Promorphology of Crystals Preparation X

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
10

Sequel to the Plane Group P3m1
Before we continue our discussion of the Plane Group P3m1 we will reproduce our example of a motif pattern compatible with, and according to, this Plane Group :

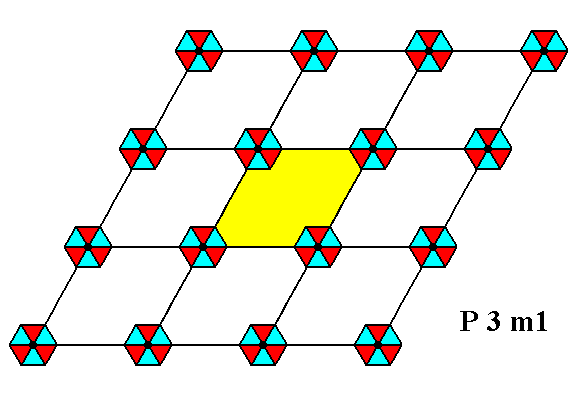
Figure 1. Periodic two-dimensional pattern according to the Plane Group P3m1. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).

The P3m1 Plane Group is compatible with many motifs, as long as they possess a 3m symmetry and are oriented and arranged like the motifs we discussed above (as in Figure 1, and in Figure 12 of the previous document).
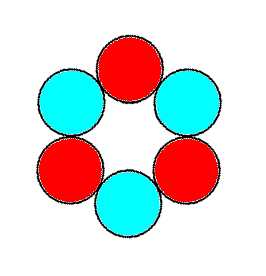
One very obvious 2-D motif compatible with this Plane Group, and in essence the same as the motifs in the just mentioned Figure 12 (previous document), consists of six discs arranged according to the corners of a regular hexagon. These discs are of two sorts : they alternate between red and blue.
The next Figure depicts this motif.

Figure 2. A 3m motif compatible with the Hexagonal Plane Lattice. When repeated according to that lattice it forms a P3m1 pattern. Compare with next Figure.

The motif of Figure 2 is, as has been said, essentially identical to our extended tri-radiate motive of the above discussions :

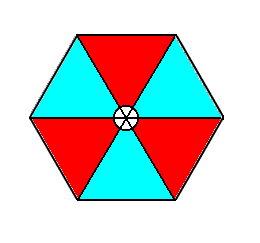
Figure 3. The extended tri-radiate 3m motif of earlier discussions. The small circular center is considered to belong to the motif's structural elements.

When the motif of Figure 2 is repeated, we get a periodic pattern according to the Plane Group P3m1, as the next Figure illustrates.

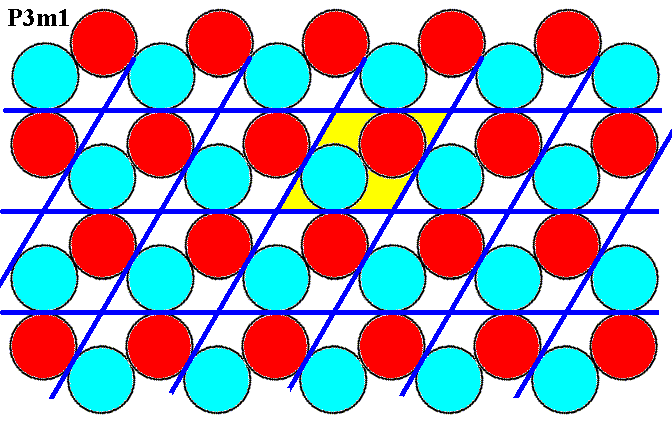
Figure 4. Repetition of the motif of Figure 2 generates a P3m1 pattern of discs.
A rhomb-shaped unit cell is indicated (yellow). It consists of two discs, one of each sort.

The way of repeat of the motif of Figure 2 is indicated in the next Figure :

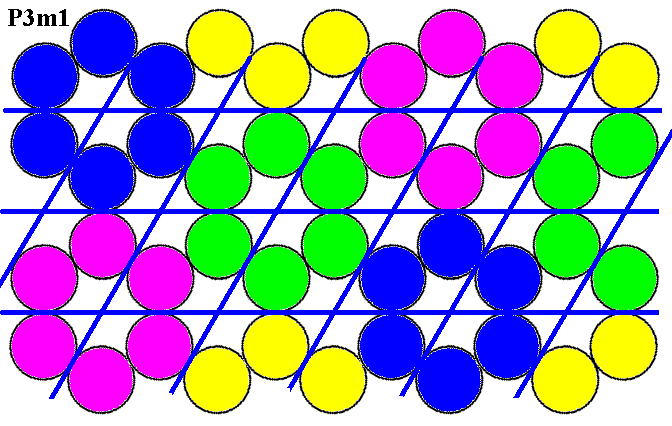
Figure 4-1. The mode of repetition of the motif of Figure 2, resulting in the P3m1 pattern of the previous Figure, is indicated.

In the pattern of Figure 4 there are two more possible unit cells detectable as the next Figure shows :

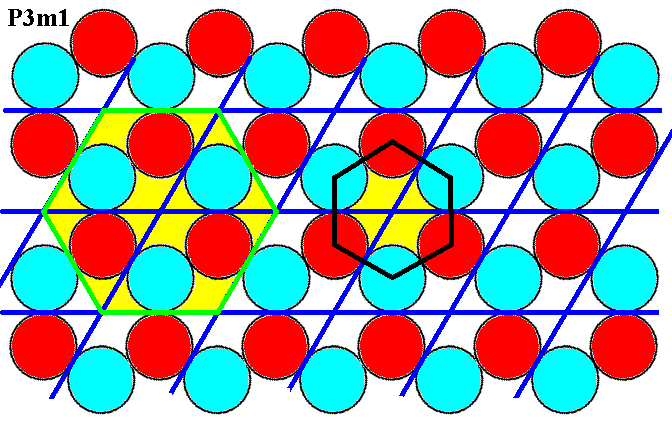
Figure 4a. In addition to a rhomb-shaped unit cell consisting of two discs ('atoms'), there are two other unit cells possible : A hexagonal unit cell can be constructed by connecting the centers of the six motif units (discs, atoms), as is depicted at the right of the image. A second possible hexagonal unit cell is depicted at the left of the image. Is the latter a proper unit cell of the pattern as a P3m1 pattern?

To investigate all this further, we will now take a smaller version of the motif as was depicted in Figure 2 :

Figure 5. A smaller version of the motif depicted in Figure 2, compatible with the Hexagonal Plane Lattice. When repeated according to that lattice it forms a P3m1 pattern. We will do that in the next Figure.

Figure 6. A periodic repetition of the motif of Figure 5, according to the Plane Group P3m1.

The above arrangement of two kinds of discs -- red and blue -- is analogous to an arrangement we can find in three-dimensional i o n i c crystals. Our 2-D arrangement thus depicts a two-dimensional i o n i c crystal structure, where a red disc could be considered as a negatively charged ion, while a blue disc could stand for a positively charged ion. In the structure we can see that the red atoms (ions) -- having an electrical charge of the same sign -- repel each other, and attract atoms (ions) of the opposite sign (blue atoms). The same goes for the blue atoms. Said differently, red atoms want to gather as much blue atoms in their vicinity as possible, and want to stand away as far as possible from their red fellows. The same goes for the blue atoms. So with our structure, as depicted in Figure 6, we have a nice analogue to the structure of 3-D ionic crystals. That's why we above said that the motif is "obvious".
The next Figure shows that the motifs are arranged according to the Primitive Hexagonal Point Lattice (Net).

Figure 7. A periodic repetition of the motif of Figure 5, according to the Plane Group P3m1. The motifs are arranged according to the Hexagonal Net. A rhomb-shaped mesh can serve as unit cell. It contains two (whole) 'atoms', one of each sort. A larger unit cell, a hexagon (yellow), can also be chosen. It consists of six whole atoms, three red and three blue ones. These six atoms constitute the repeated tri-radiate motif of the periodic pattern (Compare with Figure 4a). We can also interpret this unit cell as a total motif. But as such this total motif seems to repeat itself according to a differently oriented (but still hexagonal) net (point lattice), as the next two Figures show.

Figure 7a. Tiling of the plane by the total motif, as outlined in the previous Figure.

The next Figure shows that the tiling of the plane by that hexagonal total motif, as outlined in Figure 7 and 7a, seems to be according to a hexagonal net, it is true, but a net that is differently oriented and with rhomb-shaped meshes of other dimensions. Such a rhomb-shaped mesh can be interpreted as a possible unit cell. And it appears that we have now to do with the Plane Group P31m instead of P3m1.

Figure 7b. Tiling of the plane by the hexagonal total motif, as outlined in the previous Figure, seems to result in a repeat of that motif according to a different net (but still hexagonal and with a rhomb-shaped unit cell (outlined black)).

The next Figure depicts the hexagonal total motif of the above Figures on its own :

Figure 7c. The total motif (choice) of the above Figures isolated. It consists of six whole discs (atoms). Three of each kind.

In the next Figures we will investigate whether the pattern of Figure 6, associated with a net (black) according to Figure 7b, indeed belongs to the Plane Group P31m or maybe not so.
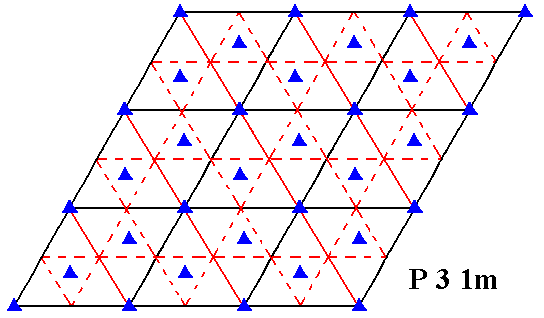
First we give the symmetry diagram for the Plane Group P31m :

Figure 7d. Symmetry content of 2-D patterns according to the Plane Group P31m. Glide lines are indicated by dashed lines. Mirror lines are indicated by red and by black solid lines, while the 3-fold rotation axes are indicated by small triangles.

First we depict a magnification of the rhomb-shaped unit cell, outlined in black, as we saw it appear in Figure 7b :

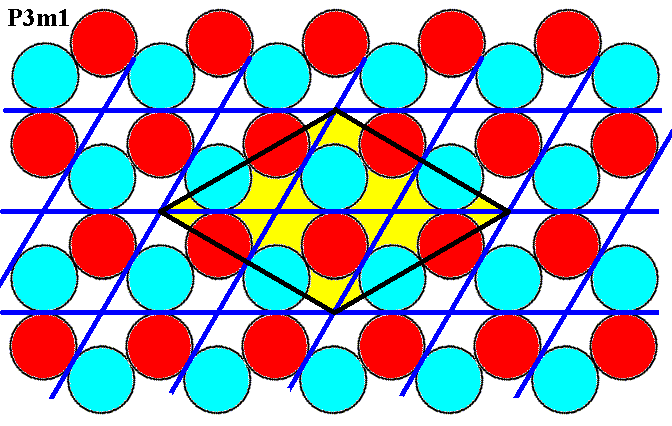
Figure 7e. Magnified portion of Figure 7b.
The blue lines indicate the initial hexagonal net, while the black lines indicate a second net, based on the yellow colored unit cell.

In order to compare Figure 7e with Figure 7d (symmetry diagram of P31m) we must be aware that the two images are somewhat differently oriented (This is immaterial, because everything in them is so differently oriented -- you can rotate your monitor in one of the two cases in order to align all orientations!).
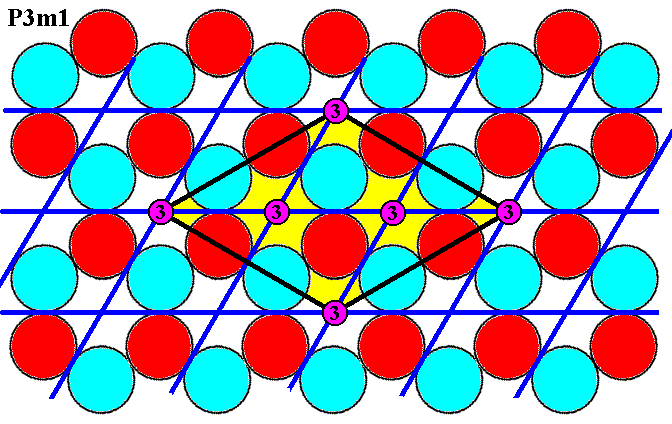
In Figure 7e you can easily see that all the 3-fold rotation axes and mirror lines are in place. The rotation axes are shown in the following Figure.

Figure 7e1. The three-fold rotation axes, as demanded by the symmetry diagram of P31m (but also by that of P3m1), are present.

The next Figure shows that also the glide lines (illustrated by one such line) parallel to, but not coincident with, the edges of the rhomb-shaped unit cell, are present.

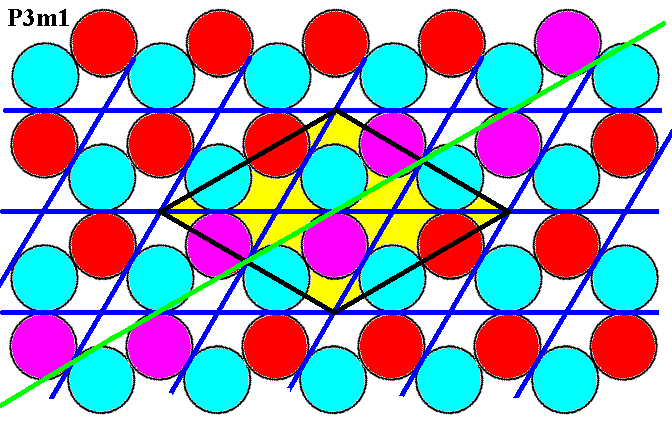
Figure 7f. Glide lines parallel to the edges of the unit cell (yellow) are present, as illustrated for one such line (purple discs).

Finally, also the glide lines connecting the centers of adjacent edges of the rhomb-shaped unit cell are present as the next Figure shows.

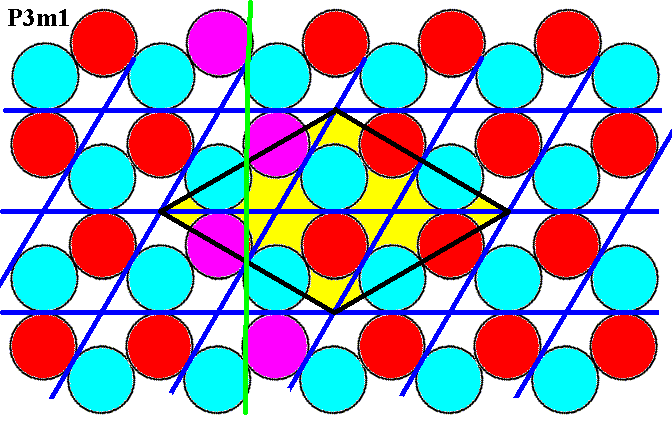
Figure 7g. Glide lines connecting the centers of adjacent edges of the unit cell (yellow) are present, as illustrated for one such line (purple discs).

So we have found all the symmetry elements being present, and also in the right places, for the pattern to comply with the Plane Group P31m.
But this is not enough.
We must demonstrate that these are the ONLY symmetry elements present. And this turns out not to be the case : In addition to the demonstrated symmetries there are extra symmetries present, namely extra 3-fold rotation axes, as the next Figure shows.

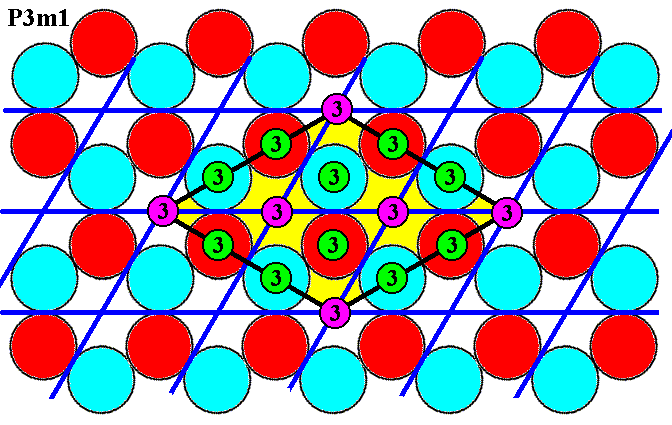
Figure 7h. I n a d d i t i o n to the 3-fold rotation axes (purple), present at the corners of the rhomb-shaped unit cell -- this cell is indicated by yellow coloring -- and two in its center (purple), and as such complying with the location of them in the symmetry configuration of the Plane Group P31m (but also of the Plane Group P3m1), there are a l s o many o t h e r locations of 3-fold rotation axes (green).

The above Figure shows that there are many additional 3-fold rotation axes (green) over and above the ones that are at the corners (purple) and the two in the center (purple) of the unit cell. So although the net, based on that unit cell (yellow in the Figure), properly describes the way by which that unit cell, and its associated total motifs (depicted in Figure 7b and Figure 7c), are repeated, the choice of that unit cell and its associated total motifs does NOT bring about a transformation of P3m1 into P31m with respect to the pattern of Figure 6.
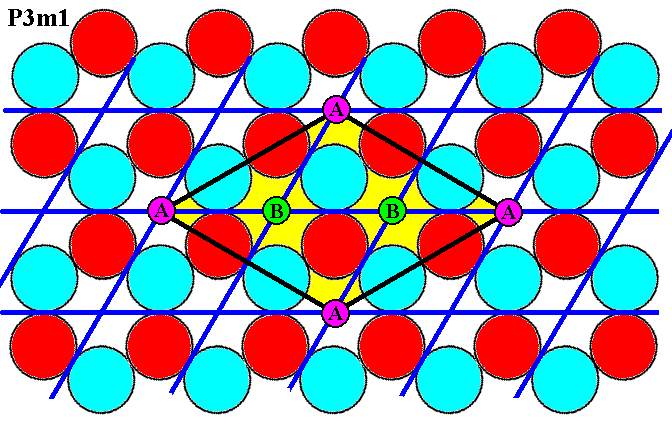
Moreover, in addition to the foregoing (concerning the presence of extra 3-fold rotation axes), there is yet another indication that the choice of the unit cell and total motifs as was done in Figure 7b (black) and Figure 7c, does not bring about a change in Plane Group. See next Figure.

Figure 7i. In the pattern of discs we can see that the points, marked by either A or B, are fully equivalent (i.e. the A's are equivalent to the B's). This implies that the points marked B are l a t t i c e p o i n t s, which would entail either that our rhomb-shaped unit cell (yellow) has nodes in its center and would then represent a sort of centered net which is, however, not one of the five possible unique two-dimensional nets, or we have to consider the points marked B as not equivalent to the points marked A, but then we have a qualitatively DIFFERENT pattern, i.e. we have changed the pattern. And only as so changed it is a pattern according to the Plane Group P31m.

What we have shown is the fact that when we have a pattern, as in Figure 6 and Figure 7, we can, if convenient, choose a larger -- hexagonal -- unit cell, larger than the rhomb-shaped unit cell of the hexagonal net. Indeed, as Figure 7a shows, such a larger (hexagonal) unit cell is a genuine repeat unit. And it can also be interpreted as a total motif that neatly tiles the plane. Such a choice of unit cell (or total motif) is necessary for finding the Complex Motif, because it is more symmetric than the rhomb-shaped unit cell, and can thus reflect all the given crystal's point symmetry. But such a choice DOES NOT IMPLY A TRANSITION FROM ONE PLANE GROUP TO ANOTHER.
We will see that the difference between the Plane Groups P3m1 and P31m can be described as a difference in orientation of their motifs s.str. This difference is equal to a rotation of those motifs (in one Plane Group) by 30⁰ with respect to those of the other Plane Group. But this rotation only involves the motifs s.str., it does NOT involve their background. And this is the reason why the corresponding patterns of P3m1 and of P31m are not just rotated with respect to each other, i.e. the one pattern is not just a rotated version of the other. They are different patterns. The fact that in the transformation of P3m1 into P31m, or vice versa, only the motif s.str. is rotated and not its background, implies that the PATTERN HAS CHANGED, although the total symmetry content has remained the same. We will return to these matters when treating of the Plane Group P31m.

Now we must demonstrate that the pattern of Figure 6 belongs to the Plane Group P3m1 indicated by the net according to Figure 7. The (smallest) unit cell of this net is rhomb-shaped, and contains two discs, one of each sort.
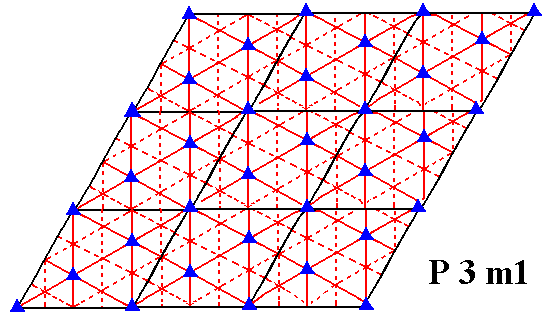
First we depict the symmetry diagram of the Plane Group P3m1 :

Figure 7j. Symmetry content of the Plane Group P3m1. Glide lines are indicated by dashed lines. Mirror lines are indicated by red solid lines, and the 3-fold rotation axes by small triangles.

The next Figure shows that the vertical glide line is present.

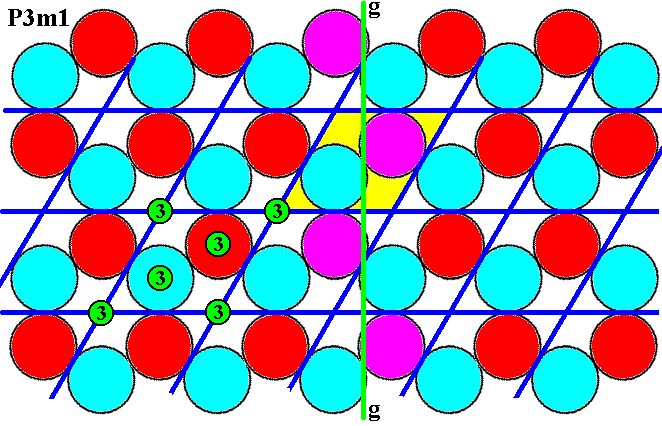
Figure 7k. (Magnified) pattern of Figure 6. Vertical glide line (green, g), indicated by the purple discs.

From the above Figure we can also see that the 3-fold rotation axes (some are indicated) and mirror lines, as demanded by the symmetry diagram, are present. There are no extra 3-fold axes. The next Figure shows that the NW-SE glide line is also present.

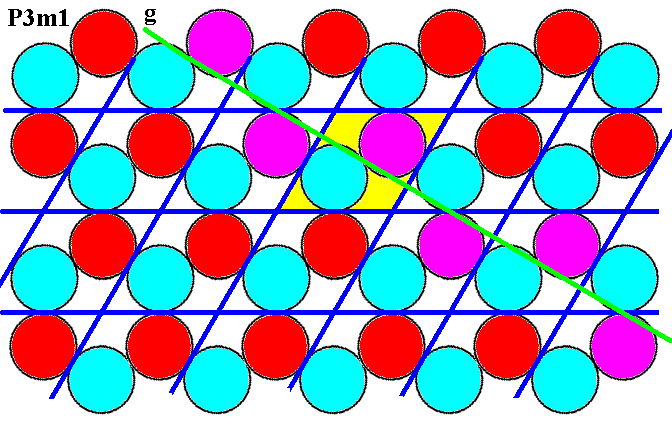
Figure 7m. (Magnified) pattern of Figure 6. NW-SE glide line (green, g), indicated by the purple discs.

Finally, the SW-NE glide line is also present, as the next Figure shows.

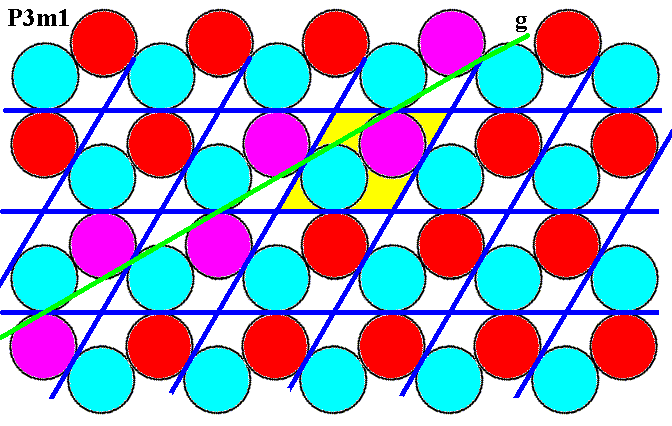
Figure 7n. (Magnified) pattern of Figure 6. SW-NE glide line (green, g), indicated by the purple discs.

So we now have demonstrated that the motif pattern of Figure 6, associated with a net according to Figure 7 belongs to the Plane Group P3m1.
It allows for two types of unit cell, a hexagonal unit cell consisting of 6x1/3=2 discs ('atoms'), and a rhomb-shaped unit cell consisting of two whole discs ('atoms'). The rhomb-shaped unit cell is indicated in the above Figures. The hexagonal unit cell for the P3m1 structure, and its way of repeating are shown in the next Figure.

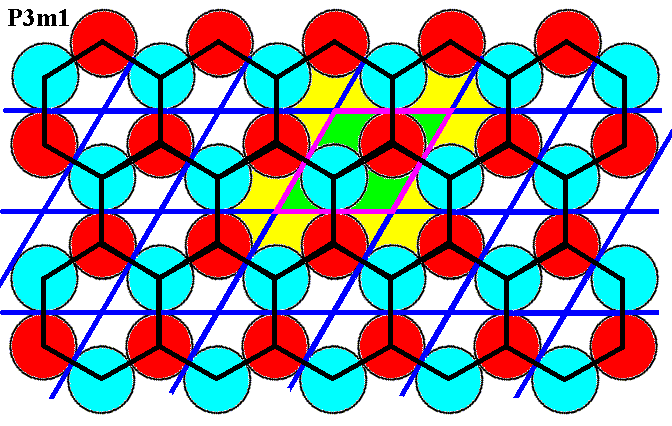
Figure 7o. (Magnified) pattern of Figure 6. A hexagonal unit cell (black) and its repetition are given. One can see that this unit cell (hexagons) repeats according to the same net based on the rhomb-shaped unit cell (purple). The hexagonal unit cell can also be interpreted as the total motif associated with a lattice point. Four such total motifs are highlighted.

The hexagonal unit cell of the P3m1 pattern of Figure 6, is the most symmetric unit cell. When we isolate this cell we have the (penultimate) Complex Motif of our pattern. See next Figure.

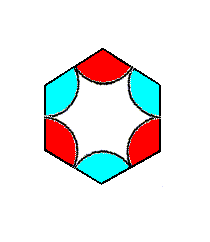
Figure 7p. Isolated hexagonal unit cell of the P3m1 periodic motif pattern of Figure 6 (With respect to that pattern the depicted unit cell or repeating unit is of course a magnified version). It is the Complex Motif of this pattern.

It is perhaps instructive to compare this Complex Motif with that of the P3m1 pattern studied earlier, namely in Part Eight of the present series of documents :

Figure 7q. Penultimate Complex Motif of the P3m1 pattern studied earlier (Part Eight). It consists of one whole motif s.str. plus its corresponding background.

This Complex Motif tiles the plane as follows :

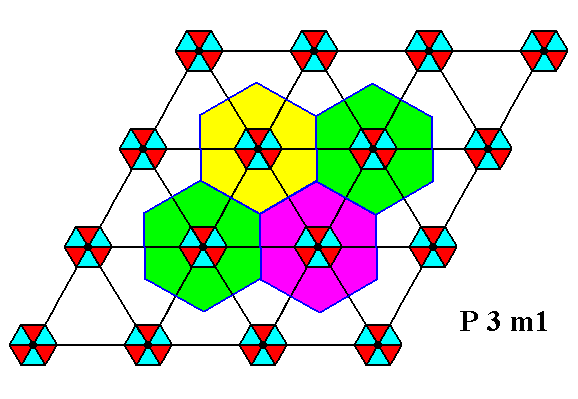
Figure 7r. Indication of total motifs (that can serve as representing the Complex Motif) associated with the lattice points. Such a total motif consists of a motif s.str. plus corresponding background. The motif s.str. here is accordingly a non-extended motif.

The next Figure depicts both Complex Motifs together for easy comparison :

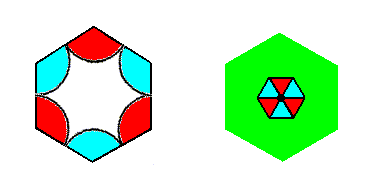
Figure 7s.
Left image : Complex Motif of the P3m1 periodic pattern of Figure 6.
Right image : Complex Motif of the first P3m1 periodic pattern studied (Studied in Part 8).

The motif of the left image of the above Figure is, what we can call an e x t e n d e d m o t i f, which means that the motif s.str. has fully extended over its background. The interior of this motif is not interpreted as background.
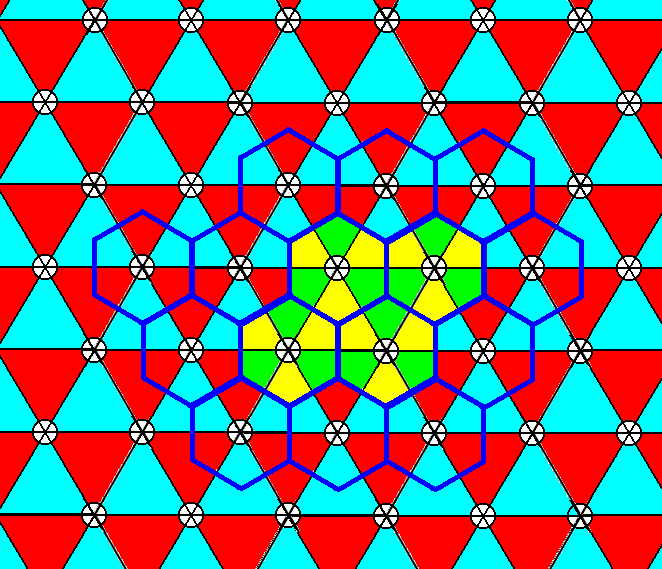
The motif of the right image of the above Figure is a non-extended motif, which means that we have to do with a motif in the stricter sense (a motif s.str.) and its background. The only specific feature of such a background is its shape.
At the end of Part Nine of the present series of documents we found out that if we extend the motif s.str. (right image of above Figure) properly, it will tile the plane and still arranges according to Plane Group P3m1. See next Figure (The scales of the underlying net of the pattern where the right image of Figure 7r came from, and of the net underlying the pattern of the next Figure, differ a little, but this is immaterial for our discussion).

Figure 7t. When the motifs of the P3m1 periodic pattern of Figure 7r are properly extended, and invade the whole of their corresponding backgrounds, they tile the plane neatly and still arrange according to Plane Group P3m1. See also Figure 23 of the previous document

The extended motif of the above Figure (6s) is at the same time the most symmetric unit cell, and can serve directly as Complex Motif, because elimination of the glide lines will not have any effect on the symmetry, as was established in Part Eight.
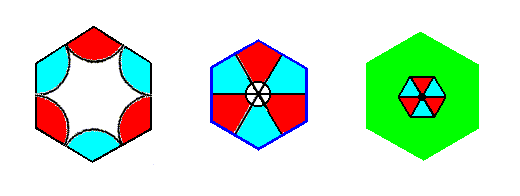
The next Figure adds this extended motif (as indicated in Figure 6s) to the other two for comparison.

Figure 7u.
First image to the left : Complex Motif of the P3m1 periodic pattern of Figure 6. Extended motif.
Second image : Complex Motif as established in Figure 6s. Extended motif.
Third image : Complex Motif of the first P3m1 periodic pattern studied. Non-extended motif.
The slight differences in scale come from the different origins from where those Complex Motifs were derived. As has been said, they are immaterial for the present discussion.

After this diversion and comparison of the two P3m1 periodic patterns, let us continue with the second of them, the pattern of two sorts of discs (red and blue), that can stand for the structure of a two-dimensional ionic crystal.
If we look to that structure, as depicted in Figure 6, carefully, we can detect several different d i r e c t i o n s that could become 'faces' of the crystal possessing this structure, i.e. the P3m1 structure. These directions present several different atomic aspects to the nutrient environment of the growing crystal. Faces displaying such different atomic aspects will in most cases grow at a different rate. And this is decisive for the s h a p e that the crystal will finally adopt : The slowest growing faces will eventually survive the faster growing faces (except when they are perpendicular to each other). The latter disappear after prolonged growth (See for this phenomenon the next Figure, and also the document on the Morphology of Crystals in the SPECIAL SERIES of the First Part of this website, accessible by clicking on back to homepage).

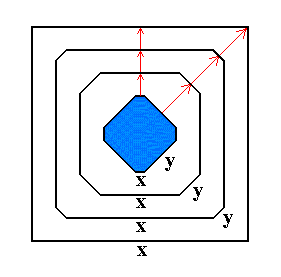
Figure 7v. A growing 2-dimensional crystal. Because its y-faces grow faster than its x-faces, the y-faces will eventually grow themselves out of existence.

The next Figure depicts our structure and shows that it supports three types of faces, each presenting a different atomic aspect to the nutrient environment of the growing crystal.

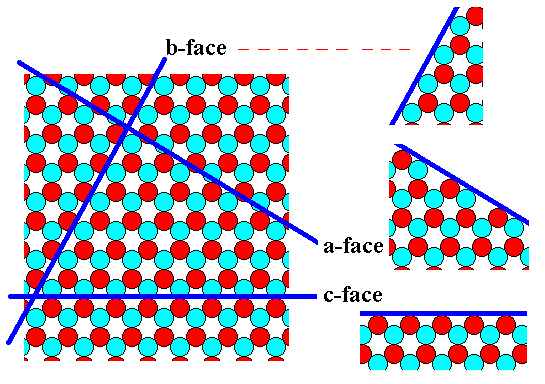
Figure 8. A periodic repetition of the motif of Figure 5, according to the Plane Group P3m1. The motif pattern (depicted in Figure 6) supports three different types of crystal faces associated with different atomic aspects presented to the nutrient environment.

The point symmetry of 2-D crystals having this internal structure -- a structure according to the Plane Group P3m1 -- is 3m (which is the translation-free residue of all isogonal Plane Groups, which here means of the Plane Groups P3m1 and P31m). So a certain possible crystal face (belonging to one of the three types found in Figure 8) will configure with its fellows such that the resulting face configuration has 3m symmetry. If the faces of such a configuration are all of the same type, say a-faces, then such a configuration is called a (simple) FORM. When more than one type of faces is involved in such a configuration we call it a COMBINATION (a combination of FORMS). A simple FORM or a COMBINATION can only exist as a crystal (For 2-D crystals this is of course an analogue of 'existing') when it is closed, i.e. when it encloses space completely (For 2-D crystal, 2-D space, for 3-D crystals, 3-D space).
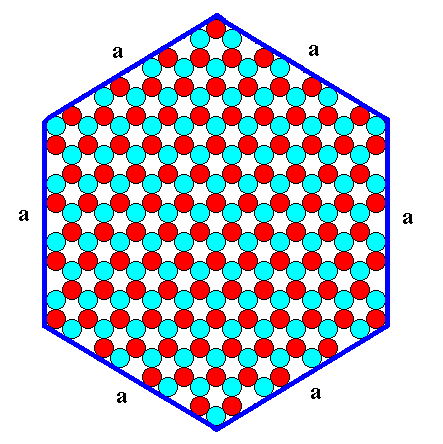
There are six differently oriented faces capable of presenting the aspect "a" to the nutrient environment, implying that hexagonal crystals can be formed, bounded by these faces. Although this FORM has a hexagonal shape it has a 3m symmetry (not a 6mm symmetry), which can be verified by inspecting the internal structure. Because it is closed, it can 'occur' as a crystal. The next Figure shows this hexagonal FORM.

Figure 9. A hexagonal two-dimensional ionic crystal with an internal structure of which the symmetry is according to the Plane Group P3m1. The crystal has six equivalent faces (a-faces) presenting the same atomic aspect to the environment.

A smaller hexagonal ionic crystal with the same internal structure (P3m1) looks like this :

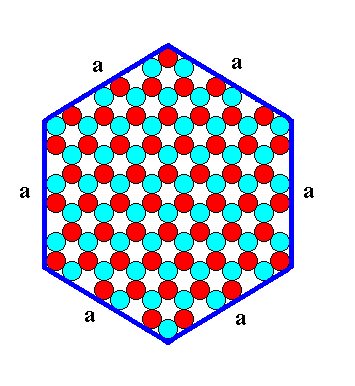
Figure 9a. A hexagonal two-dimensional ionic crystal with an internal structure of which the symmetry is according to the Plane Group P3m1. The crystal has six equivalent faces (a-faces) presenting the same atomic aspect to the environment. It is the same as in Figure 9, but smaller.

We just stated that the structure of the above (Figure 9, and also Figure 9a) depicted hexagonal 2-D crystal has a symmetry "according to the Plane Group P3m1", which means that there are numerous glide lines, mirror lines, 3-fold rotation axes, etc. Of course this is only valid when we have a crystal of macroscopic dimensions, consisting of microscopic atoms, resulting in there being almost an infinity of atoms and unit cells. So in the Figure the depicted crystal is much too small, implying that there is only a small finite number of repeating units. Indeed in a finitely (and uniformly) extended P3m1 structure (as well as in a finitely extended P31m structure) there can be only one 3-fold axis, and only mirror planes that go through the center of the structure. There can be no mirror lines parallel to each other, and no rotation axes parallel to each other. So a crystal (and this is also valid for 3-dimensional crystals) inherently has several different atomic aspects, and each aspect can have copies that are regularly distributed across the structure in accordance with its point symmetry, and resulting in regularly distributed crystal faces as we saw in Figure 9 and 9a with respect to the a-faces.
Now we could be tempted to consider these regularly distributed aspects as representing the crystal's a n t i m e r s or counterparts, suggesting that a crystal d i r e c t l y reveals its t e c t o l o g y, which here means : the number, shape and configuration of its antimers, from which the promorph or planimetric basic form could be directly read off. And so there would be no need to derive the C o m p l e x M o t i f in order to determine the crystal's promorph. However, this is only seemingly so. The following will demonstrate this :
If we consider the number of regularly distributed aspects of the same sort, which have given rise to the six equivalent faces of the hexagonal crystal of Figure 9 and also of Figure 9a, as the homotypic number of the crystal, in other words if we consider the six regularly distributed copies of the aspect "a" (giving rise to six a-faces) as representing the crystal's antimers, then the crystal would have six antimers and would consequently possess an axis of six-fold symmetry (a 6-fold rotation axis). But we know from the internal structure of the crystal that it does not have a 6-fold rotation axis but a 3-fold rotation axis. Indeed, if we follow the six aspects of the hexagonal crystal in Figure 9a, we see that they are, it is true, all of the same aspect, but their orientation is different in such a way that they are not repeated around some axis : If we call a red disc A and a blue disc B, and follow them around the crystal of Figure 9a, then we get the following sequence :
AB AB ABA BA BAB AB ABA BA BAB AB ABA BA B
So the aspect is not properly repeated around the axis going through the center of the crystal normal to the plane of the drawing. Only alternate aspects are exactly repeated :
AB AB ABa ba bAB AB ABa ba bAB AB ABa ba b
and also :
Ab ab aBA BA BAb ab aBA BA BAb ab aBA BA B
So the crystal has a three-fold rotation axis and thus has t h r e e antimers and not six. And this, in virtue of its i n t e r n a l structure.
If we want to indicate (and recognize) the three ANTIMERS in the 2-D hexagonal crystal of Figure 9a as a whole, we must divide the crystal in three congruent parts, that repeat around the 3-fold axis :

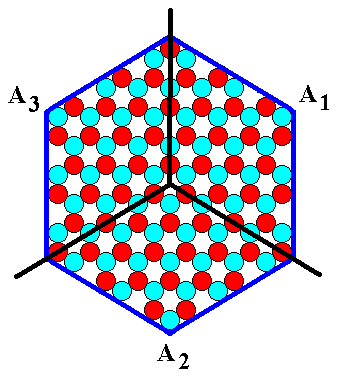
Figure 9b. A hexagonal two-dimensional ionic crystal with an internal structure of which the symmetry is according to the Plane Group P3m1. In accordance with its internal structure we could indicate three congruent a n t i m e r s in the crystal of Figure 9a.

The 'antimers' of the crystal, as depicted in the above Figure, do not look very much like the antimers as we see them in organisms, like polypes, flowers, echinoderms etc. Those genuine antimers much more look like this :

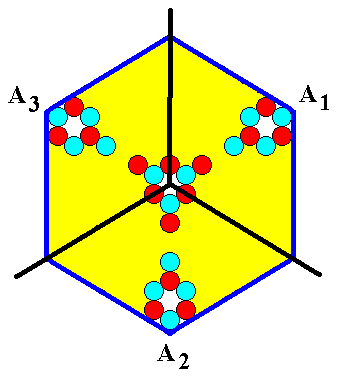
Figure 9c. A structure, akin to that of Figure 9b, with genuine a n t i m e r s. These antimers are repeated around a three-fold axis. The structure, also when it is imagined to be infinitely extended in 2-D space, is NOT periodic, while the crystal -- when imagined to be extended in 2-D space indefinitely -- IS. The next Figure emphasizes this fact.

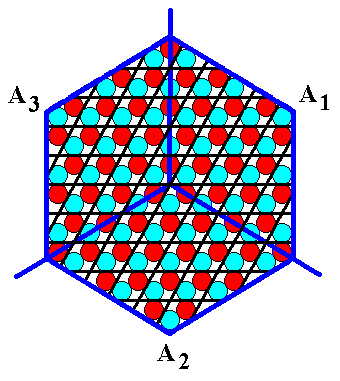
Figure 9d. The crystal of Figure 9b furnished with the appropriate hexagonal net (point lattice). The possibility of letting the structure be underlied by a point lattice emphasizes the periodic nature of the crystal, and consequently its non-tectological structure. The net thereby expresses that the 'antimers' are not genuine antimers, at least not antimers just like that.

In Organic Tectology, as laid down on this website, subordinated f o r m i n d i v i d u a l s of several types are being distinguished within an organismic body. The antimers are such subordinated individuals (to be precisely, third-order form individuals). Well, as can be seen in Figure 9b, the 'antimers' do not show any i n d i v i d u a l i t y whatsoever. Even in organisms or parts thereof that have only two antimers (unlike, for instance, star-fishes), which show up as simply to be their left and right body halves, the boundary between those two antimers is often materialized, for instance in the form of the spine in vertebrates or as the main vein in many plant leafs. In this way the antimers stand out clearly. Crystals on the other hand, especially when they are considered from a macroscopical view, are in fact homogeneous bodies. And, moreover, in organisms, also when they are inspected microscopically, there is no sign of a p e r i o d i c structure as is typical for crystals.
The C o m p l e x M o t i f of crystals on the other hand, shows a true tectological (i.e. non-periodic) structure with genuine individualized antimers, as we showed already for two-dimensional crystals, and will show for three-dimensional crystals as well. See the series of documents treating of 3-D crystals by clicking HERE to begin with. Our discussions of two-dimensional crystals is an instructive preamble to the structure of 3-D crystals and their Complex Motif, and thus their Tectology and Promorphology.

All this points to the fact that if we want to consider CRYSTALS promorphologically, like we did in the case of ORGANISMS, we must look for a true tectological aspect in crystals, an aspect that shows genuine antimers. And this indeed is our C o m p l e x M o t i f.
The crystal of Figure 9a (or Figure 9 for that matter) has an external shape (namely hexagonal) that does as such not reflect the true symmetry of the crystal, which is 3m. This 3m symmetry was revealed by its internal structure.
But there are other crystals, possessing our P3m1 structure, (or some conditions acting on the same crystal) that can be imagined to show this lower symmetry already by their geometrical shape : The faces, corresponding to the 'b-aspect', the b-faces (an example of which is shown in Figure 8, and of which there are only three in different directions) may grow slowly enough to appear at the growing crystal. These faces differ from the "a's" in two important ways. In the first place, they present a quite different atomic aspect to the environment. They will almost certainly grow at a different rate from the a-faces. In the second place, there are only three faces capable of presenting that aspect in different directions. They define a triangle, not a hexagon. From the three faces that would like to be like the b-faces, if the crystal had a 6-fold axis of symmetry, one is indicated as "c" in Figure 8. Clearly the c-faces and the b-faces present different atomic aspects to the nutrient environment. It would be very improbable to find these two sorts of faces growing at the same rate. The environment would probably behave quite differently toward a face of 'blue' ions and a face of 'red' ions. Even if you visualize coating the two sorts of faces with the same sort of ions, you will reach the same conclusion. There is a different disposition of the red ions directly beneath the blue ions in the coatings, and the nutrient environment will respond to that difference also. The nutrient environment sees through the coating as it were. So we can imagine that -- in a second case -- in addition to the six a-faces, the three b-faces also appear at the crystal, while the c-faces don't (because their relative growth rate is too high) : We in this way obtain a second habit (The first habit was the hexagonal shape of the crystal): The crystal consists of six a-faces while three of the six potential corners (of the "a-hexagon") are cut off by the "b-triangle", as the next Figure shows.

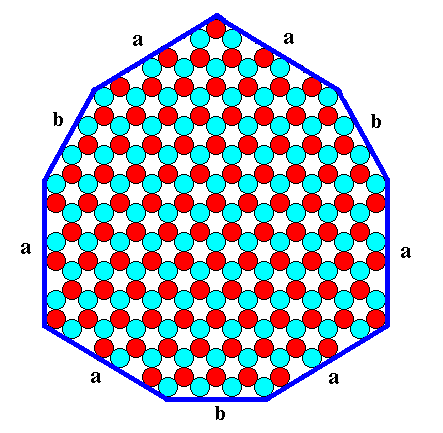
Figure 10. A two-dimensional ionic crystal with a symmetry of its internal structure according to the Plane Group P3m1. Two types of faces, six a-faces and three b-faces, have appeared. They reveal the true symmetry of the crystal, namely 3m (three equivalent mirror lines and a 3-fold rotation axis).

A third habit can emerge when the b-faces are the slowest growing faces, while the others grow much faster (In real crystals this could -- as in the case of the second habit -- be so either because the solution in which the crystal grows contains some ingredients that affect the relative growth rates, or because we have to do with a crystal of a different chemical substance all together). Because there are only three directions in which b-faces can occur in our structure (i.e. the structure depicted in Figure 6) the b-faces form, when they alone appear, a triangle. In our case an equilateral triangle (in accordance with the 3m symmetry), as the next Figure shows.

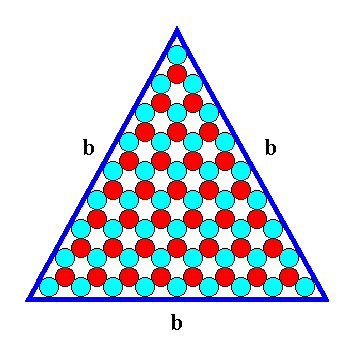
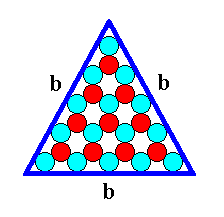
Figure 11. A two-dimensional ionic crystal with a symmetry of its internal structure according to the Plane Group P3m1. Only one type of faces, b-faces, have appeared. They are three in number and equal, and form a triangular 2-D crystal. They reveal the true symmetry of the crystal, namely 3m (three equivalent mirror lines and a 3-fold rotation axis). The size of the crystal's faces is 9 atoms (discs) long. We call it a b-9 (triangular) crystal. This crystal can be considered as a (simple) FORM of the 2-D Crystal Class 3m.

From the foregoing we see that the number of a n t i m e r s (counterparts) of a crystal is not in a constant way determined by the number of possible directions of a certain atomic aspect, because that number can be different for different aspects : In our case, six for the a-aspect, three for the b-aspect, and three for the c-aspect.
If on the other hand, the c-faces are the slowest growing faces, while the a- and b-faces grow much faster, then, eventually, only the c-faces appear on the crystal, three in number, because also c-faces have -- in our case -- only three possible directions. So also in this case a triangular crystal will finally appear. See next Figure.

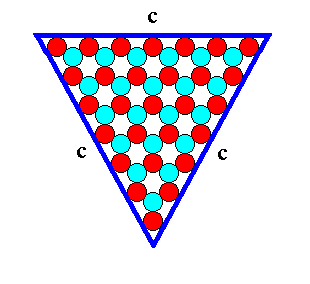
Figure 12. A two-dimensional ionic crystal (and also a -- closed -- FORM) of the 2-D Crystal Class 3m, with a symmetry of its internal structure according to the Plane Group P3m1. Only one type of faces, c-faces, have appeared. They are three in number and equal, and form a triangular 2-D crystal. They reveal the true symmetry of the crystal, namely 3m. The size of the crystal's faces is 7 atoms. We call it a (triangular) c-7 crystal.

The next Figure gives a slightly larger version of the triangular crystal consisting of c-faces :

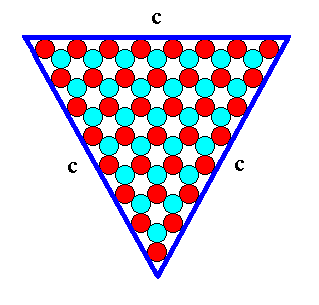
Figure 13. A two-dimensional ionic crystal (and also a -- closed -- FORM) of the 2-D Crystal Class 3m, with a symmetry of its internal structure according to the Plane Group P3m1. Only one type of faces, c-faces, have appeared. The size of the crystal's faces is 8 atoms. We call it a c-8 crystal.

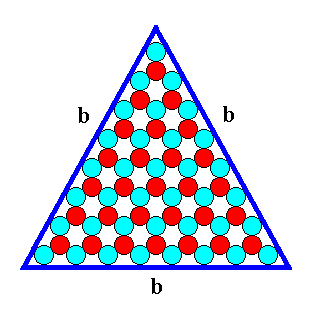
Figure 14. A two-dimensional ionic crystal (and also a -- closed -- FORM) of the 2-D Crystal Class 3m, with a symmetry of its internal structure according to the Plane Group P3m1. Only one type of faces, b-faces, have appeared. The size of the crystal's faces is 8 atoms. We call it a b-8 crystal.

If the a-faces grow fast enough to finally disappear, while the growth rates of the b- and c-faces differ little from each other but are markedly lower than that of the a-faces, then we will see a combination of a b-triangle (a b-FORM) and a c-triangle (c-FORM) cutting off each other's corners. In the next Figure we combine a b-8 FORM (Figure 14) with a c-7 FORM (Figure 12).
Initially we meant by "8" in "b-8", "c-8", etc. the size of the crystal represented by the FORM. But at the same time we can also let those numbers indicate the (relative) g r o w t h r a t e of the faces of the given FORM or crystal. So speaking about a combination of a b-8 FORM and a c-7 FORM means that a FORM, presenting with its faces the structure's atomic aspect "b" to the nutrient environment, combines with another FORM of the same crystal Class, presenting with its faces the structure's atomic aspect "c" to the nutrient environment, whereby the (faces of the) first FORM grow faster than (those of) the second FORM. The faces of the latter, i.e. of the c-FORM, will finally survive, while the b-faces disappear. Well, let us look to a b-8 / c-7 combination of FORMS (Of the Class 3m).

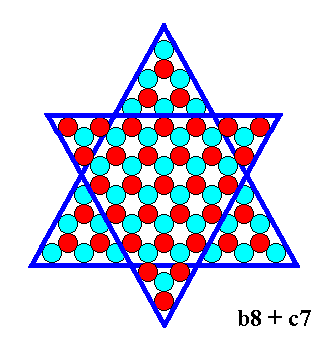
Figure 15. A b-face triangle of size 8 (i.e. each of its faces is 8 atoms long), and a c-face triangle of size 7 combine. They will cut off each other's corners (See next Figure).

The result of the combination is given in the next Figure.

Figure 16. Result of the combination indicated in the previous Figure. We can call it a b-8 + c-7 crystal.

Let's summarize some features.
The six possible a-faces, showing the structure's atomic aspect "a", together constitute a (simple) FORM of the present symmetry Class, namely 3m. In this case the FORM is a regular hexagon.
The three possible b-faces, showing the structure's atomic aspect "b", also constitute a FORM of the Class 3m. That FORM is a regular triangle.
The three possible c-faces, finally, showing the structure's atomic aspect "c", constitute a third FORM of the Class 3m. It is also a regular triangle.
As in three-dimensional crystals, these 2-D FORMS (analogically) can -- as has been said earlier -- when they are closed FORMS (i.e. when they enclose space completely), occur alone (i.e. not in combination with other FORMS), as crystals, or, they can, as long as they belong to the same Crystal Class, enter in combinations with other FORMS, but can only exist as crystals when the combinations are closed. Each FORM is a set of equivalent faces, representing a certain a t o m i c a s p e c t that is presented to the environment. In most cases different atomic aspects, and thus different FORMS, have different growth rates. And because the relative growth rates of the faces of a crystal determine its final shape, the presence of FORMS and their configuration determines that final shape of the given crystal.
It is worthwile to dwell a little longer upon the combination of two equilateral triangular FORMS having a P3m1 structure. One FORM effects b-triangles (i.e. its sides are b-faces), the other FORM effects c-triangles (i.e. its sides are c-faces).
A triangle denoted (in our Figures) as a "b-x triangle", i.e. an equilateral b-triangle having sides of x atoms long, grows, by definition slower (and will accordingly likely to remain present at the growing crystal) than a triangle denoted as a "c-(x+n) triangle", i.e. a c-triangle having sides longer than x atoms.
The triangular 2-D crystals can only combine with each other when they are c o n c e n t r i c. One will think that (two) equal triangles, say b9 and b9, will always combine, but this is not so : 3-b + 3c is possible, 6-b + 6c is possible, 9-b + 9c is possible, etc. But 4-b + 4c is not possible, 5-b + 5c is not possible, and 7-b + 7c is not possible. In crystals we will only seldom encounter a combination of equal triangles (resulting -- after chopping off each others corners -- in a regular hexagon), because the atomic aspects presented to the environment (in our case the b- and c-aspects) are different and the environment will almost certainly respond differently to them, resulting in different growth rates, and thus in a b-x triangle + c-(x+n) triangle, or a b-(x+n) triangle + a c-x triangle, and will be depicted in our Figures as triangles of different sizes.
So we concentrate on the combination of different sized triangles (and consequently having different growth rates). The smallest unequal triangles that so combine are triangles having sides with a length of respectively 4 and 5 atoms. See next Figures.

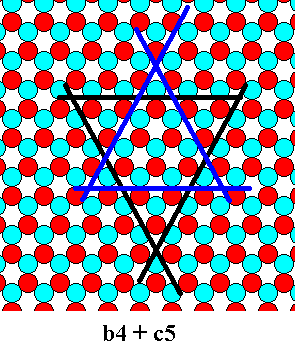
Figure 17. Combination of a b-4 triangle and a c-5 triangle. The triangles will cut off each other's corners. See next Figure.

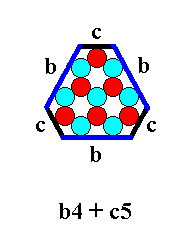
Figure 18. Result of the combination of a b-4 triangle and a c-5 triangle. The triangles have cut off each other's corners.

Combinations of larger triangles can only as such exist when they are, to begin with, concentric with the b-4 and c-5 triangles (The same applies when we start with a combination of a c-4 triangle with a b-5 triangle). Well, a b-x triangle is only concentric with a b-(x+3n) triangle, i.e. with a b-triangle having sides three atoms, or a multiple thereof, longer than those of the b-x triangle. The same applies to a c-x triangle. Concentric with this triangle are all the c-(x+3n) triangles. The next Figure shows why this is so.

Figure 19. Concentric triangular 2-D crystal FORMS of the b-type.
The smallest b-triangle that can be combined with larger c-triangles has sides that are 4 atoms long. The next larger b-triangle that allows such a combination is one layer thicker than the initial triangle. One layer thicker implies that each side of the new triangle is t h r e e atoms (discs) longer than the sides of the initial triangle.
So the b-4 triangle (yellow) is followed by a b-(4+3) triangle i.e. by a b-7 triangle (black), a triangle having sides of seven atoms long. The next larger concentric triangle (green) is a b-(7+3) triangle, i.e. a b-10 triangle having sides of ten atoms long.

So if we start with a b-4---c-5 combination as in Figure 17 and 18, we can determine which other combinations are possible, by adding three to one of them or to both. In doing so we get the possible combinations. In listing these combinations we can omit the letters b and c, and just list the sizes expressed by the atomic length of a side (The triangles are equilateral, so all three sides of such a triangle are equal). In the next list "+" means "combined with" :
4 + 5
7 + 5
4 + 8 (one triangle falls exactly within the other)
7 + 8
10 + 8
10 + 11
etc.
So it is clear that the following combinations of two triangles of different size are not possible, because the lengths of their sides cannot be derived from the 4 + 5 combination (or from the 3 + 3 combination), by (repeatedly) adding 3 :
7 + 9
8 + 9
8 + 11
etc.
As we've said, the combination of equal triangles, say, b-6 + c-6, means that we have to do with different atomic aspects (presented to the nutrient environment) having the same growth rate. This will not occur often, but is possible. The smallest combination of equal triangles is 3 + 3 :

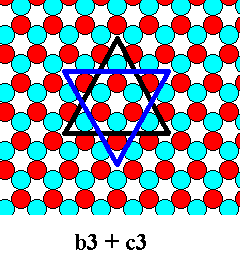
Figure 20. The smallest possible equal triangles.

From 3 + 3 we can deduce other possible combinations :
6 + 3 (Here one triangle fits precisely within the other)
6 + 6
9 + 6
etc.
The last mentioned combination can be exemplified by the b-9 (Figure 11) triangle combined with a c-6 triangle :

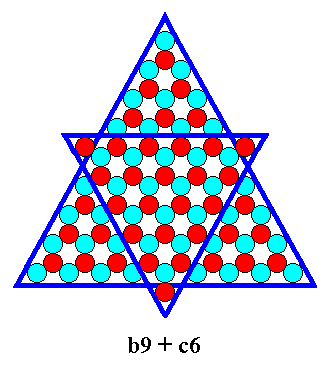
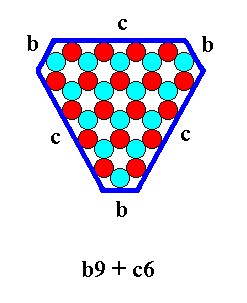
Figure 21. Combining the b-9 and c-6 triangles.

Figure 22. Result of the combination of b-9 and c-6 triangles.

As a further example of combining ionic triangles we can put together a c-7 triangle (Figure 12) and a b-5 triangle (Figure 23).

Figure 23. A b-5 triangle (as a FORM) of the 2-D Crystal Class 3m.

The next Figures give the b5 + c7 combination.

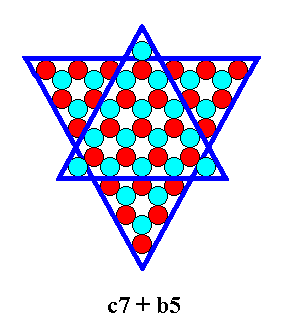
Figure 24. Combination of two 2-dimensional crystal FORMS of the Crystal Class 3m. The forms will cut off each other's corners as the next Figure shows.

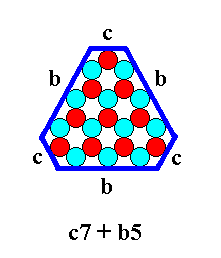
Figure 25. Two-dimensional crystal of the Crystal Class 3m. It is a combination of two 2-dimensional crystal FORMS of that Crystal Class.

Similar situations as described above for two-dimensional crystals often arise among real crystals, i.e. among three-dimensional crystals : Sodium Chlorate and Sodium Bromate are good examples (HOLDEN & MORRISON, 1982, Crystals and Crystal Growing, p.p. 253).
The c u b i c a l habit of Sodium Chlorate is analogous to the habit of the two-dimensional crystal shown in Figure 9a. Those habits have higher symmetries than the structures. The faces that appear belong to special sets (FORMS) forming highly symmetrical (geometric) figures.
Adding a little Borax to te growing solution for Sodium Chlorate reduces the relative growth rate of the tetrahedron faces to the point where they appear on the crystal, cutting off four of the corners of the cube, as shown in the next Figure.

Figure 26. Two habits of Sodium Chlorate. The one on the right is modified by Borax. With increasing amounts of Borax in the solution, the tetrahedron faces become more and more prominent.

This behavior is similar to the development of the habit on the two-dimensional crystal of Figure 10.
On the other hand, the habit of Sodium Bromate is analogous to the habit of the two-dimensional crystal of Figure 16 or of Figure 22. Usually the crystal forms a tetrahedron whose corners are cut off by another tetrahedron. If the two tetrahedra had the same size, they would combine to produce an octahedron ( = a polyhedron with eight triangular faces ). But the structure has a lower symmetry than an octahedron. The two tetrahedra grow at different rates, as do the two triangles which form the habit as depicted in the just mentioned Figures.
It is reasonable that Sodium Chlorate and Sodium Bromate should both exhibit a tetrahedral habit. X-ray investigations show that they both have the same crystal structure, in which Chlorine and Bromine alternatively plays the same role. But it is unexpected that when they grow from pure solutions, the cube faces grow more slowly than the tetrahedron faces on the Chlorate, and the relative growth rates are reversed on the Bromate. Together they show dramatically that the relative growth rates on crystal faces can be very sensitive to small influences : Bromine versus Chlorine in the compounds mentioned.
In the case discussed, when habit ( = geometric shape) has failed to reveal the true symmetry of the crystal (as in Sodium Chlorate, and in the 2-D crystal of Figure 9a), it has suggested too high a symmetry. Our above discussion of the fictitious two-dimensional crystals has shown why. The slowest growing faces, dominating the crystal shape, may happen to be a set forming a figure consistent with several crystal Classes (in the case depicted in Figure 9a these are the 2-D Classes 3m, 3, 6mm and 6), and therefore in particular with a Class having high symmetry (for instance 6mm, which is the symmetry of a pure hexagon).
Much more rarely a crystal may have a habit suggesting a symmetry lower than its true symmetry. Nobody knows why this occurs. An example is Potassium Chloride, known to mineralogists as Sylvine. Repeated observation of habit led early crystallographers to assign Potassium Chloride to a cubic Class having no plane of symmetry. But X-ray investigations have shown it to have the structure of Sodium Chloride, and have thus placed it in the Class that has the full symmetry of a cube. And a cube does have planes of symmetry.

In the next document we will discuss the Plane Group P31m of which we spoke already on many occasions in the present and previous documents. Also with respect to periodic 2-dimensional motif patterns according to that Plane Group (P31m) we will search for the C o m p l e x M o t i f which is the tectological aspect of the corresponding (2-D) crystals, and which legitimates the promorphological treatment of such crystals, and with them of their 3-D analogues.

To continue click HERE to proceed with the next Plane Groups.

e-mail :