REMARK : When the reader feels satisfied with our established theoretical foundation (done in the previous two documents) that allows (single, non-twinned) Crystals to be promorphologically assessed, he or she can skip all the following, and directly proceed with The Promorphology of Crystals.
The Plane Group Cm
The symmetry of periodic patterns of motifs according to the Plane Group Cm is based on one or another version of the Centered Rectangular Point Lattice (Net). See the next Figures.

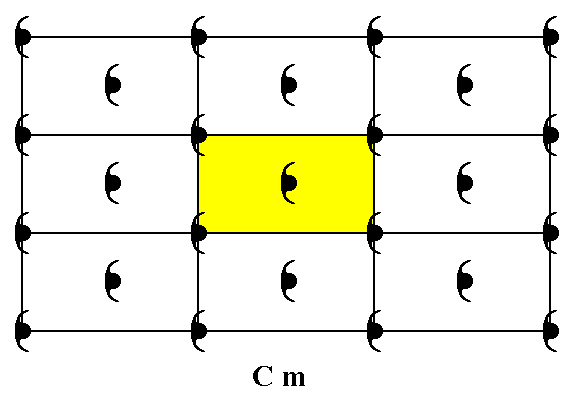
Figure 1. Periodic two-dimensional pattern according to the Plane Group Cm. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).
The pattern of Figure 1 contains one set of glide lines, as is indicated in the next Figure (These glide lines are just implied in virtue of the centering, they are not mentioned in the Plane Group symbol).
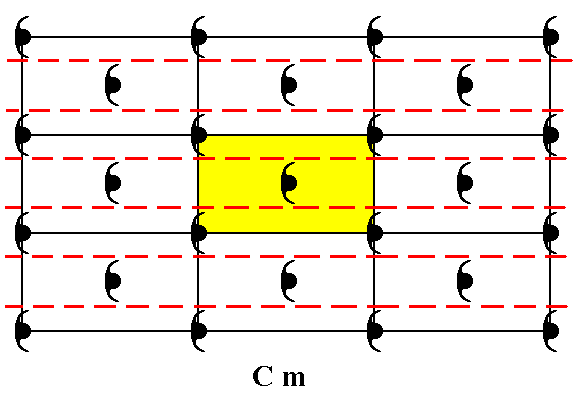
Figure 2. Periodic two-dimensional pattern according to the Plane Group Cm. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow). The pattern contains one set of glide lines (red dashed lines). The horizontal black lines of the net are at the same time mirror lines (They are interleaved with additional mirror lines (not shown). The lattice was chosen such that its nodes come to lie on mirror lines. The glide lines are parallel to existing mirror lines, so they will not increase the symmetry when their translations are made undone. So in deriving the Complex Motif we do not have to consider those glide lines.
Although we do not have to concern ourselves with the glide lines of the Cm pattern, it is nevertheless instructive to see what actually happens when we eliminate the translations involved with these glide lines. We will do this by our Copy-Shift-Superimpose method, in our case the Copy-horizontal-Shift-Superimpose method, because we have to do with horizontal glide translations. According to this method we will do the following : We make a copy of the periodic pattern, then we shift this copy horizontally by half the horizontal side of the unit cell, and finally we superimpose the shifted copy onto the original. In actually executing this whole operation we only need to involve a part, i.e. a fragment (bigger than one unit cell) of the pattern, because it is periodic. In this way we will effect an undoing (i.e.elimination) of the glide translation involved in the horizontal glide lines of the pattern. The next two Figures illustrate the process.
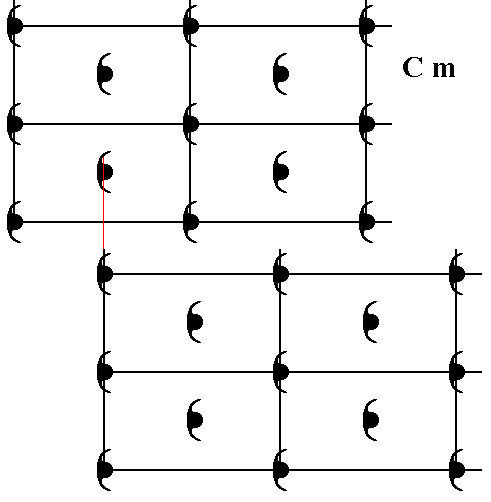
Figure 2a. A copy is made of the Cm pattern of Figure 1, and shifted horizontally by one-half of the length of the horizontal side of the unit cell.
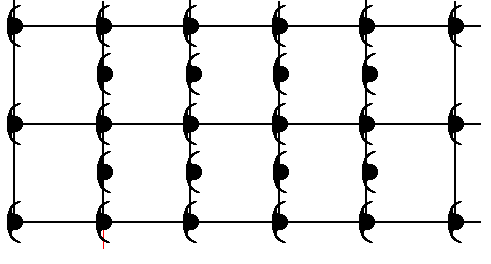
Figure 2b. The shifted copy is superimposed onto the original.
The next Figure isolates the area actually involved in the superposition (of course the w h o l e infinite pattern is supposed to be involved in the copy-shift-superimpose operation).
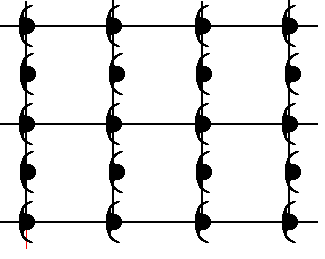
Figure 2c. The proper effect of the copy-horizontal-shift-superimpose operation on the pattern of Figure 1. Indeed, the glide lines have now become mirror lines (The small discrepancies, visible in the Figure are not intrinsic, they are caused by small inaccuracies in the drawings).
In order to find a repeated unit in the pattern just obtained (Figure 2c) we connect equivalent points. The result is a net which clearly indicates possible repeating units, namely the content of any rectangle of this net :
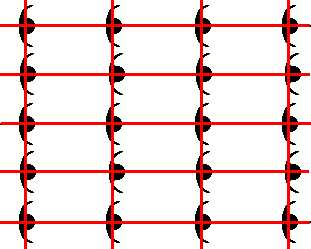
Figure 2d. Evidently equivalent points form a net, indicating the periodic repeat within the pattern of Figure 2c.
Although we now have found a possible repeating unit (the content of any rectangle of the net), a more satisfactory and fully equivalent unit, in which no parts, i.e. fragments of the motif s.str. are involved, can also be found. It involves only whole motifs s.str. To actually find such a repeating unit we first isolate the net itself :
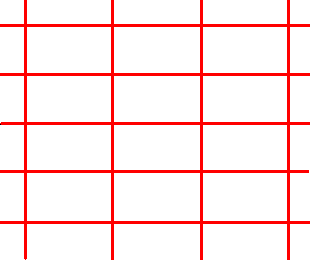
Figure 2e. Isolated net of the previous Figure.
The net reflects the periodic nature of our pattern of Figure 2c. We can lay the net over the pattern as we please, as long as the net is not turned with respect to the pattern. So we can lay it over the pattern in such a way that whole mitifs s.str. fall within the cells of the net. See next Figure.
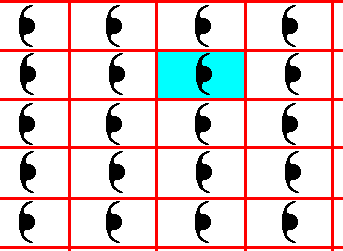
Figure 2f. The isolated net of the previous Figure is laid over the motif pattern of Figure 2c. After erasion of the lines of the old net we can easily detect a repeating unit containing a whole (i.e. not fragmented) motif s.str. One such repeating unit is indicated.
The repeating unit as indicated in the previous Figure is in fact our u l t i m a t e Complex Motif. It consists of the motif s.str. (black) plus background (light blue). The next Figure isolates this Complex Motif, thereby at the same time eliminating all simple translations.

Figure 2g. Isolated repeating unit of the pattern of Figure 2f. This is the final Complex Motif. It consists of one whole motif s.str. (black) plus its corresponding background (light blue). Its symmetry is m.
The symmetry of this Complex Motif is m, i.e. its only symmetry element is a mirror line. This Complex Motif is derived from the Cm pattern (Figure 1) by eliminating the horizontal translation involved in the pattern's horizontal glide lines. We did this by applying our Copy-Shift-Superimpose method. But because the pattern has mirror lines parallel to the glide lines, it is to be expected that elimination of the glide translations will not increase the symmetry any further. And all what matters is that we end up with a finite tectological figure having the full symmetry indicated by the Crystal Class of the given crystal, i.e. by its point symmetry. From the Plane Group symbol -- Cm -- we can deduce that this point symmetry must be m. Indeed if we directly read the Complex Motif from the Cm pattern of Figure 1, then we have a motif already possessing the symmetry m.

Figure 2h. Isolated repeating unit of the pattern of Figure 1. This is a possible Complex Motif. It consists of one whole motif s.str. (black) plus 4x1/4 motif s.str. (black) plus the corresponding background (light blue). Its symmetry is m.
When we take the total motif, i.e. the complete motif associated with a lattice point, we get the same Complex Motif as was obtained in the previous Figure :
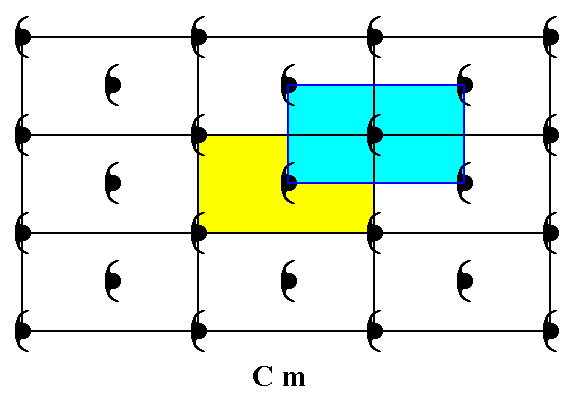
Figure 2i. When we take the total motif (light blue), we get the same Complex Motif as we obtained in Figure 2h. Its symmetry is m.
If we choose a different rectangular unit cell (i.e. if we shift the location of the net -- without turning it -- across the pattern), we still have to do with a c e n t e r e d rectangular net. The following Figures illustrate this.
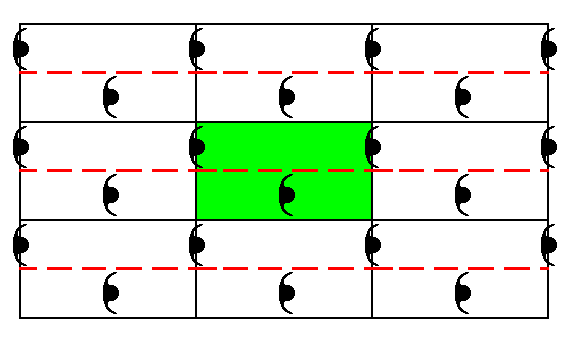
Figure 3. The alternative unit cell choice in the periodic motif pattern of Figure 1 (i.e. just as a Cm pattern) implies a new net position with respect to the motifs. One of the glide lines (dashed red line) passes through the center of the unit cell (green).
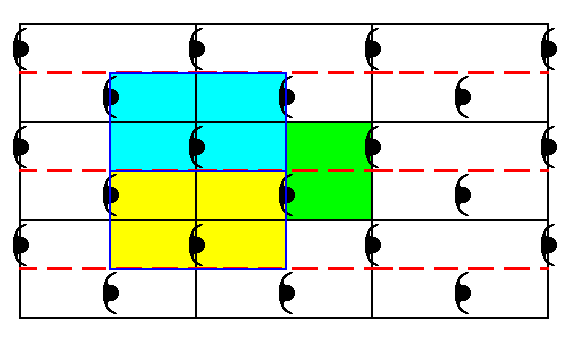
Figure 4. In the new net, based on the alternative unit cell choice in the pattern of Figure 1, two total motifs are indicated (a "total motif" is the motif in the strict sense plus its corresponding background) : one (light blue) associated with the upper left corner of the unit cell (The unit cell, as given in Figure 3), the other (yellow) associated with the lower left corner. We can see that they are identical to each other and to the unit cell.
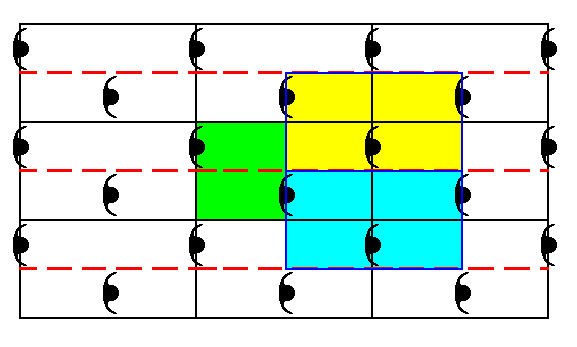
Figure 5. In the new net, based on the alternative unit cell choice in the pattern of Figure 1, two other total motifs are indicated : one (light blue) associated with the lower right corner of the unit cell (as given in Figure 3), the other (yellow) associated with the upper right corner. We can see that they are identical to each other and to the unit cell.
So we have established five total motifs, associated with the unit cell : one at each corner, and one in its center (the latter is equivalent to the unit cell itself). All five total motifs are identical with respect to shape, symmetry and content. So we indeed have still to do with a centered rectangular net.
The next Figure shows all five total motifs associated with the nodes of the centered rectangular net.
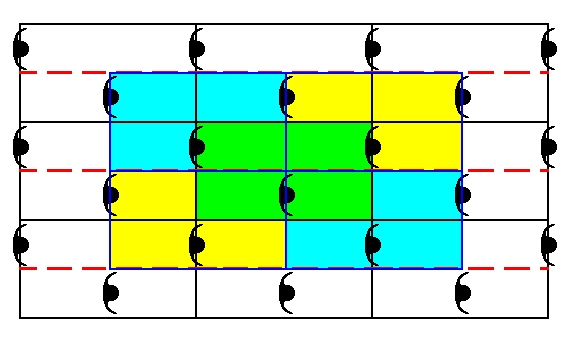
Figure 6. The five total motifs. Their equivalence and distribution shows that we have to do with a centered rectangular net.
When we isolate the unit cell of Figure 3 -- which is fully equivalent to a total motif -- we see that it contains of 1/2+1/2+1=2 motifs s.str. See next Figure.
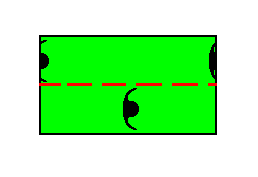
Figure 7. An isolated unit cell or total motif, from the pattern of Figure 3 (which is the same pattern as that of Figure 1).
The repeating unit depicted in Figure 7 consists of 1/2+1/2+1=2 motifs s.str., while the repeating unit that we obtained in Figure 2h, derived from the same pattern but with the net placed in the original position (Figure 1), contains 4x1/4+1=2 motifs s.str. But while the symmetry of the latter (Figure 2h) is m, i.e. it has one mirror plane, there is no symmetry at all in the former (Figure 7). So as unit cells these two units are equivalent, but as Complex Motif not : The unit of Figure 7 is not a Complex Motif, because it has not yet the symmetry of the Class, which is m. It therefore turns out that in order to find the Complex Motif we must take that net (point lattice) position which has the highest symmetric unit cell. And indeed we see that the unit cell of the alternative (position of the) net -- see Figure 3 -- is less symmetric than the one of the initially chosen net (position) (Figure 1). The Complex Motif obtained from the latter, and obtained without eliminating the glide translations, can be considered as the p e n u l t i m a t e Complex Motif, while the Complex Motif obtained by eliminating the glide translations can be considered as the u l t i m a t e Complex Motif (Figure 2f and, finally, Figure 2g). The penultimate Complex motif already possesses the symmetry of the Crystal Class associated with the Plane Group Cm, namely m, so the elimination of the glide translation was not strictly necessary.
The next Figure recapitulates the penultimate Complex Motif and the ultimate Complex Motif :
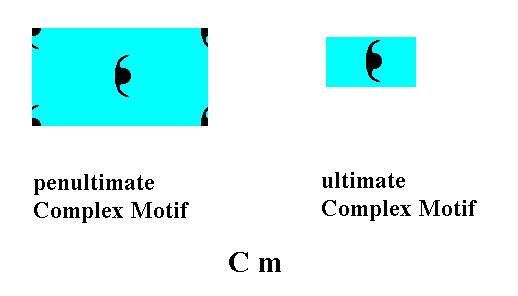
Figure 8. The penultimate Complex Motif and the ultimate Complex Motif associated with Plane Group Cm.
The symmetry of the Complex Motif consists of one mirror line as its only symmetry element. The planimetric Figure that geometrically represents this symmetry is the Isosceles Triangle. The isosceles triangle is accordingly the promorph or planimetric basic form of all 2-D crystals belonging to Plane Group Cm, and with it to the Class m.

Figure 9. The Isosceles Triangle as the promorph or planimetric basic form of all 2-D crystals with a total symmetry described by Plane Group Cm, and with it belonging to the Class m.
The Plane Group P2gg
Periodic patterns of motifs according to Plane Group P2gg are based on a representative of the Primitive Rectangular Point lattice. See next Figures.
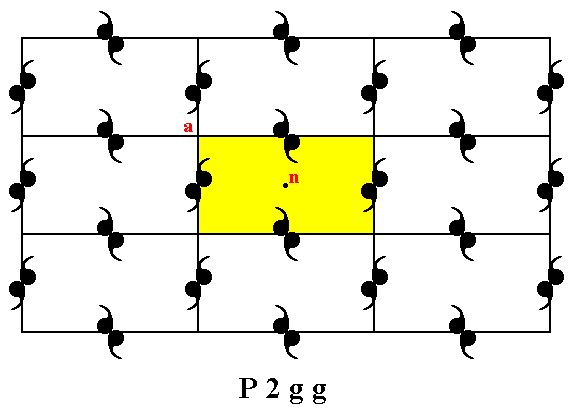
Figure 10. Periodic two-dimensional pattern according to the Plane Group P2gg. The pattern must be considered as indefinitely extended in 2-D space. A unit mesh choice is given (yellow). This unit mesh is primitive and has a point symmetry of 2.
Point n is not equivalent to point a, because the orientations of the motifs left and right to them are different. So indeed the unit mesh is primitive.
The P2gg pattern contains two sets of glide lines, indicated in the next Figure.
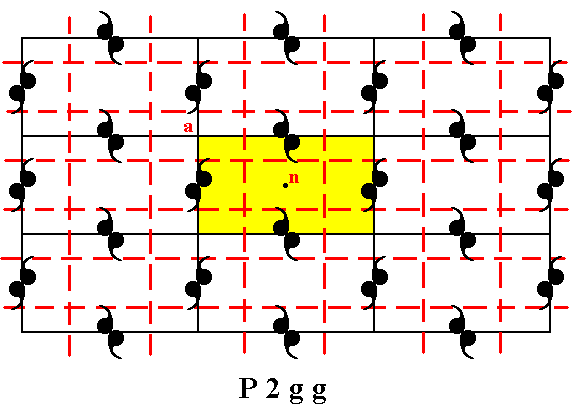
Figure 11. Periodic two-dimensional pattern according to the Plane Group P2gg. The pattern must be considered as indefinitely extended in 2-D space. The pattern possesses two sets of g l i d e l i n e s, indicated by red dashed lines.
Because there are no mirror lines parallel to the glide lines we know that the Complex Motif is drawn apart by these glide lines and effecting a lower symmetry, as can be seen by the fact that the symmetry of the unit cell is 2, and thus not possessing the point symmetry of the crystal -- 2mm -- as can be deduced from the Plane Group symbol. So to obtain the Complex Motif we must undo the glide translations. We first handle the vertical translation involved in the vertical glide lines : We take a copy of the pattern, shift it vertically by half a vertical unit cell edge in order to undo the vertical translation, and superimpose the shifted copy of the pattern onto the original. Then we make a copy of the just obtained result, shift that copy horizontally by half a horizontal edge of the unit cell, and superimpose this shifted copy onto the first result. We then obtain a pattern of which the smallest repeated unit is the Complex Motif, i.e. the condition of being drawn apart of the motif is now undone. In all this it is sufficient to just take a p a r t of the pattern of unit cell size or a little bigger, because the pattern is periodic. The next Figures illustrate this whole process.
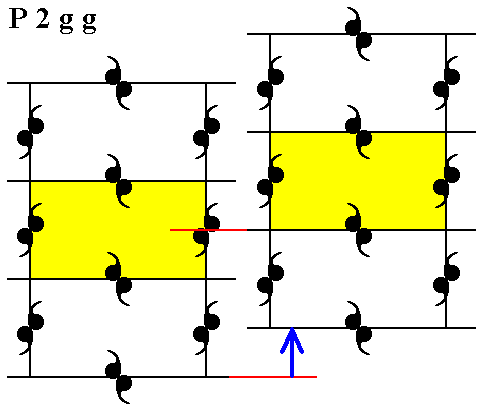
Figure 12. A copy of the pattern (P2gg) is shifted upward (indicated by the blue arrow) by half the vertical length of the unit cell.
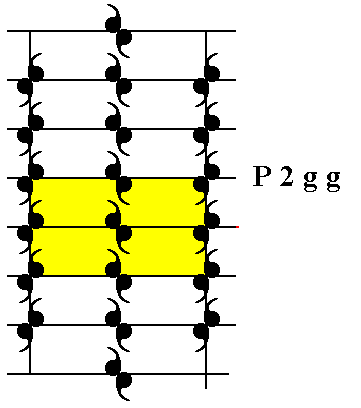
Figure 13. The shifted copy of the pattern (P2gg) is superimposed upon the original. An area of the size of the unit cell is indicated.
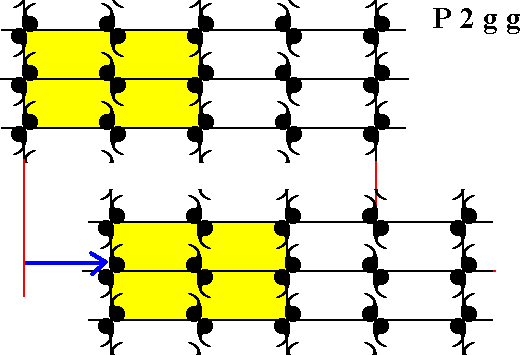
Figure 14. We make a copy of the result of the previous Figure and shift it to the right (indicated by the arrow) by half the length of the horizontal unit cell edge.
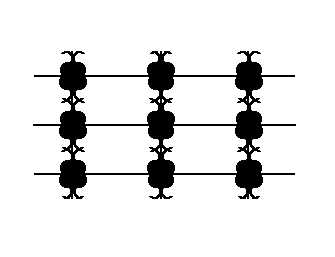
Figure 15. We superimpose the shifted copy onto the the first result (i.e. onto the original with respect to that copy).
From the just obtained result we can easily recognize the Complex Motif. It is depicted in the next Figure.

Figure 16. The Complex Motif of the P2gg pattern as given above. Its symmetry is 2mm, which means that it possesses a 2-fold rotation axis in its center (normal to the plane of the drawing), and two mirror lines intersecting in the motif's center. The light blue surroundings also belong to the Complex Motif.
We stated that the symmetry of the Complex Motif is 2mm. However, when we look carefully to its drawing we see a slight discrepancy with respect to its symmetry. But this is resulting from slight errors (inaccuracies) that can easily creep in while making digital drawings. From all the foregoing Figures it is clear that the symmetry of the Complex Motif is 2mm.
The simplest planimetric figures that geometrically express this (2mm) symmetry are the Rectangle and the Rhombus.
Although the Rectangle and the Rhombus both possess the same symmetry, namely 2mm, Promorphology discriminates between them. Let us explain this.
The shape of the Rectangle as well as of the Rhombus allows for two homopolar axes -- the d i r e c t i o n a l a x e s -- to be distinguished. They are perpendicular to each other and coincide with the two mirror lines. Motif units, insofar as they are the Complex Motif's a n t i m e r s (counterparts), can have different relations to these two directional axes. When the Complex Motif has f o u r antimers we can state the following : Whether the promorph must be represented by a Rectangle or by a Rhombus depends on the fact whether the directional axes of the Complex Motif are i n t e r r a d i a l or r a d i a l, which means that they either go between the antimers of the Complex Motif, or they go right through them ( See also Figure 27 ). When the Complex motif -- with symmetry 2mm -- has only t w o (congruent) antimers, one directional axis is radial -- it passes through the two antimers, while the other directional axis is interradial --it passes between the two antimers, and the promorph must be expressed by a Rhombus ( See Figure 28 ).
And so the R h o m b u s accordingly represents the promorph or planimetric basic form of all the 2-D crystals possessing a 2mm Complex Motif having either four antimers, provided that its two directional axes are radial, or (having) two antimers. And thus a promorph based on a Rhombus-just-like-that, consists of two species, one with four and one with two antimers, depending on the tectology of the Complex Motif. When none of the two directional axes are radial the promorph must be represented by a R e c t a n g l e, and in that case there are always four antimers present.
See next Figures.
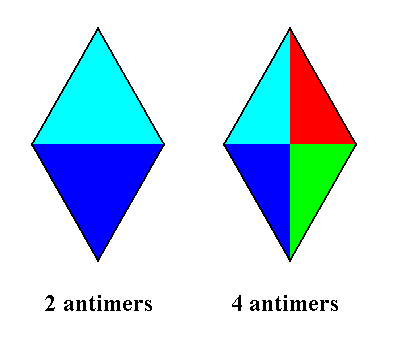

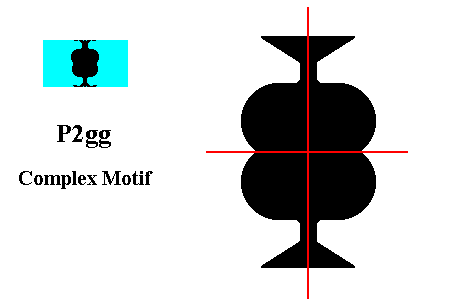
Figure 18. The Complex Motif of the P2gg pattern as given above, and its magnification. The two d i r e c t i o n a l a x e s (red) are indicated in the magnification.
To judge from the Complex Motif's magnification it consists of two oppositely positioned antimers, analogous to the (3-D) Orthostaura diphragma (Heteropola heterostaura autopola), or amphitect pyramids with only two antimers (The latter feature is dictated by the given organism or inorganism). See next Figures.
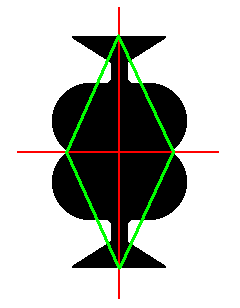
Figure 19. We can inscribe a Rhombus in the Complex Motif of the P2gg pattern to express the radiality of at least one directional axis.
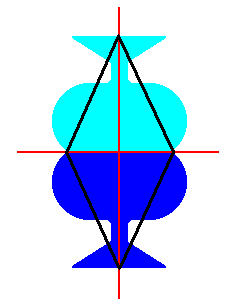
The Complex Motif derived from the P2gg motif pattern of Figure 10 has two antimers (Figure 20), so its promorph or planimetric basic form must be represented by a Rhombus in which the TWO antimers are indicated :

Figure 21. The Rhombus as the promorph or planimetric basic form of all 2-D crystals of Plane Group P2gg, and of the Class 2mm, with two antimers.
The Plane Group P2mm
Two-dimensional periodic motif patterns according to the Plane Group P2mm are based on the Primitive Rectangular Point lattice. The next Figure displays such a pattern.
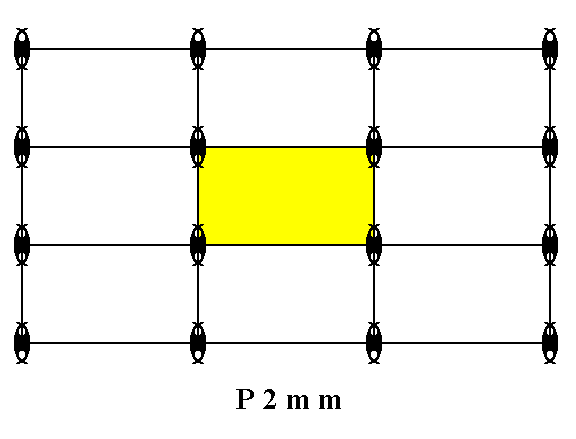
Figure 22. Motif pattern according to the Plane Group P2mm. A unit cell (mesh) is indicated (yellow). The pattern must be imagined as indefinitely extended in 2-D space.
The P2mm pattern does not possess glide lines. So the Complex Motif is identical to the content of a unit cell (which always means the most symmetric unit cell, if there are several possible choices of unit cell).
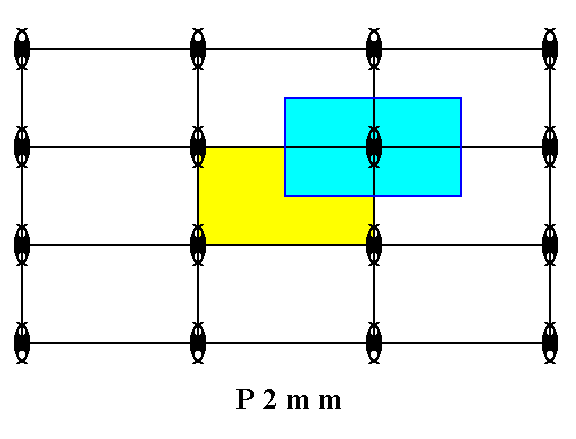
Figure 23. A total motif, associated with the upper right lattice point of the unit cell (Recall that all lattice points are equivalent, and also all lattice points + their corresponding complete surroundings. Such a complete environment (surroundings) consists of the motif s.str. or parts thereof + its corresponding background).
The total motif, as established in the previous Figure, is equivalent to the C o m p l e x M o t i f of the pattern of Figure 22.

Figure 24. The Complex Motif of the periodic pattern of Figure 22. The symmetry of the motif s.str. dictates the symmetry of the whole motif.
The Complex Motif, as established in Figure 24, has a symmetry of 2mm, which means that it has two non-equivalent mirror lines and a two-fold rotation axis going through the intersection of these mirror lines and normal to the plane of the drawing. To judge from the morphology of the motif s.str. the Complex Motif has two antimers, so the promorph or planimetric basic form must be expressed by a Rhombus in which the presence of the two antimers is indicated. See next Figures.
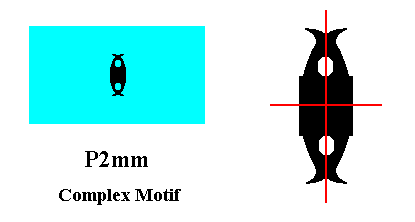
Figure 25. The Complex Motif of the periodic pattern of Figure 22, and a magnification of it to show tectological features. In the magnification the two directional axes are indicated (red lines). They coincide with the two mirror lines.
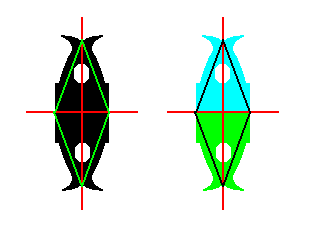
Figure 26. Complex Motif of the P2mm pattern of Figure 22.
Left image : In the Complex Motif a Rhombus can be inscribed, indicating the radiality of at least one directional axis.
Right image : The motif s.str. indicates the presence of two antimers. Therefore one directional axis is radial, the other interradial.
It is perhaps instructive to enumerate the other two possible promorphs for the 2mm symmetry. See next Figure.
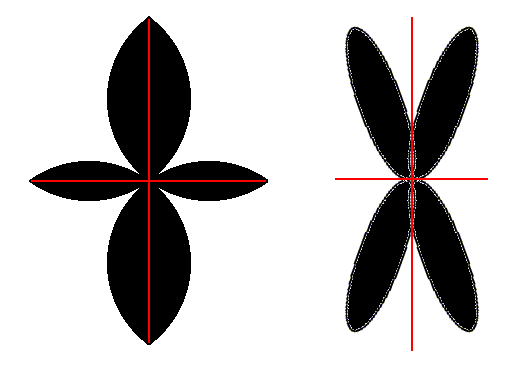
Figure 27. Possible 2-D motifs with 2mm symmetry ( = two mirror lines perpendicular to each other, and one 2-fold rotation axis that contains the intersection of the mirror lines and is perpendicular to the plane of the drawing ). Both motifs consist of four antimers. The directional axes are indicated by red lines. They coincide with the two mirror lines.
In the left image the directional axes are r a d i a l, which means that they pass through the antimers. The promorph must accordingly be expressed by a Rhombus.
In the right image the directional axes are i n t e r r a d i a l, which means that they pass between the antimers. The promorph must accordingly be expressed by a Rectangle ( See also Figure 17a ).
A motif clearly displaying its composition out of only t w o antimers is shown in the next Figure. Here one directional axis is radial, while the other is interradial.
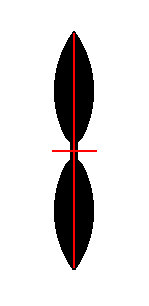
Figure 28. A third possibility for the morphology of 2mm motifs. The motif consists of only two (congruent) antimers. Directional axes are indicated by red lines. One directional axis is radial, it passes through the antimers, while the other is interradial, it passes beteen the antimers. The promorph must be expressed by a Rhombus. Our derived Complex Motif (derived from the P2mm pattern of Figure 22, and depicted in the Figures 24, 25 and 26) belongs to this type (be it less clearly).
In the next Figure we depict the planimetric figure which expresses the 2mm symmetry of the Complex Motif (Figures 24, 25 and 26) of the P2mm pattern of Figure 22 , and which shows (i.e. expresses the fact) that the Complex Motif consists of two antimers.

Figure 29. The Rhombus provided with the indication of the presence (in the Complex Motif) of two antimers, is the planimetric basic form of all 2-D crystals of the Plane Group P2mm, and with it of the Crystal Class 2mm, of which the Complex Motif consists of two antimers.
The Plane Group P2mg
The symmetry of two-dimensional periodic patterns according to the Plane Group P2mg is based on the Primitive Rectangular Point Lattice. The next Figure depicts such a pattern.
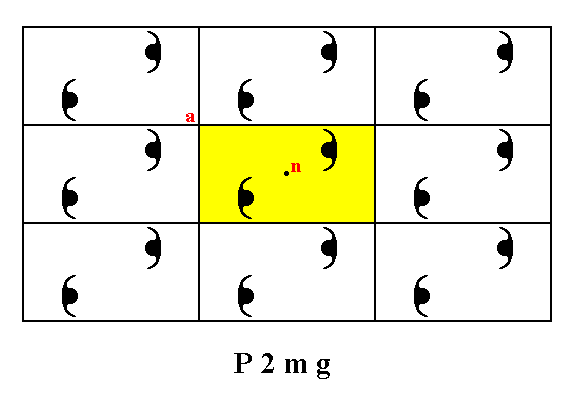
Figure 30. A motif pattern according to the Plane Group P2mg. A unit cell is indicated (yellow). The pattern must be imagined as indefinitely extended in 2-D space.
The point n is not equivalent to the point a, which is evident in their different surroundings. This means that if the point a is a lattice point, then the point n is not a lattice point, so the net is not centered.
This pattern has vertical glide lines :
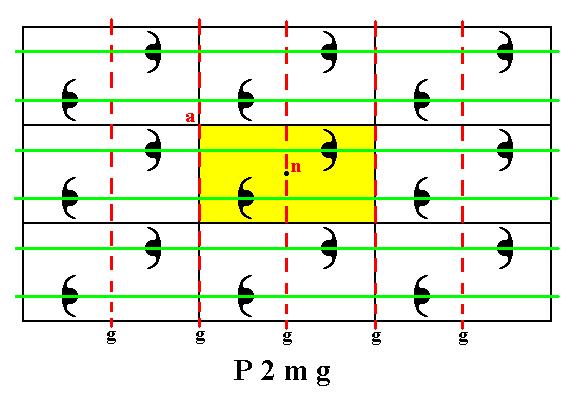
Figure 31. A motif pattern according to the Plane Group P2mg. A unit cell is indicated (yellow). The pattern must be imagined as indefinitely extended in 2-D space.
In addition to horizontal mirror lines (green lines) there are vertical glide lines (g), indicated by red dashed lines (The pattern also has 2-fold rotation axes, but these are not shown here).
In order to find the Complex Motif we must undo the translations involved in the glide lines. We accomplish this by our Copy-Shift-Superimpose method. And in the present case the shift must be a vertical one. The length of the shift is equal to the length of one-half of the vertical side of the unit cell. See next Figures.
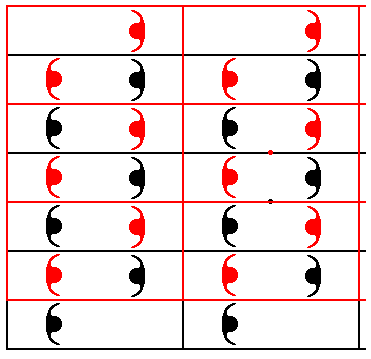
Figure 32. A copy (red) is made of the P2mg pattern of Figure 30. The copy is shifted vertically (upward), and then copied onto the original. The fact that small areas (top and bottom) are not involved in the superposition is a consequence of the fact that we use only a finite part of the pattern. This is legitimate because the pattern is periodic. The next Figure properly gives the final result.
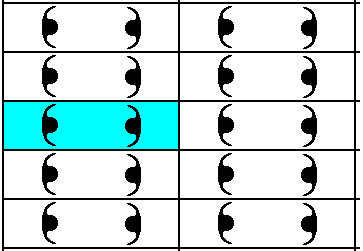
Figure 33. Final result of the Copy-Shift-Superimpose operation applied to the motif pattern of Figure 30. One repeating unit is highlighted (light blue).
One can see that the vertical glide lines that were initially present are now transformed into mirror planes as an effect of the Copy-Shift-Superimpose operation. See next Figure.
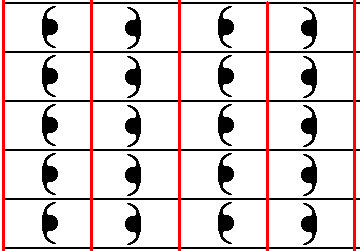
Figure 34. The initial vertical glide lines are now turned into vertical mirror lines (indicated by red solid lines). The black lines indicate the mirror lines that were originally present (See Figure 31).
The repeating unit, as indicated in Figure 33, is our sought for Complex Motif. If we isolate this motif, then at the same time all simple translations are also eliminated :

As we can see from Figure 35 the symmetry of the Complex Motif is 2mm : two mirror lines perpendicular to one another, and one 2-fold rotation axis going through the intersection point of the mirror lines while perpendicilar to the plane of the drawing.
As we know from the foregoing, in order to determine the precise promorph, we must inspect the tectology of the Complex Motif, which here means that we must look for antimers, their number and configuration. The Complex Motif, as we see it in Figure 35, suggests two antimers. Consequently the promorph must -- as was explained earlier -- be represented by a Rhombus provided with an indication that the Complex Motif has two (and not four) antimers :

Figure 36. The Rhombus provided with the indication of the presence (in the Complex Motif) of two antimers, is the planimetric basic form of all 2-D crystals of the Plane Group P2mg, and with it of the Crystal Class 2mm, of which the Complex Motif consists of two antimers.
The Plane Group C2mm
The symmetry of two-dimensional motif patterns according to the Plane Group C2mm is based on the Centered Rectangular Point Lattice (When we choose, instead of a centered rectangular unit cell, a rhomb-shaped unit cell, then we put a primitive point lattice at the basis of the pattern's symmetry -- click HERE to see it.
A pattern according to the Plane Group C2mm is depicted in the next Figure.
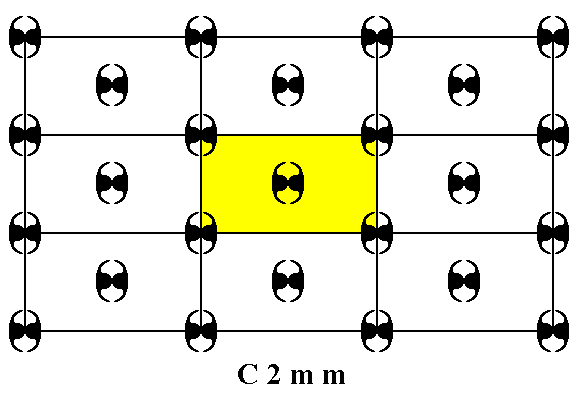
Figure 37. Motif pattern according to the Plane Group C2mm. A unit cell is indicated (yellow). The pattern must be imagined to extend indefinitely in 2-D space. Because of our choice of unit cell the periodicity of the pattern is described by a centered rectangular net.
In addition to 2-fold rotation axes and mirror planes, the pattern has two sets of glide lines : vertical glide lines and horizontal glide lines. The pattern's mirror lines are parallel to these glide lines. But because the latter are just implied because of the centering, they are not mentioned in the Plane Group symbol. See next Figure.
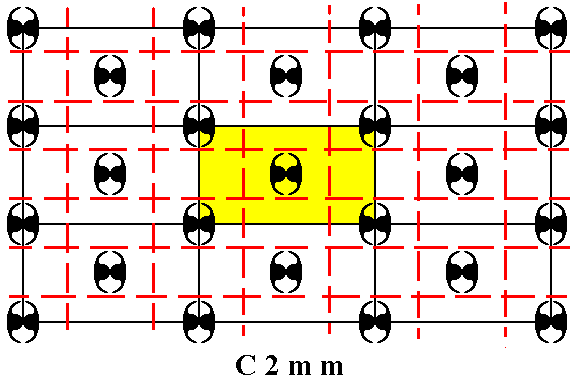
Figure 38. Motif pattern according to the Plane Group C2mm. A unit cell is indicated (yellow). The pattern must be imagined to extend indefinitely in 2-D space. Because of our choice of unit cell the periodicity of the pattern is described by a centered rectangular net.
Implied g l i d e l i n e s are indicated by red dashed lines. In addition to 2-fold rotation axes the pattern also contains mirror lines (not shown) passing vertically and horizontally through each motif s.str.
Although it is to be expected that the symmetry of a repeating unit will not be increased by the elimination of the glide translations (because parallel to all the glide lines there are mirror lines), meaning that such a repeating unit of the pattern of Figure 37 is already the Complex Motif (penultimate Complex Motif), we will nevertheless eliminate those translations, in order to obtain the ultimate Complex Motif.
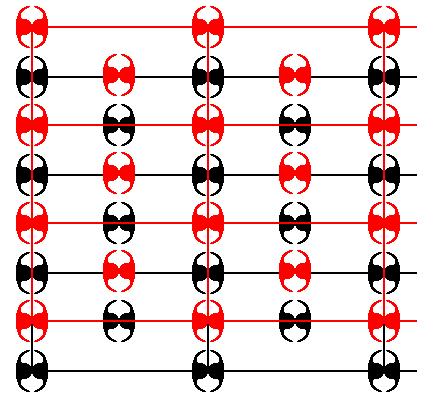
Figure 39. A copy (red) is made of the pattern of Figure 37, and shifted upward by half the length of the vertical unit cell side. The shifted copy is then superimposed upon the original.
After processing the just obtained result we get the following (indefinitely extended) pattern :
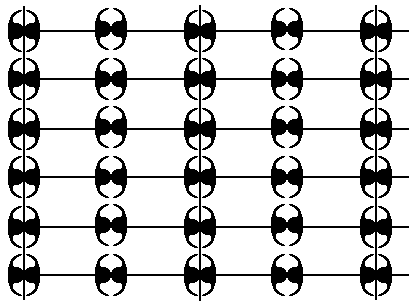
Figure 40. Result of the Copy-vertical-Shift-Superimpose operation on the pattern of Figure 37, in order to undo the vertical translations involved in the vertical glide lines.
We will now turn to the horizontal glide translations. In order to eliminate them we apply the Copy-Shift-Superimpose operation to the just obtained result (as given in Figure 40), while the shift is now horizontal over a distance of half a horizontal side of the unit cell :
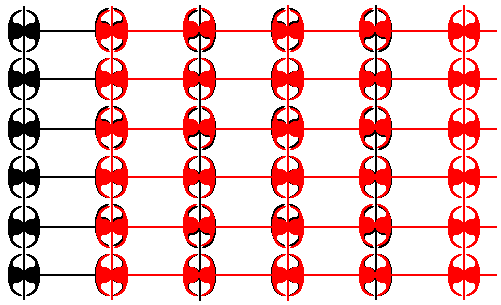
Figure 41. Result of the Copy-horizontal-Shift-Superimpose operation on the result of Figure 40, in order to undo the horizontal translations involved in the horizontal glide lines.
After processing, the final result looks like this :
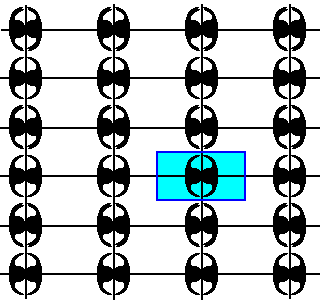
Figure 42. Final result of the eliminations of all glide translations (vertical and horizontal) in the pattern of Figure 37. A repeating unit is indicated.
As was to be expected, the pattern just obtained is identical to the one obtained after eliminating the vertical translations (Figure 40) : elimination of the vertical translations implies the elimination of the horizontal translations.
While the penultimate Complex Motif consists of 4x1/4+1=2 motifs s.str. (which is the content of the unit cell as given in Figure 37), the ultimate Complex Motif consists of only one motif s.str. This is because we telescoped the structure back along the glide lines. These glide lines are, however, in our context of the derivation of te Complex Motif, NOT fundamental. This is evident from the fact that we can choose for our periodic motif pattern another unit cell, namely a primitive rhomb-shaped unit cell -- and, consequently another net, the Diamond Net : Such a primitive unit cell only has lattice points at its corners, and this implies that the content of such a unit cell is o n e motif s.str., either 4x1/4 or just one whole. So the content of the ultimate Complex Motif (Figure 42) is the same as that of the primitive unit cell afterall, without eliminating any glide translations.
We obtain the ultimate Complex Motif by isolating the repeating unit as indicated in Figure 42 :

We obtain the same Complex Motif when we apply the Diamond Net to our periodic pattern, i.e. the alternative net referred to above, such that the motifs s.str. come to lie in the centers of the rhombi composing the net. The only difference would be that the shape of the proper surroundings of the motif s.str. would be a rhombus instead of a rectangle as was the case in the Figures 42 and 43. But the symmetry of a rhombus is identical to that of a rectangle, namely 2mm.
From Figure 43 we can see that the symmetry of the Complex Motif is 2mm, i.e. it contains two non-equivalent mirror lines (perpendicular to each other) and a 2-fold rotation axis normal to the plane of the drawing and passing through the intersection point of the mirror lines.
To judge from the morphology of the motif s.str. in the Complex Motif, the latter has two antimers. Combined with its 2mm symmetry we can deduce that one directional axis (coinciding with a mirror line) is radial, i.e. passes through the antimers, while the other directional axis (coinciding with the other mirror line) is interradial. So the promorph of all 2-D crystals belonging to the Plane Group C2mm must be represented by a Rhombus in which the presence of the two (instead of four) antimers is indicated. See next Figure.

Figure 44. The Rhombus provided with the indication of the presence (in the Complex Motif) of two antimers, is the planimetric basic form of all 2-D crystals of the Plane Group C2mm, and with it of the Crystal Class 2mm, of which the Complex Motif consists of only two antimers.
To continue click HERE to study the next Plane Groups concentrating on the derivation of the Complex Motif.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)
back to Allopola amphipleura and zygopleura
back to the Basic Forms of Cells I
back to the Basic Forms of Cells II
back to the Basic Forms of Organs
back to the Basic Forms of Antimers
back to the Basic Forms of Metamers
back to the Basic Forms of Persons
back to the Basic Forms of Colonies
back to the first part of the Preparation to the Promorphology of Crystals
back to the second part of the Preparation to the Promorphology of Crystals
back to the third part of the Preparation to the Promorphology of Crystals
back to the fourth part of the Preparation to the Promorphology of Crystals