Promorphology II

Stereometric Basic forms of the six Individuality Orders

Basic Forms of Cells
I

P r o m o r p h s o f f i r s t - o r d e r f o r m i n d i v i d u a l s

Arachnoidiscus, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

REMARK : To understand the following documents on the Promorphology of the Six Individuality Orders, the reader should be familiar with the Tectology of Organisms. I have treated these in a series of documents on the Morphological Individality in Organisms, beginning with an Introduction to Tectology.
REMARK : When we, in the course of the ensuing discussions, quote a certain promorph (= stereometric basic form or promorphological category), we will set it as a LINK. This link will bring the reader to the relevant place within the Promorphological System, so that he or she can orient him- or herself as to where that category is situated within the System.
The c e l l s constitute as first-order form individuals the ultimate building blocks of (multicellular) organismic bodies. They are in this particular sense "ultimate" because below the level of the cell we do not find genuine undisputed l i v i n g entities. Cells as building blocks are as important to Promorphology as to Tectology. The basic forms (underlying their outer shapes) of all second- to sixth-order form individuals ultimately result in the same way from the basic form, number, positioning and way of connection of the constituent cells as the basic form of the latter result from the number, positioning and way of connection of the cell constituents (organelles). One would expect that the cells, because they are just the building blocks of higher organisms, show only a low diversity with respect to their basic form (promorph). Cells however are not rigid entities, but complex dynamic beings, they are plasic (that's why Haeckel called them plastids (a term, unfortunately now used to signify other biological structures). Indeed there is not a single promorph, as known from the domain of promorphs of multicellular organisms, that is not represented by single cells. We only have to think about Radiolarians and Foraminiferans (insofar as they are genuinely unicellular, i.e. containing only one nucleus), of solitary Diatomeans and many others. So even the single cell has already a maximum potential with respect to form. Also when they occur within a multicellular body they often display a variety of basic forms. So in higher organisms it is not so much their diversity of basic forms that is remarkable, but the fact that a relative large organismic body can be generated that complies to certain symmetries over relatively large distances across the body, distances far more greater than the range of molecular forces. So in small bodies (cells) a diverse form generation is indeed to be expected.

We said that the basic form of higher-order form individuals (organs, antimers, metamers, persons and colonies) ultimately depend on the basic forms of the constituent cells. But because cells are plastic entities their basic forms, insofar as the cells are constituents of a larger whole, are also determined by that whole.

In the protists as also in the plantkingdom as well as in the animal kingdom we can find almost every basic form discussed in the previous documents : from the lowest and simplest, the Anaxonia and Homaxonia all the way up tho the highest and most perfect, the Amphipleura and Zygopleura. This remarkable diversity of basic form, by which the first-order form individuals stand out with respect to the other individality orders, is mainly determined by two factors. Firstly by the fact that the first-order form individuals are in a higher degree subject to the most diverse adaptational relationships, secondly by the fact that most cells which elevate themselves to a higher basic form, must pass through a series of lower basic forms.

In Chapter V, The forms of cells, of the outstanding work of D'ARCY THOMPSON, 1942, On growth and Form, the forms (shapes) of organic cells is discussed in a causal way as an effect of surface-tension. Later it turned out (See BONNER, J., 1961, reprinted 1975, editing an abridged edition of On Growth and Form) that in addition to surface-tension (reigning in the semi-liquid organic material) also so-called membrane tension plays a part. These forces are however extremely low, far too low to account by themselves for cell shape. Instead, then, we must look to the microstructure of the cell periphery for an understanding of cell form. The consideration of the generation of cell forms (shapes) along surface-tension features nevertheless has its value as long as we interpret it as representing a model, or an analogy, rather than a reality.
Our treatment concerning the basic form of cells (and of all other organismic entities) is not a causal treatment, but a descriptional one. It documents all organic basic forms actually encountered in Nature, and tries to classify them. It is a morphology, not a physiology, i.e. not a biophysics.

An important promorphological characteristic of cells is the preponderance of lower basic forms (promorphs). Although all higher, even the highest and most perfect promorphs, are materialized in certain cells, they form a minority with respect to the abundance of lower ones. Only the those cells that as free and isolated life units form the substrate of actual bionts, generally display a larger wealth of higjer basic forms, while the great majority of the remaining cells, which constitute organs and higher-order form individuals anyway, most offen stick to lower promorphs.
If one could compare and statistically order all existing cells with respect to their promorph, then the result would probably be that the majority of all cells possesses either the completely amorphous basic form of the Anaxonia ( Anaxonia acentra ), or the absolutely regular shape of the sphere, that is the basic form of the Homaxonia, and the one that imediately connects with the latter, the Monaxonia. Further it probably would turn out that the spherical form is predominant in those cells that can develop their form (shape) unimpeded by external non-uniform pressure freely out into all directions of space, for instance those that exist freely in a liquid, while, on the other hand the monaxonic form and the anaxonic form predominates in those cells that must, in their overall growth, conform with the external constraints, imposed on them by the spatial situation of the adjacent cells.

As has been said the spherical shape of cells is to be expected in cases where they live freely, except when such a cell is enclosed in a shell, like in many radiolarians, foraminiferans and solitary diatomeans (See Figure 1).

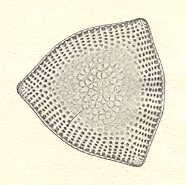
Figure 1. Stictodiscus, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

The spherical shape we see in many virtual bionts (physiological individuals that can develop into the corresponding mature forms) that play a role in the reproduction of organisms, namely (many) eggs and spores. Among partial bionts (physiological individuals that can maintain themselves for some time, but which cannot independently develop into the mature form of the species) we can indicate many pollen grains having this spherical shape.
As the most regular basic forms, which immediately connect to the form of the sphere, we have indicated in the previous documents the Polyaxonia, the irregular and regular endospheric polyhedra. Also these are often materialized in cells,, especially again in the above mentioned virtual and partial bionts, the eggs and spores, and the pollen grains.
From the large form group of the Protaxonia it is especially the Monaxonia that form the promorphs of many cells, and as such the homopolar ( Monaxonia haplopola ) as well as the heteropolar ( Monaxonia diplopola ) forms. Examples, among cells, of the Diplopola anepipeda are the eggs of birds.
More seldom than the Monaxonic form, which can be derived from the Homaxonia by slight modifications, we will find the Stauraxonic form ( Stauraxonia ) be materialized in cells. We see them for example in diatoms and pollengrains. We will show below the diversity of cell forms even within a single group : The Diatoms. These latter are vegetable unicellular (sometimes forming colonies) aquatic organisms. The cell of such a diatomean is enclosed within a pillbox-like shell of silica. The next Figures are photographs depicting diatomean cells. The magnification ranges from 200 to 500.

Figure 2. Actinoptychus, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 3. Didymosphenia, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 4. Auliscus, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 5. Coscinodiscus, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 6. Hemidiscus, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 7. Triceratium, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 8. Asteromphalus, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 9. Frustulia, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

Figure 10. Gyrosigma, a diatomean cell.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

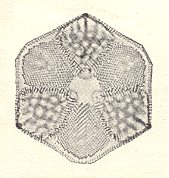
Although the most differentiated basic forms like the Heterostaura autopola and the Heterostaura allopola are materialized in some cells, their proportion is low with respect to the simple and regular promorphs, and also with respect to the absolutely irregular Anaxonia, which are the dominating promorphs in the first-order form individuals.
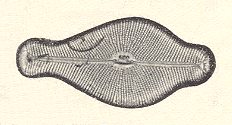
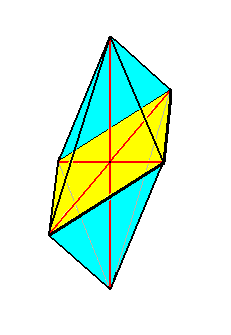
The diatomean Gyrosigma, displayed in Figure 10, is promorphologically very remarkable. If we consider the top and bottom halves (only one of them being visible in the photograph) as being symmetrical with respect to each other, then they are separated by a mirror plane (parallel to the plane of the photograph). Perpendicular to this mirror plane we can detect a 2-fold rotation axis as a second symmetry element of the individual. This axis can be considered as to coincide with the individual's main body axis. If that main axis were to coincide with the line of intersection of two mirror planes perpendicular to each other, implying in the organism under consideration the presence of two unequal ideal (i.e. directional) cross axes perpendicular to each other, and each one moreover being homopolar, then the stereometric basic form would belong to the Allostaura octopleura (Stauraxonia homopola), which are geometrically represented by an 8-sided amphitect bipyramid. See next Figure.

Figure 11. The eight-sided amphitect bipyramid (Rhombic Octahedron). The equatorial plane is emphasized (yellow). The ideal cross axes (Euthini) are contained in the equatorial plane.

But, as can be seen in the photograph, the mentioned mirror planes (containing the body's main axis) are not present, because of the sigmoid form of the individual. Besides the equatorial mirror plane, the only symmetry element of the individual (as represented by Gyrosigma) is a 2-fold rotation axis (which means that when the individual is rotated by 180⁰ about that axis, the result will be identical to the initial state, i.e. the individual will be mapped onto itself). Crystallographically the symmetry of the individual can be indicated by the symbol 2/m which corresponds to the Prismatic Class of the Monoclinic Crystal System [ See the Special Series of the First Part of this website, accessible via back to homepage.For a Promorphological consideration of (single) Crystals, see the document onThe Promorphology of Crystals ]. Such a form, i.e. such symmetry content, we will seldom encounter in organisms. If we consider only the axes and their poles, i.e. only the relative lengths of the body axes and the quality of their poles (homopolar or heteropolar), as we normally do in Promorphology, then the given individual, representing the diatomean genus Gyrosigma, has only one homopolar body axis, namely its main axis. Its basic form would then belong to the Eudipleura. As a consequence we then should interpret the homopolar axis as the lateral axis of the body. As such the symmetry would correspond to the Domatic Class (m) of the Monoclinic Crystal System.
Analogous considerations as the ones we just had, apply when we discriminate between the top and bottom parts of the diatomean shell. The top part is a lid that encloses the bottom part and is consequently a little wider than the latter. The 2-fold rotation axis is then heteropolar.
The next Figure shows some more detail of Gyrosigma

Figure 12. Gyrosigma, a diatomean cell. Detail.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))

To accomodate for forms like Gyrosigma we have erected a special promorphological category, whereby we consider the two diatomean valves (the top and bottom valve) as promorphologically equal (In most Diatoms they only differ slightly with respect to size). The new category mentioned will be called S i g m o s t a u r a, expressing the fact that at least one cross axis has a sigmoid shape. The Sigmostaura will belong to the Stauraxonia homopola, and will be a sister group of the Homopola isostaura and the Homopola allostaura, i.e. our new category can be comprehensively called Homopola sigmostaura. The reader can find the treatment of this category HERE.

To continue click HERE for the Basic Forms of Cells II

e-mail :