Promorphology of Crystals Preparation XIII

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
13

e-mail :

Sequel to the Plane Group P31m

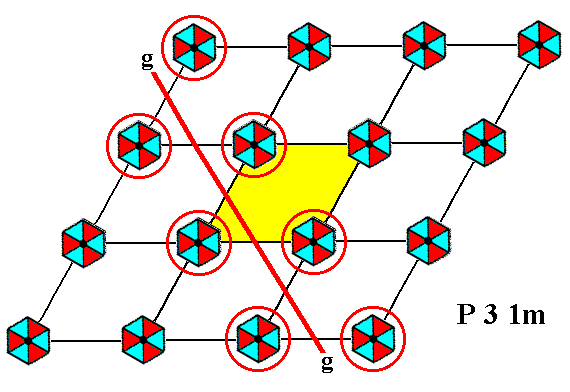
We will now -- in order to find the ultimate Complex Motif of the P31m pattern of Figure 2 of the previous document -- eliminate all glide translations inherent in the pattern. First we will eliminate the translation involved in the diagonal glide line. This glide line is shown in the next Figure.

Figure 1. The pattern of Figure 2 of the previous document has glide lines parallel to, but not coincident with, the shorter diagonal of the unit cell, in accordance with the symmetry diagram for the Plane Group P31m, depicted in Figure 3 of the previous document. Only one such glide line is indicated.

To eliminate this translation we will use our Copy-Shift-Superimpose method :
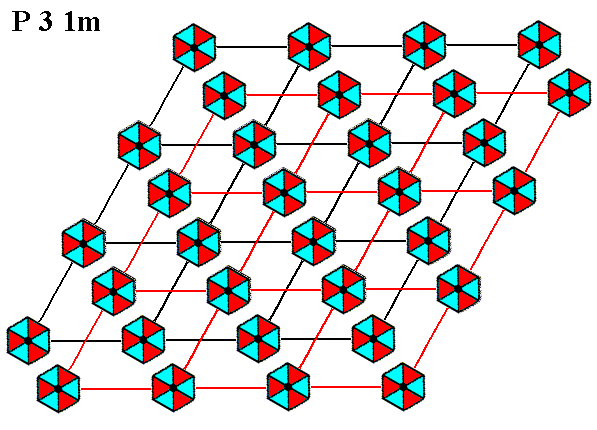
We make a copy of the P31m pattern, shift it by half the shorter unit cell diagonal ( = the shorter diagonal of the rhomb-shaped unit cell ), and then superimpose the shifted copy onto the original :

Figure 2. Elimination of the diagonal translation by the Copy-Shift-Superimpose method. The shift is diagonal by half the length of the shorter diagonal of the unit cell. In this way the translation, involved in the glide line is undone.

After some processing the result looks like this :

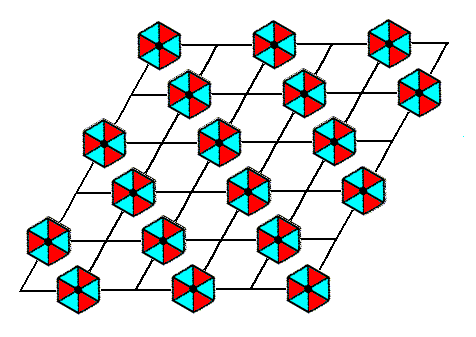
Figure 3. Elimination of the diagonal translation by the Copy-Shift-Superimpose method. Final result.

Now we subject the just obtained result again by a Copy-Shift-Superimpose operation, in which the shift is in the SW-NE direction parallel to one of the edges of the rhomb-shaped unit cell. When we have done so we will have eliminated the corresponding SW-NE translation, and, as will be evident, at the same time also the translation parallel to the other edge of the unit cell, the horizontal edge. See next Figure.

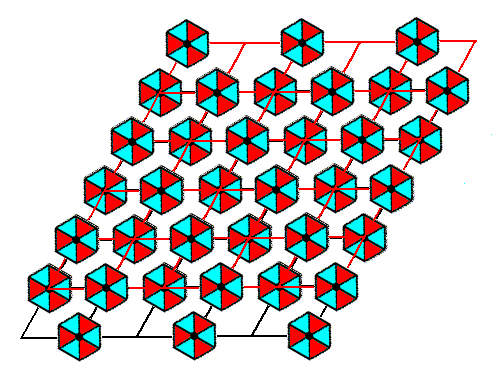
Figure 4. Elimination of the SW-NE translation by the Copy-Shift-Superimpose method.

After some processing the result looks like this :

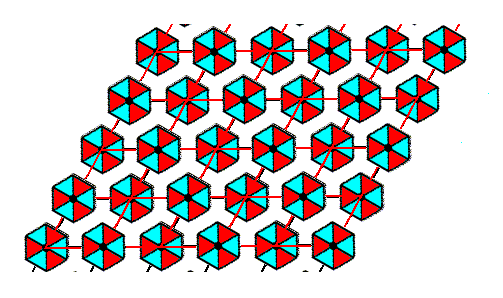
Figure 5. Elimination of the SW-NE translation by the Copy-Shift-Superimpose method. Final result.

As has been said (and as can be directly seen from the result depicted in Figure 5), the application of the Copy-Shift-Superimpose operation with respect to the horizontal translation will not have any further effect. That translation is already automatically eliminated. So the pattern of Figure 5 (minus the lines that belonged to the connection lines of the point lattice) is our pattern that is free from glide translations.
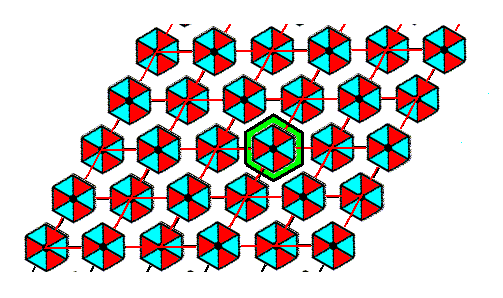
When we finally isolate from this pattern a proper repeating unit, we then have also eliminated all simple translations and obtain the (ultimate) Complex Motif.

Figure 6. A repeat unit is indicated in the pattern of Figure 5.

This repeat unit is the (ultimate) Complex Motif of the P31m pattern of Figure 2 of the previous document. See next Figure.

Figure 7. The (ultimate) Complex Motif of the P31m periodic motif pattern of Figure 2 of the previous document, after elimination of all glide as well as simple translations.

It is again instructive to compare this ultimate Complex Motif with the ultimate Complex Motif of the P3m1 periodic pattern having the same motifs s.str. Both Complex Motifs are obtained by eliminating all simple as well as all glide translations. This P3m1 ultimate Complex Motif was found in Figure 14 of Part 8. The comparison is given in the next Figure.

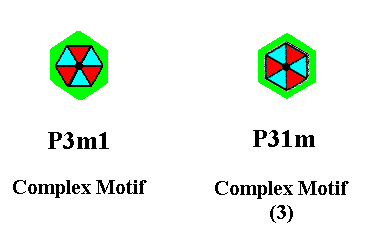
Figure 8. The ultimate Complex Motif of the P31m periodic motif pattern of Figure 2 of the previous document (right) is compared with the ultimate Complex Motif of the P3m1 periodic motif pattern of Figure 1 of Part 8 (left).

Also here (Figure 8) we see that the difference between the Plane Groups P3m1 and P31m consists in a difference of orientation of the motif s.str. with respect to its background. This difference is a 30⁰ rotation.
The next Figure shows the symmetry of the P31m Complex Motif (Figure 7).

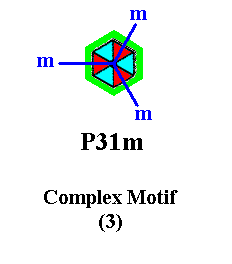
Figure 9. The ultimate Complex Motif of the P31m periodic motif pattern and also the P31m Complex Motifs as found earlier in Figure 14 of the previous Part have a 3m symmetry (point symmetry) : Three mirror lines at angles of 120⁰, and a 3-fold rotation axis.

While different P31m periodic patterns can have different Complex Motifs, the symmetry of the P31m Complex Motif is always 3m. The simplest planimetric figure expressing this symmetry is the Equilateral Triangle, which is accordingly the promorph or planimetric basic form of all the 2-D crystals belonging to the Plane Group P31m and with it to the Crystal Class 3m. See next Figure.

Figure 10. The promorph or planimetric basic form of all crystals of the Plane Group P31m, and with it of the Class 3m (Indeed, also of the Plane Group P3m1, implying the same Crystal Class, 3m, the promorph was found to be the Equilateral Triangle).

As we did with respect to the Plane Group P3m1, we will discuss a 2-D periodic pattern that can stand for two-dimensional i o n i c c r y s t a l s, and whose total symmetry and its distribution seems to be that of the present Plane Group, P31m.
The pattern is the same as that of Figure 6 in Part 10, but it is rotated by 30⁰, as the next Figure shows.

Figure 11. A periodic pattern representing the structure of a two-dimensional ionic crystal. The two ionic species are indicated by red and grey.

The repetitional aspect of the pattern of Figure 11 can be described by a hexagonal net (point lattice) :

Figure 12. The periodic pattern of Figure 11, representing the structure of a two-dimensional ionic crystal, can be based on a hexagonal net with a rhomb-shaped unit cell. Such a unit cell contains two whole atoms (ions), one of each sort.

As we saw earlier, such a pattern exhibits several possible faces, corresponding with different atomic aspects presented to the nutrient environment :

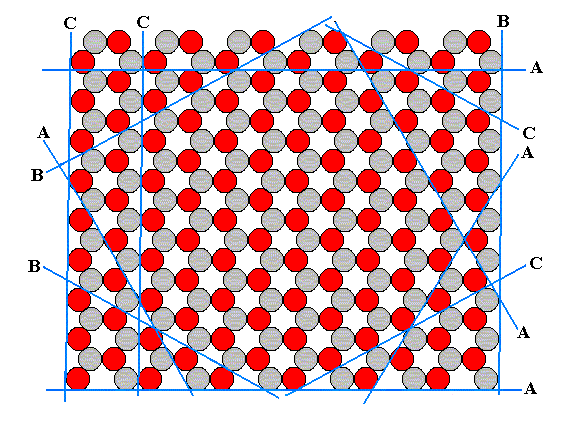
Figure 13. The periodic pattern of Figure 11 has several potential crystal faces corresponding with different atomic aspects presented to the environment.

In Part 10 we explained how crystals can be formed from such faces.
The next Figure gives a magnification of the ionic pattern of Figure 11. The pattern consists of two types of discs (atoms, ions), here indicated by red and blue.

Figure 14. The periodic pattern of Figure 11 magnified. The two ions, negative and positive, are indicated by colors, here red and blue.

In Figure 12 we showed a net, indicating the repeat of a unit. This unit consists of two whole atoms, and its shape is a rhombus. This shape has not all the symmetry that a crystal having this stucture has in store, namely 3m. The next Figure suggests a larger, and, especially, more symmetric repeat unit, consisting of six whole atoms (ions) three of each of the two sorts.

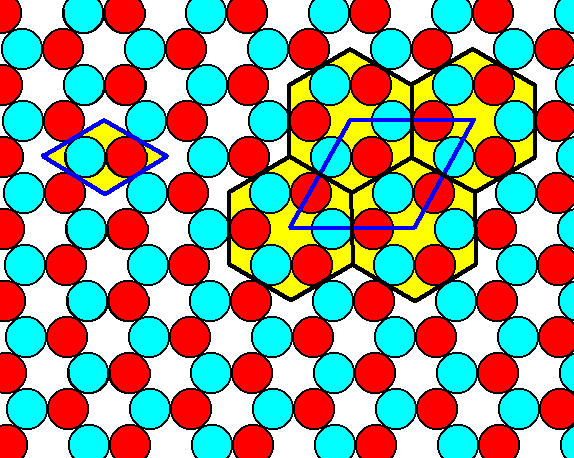
Figure 15. The periodic pattern of 'ions' also allows for a larger more symmetric repeat unit, consisting of six atoms (three of each sort). The symmetry of this repeat unit fully complies with the point symmetry of any crystal having this structure. The unit cell choice as in Figure 12 is also indicated here (left in the image).

The hexagonal repeat units of the previous Figure repeat according to the net indicated (dark blue in the Figure). Compare this Figure with Figure 2 of the previous document. This comparison shows that when the motifs s.str. extend till they meet, we can still repeat these motifs according to the net indicated in that Figure 2, but some points, which are in fact equivalent, like the centers of the hexagons in the above Figure being equivalent to the meeting points of those hexagons, are not (considered to be) equivalent anymore (only the points at the corners of the rhombus are equivalent). Nevertheless the hexagonal repeat unit is a good candidate for turning out to represent the Complex Motif of our present periodic pattern.
But first we must investigate whether our ionic pattern related to the proper net (in which all points that initially were equivalent remain equivalent), indeed belongs to the Plane Group P31m.
First we give again the symmetry diagram for the Plane Group P31m.

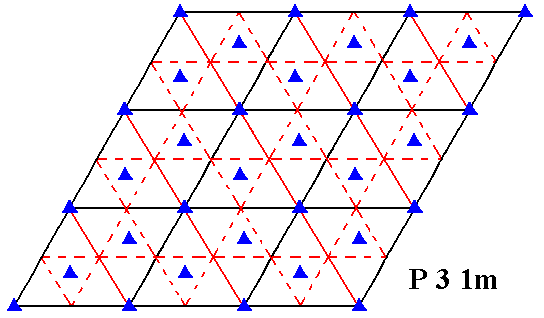
Figure 16. Symmetry content of 2-D patterns according to the Plane Group P31m. Glide lines are indicated by dashed lines. Mirror lines are indicated by red and by black solid lines, while the 3-fold rotation axes are indicated by small triangles.

The next Figure shows that the 3-fold rotation axes, as given (and demanded) by the symmetry diagram, are indeed present in our ionic structure. The positions of the 3-fold rotation axes, however, do not discriminate between the Plane Groups P3m1 and P31m, because they are the same in both Groups.

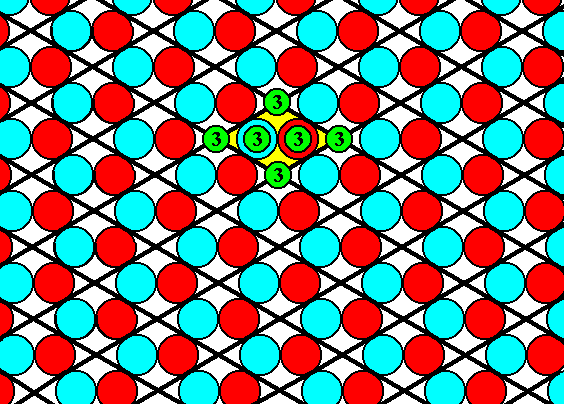
Figure 17. The ionic pattern of discs, as given in the Figures 11 and 14, indeed possesses the 3-fold rotation axes as demanded by the symmetry diagram.

But the mirror lines, as given in the symmetry diagram, are NOT present :

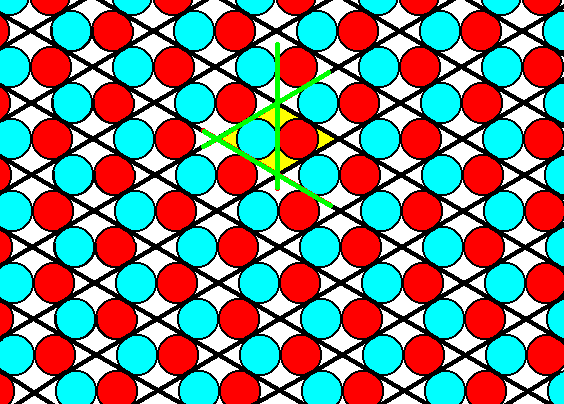
Figure 18. The ionic pattern of discs, as given in the Figures 11 and 14, does NOT possess the mirror lines as demanded by the symmetry diagram.

In fact the pattern turns out NOT to be according to the Plane Group P31m, but to the Plane Group P3m1. Let's demonstrate that.
We first give the symmetry diagram for the Plane Group P3m1.

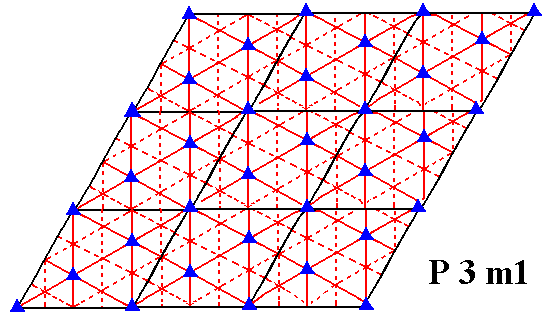
Figure 19. Symmetry content of the Plane Group P3m1. Glide lines are indicated by dashed lines. Mirror lines are indicated by red solid lines, and the 3-fold rotation axes by small triangles.

First we already know that the positions of the 3-fold rotation axes comply with the symmetry diagram for P3m1 (as they do also with respect to p31m).
Next we check the position of existing mirror lines :

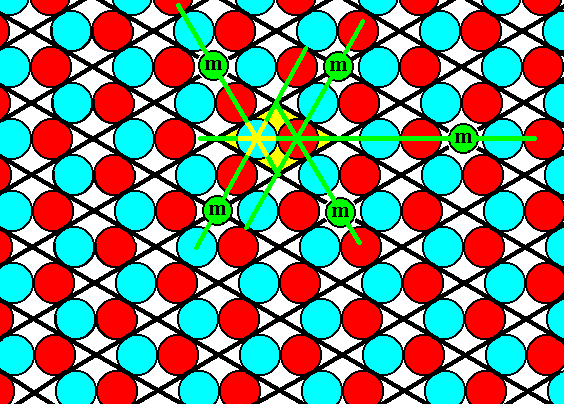
Figure 20. The pattern indeed has the mirror lines where they should be according to the symmetry diagram for P3m1.

The next Figures show that all the glide lines indicated in the symmetry diagram for P3m1 are present.

Figure 21. Glide lines (one indicated) complying with the symmetry diagram for the Plane Group P3m1.

Figure 22. Glide lines (one indicated) complying with the symmetry diagram for the Plane Group P3m1.

Figure 23. Glide lines (one indicated) complying with the symmetry diagram for the Plane Group P3m1.

Figure 24. Glide lines (one indicated) complying with the symmetry diagram for the Plane Group P3m1.

We have now demonstrated that the pattern of Figure 11 and Figure 14 must be described with the Plane Group P3m1.
The next Figure shows what the motifs (the total motifs) really are. Each of them is associated with a lattice point.

Figure 25. Indication of the total motifs, and how they are associated with each lattice point.

If we now look to Figure 15 we see that the unit cell at the right of the image complies with the symmetry diagram for the Plane Group P31m, but the points in the centers of the hexagons are equivalent to the junction points of the hexagons. And this means that inside the rhomb-shaped unit cell (at the right side of the image) there are lattice nodes (because the nodes should represent all equivalent points in the pattern). This indicates that our ionic pattern does not belong to the Plane Group P31m (but to P3m1) as was observed earlier. The Figure (Figure 15), however, suggests a way of transforming the pattern into a true P31m pattern. We can do this by insisting that the two sets of points mentioned are not equivalent, and then indeed we have a pattern that fully complies with the Plane Group P31m. But of course we then have changed our initial pattern into a different one, not representing the ionic structure consisting of two oppositely charged ions anymore. Both patterns, however (the initial ionic pattern, and the transformed pattern) possess the same total symmetry content (KLEIN, C. & HURLBUT, C., 1999, Manual of Mineralogy, p. 122) , expressed by the symbols of their Plane Groups, P3m1 and P31m.
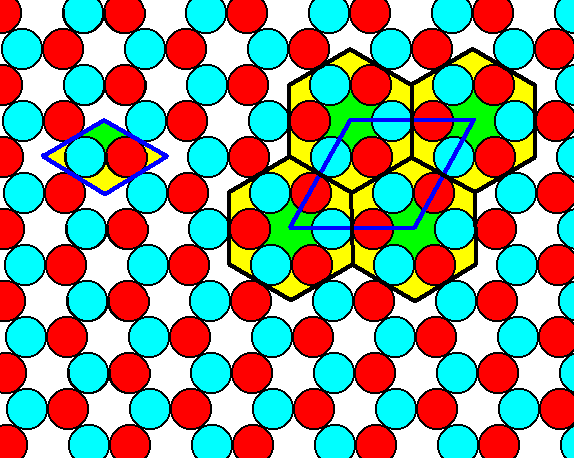
The change can be brought about by distinguishing between the center part of a hexagonal motif (as depicted in Figure 15) and the pieces of background at the periphery of such a hexagonal motif. Indeed if we do that we get a periodic pattern complying with Plane Group P31m. See next Figure.

Figure 26. By qualitatively changing the hexagonal total motifs associated with the corners of the rhomb-shaped unit cell at the right of the image, we transform the P3m1 pattern into a P31m pattern. The result is a new and different pattern but with the same total symmetry content. The qualitative change of the motifs is indicated by the green color of the center of the hexagonal repeat unit (The coloration is done only for a few such units. Of course it must be imagined to have been done for all those hexagonal repeat units).

The adapted pattern will now look like this :

Figure 27. By accomplishing the above described qualitative change of the hexagonal total motifs we obtain a pattern according to the Plane Group P31m.

The next Figure gives this same pattern now furnished with the appropriate net (point lattice). The pattern consists of three qualitatively different elements, red discs, blue discs and green 'stars'.

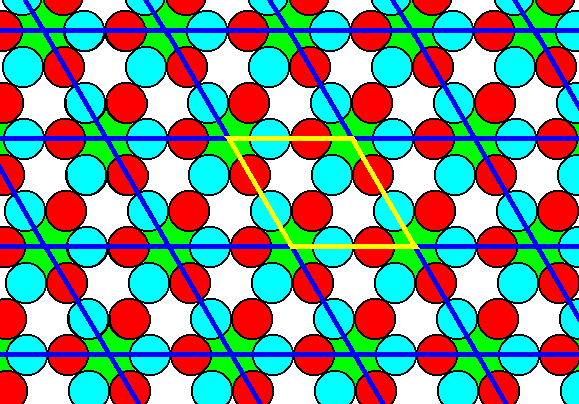
Figure 28. The P31m pattern of Figure 27 furnished with its appropriate hexagonal point lattice. A unit cell is indicated.

In the next document we will demonstrate that the pattern of Figure 28 indeed belongs to the Plane Group P31m.

e-mail : lovelace@hetnet.nl

To continue click HERE to further investigate the Plane Group P31m.

e-mail :

back to homepage

back to retrospect and continuation page

back to Internal Structure of 3-D Crystals

back to The Shapes of 3-D Crystals

back to The Thermodynamics of Crystals

back to Tectology

back to Introduction to Promorphology

back to Anaxonia, Homaxonia, Polyaxonia

back to Protaxonia : Monaxonia

back to Stauraxonia homopola