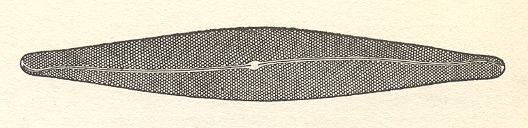
The Diatomeans (Diatoms, Bacillariales) are a group of vegetable unicells of great diversity of shape. They also exist as linear or fan-shaped colonies (of the tectological order of an organ). They are notable for the possession of two silicified walls (frustules) inside the external cell membrane : one of these frustules (epitheca) overlaps the other (hypotheca) like the lid of a box or tin. The cell looks very different according to whether it is viewed from above or below -- the valve-view -- or from the sides -- the girdle-view. Between the valve and girdle intercalary bands sometimes occur. In some species these bear septa projecting into the cell. The siliceous wall, especially in valve-view, is seen to bear extremely fine and complicated structures, often arranged in rows. These may consist of minute chambers, either open or closed above or below. If closed they are perforated by minute pores.
Frequently a groove or 'raphe' runs along the line of symmetry of the valve. The fine structure of this varies greatly in different genera. It is supposed that the extrusion of cytoplasm through the raphe causes the characteristic gliding motion which is peculiar to the Pennatae (A subgroup of the diatoms). [Strasburger's Textbook of Botany, New English Edition, 1976]
The next Figures schematize the global morphology of Diatoms.

Figure 1. Every Diatom shell consists of two main parts, a 'box' (hypotheca) and its 'lid' (epitheca). These two parts generally are very much alike, they only differ a little in size.
In the literature on Diatoms the body axes of a diatomean cell have special names. We will present those given by HUSTEDT, 1956. We will use them to identify the corresponding promorphological axes. The next Figure depicts these axes. The cell is simplified such as consisting of two equal halves on top of each other. These halves represent the epitheca and hypotheca with their respective sides (considered to be identical) coinciding. The top part of the epitheca is the upper v a l v e, while the bottom part of the hypotheca is the bottom v a l v e. So the axis connecting top valve and bottom valve (the pervalvarous axis) is vertical in the Figure.
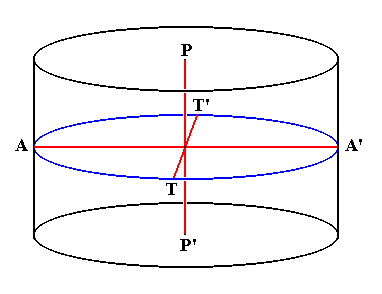
Figure 2. Axes within the diatomean cell. The outline of this cell should here be imagined to be elliptical (not circular).
P-P' (running from top valve to bottom valve): Pervalvarous Axis.
A-A' (representing the longer diameter of the cell) : Apical Axis.
T-T' (representing the shorter diameter of the cell) : Transapical Axis.
A diatom, when present singly (often they form loose colonies), is a single c e l l with a nucleus. The next Figure is a diagram of the inner parts of such a cell.
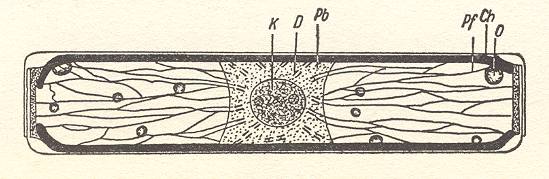
Figure 3. Cell interior of Pinnularia.
K, Nucleus, D, double bars, Pb, Plasma bridge, Pf, Plasma threads, O, Oil drop, Ch, Edges of the chromatophore plate, lying along the girdle side, but which is here omitted, in order to allow a view into the cell interior.
( After HUSTEDT, F., 1956, Kieselalgen (Diatomeen))
The Diatoms divide into two groups :
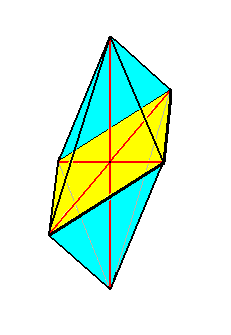
Figure 4. The eight-sided amphitect bipyramid (Rhombic Octahedron). The equatorial plane is emphasized (yellow). The ideal cross axes (Euthini) are contained in the equatorial plane. The total symmetry content is : three mirror planes perpendicular to each other, and three 2-fold rotation axes (coinciding with cross axes and main axis) each perpendicular to one of the just mentioned mirror planes. This symmetry content is symbolized by 2/m 2/m 2/m, where " 2 " stands for a 2-fold rotation axis, and " m " stands for a mirror plane.
The Allostaura octopleura are Allostaura (amphitect bipyramids) in which the radial cross axes intersect at right angles.
In crystals the Rhombic Octahedron is the basic form of the Orthorhombic Crystal System : The two radial cross axes together with the main axis form an orthorhombic crystallographic axial system, and this means that the three axes are different, but none of them stands out as a main axis.
So the Rhombic Octahedron is the point of departure when it comes to promorphologically assess a pennate diatom.
(The symmetry of) this Rhombic Octahedron, as the basic form of the Allostaura octopleura, we find materialized pretty accurate in Navicula and others. See the next Figure.

The Rhombic Octahedron indeed forms the general promorphological background form of the pennate diatoms.
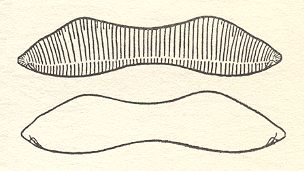
Figure 6. Eunotia didyma.
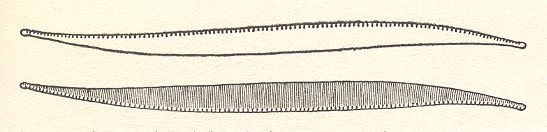
The two valves of the shell. Valve form and position of raphes of the hypotheca (lower image) are the mirror image of the epitheca (upper image).
( After HUSTEDT, F., 1956, Kieselalgen (Diatomeen))
In the following we will discuss the above mentioned diatom (Eunotia) and some other diatoms in orther to expound the symmetries that prevail in them and how to assess them promorphologically. When a diatom is viewed in valve view through a microscope we see the outer side of the top valve, when the microscope is adjusted 'high', while we see the inner side of the bottom valve when the microscope is adjusted 'low'. Both valves of each species under scrutinity are considered to be exactly equal, i.e. their s h a p e is considered equal. While having this identical shape, they could however differ in their respective sculptures and in the position and structure of the r a p h e.
That valve that (at that moment of observation) lies a b o v e, i.e. towards the observer, is called A.
That valve that (at that moment of observation) lies u n d e r, i.e. away from the observer, is called B. See next Figure.
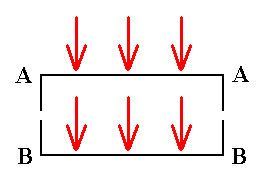
Figure 7. Direction of observation of a diatom in valve view.
Turned-towards-viewer face is called A.
Turned-away-from-viewer face is called B.
Also when the object is flipped, i.e. also when the two valves swap their position, the turned-towards-viewer face will be denoted by A, while the turned-away-from-viewer face will be denoted by B. So sometimes the epitheca will be associated with the symbol A, sometimes the hypotheca.
During the consideration of the w h o l e cell, i.e. both valves (or both epitheca and hypotheca for that matter), applies :
Of A we always see only the o u t e r side.
Of B we always see only the i n n e r side.
We can never see the inner side of A (Recall that A is not a particular valve, A refers to the position with respect to the observer). This is so because when we flip the cell upside down (i.e. the set comprising its two valves), then A becomes B and vice versa.
When, on the other hand, we consider o n e s i n g l e valve, then we can also always see the inner side of the valve after having it flipped upside down, i.e. we can see its outer and inner side. So we must discriminate between a consideration of one valve only and of the cell's two valves at the same time.
After having set all this we can now proceed with more detailed symmetry considerations.
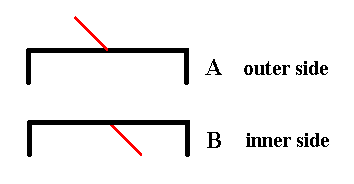
Figure 8. The two valves of Eunotia didyma (in valve view) as far as their symmetry is concerned. Each valve has as its only symmetry element a mirror plane perpendicular to the plane of the drawing (and as such it is symbolized by the hooked black line, i.e. the form of this line expresses the symmetry of the valve.
The appended short red line symbolizes the third spatial dimension, i.e. features of the valve situated along that dimension (the three spatial dimensions are perpendicular to each other). It also symbolizes the outer side or inner side of the valve. If the red line is directed upwards, as seen in the drawing, then we have to do with the outer side of the given valve, if, on the other hand, it is directed downwards, as seen in the drawing, then we have to do with the inner side of the given valve.
The red line being directed upwards as seen in the drawing, in fact is supposed to point right to the observer, while the red line being directed downwards as seen in the drawing, in fact is supposed to point right away from the observer. In both cases it is supposed to be p e r p e n d i c u l a r to the plane of the drawing.
When we want to assess the symmetric relationship between the valves we must compare outer side with outer side, or inner side with inner side.
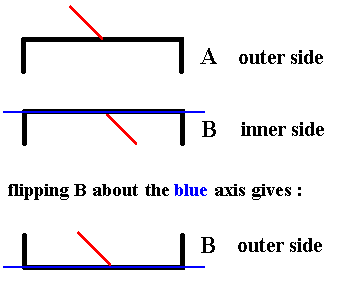
Figure 9. In order to be able to compare an outer side with an outer side (or an inner side with an inner side) we flip B about the axis indicated, which means that we rotate B about that axis by 1800. The outer side of it will now become visible Indicated by the red line being directed 'upwards'. So the result is : the outer side of B.
When we now compare the outer side of A with the outer side of B we see that they are related by mirror symmetry :
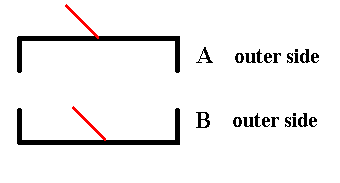
Figure 10. The outer side of A and the outer side of B are symmetric with respect to each other.
The red lines are supposed to stand perpendicular to the plane of the drawing (Recall that they represent the third spatial dimension). Here they both point right to the observer.
In order to explicitly show that the two valves (as they are with respect to their outer side) are symmetrically related to each other, we show that when one of them is mirrored the result will be such that it is identical to the other valve, i.e. we have complete covering, or in other words the valves will be mapped onto each other by subjecting each of them to mirror symmetry.
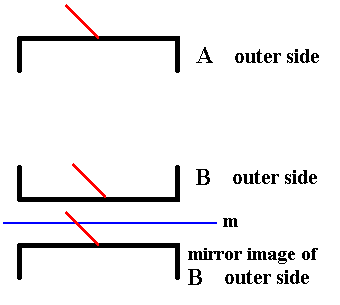
Figure 11. The outer side of A and the outer side of B are symmetric with respect to each other.
The red lines are supposed to stand perpendicular to the plane of the drawing (Recall that they represent the third spatial dimension). Here they both point right to the observer.
In order to show this symmetry we create a mirror image of one of the valves (here B) and indeed see that the result is exactly identical (i.e. congruent ) to the other other valve (A). The mirror operation does not swap inner side with outer side (indicated by the red line).
When we do the same with valve A, then we will get a same result :
The mirror image of A will be completely identical (congruent) to B.
As we can see from Figure 6 and from Figure 10, the mirror plane situated between the valves, is not the only mirror plane : another one runs across the valves as the next Figure illustrates.
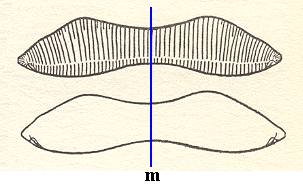
Figure 12. Eunotia didyma.
The two valves of the shell. Valve form and position of raphes of the hypotheca (lower image) are the mirror image of the epitheca (upper image). There is yet another mirror plane as indicated by the red line (the plane is normal to the plane of the drawing, and normal to the other mirror plane.).
A third symmetry element is now implied by these two mirror planes, namely a 2-fold rotation axis coinciding with the line of intersection of the two mirror planes. Consequently the stereometric body representing these symmetries is a single amphitect pyramid with two antimers, a Rhombic Pyramid, the basic form of the (Autopola) Orthostaura diphragma.
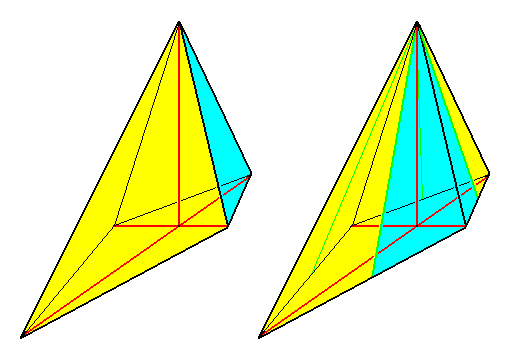
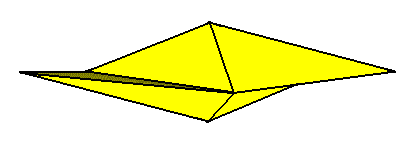
Figure 13. Perspectivic view of a Rhombic pyramid.
Left image : Rhombic pyramid with t w o antimers, representing the basic form of the D i p h r a g m a.
Right image : Rhombic pyramid with four antimers (basic form of the Tetraphragma).
The left image of the above Figure symbolizes promorphologically the cell (with its two valves) of Eunotia didyma. One valve (i.e. its promorphological symbol) is colored blue, the other yellow.
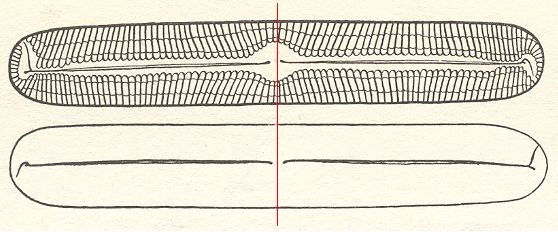
Figure 14. Pinnularia flamma.
The two valves of the shell. The course of the raphe is opposite on both valves. The valves as drawn must be imagined to be superimposed upon each other. The 2-fold rotation axis is indicated by a thin red line, and should be imagined to run between the valves. It is the only symmetry element of the cell.
( After HUSTEDT, F., 1956, Kieselalgen (Diatomeen))
The diatom Pinnularia flamma as depicted above possesses -- when all details, especially those of the raphe, are taken into account -- only one symmetry element, namely a two-fold rotation axis, running between the valves along their short diameter (This rotation axis is indicated as a red line in the above Figure). The symmetry can be symbolized by the following diagram representing the girdle-view of the cell, i.e. we now look along the direction of the 2-fold rotation axis.
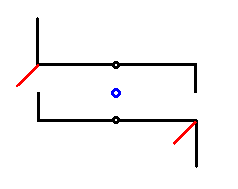
Figure 15. Symmetry diagram of Pinnularia flamma. Girdle-view. The two valves of the shell are symbolized by the two hooked lines, one above the other. The 2-fold rotation axis is indicated by a small blue circle in the center of the image, and should be imagined to run between the valves. It is the only symmetry element of the cell. The short red lines project into the third dimension (normal to the plane of the drawing). They represent features of the raphe, and at the same time show that the whole structure does not contain a center of symmetry (See next Figure).
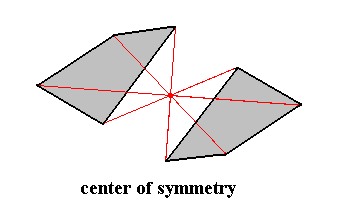
Figure 16. Center of Symmetry.
The item possessing a center of symmetry (and only a center of symmetry) consists of two asymmetric faces related to each other by a center of symmetry, which means that every point of such a face is reflected in a same point, the center of symmetry (indicated by the red lines and their point of intersection. Every part of the item can also be found at the opposite side of that point at the same distance.
The symmetry diagram of Pinnularia flamma, as depicted in Figure 15 can now be further compressed, resulting in the following :
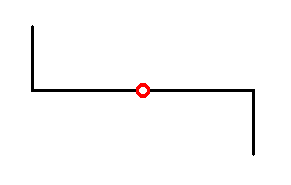
Figure 17. Compressed symmetry diagram of Pinnularia flamma. Girdle-view. The 2-fold rotation axis is normal to the plane of the drawing, and is indicated by the small red circle.
We shall now elaborate further on the symmetry content of a cell of Pinnularia flamma, making sure that we do not confuse inner and outer sides of the valves. The next Figure is a diagram, expressing the symmetry of the valves as they are depicted in Figure 14.
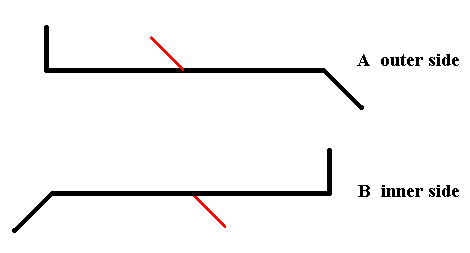
Figure 18. Diagram symbolizing the symmetry of Pinnularia flamma as depicted in Figure 14.
We will now flip B in order to see its outer side. See next Figure.
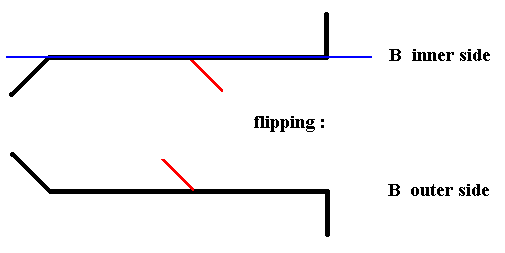
Figure 19. Diagram symbolizing the flipping of valve B of Pinnularia flamma, about the axis indicated in blue, i.e. rotating it about that axis by 1800, resulting in the outer side of B.
We now have the outer side of A and the outerside of B :
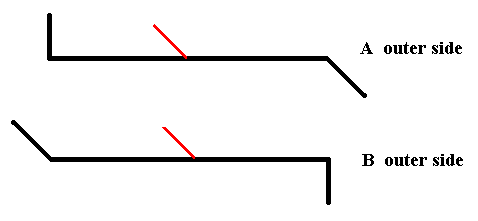
Figure 20. The outer side of A and the outer side of B.
As can be seen from the above Figure the outer side of A is not symmetrically related with the outer side of B. So there is no mirror plane situated between the two valves of Pinnularia flamma.
If we find a symmetry operation that transduces the outer side of A and the inner side of B into each other, i.e. maps them onto each other, then we have found a symmetry element of the whole cell (here represented by its two valves). Let's try to transduce the inner side of B into the outer side of A :
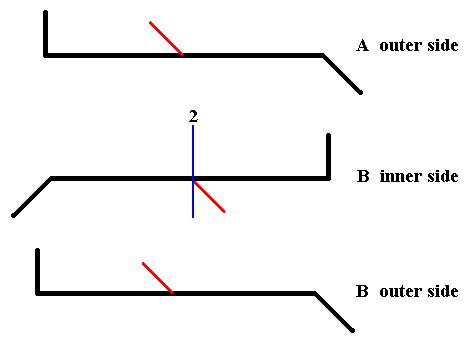
Figure 21. After rotating the inner side of B about the axis indicated in blue by 1800, we get the outer side of B (but with its apices exchanged). And now we see that this outer side of B (but with its apices exchanged) is exactly identical to the outer side of A. And this means that rotation of the inner side of B by 1800 about the axis indicated in blue, results in the outer side of A.
In the above Figure we see that the inner side of B can be transduced into the outer side of A by a rotation about the axis indicated in blue. It is clear that the same applies when we subject the outer side of A to that same rotation : It will be transduced into the inner side of B. And this means that if we subject the whole cell, as represented by its two valves, to a rotation of 1800 about the mentioned axis, then this whole cell will be transduced into itself, i.e. it will be mapped onto itself, and this in turn means that this 2-fold rotation axis is a symmetry element of the whole cell (of Pinnularia flamma) (In all this we did not consider the girdle bands, but these do not limit the cell's symmetry).
We will now subject the whole cell (represented by its two silicified valves) to a rotation by 1800 about the axis as established above (i.e. as in Figure 20). The cell should be mapped onto itself. We'll start with a symmetry diagram of the the cell (its two valves) as was given earlier and which corresponds to Figure 14, and then subject this whole to the operation mentioned.
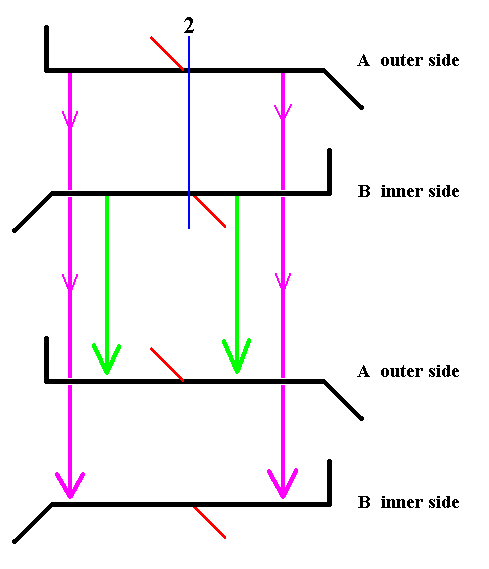
Figure 22. Diagram symbolizing the symmetry of Pinnularia flamma as depicted in Figure 14. The 2-fold axis of rotation is indicated in blue. The whole structure is rotated 1800 about that axis. The valves are transduced as indicated by the arrows. Thereby B becomes A (green arrows), and A becomes B (pink arrows).
If we rotate the whole structure 1800 about the indicated axis which runs between the two valves, then B comes to lie up, and consequently becomes A, and should be depicted as lying above.
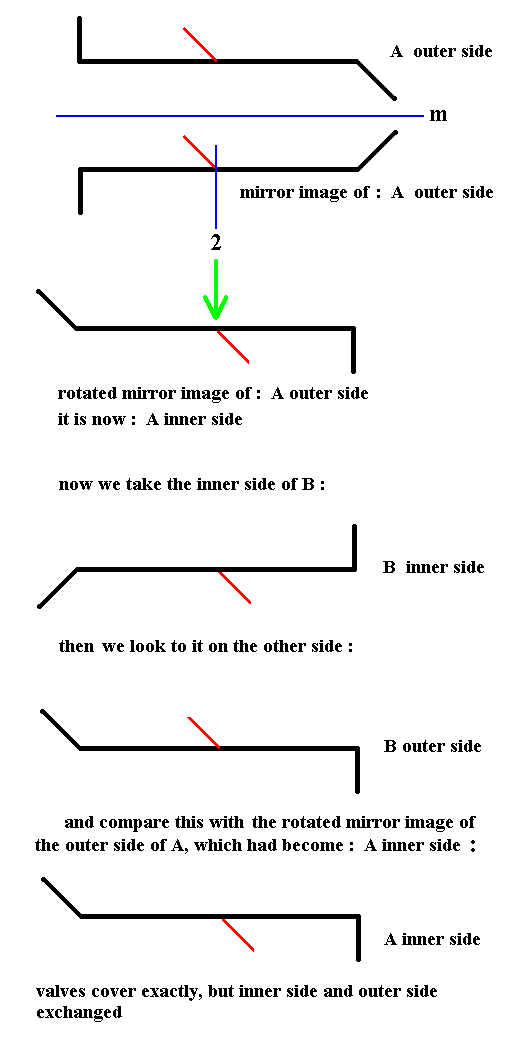
Rotation of the mirror image of one of the valves seems to transduce this valve into the other one, but this is not a genuine covering because inner side and outer side are exchanged, implying that the result of rotation of the mirror image is not identical to the other valve. The next Figure illustrates this.
The Rhombic Octahedron is still further deformed in the Diatom Nitzschia sigma. The latter has a sigmoid shape (Figure 25), but because of the position of the raphe on either valve, its only symmetry element is a center of symmetry. So Nitzschia sigma promorphologically belongs to the Anaxonia centrostigma.
It is perhaps useful to dwell a little longer on the symmetry of Nitzschia sigma (Figure 25).
Also here we will symbolize the symmetry and shape of its two valves, like we did with respect to Pinnularia flamma :
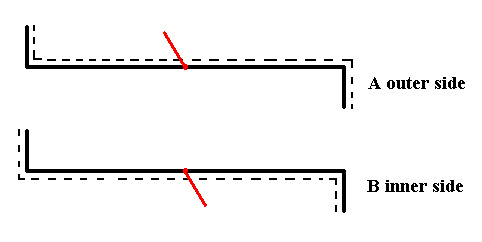
Figure 27. Symmetry scheme of Nitzschia sigma. Upper and lower valve (See Figure 25). The dashed line symbolizes the position of the raphe.
If we take the mirror image of the outer side of A, and rotate it 1800 about an axis perpendicular to the mirror plane (that was involved in the mirroring just mentioned), then the result will be identical to the inner side of B. See the next Figure.
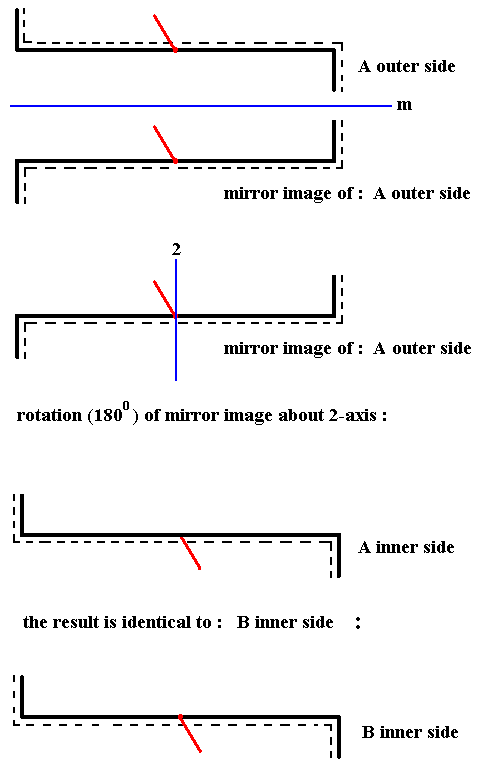
Figure 28. Demonstration of the symmetry of a cell of Nitzschia sigma. Reflection in a mirror plane m followed by a rotation of 1800 about an axis perpendicular to m transduces the outer side of A into the inner side of B, which means that the whole cell has a center of symmetry. There are no other symmetry elements present.
The same will apply to the innerside of A : reflection and rotation (1800) will result in something that is exactly identical to the outer side of B. This means that this reflection + rotation transduces the whole cell (represented by its two valves), as depicted in Figures 25 and 27, into itself. The described operation of reflection + rotation is a symmetry element that is equivalent to a center of symmetry. So the cell of Nitzschia sigma has a center of symmetry. It is obvious (after inspection of the Figures) that there are no other symmetry elements present, so the symmetry of the cell of Nitzschia sigma is equal to that of crystals of the Pinacoidal Class of the Triclinic Crystal System. The promorph is accordingly that of the Anaxonia centrostigma.
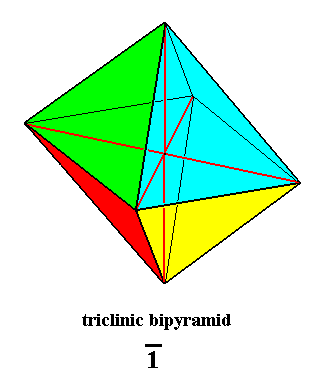
Figure 29. Triclinic Bipyramid, basic form of the Anaxonia centrostigma. Its only symmetry element is a center of symmetry, which is equivalent to a 1-fold rotoinversion axis, or to a combination of reflection and rotation as described above.
The characterization of the basic form of a cell of Nitzschia sigma as a member of the Anaxonia centrostigma needs some additional information about its having a sigmoid shape. If the raphe were situated along the mid-line of the valves, then the basic form would be such as to belong to the Allosigmostaura duamphimera (Stauraxonia homopola sigmostaura). So the basic form of the Allosigmostaura duamphimera, which is an amphitect gyroid bipyramid, is the b a c k g r o u n d f o r m of the cell of Nitzschia sigma, i.e. its Anaxonic centrostigmic basic form is embedded in a form that belongs to the Allosigmostaura.
To v e r i f y the above assessment of the exact symmetry of the shell of Nitzschia sigma, namely that the only symmetry element it possesses is a center of symmetry, we apply this operation to the whole shell (cell). To do this we first reflect this whole shell as it is represented in Figure 27, and rotate the result 1800 about an axis perpendicular to the mirror plane. See next Figure.
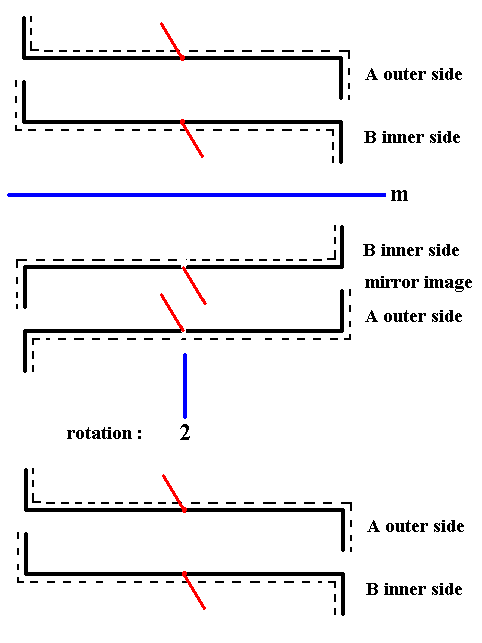
Figure 29a. When we apply the symmetry operation that corresponds to a center of symmetry to the whole shell of Nitzschia sigma as it is diagrammed in Figure 27, we will see that this whole shell will be mapped onto itself, i.e. the result is identical to that with which we began. So the shell as a whole has a center of symmetry.
Clarification of the rotational operation (1800) of the whole shell of Nitzschia sigma.
The rotation by 1800 of the whole shell brings about the fact that the inner side of B, which, also after reflection, lies under, i.e. away from the beholder, will now come to lie UP and consequently becomes A, seen as the outer side of A. See next Figure.
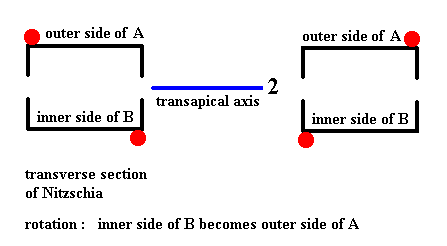
Figure 29b. Clarification of the rotation of the whole shell by 1800 as was done in Figure 29a.
Among the many Diatoms there are some that should be discussed briefly, because of their aberrant promorphology. These are Actinoptychus and Coscinodiscus. They are centric diatoms (Centrales).
The shell of Actinoptychus is clearly triradiate. In the species of Figure 30 this is moreover emphasized by its hexagonal outline (where, accordingly a unit consisting of two 600 sections is repeated three times around the pervalvarous axis). Its girdle view (See Figure above) is however peculiar.
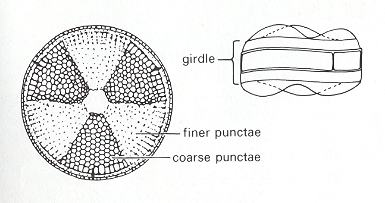
In the next Figure we depict a species of the genus Coscinodiscus.
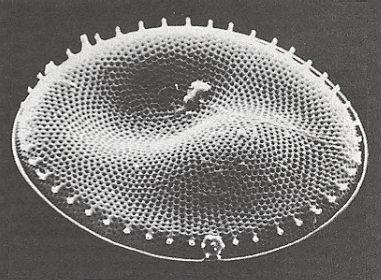
Figure 32. Photograph of the Diatom Coscinodiscus lacustris, valve view, made with the electron microscope of the Geological-Paleontological Institute of the University of Kiel (Germany). Original diameter 0.08 millimetre. This alga lives suspended near the surface of water with various salinity and is frequently found in the Baltic Sea. Photograph : Hans-J. Schrader.
( After JANTSCH, E., (1980) 1987, The Self-organizing Universe )
To judge from the photograph it seems that the shell of Coscinodiscus lacustris has the same basic form features as we just saw in the case of Actinoptychus. Its shell is however not radiate, i.e. it does not have a specific number of definite cross axes. So its stereometric basic form approaches that of a (flat) cylinder ( Monaxonia haplopola ). Of course its wavy valve surfaces are peculiar promorphologically. It reminds us of the Scalenoidea (Stauraxonia homopola), especially when its girdle view turns out to look like that of the Actinoptychus depicted in Figure 31.
To continue click HERE for the Basic Forms of Organs
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)
back to Allopola amphipleura and zygopleura
back to basic forms of cells I