REMARK : When we, in the course of the ensuing discussions, quote a certain promorph (= stereometric basic form or promorphological category), we will set it as a LINK. This link will bring the reader to the relevant place within the Promorphological System, so that he or she can orient him- or herself as to where that category is situated within the System.
The Antimers or counterparts, i.e. third-order form individuals , show, with respect to their stereometric basic form or promorph a very conspicuous contrast with respect to those of first and second order (cells and organs). In contradistinction to the unlimited promorphological diversity of organs and cells, in antimers (and also in paramers) we find only a very limited number of stereometric basic form realized. This state of affairs is immediately caused by the determined relations which always obtain between the third-order form individuals and the fourth-order form individuals, and especially between the third-order form individuals themselves. Because (1) the body of all higher form individuals (fourth- and fifth-order) is composed of two or more antimers, (2) the specific number of antimers (the homotypic basic number), and also their connection, is very constant within a same biological species, and, finally because (3), in virtue of this connection, the basic form of the metamer and person is determined, -- the basic form of the antimer itself must necessarily be a very determined one, i.e. it can only be very uniform (Differently expressed : The range of possible basic forms in antimers is very limited). All antimers that compose a metamer or a person must meet each other in definite planes, and they further must exhibit certain definite common positional relationships with respect to the center, which is their common element. The basic form of the antimers will show definite differences as to when this centrum is a point, a line or a plane. So within the form groups of the Centrostigma, Centraxonia and Centrepipeda we can expect definite promorphological differences in their antimers. Because of the paramount role that antimers play in determining the promorph of fourth- and fifth-order form individuals (and the paramers in first- and second-order form individuals) it is instructive to inspect these three major form groups with respect to the promorph of their antimers.
Centrostigma
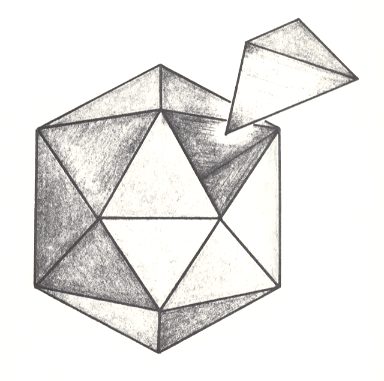
The form group of the C e n t r o s t i g m a, the members of which distinguish themselves by their centrum being a p o i n t, consists of the two departments of the Homaxonia (spheres) and the Polyaxonia (endospheric polyhedra). In addition to these two departments we have the Anaxonia centrostigma in which the center is also a point, namely its center of symmetry, as its only symmetry element. But although the latter do have a definite body center, they do not admit of definite antimers, because the lines we can draw through that center (of symmetry) all connect (via the center of symmetry) equal body parts, and we can draw as many such lines as we wish to. If some of these lines connect certain definite body parts, that are clearly distinguished morphologically from other body parts, then the promorph will automatically not belong to the Anaxonia centrostigma anymore, but either to the Polyaxonia or to the Heteraxonia. Such bodies then still possess a center of symmetry, but not as their only symmetry element (for example all bipyramids (Stauraxonia homopola)). Also the Homaxonia do not possess genuine antimers, because here also we can draw infinitely many lines that could each for themselves represent an antimer (If some such lines connect certain definite body parts different from others, then the promorph will be that of the Polyaxonia). So the only Centrostigma that possess genuine antimers (or paramers) are the P o l y a x o n i a. In these, generally every antimer is a pyramid. In the rhythmic polyhedra (Polyaxonia rhythmica) they are regular pyramids, while in the arrhythmic polyhedra (Polyaxonia arrhythma) they are either regular or irregular pyramids. See next Figure.

In the above Figure we see one of the antimers isolated from a polyhedron. The faces of the polyhedron represent specific body parts, and as such they represent the antimers of the given organic body.
Centraxonia
The form group of the C e n t r a x o n i a, which distinguishes itself by the fact that the center of the body is a l i n e (either the only axis present, or the main axis, length axis), consists of the five divisions of the Monaxonia, the Stauraxonia homopola (bipyramids), the (Stauraxonia) Heteropola homostaura (regular single pyramids), the Heterostaura autopola (i.e. amphitect single pyramids, also belonging to the Stauraxonia heteropola) and the (Stauraxonia) Heteropola gyrostaura (pyramidal bodies with at least one sigmoid cross axis). Of these only the last four are relevant, because in the Monaxonia, which do not posses genuine cross axes, but only a main axis), we cannot distinguish antimers.
The promorph of the homopolar stauraxonians is the bipyramid. So all these forms are composed of two congruent pyramids. These constituent pyramids could be thought of as two m e t a m e r s, but one can dispute whether such an interpretation is fully correct : The two pyramids have opposite orientations with respect to each other, which one should not expect of metamers. The orientation of the latter is normally the same, i.e. they all point in the same direction. If we do not accept that the two single pyramids necessarily represent two metamers, and consider the bipyramid as a whole, then an antimer must be conceived as the next Figure indicates :
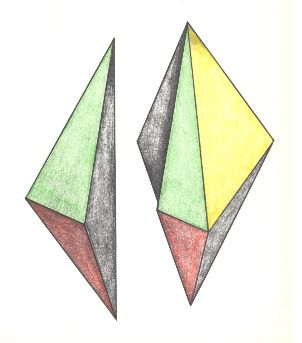
To describe antimers of bipyramidal forms (Stauraxonia homopola), however, it is more convenient to consider the constituent single pyramids apart, which boils down to consider just one constituent single pyramid, and determine its antimers.
IN ALL THIS WE MUST REALIZE THAT WE CONSIDER THE ANTIMERS AS THEY ARE PRESENT IN THE GIVEN ORGANIC INDIVIDUAL, AND NOT AS WE FIND THEM IN THE STEREOMETRIC REPRESENTATION OF THE PROMORPH OF THAT ORGANIC INDIVIDUAL.
So according to the convenience just mentioned we will consider that part of the given organic, and promorphologically bipyramidal individual that promorphologically corresponds to one of the two single bipyramids, and consider the antimers of such a single pyramid. Such a pyramid consists of at least three antimers. These must be themselves also pyramids, and they must moreover be three-fold pyramids (This is because each antimer of every bipyramidal organic form, but also of just a pyramidal form -- think of starfishes -- as it is in its organic reality, has a bilateral form -- as it turns out in organisms -- such that its basic form is that of a three-fold pyramid, regular or irregular). In the Isostaura (regular bipyramids) the promorph of every antimer is an isosceles pyramid (Half a rhombic pyramid), while in the Allostaura (amphitect bipyramids) they are either an isosceles or unequally sided three-fold pyramid.
The next Figure shows an antimer from one of the pyramids constituting the bipyramid, as it is obtained from the promorph of the whole. As such this antimer is a four-fold pyramid (instead of a three-fold pyramid). The organic part that such an 'antimer' represents is, however such that its promorph is a three-fold pyramid. As in bipyramids (Stauraxonia homopola), this also applies to pyramids (Stauraxonia heteropola).
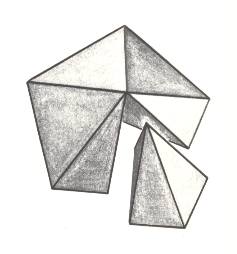
Figure 3. Slightly oblique top view of a five-fold regular pyramid. One antimer is taken out. It is, as such, a four-fold pyramid.
In the homostauric heteropoles ((Stauraxonia) heteropola homostaura), of which the basic form is the single regular pyramid (materialized by all regular radiate animals and flowers), every antimer must promorphologically be represented by an isosceles pyramid (half a rhombic pyramid). Finally, in the autopolar heterostaurs ((Heteropola) heterostaura autopola), the highest form group of the Centraxonia, of which the basic form is the single amphitect pyramid, materialized for instance in Ctenophores and Madrepores (Madreporaria, Corals), the promorph of every antimer must either be an isosceles pyramid (for instance both lateral antimers of the madrepores, right and left one), or an unequally sided three-fold pyramid (for instance both dorsal and both ventral antimers of madrepores). See next Figure.
( After HAECKEL, 1866, Generelle Morphologie der Organismen, Fig. 2 from Tafel I. )
In the above Figure we can see that each of the Madrepora's two lateral antimers (right and left), as it is organically materialized, has as its only symmetry element a mirror plane. It clearly has an axis that lends itself to be interpreted as a heteropolar (main) axis (of the antimer). Well, the simplest geometric body that directly displays this symmetry content is the isosceles three-fold single pyramid, i.e. half a rhombic pyramid. Each of the dorsal or ventral antimers of the Madrepora is easily assessible promorphologically, when we compare it with the lateral antimers. The promorph of a dorsal or ventral antimer is accordingly an unequally sided three-fold pyramid. The latter can be represented by a quarter of a rhombic pyramid.
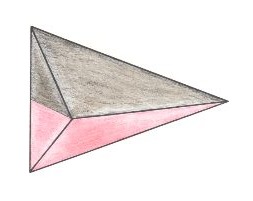
Figure 5. Half a rhombic pyramid, the promorph of (for instance) a lateral antimer of the Madrepora of the above Figure. This pyramid has only one mirror plane which separates its two halves (indicated by coloration). The pyramidal main axis points obliquely to the beholder, its symmetrical sides are indicated by the coloring mentioned.
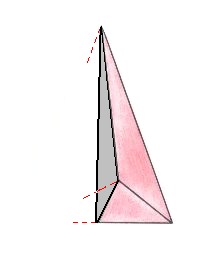
Figure 6. A quarter of a rhombic pyramid, the promorph of (for instance) a dorsal antimer of the Madrepora of the above Figure 4. This pyramid has no symmetry elements, but is clearly derived from half a rhombic pyramid. The pyramidal main axis points obliquely to the beholder. It is an unequally sided three-fold pyramid.
In the centraxonians we also have the Sigmostaura ((Stauraxonia) Homopola sigmostaura) in which one or more cross axes have a sigmoid form. Their antimers (as considered in the constituent pyramids, and also as they are organically materialized) are consequently dysdipleural ( (Zygopleura) Dipleura dysdipleura ) with respect to their promorph (which consequently is an unequally sided three-fold pyramid). See next Figure.
Figure 6a. Diagram of a sigmoid form with two equal antimers. One antimer is emphasized. Its stereometric basic form is clearly that of the Dysdipleura.
Exactly the same situation we find in the (Stauraxonia) Heteropola gyrostaura. Also there an antimer promorphologically belongs to the Dysdipleura.
So in all Centraxonians, without exception, the general promorph of their antimers (and also of the paramers) is the three-fold pyramid, either half a rhombic pyramid (Eudipleural form), or the unequally sided three-fold pyramid (Dysdipleural form).
Centrepipeda
The form group of the C e n t r e p i p e d a or Z e u g i t a, i.e. the allopolar heterostaurs ((Heteropola) heterostaura allopola), which distinguish themselves by their center being a p l a n e (The median plane or sagittal plane), consists of the two divisions of the Amphipleura and the Zygopleura. In the Amphipleura the body consists of three, five or more, in the Zygopleura of two or four antimers. In the Amphipleura the basic form of every antimer is either an isosceles pyramid (half a rhombic pyramid), for instance the ventral antimer of the pentamphipleural echinoderms (this is the unpaired antimer), or an unequally sided three-fold pyramid, for instance the paired antimers of the pentamphipleural echinoderms. In the Zygopleura the antimers are almost always unequally sided three-fold pyramids. The only exception is the dorsal and ventral antimer in the Eutetrapleura radialia, for example in the flowers of Reseda (next Figure), where the promorph of these antimers is an isosceles pyramid.

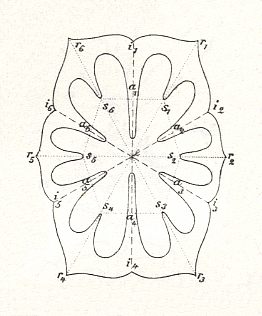
Figure 7. Eutetrapleura radialia.
The basic form of the Eutetrapleura radialia illustrated by the morphological scheme of a Reseda flower. In the median plane (r1 r3) lies the ventral petal (small and two-split) and opposite to it the dorsal petal (big and six-split). In the lateral plane (r2 r4) on the other hand lie the two symmetrically equal three-split lateral petals, the right one and left one. In the two interradial cross planes (i1 i3 and i2 i4) lie the four calyx leaves and the four leaves associated with the female genitals. The interradial cross planes separate the four antimers.
( After HAECKEL, 1866, Generelle Morphologie, Table I, fig. 11 )
In the eudipleural promorph, the most important of all promorphs, each of the symmetrically similar body halves (i.e. the two antimers) possesses the dysdipleural promorph.
With all this we accordingly obtain the important promorphological rule, that the general stereometric basic form of all antimers, without exception (and also all paramers), is the s i n g l e p y r a m i d, thereby it is in most cases the three-fold (Dipleural form, i.e. eudipleural or dysdipleural), seldom (only in some Centrostigma) the many-fold pyramid. Normally the three-fold pyramid is unequally sided (dysdipleural form), less often isosceles (eudipleural form). In the first case the base of the pyramid is an unequally sided triangle, in the second case it is an isosceles triangle.
So a p a r a m e r or a n t i m e r can n e v e r possess promorphs belonging to the following categories :
To continue click HERE for the Basic Forms of Metamers
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)
back to Allopola amphipleura and zygopleura
back to the Basic Forms of Cells I
back to the Basic Forms of Cells II
back to the Basic Forms of Organs