Against the small group of Polyaxonia there is the other, uncomparable more diverse and important order of the Heteraxonia, namely the large and rich group called Protaxonia. They show a differentiation of a single, in one or another way outstanding, axis, the m a i n a x i s, and this feature distinguishes them clearly from the Polyaxonia. All Polyaxonia, despite in whatever the faces of the polyhedron may differ in number and shape, agree in their polyhedron being endospheric, implying that all corners hit a single shpere (i.e. they all lie on the surface of a single sphere). They also agree in the fact that the center of that sphere is at the same time the center of the polyhedron. And in virtue of all this, all main axes, of which at least three must be present, have the same length. By reason of the latter, and by reason of the fact that their center is a point, the Polyaxonia are closest to the Homaxonia.
In the Protaxonia, on the other hand, the basic form can never be an endospheric polyhedron or sphere. When the basic form of the Protaxonia is a regular or irregular polyhedron, its corners never lie on the surface of a sphere. When the basic form is bounded by a curved surface, the latter is never a complete sphere, but only a part of a sphere (shperical segment, hemisphere, or a spheroid (ellipsoid, lens), or an egg, etc.
In all Protaxonia the body center is not a point anymore, but a line, or (in the Heterostaura allopola) a surface (normally a plane). This line or plane is totally different from all other lines or planes that we could draw through the body. All parts of the body are in a special and characteristic way related to this central line or plane, and all bisection planes of the body must go through that median line or plane.
In the Protaxonia with a median line (Centraxonia) several, at least two, bisection planes of the body are present. In the Protaxonia with a median plane (Centrepipeda or Heterostaura allopola) only one bisection plane is present, and the latter is identical to the median plane.
The main axis ( A x o n p r i n c i p a l i s ), which characterizes the Protaxonia as such, and which distinguishes them from all other previously discussed basic forms, is in the Centraxonia identical to the median line, while in the Centrepipeda it lies in the median plane. Although it is not easy to further characterize the main axis for all Protaxonia in general, because it has very different properties in its different subgroups, it is in all individual cases always possible, and in most of them very easy, to indicate it unequivocally. Where only one body axis at all is present, as in the Monaxonia, it is at the same time the main axis. Where the body consists of more than two congruent antimers, like in all Stauraxonia homopola and in the Heteropola homostaura, the main axis is always that line that is commonly possessed by all antimers, and in which they come together. Where it is possible to indicate in the body three different ideal cross axes which are perpendicular to each other, as in the Heterostaura, the main axis is one of them (which correspond to the three spatial directions -- dimensions -- of space). In the latter case it always is the longitudinal dimension that is determined by the main axis, so we can call it also the longitudinal axis ( A x o n l o n g i t u d i n a l i s ). In most cases the longitudinal axis is longer than all other axes, but often significantly shorter, implying that we cannot generally characterize it as the longest of all axes.
Also the quality of both its poles does not allow a general determination (assessment) of it as main axis. In the majority of all Protaxonia among animals, a head, or at least a head-end is differentiated, and one pole of the main axis lies in this head-end. In the majority of the remaining Protaxonia, the headless Protaxonia, a mouth is present at one end of the body or somewhere near it, an then one pole of the main axis lies in the mouth (in the Homostaura in the center of the mouth), or in its vicinity. Also in many mouthless Protaxonia, for example in most protaxonic radiolarians, we still can find a 'mouth' of the shell (i.e. its oral aperture), that in more than one respect represents the location of the mouth. In flowers this pole is situated in the open end of them, and so in general the free end in all sedentary protaxonic plant individuals. No organ is so persistent in the whole protaxonic series as the mouth (or its equivalent), so it is most appropriate to determine the first pole of the main axis as mouth pole ( P o l u s p e r i s t o m i u s, or P o l u s o r a l i s ), and to determine the body part in which it lies as mouth-end or oral end ( P e r i s t o m i u m, S u p e r f i c i e s o r a l i s ). With respect to the opposite second pole of the main axis it is less easy to find a generally fitting positive notion. In the majority of protaxonic animals the anus coincides with the second pole or lies in its vicinity, so one could call it the anal pole. But because in many protaxonic animals the anus is wholly absent, or far away from the second axial pole, and often much closer to the mouth pole, and because in sedentary protaxonic plant individuals the end part, lying opposite to the mouth pole, is the non-free end part, the basal part (in the main off-shoot the root), the second pole of the main axis can best be denoted by contra mouth pole ( P o l u s a n t i s t o m i u s, or P o l u s a b o r a l i s ), and the body part in which it lies by contra mouth-end ( A n t i s t o m i u m, S u p e r f i c i e s a b o r a l i s ).
The many diverse basic forms that are comprised within the Protaxonia divide into three large main sections, namely forms having only one (straight) axis, Monaxonia, forms that have in addition to the (straight) main axis several cross axes, the Stauraxonia, and forms that have their main axis spirally curved, the Spiraxonia.
If we denote the planes that are perpendicular to the main axis, and which we can lay through the body of all protaxonians, as transverse planes ( P l a n a t r a n s v e r s a l i a ), and (when we denote) all straight lines that lie in these planes as tranverse axes ( A x o n e s t r a n s v e r s a l e s ), then in the Monaxonia all transverse axes, that lie in one and the same transverse plane, are equal, while in the Stauraxonia (either in some transverse planes or in all) some of those transverse axes are different from the others lying in the same plane. Among these differentiated transverse axes we denote those axes that stand out in some way or another, and to which the neighboring different transverse axes relate symmetrically, as cross axes ( S t a u r i ). In the Monaxonic Protaxonia all transverse planes are discs (i.e. they are bounded by a circle), while in the Stauraxonic Protaxonia at least a part of the transverse planes are not discs, but (areas enclosed by) polygons or ellipses or still more complex forms.
If we indicate those planes that go through the main axis, i.e. that contain the main axis, as meridian planes ( P l a n a m e r i d i a n a ), then we see that in the Monaxonia all these planes are equal. In the Stauraxonia, on the other hand, we see that a part of the meridian planes is different from the others. Those meridian planes of the Stauraxonia that go through the cross axes, and that are consequently characteristic, we call cross planes ( P l a n a s t a u r o t a ).
In the Stauraxonia the body is always composed of a definite number of antimers, that meet each other in the main axis, while in the Monaxonia their number is infinite. The number of cross axes indicates the number of antimers, if we interpret as cross axes those transverse axes that lie in the median planes of the individual antimers, as well as those that lie in the boundary planes between every two neighboring antimers.
In all Stauraxonia we denote that half of a cross axis, that lies in the median plane of an antimer, as radius, and (we denote) that half of a cross axis, that lies in the boundary plane between two neighboring antimers, as interradius. Those meridian planes which contains two radii, and which are then at the same time median planes of two antimers, are preferredly called (for instance in the anatomy of Coelenterates, etc) radial planes ( P l a n a r a d i a l i a ). Those meridian planes, on the other hand, which contain two interradii, and which are then at the same time the boundary planes of two pairs of antimers, we call interradial planes ( P l a n a i n t e r r a d i a l i a ). A third kind of meridian planes are those that contain one radius and one interradius. We can call these planes semiradial planes ( P l a n a s e m i r a d i a l i a ). The cross axes, that lie in the semiradial planes, are neither radial nor interradial, but semiradial, because one half of such a cross axis is a radius, and the other an interradial.
The number of antimers in the Stauraxonia should now always be equal to the number of cross axes or cross planes. This law is valid for all Stauraxonia, which, though, follows from different factors, namely whether the homotypic basic number is even or uneven : If the number of antimers is even ( 4, 6, 8 and in general 2n ), like for instance in Coelenterates, then each cross axis consists either of two radii or of two interradii, and thus there always are two kinds of cross planes present, regularly alternating with each other, which means that between every two radial planes lies an interradial plane. So we have for example in the 4-fold dicotyledone flowers and also in the common medusae, two radial planes perpendicular to each other, that in the latter go through the middle lines of two neighboring radial vessels, and two interradial planes, that are also perpendicular to each other, that are determined by the interradial lines that lie in the middle between the mentioned vessels. Those interradial planes make angles of 450 with the radial planes. So we have four cross planes in all, and correspondingly also four antimers. If, on the other hand, the number of antimers is uneven ( 3, 5 and in general 2n-1 ), for example in Echinoderms, the five-fold dicotyledone flowers, then each cross axis contains one radius (forming one half of it) and one interradius (forming the other half), so all cross planes are of the same kind, namely semiradial. Each single cross plane is half radial, half interradial. So, in for instance Echinoderms, the number of cross planes, namely 5, each of them being for one half radial and for the other half interradial, is identical to the number of antimers, namely 5, of which the body is composed.
We will, below, in our general treatment of the Stauraxonia, explain all this still further.
In the Spiraxonia the main body axis is spirally curved. In this way we have to do (roughly) with a 'tube' that is coiled up. This coiling up can take place either in the same plane, resulting in flat spirals, as we see in many Ammonites, or be such that in addition to the formation of a spiral a screw is added, resulting in the form as a whole becoming more or less conical, as we see in many snails. The transverse section of the mentioned tube can have any shape, for example a circle, an ellipse an irregular polygon or a totally irregular shape. Two types of spirals could be encountered in the organic nature, the Archimedian Spiral and the Equiangular Spiral. The latter is by far the most important.
So the Protaxonia are divided into three Suborders :
Rotational bodies. Such a body remains the same (which here means that it will cover itself completely) after it is subjected to a rotation of whatever number of degrees about a certain axis.
The suborder of the singly axial Protaxonia only comprises such basic forms that, while displaying a clearly expressed straight longitudinal axis or main axis, lacks any indication of determined cross axes, implying that all transverse axes lying in one or another transverse plane are equal, which in turn implies that all transverse planes are discs (i.e. planes bounded by a circle). Because in such bodies all meridian must be equal, one can imagine that such a bodie consists of infinitely many congruent antimers, all having only one straight boundary line, the main axis, in common. The boundary surfaces of the monaxonic forms must either all be curved surfaces, or only those boundary faces that are perpendicular to the main axis, and that are consequently parallel to the transverse planes, can be planes.
Because we only have the two poles of the main axis, only two plane boundary surfaces could be present in monaxonic bodies. These planes, that must be discs, can be denoted as bases or polar planes ( P l a n a p o l a r i a ). One of them is the oral surface or peristomial surface, the other is the aboral or antistomial surface. The coherent curved boundary surface of the monaxonic form can generally be denoted as casing ( P a l l i u m ).
With respect to the surfacial bordering of the Monaxonia three cases are possible :
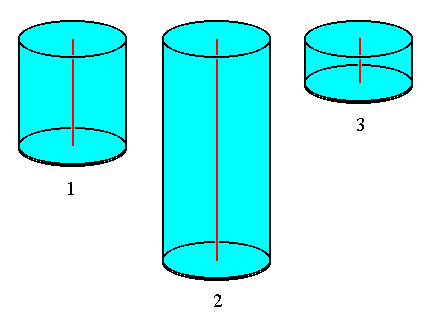
If we, for the time being, give up the above three-fold division of the Monaxonia on the basis of their surfaces, and first of all concentrate again on the axes and their poles, then we find as the simplest and most natural criterion of division the equality or non-equality of the poles of the main axis. In the equipolar or simply-polar forms, the Monaxonia haplopola, both poles of the main axis, and the corresponding polar surfaces, are equal, while in the non-equipolar or twofold forms, the Monaxonia diplopola they are unequal. To the former belong the spheroidal forms (Ellipsoid, Lens), the Bicone and the Cylinder, to the latter belong the hemispheroidal forms and generally all truncated spheroidal forms, further the Cone and the Egg.
Important for the assessment of monaxonic forms is that transverse plane that goes through the mid-point of the main axis, and that we denote as equatorial plane ( P l a n u m a e q u a t o r i a l e ). The transverse axes that lie in the equatorial plane are called equatorial axes. The equatorial plane divides the body of the Monaxonia haplopola in two congruent parts, while it divides the body of the Monaxonia diplopola in two unequal parts. The simplest stereometric basic form of the Monaxonia haplopola is the C y l i n d e r, the one of the diplopola is the C o n e.
Rotational bodies with a homopolar main axis.
The form group of equipolar Monaxonia, or, succinctly expressed, Haplopola, the body of which is divided in two congruent halves by the equatoral plane as wel as by any meridian plane, is seldom assumed by higher-order individuals, but is, on the other hand, often found in lower-order individuals (cells and organs). As subordinated modifications of this basic form we can distinguish two form groups, according to the body (surface) being bordered by just one curved surface (casing), or, in addition to that, by two equal planes (bases).
Remark : Here we see, by the way, that Haeckel's Promorphology is not just a consideration of body shapes according to their mirror symmetry -- it would then be just a part of Geometry. Actual organic shapes, as found in nature, are taken into account. Not only axial relations matter, but also the quality of surfaces encountered in real organisms. And, further down, when discussing the Haplopola anepipeds, and, later the Eudipleura, we will moreover make distinctions on the basis of axial ratios, i.e. their relative length (these latter distinctions are not (systematically) discussed by Haeckel in the case of the Eudipleura).
Forms possessing only one such plane cannot occur in the present forms (haplopola), because in that case the main axis would become non-equipolar. All such forms belong to the Diplopola.
The haplopolar forms without (possessing) such a plane, the Anepipeda, are represented by the different kinds of Spheroids (Ellipsoid, Lens, etc.) and by the Basal Bicone (i.e. two congruent cones placed such that they share their congruent bases).
The haplopolar forms having two planes taking part in (the constitution of) their body surface, the Amphepipeda, are represented by the Straight Cylinder and the forms that can be derived from it, the Apical Bicone (i.e. two congruent cones placed such that they meet at their apices and in which the main axis of one is the straight continuation of the other), etc.
Rotational bodies with a homopolar main axis and bordered by a single curved surface.
To begin with we will present some images of the possible shapes belonging to the present Subfamily.

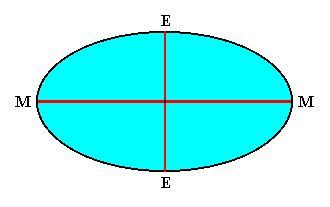
The Haplopola anepipeda appear in two different main forms, namely in the simple form of the Basal Bicone, and in the more complex form of the Spheroid. The Straight Basal Bicone can be defined as that kind of stereometric basic form that consists of two congruent straight cones that are united by their bases. Each meridian plane of such a body is a rhombus. See Figure 4.
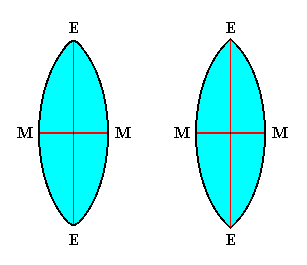
From the basic form of the Basal Straight Bicone, as also from that of the single straight cone, we can distinguish three different species, according to the main axis being as long as, longer than or shorter than the equatorial axis.
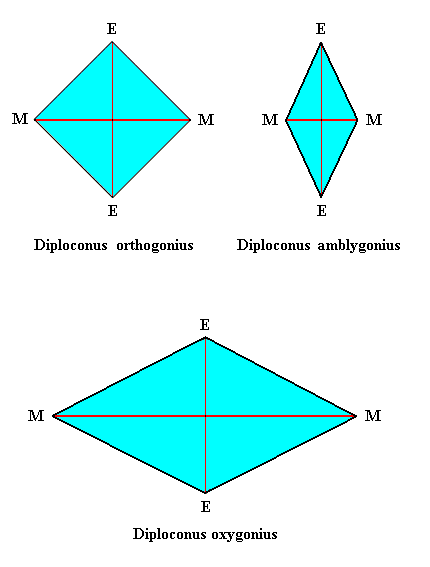
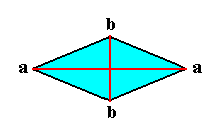
The basic form ( p r o m o r p h o n t ) of the Straight Basal Bicone is seldomly represented in organic forms. Even in lower-order form individuals, cells and organs, we only find few cases where it is realized. The other main form of the Haplopola anepipeda, the Spheroid, is realized in many cases. The spheroidal form belongs to the simplest organic basic forms and is most akin to the Homaxonic form, the Sphere, from which it can be derived when we extend or shorten one axis of the sphere equally in both directions, implying its poles to be equally distant from the center, and the equatorial plane dividing the whole body in two congruent hemispheroids. When the main axis of the spheroid is longer than the equatorial axis, we have the E l l i p s o i d, when it is shorter we have the L e n s. When the curved equatorial edge of the Lens sharpens, the transition to the Basal Straight Bicone becomes apparent (See Figure 2). The meridian plane of the Spheroid generally is an ellipse. In the Lens it can assume a little different outline.
The realization of the spheroidal form in first- and second-order organic individuals (cells and organs) is so wide-spread that we do not have to give examples. Also in juvenile stages (embryo's) of higher organisms the Ellipsoid or Lens is wide-spread. With respect to adult organisms we find the Spheroid in Radiolarians.
Rotational bodies with a homopolar main axis and bordered by two flat surfaces.
The equipolar monaxonic forms with two flat surfaces (in addition to their casing (Pallium)) appear either as the simple basic form of the Straight Cylinder, or as more complicated forms that can be seen in equipolar modifications of the Cylinder.
The S t r a i g h t C y l i n d e r of Geometry, the meridian plane of which is a rectangle, while its main axis is perpendicular to both, congruent and parallel, circular bases and going through their centers, is often realized in a very pure form in organisms, but, while seldom realized as material substrate of adult organisms, it abounds in lower-order form individuals composing a whole organism, especially cells and organs. Also in for example single celled algae we can find the Cylinder.
Also in cylindric forms we can distinguish several species, according to their axial ratio, i.e. the ratio between the length of the main axis and that of the equatorial axis (which is equal to the diameter of either basis).
In this way we distinguish three species of Straight Cylinder :
Even more common, especially in cells, are the m o d i f i e d Straight Cylinders. In them the polar halves are modified symmetrically, either by bendings of the casing surface, or by constrictions on both sides of the equatorial plane, or other (symmetrical) deformations. To these belong all the forms of the Haplopola anepipeda as soon as they are subjected to truncations symmetric with respect to the equatorial plane and parallel to it. Most of such forms, displaying great diversity, will resist an easy geometrical precise description.
The axes of the individual partner-cones lie in each others direction.
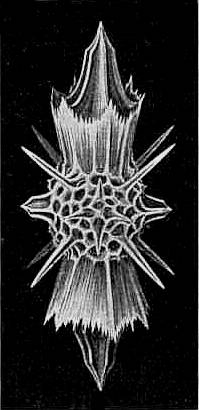
We can see the Apical Bicone realized in a Radiolarian :
How different the curvings of the casings, in the modified straight cylinders, may be, all these forms correspond to the Straight Cylinder by the fact that their body is partitioned in two congruent halves by the equatorial plane.
Rotational bodies with a heteropolar main axis.
The form group of the Diplopola or non-equipolar monaxonic forms, the simplest basic form of which is the C o n e, is more commonly than the Haplopola represented in higher-order form individuals (Persons and Colonies), and in addition to this also preferably in lower-order form individuals, Cells and Organs.
Because the poles of the main axis always differ from each other, the body never is divided in two congruent halves by the equatorial plane. Here, for the first time, the polar surfaces, that were still congruent in the Haplopola, are distinguished from each other : The mouth pole is the center of the peristomium or A r e a o r a l i s, the contra-mouth pole is the center of the Antistomium or A r e a a b o r a l i s.
The different forms of the diplopolar monaxonians are divided among three groups, according to the body being bordered just by a curved casing, or in addition to it by one or by two flat surfaces, i.e. planes (bases, polar planes). The simplest basic form of the bodies without planar surfaces ( A n e p i p e d a ) is the E g g. The simplest basic form of the M o n e p i p e d a (with one polar plane) is the single S t r a i g h t C o n e. The simplest basic form of the A m p h e p i p e d a (with two polar planes) finally, is the S t r a i g h t T r u n c a t e d C o n e.
Rotational bodies with a heteropolar main axis, but without polar planes.


The simplest regular body, that is enclosed by just one curved surface, and that has only one axis, with two different poles, is the E g g. The degree of curving of the casing ( p a l l i u m ) can be very different (See the above Figures). But it always is limited in virtue of the fact that every transverse plane of the body must remain a disc (i.e. a figure enclosed by a circle). This implies that all meridian planes of the Egg must be congruent. The lowest-order individuals, the cells, appear so often in the form of an Egg, that, as examples, the above Figures are amply sufficient. Also organs and colonies are very often egg-shaped.
The derived egg shapes or m o d i f i c a t i o n s o f t h e E g g f o r m, that also are very often realized in organisms, distinguish themselves from the pure geometrical egg form by the fact that the decline of the diameter of the parallel circular planes towards the poles is not proceeding evenly, but unevenly. This can result in alternating constrictions or bulges on the egg's surface.
If one wants to distinguish between different sorts of egg forms, then one can set up three types of Eggs :
Rotational bodies with a heteropolar main axis, and having one polar plane.
One of the basic forms that is most often realized in cells and organs, but also in colonies ( C o r m i ) is that regular diplopolar form the surface of which is bounded by one curved casing ( P a l l i u m ) and by one plane surface. As the simplest geometric form of this group one can take either the S t r a i g h t C o n e, or the H e m i s p h e r e. In both the plane that coresponds to the oral pole, and which we therefore call A r e a o r a l i s, is a disc. The meridian plane of the Straight Cone is an isosceles triangle, the one of the Hemisphere is a hemidisc.
The S t r a i g h t C o n e ( C o n u s ) is as basic form of cells and organs very common. Also genuine colonies ( C o r m i ) show this form often more or less pure, as can be seen in plant colonies, especially in many Conifers.
The external shape of the body, determined by the casing ( P a l l i u m ), indicates the straight cone also in those cases (for instance in many Coelenterates and Echinoderms), where in virtue of the internal structure of the body (consisting of a definite number of congruent antimers) in fact the form of the S t a u r a x o n i a h o m o s t a u r a i.e. a regular pyramid (and so not a monaxon form) is indicated.
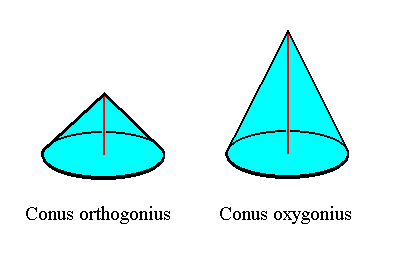
Each of the different forms belonging to the group of Straight Cones can be reduced to one of the three species of Straight Cone, that are also determined as such in geometry, namely according to the ratio of the height of the cone and the radius
( See REMARK ) of its basis. These three species are :
The next two Figures depict these three types of Cone :
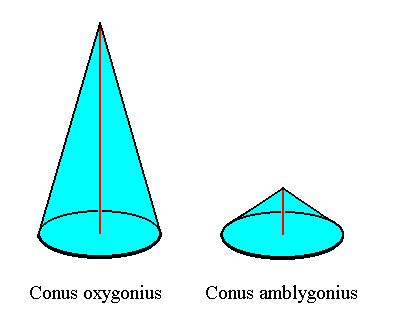
The H e m i s p h e r e ( H e m i s p h a e r a ) is less commonly realized (in a pure geometrical form) in organisms than the Cone. The next Figure depicts a meridian plane of the Hemisphere :
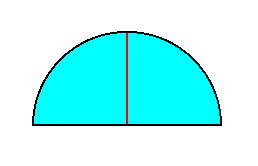
Much more often organically realized is the H e m i s p h e r o i d when we mean by it, on the one hand any spherical segment that is smaller or greater than a hemisphere, and on the other hand any form that can be derived from the Spheroid (Ellipsoid, Lens), or from the Egg by truncating it through a transverse plane (a plane that is parallel to the equatorial plane). The next Figures depict several possible Hemispheroids.
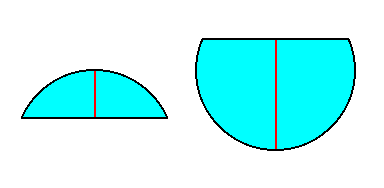
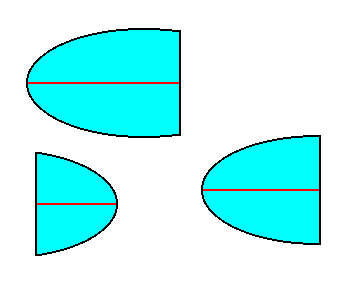
The external shape of the pallium (casing) of most Hydromedusae and Ctenophores (when we do not consider the pyramidal basic form of the whole organism, based on the radial composition of their bodies, i.e. their being composed of a finite number of antimers) could be reduced to such highly diverse hemispheroidal forms, partly also to pure Hemispheres.
If one wants to distinguish several different species of Hemispheroid (in the broadest sense of the term), then the following could be indicated :
Rotational bodies with a heteropolar main axis, and having two polar planes.
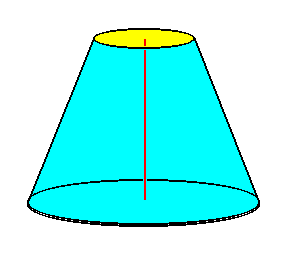
The highest differentiated monaxonic form is represented by those heteropolar monaxonians, that, in addition to the curved surface (casing), is enclosed by two different flat surfaces (bases). The simplest geometric basic form of these Diplopola amphepipeda is the s t r a i g h t t r u n c a t e d c o n e,
In addition to the straight truncated cone and the forms that can be derived from it by a hollowing out or bulging of the casing surface, also those d o u b l y t r u n c a t e d s p h e r o i d a l f o r m s belong to the present group, that one can obtain by truncating the several modifications of the Spheroid (Ellipsoid, Phacoid), as well as the Egg, towards both poles by two planes whose distances from the equatorial plane (which is parallel to them) are unequal.
Also these forms, are, just like the truncated straight cone, represented in the shapes of the first-, second- and sixth-order form individuals, i.e. in cells, organs and colonies, for example plant colonies (i.e. certain trees).
To continue click HERE to proceed further with the systematic Promorphology.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia