Spiraxonia isogonia

Second Family of the Spiraxonia

Spiraxonia isogonia

Stereometric Basic Form : Equiangular spiral

Forms with their main axis regularly spirally curved according to the equiangular spiral (also called logarithmic spiral).
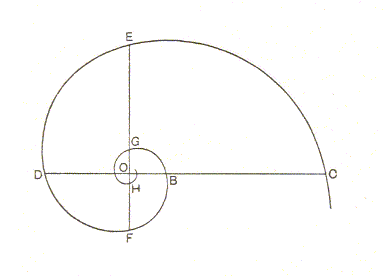
The S p i r a x o n i a i s o g o n i a have as their stereometric basic form the e q u i a n g u l a r s p i r a l. In such spirals the angle between the tangents to the whorls in the points of intersection with a radius remains constant while the spiral recedes from its point of origin. The breadth of the whorls (in fact the distance between successive whorls of the spiral curve) increases in a constant ratio according to r = a^THETA, in which a is some constant (i.e. a factor of multiplication), and THETA is the vectorial angle, i.e. the angle of revolution of the spiral.
The o r i g i n o f t h e (equiangular) s p i r a l is called the p o l e (O). It is one of the two poles of the spirally coiled main body axis. The a x i s o f t h e s p i r a l is a straight line going through the pole, and perpendicular to the plane of the spiral (The latter considered as a planar curve). About this axis a straight line, perpendicular to this axis, can be imagined to revolve. This line is called the r a d i u s v e c t o r (r). The planar spiral is geometrically produced by the trace of a point moving along the radius vector as the latter revolves uniformly about the pole.
Now we can define the e q u i a n g u l a r s p i r a l as follows:
"If, instead of travelling with a uniform velocity (as in the Archimedian spiral), our point move along the radius vector with a velocity i n c r e a s i n g a s i t s d i s t a n c e f r o m t h e p o l e, then the path described is called an equiangular spiral".
Each whorl which the radius vector intersects will be broader than its predecessor in a definite ratio. The radius vector will increase in length in g e o m e t r i c a l progression, as it sweeps through the successive equal angles.
As the spiral grows the form as a whole does not change.

Figure 1. The equiangular spiral. ( After D'ARCY THOMPSON, 1942 )

Many shells of organisms, like snails, Nautilus and the Ammonites, but also most Foraminifers, are built according to the equiangular spiral, the basic form of the Spiraxonia isogonia.
This spiral, representing the spirally curved main axis of the relevant organisms, can have its whorls either in one and the same plane, resulting in discoid forms ( I s o g o n i a p l a n a t a ), or be drawn out into the third dimension in order to leave room for previous whorls, resulting in turbinate forms ( i s o g o n i a a p l a n a t a ).

Of course there are many possible equiangular spirals, differing in the value of (the parameter) WHORL, which is equivalent to a in the equation to the equiangular spiral as given above. When WHORL increases, the curvature of the spiral can become very low indeed. In spiral organisms with such a high WHORL-value, like (the shells of) cockles, the first concrete whorl is never completed, so that the actual spiral form of the shell is hardly recognizable (See for more details of the equiangular spiral our general introduction to the Spiraxonia).

First Genus of the Spiraxonia isogonia

Isogonia planata

Stereometric Basic Form : Planar equiangular spiral

Forms with a spirally coiled main axis according to the equiangular spiral with all its whorls in the same plane .
To the I s o g o n i a p l a n a t a we assign all organismic (form) individuals that are built according to a p l a n a r e q u i a n g u l a r s p i r a l.
Such organic forms can roughly be thought of as a cone that is coiled up into a spiral. This cone can in principle be a genuine cone and thus causing the 'tube' to have a circle as the form of its cross section. As such it is the cross section of the whorls of a shell. The tube can also be a flattened cone, causing its cross section to be an ellipse, or the tube can be some regular or irregular pyramid (coiled up into a spiral), causing the cross section to be a regular or irregular polygon. The tube can be such as to fit neatly in the space permitted by the given spiral, or leave gaps between the successive whorls.
In the introduction to the Spiraxonia we defined the parameter WORM as follows :
A WORM-value of, say, 0.7 means that the distance between the origin of the spiral (the pole) and the inner wall of the tube is 70% of the distance between the origin of the spiral and the outer wall of the tube. The WORM-value is equal for the whole shell, regardless of the particular part of the tube where we do our measurements. Logically speaking, this is not necessary, but appears to hold so many times in real shells, that we will take it as point of departure, unless otherwise indicated.
Only when this WORM-value is the reciprocal of the WHORL-value the whorls will neatly fit and be contiguous into the space permitted by the spiral. When the value is higher we will see gaps between the whorls, and when it is lower the actual whorls (formed by the coiled tube) will get in each others way. In the planar spiral organic forms this problem is solved by letting the whorls partly enclose previuos whorls.
When the last whorl encloses all the previous whorls the spiral is called an i n v o l u t e s p i r a l. When on the other hand, all the whorls remain visible the spiral is called an e v o l u t e s p i r a l.
The Isogonia planata are materialized mainly in Cephalopods, like Nautilus and the Ammonites, but also in many Foraminifers. In snails this basic form is less common.

Figure 2. Ammonite. Lytoceras fimbriatus ( Lower Lias ), Lyme Regis, England.
A representative of one of the two deep-water stocks from which many Ammonitina arose.
( After CLARKSON, E., 1979, Invertebrate palaentology and evolution )

Figure 3. Nautilus pompilius (Recent). Shell sectioned subcentrally. ( After CLARKSON, E., 1979, Invertebrate palaentology and evolution )

Figure 4. Ammonoid morphology reconstructed on the basis of the anatomy of Nautilus, showing marginal siphuncle and inferred organization of soft parts. ( After CLARKSON, E., 1979, Invertebrate palaentology and evolution )

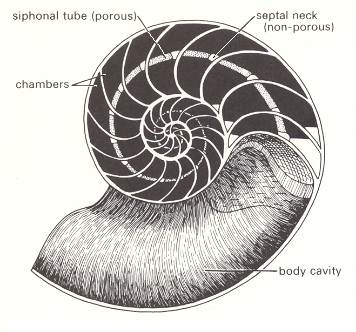
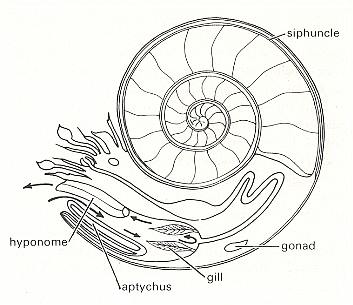
Figure 4 shows that the animal itself (except its siphuncle) lives in the last shell chamber only. As far as can be inferred this soft body has a basic form, not of a spiral, but of one belonging to the Dipleura (Stauraxonia). Its siphuncle, however, which is a single calcified strand of living tissue extending from the body to the center of the shell's spiral, and carrying a rich blood supply, is spirally curved, following the shell's spiral. So in a sense the soft body as a whole is spirally formed after all. For a section through the siphuncle see next Figure.

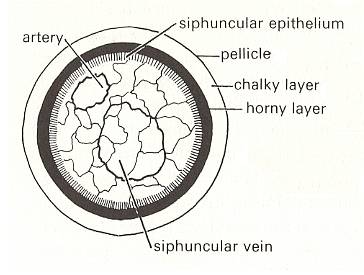
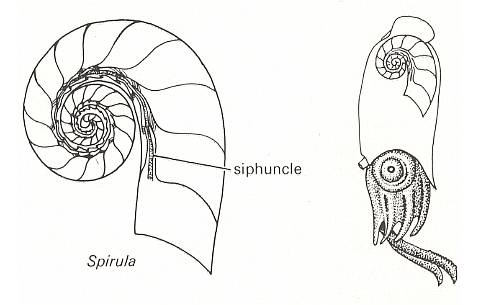
Figure 5. Anatomy of Nautilus siphuncle. Transverse section of siphonal tube. The siphuncle is used to regulate the buoyancy of the animal. ( After CLARKSON, E., 1979, Invertebrate palaentology and evolution )

Figure 6.
Left image : Shell structure in Spirula with siphuncle.
Right image : Spirula : in life position showing the location of the shell.
( After CLARKSON, E., 1979, Invertebrate palaentology and evolution)

In Figure 6 we see that in Spirula the shell is an interior structure. So especially in such cases the shell clearly is just an o r g a n, morphologically as well as physiologically. This organ (second-order form individual) has the basic form of the Isogonia planata (Spiraxonia), while the (soft) animal itself apparently belongs to the Dipleura (Stauraxonia).

Second Genus of the Spiraxonia isogonia

Isogonia aplanata

Stereometric Basic Form : Aplanar equiangular spiral

Forms with a spirally coiled main axis according to the equiangular spiral with its whorls drawn into a third dimension.

Figure 7. Common land snail

To the I s o g o n i a a p l a n a t a we assign all organismic (form) individuals that are built according to an a p l a n a r e q u i a n g u l a r s p i r a l.
In these forms the solution to the above mentioned problem that appears when the value of WORM is smaller the the reciprocal of the value of WHORL, causing the actual (more or less tubular) whorls to get in each other's way, is solved by giving way to the third dimension of subsequent whorls, resulting in a turbinate structure of a more or less conical overall shape.
Most marine and land snails display such turbinate forms. Their overall shape is indeed more or less conical. We can imagine the tube being coiled up along a cone. In this they show several degrees, that can be quantified with the parameter TOP.
TOP indicates the speed with which the consecutive whorls of the spiral are displaced along the length of the cone. We can measure TOP by determining the angle BETA between the common tangent to the whorls of the shell and the axis of the spiral. Nautilus has a TOP-value of 90⁰, because all the whorls lie in one and the same plane. But Turritella, having a sharply pointed shell, has a much smaller value.

Figure 8. Turritella duplicata
( After D'ARCY THOMPSON, 1942, On Growth and Form )

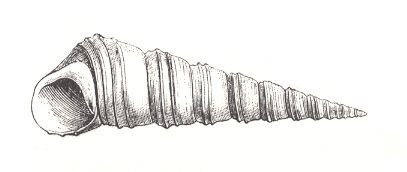
With all this we must bear in mind that in many shells the value of TOP is not precisely constant during the growth of the individual. The result is a more or less concave or convex outline of the cone. See next Figure.

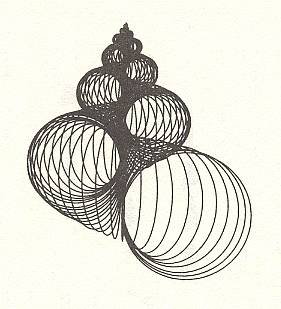
Figure 9. Turbinella napus. An Indian chank shell.
( After D'ARCY THOMPSON, 1942, On Growth and Form )

In the next four Figures images are given of computer-generated shells. Implementation of different values of the three parameters WHORL, WORM and TOP results in different shell shapes. TOP is given as cot(BETA), i.e. the cotangens of the angle between the axis of the spiral and the common tangent to the whorls. It measures the pointedness of the shell, i.e. the extent to which its whorls are drawn out into the third dimension.

Figure 10. A computer-generated shell.
WHORL = 2 WORM = 0 TOP = 3
( After DAWKINS, R., 1996, Climbing Mount Improbable )

Figure 11. A computer-generated shell.
WHORL = 1.3 WORM = 0 TOP = 8.2
( After DAWKINS, R., 1996, Climbing Mount Improbable )

Figure 12. A computer-generated shell.
WHORL = 1000 WORM = 0 TOP = 0.5
( After DAWKINS, R., 1996, Climbing Mount Improbable )

Figure 13. A computer-generated shell.
WHORL = 2 WORM = 0.25 TOP = 1.5
( After DAWKINS, R., 1996, Climbing Mount Improbable )

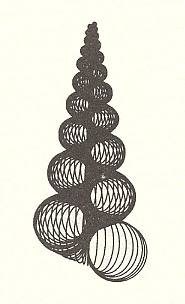
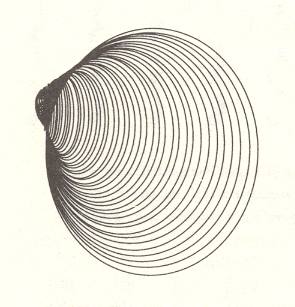
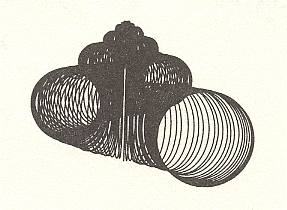
Within the Isogonia aplanata there is an enormous diversity to be found, especially among the turbinate shells of (land, fresh water or sea) snails. But their common basic form (promorphont) is the non-planar equiangular spiral.

With the Isogonia aplanata we have concluded our investigation of the last Suborder of the Protaxonia, and with it we have c o m p l e t e d the Promorphological System of Stereometric Basic Forms.
Every conceivable organism or part of it can have a place in this System, whether it comes from our planet or from any other. The only condition for it to have a place, is that it must be built in a t e c t o l o g i c a l way, i.e. it should consist of body parts that, while being (morphologically) identical or more or less similar, are repeated a b o u t a n ( i m a g i n a r y ) a x i s that can be conceived as the main axis, or about a point representing the body center. Such a way of repeating (namely about an axis or point) distinguishes itself clearly from a p e r i o d i c repetition as we see in crystals. The identical or more or less similar body parts that are repeated about an axis are called a n t i m e r s, and we have seen how important they are in a promorphological inquiry.
The Promorphological System of Basic Forms shows an increasing differentiation of body parts, promorphologically expressed by the non-equivalence of axes and of their poles.
The basic forms express a spatial ordering of (the parts of) the developing organisms. How this exactly comes about we don't know. Probably we should think of it in terms of (organisms as being) reaction-diffusion systems. These systems can indeed generate patterns on the basis of slow diffusion of reaction products and subsequent interaction of these products when they finally encounter each other. Also a foamy matrix could be an important condition for the formation of shells or skeletons which impose FORM onto the given organic individual.
A Promorphology as presented here, should precede any morphological investigation (that's why it is called "Promorphology"), i.e. any special morphological investigation must be embedded into a general promorphological context.
Throughout the first half of this website, (and directly) beginning with the HOMEPAGE, we have developed a theory about the E s s e n c e o f a t h i n g. If a thing indeed has an Essence, then such a thing is a genuine b e i n g. We have found out that the Essence of a being is the Dynamical Law of that dynamical system that has generated, or could generate, that being or thing. This Dynamical Law or Essence resides at the 'genotypical level' of that being, i.e. it exists in an abstract way in the given thing, while its e f f e c t s reside at the 'phenotypical level' of the thing, and are as such directly visible. There are many such phenotypical effects of the Dynamical Law of any one thing. And on this website we have choosen to concentrate on two heavily interrelated phenotypic effects in things, that we could call (1) STRUCTURE, and (2) SYMMETRY AND FORM. We have investigated these effects in Crystals by means of Crystallography [internal form (= structure) and external form], and in Organisms by means of Tectology [concerns general macroscopic internal form (= structure)] and Promorphology [concerns general external form].

Promorphology and Tectology
Preceding Promorphology we have studied the general, global internal form, i.e. global structure, of organisms. This study was called Tectology. There we established that the general internal structure of organisms boils down to recognizing an organism as being built up by subordinated form individuals.
Six orders were found :

Cells. They are the units or ultimate building blocks recognized in Tectology.
Organs. Interpreted morphologically (as are all these orders).
Antimers. I.e. counterparts or homotypic pars.
Metamers. I.e. sequentional parts or homodynamic parts.
Persons. Including off-shoots.
Cormi. I.e. genuine colonies.
In Promorphology especially the antimers are -- as we have seen -- of great importance.
Within Tectology we have further distinguished between morphological individuals and physiological individuals. The latter were called bionts. Among these bionts we distinguished in turn actual bionts, virtual bionts and partial bionts.
In Promorphology, as was done above, we established the possible basic forms of organisms, without explicitly referring either to certain parts of them or to the whole organism. It was just a consideration of the possible stereometric basic forms that can be expected to occur in the organic domain.
In the following document we will again consider the basic forms, but this time by involving explicitly the parts of the organismic bodies possessing these forms. This boils down to study the possible basic forms in each individuality order, as established in (the documents on) Tectology, and enumerated above. So we will consecutively study :

The stereometric basic forms of Cells.
The stereometric basic forms of Organs.
The stereometric basic forms of Antimers.
The stereometric basic forms of Metamers.
The stereometric basic forms of Persons.
The stereometric basic forms of Colonies.

To study the Basic Forms of the six orders of Individuality, click HERE

e-mail :