In order to deal adequately with the content of the present and following documents, the reader should consult the Special Series of the First Part of this website, accessible via back to homepage, especially the introductory document, and all the ones that deal explicitly with all the Crystal Classes (He or she should not necessarily read the documents of the derivation of those Classes).
Introduction
In the foregoing series of documents we have set up a Promorphological System of Organic Forms, based on the symmetry and tectology of organic individuals of all individuality orders. But although it is an ORGANIC system we would like to extend it in order to accommodate also for inorganic forms. With the latter we mean the forms (shapes) of genuine inorganic beings, beings that seem to defy any incorporation of them into the Promorphological System because they do not have a TECTOLOGICAL structure, but instead a PERIODIC structure : Crystals (especially single --in contradistinction to twinned -- crystals). They are composed of periodically repeated morphological units, i.e. units that all have exactly the same orientation within the total pattern.
Organisms on the other hand, are composed of non-periodically repeated units, i.e. units that generally have different orientations with respect to each other. This is most clearly exhibited by their possessing ANTIMERS, i.e. identical parts distributed in a regular way around a certain body axis.
But despite the fact that single crystals (again, in contradistinction to many twinned crystals) do not have a tectological structure providing the basis for a promorphological consideration of them, they can nevertheless be incorporated into a promorphological framework, because they, however strange it may sound, possess a tectological feature deep down buried within them, so that they have (in a way) a tectological structure after all! But this structure must be 'dug up', and only when this has been successfully accomplished we can start to think about the incorporation of crystal forms into the Promorphological System, i.e. to establish a connection between the Crystallographic Scheme of Crystal Forms and the Promorphological Scheme of Organic Forms.
In the first document that actually will do so, we will further introduce this idea of connecting the to Schemes.
In the present document we will investigate in what way single crystals possess a tectological structure, despite their periodic structure, and so prepare ourselves to connect the mentioned Form Schemes.
For the purpose of this investigation a study of 2-dimensional crystals (i.e. two-dimensional analogues to (real) three-dimensional crystals) will do perfectly. The advantage of using 2-dimensional crystals (which are of course not really existing in the natural world) is that they are much more transparent than 3-dimensional crystals are, while retaining to be instructive for the present problem.
To uderstand the following considerations, some knowledge about the i n t e r n a l s t r u c t u r e of 2-dimensional crystals (their point symmetries and translational symmetries, Planar Point Groups and Plane Groups) is necessary. The reader will find an introduction to these matters in the mentioned Series of Essays (documents) in the First Part of this website, accessible via back to homepage : Special Series, the documents on the Internal Structure of Crystals.
In the following considerations we'll discuss some examples of two-dimensional crystals and their respective Plane Groups. We will depict these crystals as 2-dimensional periodic arrays of m o t i f s. These (graphical) motifs are the 2-dimensional analogues to c h e m i c a l motifs in real 3-dimensional crystals.
From our considerations in the mentioned documents on Crystals we know that the point symmetry of a given 3-dimensional (single) crystal, i.e. the symmetry expressed by the Crystal Class or Point Group to which it belongs, is the translation-free residue of the total symmetry as expressed by the Space Group to which the given crystal belongs. The Space Group expresses the point symmetry as well as all translational symmetry and also the configuration of the symmetry elements within the crystal lattice (The latter boils down to the orientation of chemical motifs within the lattice).
An analogous case we have with respect to 2-dimensional crystals : The planar point symmetry of such a crystal is the translation-free residue of the total symmetry as expressed by the Plane Group to which the given crystal belongs.
The internal structure of a 2-dimensional crystal can be seen as an array of motifs arranged according to one or another p o i n t l a t t i c e (or net). Or, in other words, we have a point net, provided with motifs, in such a way that each lattice point (node) and its associated motif (which could consist of a collection of motif units grouped around the lattice point (node)) is fully equivalent to any other lattice point, which means that all the lattice points have identical surroundings. The smallest repeated unit that has the same dimensionality as the net itself is called the unit cell. Sometimes a unit cell comes in several possible choices.
Well, if we take a 2-dimensional periodic array of motifs, representing the internal structure of some 2-dimensional crystal, then we have before us motifs (and motif units) separated by t r a n s l a t i o n s. These translations can be of two sorts :
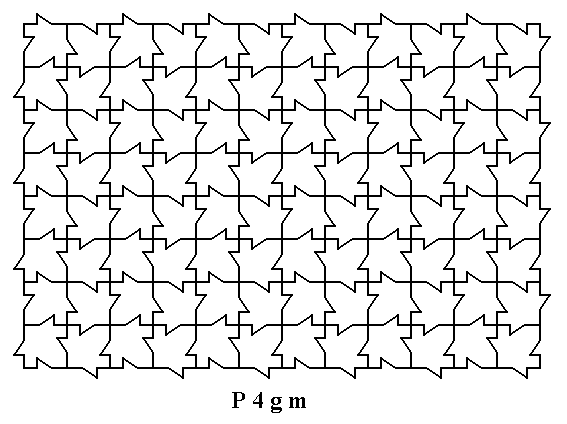
The next 2-D array of periodically repeated motifs consists of canadian maple leaves (each such a leaf is a 2-D analogue to a chemical unit in 3-D crystals) :

Figure 1. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. The array must be considered as indefinitely extended in (2-D) space
( Adapted from BRISSE, F., 1981, La Symétrie bidimensionelle et le Canada, redrawn in KLEIN, C., & HURLBUT, C., 1999, Manual of Mineralogy )
As noted just above, the array must be imagined as i n d e f i n i t e l y e x t e n d i n g across 2-dimensional space. When we find ourselves in the microscopical dimension this idea of infinite extension is reasonable, because (reasoning from 3-D crystals) the number of lattice nodes is very large indeed. The next Figure illustrates this.
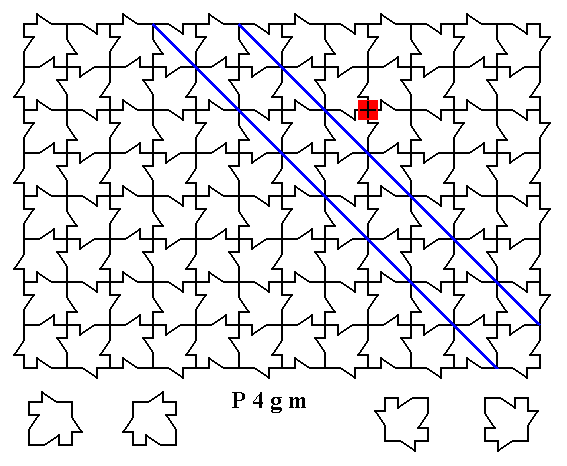
Figure 1a. A two-dimensional array of canadian maple leaves. As such, a 4-fold rotation axis, as indicated by the small red square, is not possible (wherever we imagine such an axis to be present in the array). Already the rectangular outline of the pattern as drawn forbids the presence of such axes. Also the two suggested mirror lines (solid blue lines) are not possible for such a pattern as it stands, i.e. as it is drawn (namely as a finite pattern). The array must be considered as indefinitely extended in (2-D) space, and then the drawn symmetry elements are possible.
In the presently considered array we can distinguish (and choose between several possibilities) lattice points.
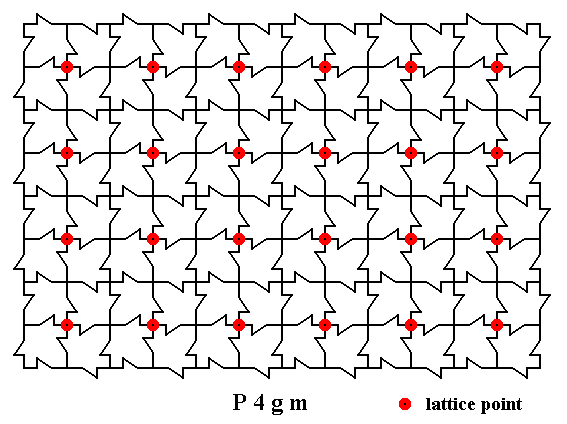
Figure 2. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs. We obtain the point lattice by connecting these points non-diagonally. See next Figure.
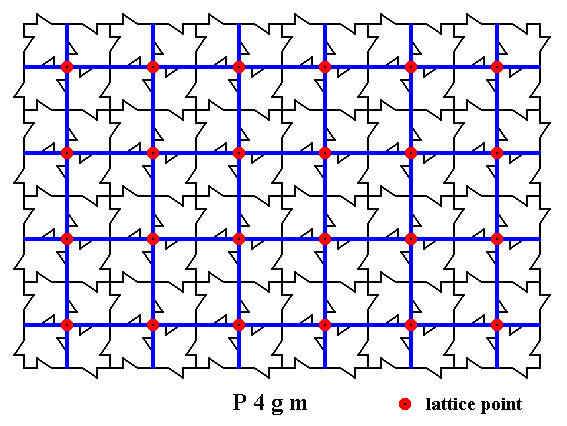
Figure 3. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs. These lattice points are now connected as indicated (blue lines), revealing a Primitive Square Lattice, supporting the motif pattern.
In the present pattern of maple leaves we clearly see the presence of a 4-fold rotation axis at each node. In the center of each unit cell we also see a 4-fold rotation axis. But while the former are directed clockwise the latter are directed anti-clockwise, so the involved points are not equivalent, which here means that the central point is not a lattice point, so the lattice is not centered.
In our array a m o t i f consists of four maple leaves centered around each lattice node. Each single maple leaf can be considered as a motif unit. In the next Figure these units are given in different colors :
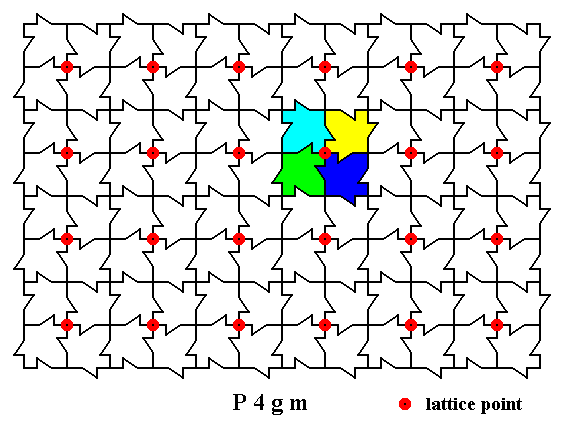
Figure 4. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
Each node (lattice point) is associated with a motif consisting of four motif units. One such motif is indicated.
The next Figure shows the periodic repetition of motifs according to the point lattice.
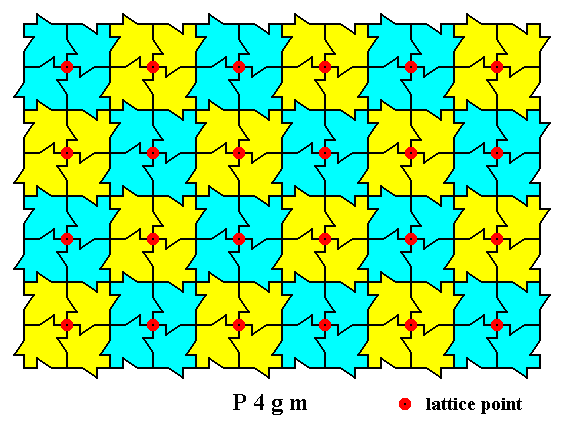
Figure 5. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
Each node (lattice point) is associated with a motif consisting of four motif units. The array consists of a periodic repetition of equivalent motifs, as indicated.
What we have depicted in Figure 4 is the t o t a l m o t i f, which here means the complete surroundings of the lattice point. That's why this motif neatly adjoins to the next (total) motif belonging to the next lattice point. And of course we can let the boundary of the total motif coincide with the perimeter of the square -- as the next Figure shows -- because all what we're looking for is a unit that is periodically repeated throughout the structure.
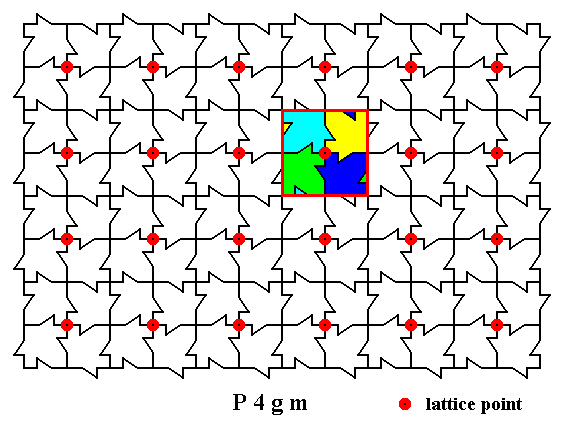
Figure 5a. A second (but equivalent) way to conceive the total motif as the complete surroundings of a lattice point. The boundary of such a total motif is indicated by red lines forming a square.
The next Figure shows the net and its nodes (as in Figure 3), it shows the motifs, and it outlines a possible u n i t c e l l.
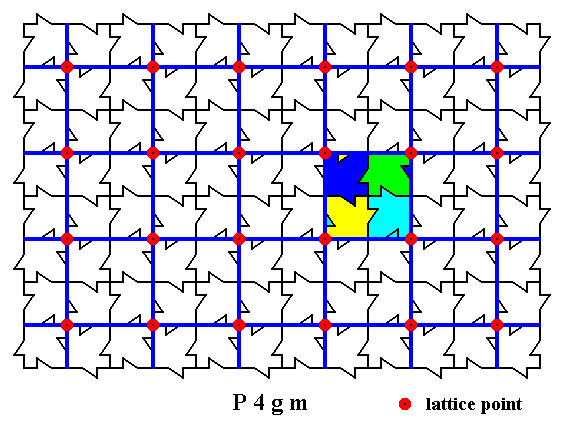
Figure 5b. A possible unit cell is outlined. By repeating this unit cell periodically, we obtain our structure (pattern) of maple leaves.
If we now compare the total motif as depicted in Figure 5a and a possible unit cell as depicted in Figure 5b, then we see that they are exactly equal in size and equivalent with respect to content, which means that THE TOTAL MOTIF IS EQUIVALENT TO A POSSIBLE UNIT CELL. Such a total motif are the complete surroundings of a lattice point. All this implies that when we telescope a crystal structure back, i.e. eliminate all translations (in order to find the c o m p l e x motif, and on the basis of it the crystal's tectology), we cannot push this so far as to even sqeeze a unit cell. The process stops at the unit cell (Recall that choosing a smaller unit cell than some given unit cell, has nothing to do with an elimination of translations). The smallest part of the lattice is the lattice point. And as soon as we include content to a point lattice, each lattice point is associated with its surroundings (which have, and represent, content). These surroundings are the total motif of the structure (i.e. the given point lattice provided with content). So the total motif is the smallest unity that we can get by eliminating translations, and this total motif is -- as we just saw -- equivalent to a possible unit cell.
We can see that the pattern (imagined to be extended indefinitely) possesses m i r r o r l i n e s in the two diagonal directions :
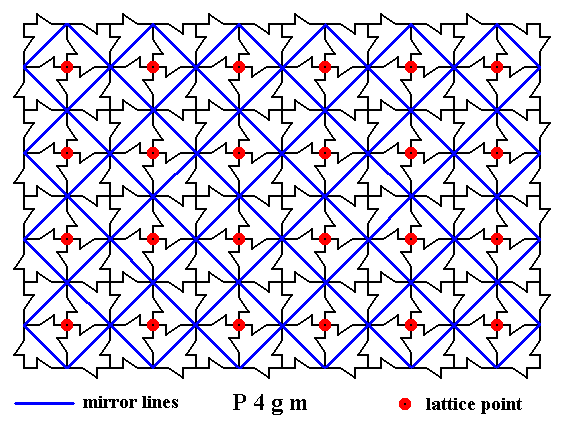
Figure 6. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
The pattern possesses mirror lines as indicated (blue solid lines).
The pattern also possesses g l i d e l i n e s (glide reflections). They come in two varieties, diagonal and non-diagonal (= horizontal and vertical). Let us first concentrate on the diagonal ones. The next Figure depicts one such diagonal glide line.
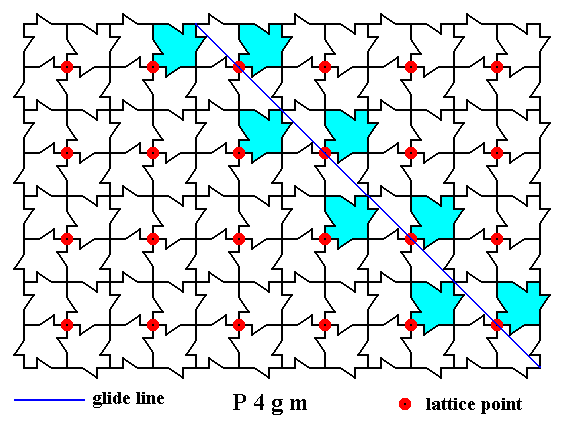
Figure 7. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
In addition to mirror lines the pattern possesses glide lines. One such glide line is indicated (thin blue solid line).
The next Figure depicts all the glide lines in one diagonal direction :
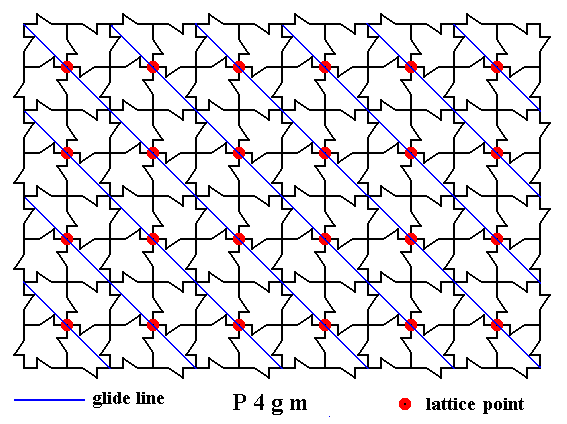
Figure 8. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
In addition to mirror lines the pattern possesses glide lines. All the glide lines in one diagonal direction are indicated (thin blue solid lines).
The other diagonal glide lines are situated as follows :
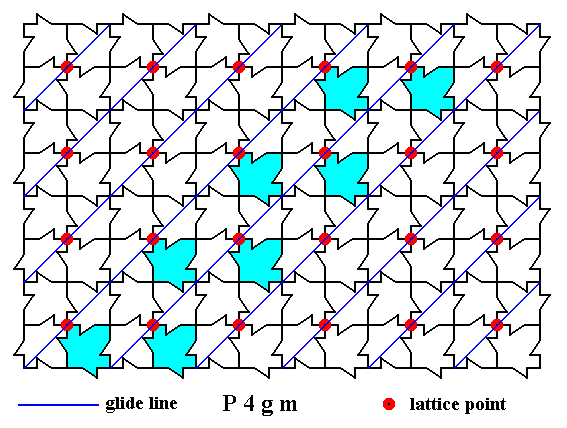
Figure 9. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
Indicated are the other diagonal glide lines.
The next Figure gives all the diagonal glide lines :
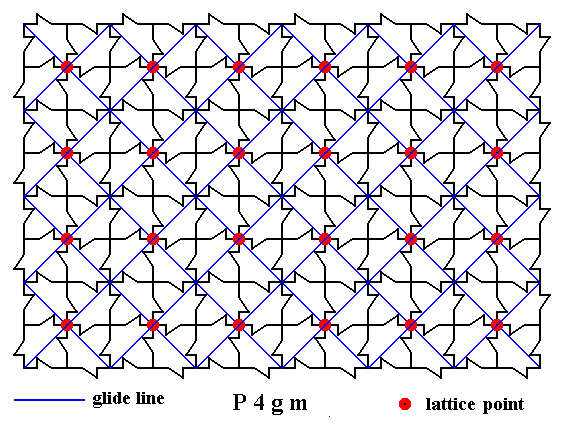
Figure 10. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
Indicated are all the diagonal glide lines.
There are also non-diagonal glide lines to be found in the pattern. One of them is depicted in the next Figure.
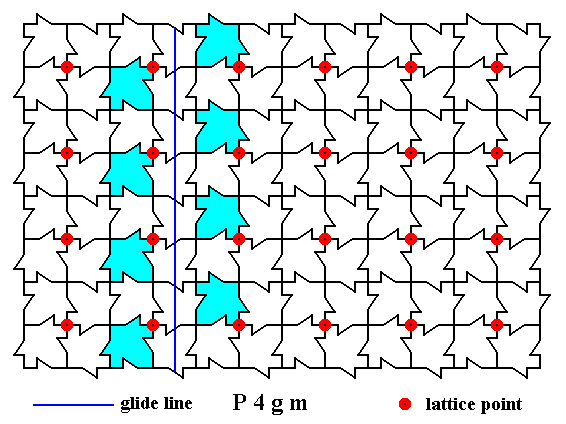
Figure 11. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
One non-diagonal glide line is indicated.
Next we indicate all the non-diagonal glide lines in one direction :
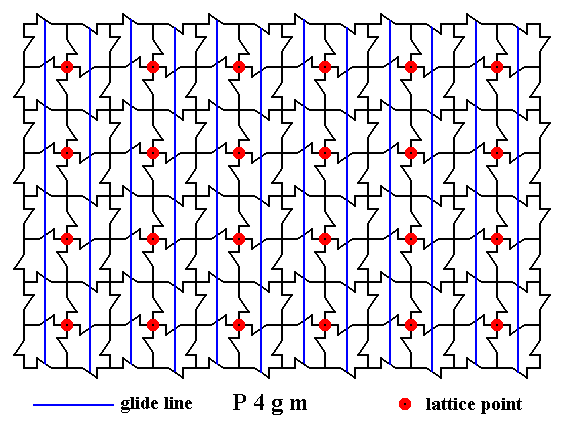
Figure 12. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
All non-diagonal glide lines in one direction are indicated.
Next we show all the non-diagonal glide lines in the other direction :
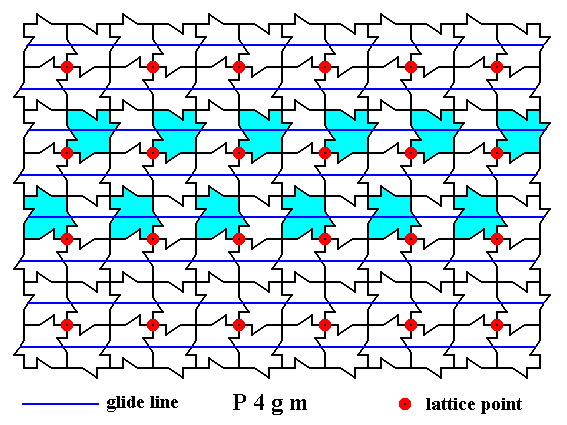
Figure 13. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
All non-diagonal glide lines in the other direction are indicated.
The next Figure gives all the non-diagonal glide lines of the pattern.
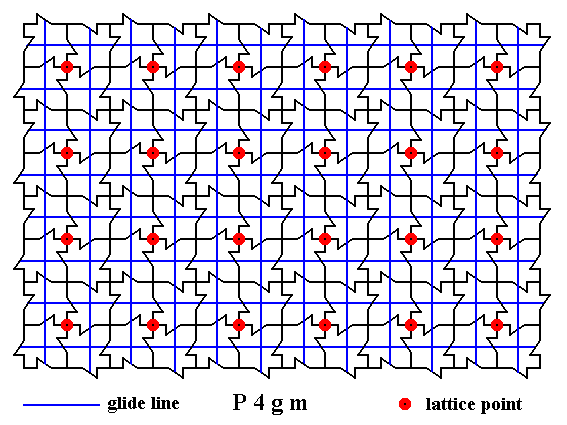
Figure 14. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
All non-diagonal glide lines inherent in the pattern are indicated.
The next Figure gives ALL the glide lines (diagonal and non-diagonal) inherent in the pattern.
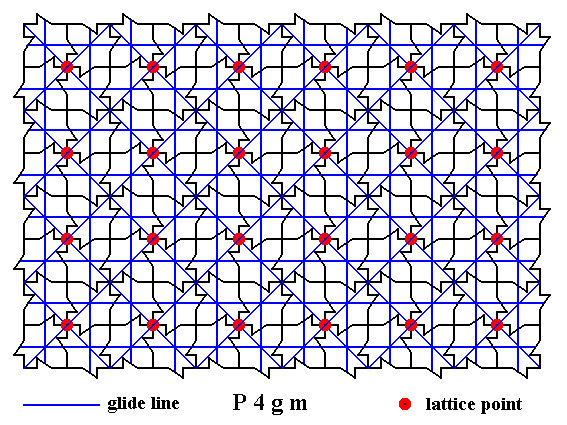
Figure 14a. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
All glide lines inherent in the pattern are indicated.
The next Figures, finally give ALL the mirror lines and ALL the glide lines inherent in the pattern.
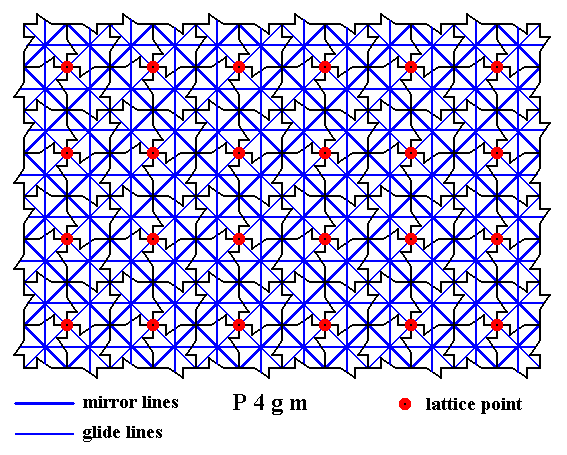
Figure 15. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
All mirror lines and glide lines inherent in the pattern are indicated.
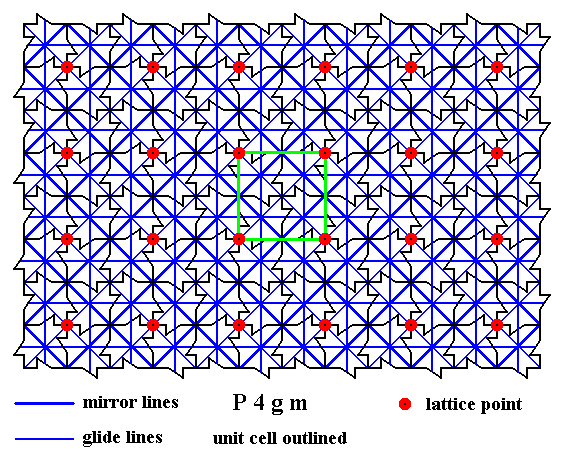
Figure 16. A two-dimensional array of canadian maple leaves. The pattern can be described and characterized by the Plane Group P4gm. Nodes (lattice points) are indicated by small red discs.
All mirror lines and glide lines inherent in the pattern are indicated.
The UNIT CELL is indicated (green lines).
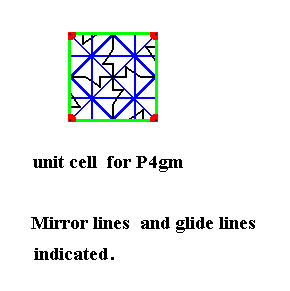
Figure 17. Isolated UNIT CELL of the maple leaf pattern of the above Figures. The pattern belongs to the Plane Group P4gm.
All mirror lines and glide lines inherent in the pattern are indicated.
The unit cell is primitive, it has nodes only at its corners. It is moreover square, so we have to do with the Square Net, representing the point lattice of the pattern. At each node there is a 4-fold rotation axis. In addition to these there is a 4-fold rotation axis in the center of the unit cell. At the center of each side of the unit cell there is a 2-fold rotation axis. See next Figure for those axes.
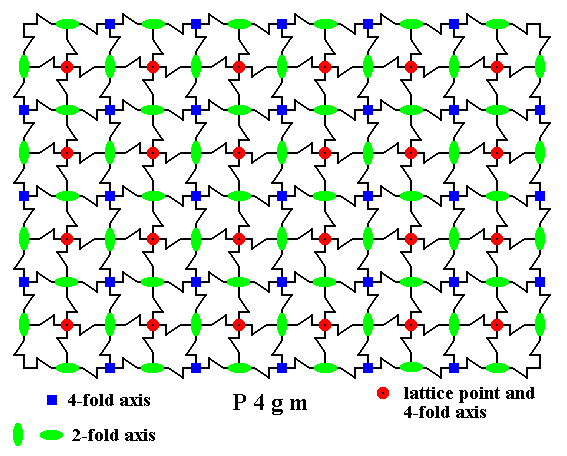
Figure 18. 4-fold and 2-fold rotation axes (perpendicular to the plane of the drawing) in the pattern of maple leaves belonging to Plane Group P4gm. The 4-fold rotation axes occur at the center of each unit cell as well as at each corner of that cell, i.e. at each node.
The 4-fold rotation axes are given as small blue squares or as small red discs.
The 2-fold rotation axes are given as small green ovals.
The next Figure depicts a (very small) crystal corresponding to our pattern of maple leaves :
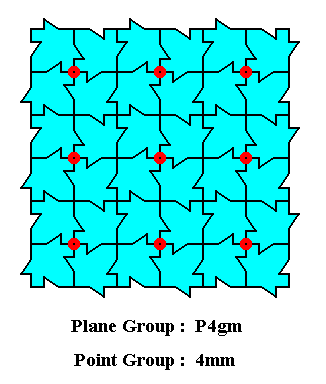
Figure 18a. A (very small) 2-dimensional crystal corresponding to the pattern of maple leaves.
The general outline of the 2-dimensional crystal of the above Figure is a square. The small zig-zag features at its margins ('faces') are macroscopically not visible, i.e. not visible when we take, instead of this microscopical crystal, a macroscopical version of it, i.e. when we let involve much more of its unit cells (and this means millions of them). To consider such a macroscopical version is equivalent to an elimination of all translations and thus the smoothing out of all features connected with them. The square has a point symmetry of 4mm : it possesses a 4-fold rotation axis at its center and two groups of mirror lines, diagonal and non-diagonal.
Based on the results so far obtained, the next document will be devoted to find the t e c t o l o g i c a l a s p e c t that must, in some way or another, be inherent in our periodic array of maple leaves (as it must be inherent in any periodic pattern).
To continue click HERE to proceed further with the preparation to the Promorphology of Crystals.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)
back to Allopola amphipleura and zygopleura
back to the Basic Forms of Cells I
back to the Basic Forms of Cells II
back to the Basic Forms of Organs
back to the Basic Forms of Antimers
back to the Basic Forms of Metamers
back to the Basic Forms of Persons
back to the Basic Forms of Colonies