Spiraxonia allogonia

First Family of the Spiraxonia

Stereometric Basic Form : Irregular spiral

Forms with an irregularly spirally curved main axis.
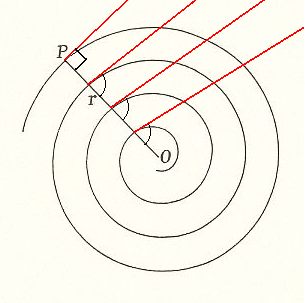
All organismic individuals of which the main body axis is coiled up into an irregular spiral belong promorphologically to the S p i r a x o n i a a l l o g o n i a. By "irregular spiral" we mean a spiral in which the angle between the radius vector and the tangent of the curve (in the point where the radius vector intersects the curve), i.e. the angle ALPHA, v a r i e s within the same individual (but does that in the same way in every individual of the given biological species). In the case where it varies in a regular way such that the angle increases gradually as the curve widens, and in the limit becomes 90⁰, we have to do with a limiting case (of the category of irregular spirals), the equable or Archimedian spiral. Although this spiral is, in a sense, regular, we we place it in the Allogonia because of its varying angle ALPHA. It is as has been said a limiting case of the Allogonia. See the next Figure.

Figure 1. The spiral of Archimedes. The red lines are the tangents to the whorls. The angles which they make with the radius vector change slowly as the spiral widens and in the limit become 90⁰. This limit is of course never reached, but is here symbolized in the last whorl drawn. ( Adapted from D'ARCY THOMPSON, 1942 )

In an Archimedian spiral the breadth of the whorls (i.e. the distance between the curve's points of intersection with one and the same radius) remains the same as the spiral widens. Almost all shells, on the other hand, have the form of an equiangular spiral (and as such belong promorphologically to the Isogonia). In such a spiral the breadth of the whorls increases in a constant ratio as the spiral widens. If the whorls of such a shell increase very slowly, the equiangular spiral will come to look like a spiral of Archimedes. The Nummulite is a case in point (A Nummulite is a relatively large unicellular coin-shaped shell-bearing organism, belonging to the Foraminifera). Here we have a large number of whorls, very narrow, very close together, and apparently of equal breadth, which give rise to an appearance similar to that of a coiled rope. And (D'ARCY THOMPSON, p. 754), in a case of this kind, we might actually find that the whorls were of equal breadth, being produced (as is apparently the case in the Nummulite) not by any very slow and gradual growth in thickness of a continuous tube, but by a succession of similar chambers laid on, round and round, determined as to their size by constant surface tension conditions and therefore of unvarying dimensions (The chambers in the shell of a Nummulite could have originated from a foamy protoplasmic mass in which favourable conditions for the accretion of calcarous matter may arise). See next Figures.

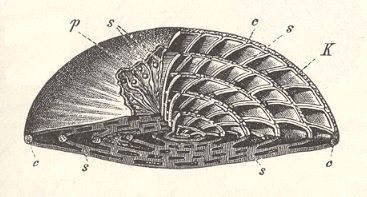
Figure 2. Nummulites sp.
K chamber position in the equatorial plane of the spiral.
s septa.
p pillar.
( After WEDEKIND, R., 1913 in Handwörterbuch der Naturwissenschaften, Band 8, p. 453 )

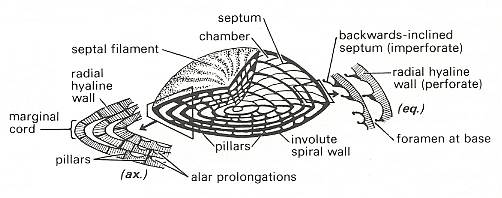
Figure 3. Nummulites sp.
Center : Test of Nummulites, showing axial (ax.) and equatorial (eq.) sections.
Left : detail of axial section.
Right : detail of spiral section.
( After BRASIER, M., 1980, Microfossils )

Figure 4. A fossil Nummulite from Egypt. (Approx. x 1.3).

The more typical members of the Allogonia are the g e n u i n e i r r e g u l a r s p i r a l s as they are materialized in some organisms. See the next Figures, that depict some aberrant Ammonites that should be assigned to the Allogonia (The overwhelming majority of species of Ammonites are built according to a (flat) equiangular spiral, and thus should be assigned to the Isogonia).

Figure 5. Heteromorphic ammonite.
( After CLARKSON, E., 1979, Invertebrate palaeontology and evolution )

Figure 6. Heteromorphic ammonite.
( After CLARKSON, E., 1979, Invertebrate palaeontology and evolution )

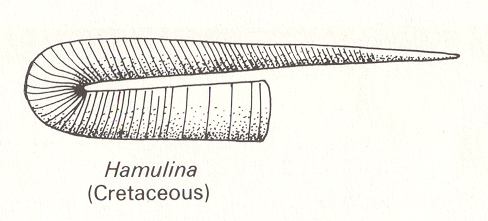
In Figure 3 the depicted form is not strongly reminiscent of a spiral. Its promorphological assignment to the Spiraxonia is biologically motivated : The given organism biologically belongs to a group (Ammonites) that is intimately connected with a spiral form.

To continue click HERE to proceed further with the systematic Promorphology.

e-mail :