The basic forms possessing c r o s s a x e s namely the Stauraxonia, that represent the other main division of the Protaxonia, are uncomparably more important and interesting than the Monaxonia, already because of the enormous diversity of different forms, which owe their origin to the many different possibilies of differentiation of certain cross axes. The diversity of shapes of all until now investigated basic forms is insignificant with respect to the extremely diverse animal and plant forms of the stauraxonic group. With the increasing possibility of "form bending" in different directions, also, it is true, the difficulty in assessing their basic form increases, explaining the fact that until now (1866) the geometric basic form that lies beneath all Stauraxonia is not as such recognized.
REMARK : I fear that even today -- 2002 -- this statement of Haeckel is still valid, especially because organic morphology is not much further developed scientifically since, if not, set back, with respect to that of Haeckel.
The Stauraxonia distinguish themselves from the Monaxonia first of all by the fact that in addition to the main axis (common to both groups) also other determined body axes are present, that are perpendicular to the former and that are different from the ones that lie between them (in the same transversal plane). The n u m b e r of such axes, that we call c r o s s a x e s ( S t a u r i ), is always equal to the number of a n t i m e r s, a number that is always finite, while it is infinite in the Monaxonia. In the previous Essay where the Protaxonia were introduced it was demonstrated why that statement is universally valid, despite the fact that the cross axes, and the meridian planes that contains them, come in two, or in fact three, varieties, depending on the number of antimers being even or uneven. Because of the importance of this relation for an understanding of stauraxonic forms it is necessary to establish it in a comprehensive way. In it we focus on the a n t i m e r s, that as third-order form individuals make up the metamers and persons (i.e. fourth-order and fifth-order form individuals). And what is valid for the antimers is at the same time also valid for the p a r a m e r s, that play an analogous role in second-order and first-order form individuals (organs and cells).
The c r o s s a x e s of the Stauraxonia either lie in the median plane of an antimer (half a radial plane) or in the boundary plane between two neighboring antimers (half an interradial plane), or, finally, half of it in a radial, half of it in an interradial cross plane. In order to precisely assess the relation between cross axes and antimers it is necessary to define in a precise way the concepts of r a d i u s and i n t e r r a d i u s (often used in different senses).
As r a d i u s we denote that half of a cross axis that lies in the median plane of an antimer.
As i n t e r r a d i u s we denote that half of a cross axis that lies in the boundary plane between two neighboring antimers.
In any particular case one can construct the r a d i u s of the antimer by drawing in the antimer's median plane (in the meridian plane containing both the mid-line of the antimer and the main axis of the metamer or person) a perpendicular onto the mid-point of the main axis, while the i n t e r r a d i u s can be constructed by drawing a perpendicular onto that same mid-point of the main axis, but now lying in the boundary plane between two neighboring antimers. The median plane of every antimer consequently is half a radial meridian plane, while the boundary plane between two neighboring antimers is half an interradial meridian plane.
Now we can discriminate three species of c r o s s a x e s ( S t a u r i ) as well as the three species of meridian planes corresponding to them, meridian planes that we call c r o s s p l a n e s ( P l a n a c r u c i a t a or s t a u r o t a ) :

Corresponding to these three types of cross axes we also can distinguish the three types of cross planes (meridian planes, that contain the cross axes) :
The number of antimers ( or the h o m o t y p i c b a s i c n u m b e r ) is equal to the number of cross axes (or to the number of cross planes), regardless whether this number is even (2n) or uneven (2n-1).
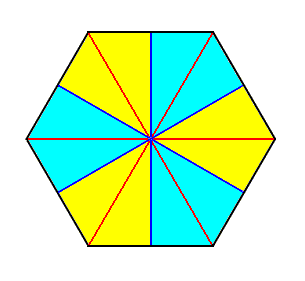
When the number of antimers is even (= 2n), as in most Coelenterates, the cross axes come in two types, half of them is radial, half of them interradial, resulting in the alternation of radial and interradial cross axes (See Figure 1 for six-fold forms).
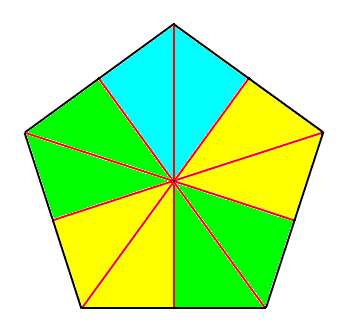
When, on the other hand, the homotypical basic number is uneven (2n-1), as in most Echinoderms, all cross axes belong to one type only, namely semiradial, and half of each cross axis is a radius, while the other half is an interradius (See Figure2).
In the next Figure we depict a six-fold pyramid and one of its meridian planes.
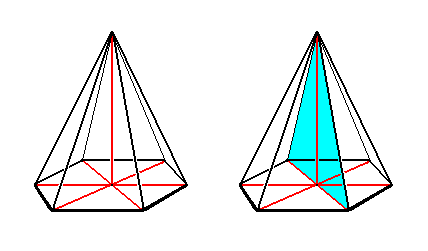
Remark : To this law we must add a pecularity. It occurs in a very small part of the Stauraxonia namely in a small part of the Centrepipeda or Heterostaura allopola, and among them only in a part of the Pentamphipleura (for example in irregular Echinoderms -- Spatangids etc.). This pecularity seems to represent an exception to that law, because, strictly speaking, the number of cross planes is twice as big as the number of antimers, by reason of the fact that the radii do not lie exactly opposite to the corresponding interradii, but instead making an angle with them. See Figures 4 and 5.
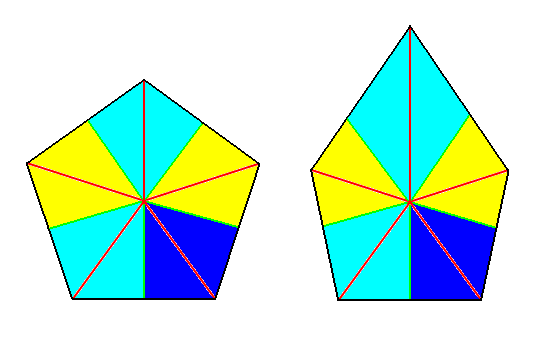
Figure 4. Left image : Base of a regular five-fold pyramid. The cross axes are semiradial. The interradial halves are straight continuations (extensions) of the corresponding radial halves. The five cross axes make angles of 360. The pyramid belongs to the P e n t a c t i n o t a. Right image : Base of an irregular five-fold pyramid possessing however the same angles ( 360 ) between the semiradial cross axes. Also here the interradial parts of the semiradial cross axes are straight continuations (extensions) of the corresponding radial parts. The pyramid belongs to the P e n t a m p h i p l e u r a.
The antimers are indicated by coloration.
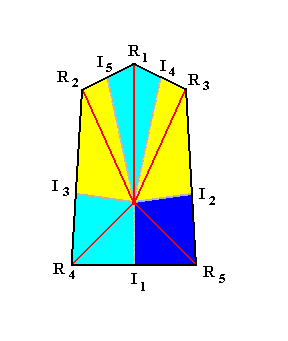
Figure 5. Base of an irregular five-fold pyramid. The five cross axes make angles different from 360. The interradial parts ( I ) of the cross axes are not straight continuations (extensions) of the corresponding radial parts ( R ) -- except with respect to the first cross axis ( R1I1 ) -- , but make an angle with them.
The pyramid belongs to ( a more irregular species of ) the P e n t a m p h i p l e u r a.
The antimers are indicated by coloration.
In Figure 5 we see that the radial part (R2) of the second cross axis makes an angle with its interradial counterpart (I2). The same phenomenon we see with respect to R3I3, R4I4 and R5I5. Only I1 is a straight continuation (extension) of R1.
R1I1, R2I2, R3I3, R4I4, R5I5
In classifying the Stauraxonia in subordinated form groups, important directives are the equality or unequality of the cross axes and their poles, as well as the number of cross axes. Still more important is the equality or unequality of the poles of the main axis according to which we can, just like in the Monaxonia, distinguish two main groups : equipolar (homopolar) and non-equiplolar (heteropolar) Stauraxonia, i.e. stauraxonic forms possessing equal poles and equal polar surfaces with respect to the main axis, and Stauraxonic forms possessing unequal poles and unequal polar surfaces with respect to the main axis.
In the S t a u r a x o n i a h o m o p o l a, corresponding to the Monaxonia haplopola in this respect, it is thus to be expected that the peristomial surface is equal to the antistomial surface. In the S t a u r a x o n i a h e t e r o p o l a, on the other hand, that are analogous to the Monaxonia diplopola, they are unequal.
In the first group the body is divided into two congruent halves by the equatorial plane (i.e. the transversal plane, perpendicular to the main axis, and containing its mid-point). In the Stauraxonia heteropola it is divided in two unequal parts.
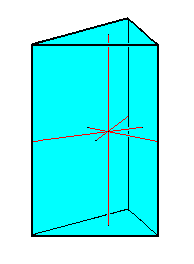
Remark : Here we consider the origin of the axial system to lie at the mid-point of the main axis. From this mid-point then radiate the cross axes. This should in any case be done in the case bipyramids, Stauraxonia homopola (as also in bicones). In the case of single pyramids, Stauraxonia heteropola (as also in single cones), we also can set the origin at the mid-point of the main axis, but here it could be convenient, to set the origin at the point on the base where the latter is pierced by the main axis. The cross axes then radiate from this point, and consequently lie in the base of the single pyramid instead of lying half way up inside the pyramid.
When we, after the forgoing discussion concerning the general characteristic properties of the Stauraxonia, want to find, within Stereometry, the simplest mathematical body possessing all those properties, it will be the s t r a i g h t p y r a m i d. Therby we must accept as basic form of the h e t e r o p o l a r stauraxonians the s i n g l e s t r a i g h t p y r a m i d, while that of the h o m o p o l a r stauraxonians should be the s t r a i g h t b i p y r a m i d.
We thus encounter also here the same general form law as in the case of the Monaxonia, namely that the lesser differentiated monaxonia haplopola (Bicone, Spheroid) appear to be composed of two congruent individuals, united by a polar plane, two individuals of the corresponding diplopolar (i.e. non-equipolar) forms (Cone, Hemispheroid). See the next Figure that depicts such a composition in the Stauraxonia.
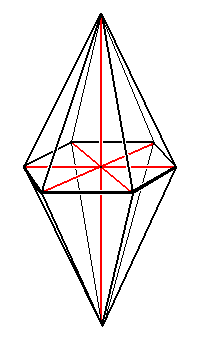
The main axis of the Stauraxonia is identical to that line that in Stereometry is simply called the axis of the straight pyramid. It is the line originating at the apex and perpendicular to the base of the pyramid and intersecting the center of the base.
Remark : "amphitectos" means : sharpened at both sides (edges), referring to a certain ancient type of sword.
All diagonals of the amphitect polygon intersect in its mid-point. The two sides at either end of each diagonal are pair-wise equal and parallel, implying that the angles, connected by such a diagonal, are equal.
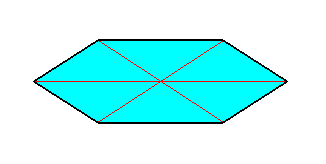
Strictly speaking only two of the four polygons that constitute every amphitect polygon are a b s o l u t e l y c o n g r u e n t, namely the ones that lie opposite to each other, while the neighboring polygons are s y m m e t r i c c o n g r u e n t, which means that they must be flipped in order to cover each other.
Those straight pyramids, of wich the base is an amphitect polygon, are called a m p h i t e c t p y r a m i d s.
The consideration of such pyramids is important, because this basic form is wide-spread. An eight-fold amphitect pyramid, is, for instance, the basic form of the Ctenophores (sea-gooseberries or comb-jellies) ( See Figure 9 ).
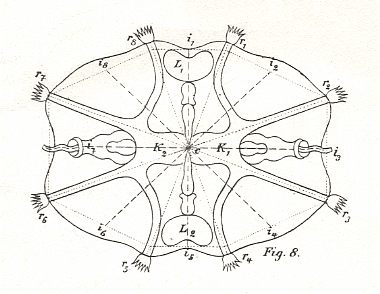
( After HAECKEL, 1866, Generelle Morphologie der Organismen, Fig. 8 from Tafel I. )
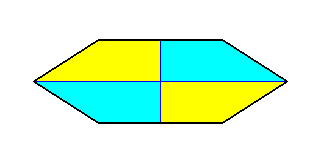
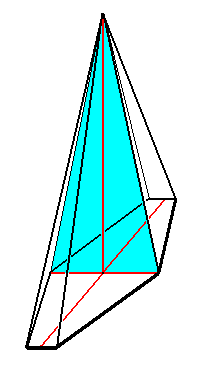
The main axis of these Stauraxonia is that line that connects the apex of the pyramid with the center of its base. The pyramid's apex is its aboral, its base its oral pole. The two meridian planes, that are perpendicular to each other, and that contain the main axis and both ideal cross axes of the amphitect pyramid, we can call d i r e c t i o n a l p l a n e s ( P l a n a e u t h y p h o r a ) or i d e a l c r o s s p l a n e s, in contradistinction to the r e a l c r o s s p l a n e s, that go through all the edges and through the mid-lines of all the sides of the pyramid, and, of course through its main axis ( See Figure 7 and 12 where the traces of the real cross planes are indicated in the amphitect pyramid's base ). The r e a l c r o s s a x e s (or cross axes in a narrower sense) are those lines perpendicular to the main axis, that are contained in the real cross planes and go through the edges of the pyramid as well as exactly between them. In an amphitect pyramid half of the the r e a l cross axes are r a d i a l , half of them are i n t e r r a d i a l (See also Figure 12 where this is illustrated by showing the b a s e s of some possible amphitect pyramids). The base of such a pyramid is p o i n t s y m m e t r i c which means that every two features that lie oposite to each other with respect to the center of the base are equal. That's why there are no semiradial cross axes.
The next two Figures depict some possible amphitect polygons representing bases of possible amphitect pyramids. In the first Figure the ideal cross axes are indicated, while the real cross axes and antimers are indicated in the second Figure.
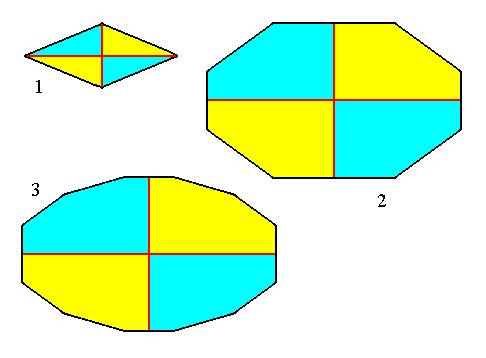
Figure 11. Some amphitect polygons representing bases of possible amphitect pyramids.
(1). Four-sided amphitect polygon (Rhombus).
(2). Eight-sided amphitect polygon.
(3). twelve-sided amphitect polygon.
The ideal cross axes ( E u t h y n i ) are indicated in red. In each case they bring about a partition into four sub-polygons.
In (1) the (two) ideal cross axes are both radial, in (2) they are interradial, and in (3) they are also interradial. In six-sided amphitect polygons, like we see in Figure 8, one ideal cross axis is radial, while the other is interradial.
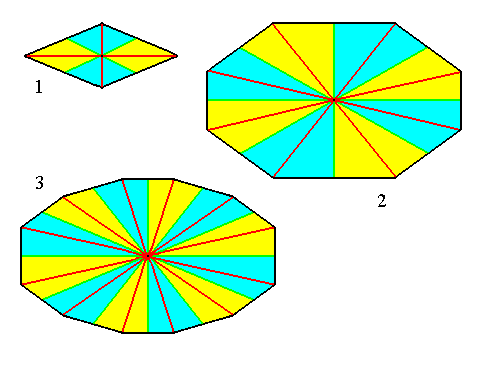
Figure 12. Some amphitect polygons ( the same as the ones in the previous Figure ) representing bases of possible amphitect pyramids. Radial and interradial cross axes and antimers are indicated.
(1). Four-sided amphitect polygon (Rhombus). Four antimers.
(2). Eight-sided amphitect polygon. Eight antimers.
(3). Twelve-sided amphitect polygon. Twelve antimers.
Radial cross axes are indicated in red. Interradial cross axes are indicated in green. The radial cross planes ( containing the radial cross axes ) are the median planes of the antimers. The interradial cross planes ( containing the interradial cross axes ) are the planes separating adjacent antimers. The antimers are indicated in yellow and blue.
The r e g u l a r p y r a m i d that lies at the basis of a part of the Stauraxonia, is, as is stated in Geometry, a pyramid of which the base is a regular polygon and of which its sides are all isosceles triangles that are congruent with respect to each other.
The above considerations with respect to the most important features of the regular and the amphitect pyramid, as the general basic form of the Stauraxonia, are valid for the single pyramid, i.e. the heteropolar form, as well as for the bipyramid of the homopolar stauraxonians. The latter can in all cases be interpreted as an aggregate of two congruent straight pyramids united with their bases. Among the simple (heteropolar) straight pyramids as well as among the straight bipyramids (homopolar), there are regular and amphitect forms. The former with equal, the latter with unequal ideal cross axes.
Pyramidal bodies with a homopolar main axis.
The homopolar stauraxonians are just a small group when compared with that of the heteropolar stauraxonians. A large numger of Protists, especially Diatomeans and Radiolarians belongs to it. They are interesting because of the fact that they express the geometric forms neatly and because of their conformity with certain crystal forms.
Remark : Haeckel laid much emphasis on a comparison of organic forms with those of crystals, but we must stress that crystals possess a p e r i o d i c structure while organisms do not. Their structure is t e c t o l o g i c a l , i.e. they are generally constituted by similar units that group themselves about an axis ans so have different orientations with respect to one another or are symmetrically placed with respect to a plane and thus are not related to each other by a linear translation.
The pattern of atoms in crystals and their resulting outward form can be explained by several possible stacking procedures effecting close packing and a minimum of potential energy, while the stereometric form of organisms cannot be so explained.
The basic form of the present promorphological category is a straight bipyramid, either regular or amphitect. Such a type pyramid shows a rich diversity with respect to the number of sides, implying a different number of antimers. When this number is four the basic form is an octahedron. The main axis of which the poles and polar surfaces are always equal can be greater or smaller than the cross axes.
The homopolar stauraxonians divide into two groups, I s o s t a u r a and A l l o s t a u r a, according to the ideal cross axes being equal or unequal. The basic form of the Isostaura is the regular bipyramid, the basic form of the Allostaura on the other hand is the amphitect bipyramid. The common base of the united congruent pyramids of which the body of the homopolar stauraxonians is composed is a regular polygon in the Isostaura, while it is an amphitect polygon in the Allostaura.
When we, in the homopolar stauraxonians, do not consider the real cross axes and the corresponding number of antimers, but only their ideal cross axes, then the agreement of their basic form with the form of certain crystals is conspicuous. We only need to connect the poles of the main axis with those of the ideal cross axes by straight lines and put a plane through every two neighboring connecting lines, to obtain the crystal form of the octahedron, which is determined by three perpendicular homopolar axes that divide each other in equal halves. When all three axes are different, as in all Allostaura, then the equatorial plane is a rhombus (i.e. in all cases of Allostaura where the ideal cross axes are the only (radial) cross axes in the given form) and the corresponding stereometric basic form then is the rhombic octahedron as the general form of the Orthorhombic Crystal System.
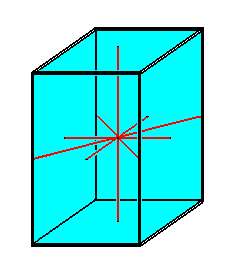
When, on the other hand, the ideal cross axes are equal, and only the main axis different, as in all Isostaura, the equatorial plane is a square (i.e. in all cases of Isostaura where the ideal cross axes are the only (radial) cross axes in the given form), and the corresponding stereometric basic form then is the quadratic octahedron as the general form of the Tetragonal Crystal System (also called the Quadratic System).
When, finally, all three axes are equal, the stereometric basic form is the regular octahedron as the general form of the Isometric Crystal System (also called the Tesseral or Cubic System). But the latter form does not belong to the present promorphological category anymore, because the main axis does not stand out. It belongs to the Polyaxonia rhythmica. It is mentioned again here to emphasize the close geometric kinship of these basic forms, a kinship namely between the absolutely regular Polyaxon forms and the almost regular Stauraxon forms.
The Quadratic Octahedron of the homopolar stauraxonians can be derived from the Regular Octahedon of the rhythmic polyaxonians by elongating one of the equal axes of the latter towards both poles by the same amount, making it the main axis.
In the Tetragonal and Orthorhombic crystal systems the Octahedron occurs as one of their F o r m s. Such a Form can be generated by subjecting an initial face to the symmetry elements of a given crystal class belonging to a given Crystal System. When we subject an initial face, that has the most general orientation (in contradistinction to a special orientation) with respect to the axial system of the Tetragonal Crystal System, to the symmetry elements of its most symmetric class we'll end up with a Quadratic Octahedron. When we perform the same operation, but now within the confines of the Orthorhombic Crystal System, we'll end up with a Rhombic Octahedron. When, on the other hand, we choose as initial face a face parallel to the crystallographic main axis (and thus a face with a special orientation), then we will end up with a prismatic column. Whithin the Tetragonal System that will be a column of which the base is a Square, while within the Orthorhombic System its base is a Rhombus. The Quadratic Prism of the Tetragonal Crystal System could then, in addition to the Quadratic Octahedron of that same System, alternatively be seen as the Basic Form of the (next to be discussed) Isostaura, while the Rhombic Prism of the Orthorhombic Crystal System could, in addition to the Rhombic Octahedron of that same System, alternatively be seen the Basic Form of the (later to be discussed) Allostaura. The Isostaura and the Allostaura are the two subdivisions of the Stauraxonia homopola, and, according to what has just been said, their respective Basic Form can either be seen as an octahedron (quadratic, respectively rhombic) or a prism (quadratic, respectively rhombic). And indeed we find (according to Haeckel) both prismatic forms realized in certain Radiolarians.
While of the Stauraxonia the h e t e r o p o l a r stauraxonians (monopyramids) enjoyed most of the attention of morphologists, the homopolar stauraxonians were more or less neglected. They are however interesting because of the above mentioned ties with the axial systems of the mentioned Crystal Systems.
Regular Pyramidal bodies with a homopolar main axis.
The Stauraxonia homopola with either equal radial, or equal interradial, or equal semiradial cross axes, which are called I s o s t a u r a, have as their Basic Form the r e g u l a r b i p y r a m i d, or, when we only consider the two ideal cross axes, the Q u a d r a t i c O c t a h e d r o n, or, as we saw above, the Q u a d r a t i c P r i s m.
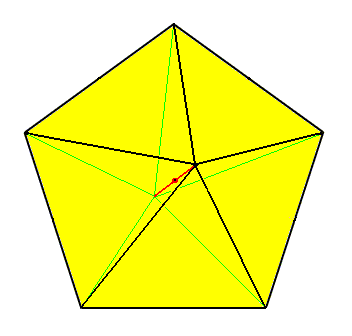
The next Figure gives a possible member of the Homopola Isostaura, the Pentagonal Bipyramid. It does not and cannot (also) occur as a Form in any Crystal System.
The next Figure depicts a possible member of the Homopola Isostaura, the Hexagonal Bipyramid. It is also one of the possible Forms in the Hexagonal Crystal System.


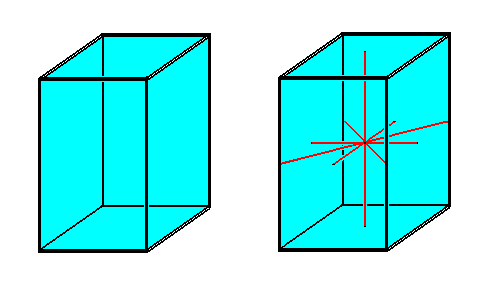
The next Figure gives the Quadratic Prism which has the same axial system as the Quadratic Octahedron. Its four vertical sides together make up one of the possible (open) Forms in the Tetragonal Crystal System.
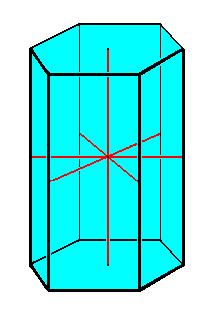
The next Figure depicts yet another possible member of the Homopola Isostaura, the Hexagonal Prism. Its six vertical sides together make up also one of the (open> Forms in the Hexagonal Crystal System.
In a natural way we can divide the Isostaura into two groups according to the homotypic basic number (i.e. according to the number of antimers) being f o u r or some other number.
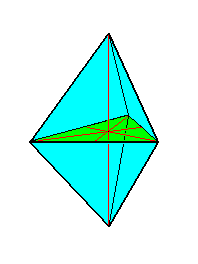
Those homopolar stauraxonians that belong to the Isostaura polypleura (also called I s o s t a u r a o x y g o n i a ) have as their basic form a regular bipyramid with six, ten, twelve or more (generally 8+2n) congruent sides. The number of antimers consequently will be three, five, six or more. The number of real cross axes is equal to that number. These real cross axes either do not at all or only partly coincide with the ideal cross axes, and consequently meet at acute angles (Oxygonia). The next Figure depicts a 3-fold bipyramid as a possible member of the Isostaura polypleura. It is at the same time a possible Form in the Hexagonal Crystal System. Its equatorial plane is an equilateral triangle.
Another possible member of the Isostaura polypleura (as depicted earlier) is the 6-fold bipyramid (Hexagonal Dodecahedron), that is also a possible Form in the Hexagonal Crystal System. It is materialized in certain pollen cells.

So to the present group belong all regular bipyramids except the eight-sided ones.
Of all organisms it is again the Radiolarians, then the Diatomeans and many pollen grains, that materialize the polypleural isostaurs very well. One time as regular bipyramid, another time as regular prism.
Among all species of bipyramids the one with eight equal faces shows the simplest relations and immediately connects itself to the regular octahedron of the rhythmic polyaxonians. The basic Form of the octopleural isostaurs is the Quadratic Octahedron, that is, as has been said, also a possible Form in the Tetragonal Crystal System.

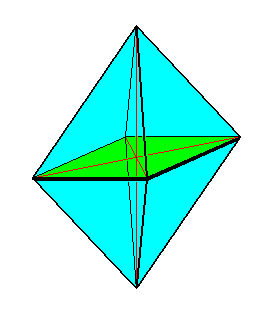
The radial real cross axes coincide with the ideal cross axes and meet at right angles, so these forms can also called I s o s t a u r a o r t h o g o n i a. These cross axes are the diagonals of the square which is the equatorial plane of the octahedron. The main axis is in those animal forms that belong to the present group very diversely developed, sometimes longer, sometimes significantly shorter than the radial cross axes (which are equal).
The Quadratic Prism is the basic form of many single cells like Diatomeans and pollen cells.
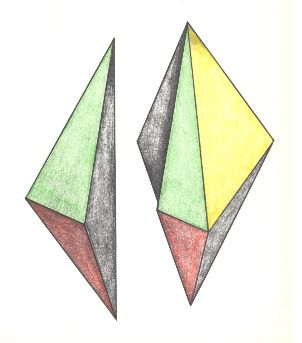
More or less linked to the Homopola isostaura are some forms looking like a Scalenohedron. Their equatorial plane is not planar. Apart from this, the forms look like (more or less regular) bipyramids. We see these forms in certain Crystals. Because no organisms are expected to realize these forms we introduce them in the INFRAME below. The reason why they are introduced into a system of ORGANIC forms is to connect this system with the forms of the inorganic world. After all, a number of inorganic promorphs do occur in some Organisms as well. So inorganic morphology is crossing the border here and there to organic morphology. Because of this we want to make the Promorphological System susceptible to all inorganic forms (i.e. forms of inorganic true beings).
The homopolar stauraxonians with unequal cross axes, which we will call Allostaura for short, have as a definite basic form the a m p h i t e c t b i p y r a m i d, or, when we only consider the (two) ideal cross axes and not the real cross axes, the r h o m b i c o c t a h e d r o n. So the axial system of this group corresponds to that of the Orthorhombic Crystal System, in which, among others Sulphur and Aragonite crystallize.
The Allostaura devide into two groups, depending on whether the homotypic basic number ( = number of antimers) is four or some other number. These two groups consequently correspond to the two divisions of the Isostaura. They can be repectively named as Allostaura octopleura and Allostaura polypleura. In the a l l o s t a u r a o c t o p l e u r a or the eight-sided amphitect bipyramids (with four antimers), that are consequently Rhombic Octahedrons, the unequal radial axes (i.e. the radial real cross axes) coincide with the two ideal cross axes and meet at right angles. By reason of this fact they could also be called o r t h o g o n i a.
In the a l l o s t a u r a p o l y p l e u r a, or the many-sided amphitect bipyramids, that contrast with the orthogonia as o x y g o n i a, the radial axes (the radial real cross axes) meet in acute angles, because their number is at least three, implying that they either cannot at all or only partially coincide with the two ideal cross axes. Because the homotypic basic number should always be even (2n), half of the real cross axes is radial, half of them interradial. The minimum number of antimers in the Allostaura polypleura is consequently six, then eight, ten, twelve, etc. (2n, in which n is minimal 3).
As in the Isostaura, we can also in the allostaura assess the octopleura as a special form of the polypleura, namely as the simplest of them, and closest to the regular polyhedra.
Those homopolar stauraxonians that represent the division of the Allostaura polypleura (or oxygonia) have as their basic form the m a n y - s i d e d a m p h i t e c t b i p y r a m i d. Its general properties are already treated of above.
Because the eight-sided amphitect bipyramid or rhombic octahedron as the special simple form representing the special group of the Allostaura octopleura, is excluded, and because the number of antimers in the amphitect bipyramid is always even, a member of the Allostaura polypleura always must consist of at least six, then eight, ten, twelve, and generally of 4+2n antimers. The number of sides, that is twice the number of antimers, must minimal be twelve, then sixteen, twenty, etc., generally 8+4n.
Because at least three radial cross axes must be present, the either cannot at all, or only partially coincide with the two ideal cross axes and must therefore meet at acute angles. See the Figures below.
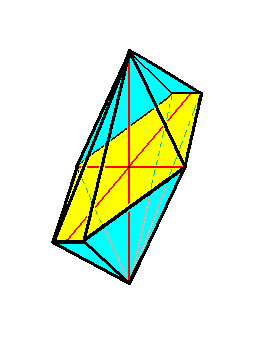
The corresponding amphitect prism is depicted in the next Figure.
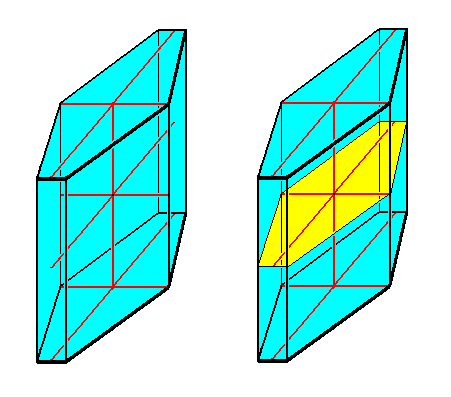
Figure 25. The six-sided amphitect prism. The equatorial plane is emphasized (yellow) in the right image. The ideal cross axes (Euthini) are contained in the equatorial plane (they are repeated in the bases for reasons of clarity).
The polypleural allostaura form is among all homopolar stauraxonians the least common in the organic world. It only occurs in a few types of pollen grains and in some Radiolarians.
The eight-sided amphitect bipyramids, that represent the special form of the Rhombic Octahedron, relate to the more general forms, the polypleura, (having at least twelve, and generally 8+4n sides), in the same way as do the octopleural isostaurs to the polypleura. In both cases, in the Isostaura as well as in the Allostaura, the essential difference between the octopleura and the polypleura consists of the fact that in the octopleura only two radial cross axes are present, meeting at right angles, and coinciding with both ideal cross axes, while in the polypleura more than two radial (or semiradial) do exist, that meet at acute angles.
The next Figures depict some members of the present group.
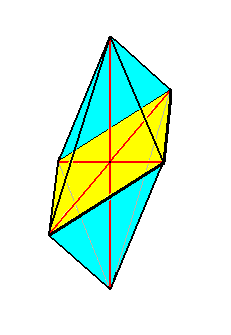
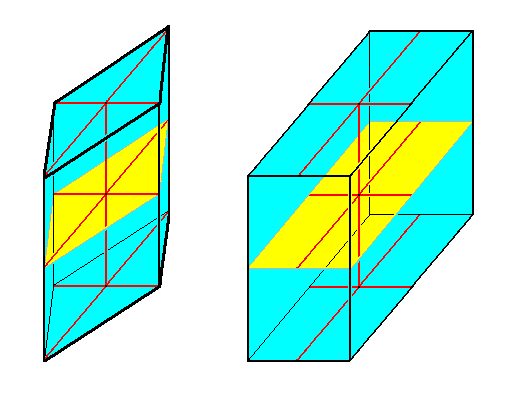
Figure 27. Two symmetrically equivalent variants of the Allostaura octopleura.
Left image : A Rhombic Prism. Its base (and also its equatorial plane) is a Rhombus.
Right image : Rectangular Prism. Its base (and also its equatorial plane) is a Rectangle.
The equatorial plane is indicated in yellow. The main axis and the ideal cross axes are given in red. All the cross axes originate from the mid-point of the main axis and lie in the equatorial plane. They are repeated in the top and bottom planes (bases) for reasons of clarity.
The two geometrical objects depicted in the above Figure have the same axial relations : three non-equivalent and homopolar axes perpendicular to each other. Several shapes can be based on such an axial system : Rhombic Bipyramid (Figure 26), Rhombic Prism (Figure 27) and Rectangular Prism (Figure 27). We depict those different shapes in order to clearly understand the symmetry involved in objects allowing for the just described axial system, and to anticipate possible organic representatives. The difference between the two prisms depicted above should be a reflection of a corresponding organic difference. The next Figure shows the equatorial planes of such prisms and indicates the a n t i m e r s. We can see that the latter are different in each case : while the antimers of the Rhombic Prism are each for themselves symmetric with respect to their median plane (in the figure we see its trace, a line), in the Rectangular Prism they are not so symmetric.
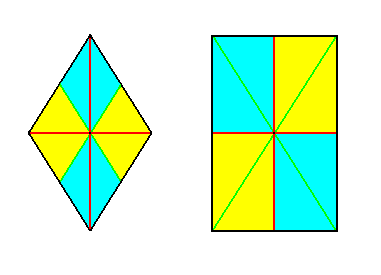
Figure 28. Equatorial planes of two symmetrically equivalent variants of the Allostaura octopleura.
Left image : Equatorial plane (or base for that matter) of a Rhombic Prism.
Right image : Equatorial plane (or base for that matter) of a Rectangular Prism.
The antimers are indicated as yellow and blue. The ideal cross axes (directional axes) are indicated in red. In the Rhombic Prism they are radial, while in the Rectangular prism they are interradial. The other cross axes are indicated in green. In both case there are four cross axes present, and consequently four antimers. But while the antimers of the Rhombic Prism are severally symmetrical, they are asymmetrical in the Rectangular Prism with respect to their median planes (here depicted as lines).
In the next Figure one a n t i m e r is emphasized in an eight-sided bipyramid (Rhombic Octahedron).
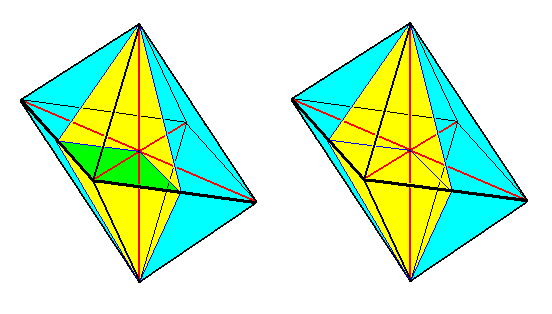
Figure 29.
Left image : Rhombic Octahedron (basic form of the Allostaura octopleura) with one antimer indicated (yellow). The equatorial plane of that antimer is indicated in green.
Right image : The same as left image, but now the indication of the antimer's equatorial plane omitted.
The axial system of the Allostaura octopleura, insofar as it consists of the main axis and the ideal cross axes, is exactly the same as the axial system characterizing the Orthorhombic Crystal System : three non-equivalent axes perpendicular to each other. In the Rhombic-bipyramidal Class of that crystal system all three axes are moreover homopolar, like they are in all Allostaura octopleura.
In the above we have presented two subgroups of the Stauraxonia homopola, namely the Homopola isostaura and the Homopola allostaura.
To continue click HERE to proceed further with the systematic Promorphology (Homopola sigmostaura).
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia