

The forms that are about to be considered are SPIRALS.
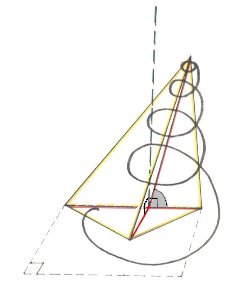
Figure 1. Lateral view of an oblique 3-sided pyramid. The one oblique main axis causes the axial system to be identical to the crystalligraphic axial system of the Monoclinic Crystal System. The Ortho-axis is pointed to the beholder, while the Clino-axis is drawn obliquely upright (The axis that is here drawn horizontally corresponds to the crystallographic Vertical Axis). This oblique pyramid was supposed to be basic form of all turbinate molluscan shells.
In this way PRZIBRAM proposed to separate from Haeckel's Dysdipleura a group called (by him) "Dyspleura". But this proposal leads to the total neglect of the s p i r a l itself and concentrates exclusively on the symmetry of the global outer, more or less conical, shape that results from the coiling up of something into a spiral while translating along the spiral's axis.
So although they are, in a way, promorphologically akin to dysdipleural forms, it is evident that the s p i r a l s deserve a promorphological category of their own : The Spiral, that we can draw as a curved line running through the relevant organismic form individual, is the m a i n a x i s of that individual. This main axis has the form of a spiral, either of an a r c h i m e d i a n s p i r a l or of an e q u i a n g u l a r s p i r a l, or, finally, of an irregular spiral. This spiral main axis can either lie in the same plane, resulting in a discoid form, like in Ammonites, or be drawn out into a third dimension, resulting in a turbinate form, like in most snails.
So the spiral forms are a special division (i.e. subgroup) of Protaxonians.
Two divisions of the Protaxonians are already dealt with : Monaxonia and Stauraxonia. The third division we will call "S p i r a x o n i a" ( from spira = coil ). It is the last division (Suborder) of the Protaxonia, and concludes our promorphological Scheme.
Before we elaborate in more detail on the features of spirals, we give a succinct overview of the possible subgroups of the Spiraxonia :
This main axis is spirally coiled up, and it is this spiral that we will further investigate. In so doing we will base ourselves heavily on D'ARCY THOMPSON, 1942, On Growth and Form, where he, in Chapter XI, treats of the properties of spirals, especially the equiangular spiral, in connection with organisms.
General definition of a Spiral.
A Spiral is a curve which, starting from a point of origin, continually diminishes in curvature as it recedes from that point. Or in other words, whose r a d i u s o f c u r v a t u r e continually increases.
This definition is wide enough to include a number of different curves, but on the other hand it excludes at least one which in popular speech we are apt to confuse with a true spiral. This latter curve is the simple cylindrical screw, or cylindrical helix, which curve neither starts from a definite origin nor changes its curvature as it proceeds.
The spirals of which we will treat should be permanent spirals, this means that we exclude from consideration the coil of an elephant's trunk (but not that of its tusks), the coils of a cuttle fish's arm or of a monkey's or a chameleon's tail. Such non-permanent coils relate more to a position or an attitude than to a f o r m.
Further there is a difference between such a spiral conformation as is built up by the separate and successive florets in the sunflower, and that which, in the snail or Nautilus shell, is apparently a single and indivisible unit. And a similar if not identical difference is apparent between the Nautilus shell and the minute shells of the Foraminifera which so closely simulate it : inasmuch as the spiral shells of these latter are composite structures, combined out of successive and separate chambers, while the molluscan shell (snails), though it may (as also in Nautilus) become secondarily subdivided, has grown as one continuous tube.
In the elementary mathematics of a spiral, we speak of the point of origin as the p o l e (O). This pole is, promorphologically one of the two poles of the main axis of a spiral organic individual. A straight line having its extremity in the pole, and revolving about it, is called the r a d i u s v e c t o r (r). A point (P), travelling along the radius vector under definite conditions of velocity, will then describe a spiral curve.
Of several mathematical curves whose form and development may be so conceived, the two most important (and the only two with which we need to deal) are those which are known as (1) the equable spirals, or spirals of Archimedes ( S p i r a x o n i a a l l o g o n i a ), and (2) the equiangular or logarithmic spirals ( S p i r a x o n i a i s o g o n i a ).
The spiral of Archimedes may be roughly illustrated by the way a sailor coils a rope upon the deck. Each whorl is of the same breadth as that which precedes it and as that which follows it.
Using its ancient definition, we may define it by saying, that "If a straight line revolve uniformly about its extremity, a point which likewise travels uniformly along it, will describe the equable spiral". Or, putting the same thing into our more modern words, "If, while the radius vector revolve uniformly about the pole, a point (P) travel with uniform velocity along it, the curve described will be that called the equable spiral or spiral of Archimedes". See next Figure.
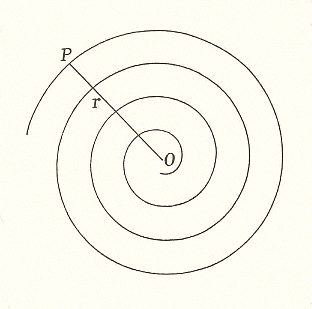
It is plain that the s p i r a l o f A r c h i m e d e s may be compared, although roughly, to a cylinder coiled up. It is plain also that a radius ( r = OP ), made up of the successive and equal whorls, will increase in a r i t h m e t i c a l progression : and will equal a certain constant quantity (a) multiplied by the whole number of whorls, (or more strictly speaking) multiplied by the whole angle (THETA) through which it has revolved : so that r = a(THETA). And it is also plain that the radius meets the curve (or its tangent) at an angle which changes slowly but continuously, and which tends towards a right angle as the whorls increase in number and become more and more circular.
But, in contrast to this, in the e q u i a n g u l a r s p i r a l of the Nautilus (Figure 4) or the snail shell or the foraminifer Globigerina, the whorls continually increase in breadth, and do so in a steady and unchanging ratio. We can define it as follows:
"If, instead of travelling with a uniform velocity, our point move along the radius vector with a velocity i n c r e a s i n g a s i t s d i s t a n c e f r o m t h e p o l e, then the path described is called an equiangular spiral".
Each whorl which the radius vector intersects will be broader than its predecessor in a definite ratio. The radius vector will increase in length in g e o m e t r i c a l progression, as it sweeps through the successive equal angles. And the equation to the spiral will be r = aTHETA [ i.e. the length of a radius, made up of successive whorls (and thus a part of the radius vector), is proportional to the constant a brought to the power of THETA, where THETA is the whole angle through which the radius vector has revolved ].
As the spiral of Archimedes, in our example of the coiled rope, might be looked upon as a coiled cylinder, so (but equally roughly) may the equiangular spiral, in the case of the shell, be pictured as a cone coiled upon itself. For the equiangular spiral, see the next Figure.
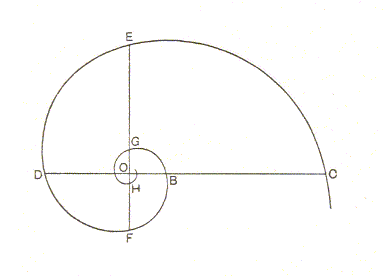
Starting with the conception of a g r o w i n g curve which should cut each radius vector at a constant angle ( ALPHA ), DESCARTES showed how it would necessarily follow that radii at equal angles to one another at the pole would be in continued proportion and that the same is therefore true of the parts cut off from a common radius vector by successive whorls or convolutions of the spire. And furthermore, that distances measured along the curve from its origin, and intercepted by any radii, as at B, C, (Figure 3), are proportional to the lengths of these radii, OB, OC. It follows that the sectors cut off by successive radii, at equal vectorial angles (i.e. angles of rotation), are similar to one another in every respect. And it further follows that the figure may be conceived as growing continuously without ever changing its shape the while.

The many specific properties of the equiangular spiral are so interrelated to one another that we may choose pretty well any one of them as the basis of our definition, and deduce the others from it by analytical methods or by elementary geometry.
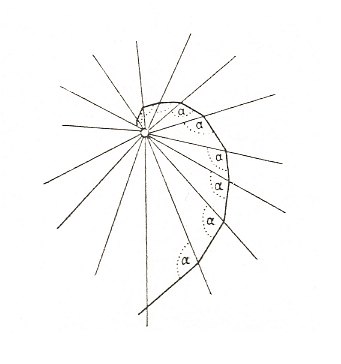
The equiangularity of the logarithmic spiral is well illustrated by the path of certain insects as they draw towards a light. Owing to the structure of their compound eyes, these insects do not look straight ahead but make for a light which they see abeam, at a certain angle. As they continually adjust their path to this constant angle, a spiral pathway brings them to their destination at last (D'ARCY THOMPSON, 1942, p. 756). See the next Figure.
In mechanical structures, c u r v a t u r e is essentially a mechanical phenomenon. It is found in flexible structures as the result of b e n d i n g, or it may be introduced into the construction for the purpose of resisting such a bending-moment. But neither shell nor tooth nor claw are flexible structures. They have not been b e n t into their peculiar curvature, they have g r o w n into it.
In the case of the equiangular spiral we encounter a very remarkable property : the shell, like the creature within it, grows in size b u t d o e s n o t c h a n g e i t s s h a p e.
We can express this mathematically as follows :
"Any [plane] curve proceeding from a fixed point (which is called the pole), and such that the arc intercepted between any two radii at a given angle to one another is always similar to itself, is called an equiangular, or logarithmic spiral".
In this definition, we have the most fundamental and intrinsic property of the curve, namely the property of continual similarity, and the very property by reason of which it is associated with organic growth in such structures as the horn or the shell. For it is peculiarly characteristic of the spiral shell, for instance, that it does not alter as it grows. Each increment is similar to its predecessor, and the whole, after every spurt of growth, is just like what it was before.
The shell retains its unchanging form in spite of its a s s y m e t r i c a l growth. It grows at one end only, and so does the horn. And this remarkable property of increasing by t e r m i n a l growth, but nevertheless retaining unchanged the form of the entire figure, is characteristic of the equiangular spiral, and of no other mathematical curve.
If we add something, let us call it G, to a given figure ( F ), such that the figure will increase in size, but will retain its original shape, then we call G a gnomon to F.
So every growth increment in the shell is a gnomon to the preceding form of the shell, i.e. to the form of the shell that it had just before the increment was added. The next Figure shows that the equiangular spiral is intimately connected with the generation of gnomons to a given structure.
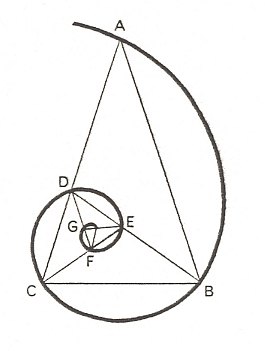
Let us consider an isosceles triangle ABC (Figure 6) having one angle of 360, and the other two angles, therefore, each equal to 720. Then by bisecting one of the angles of the base, we subdivide the large isosceles triangle into two isosceles triangles, of which one, namely DBC, is similar to the whole figure ABC, while the other, ABD, is the gnomon to DBC. So if we take this isosceles triangle ABC (but the same is possible with many other gnomic figures), and add to it (or subtract from it) in succession a series of gnomons, so converting it into larger and larger (or smaller and smaller) triangles all similar to the first, we find that the apices (or other corresponding points) of all these triangles have their l o c u s upon an equiangular spiral.
As has been said, the spirally curved main body axis, whether it be according to the Archmedian spiral (Spiraxonia allogonia) or to the equiangular spiral (Spiraxonia isogonia), can, as a spiral, lie wholly in one plane (Spiraxonia planata), like we see in most Ammonites, or be subjected to screw translation along the axis of the spiral (Spiraxonia aplanata), like we see in most snails.
Because the S p i r a x o n i a i s o g o n i a (the forms based on an equiangular spiral) are much more important than the Spiraxonia allogonia (the forms based on an Archimedian spiral, or on irregular spirals), we will concentrate on the former.
A shell of a gastropod can be imagined as a tube that is coiled up into an equiangular spiral. As has been said earlier, the shape of the transverse section of that tube can be any form. For convenience we take it, for the time being, to be a circle.
In fact there are three parameters that together can, in many cases, describe the overall shape of an organism or a part thereof (for example its shell) when this shape contains as its main ingredient an e q u i a n g u l a r s p i r a l.
These three parameters we can call WHORL, WORM and TOP ( See for this : DAWKINS, R, 1996, Climbing Mount Improbable, Chapter 6 ).

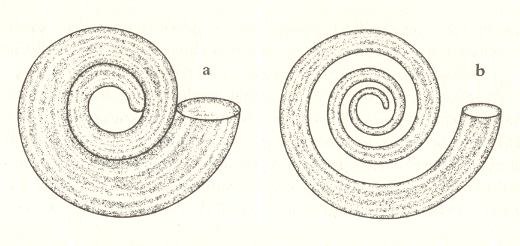
Figure 8.
8a. Tube of a shell coiled according to an equiangular spiral with WHORL = 2.
WORM = 0.5
8b. Tube of a shell coiled according to an equiangular spiral with WHORL = 2.
WORM = 0.7
( After DAWKINS, 1996 )
WHORL indicates the expansion rate of the spiral. When WHORL = 2, it means that the spiral widens such that it will have twice the diameter it initially had, after every complete revolution of the radius vector. This is the case in Figure 7a. Figure 7b displays a much more weaker curvature, it has WHORL = 10. After every complete revolution of the radios vector the diameter of the spiral increases with a factor equal to 10 (Although such a spiral never completes even a first revolution, as we see in a cockle's shell : its curvature is so weak -- its WHORL is somewhere in the thousands -- that we do not at first sight recognize it as a spiral at all).
WHORL has nothing to say about the increase of the shell's t u b e.
For that we need a second parameter, WORM. We need WORM, because the tube does not necessarily have to fit into the space allowed by the given curvature of the spiral. The shell can show gaps like in Figure 8b. The values of WHORL are equal in Figure 8a and 8b, namely 2, but Figure 8b displays a higher value of WORM, namely 0.7, than Figure 8a does, which is 0.5. A WORM-value of 0.7 means that the distance between the origin of the spiral (the pole) and the inner wall of the tube is 70% of the distance between the origin of the spiral and the outer wall of the tube. The WORM-value is equal for the whole shell, regardless of the particular part of the tube where we do our measurements. Logically speaking, this is not necessary, but appears to hold so many times in real shells, that we will take it as point of departure, unless otherwise indicated. It is clear that a WORM-value of 0.99 yields a thin wire-like tube, because the distance between the origin of the spiral and the inner wall of the tube is 99% of the distance between the origin of the spiral and the outer wall of the tube.
What WORM-value is needed to get a precisely fitting spiral as in Figure 8a? That depends on the value of WHORL : The critical value of WORM for effecting a precise fit is the reciprocal of the given value of WHORL. In Figure 8a, as well as in Figure 8b, the value of WHORL is 2, so the critical value of WORM for a precise fit is 0.5. The shell of Figure 8b has a WORM-value that is a little higher than the 'fit-value', and consequently shows gaps. When we have a shell, built according to the spiral in Figure 7b, and thus having WHORL = 10, its whorls will lie neatly adjacent to each other without leaving gaps, only when its WORM-value is 0.1.
But what happens when the value of WORM lies below the fit-value? Can we imagine a tube that is so thick that the whorls of the spiral get in the way of each other so that they must use the space of previous whorls? Is there a spiral as the two in Figure 8 (having WHORL = 2) with a WORM-value of, say, 0.4? There are two solutions to prevent disaster.
One is that the tube encloses previous whorls, like Nautilus does. In this case the transverse section of the tube is a circle from which a chunk is removed. So it is not a circle anymore. And indeed Molluscs live happily in a non-circular tube.
The other solution to the problem of the obtrusiveness of previous whorls is to give way to the third dimension, resulting in turbinate, instead of discoid shells. This brings us to the third parameter determining the shape of shells, TOP. It is a measure of the screw translation of the equiangular spiral, i.e., to the movement of the equiangular spiral, that is to say, of its radius vector, is added a translation parallel to the axis of the spiral (that goes through the spiral's pole). The result of such a translation is that the overall shape of the shell becomes more or less conical. TOP indicates the speed with which the consecutive whorls of the spiral are displaced along the length of the cone. We can measure TOP by determining the angle BETA between the tangent to the whorls of the shell and the axis of the spiral. Nautilus has a TOP-value of 900, because all the whorls lie in one and the same plane. But Turritella, having a sharply pointed shell, has a much smaller value.
With all this we must bear in mind that in many shells the value of TOP is not precisely constant during the growth of the individual. The result is a more or less concave or convex outline of the cone.
So when the value of WORM is lower than the reciprocal value of WHORL, implying that the whorls are going to get in each other's way, one of the two mentioned solutions will be applied by Nature. And if she solves the problem by giving way to the third dimension, then we witness the transition from S p i r a x o n i a p l a n a t a (discoid shells) to S p i r a x o n i a a p l a n a t a (turbinate shells). In both cases the main axis of the body is spirally curved about an imaginary axis of the (resultant) spiral. If nature solves the problem by altering the transverse shape of the tube such that previous whorls are going to be enclosed, the shell can remain planar.
Somtimes the relevant WORM-value can vary in one and the same individual such that the last whorl entirely covers all the former whorls. Such a shell is called i n v o l u t e. In e v o l u t e shells the former whorls are all visible.
If the (spirally curved) main body axis is at the same time the center of the body, and if the transverse section of the tube -- and thus of the body -- is not a circle, then it will be surrounded by the body's a n t i m e r s. Also in the case that the body center is not its main axis but a plane containing the main axis, this main axis will have antimers around it, the number of which could be as low as two. We shall, in the sequel, however, not pursue these antimers, and consequently any cross axes, any further, which boils down to not going to distinguish between the Spiraxonia astaurota (no definite number of cross axes present) and the Spiraxonia staurota (a definite number of cross axes present).
We, when considering antimers anyway, should bear in mind that there are many animals, while bearing a spiral shell, have their (soft) body not spirally coiled up : Nautilus, Spirula, and all ammonites live in their most recent chamber, and the basic form of their (soft) body is, as it seems, such that it belongs to the Dipleura (and thus to the Stauraxonia instead of the Spiraxonia) : It is not spirally coiled up except for that part of it that extends into the siphuncle as a thin organic thread (with blood vessels) and following the spiral shell (while lying inside it) all the way to the shell's beginning. So, in a way, the (soft) body of the animal is spirally coiled up after all.
Within the category of the Spiraxonia allogonia (Archimedian spirals) we will not distinguish between planata and aplanata, nor set up any other subcategory of them, because of the relative unimportance of these spirals in the organic nature.
There are 'spirals' that are, to be sure, predispositioned as spirals -- in almost every case as equiangular spirals -- but deviating strongly from it during subsequent growth of the individual, not as an individual deviation, but as a characteristic feature of the given species. Such 'spirals' in fact show a (strong) variation of the angle ALPHA within one and the same shell, i.e. the angle between the radius vector and the whorls, or, more precisely expressed, the angle between the radius vector and the tangents to the whorls where the radius vector intersects the whorls. This angle changes strongly during the growth of the individual.
It is evident that such shells (and the animals bearing them) should promorphologically be classified as Spiraxonia allogonia.
To continue click HERE to proceed further with the systematic Promorphology.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)
back to Allopola amphipleura and zygopleura