Promorphology of Crystals Preparation XVI

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
16

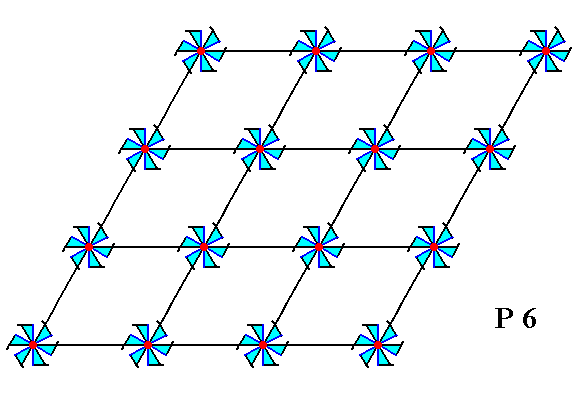
The Plane Group P6

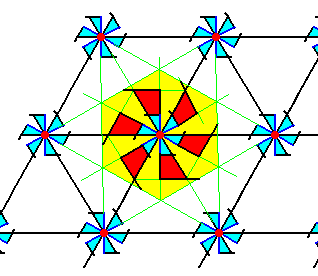
Figure 1. Inserting motifs with point symmetry 6 in a 2-D hexagonal lattice, yields a periodic pattern representing Plane Group P6. The pattern must be imagined to be extended indefinitely in 2-D space. The smallest unit cell is a rhomb-shaped mesh of the net.

The symmetry diagram for the Plane Group P6 is as follows :

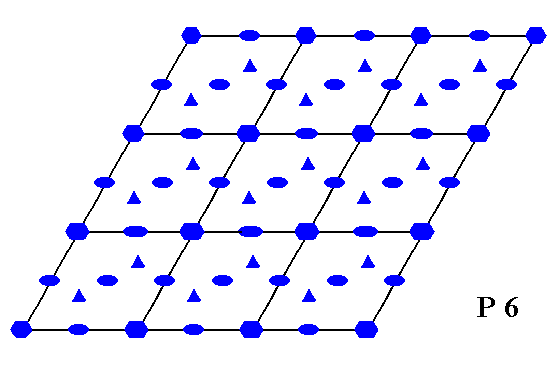
Figure 2. Total symmetry content of Plane Group P6.

Because there are no glide lines in P6 patterns, we only have to eliminate the simple translations, which means that we must isolate one unit cell, in order to obtain the Complex Motif of the pattern --which (Complex Motif) lies at the base of the promorph or planimetric basic form of all 2-D crystals belonging to the Plane Group P6. But because the Complex Motif must express all the symmetry that such a crystal has in store, we must consider the most symmetric unit cell, and this is a hexagonal unit cell (instead of a rhomb-shaped unit cell). See next Figure.

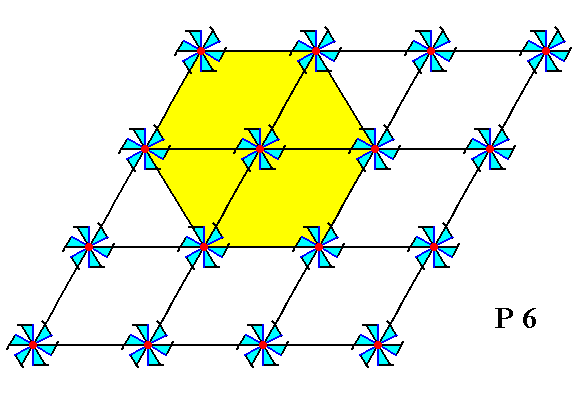
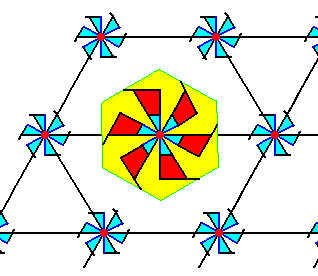
Figure 3. A larger, and hexagonal unit cell of the P6 pattern of Figure 1.

The unit cell depicted in Figure 3 is hexagonal and consists of 6x1/3+1=3 motifs s.str. plus corresponding background. Although the shape of this unit cell is suited for our search of the Complex Motif, it consists of three motifs s.str. It is clear that we must look for a repeating unit that, in addition to being hexagonal, contains just one motif s.str. plus corresponding background. The next Figure gives such a unit.

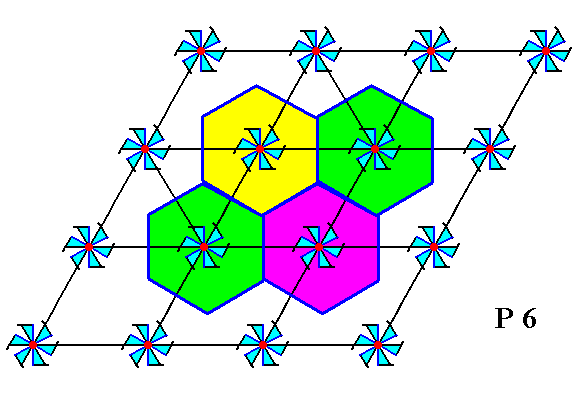
Figure 4. The larger, hexagonal unit cell of the P6 pattern of Figure 1 suggests a repeat unit, smaller again, but still hexagonal.

Isolating such a repeat unit implies eliminating the simple translations and (so implies) obtaining the Complex Motif of the P6 pattern of Figure 1 :

Figure 5. The Complex Motif of the periodic P6 pattern of Figure 1. It consists of a motif s.str. plus a hexagonal background. The line bounding this background does not belong to the motif nor to the (periodic) pattern.

The (point) symmetry of the Complex Motif is 6, which means that it possesses one 6-fold rotation axis as its only symmetry element. It does not have mirror lines.
The simplest planimetric figure expressing this symmetry geometrically is the Twisted Hexagon. The latter is accordingly the promorph of all the crystals belonging to the Plane Group P6. See next Figure.

Figure 6. The Twisted Hexagon as the planimetric basic form or promorph of all the 2-D crystals with a total symmetry according to the Plane Group P6 (and, consequently, belonging to the 2-D Crystal Class 6).

The P6 pattern of Figure 1 consists of motifs s.str. plus corresponding background. The background of each motif s.str. has a definite shape but apart from that it has no structure.
It is interesting to fill this background with structure and see what pattern we get. This means that we are going to e x t e n d the motifs s.str. See next Figures.

Figure 6a. Construction of an extended motif in the P6 pattern of Figure 1.

The next Figure depicts the finished extension.

Figure 6b. Extended motif of the P6 pattern of Figure 1.

The extended motifs plus some remaining background tile the plane neatly, as the next Figure shows.

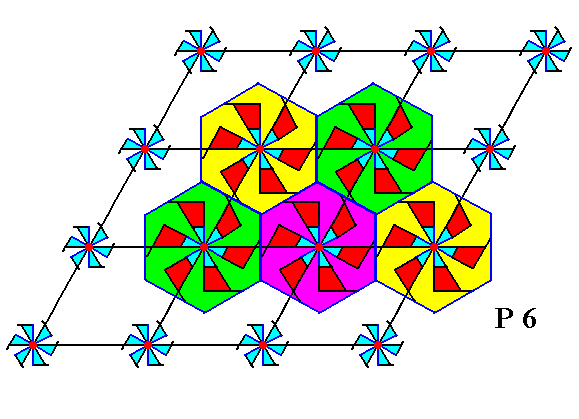
Figure 6c. The extended motifs tile the plane according to the ordering of the P6 pattern of Figure 1. They are true repeat units.

To derive the Complex Motif of our P6 pattern of extended motifs, the only translations that must be undone are the simple translations, because P6 patterns have no glide lines. So in isolating the just established repeat unit we automatically eliminate the simple translations and wind up with the Complex Motif of our pattern (That pattern is partially depicted in Figure 6c). Indeed, because there are no glide lines, the motif is not (partly) telescoped outward, i.e. it is not drawn out, and thus needs not to be compressed (i.e. telescoped inward) again in order to obtain the translation-free residue that can represent the Complex Motif of the pattern. The latter is depicted in the next Figure.

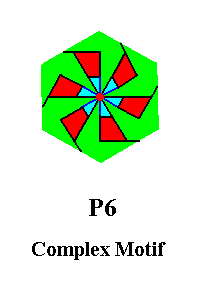
Figure 6d. The Complex motif of the pattern of Figure 6c, which is a pattern consisting of a periodic repetition of extended motifs.

The (point) symmetry of the just derived Complex Motif of the P6 pattern of Figure 6c is 6, which means that its only symmetry element is a 6-fold rotation axis. The simplest planimetric figure that expresses this symmetry geometrically is the Twisted Hexagon, already depicted in Figure 6.

The Plane Group P6mm
A pattern according to Plane Group P6mm is given in the next Figure.

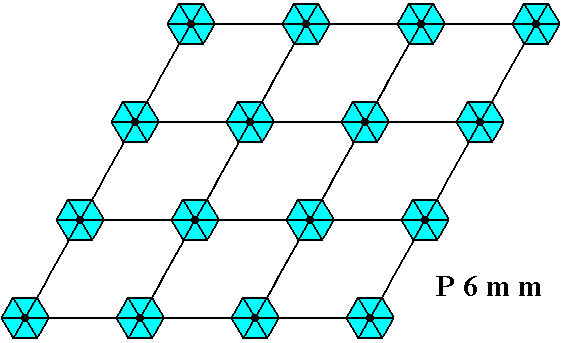
Figure 7. Motifs with point symmetry 6mm inserted in a hexagonal net, in such a way that each lattice point is associated with such a motif, yields a periodic motif pattern according to the Plane Group P6mm. A mesh of the net can serve as unit cell.

The total symmetry content of Plane Group P6mm is depicted in Figure 8.

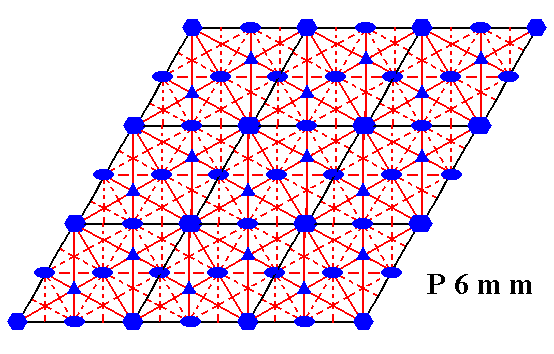
Figure 8. Total symmetry content of the Plane Group P6mm.
All rotation axes are perpendicular to the plane of the drawing.
6-fold rotation axes are indicated by small blue solid hexagons.
3-fold rotation axes are indicated by small blue solid triangles.
2-fold rotation axes are indicated by small blue solid ellipses.
Glide lines are indicated by red dashed lines.
Mirror lines are indicated by solid lines (red and black).
(One should not worry about the small discrepancies at some places in the drawing.)

In order to derive the Complex Motif of the P6mm pattern of Figure 7 we can concentrate directly on a suitable repeat unit (which should possess all the point symmetry that crystals belonging to this Plane Group have in store, and that is : 6mm, i.e. one 6-fold rotation axis and two sets of mirror lines, each set consisting of three equivalent mirror lines at 120⁰ to each other). We can do so because parallel to each existing glide line inherent in any P6mm pattern there exists a mirror line.
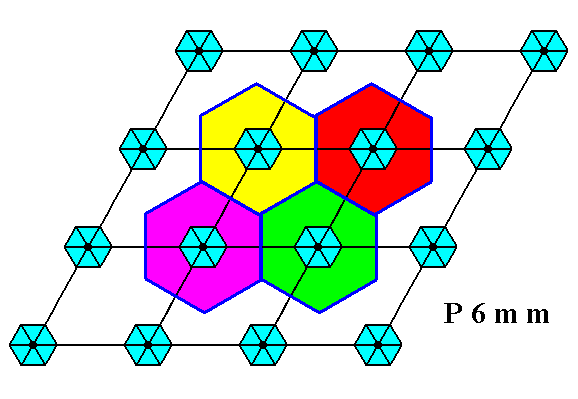
The next Figure gives the repeat unit that can represent the Complex Motif of the P6mm pattern of Figure 7.

Figure 9. Hexagonal repeat units of the P6mm pattern of Figure 7. Such a unit consists of one whole motif s.str. plus proper background. The orientation of the hexagonal outline of this background is such that the unit can tile the plane, which means that it is a true repeat unit.

When we isolate such a repeat unit we automatically eliminate the simple translations inherent in the P6mm pattern of Figure 7, and end up with the Complex Motif of that pattern :

Figure 10. Complex Motif of the periodic P6mm pattern of Figure 7. The blue line bounding the background is not a structural element of the motif. Note that the hexagonal outline is turned by 30⁰ with respect to the hexagonal outline of the motif s.str.

The point symmetry of the Complex Motif of Figure 10 is 6mm (one 6-fold rotation axis and two sets of mirror lines, each set consisting of three equivalent mirror lines).
The simplest planimetric figure expressing this symmetry geometrically is the Regular Hexagon. The Regular Hexagon is accordingly the promorph or planimetric basic Form of all 2-D crystals belonging to the Plane Group P6mm and with it to the Crystal Class 6mm. See next Figure.

Figure 11. The Regular Hexagon as the promorph or planimetric basic form of all crystals of the Plane Group P6mm an with it of the Crystal Class 6mm.

In the next document we will e x t e n d the motifs s.str. of Figure 7, and see what pattern will arise.

To continue click HERE to further investigate the Plane Group P6mm.

e-mail :