Promorphology of Crystals Preparation II

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
2

Now that we know the total symmetry content of our pattern, our next step is to find the t e c t o l o g i c a l e l e m e n t inherent somewhere in the pattern. To find this element we must eliminate all translations. There are two types of translation present in the pattern : a simple translation and a translational component of the glide lines.
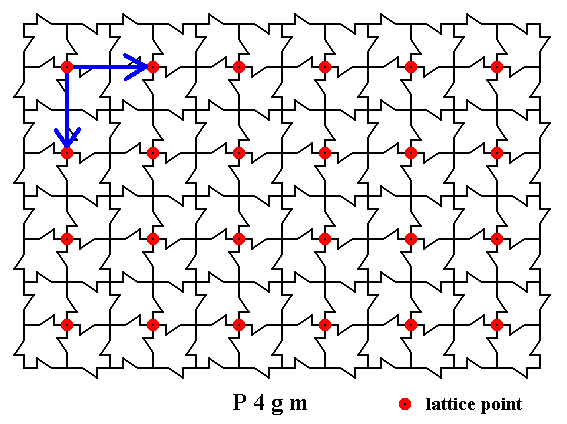
The simple translations are indicated in the next Figure :

Figure 19. The simple translations, that generate the Square Net, supporting the pattern of maple leaves. The two simple translations multiply one point, resulting in a two-dimensional square point lattice. The maple leaves are superimposed on this point lattice.

We will first eliminate the translational components of the glide lines. After that has been accomplished we will also eliminate the simple translations, and then see what we get.
When we elimimate the translational component of the glide lines, these glide lines become m i r r o r l i n e s. The simple translations, however, remain (for the time being), and this means that the motif units (= single maple leaves) are becoming superimposed in the process of the elimination of the mentioned translational components : they are not replaced.
Let us start with eliminating the translational components of the diagonal glide lines. Thereby we concentrate on the surroundings (= four maple leaves) of ONE node only (And in all what follows we concentrate on that same one node).
A glide line connects, (to begin with) two motif units X and Y, in such a way that when one motif, say X, is reflected in that line, and then shifted (translated) a certain distance along that line, it will end up as motif unit Y. So the glide line symmetry operation transduces motif unit X into Y. This is the case with all the motif units along that glide line. So the execution of the glide line symmetry operation will transduce the whole pattern into itself, and this is what we mean by saying that a certain pattern has glide lines.
In the next Figure we see the execution of one of the occurring glide lines of our pattern of maple leaves with respect to the one lattice node we concentrate on.

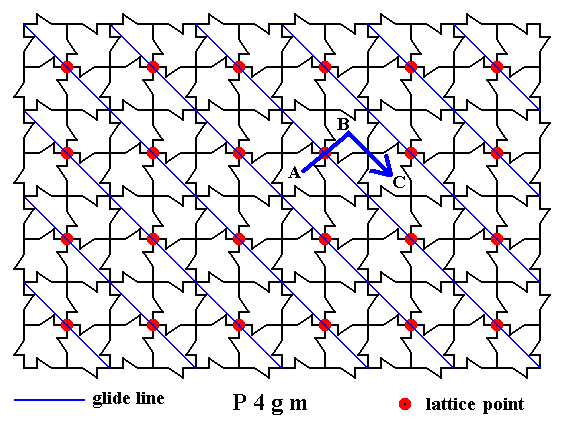
Figure 19a. Motif unit A is reflected (across the relevant glide line) to B as indicated. This reflection is immediately followed by a translation from B to C.

In order to eliminate the translational element we must make the translation from B to C (in Figure 19a) undone. We 'pull it back' as it were. This we do in the next Figure, and at the same time we do the same with the other motif unit that lies opposite to the first motif unit and which has the same relation with the glide line.

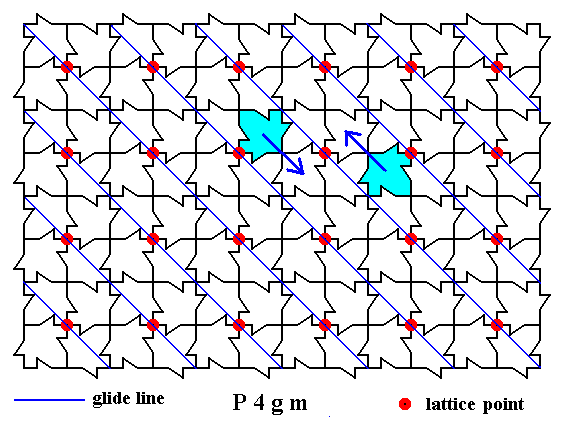
Figure 20. Each of two motif units (maple leaves) are superimposed on another as indicated by the arrows.

In doing all this, we have to do with two superpositions of motif units onto each other :

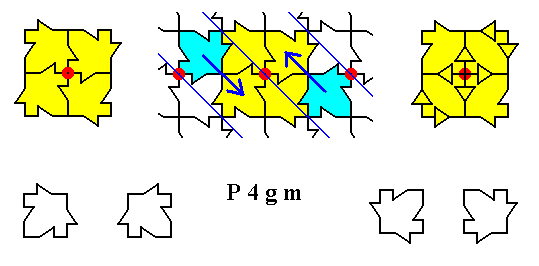
Figure 20a. Superposition of motif units as indicated in Figure 20. The complex motif resulting from this superposition is drawn to the right.
Bottom of Figure : Motif units (single maple leaves).

The result of this superposition in the context of the whole pattern is depicted in the next Figure :

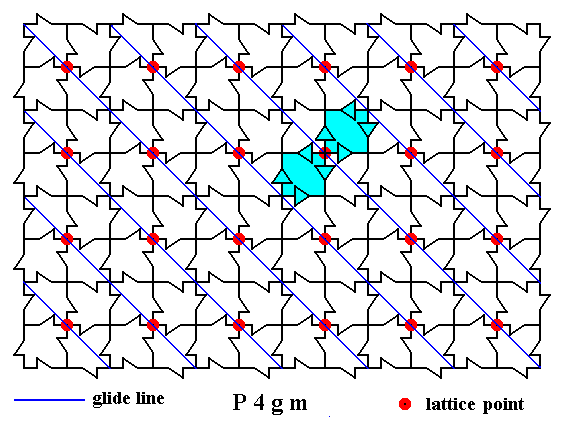
Figure 21. Result of the superpositions.

In the next three Figures we do the same with the other diagonal glide line :

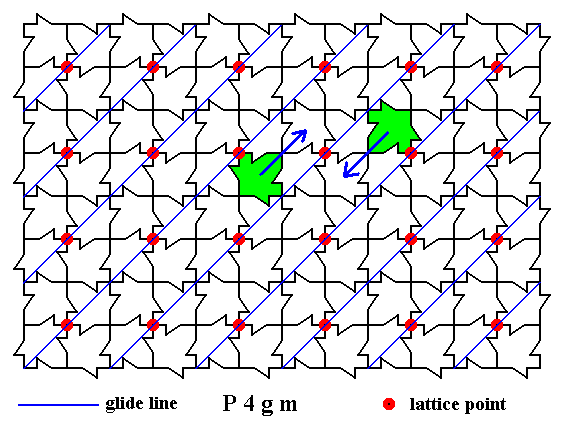
Figure 22. Superposition of motif units with respect to the elimination of translational components from the other diagonal glide lines, illustrated by the surroundings of one node only (the same node as was considered above).

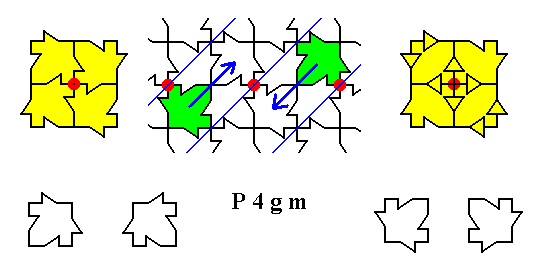
Figure 22a. Superimposing the motif units as indicated above. The result is shown on the right.

The next Figure shows this result in the context of the whole pattern.

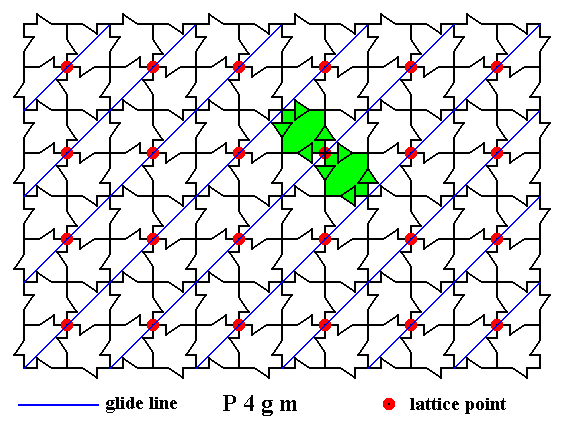
Figure 23. Result of the superpositions.

The total result of eliminating the translations of the glide lines in both diagonal directions is given in the next Figures. It is obtained by superimposing the separate results onto each other.

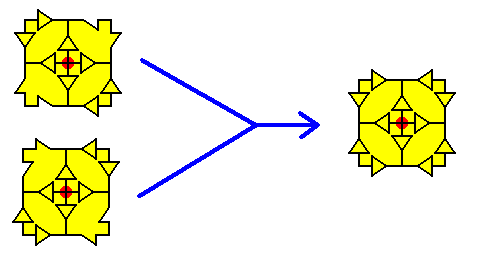
Figure 23a. Result of the superposition of the above results.

Figure 21 and 23 together result accordingly in the following (same result as in Figure 23a, but now in the context of the whole pattern) :

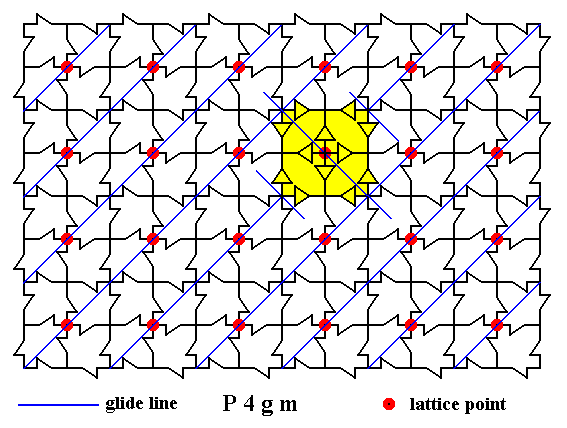
Figure 24. Result of the superpositions executed in Figure 21 and 23.

Now we eliminate the translational components of the non-diagonal glide lines, again concentrating on the same node :
The next Figure shows how such a non-diagonal glide line works :

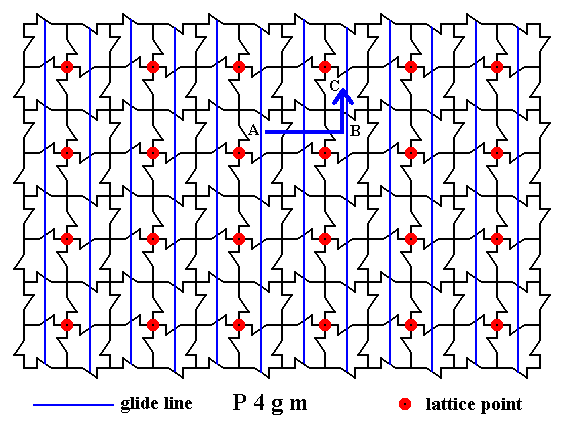
Figure 24a. Because of a (non-diagonal) glide line a motif unit is reflected from A to B, and then immediately translated over a certain distance. When we want to eliminate the translational component of this operation, we must 'pull the motif back' as it were from C to B, resulting in superposition. We do this in the next Figure.

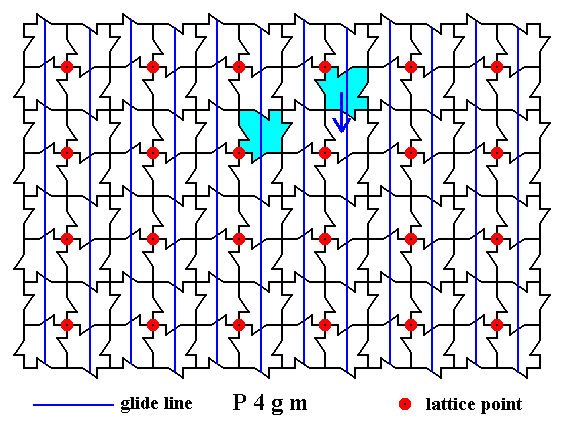
Figure 25. Superposition of a motif unit as indicated.

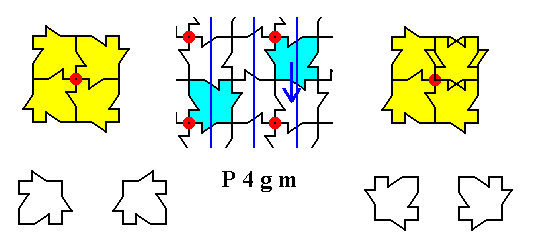
Figure 25a. Result of the superposition of a motif unit as indicated in the above Figure. The result is drawn on the right.

The next Figure gives this same result, but now in the context of the whole pattern.

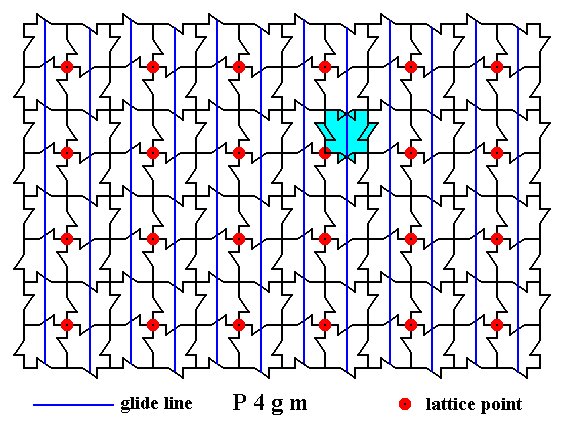
Figure 26. Result of the superposition.

We do the same with respect to the three other motif units associated with the node.

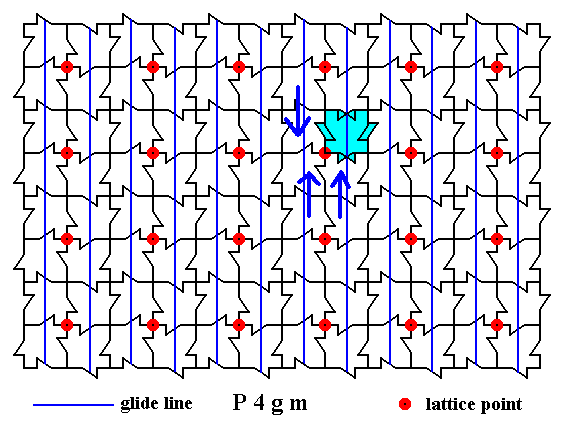
Figure 26a. Superposition with respect to the other three motif units, as indicated by arrows.

The result is given in the next Figure.

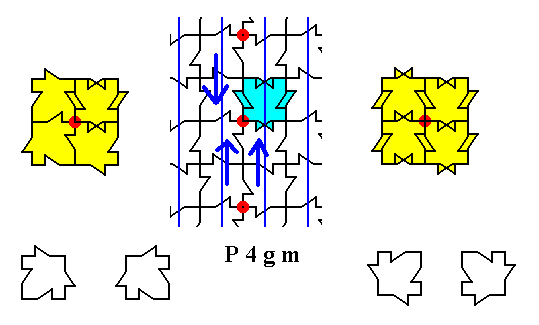
Figure 26b. Result of the superposition with respect to the other three motif units.

The next Figure depicts this result in the context of the whole pattern.

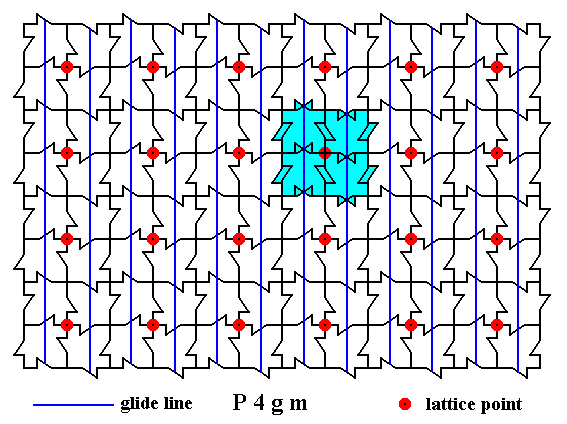
Figure 27. Result of the elimination of the translational components of the (vertical) non-diagonal glide lines.

Now we do the same with the other non-diagonal glide lines :

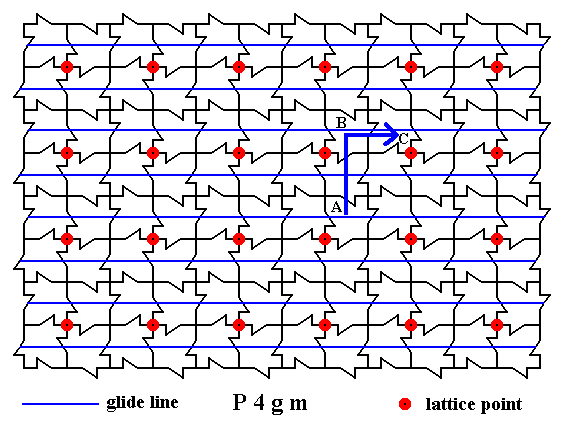
Figure 28. The working of a horizontal glide line.
A motif unit is reflected from A to B, and then immediately translated from B to C. When we want to eliminate the translational component of this operation, we have to 'pull the motif back' as it were from C to B, resulting in a superposition. For two motif units this is shown below.

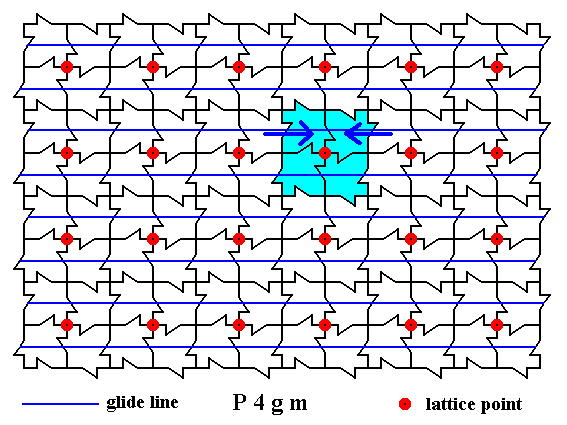
Figure 28a. Superposition -- indicated by arrows -- with respect to two motif units, as a result of the elimination of the translational components of the glide operations.

The result of these two superpositions is shown in the next Figure.

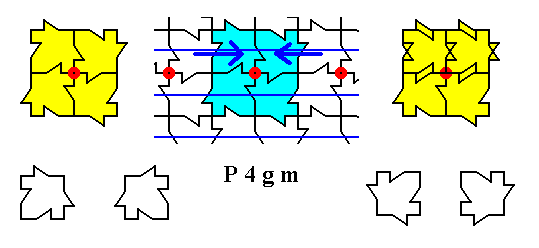
Figure 28b. Result (shown right) of the two superpositions described above.

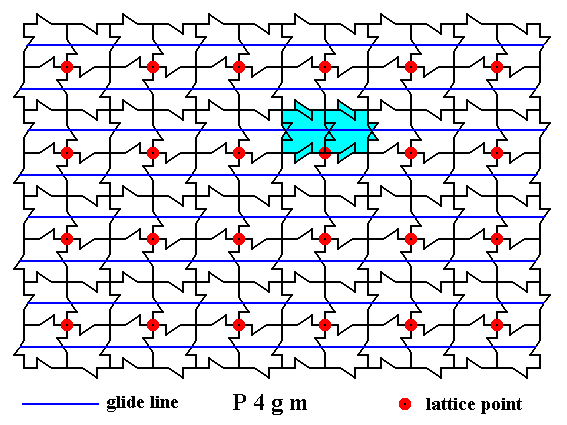
Figure 29. Result of the two superpositions in the context of the whole pattern.

Concerning the other two motif units the superpositions should be carried out as indicated by the arrows in the next Figure.

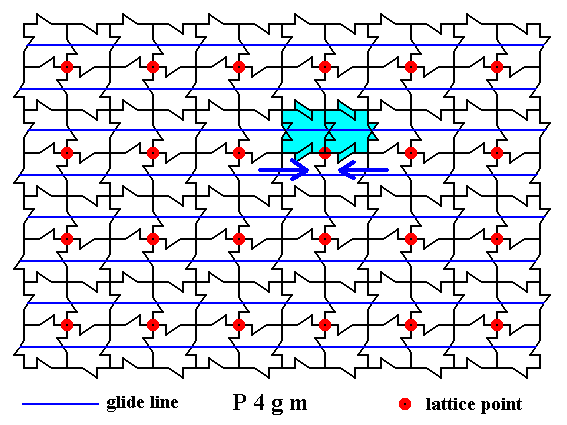
Figure 29a. The two superpositions (indicated by arrows), implied by the elimination of the translational component of the relevant horizontal glide line with respect to the the other two motif units (from the surroundings of our lattice point).

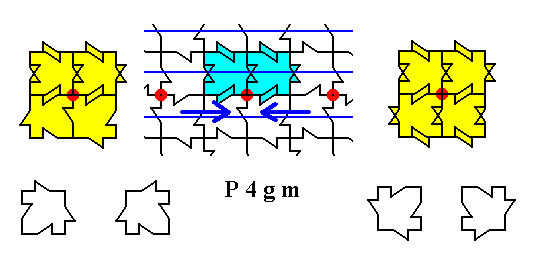
Figure 29b. Result (drawn on the right) of the two superpositions described above.

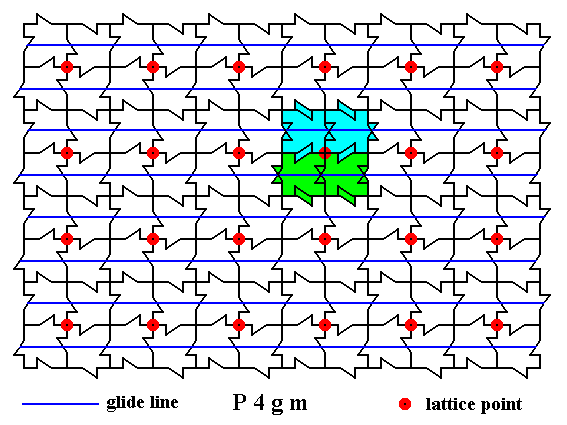
Figure 30. Result of the superpositions described above, now in the context of the whole pattern.

We now must superimpose the result of elimination of the translational components of the horizontal glide lines onto the result of the elimination of the translational components of the vertical glide lines, to obtain the total result of the elimination of the translation components of all non-diagonal glide lines. The next Figures show the result of this superposition.

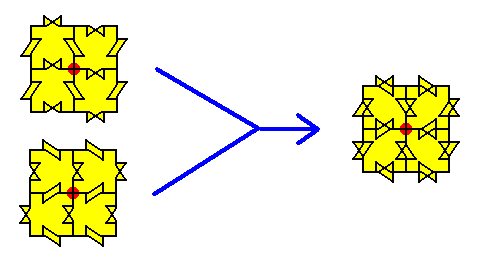
Figure 30a. Result of the superposition of the two results obtained above with respect to the non-diagonal glide lines.

Superposition of the result in Figure 30 onto the result obtained in Figure 27 gives this same total result of the elimination of the translational components from the non-diagonal glide lines, now seen in the context of the whole pattern :

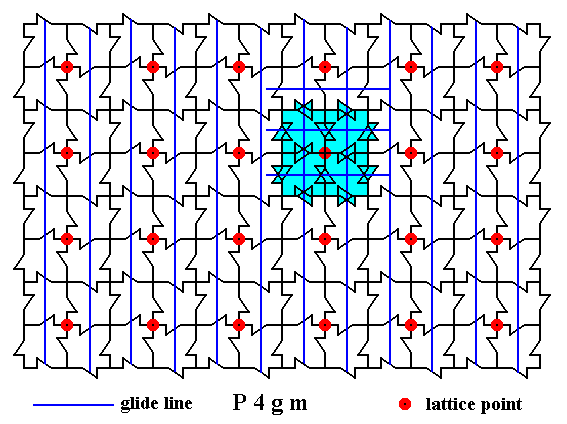
Figure 31. Result of the elimination of the translational components from the non-diagonal glide lines.

We now must combine, i.e. superimpose (1) the result concerning all the non-diagonal glide lines and (2) the result concerning all diagonal glide lines. We will do this in the next Figures.

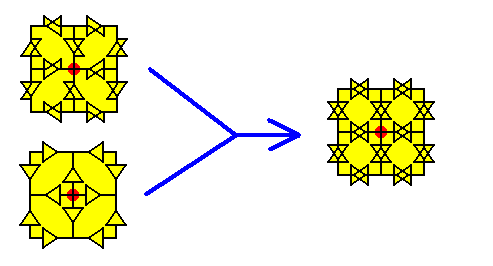
Figure 31a. Result of the elimination of the translational components from ALL the glide lines with respect to one node of the net. This result is obtained by superimposing the results with respect to the non-diagonal glide lines and the diagonal glide lines.

In the context of the repetition of this complex motif we will see that some overlappings occur, so the real complex motif neatly fits into a square of the net and is as such periodically repeated. It looks like this :

Figure 31b. Complex motif, as it is repeated according to the Square Net.

So we now have found how the surroundings of our node look like after elimination of the translational components of all glide lines.
By superposition of the result of Figure 31 (concerning non-diagonal glide lines) onto the result of Figure 24 (concerning diagonal glide lines), we also will obtain those surroundings of our node after elimination of all translational components of the glide lines, and now moreover in the context of the whole pattern. See next Figure.

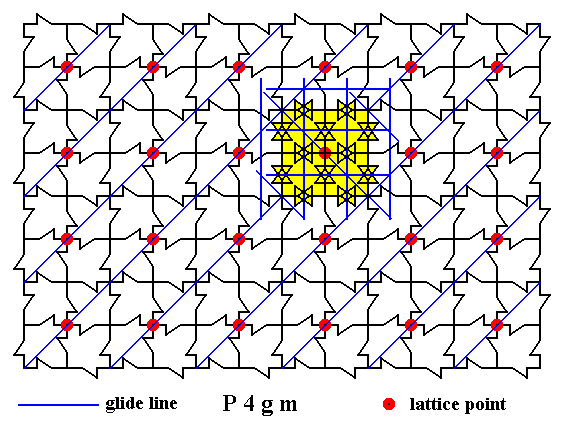
Figure 32. Result of the elimination of the translational components from ALL the glide lines, with respect to one node. This result is a complex motif, associated with that node. When this elimination is done with respect to every node of the lattice, then every node is associated with such a complex motif. These complex motifs are all identical. See next Figure.

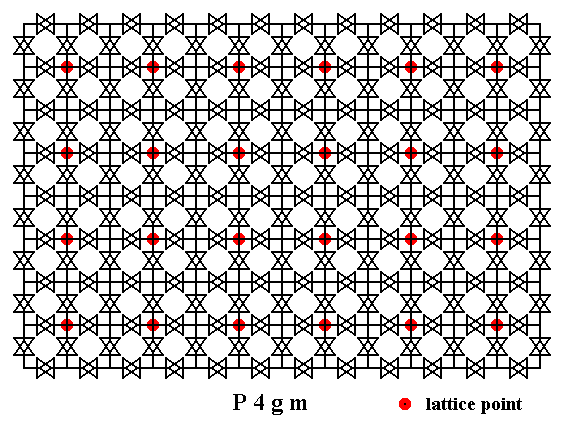
Figure 32a. Result of the elimination of the translational components from ALL the glide lines, with respect to EVERY node.

So in the above Figure the translational components of all the glide lines are eliminated. Those glide lines are now transformed into mirror lines.
The s i m p l e t r a n s l a t i o n s, however, are still there, and are responsible for the periodic repetition of the complex motif. This repetition is according to the Square Net.
We can show this repetition in several ways, as the next Figures illustrate.

Figure 32b. Periodic repetition of the complex motif according to the Square Point Lattice.

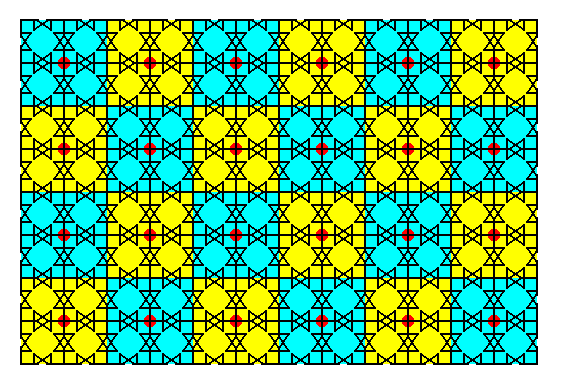
Figure 32c. Periodic repetition of the complex motif according to the Square Point Lattice.

The above Figure (32c), finally, precisely and correctly depicts the repetition of the complex motif.
When we now eliminate also all the simple translations, we'll end up with ONE complex motif only. This elimination of the simple translations boils down to isolating one of the complex motifs.

Figure 33. The isolation of one complex motif (which is the same as eliminating all simple translations). The result is the translation-free residue of the periodic pattern of maple leaves. Elimination of all simple translations means the superposition of all lattice points, resulting in one lattice point only. Because this point does not represent a lattice anymore we can remove it from the motif :

Figure 33a. The complex motif.

If we study the complex motif of Figure 33a, closely, we see that its (point) symmetry is 4mm, which is to be expected from the Plane Group of our maple leaf pattern : P4gm : Eliminating the translational component of all glide lines turns g into m. Eliminating all simple translations removes the lattice (i.e. turns it into one point), and thus removes P from the symbol. What is left is indeed 4mm.

Promorphology of single Crystals
Now, at last, with obtaining this complex motif, we have found the t e c t o l o g i c a l a s p e c t, which underlies the possiblity and legitimacy to consider (single) c r y s t a l s promorphologically : The complex motif has indeed a tectological structure (in contradistinction to a periodic). Our particular complex motif consists of four a n t i m e r s, as the next Figure shows :

Figure 34. The complex motif, as the translation-free residue of the periodic pattern of maple leaves, has a tectological structure. It has four antimers.

When we look at a concrete (single) crystal, i.e. when we consider the crystal macroscopically, the translations involved in glide lines (and in 3-D crystals the translations involved in glide planes and screw axes) are not as such visible (they are much too small). This means that we see glide lines as mirror lines (and in 3-D crystals glide planes as mirror planes, and screw axes as rotational axes), i.e. we eliminate the translational components of those operations (as we have done above). But we do not (when observing the crystal macroscopically) eliminate the simple translations just like that. It is true that we do not see them as repetitions (because the simple translations are also too small to be visible as such). But we do see one effect of these translations, namely the fact that in virtue of these translations (repetitions according to the given net) the crystal is bulky, which means that it -- as a visible crystal -- is not of a microscopical magnitude. It would have this microscopical magnitude if in addition to the mentioned translation components of glide (and for 3-D also -- screw) operations also the simple translations would be eliminated (We are then left with the mentioned complex motif). So when we observe a crystal macroscopically the simple translations are retained.
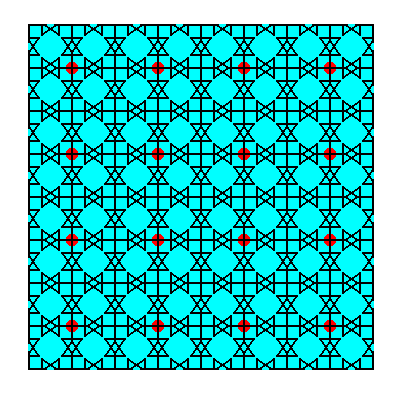
The next Figure shows a 2-D crystal based on the -- now all too familiar -- pattern of maple leaves, macroscopically (of course we still draw too small a number of repeated motifs, there should be millions of them). The crystal is supposed to have grown undisturbedly in a uniform medium, resulting in the outer shape of the crystal being a square, in line with the underlying (square) lattice.

Figure 35. A two-dimensional crystal, based on the maple leaf pattern (P4gm), considered macroscopically. The simple translations effect the bulky nature of the crystal. We can see that the POINT SYMMETRY of the crystal is 4mm : It has a 4-fold rotation axis at its center (perpendicular to the plane of the drawing) and two sets of mirror lines, diagonal and non-diagonal. See for this point symmetry the next Figure.

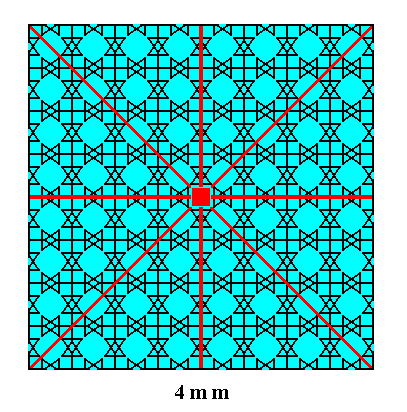
Figure 36. A two-dimensional crystal, based on the maple leaf pattern (P4gm), considered macroscopically. The simple translations effect the bulky nature of the crystal. The POINT SYMMETRY of the crystal (4mm) is indicated : It has a 4-fold rotation axis (small red square) at its center (perpendicular to the plane of the drawing) and two sets of mirror lines (solid red lines), diagonal and non-diagonal.

In the Figure above, which depicts a crystal considered macroscopically, we cannot set any other symmetry axes and mirror lines than those that are already indicated. We cannot for example set (i.e. detect) some other 4-fold axes in addition to the one in the center, because now the crystal, and with it the point lattice (sustained by the simple translations), is finite with respect to its spatial extension, i.e. we now do not consider the lattice as indefinitely extending (which can be so considered as soon as we find ourselves in the microscopical dimension). The same applies to the mirror lines.

On the basis of the symmetry of the complex motif we have determined the point symmetry of 2-D crystals belonging to the Plane Group P4gm. It is 4mm. If we examine a pattern based on the Plane Group P4mm, we will obtain -- qua symmetry -- the same result : The resulting (complex) motif will have 4mm symmetry. So the crystals of either of the two mentioned Plane Groups, P4gm and P4mm, belong to the same 2-D Crystal Class. Their (point) symmetry is 4mm, and the two-dimensional geometric figure that fully expresses this symmetry will be seen as the two-dimensional p r o m o r p h (= stereometric basic form) of all the single non-twinned crystals of this Class (4mm), whether they belong to the Plane Group P4gm or P4mm. Such a promorphological assessment is legitimate because it is ultimately based on the symmetry of the complex motif, and this motif has indeed a tectological structure and as such allows for a promorphological consideration. The mentioned g e o m e t r i c f i g u r e, representing the p r o m o r p h or planimetric basic form of 2-D crystals of the Class 4mm is the S q u a r e. See next Figure.

Figure 37. The two-dimensional promorph (the Square) of all the single non-twinned crystals of the 2-D Crystal Class 4mm, either belonging to the Plane Group P4mm, or to the Plane Group P4gm.

Three-dimensional Crystals
All our results have been demonstrated of 2-dimensional crystals. The same, however, applies to 3-dimensional crystals. In addition to glide planes we have in many 3-D crystals to do with screw axes. Screw axes are symmetry elements consisting of a combination of a rotation and translation along the axis of that rotation.
So we have finally laid down the theoretical legitimacy to consider three-dimensional single crystals (which here means : not only twinned crystals but also all non-twinned crystals) (also) in a promorphological way, because their point symmetry (which determines to which Crystal Class the given crystal belongs) is based on a (chemical) motif, which in the case of the presence of glide planes and/or screw axes is a complex motif, obtained by telescoping the structure back along glide planes and screw axes. And this motif has a tectological structure.

In order to consolidate still further our theoretical legitimacy to consider crystals promorphologically, we will, in what is coming next, derive the tectological aspect from all 2-dimensional Plane Groups. If the reader feels already satisfied with all the relevant discussions so far laid down, he or she can skip it and proceed directly with the documents in which we explain and define how to assess a (single) 3-D crystal promorphologically, and in which this assessment is actually executed : The Promorphology of Crystals.

To continue click HERE to further theoretically prepare for the Promorphology of Crystals.

e-mail :