Promorphology of Crystals Preparation VIII

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
8

REMARK : When the reader feels satisfied with our established theoretical foundation (done in the previous two documents) that allows (single, non-twinned) Crystals to be promorphologically assessed, he or she can skip all the following, and directly proceed with The Promorphology of Crystals.

The Plane Group P3m1
The symmetry of periodic patterns of motifs according to the Plane Group P3m1 are based on one or another version of the Primitive Hexagonal Point Lattice (Net). See the next Figures.

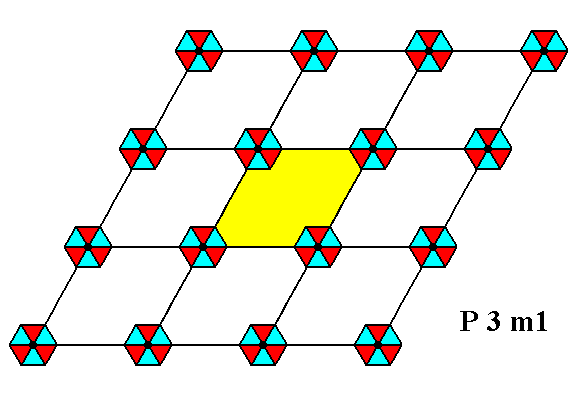
Figure 1. Periodic two-dimensional pattern according to the Plane Group P3m1. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).

The "1" in the Plane Group symbol serves to distinguish it from another Plane Group, which has the same symmetry content, but has a different orientation of the motifs s.str. (This is equivalent to stating that the same total symmetry is differently configured). This other Plane Group is P31m.
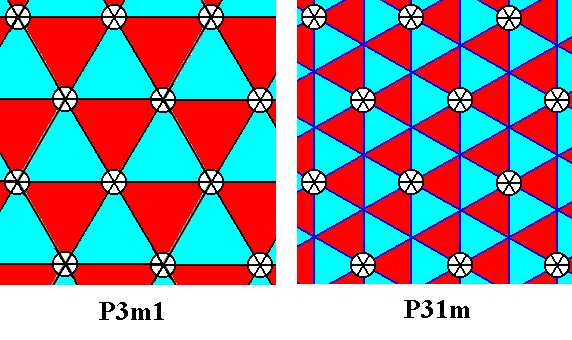
Indeed the 2-D Crystal Class 3m admits of two Plane Groups to be possible. Because their total symmetry content is the same, it is not easy to distinguish them by a clear definition. But in themselves they are truly distinguished, they represent different patterns. To get an idea of the difference of these patterns, we give a Figure, illustrating it with respect to a space-filling pattern. Later (Part 15) it will be fully discussed.

Figure 1a. A pattern representing Plane Group P3m1 (left), and another pattern representing Plane Group P31m (right).

Because of the mentioned difficulty of clearly and unambiguously discriminate between patterns representing these two Plane Groups (P3m1 and P31m), but also because of their intrinsic subtleness, and especially their connection with ionic crystals, we will devote several documents to them : In addition to the present document, also the ensuing documents representing Part 9, 10, 11, 12, 13, 14 and 15, will be devoted to these two Plane Groups.
The P3m1 pattern of Figure 1 admits of three sets of glide lines parallel to the three mirror lines that go through the motifs. The next three Figures depict these sets separately.

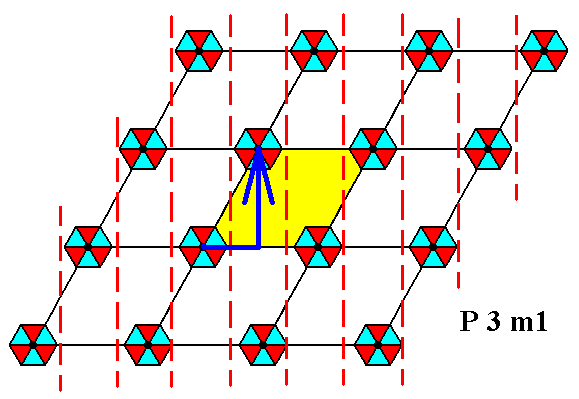
Figure 2. Periodic two-dimensional pattern according to the Plane Group P3m1. The pattern must be considered as indefinitely extended in 2-D space. Vertical glide lines, inherent in the pattern, are shown. The blue hooked arrow indicates the glide operation : Reflection across the glide line immediately followed by a translation parallel to the glide line by a distance equal to the hight of the unit cell.
The next two Figures show the other two sets of glide lines.

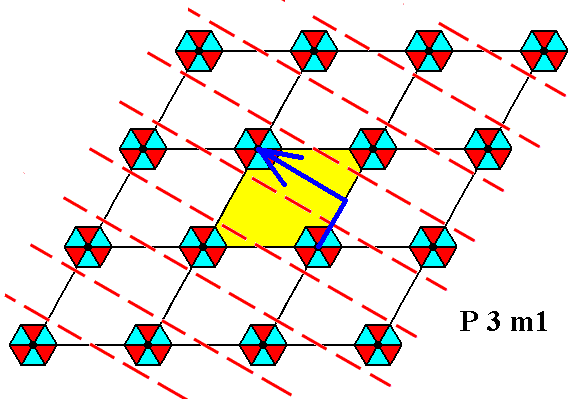
Figure 3. Periodic two-dimensional pattern according to the Plane Group P3m1. The pattern must be considered as indefinitely extended in 2-D space. A second set of glide lines, inherent in the pattern, is shown. The blue hooked arrow indicates the glide operation : Reflection across the glide line immediately followed by a translation parallel to the glide line and equal to the width of the rhomb-shaped unit cell as depicted in Figure 1. The next Figure shows the third and last set of glide lines.

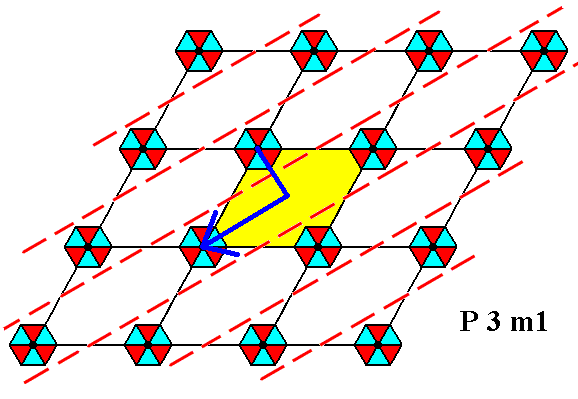
Figure 4. Periodic two-dimensional pattern according to the Plane Group P3m1. The pattern must be considered as indefinitely extended in 2-D space. A third and last set of glide lines, inherent in the pattern, is shown. The glide operation is indicated by the hooked blue arrow : reflection across the glide line immediately followed by a translation parallel to the glide line over half the longer diagonal of te unit cell.

As we know from the treatment of the Plane Group P3 (previous document), we must -- in order to find the Complex Motif -- choose a more symmetrical (in fact the most symmetrical) unit cell, namely the hexagonal unit cell. This cell defines a centered hexagonal net (lattice), i.e. the net consists of centered hexagons, which is however fully equivalent to the net based on the rhomb-shaped unit cell. This hexagonal cell is depicted in the next Figure.

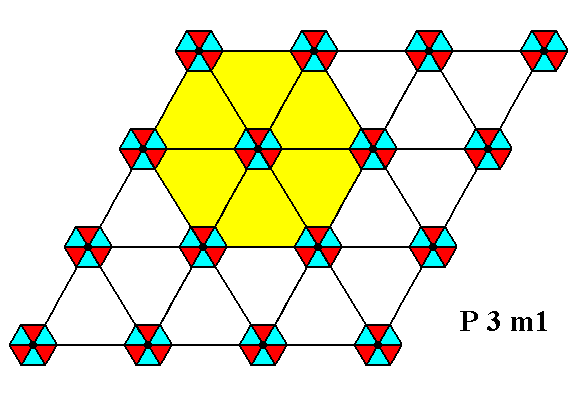
Figure 5. Periodic two-dimensional pattern according to the Plane Group P3m1. The pattern must be considered as indefinitely extended in 2-D space. A larger unit cell, or repeat unit (yellow) -- the most symmetric unit -- is chosen.

Because the pattern has mirror lines parallel to all glide lines, we do not expect the symmetry of the Complex Motif, as it is derived by eliminating all the translations involved in those glide lines, to be increased with respect to that of the hexagonal unit cell, and so this unit cell will already represent the Complex Motif (albeit the penultimate Complex Motif). When we isolate this unit cell and with it effecting automatically the elimination of all simple translations (responsible for the periodic repetition of the unit cell), we will obtain the (penultimate) Complex Motif (The elimination of all simple translations, by isolating the repeat unit, means that the resulting pattern -- the repeat unit all by itself -- will not be mapped onto itself by such a translation : The image will be shifted with respect to the original, while in an infinite periodic pattern the pattern will be mapped onto itself) :

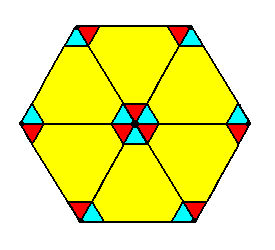
Figure 6. The isolated hexagonal unit cell of the periodic pattern of Figure 1 (and 5) is the penultimate Complex Motif. It consists of 6x1/3+1=3 motifs s.str.

We just had chosen the most symmetrical unit cell -- in fact just a possible repeat unit -- (Figure 5 and 6). The shape of this unit cell must be the shape of the Complex Motif. Indeed this unit cell can represent the Complex Motif. However, it in fact only represents (and prescribes) the symmetry of the Complex Motif, because the motif itself consists, in addition to one whole motif s.str, of thirds of motifs s.str. So the content of this unit cell represents the Complex Motif only in a formal way, not in a concrete way (because half or third motifs do not as such occur in reality, and, analogously, not in the world of 2-D crystals). Thus, while now knowing that the Complex Motif must have a hexagonal shape, we must consider again Figure 1, where we had chosen a rhomb-shaped unit cell, and a lattice according to this unit cell. And this rhomb-shaped unit cell defines hexagonal t o t a l m o t i f s associated with its lattice points. Such a total motif is the complete surroundings of a lattice point. It tiles the plane neatly. But of course we can also interpret these total motifs as those of the hexagonal repeat unit (Figure 6 and 5). See next Figure.

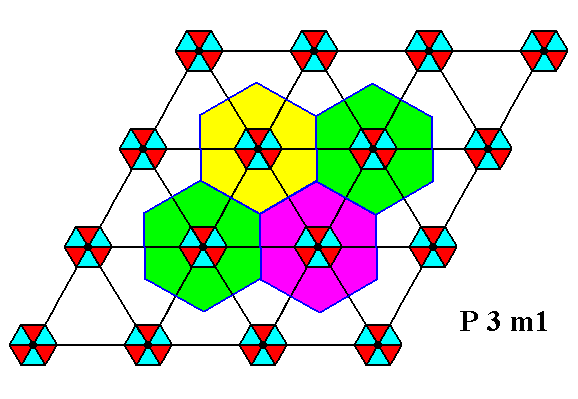
Figure 6a. Indication of total motifs associated with the lattice points of the net of Figure 1. They are at the same time total motifs of the hexagonal repeat unit of Figure 6 and 5. Four of the seven total motifs associated with that hexagonal repeat unit are indicated. At the same time they are all the total motifs associated with the rhomb-shaped unit cell.

Although the total motif, as depicted in Figure 6a, is a genuine repeating unit, it is not a p r e f e r a b l e unit cell choice because of the following reason (to which we referred already when treating of the Plane Group P3) : The corners of the hexagon (as can be seen in Figure 6a) are not equivalent to the central point, because in that point something is present which is absent in the corner points. This implies that the hexagonal net (point lattice) based on such a unit cell would necessarily be primitive, i.e. the central point -- which is furnished with a motif s.str. -- is not a lattice point. All this further implies that the motifs s.str. do not coincide with the lattice points. Although such a coincidence is theoretically not mandatory it is very convenient and instructive.
But in spite of the fact that the total motif is less suited to figure as unit cell (and as such defining a lattice (i.e. a net)), it can figure -- and preferable so -- as C o m p l e x M o t i f. It is smaller than that of Figure 6. Instead of 3, it consists of just one whole motif s.str. (So it does not contain half or third motifs.str.). If we isolate such a total motif we indeed have a preferable version of the (penultimate) Complex Motif. See next Figure.

Figure 6b. Preferable (because smaller, and because it does not contain halfs or thirds of motifs s.str.) penultimate Complex Motif (equivalent to a total motif of the rhomb-shaped unit cell (Figure 1), or of the (larger) hexagonal repeat unit (Figure 5)). It consists of one whole motif s.str. plus corresponding background. Note that the shape of the background is, as is the shape of the motif s.str., hexagonal, but differently orientated by 30⁰.

Although we now have the Complex Motif, it will nevertheless be instructive to eliminate all glide translations and see what happens. We will do this with our method of Copy-Shift-Superimpose.
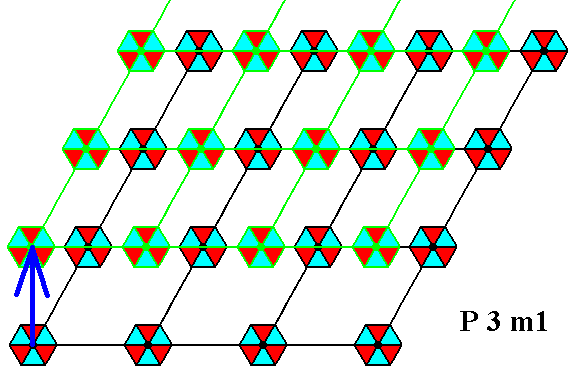
Let's start with the first (out of three) set of glide lines (Figure 2) :

Figure 7. A copy is made of the pattern of Figure 1 and shifted by the height of the rhomb-shaped unit cell (as depicted in Figure 1) -- the shift is indicated by the blue arrow --, and then superimposed onto the original. Compare with Figure 2.

In Figure 7 we shifted the copy upward. Exactly the same result will be obtained when we shift it downward. This is easy to grasp : If we, in Figure 7, consider the copy to be the original, and the original to be the copy, then the copy has been shifted downward. This corresponds to the translation direction of any such glide line : We can read this symmetry operation as REFLECT AND TRANSLATE UPWARD (See Figure 2), but we can also read it as TRANSLATE DOWNWARD AND REFLECT.
After a bit of processing, the result of Figure 7 looks as follows :

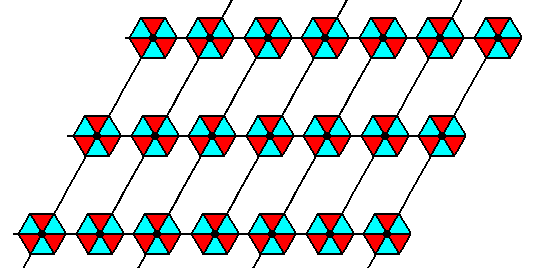
Figure 8. Final result of the Copy-Shift-Superimpose operation on the pattern of Figure 1, with respect to the vertical direction. The vertical glide translations (as indicated in Figure 2) are now undone, resulting in the glide lines to be transformed into mirror lines, as the next Figure shows.

Figure 9. Final result of the Copy-Shift-Superimpose operation on the pattern of Figure 1, with respect to the vertical direction. The vertical glide lines are transformed into mirror lines (m).

The result of Figure 8 will now in turn be subjected to a Copy-Shift-Superimpose operation, now with respect to the second set of glide lines (Figure 3):

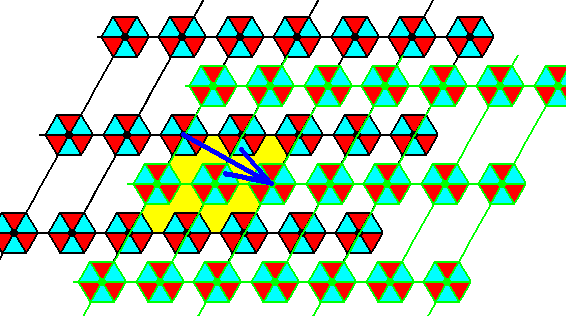
Figure 10. The result, as depicted in Figure 8, is subjected to the elimination of the second set of glide translations. A copy is made of the result of Figure 8, and shifted according to the blue arrow, and then superimposed upon that result.

After processing we get the following result :

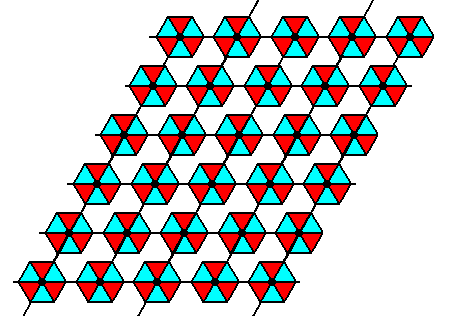
Figure 11. Final result of the Copy-Shift-Superimpose operation on the result of Figure 8. We have now eliminated the second set of glide lines as they were present in our initial pattern (Figure 1).

Finally, the result of Figure 11 will be subjected to yet another Copy-Shift-Superimpose operation with respect to the third set of glide lines as they are present in the initial pattern (Figure 4). The shift must be parallel to the longer diagonal of the rhomb-shaped unit cell by half that diagonal's length. See Figure 4. As can be seen in the next Figure, the pattern will be unchanged by this last operation, so with the result of Figure 11 we have our definitive result.

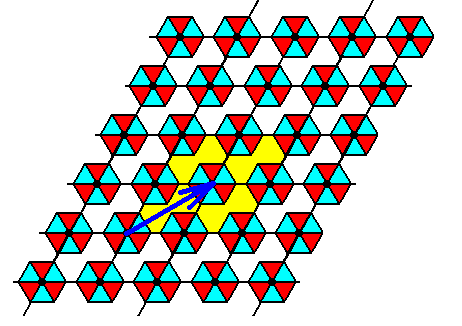
Figure 12. A Copy-Shift-Superimpose operation on the result of Figure 11, parallel to the longer diagonal of the unit cell by half that diagonal's length, in order to eliminate the third set of glide translations (Figure 4) does not have any effect (i.e. our recursive Copy-Shift-Superimpose process ended up at a steady state). So we had already eliminated the third set of glide translations, and with it ALL glide translations of our initial motif pattern (Figure 1).

In order to find the Complex Motif we must determine the r e p e a t i n g u n i t in our final pattern (Figure 11). The next Figure indicates this repeating unit.

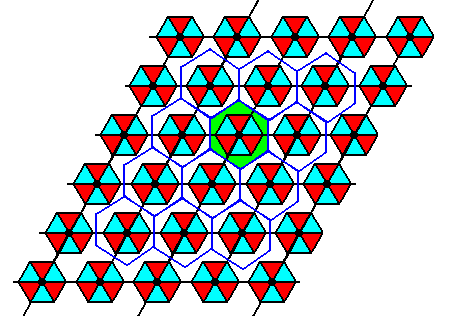
Figure 13. In the final pattern of Figure 11 a repeating unit (green) is indicated.

When we isolate this repeating unit, co-effecting the elimination of all simple translations, we get the Complex Motif of our periodic pattern of Figure 1 :

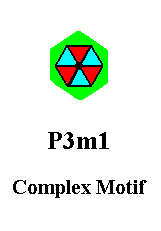
Figure 14. Ultimate Complex Motif of the P3m1 periodic pattern of Figure 1.

Our penultimate Complex Motif of Figure 6b, as well as our ultimate Complex Motif of Figure 14 only differ in the extension of the motif background. Both display a 3m symmetry, which means that each of them possesses three equivalent mirror lines and a 3-fold rotation axis going through their point of intersection and perpendicular to the plane of the drawing. Tectologically the Complex Motif consists of three antimers. These are indicated in the next Figure.

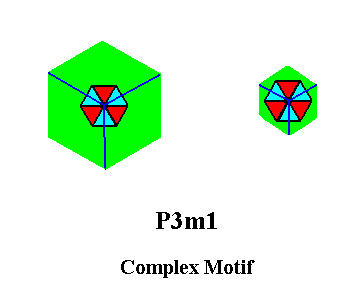
Figure 15. Composition out of three a n t i m e r s of the penultimate and ultimate Complex Motif of the P3m1 periodic pattern of Figure 1.

The structure of the Complex Motif of the pattern of Figure 1 admits of several choices where to lie the boundaries of the three antimers. This is of course the case because here we have just a geometrical figure at our disposal. The antimers of a real chemical motif certainly reveal themselves clearly and unambiguously. The next Figure depicts some choices of antimer boundaries in a magnification of the motif s.str. of our Complex Motif.

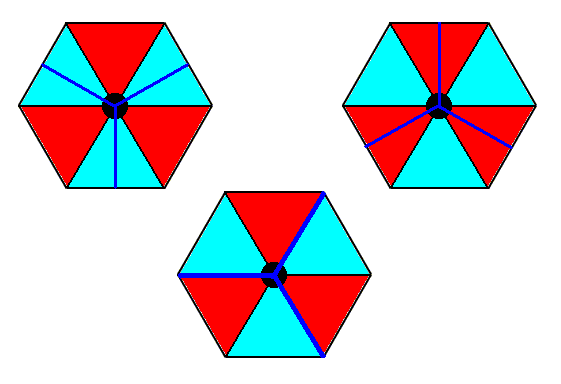
Figure 16. Several possible choices of antimer boundaries in a motif compatible with the P3m1 structure.

The next Figure indicates the symmetry content of the Complex Motif (represented by its motif s.str., which fully determines the symmetry of the Complex Motif).

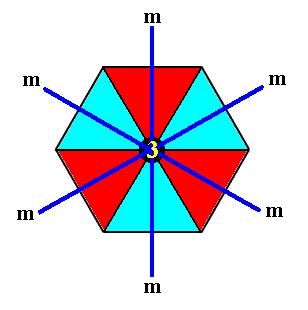
Figure 17. The symmetry content of a motif compatible with a P3m1 periodic structure. The symmetry of the motif is 3m, which means that it has three equivalent mirror lines (m) at 120⁰ to each other, and one three-fold rotation axis (3) going through the intersection point of the mirror lines, while being perpendicular to the plane of the drawing.

The simplest planimetric figure that expresses the symmetry -- 3m -- of the Complex Motif associated with the Plane Group P3m1, is the Equilateral Triangle (regular trigon), so the Equilateral Triangle is the promorph of all the 2-D crystals of the Plane Group P3m1 and with it of the Class 3m.

Figure 18. The Equilateral Triangle (regular trigon) is the promorph or planimetric basic form of all crystals belonging to the Plane Group P3m1 and with it to the Class 3m.

In the next document we will do some more research into the present Plane Group (P3m1), especially the possible motifs that can be supported by this Group. We are particulary interested in space-filling motifs (which here means that we want content also in the background). In the process we will encounter two-dimensional 'ionic' crystals, which are very instructive with respect to the general tectology and ensuing promorphology of crystals.

To continue click HERE to investigate the Plane Group P3m1 still further, including the transition to the (study of the) Plane Group P31m, with respect to the characterization of the Complex Motif.

e-mail :