
REMARK : In the documents preceding the Introduction to Promorphology, we have treated of the individuality orders in organisms (Tectology). There we distinguished -- following Haeckel, but adding many amendments -- between Cells, Organs, Antimers, Metamers, Persons and Colonies ( = the six individuality orders). In Promorphology the ANTIMERS play a prominent role in determining the stereometric basic form (promorph) of higher form individuals. In cells and organs the PARAMERS play an analogous role. But in order to make Promorpohology as little dependent on Tectology (which itself is more or less speculative) as possible, we do, in all the documents concerning the Promorphological System -- and of which the present document is the first one -- not distinguish between antimers and paramers. All of them are just called Antimers.
All the organic basic forms first of all divide in two groups, the Anaxonia and the Axonia. The Anaxonia are characterized by the absence of any definite and constant body axis, while the Axonia always possess one or more such axes, and comprise almost all form types. The Anaxonia divide into two subgroups, depending on the presence or absence of a definite and constant midpoint of the body. The first subgroup is the A n a x o n i a a c e n t r a, consisting of bodies that not only lack any body axis but also a definite and constant mid-point of their body. The Anaxonia centrostigma on the other hand, although (also) lacking any definite and constant body axis, do have a definite and constant mid-point of their body. This mid-point is their c e n t e r o f s y m m e t r y which means that any straight line passing through that point connects equivalent body parts. This center of symmetry, as the only symmetry element of the Anaxonia centrostigma, is one of the four types of body centra that can be found in organic forms. The three others (not occurring in the Anaxonia centrostigma, and of course also not in the Anaxonia acentra) are : (1) The point of intersection of the axes in the Polyaxonia (endospheric polyhedra), (2) the line representing the only axis present in the Monaxonia, and the main axis of all Stauraxonia, except the Heterostaura allopola, (3) the plane of symmetry in all Heterostaura allopola.
The Homaxonia (spheres), and some Polyaxonia do have a center of symmetry, but in addition to it they possess mirror planes.
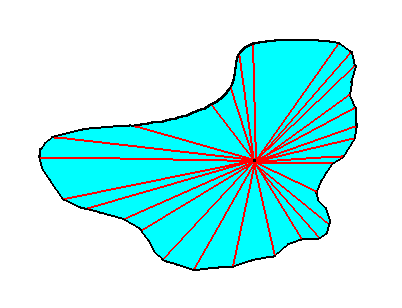
The Anaxonia acentra are completely irregular forms, lacking a constant center and showing no preferred axes. In the previous Document (Introduction to Promorphology) we derived them ultimately from the Homaxonia by an ongoing irregular differentiation of their axes and poles. The resulting forms lack any symmetry as do crystals belonging to the Asymmetric Class of the Triclinic Crystal System. This Class is indicated by the symbol 1 because of the following reason : The absence of symmetry of bodies is equivalent to their having only a 1-fold rotational axis that can be imagined to go through that body anywhere (which means every randomly chosen axis, passing through that body in any direction, will do). The possession of such a 1-fold rotation axis means that when the body is rotated about this axis by 3600, the result will be identical to the initial state before rotation, i.e. the body will be mapped onto itself.
All individual forms of organisms divide, with respect to their stereometric basic form ( p r o m o r p h o n t ) first of all in two large main groups (categories), namely Anaxonia acentra on the one hand, and the Anaxonia centrostigma + Axonia on the other. The Anaxonia acentra do not admit of any clear assessment as to their promorphont and are absolutely irregular, while the Anaxonia centrostigma + Axonia in one or another way admit of such an assessment. In the Anaxonia centrostigma and in all Axonia a definite ideal center of their body is present, a central spatial magnitude, to which all the other body parts relate. Therefore one can indicate the Anaxonia centrostigma + Axonia also as Centromorpha, i.e. as forms with a definite center (either in the form of a point or as a line or as a plane). In the other forms, that is to say the (Anxonia) acentra, such a center is not specifiable. This fundamental distinction between the highest and most general main categories of forms of organismic matter is analogous to the main form categories of inorganic matter. Also the latter either turns up in an amorphous state, or as definitely formed (i.e. with a definite intrinsic shape), and differently so formed depending on its phase (liquid or solid). The liquid inorganic individual (abiont), when it is in a condition of equilibrium, adopts a spherical form. But when the latter is transformed by crystallization from liquid to solid, it generally adopts the regular stereometrically specifiable shape of the crystal. So the Centromorpha of the organic world are analogous to the spheres, spheroidal forms, and crystals of the inorganic world, while the Anaxonia acentra of the organic world are comparable to the amorphous bodies of the inorganic world.
Remark : The Anaxonia acentra of the organic world can, as has already been said earlier, also be compared to crystals of the Asymmetric Class of the Triclinic Crystal System. But these crystals do have an internal periodic order (as do all crystals) causing them to have genuine crystal faces when grown unimpededly.
Remark : A curious intermediate situation can be found in the inorganic world : liquid crystals (rheo-crystals), also indicated as mesophase. Here we have liquid objects that possess some internal order comparable to that of solid crystals (sterro-crystals).
The organic basic forms that can be assessed to be genuine Anaxonia acentra, are in fact less common as one usually assumes. The persons, metamers and antimers, i.e. the form individuals of the fifth, fourth and third orders (See for those the previous Essay on the Introduction to Promorphology), seldom, or in fact never, are really acentric or anaxonic, because already by reason of their tectological quality certain axes are evident. Form individuals of the first and second orders (cells and organs), on the other hand, often appear to be genuine Anaxonia acentra, and also many colonies, for instance many coral colonies.
The next figure shows a well-known plant organ that is totally acentric :
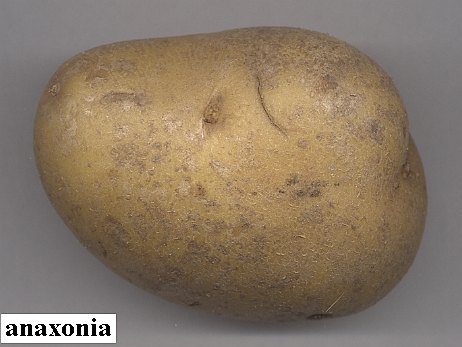
Among whole (i.e. complete) organisms the Anaxonia acentra are most diversely represented in Sponges.
The Anaxonia centrostigma are represented by bodies of which the only symmetry element is a center of symmetry. Qua external symmetry they are equivalent to crystals of the Pinacoidal Class of the Triclinic Crystal System.
A center of symmetry is illustrated by the following Figure.
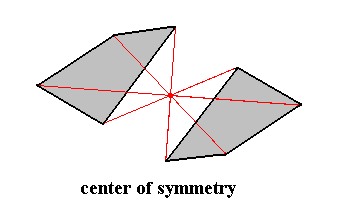
Figure 2a. Center of Symmetry.
The item, as depicted here, and possessing a center of symmetry (and only a center of symmetry) consists of two asymmetric faces related to each other by a center of symmetry, which means that every point of such a face is reflected in a same point, the center of symmetry ((all this)indicated by the red lines and their point of intersection. Every part of the item can also be found at the opposite side of that point at the same distance.
There are only a few organisms that materialize the Anaxonia centrostigma, one of them is depicted here.
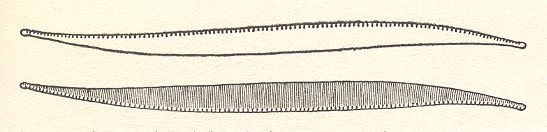
Figure 2b. Nitzschia sigma, a diatomean cell. Upper and lower valve separately depicted. The raphes ly on the edge of the valves, but on different sides, causing the symmetry content of the whole organism to consist of just a center of symmetry, implying that the organism promorphologically belongs to the Anaxonia centrostigma.
(After HUSTEDT, F., 1956, Kieselalgen (Diatomeen))
As is already the case in the Anaxonia centrostigma (which are as a group of limited importance with respect to organic Promorphology), the generation of organisms belonging to the present Class is in some way or another spatially restricted, resulting in individuals that possess a definite stereometric basic form on which their actual shapes are based. These shapes are never just lumps but are genuine shapes.
All organic forms that are not in an absolute way irregular, or do not just possess a center of symmetry, always possess a constant centrum, such that in it definite axes come together, or through which runs at least one definite axis. Therefore we call them Axonia. All parts of the body of the organic individual have a definite position with respect to that centrum and those axes, resulting in the fact that the shape of that body never is in an absolute way irregular or just centrosymmetric, but always either regular or symmetric (in its broadest sense). So by reason of this it is always possible to indicate at least one bisection plane in the body of such an individual, a bisection plane that divides the body either in two congruent halves, or in two symmetric identical halves, or in two symmetric similar halves. The center ( c e n t r u m ) of the Axonia, to which all body parts spatially relate, can either be a point ( s t i g m a ), or a line ( a x o n ), or a (internal) surface ( e p i p h a n i a ). The latter usually is a plane ( e p i p e d u m ). On the basis of this we can distinguish three essentially different main groups within the Axonia. (Remark : Some not yet discussed promorphological categories will be mentioned. They will be fully dealt with later.)
When we now want to properly understand and evaluate the further differences associated with the many basic forms that belong to the present Class, i.e. the Axonia, we must first of all further determine the properties of the axes of their body and thereafter the (properties of the) poles of those axes. According to this viewpoint all Axonia can be divided among two main groups, namely in Homaxonia (equiaxial forms) and Heteraxonia (unequiaxial forms). In the former all axes, that can be imagined to run through the body center, are absolutely equal, in the latter they are unequal. The number of equal axes, that go through the center, is in the former infinite, in the latter finite. The Homaxon form can represent only one form, namely the (bald) Sphere, while the Heteraxon form is extremely diverse in its (possible) differentiation. The Homaxonia and the Heteraxonia, as the two most pristine and general form species of the organized centromorphous matter, at the same time correspond to the two most pristine and general shapes, in which non-organized (but) formed matter appears in the liquid state (phase) and in the solid state, namely the sphere and the crystal. The spherical shape of the drop that is adopted by the inorganic individual when it is in a liquid state and in perfect equilibrium, is about the same in a homaxonic organism, especially as it often is in its first individual stadium as a semi-liquid cell. The heteraxon form in organisms can always be reduced to certain simple geometric basic forms, which remind us to the external shapes of crystals.
Bodies possessing maximal symmetry and regularity. All axes that pass through the body center are equivalent.

The properties of the sphere, which is the only possible homaxon form and at the same time the only absolutely regular (geometric) body, are so well known, that we do not have to expound them here.
Bodies possessing unequal axes, giving rise to endospheric polyhedra, ellipsoids, cylinders, cones and pyramids.
Heteraxonia or unequiaxial Axonia refer to all organic forms, that
allow us to distinguish a finite number of definite axes, which differ from all
other axes that go through the body center. In this category we place all
the shapes adopted by organized matter that are in some way comparable to
the external shapes of crystalline non-organized matter.
To assess the basic forms of the different heteraxonic organic individuals we will not primarily consider the surfaces and their relationships, but concentrate on finding the axes of the body and their poles, and see for their equality or unequality (differentiation).
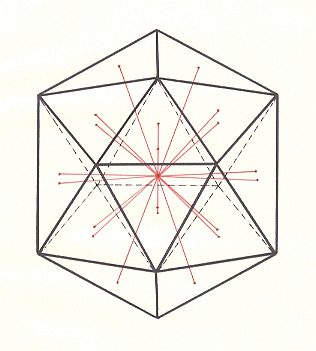
With respect to this the whole mass of heteraxonic organisms falls apart in two main groups. In the one a certain main axis can be detected that shows certain differencs with respect to all the other axes of the given body. In the other all determinable axes are equivalent, or there are several (at least three) main axes present, that distinguish themselves clearly from the remaining secondary axes, but that are equivalent to each other. The representatives of this latter group, the Heteraxonia with three or more main axes, we call the Polyaxonia, while those from the first group, the heteraxonia with only one main axis, will be called Protaxonia. In the Polyaxonia the center of the body is, like in the Homaxonia, still a point, while in the Protaxonia it is a line, or (in the Heteostaura allopola) a plane.
Bodies that are no spheres, but that neatly fit into a sphere. They are bounded by faces.
The general basic form of the Polyaxonia is an endospherical polyhedron, i.e. a polyhedron of which all corners hit the surface of a single sphere. The center of this sphere is at the same time the center of the polyhedron, and the axes of the polyhedron can be revealed when we connect all corners of it with the center by means of straight lines. Not any such axis distinguishes itself from the others in such a way that it could be assessed as the main axis. Evidently this polyaxonic basic form is first of all linked to the absolutely regular form of the sphere.
Only relatively few organismic individuals show the polyaxonic form, for example many pollen grains.
Like what has been done in Stereometry, namely to divide the endospheric polyhedra in regular and irregular forms, we can do the same with respect to those organisms in which the polyaxonic form is realized. According to that a regular polyhedron is bounded by regular and congruent polygons (i.e. all its faces are identical). It has been proven that only five species of them are at all
possible, they are called the five Platonic Polyhedra :
Bodies that fit into a sphere. Their faces are not all identical.
To the Polyaxonia arrhythma we must reckon all those endospherical polyhedra the faces of which are partially unequal. Consequently not all the faces of such a polyhedron are regular and congruent polygons. Many pollen grains belong to this group and also some spherical spores and eggs with a irregular reticulate surface, further some Radiolarians.
The many forms that are displayed in some arrhythmic polyaxonic Radiolarians can be divided in two different groups. In the first group the polygonal faces of the endospheric polyhedron are all of the same kind, i.e. all have the same number of sides and angles. In one case all faces are triangular, in another case they can be pentagonal (five sided), etc. We can therefore call them Isopolygona. In the second group, on the other hand, the faces of the polyhedron are partially or all different. The number of sides and angles of least some polygonal faces is different from that of other faces. These generally more irregular forms can be called Allopolygona.
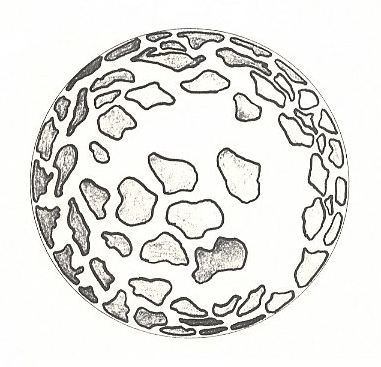
Those endospheric polyhedra, the faces of which do not all have the same number of sides and angles, and which we sum up as Allopolygona, are the basic form of many Radiolarians. Also many cells of the vegetable pollen show this form type.
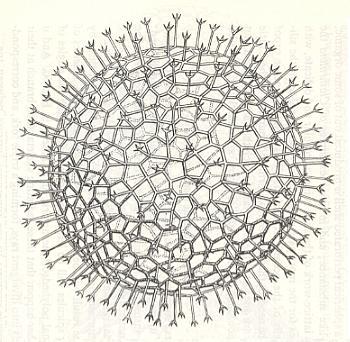
Bodies that fit into a sphere, but are irregular, but not totally so.
Still more clearly and definitely as in the Allopolygona the endospherical polyhedron form appears in those basic forms that we call Isopolygona. They are so called because the number of sides and angles that bound their faces is the same for all faces. Many of such polyhedra come close to the regular polyhedra, because the majority of their faces are formed by (regular) polygones that are very similar or partially even congruent (or rather almost congruent), and in which only those few faces, that must be inserted between the congruent ones in order to complete the spherical form, are a little different from them.
The number of sides and angles is in all Isopolygona always the same (but varying from species to species). On the basis of that number being three (i.e. the faces are then triangles), four, six, etc., we can distinguish subordinated basic forms (i.e. dividing the Isopolygona in several subgroups): trigonal, tetragonal, hexagonal species of Isopolygona. But there's a snag : No system of hexagons can enclose space. Whether the hexagons be equal or unequal, regular or irregular, it is still under all circumstances mathematically impossible. We learn from Euler : the array of hexagons may be extended as far as you please, and over a surface either plane or curved, but it never closes in (D'Arcy THOMPSON, On Growth and Form, Abridged Edition, 1975, p. 157/8).
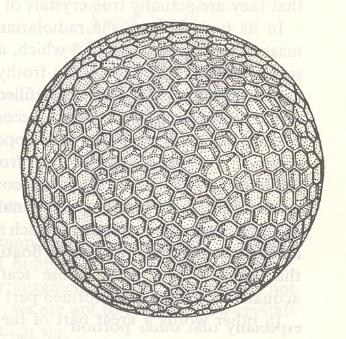
In the next Figure we see the shell of the Radiolarian Aulonia hexagona. Here we can detect many hexagonal facets, but indeed not all of them are such. In the Figure we have indicated some pentagonal facets. THOMPSON reports that "Haeckel actually states, in his brief description of his Aulonia hexagona, that a few square or pentagonal facets are to be found among the hexagons."
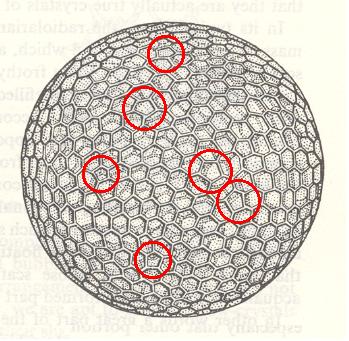
So strictly speaken, the form of Aulonia hexagona, complies, not with the Isopolygona, but with the Allopolygona.
The next Figure depicts a "triangulated" radiolarian. It complies well with an endospheric polyhedron consisting of many -- i.e. more than twenty : One actually having twenty (triangular faces) we will encounter in due course as belonging to the Icosaedra regularia, one of the five species of the Polyaxonia rhythmica -- triangular faces. So this radiolarian can be considered promorphologically as belonging to the Isopolygona.

If we look at Figure 8 we see that the spherical network of that radiolarian shell consists of triangles. At first sight these triangles appear to be grouped such that everywhere six of them form a hexagon. So the surface of the shell seems to be built up from triangulated hexagons. When we now think away all the rods that radiate from the center of each hexagon we're left with a spherical network of hexagons which we know is impossible. So in addition to the many hexagons there must be some other polygons, say pentagons, strewn between the hexagons. On closer inspection of the drawing of that radiolarian shell we indeed see at least one pentagon to be present.
Very conspicuously the Isopolygonic form appears in many pollen grains.
Bodies having the shape of one of the five "Platonic Polyhedra". After the sphere, which is has maximum symmetry, they are the most regular three-dimensional bodies.
Much more seldom than is the case with the arrhythmics, we'll see the rhythmic or regular Polyaxonia realized in organic individuals. Such perfectly regular polyhedra, while (three of them) being common among crystals of the Isometric Crystal System (also called Regular, Tesseral System), are found relatively seldom in organisms, namely in pollen grains of many higher plants, and in the silica shells of some Radiolarians. All five species of the Polyaxonia rhythmica, namely the Icosahedron, the Dodecahedron, the Octahedron, the Hexahedron and the Tetrahedron, are realized in certain organic forms.
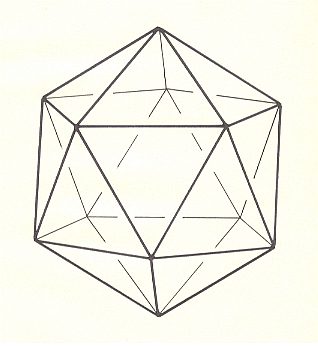
The regular Icosahedron, the 20 faces of which are equilateral and congruent triangles, is among all regular polyhedra the most uncommon form realized in organic individuals. Haeckel could find only one organism in which it indeed is realized, namely in the Radiolarian Aulosphaera icosaedra (which could -- according to Haeckel, 1866 -- be a juvenile stadium of Aulosphaera trigonopa), and maybe (it is realized) in some pollen grains.
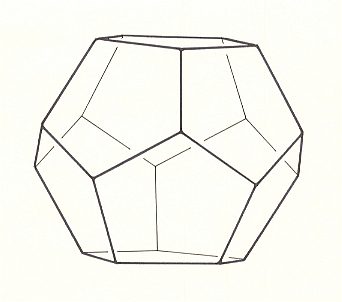
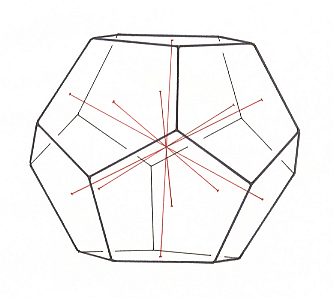
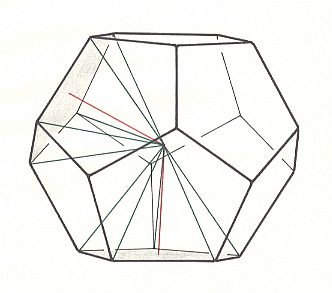
The regular Dodecahedron, or Pentagonal Dodecahedron, the twelve faces of which are equilateral and congruent pentagons, can be found in pollen grains of many higher plants. In crystals we also find a pentagonal dodecahedron, namely in many crystals of the mineral Pyrite, but it isn't a regular dodecahedron, because in genuine crystals a five-fold rotation axis (characterizing a regular pentagon) is mathematically impossible.
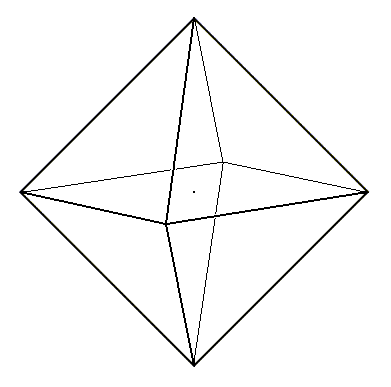
The regular Octahedron, the eight faces of which are equilateral and congruent triangles, is much more seldom realized in organisms than the Pentagonal Dodecahedron is. Also is it more sparsely realized than the next form, the cube, is, although it has the same axial relations as the latter.
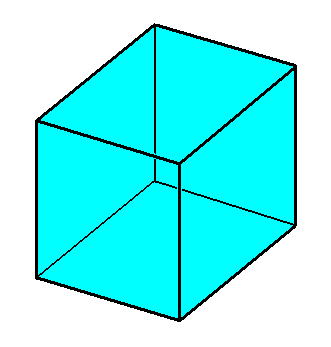
The regular Hexahedron or Cube ( C u b u s, T e s s e r a ), the six faces of which are congruent squares, is the stereometric basic form of many freely existing organic cells. It is very neatly realized in, for example, many pollen cells.
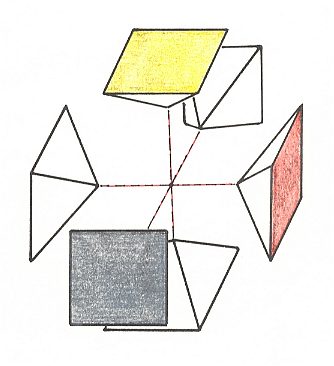
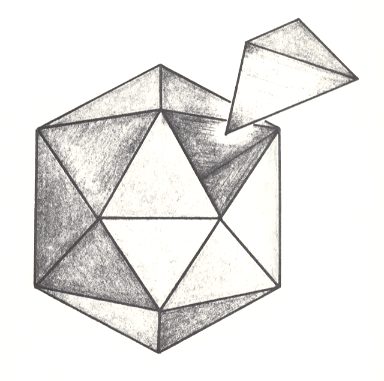
The next Figure depicts the construction of a regular tetrahedron from a cube.
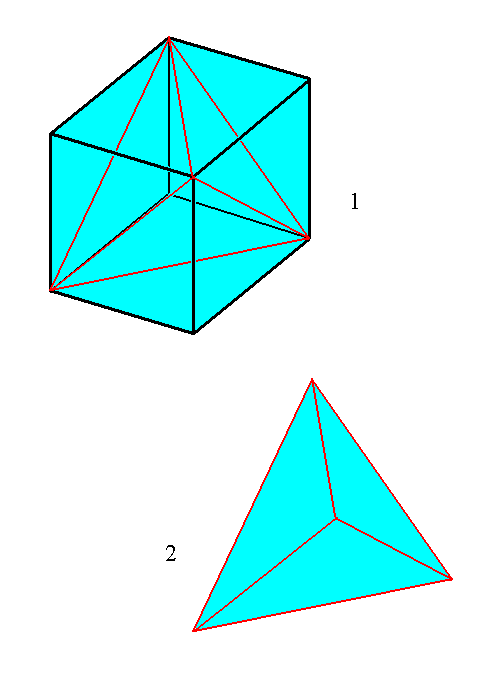
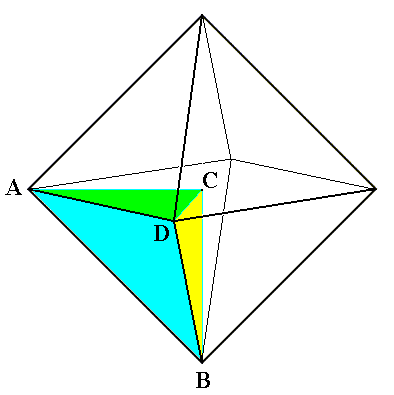
The Basic Form of the Tetraedra regularia consists of four Antimers as the next Figure shows.
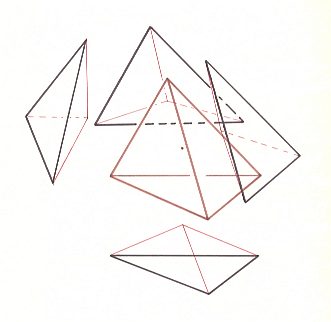
The regular Tetrahedron, the four faces of which are equilateral and congruent triangles, and which we can find as a (hemihedric) Form in the Isometric Crystal System, will not easily be encountered among adult organisms. But it seems common in many pollen cells.
In addition to ENDOSPHERIC polyhedra there can be SUBENDOSPHERIC polyhedra, i.e. polyhedra, also not showing any axis that stands out, but which in spite of that such that its corners do not lie on one sphere but on several different but concentric spheres, i.e. one group of corners lie on one sphere, whole the remaining corners lie on another sphere concentric with the first one. These subendospheric polyhedra are known in the realm of CRYSTALS. But because it is not to be expected that they are materialized in organisms we will introduce them separately in a special inframe (see below).
To continue click HERE to proceed further with the systematic Promorphology.
e-mail :

back to retrospect and continuation page
back to Introduction to Promorphology
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals