e-mail : 

REMARK
All the many documents that will now follow are headed by :  The Total Symmetry of Three-dimensional Crystals.  But it will turn out that such crystals will in fact only rarely be touched upon in these documents. Istead, two-dimensional crystals -- which do not as such exist physically -- (and group theory) are being studied there.
The study of the theoretical two-dimensional crystals and group theory together form a necessary preparation for the study of the symmetry of three-dimensional crystals, especially because the symmetry of two-dimensional crystals is much easier to understand than that of their three-dimensional counterparts. But when we began these preparatory studies we thought we could do this in just a few, say three or four, documents. All the many further documents which would then follow upon these would then explicitly turn to the study of the symmetry of three-dimensional crystals grouptheoretically. And so we could conveniently call every document of the total series, that is, the preparatory documents (2-dimensional crystals and group theory) as well as the 'true' documents (3-dimensional crystals and group theory) :  The Total Symmetry of Three-dimensional Crystals.  But, as it turned out, the preparatory study took many more documents than was initially anticipated, and we have up to now (May, 2007) even not yet begun the promised grouptheoretical study of the symmetry of three-dimensional crystals. We don't know whether we will have the opportunity for this study.
Crystals will, in all the major 'Parts' of this Website (First, Second, Third, and Fourth Part of Website), be studied mainly from a philosophical point of view, and, as I became to realize in the course of the preparatory studies and later, a study of two-dimensional crystals and (the relevant part of) group theory is probably already sufficient for the philosophical points we are planning to make.
But if the reader is not convinced of this sufficiency, or if he or she wants to study the symmetry of three-dimensional crystals anyway (for example because of purely mathematical or mineralogical interests instead of philosophical ones) the reading of the present and folowing documents named  The Total Symmetry of Three-dimensional Crystals  is still highly recommended because they provide a very clear and necessary preparation for such a study.
And indeed the present document (Part I of the present series) as far as it treats matrices is directly relevant for three-dimensional symmetry theory, while we will not use matrices in the grouptheoretical study of two-dimensional crystals.

This document will begin with the theoretical preparations necessary for a treatment of the Internal Structure of Three-dimensional Crystals.
Because this internal structure is very complicated and hard to visualize (i.e. drawings will not reveal very much of those 3-D structures), we will heavily rely on our corresponding results with respect to the internal structure of two-dimensional crystals, fully expounded in a previous series of documents (To inspect them, go back to HOMEPAGE, and see the documents on The Internal Structure of Crystals Parts I -- XX). In fact the theory of the internal structure of three-dimensional crystals is basically the same as that of two-dimensional crystals. The structure of three-dimensional crystals is, however, more complicated because of the extra dimension, and, being a consequence of it, of the possibility of screw axes (that cannot occur in two-dimensional crystals), representing an extra symmetry element, occurring in several 3-D crystals. All this implies a larger number of possible and unique combinations of symmetries :   Instead of the 17 Plane Groups of 2-D crystals, we have 230 Space Groups in the case of 3-D crystals.
So the reader should first consult the documents on the internal structure of two-dimensional crystals before going to read the present document(s).
In order to understand the internal structure of 3-D crystals, an understanding of the  s y m m e t r i e s  inherent in a given structure is paramount. This in turn demands that we should learn more about symmetry itself. A symmetry is a transformation, performed on an object, (a transformation) having certain general properties, one of them is that the object (having this symmetry) will end up precisely where it was before it was subjected to that transformation (It is mapped onto itself). So we can speak of a symmetry transformation. And the total of possible symmetry transformations that can be performed on an object has special mathematical properties that unify that total, and classify the object according to its symmetry.
A crystal (and we concentrate fully on 3-D crystals), when viewed macroscopically, and, consequently, seen as a  f i n i t e  object, has one or more symmetries. These could be rotations, roto-inversions, reflections and inversions. They constitute the  p o i n t  s y m m e t r y  of the given crystal. They involve transformations in which at least one point remains where it was. They can conveniently be described by the so-called Point Groups.
All or some of these point symmetries of that given crystal we also encounter in that same crystal's internal structure, i.e. in the periodic pattern of chemical motifs -- which is only evident in a microscopical view of the crystal. But in addition to these point symmetries the periodic motif pattern has other symmetries as well :   translational symmetries. These are symmetry operations in which not any point remains in place. All the points of the pattern move to a new location. But, because in a microscopic view the pattern of (chemical) motifs of a crystal can be considered as virtually infinite, the pattern can be mapped onto itself by an appropriate translational symmetry transformation, which then means that the pattern has that specific translational symmetry. These translational symmetries of the internal periodic pattern of the given crystal, together with the point symmetries still present in that pattern, form the  t o t a l  s y m m e t r y  of the (internal) structure of that crystal. It can be described by a Space Group.
So the external symmetry of a crystal is described by its Point Group, while the symmetry of its internal structure is described by its Space Group (of which the 2-D analogue is the Plane Group). The Point Group of a crystal describes the translation-free residue of the total symmetry of that crystal described by its Space Group.
In order to understand Point Groups and (especially) Space Groups, we must know something about the (mathematical) Theory of GROUPS.

Every object can be characterized by its  s y m m e t r y.  It contains at least one, but often several symmetries. But what then is a symmetry?
A symmetry is a certain operation, namely a rigid transformation, that can be applied to that object such, that the result is that same object occupying exactly the same space as it occupied before the transformation took place. The object has covered itself exactly, or, in other words, it is mapped onto itself. The transformation is rigid, which means that all internal distances and angles are preserved. But, except for the so-called identical transformation, most points have swapped their positions.
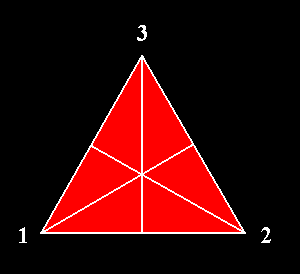
A good example are the symmetries of the Equilateral Triangle.

Figure 1.  An equilateral triangle. The three points associated with its three angle are numbered.

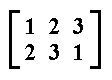
If, on the other hand, we rotate the triangle 240⁰ it will also cover the original. It again occupies the same space as before. The permutation involved is the following :

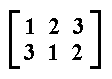
If we, finally rotate it 360⁰ we have executed an operation which is in fact equivalent to not having it rotated at all. The permutation involved is the following :

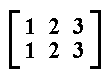
This permutation represents the identical transformation.
So to begin with the equilateral triangle has three symmetries :   three rotational symmetries, one of which -- rotation of 0 or 360 degrees -- is the identical transformation, in which no points are swapped.
But the equilateral triangle has still more symmetries.
We can detect three mirror lines (reflection lines), each one going from a tip to the center of the opposite side (Figure 1). When we reflect the triangle with respect to one such reflection line we swap the two halves of the triangle divided by that line. Also these three reflections can be expressed by permutations of the three numbered points of the triangle (Figure 1) :   When we reflect the triangle with respect to the vertical mirror line, 2 will be replaced by 1, and 1 will be replaced by 2, while 3 will be 'replaced' by itself. So we have the following permutation :

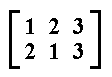
The permutations representing the other two reflections are then as follows :

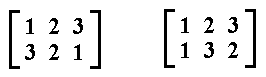
So we have six permutations with respect to the Equilateral Triangle, i.e. the equilateral triangle has six symmetries, which are rigid transformations such that the original is exactly covered by the image produced by that transformation :  three rotational symmetries (one of which is the identical transformation) and three reflectional symmetries.
In the following we list all these six permutations and identify each one of them with a letter for easy reference.

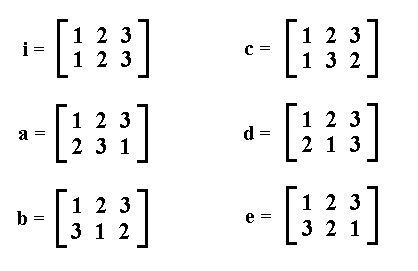
Now this set of transformations -- the permutations i, a, b, c, d, and e -- i.e. the set of symmetries possessed by the Equilateral Triangle, is not just a set, it is not just a bunch of symmetries that happen to be present at the triangle. The set has a  s t r u c t u r e,  causing it to be an intrinsic unity. Let me explain this structure.
The permutations associated with the Equilateral Triangle are related to each other in a special way :   They can be seen as elements of an  o p e r a t i o n,  in our case a binary operation, which means that the two members of each pair of permutations from our set can in some way be combined. And the result of this combination -- the product of the operation -- turns out to be identical with some one permutation already present in our set. And this combination -- this operation -- with respect to (any) two permutations of our set consists in the  s u c c e s s i v e   e x e c u t i o n  of two permutations (one after the other). The result of such an operation on any two permutations of our set turns out to be always itself a permutation already present in our set. Of course this was to be expected, because the permutations are in our case transformations of an equilateral triangle, such that the image (the product) of this transformation exactly covers the original triangle. So performing two cover transformations, one after the other, results again in a covering of the image triangle onto the original. We can say that our set of permutations is closed under the operation mentioned (which is the successive application of two permutations of the set). We can denote this operation by the letter O.
Let us subject the permutations  a and  c (in this order) to the operation O, i.e. let us successively apply the permutations  a and  c :

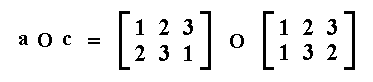
The result of the application of permutation  a  on the initial numbers  1  2  3  is :   2  3  1.  To this result we will apply permutation  c :

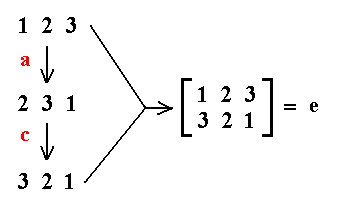
We can easily verify that the result is identical to permutation e, which already belongs to our set of permutations, so we can state :

In this way we can determine all the possible combinations of two permutations of our set. The results can conveniently be summarized in the following table :

This table reads as follows :  If we want to know the outcome of  d  O  e  we look up  d  in the column of entries to the left (i.e. left of the line), and we look up  e  in the row of entries above (i.e. above the line), and determine what is found at the intersection of the horizontal line, starting from  d,  and the vertical line, starting from  e.  We find  a.
The contents of the table immediately shows that the set is closed under the operation. But, in addition to the fact that our set of permutations is closed under the operation O, there is more to the structure of this set :

The operation O is associative, which means that to any three elements x, y and z of our set of permutations the following applies :

That our operation complies with associativity is intuitively clear : Our operation consists in the successive execution of two transformations : The end result (and that is all what matters here) is the same when we (1) shave and wash, and then, after a pauze, dress, or when we (2) shave, and, after a pauze wash and dress.

And further :  every equation

and every equation

possesses one, and not more than one solution.

We can check this for every two elements of our set by consulting the table given above.

These properties (closure, associativety and unique solutions) cause the set, having these properties, to be a  G R O U P.  In our case it is the symmetry group of the Equilateral Triangle.
A GROUP is a certain self-contained algebraic structure. It is a set of elements for which one binary operation is defined, such that the set is closed under this operation, and that this operation complies with the above mentioned conditions (associativity and unique solution). The latter conditions are called Group Axioms. From them a number of other properties can be deduced. For example, we can state that a GROUP always possesses one determined identity element (neutral element)  i. The latter can be defined as follows :

For every element of the GROUP the following holds :

In our case of the symmetry group of the Equilateral Triangle,  i  was the identity transformation, i.e. rotation of the triangle by 0⁰ (or 360⁰).

Also the following property of any GROUP can be deduced :

A GROUP always contains one determined inverse element, which here means that for every element  a  there is an inverse element a^-1, also belonging to the set, such that :

So because, for example (See our table),

b is the inverse of a and vice versa.
The inverse makes a transformation undone. In the case of a rotatation this means that we must rotate back with the same amount, effecting the net operation to be the identity operation.
In the case of undoing a reflection we must perform this same reflection again. Indeed, as can be seen in the above table,

in which c is a reflection with respect to the mirror line going through 1 of the above depicted triangle ( Figure 1 ). Indeed, if we flip (i.e. reflect) a figure and flip it again with respect to the same reflection line, then in fact nothing has happened : we have performed the identity transformation.

The symmetry group of the Equilateral Triangle is a so-called third-order Dihedral Group and is denoted in mathematics as D₃. In crystallography it is called the Point Group 3m. It is called a point group because the involved symmetry transformations always leave at least one point where it initially was (In contrast with a translational symmetry transformation, where ALL the points are shifted to a new location).

In the Group Table of the group D₃, as given above, we can detect a subgroup, i.e. a genuine subset of the elements of D₃ form a group of their own. These are presisely the elements that are the rotations (i.e. the rotational transformations), and these form a so-called cyclic group, indicated by the symbol C₃, consisting of the elements, i, a and b. The next Figure shows this subgroup C₃ within the group D₃.

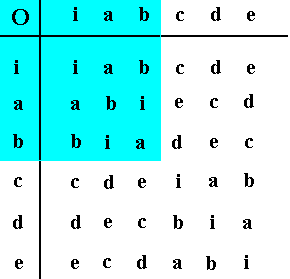
Figure 2.   The cyclic subgroup C₃ of order 3 is indicated (light blue) within the dihedral Group D₃ of order 6. The cyclic subgroup represents the rotational component of the 3m symmetry.

So the symmetry of a crystal can be described by a Group, consisting of all the symmetry transformations inherent in the given crystal. In order to develop the Group concept further we are going to describe a symmetry transformation in a more or less different (but equivalent) way, i.e. different from how we did it in our above example of the equilateral triangle. A symmetry transformation will now be described as an operator. Such an operator can act on a point, or on a crystal face, moving it to a new location (as we see it for example in a rotation or in a reflection). Each symmetry transformation is a transformation with respect to a certain geometrical feature, for example a line (in a 3-D situation), with respect to which a rotation is executed, or a plane with respect to which a reflection is executed. Such a line we call a rotation axis, and such a plane we call a mirror plane. In general such geometrical objects (lines, planes, etc.), with respect to which certain symmetry transformations are performed, like rotation axes and mirror planes, are called symmetry elements. Well each individual symmetry transformation with respect to a certain symmetry element, say a rotation of 60⁰ about some axis, or a rotation of 120⁰ about that same axis, but also a reflection across a certain plane, or a reflection across another plane, can be seen as the action of an operator acting on all the points, planes and faces of a crystal. And such an operator can most conveniently be represented by a  m a t r i x.
The coordinates of a point can also be given as a matrix. If we now multiply (according to the rules of matrix multiplication) the operator matrix with the coordinate matrix, we will obtain the coordinates of the image of the given point when it was indeed subjected to the symmetry transformation of which the mentioned matrix represents the operator.
It is clear that we should know something about matrices.

An algebraic equation is linear when the unknown -- often denoted by x -- is raised to a power of maximal 1.
A constant, say 3, figuring in such an equation, can be thought of as a number multiplied by the unknown raised to the power of zero. In our case that would be 3x⁰. And indeed, x⁰ is equal to one, no matter what the value of x is, because, generally, a^y/a^y = 1 = a^y-y = a⁰. So 3x⁰ = 3. In addition to being raised to the power of zero, resulting in a constant, the unknown x can be raised to the power of one, x¹, and this is equal to x. So in a linear equation with an unknown denoted by x, we only see x, and multiples thereof (for example 3x, 1/4x etc.) and constants, for example 2, 3 1/4, etc.).
Now suppose we have a system of linear equations (also called a linear forms) in which there are no constants (so the unknown only occurs as raised to the power of one) :

then the system of coefficients can be denoted as follows :

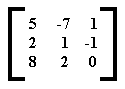
This entity we call a  m a t r i x.  It is in fact a sort of ordered table consisting of an array of elements, often numbers.
It can represent the system of linear forms completely. It has three rows and three columns.
The coefficient matrix of our general system of linear forms, as given above, would look like this :

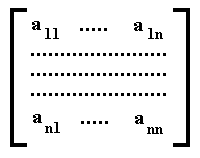
This matrix has n rows and n columns. For to be a matrix the number of rows does not need to be equal to the number of columns. Our two matrices were examples of so-called square matrices, respectively 3x3 and nxn. But there can be, say, 3x4 matrices, etc., generally mxn matrices.

Well, every matrix consists is an array of mathematical magnitudes. But a matrix itself can also be interpreted as a mathematical magnitude. And for such magnitudes we can define certain operations, which means that we combine two matrices, A and B, and obtain, as a result, matrix C.
The definition of the addition of two matrices is straightforward : Corresponding elements are added.

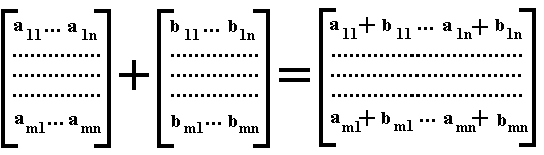
The definition of the multiplication of two matrices is less straightforward, because it will not be the multiplication of corresponding elements in the same way as we did for the addition. So the multiplication of the two just considered matrices will NOT result in the following :

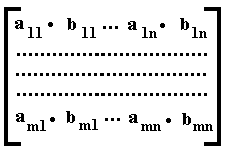
Of course we could define the addition in this way, but then there would be no connection at all with linear forms.
We will now show how we can arrive at a definition of the multiplication of two matrices while retaining their connection with linear forms.
Consider the folowing linear forms :

Horizontally the coefficients go from a₁₁, via a₁₂, a₁₃, etc. to a_1m.
Vertically they go from a₁₁, via a₂₁, a₃₁, etc. to a_k1.
Further, from a₁₂, via a₂₂, a₃₂, etc. to a_k2,
and so on.
So the matrix of the coefficients has k rows and m columns.
If we now substitute in this system the following linear forms :

we get of course again linear forms, that look generally as follows :

Now we want to know what the coefficients c₁₁ etc. really are. All we have to do is to actually carry out the substititions. The y's in our original system must be replaced by the corresponding values of those y's (y₁, y₂, etc) as given above. But of course this is a lot of calculation work!
One has, however, discovered that the matrix of the c-coefficients can be derived in a simple way from the matrix of the a-coefficients and that of the b-coefficients. This c-matrix is called the product of both other matrices.
From the substitution, as was indicated above, we can see that a multiplication of matrices, when it is equivalent to such a substitution, can only be performed when the a-matrix has m columns (whatever the value of m is) and the b-matrix precisely as many rows.

The reverse is not demanded :   The number of columns in the b-matrix does not need to be equal to the number of rows in the a-matrix :
While in the just given example the number of columns in the a-matrix (for coefficients) is m, and is indeed equal to the number of rows in the b-matrix (m),   the number of columns in the b-matrix is n, and the number of rows in the a-matrix is k.

So only when the above condition is satisfied the multiplication of two given matrices is (significantly) defined.
Now we can give a general formula that indicates the product of two matrices, but it comes out more clearly when we give an example.
Consider the following two matrices A and B :

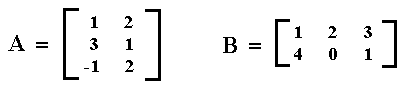
To determine the product AB (in this order!) we do the following, in which the arrows indicate which matrix elements must be multiplied :

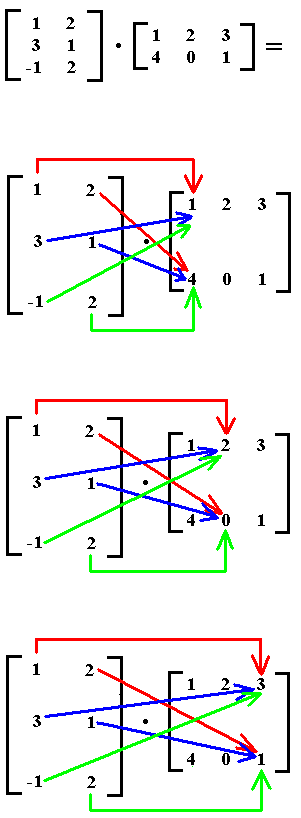
First we handle the first column of matrix B as indicated, and add the products, then we handle the second column of matrix B, and add the products, and finally we handle the third column, and add the products. We get the following result :

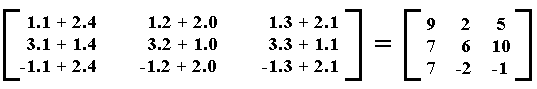
If we now determine the product BA (instead of AB) then we see that we get a different answer :

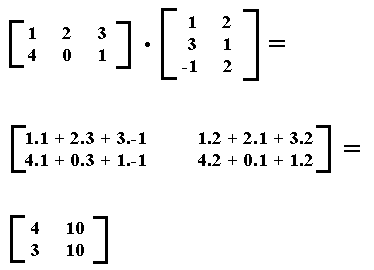
It is even a matrix with a different number of rows and columns! In such a case we say that the matrix multiplicatiom is not commutative. For an operation O to be commutative the following is demanded :
a O b = b O a  for every pair a,b of the set for which the operation is defined. So if we find already one case in which the two elements involved do not commute, the operation is non-commutative.

We have now defined two operations for matrices, addition and multiplication. But there is yet another operation to be defined. And this operation is also a multiplication, but this time a multiplication of a matrix and a number :
A matrix A is multiplied with a number c by multiplying every element of the matrix by that number.

With the help of matrices we have a means of writing down large expressions in a compact way (and we shall amply make use of this property of matrices). Say we have the following system of equations :

This system can be written down as follows :

where B is the matrix of the coefficients.  X is a so-called column matrix (or column vector), and Y is also a column matrix (column vector) :

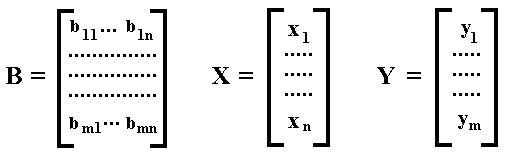
If we now apply the rule for matrix multiplication with respect to the matrices B and X we get the following :

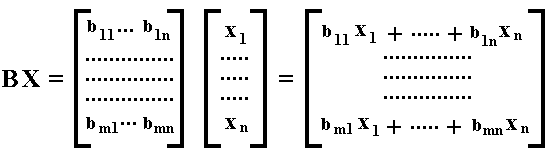
We see that we indeed get the above form insofar as it is at the left of the equality sign. Note that the result of this multiplication (BX) is a column matrix consisting of one column.
We still have to recover the complete equations.
To accomplish that we must define the equality of two matrices :
Two matrices are equal if the corresponding elements are equal.
This definition is of course only relevant when the number of rows and columns is the same (i.e. when the matrices are of the same order).
Well, the matrix Y has only one column (with m elements), and the matrix of the product BX also consists of one column (with m elements). If we now equate the corresponding elements of BX with those of Y, then we indeed get back our system of equations.

As has been said, matrices will, in our expositions concerning the internal structure of 3-D crystals, be used to express symmetry transformations, like a rotation of 120⁰ about a certain axis, a reflection across a certain plane, etc. And as such they will figure as the elements of GROUPS, under the group operation of the successive execution of two such transformations. Such a successive execution is in fact a mapping that assigns a unique symmetry transformation from the given set of symmetry transformations to a given (ordered) pair of symmetry transformations from the same set. This mapping will be equivalent to the multiplication of two matrices, each one expressing a symmetry transformation. So the mapping, i.e. the group operation fixing the relation between its elements, assigns a unique transformation matrix to an ordered pair of transformation matrices from the same set of transformation matrices constituting the given GROUP. If we represent such matrices by letters, we can conveniently set up group tables in which the group operation (the mapping just mentioned) is fully defined.

Above (click link) we described the total symmetry of the Equilateral Triangle by means of permutations of its three corners. Permutations may also be represented by matrices. So the above permutations describing the 3m symmetry of the Equilateral Triangle could be expressed as matrices that together form a Group inder the operation of matrix multiplication.
Let's see how this works out.
The permutation

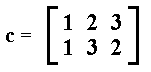
(1 becomes 1, 2 becomes 3, 3 becomes 2) can be effected by the following matrix :

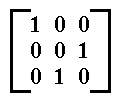
To demonstrate this we write the three numbers as column matrices (column vectors). So with respect to the just given permutation c we have two column vectors, one corresponds to the initial number sequence, 1 2 3, the other to the resulting number sequence, 1 3 2 :

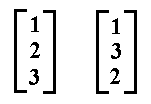
We can now show the action of the just given permutation matrix on the initial number sequence :

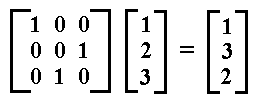
Also for the remaining five permutations we can find matrices that effect those permutations (i is the identity element):

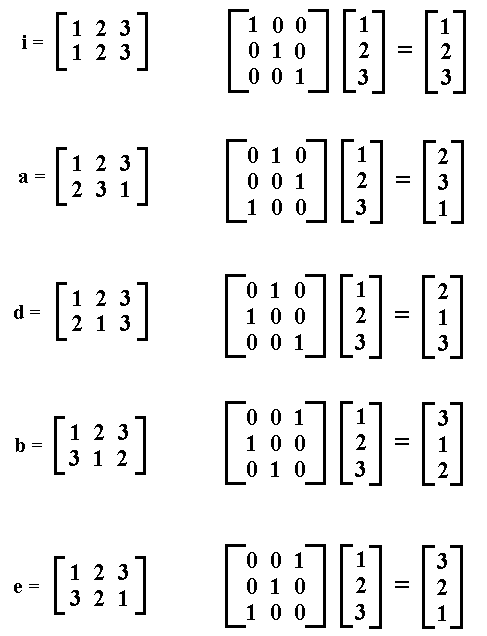
This set of six permutation matrices forms a GROUP under the composition of two permutations (first one permutation, and, executed on the result, a second permutation), which now is equivalent to a matrix multiplication, i.e. a multiplication of any two matrices of the set. We can indicate each matrix within this set with the same label as we used for the corresponding permutation. It is however customary to use capital letters for matrices. So our set of matices is { I, A, B, C, D, E }, and they form, as has been said, a GROUP under matrix multiplication. For example when we multiply the matrices A and B, i.e. if we determine the product AB, we get the following :

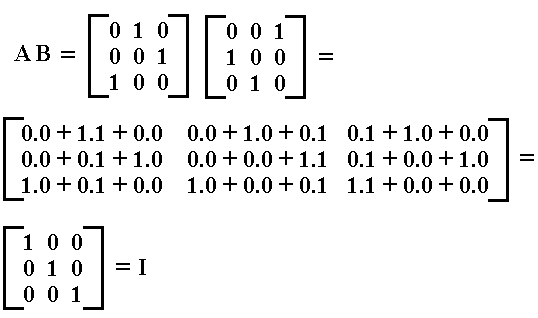
So AB = I, which means that if we first perform permutation a, which we do by subjecting the number sequence 123 to the action of permutation matrix A, and then subject the result to permutation b, which we do by subjecting it to the permutation matrix B, then we -- as it turns out -- get the original number sequence 123 back again, which means that we have done nothing at all, which is expressed by the matrix I corresponding to the permutation i, which transforms 123 into 123, i.e. which leaves any number sequence, consisting of three numbers, unchanged. I, and with it i, is the identity element of the Group of the six permutations.

Let us now determine BB, which we can also write as B² :

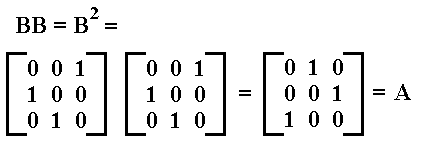
So BB = B² = A.

The matrix 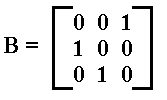  effects the permutation  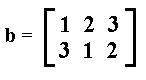 according to .
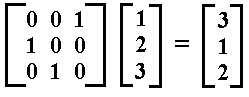If we look to the permutation b, then we see : 1 becomes 3, 3 becomes 2, and 2 becomes 1 again. Further we see that : 2 becomes 1, 1 becomes 3, and 3 becomes 2 again. Further, 3 becomes 2, 2 becomes 1, and 1 becomes 3 again. So we clearly have to do with a periodic cycle of order 3. So we can expect that b³ = i, and equivalently, that B³ = I. Indeed, when we look to the matrix I, representing the identity element, and compare it with the matrices for B and B², then we can anticipate what would be B³ :

And indeed, B³ = I  :

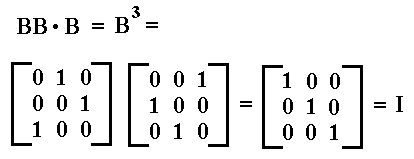
Three times the execution of permutation b has, accordingly, a net effect of no permutation at all. Said differently, after three times the original state is visited again, which means -- because the system is deterministic -- that after six times the original state is visited yet again, etc. We say that the period of element b (and equivalently, of element B) is 3, because 3 is the smallest number, such that b^x = i (identity element), or equivalently, such that B^x = I (identity element).

Let us further determine CE :

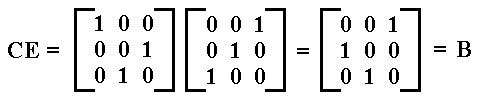
So CE = B

We can perform the remaining multiplications, and then verify that the set of matrice { I, A, B, C, D, E } is closed under the operation of matrix multiplication, i.e. every multiplication of two matrices from this set results in a matrix already present in that set.

Our set contains an identity element I, which means that for every element X of our set the following holds :

XI = IX = X

We can also verify that this multiplication is associative (the combining of transformations is always associative), i.e. for any X, Y, Z of our set of matrices applies :

(XY)Z = X(YZ)

Every element has an inverse, i.e. for every element X of the set applies that there is an element X^-1, also belonging to that set, for which applies :

XX^-1 = I (=identity element) (X can be identical to X^-1)

All this indicates that our set of permutation matrices forms a GROUP under the operation of matrix multiplication. And this particular Group described the point symmetry 3m of the Equilateral Triangle.
Now we have sufficient knowledge about matrices. They will be used for expressing symmetry transformations within a Group Theoretic framework, that ultimately aims at an understanding of the symmetry of the internal structure of three-dimensional crystals.
But before we turn to those crystals we must first give an outline of Group Theory itself. In doing so we keep on having our goal -- the symmetry of crystals -- in mind, and will accordingly consider only the relevant topics from Group Theory. Those relevant topics will consist of definitions and some theorems, which will given without proof. The whole treatment of of Group Theory on this website will accordingly be limited and informal. We will do this in the next document.

e-mail : 

back to homepage

back to retrospect and continuation page