Promorphology of Crystals Preparation XII

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
12

Sequel to the Plane Group P31m
In the previous document we found out that the difference between the Plane Group P3m1 and the present Plane Group P31m finally boils down to a difference of the o r i e n t a t i o n of the motifs s.str. by a rotation of 30⁰. Well, this is easy to see when we consider the point lattice of Figure 4 of the previous document, and furnish this lattice with the same motifs s.str., but in such a way that all those motifs are rotated by 30⁰ with respect to their background.
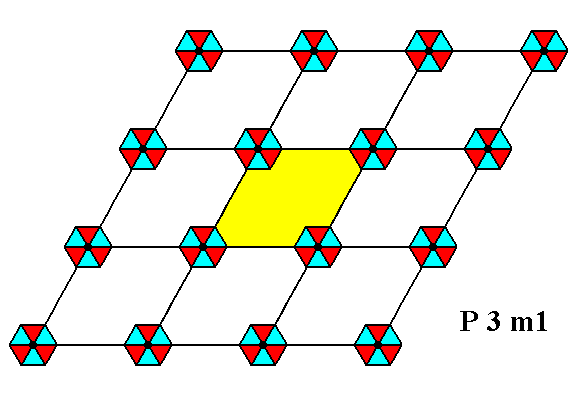
In order to see this we first reproduce the mentioned Figure :

Figure 1. The above periodic two-dimensional pattern of 3m motifs can be related to (and thus described by) a hexagonal net (point lattice) with a rhomb-shaped unit cell (yellow). The net describes only one aspect of the pattern, namely the way of r e p e t i t i o n of nodes with which motifs are associated. The total symmetry of this periodic pattern can be described by the Plane Group P3m1. The pattern must be imagined to be extended indefinitely in 2-D space.

If we now replace the motifs s.str. of this pattern (while the net remains in place) with the same motifs but now each of them rotated by 30⁰, we get the following pattern :

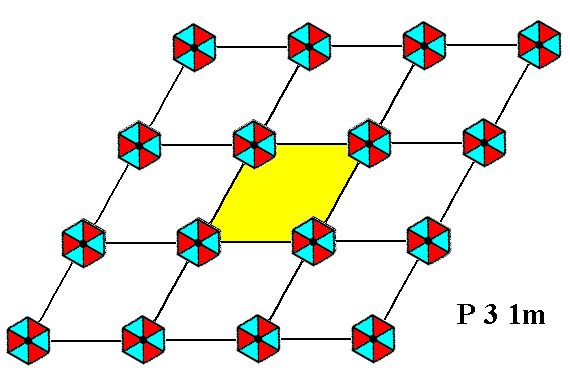
Figure 2. The depicted periodic two-dimensional pattern of 3m motifs can be related to (and thus described by) a hexagonal net (point lattice) with a rhomb-shaped unit cell (yellow). The net describes only one aspect of the pattern, namely the way of r e p e t i t i o n of nodes with which motifs are associated. The total symmetry of this periodic pattern can be described by the Plane Group P31m. The motifs s.str. of this pattern are identical to those of Figure 1, save that they are rotated by 30⁰ with respect to them. Also the applied point lattices are the same in both Figures. The pattern must be imagined to be extended indefinitely in 2-D space.

The next Figure gives the symmetry diagram for the Plane Group P31m, in which the total symmetry is indicated.

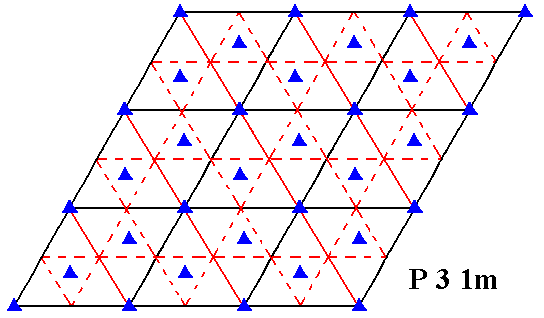
Figure 3. Symmetry content of 2-D patterns according to the Plane Group P31m. Glide lines are indicated by dashed lines. Mirror lines are indicated by red and by black solid lines, while the 3-fold rotation axes are indicated by small triangles.

We will demonstrate that the pattern of Figure 2 as related to the net as drawn in that Figure, indeed possesses the symmetry distribution of the symmetry diagram for the Plane Group P31m. See the next Figures.

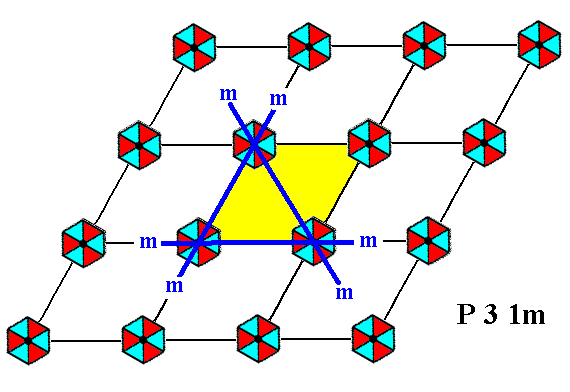
Figure 4. The pattern of Figure 2 has mirror lines (m) coinciding with the edges of the rhomb-shaped unit cell, in accordance with the symmetry diagram for the Plane Group P31m. Only two such mirror lines are indicated. Also the mirror line coincident with the shorter diagonal of the unit cell is present. For one unit cell such a mirror line is indicated.

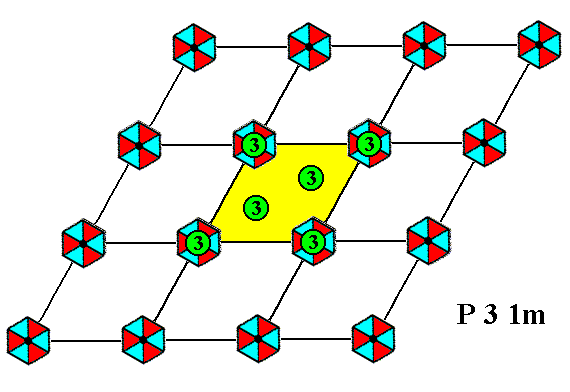
Figure 5. The pattern of Figure 2 has 3-fold rotation axes at locations in accordance with the symmetry diagram for the Plane Group P31m. Only those of the unit cell are indicated.

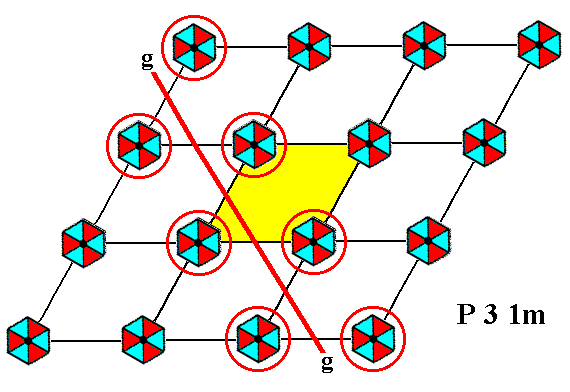
Figure 6. The pattern of Figure 2 has glide lines parallel to, but not coincident with, the shorter diagonal of the unit cell, in accordance with the symmetry diagram for the Plane Group P31m. Only one such glide line is indicated.

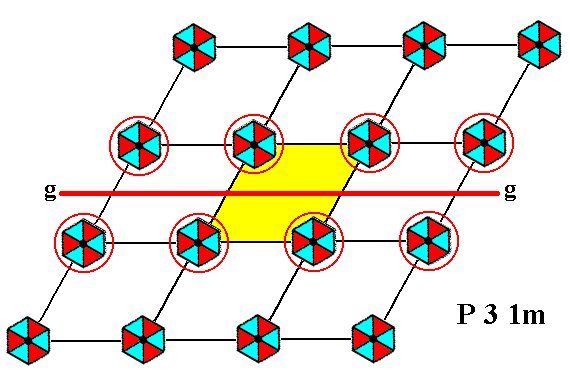
Figure 7. The pattern of Figure 2 has glide lines parallel to, but not coincident with, the edges of the unit cell, in accordance with the symmetry diagram for the Plane Group P31m. Only one such glide line, belonging to the horizontal series, is indicated. A glide line of the other series is indicated in the next Figure.

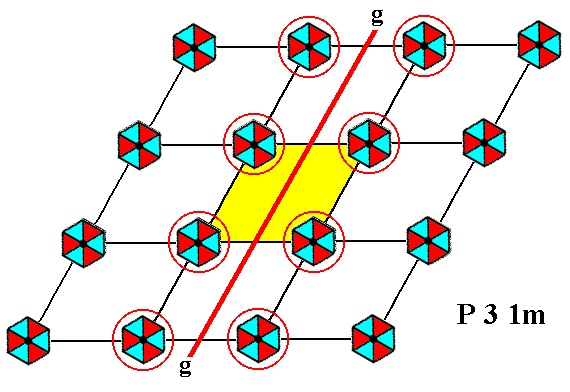
Figure 8. The pattern of Figure 2 has glide lines parallel to, but not coincident with, the edges of the unit cell, in accordance with the symmetry diagram for the Plane Group P31m. Only one such glide line, belonging to the NE-SW series, is indicated.

We have now demonstrated that the pattern as given in Figure 2 as such belongs to the Plane Group P31m.
We will now derive the C o m p l e x M o t i f of the pattern of Figure 2.
Recall that the Complex Motif is the translation-free residue of a periodic motif pattern. When this pattern is the internal structure of crystals, the Complex Motif lies at the base of the crystal's tectological aspect. The Complex Motif allows the crystal to be assessed promorphologically. It determines the number and configuration of antimers, essential for the crystal's promorph or basic form. The Complex Motif should express all point symmetry that the given crystal has in store, and it should be aperiodic in order to be tectological.
So to find the Complex Motif we must eliminate all translations inherent in the periodic pattern, glide translations and simple translations.
Because all glide lines of our pattern have mirror lines parallel to each of them, elimination of the glide translations will not increase the symmetry any further, so that we can start right away with the content of a single unit cell (by concentrating on a s i n g l e unit cell we automatically eliminate all s i m p l e translations). This unit cell must however be the most symmetrical unit cell in order to exhibit all point symmetries of the given crystal. The rhomb-shaped unit cell of Figure 2 does not have all the symmetry which the crystal has in store (which we know from the Crystal Class to which a crystal having a total symmetry of P31m belongs : 3m), so we must find another unit cell. The most obvious one is a hexagonal unit cell as depicted in the next Figure.

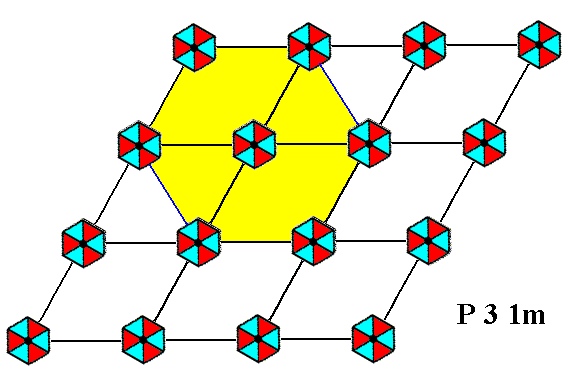
Figure 9. A hexagonal unit cell choice is possible for the pattern of Figure 2.

This unit cell -- which is not the smallest unit cell possible -- suggests a smaller, but still hexagonal repeat unit. Because the outline of this repeat unit is hexagonal, the full 3m symmetry will be preserved. There are two smaller hexagonal units possible, but only one of them is a true repeat unit of the pattern :

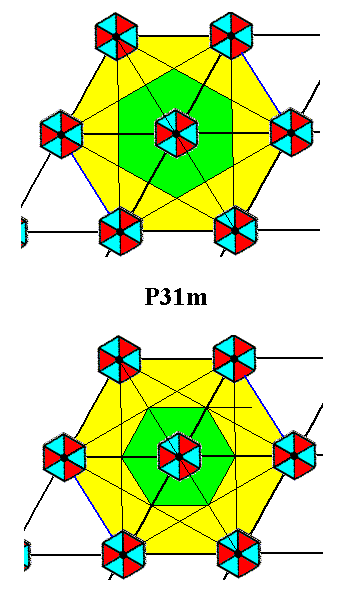
Figure 10. A hexagonal unit cell choice for the pattern of Figure 2 suggests smaller hexagonal units (green). One of them is a true repeat unit of the structure and can represent the Complex Motif.

The hexagon (green) of the lower image of Figure 10 is not a true repeating unit, as the next figure illustrates.

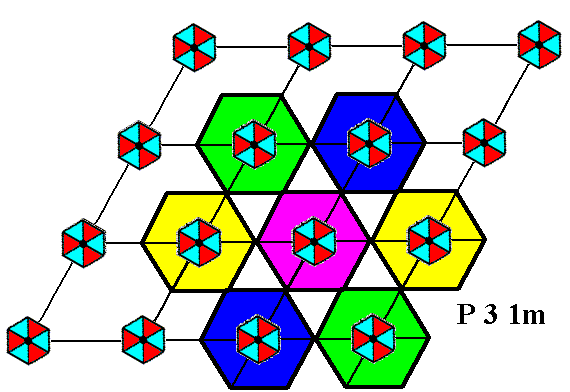
Figure 11. The hexagonal unit of the lower image of the previous Figure is not a true repeat unit, and thus cannot represent the Complex Motif.

The hexagonal unit of the upper image of Figure 10 is a true repeating unit, as the next Figure shows. It can represent the Complex Motif of our P31m structure.

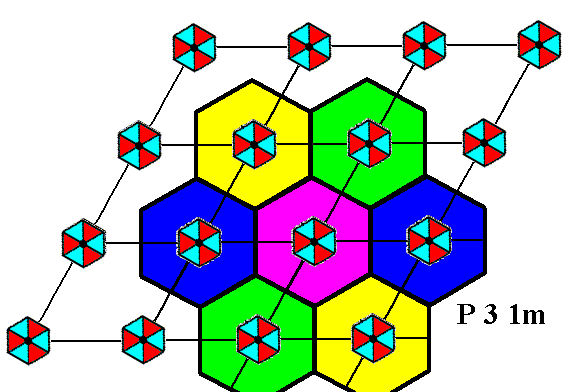
Figure 12. The hexagonal unit of the upper image of the Figure 10 is a true repeat unit, and thus can represent the Complex Motif.

If we isolate a hexagonal repeat unit as depicted in the previous Figure we automatically eliminate the simple translations and obtain the Complex Motif of our P31m pattern (of Figure 2) :

Figure 13. The Complex Motif of the periodic motif pattern of Figure 2. For the Plane Group P31m this is the second time we obtain a Complex Motif. Earlier we obtained the Complex Motif from Figure 18 of the previous document.

It is instructive to compare the above result with the result obtained earlier (Figure 25 of the previous document) :

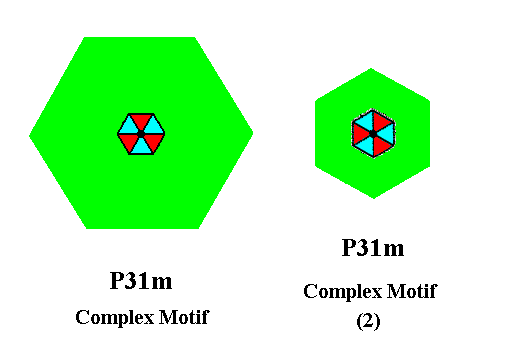
Figure 14. The Complex Motif of the periodic motif pattern of Figure 18 of the previous document (left), compared with that of the pattern of Figure 2 of the present document (right). Both belong to the Plane Group P31m.

Except for their size (and this is immaterial), the obtained Complex Motifs (Figure 14) are wholly identical. They are, it is true rotated with respect to each other, but, because everything in them is so rotated they are totally identical, which, of course, was to be expected : They both belong to the same Plane Group (P31m) and their motifs s.str. are identical.
When we now compare the Complex Motif of the P3m1 pattern with the P31m pattern (both having the same motifs s.str.) we see the precise difference between the two Plane Groups reflected in their respective Complex Motifs : The motif s.str. is rotated by 30⁰ with respect to the background. See next Figure.

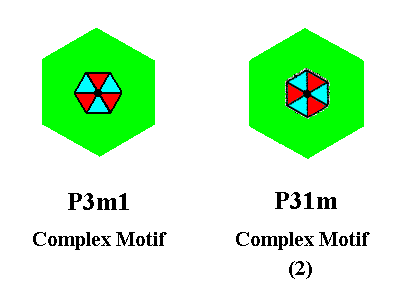
Figure 15. The Complex Motif of the P3m1 periodic motif pattern of Figure 1 of Part Eight (where the Complex Motif itself is depicted in Figure 6b), compared with that of the P31m pattern of Figure 2 of the present document. The difference between them is a rotation of the motif s.str. by 30⁰ with respect to the background. This difference precisely reflects the difference between the two Plane Groups P3m1 and P31m. When we transform the one Plane Group into the other we rotate the motifs s.str. by 30⁰, WITHOUT ROTATING THE BACKGROUND. And this means that the total motif is NOT simply rotated but only a part of it, resulting in a DIFFERENT pattern but possessing the same total symmetry.

Although, as has been said, we now have the Complex Motif of our P31m pattern of Figure 2 of the present document, it is nevertheless instructive to explicitly eliminate the translations involved in the glide lines of the structure, and see what emerges. We will do that in the next document.

To continue click HERE to further investigate the Plane Group P31m.

e-mail :