Although the division of the amphipleural zeugites or A m p h i p l e u r a, as we will call them for short, lags far behind that of the zygopleural zeugites, it contains a number of interesting and important basic forms, that caused troubles in those morphological enquiries that were based on the outer shape alone while neglecting the axes.
The basic form of all Amphipleura is half an amphitect pyramid that has 4+2n sides. The number of sides must be twice as much as the number of antimers in the forms that result from halving such pyramids. So the basic form of the 3-fold amphipleurals (Triamphipleura) is half a six-sided, that of the 5-fold amphipleurals (Pentamphipleura) half a ten-sided amphitect pyramid, etc. Here we used real bisection. When we want to use ideal bisection, then our original pyramid should have the same number of sides as the number of antimers of the resulting amphipleural form. And because the lowest number of sides of an amphitect pyramid is four, we cannot obtain a triamphipleural form by ideal bisection. We can also not obtain a pentamphipleural form by ideal bisection, because our original pyramid should have five sides, but there are no amphitect pyramids with an uneven number of sides. A hexamphipleural form on the other hand can be obtained by ideal bisection of a six-sided amphitect pyramid. Indeed from all amphitect pyramids with an even number of sides (and with at least one directional axis being interradial) can be derived the corresponding amphipleural form by ideal bisection, except from a four-sided amphitect pyramid, because that results in a zygopleural form, as we saw in the previous document.
Because the homotypic basic number, which is in the amphipleurals equal to 3, 5, 6, 7, or more (n), is always equal to the number of radii ( = the lines, originating in the center of the axial system and running along the mid-lines of the antimers), those radii will meet at acute angles when the center of the axial system has not moved inward. See next Figure.

Figure 1.
Left image : Base of a Pentamphipleural form. The center of the axial system lies completely to the right (it lies in fact in the center of the base of the whole original pyramid before its real bisection).
Right image : Base of a Pentamphipleural form, with the center of the axial system shifted to the left. The two radii on the right meet at an o b t u s e angle.
Also in triamphipleural forms, while having only three radii, their radii meet at acute angles (i.e. they do not admit of any obtuse angle to be present at the axial center), because, provided the axial center lies on the line of the real division -- which resulted in that triamphipleural form -- only 1800 is available for division by radii.
Of the many species of amphipleurals that are theoretically possible according to the different numbers of antimers, only a few of them -- like in the case of the amphitect pyramids -- are materialized in the organic nature, namely four different species, 7-fold, 6-fold, 5-fold and 3-fold amphipleurals. Of these the first two are on the whole seldom, while the latter two are extensively and diversely developed. Many flowers have the basic form of the Triamphipleura. The Pentamphipleura are materialized in a large number of animals and flowers.
The basic form of the Heptamphipleura is in its simplest version a non-straight pyramid with its tip precisely above the center of the lateral axis (We imagine the cross axes to lie in the base of the pyramid). And because this lateral axis is one of the sides of the base the pyramid, the latter is not a straight pyramid.
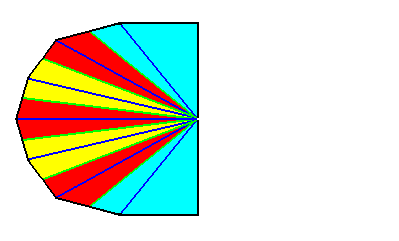
Figure 2. Base of an heptamphipleural form. The seven antimers are indicated by colors.
The seven-fold amphipleural form, is, as are all 7-fold basic forms, very seldom, but is nevertheless clearly expressed in some higher plant flowers. The general basic form of all bilateral seven-fold forms (Heptamphipleura) is half a 14-sided amphitect pyramid.
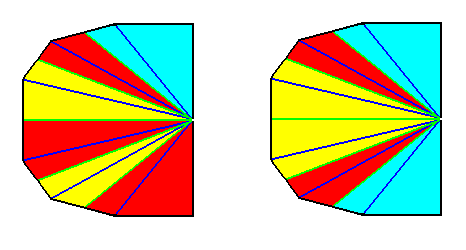
Figure 3.
Left image : Base of a Hexamphipleural form. The six antimers are indicated by colors.
Right image : Base of a Hexamphipleural form. By redistribution of the colors its symmetry with respect to the dorso-ventral axis is highlighted.
This basic form is found in some corals (coral polypes) and in some higher plant flowers. It is half a 12-sided amphitect pyramid.
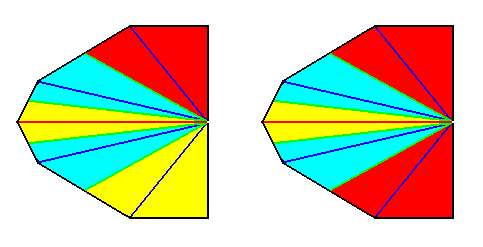
Figure 4.
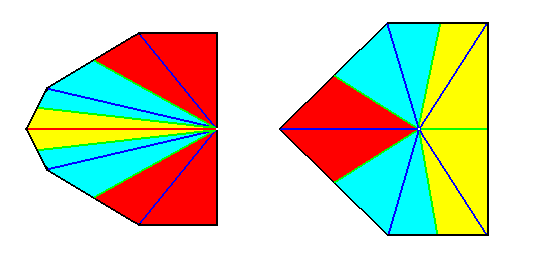
Left image : Base of a Pentamphipleural form. The five antimers are indicated by colors.
Right image : Base of a Pentamphipleural form. By redistribution of the colors its symmetry with respect to the dorso-ventral axis is highlighted.
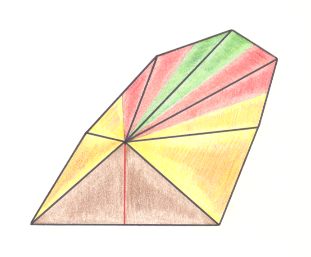
Figure 5. Oblique top view of a pentamphipleural form (half a 10-fold amphitect pyramid). The five antimers are indicated.
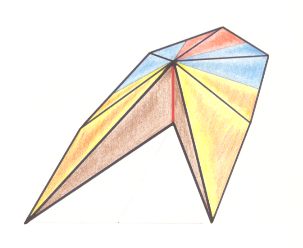
Figure 6. Oblique top view of a pentamphipleural form. The main axis is shifted towards the center of the structure. The five antimers are indicated.
Haeckel reports that of all organic basic forms probably the pentamphipleural form has caused the most troubles with respect to its proper assessment. Being widely spread over the animal kingdom, where the "bilateral" or "irregular" Echinoderms, and over the plant kingdom, where the "irregular" or "symmetric" flowers of the five-fold dicotyledones, are built according to this basic form, it has often been the subject of an inquiry, but never as such recognized because no, or not enough, emphasis has been put on a consideration about the axes and their poles. And yet the recognition of this basic form is -- as soon as one considers the latter sufficiently and is keen to look at the differentiations of the antimers -- as easy as it is interesting.

Figure 7. Top view (aboral view) of the shell of a bilateral sea urchin. The five antimers are indicated by the shell's markings.

Figure 8. Bottom view (oral view) of the sea urchin of the above Figure. Also here the five-foldness and the bilateral symmetry is indicated bt the shell's markings and outline.
The general stereometric basic form of the five-fold amphipleurals is h a l f a t e n - s i d e d a m p h i t e c t p y r a m i d. This form is always composed of five unequal antimers that distribute themselves in such a way on either side of the median plane that the body appears to be composed of two symmetrically equal halves. The pattern of antimers divides itself into two pairs that lie behind each other, and one that is unpaired and lies in front of them and in the middle.
Among dicotyledone plants the sexual persons (flower off-shoots) of many families show the pentamphipleural form, for example of Umbellifers and Labiates.
Most Pentamphipleura are purely h o m o p l e u r a l, with symmetrically equal right and left halves. Very seldom these are significantly unequal.
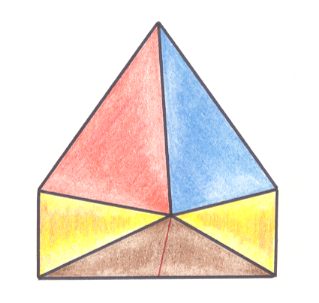
Figure 9. Oblique top view of half a six-fold amphitect pyramid. This half pyramid is the basic form of the Allopola triamphipleura. The s i d e s of this half pyramid are indicated by colors.
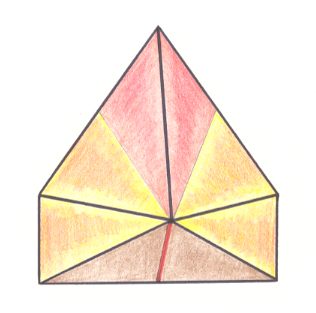
Figure 9. Oblique top view of half a six-fold amphitect pyramid. This half pyramid is the basic form of the Allopola triamphipleura. The three a n t i m e r s of this basic form are indicated by colors.
The triamphipleural form is of great significance in the plant kingdom, because a great many monocotyledone flowers (for example Orchids) show this form. In the animal kingdom on the other hand it is seldom encountered. In Protists we see it in some Radiolarians.
In most Triamphipleura the body is strictly homopleural, and then the two dorsal antimers are symmetrically equal with respect to each other.
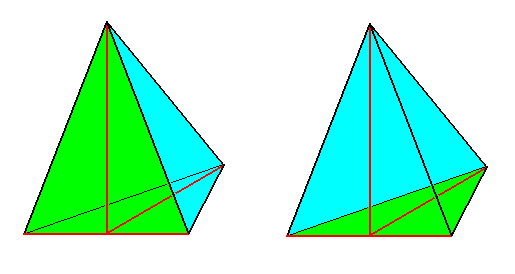
Figure 10.
The basic form of the Heterostaura allopola, illustrated by half a Rhombic Pyramid (which itself is the basic form of the Allopola zygopleura eudipleura) .
Left image : bisection face (originated by the bisection of the whole Rhombic Pyramid) emphasized (green).
Right image : Base emphasized (green).
Main axis (vertical), lateral axis (horizontal) and dorso-ventral axis are indicated in red.
The important and extensive division of the zygopleural zeugites, that we will call Z y g o p l e u r a for short, relates to the Amphipleura as do in the Autopola the Orthostaura to the Oxystaura. In the Amphipleura, as in the Oxystaura, the number of radii is such that acute angles are being involved. And while in the Amphipleura we find 3, 5, 6 or more antimers, in the Zygopleura, as in the Orthostaura, we find two or four antimers.
H a l f a R h o m b i c P y r a m i d (See Figure 10) is a pyramid the base of which is half a Rhombus, and thus an isosceles triangle. Its main axis intersects the middle of the lateral axis. The side containing the main axis and the lateral axis is also an isosceles triangle. This simple stereometric body -- which we will also call isosceles pyramid -- possesses all essential properties, which determine the character of the Zygopleura.
The isosceles pyramid can be divided into two symmetrically equal halves by only one plane. This bisection plane is the median plane, which contains the main axis (axis of the pyramid) and the mid-line of the base (i.e. the perpendicular starting at the tip of the isosceles triangle and ending at its base). Of the three sides of the isosceles pyramid (It has four faces, one of which is the base, the other three are its sides) two sides are congruent anisosceles triangles, that meet at the ventral edge, and that should be assessed as symmetrically congruent because of their opposite position with respect to that edge. These two sides correspond to the right and left body surfaces of the Zygopleura. The third side of the isosceles pyramid is an isosceles triangle the base of which coincides with the base line of the isosceles trangle that represents the pyramid's base. Because this side lies opposite to the ventral edge we must call it the dorsal side. The apex of the isosceles pyramid is, like we did in all heteropolar stauraxonians,
interpreted as the aboral end (aboral area, antistomium), while its base is interpreted as oral end (oral area, peristomium).
As we had to distinguidh in the Orthostaura two form species, the Tetraphragma with four, and the Diphragma with two antimers, so also in the Zygopleura we should separate the corresponding species, although also here the basic form is, with respect to its axes and poles, the same.
To the four-fold Orthostaura (i.e. orthostaurs with four antimers) or Tetraphragma, correspond those zygopleurals that possess four antimers, as we can see for example in most worms and in the flowers of Reseda. We call these four-fold Zygopleura T e t r a z y g o p l e u r a or T e t r a p l e u r a for short.
To the two-fold Orthostaura (i.e. orthostaurs with two antimers) or Diphragma, correspond those zygopleurals that possess two antimers, as we see for example in the persons of vertebrate animals and Arthropods, but also in many lower-order form individuals. These two-fold zygopleurals can be distinguished from the four-fold ones as D i z y g o p l e u r a or D i p l e u r a for short.
Strictly speaking, the i s o s c e l e s p y r a m i d or half a rhombic pyramid can only be interpreted as the basic form of the t w o - f o l d z y g o p l e u r a l s, and not as that of the f o u r - f o l d z y g o p l e u r a l s, because it is composed of only two antimers. If we want a special geometric expression for the T e t r a p l e u r a, then we can express such a form either as h a l f a n 8 - s i d e d a m p h i t e c t p y r a m i d, or as a b i - i s o s c e l e s p y r a m i d, i.e. a pyramid that is composed of two unequal isosceles pyramids, of which their congruent dorsal sides (i.e. that side of either isosceles pyramid that contains its main axis and its lateral axis) coincide. The b a s e of this bi-isosceles pyramid is a b i - i s o s c e l e s t r a p e z i u m, i.e. a trapezium that is composed of two unequal isosceles triangles, erected on a common base line in opposite directions. See the next Figure.
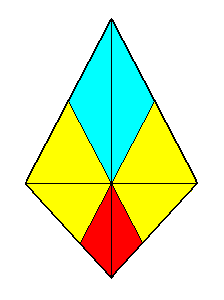
Figure 11. A bi-isosceles trapezium as base of a bi-isosceles pyramid which is the basic form of the Zygopleura tetrapleura. The four antimers are indicated by colors.
Of the four sides of the bi-isosceles pyramid every two opposite ones are unequal, the two sides meeting at the dorsal edge, on the other hand, are symmetrically congruent, as well as the two sides meeting at the ventral edge. The two right sides (dorsal and ventral) are as different from each other as are the two left sides.
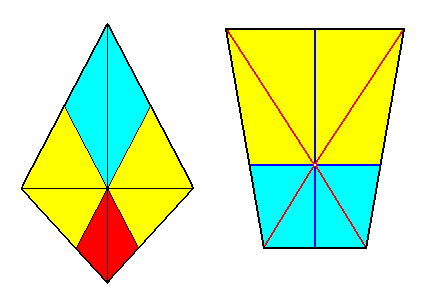
Figure 12. Bases of two possible pyramids representing the basic form of the Zygopleura tetrapleura.
Left image: Bi-isosceles trapezium as the base of a bi-isosceles pyramid representing the basic form of the Tetrapleura radialia. The four antimers are indicated: one dorsal and one ventral, and one right and one left.
Right image : Parallel-trapezium (antiparallelogram) as the base of a trapezoid pyramid (antiparallelogram pyramid) representing the basic form of the Tetrapleura interradialia. The four antimers are indicated : two dorsal and two ventral.
As is to be expected, the bi-isosceles trapezium is closely related to the parallel-trapezium. The next Figure illustrates this.
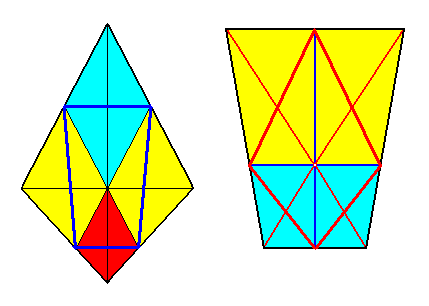
Figure 12a.
Left image : In the bi-isosceles trapezium of the Tetrapleura radialia can be inscribed (thick blue lines) the parallel-trapezium of the Tetrapleura interradialia by connecting the poles of the interradial cross axes.
Right image : In the parallel-trapezium of the Tetrapleura interradialia can be inscribed (thick red lines) the bi-isosceles trapezium of the Tetrapleura radialia by connecting the poles of the directional axes.
While the two directional planes are radial in the bi-isosceles pyramid, they are interradial in the trapezoid pyramid.

Figure 13. Tetrapleura radialia.
The basic form of the Tetrapleura radialia illustrated by the morphological scheme of a Reseda flower. In the median plane (r1 r3) lies the ventral petal (small and two-split) and opposite to it the dorsal petal (big and six-split). In the lateral plane (r2 r4) on the other hand lie the two symmetrically equal three-split lateral petals, the right one and left one. In the two interradial cross planes (i1 i3 and i2 i4) lie the four calyx leaves and the four leaves associated with the female genitals. The interradial cross planes separate the four antimers.
( After HAECKEL, 1866, Generelle Morphologie, Table I, fig. 11 )
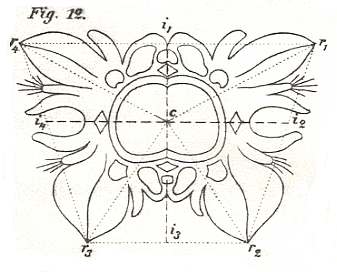
Figure 14. Tetrapleura interradialia.
The basic form of the Tetrapleura interradialia illustrated by the morphological scheme (transverse section) of an Annelid (like for instance an earthworm). The two directional planes or ideal cross planes coincide with two interradial cross planes. The (transverse sections of the) four longitudinal blood vessels are indicated by four small rhombuses surrounding the alimentary tract. The interradial cross planes separate the four antimers.
( After HAECKEL, 1866, Generelle Morphologie, Table I, fig. 12 )
For the relationships of the cross axes and the cross planes containing them, the distinction between Tetrapleura and Dipleura is also significant because in the Dipleura there is only one radial cross plane present, coinciding with the lateral plane, while the corresponding interradial cross plane, that is perpendicular to the latter, coincides with the median plane. In the Tetrapleura on the other hand, there are two radial and two corresponding interradial cross planes present, and either both radial or both interradial cross planes coincide with the two directional planes (ideal cross planes).
Although our consideration of the bi-isosceles pyramid and the related trapezoid pyramid (antiparallelogram pyramid) implies that these represent the true basic form of the four-fold zygopleurals, they are in fact just a subordinate modification of the single isosceles pyramid (half a rhombic pyramid), because the relationships of the ideal axes and their poles are the same in both cases : Of the three orthogonal axes two are unequipolar, namely the main axis and the dorso-ventral axis. The third one, the lateral axis, is equipolar.
So as the common basic form of all Z y g o p l e u r a we can set the i s o s c e l e s p y r a m i d (half a rhombic pyramid, see Figure 10), and put emphasis on the distinction between s i n g l e and d o u b l e isosceles pyramid only insofar as the first determines the homotypic two-foldness of the Dipleura, and the second the homotypic four-foldness of the Tetrapleura.
More important modifications of the general basic form than those that determine its two- or four-foldness, are implied by the fact that in the Zygopleura more often than in the Amphipleura, heteropleurals occur, i.e. the unequality of the poles of the lateral axis, in virtue of either originally unequal predisposition or by subsequent unequal growth of the two lateral halves, or in virtue of special influences determining a differentiation of left and right. Especially among the Dipleura such heterozygopleural forms are common and determine the characteristic form of, for example, the Pleuronectids (flatfishes). According to Haeckel, also the coiling of Gastropods (snails) is caused by this differentiation of left and right. The resulting form in those Gastropods, together with that of their shells, does not, however, belong to the (heteropleural) Zygopleura anymore (Haeckel asserts they do) : They even do not belong to the Stauraxonia as such. They belong to the Third Suborder of the Protaxonia (the first two are the Monaxonia and the Stauraxonia), the S p i r a x o n i a (not as such recognized by Haeckel). The Spiraxonia have their main axis curved in a regular way. In most, if not all, shell-bearing Gastropods this curve is the equiangular spiral (also called logarithmic spiral). Nevertheless it is clear that the spiraxonians are in some (morphological) way closely related to the heterozygopleural forms, especially those within the Dipleura : Dysdipleura.
Much more seldom heteropleurals will be found among the Tetrapleura.
A determined basic form for all Heterozygopleura is difficult to obtain, because the conspicuous character indicative for the Homozygopleura, the symmetric equality of both lateral sides, is lost in them. In a very general sense one could set as basic form of the Heterozygopleura an unequally three-sided pyramid, or, more precisely, as basic form of the heteropleural T e t r a p l e u r a an unequally four-sided pyramid, and as basic form of the heteropleural D i p l e u r a an unequally three-sided pyramid. But because the Heterozygopleura never deny their close kinship with the corresponding Homozygopleura, and especially because the determination (recognition) of the three unequal axes -- the main axis and the two directional axes -- despite the fact that all three axes are non-equipolar, is not subjected to any difficulty, we can indicate and name successfully the individual sides, axes and poles of the Heteropleura always by comparing them with those homopleural forms that are biologically closely related to them.
Consequently we can, because also here we must start the promorphological inquiry of the Zygopleura with a consideration of the homopleural zygopleurals, generally set the i s o s c e l e s p y r a m i d (half a rhombic pyramid) as the basic form of the Zygopleura, and signify once and for all the individual parts of it in the following way :
The many animal forms, which we, on the basis of the foregoing inquiries, should recken to the Tetrapleura, are until now (Haeckel, 1866) not being considered, in spite of the fact that they, like the Ctenophores, demand a special division for themselves within the group of so-called bilateral symmetrical animals. Most species of the large group of the Worms belongs to the present form group (Tetrapleura), and also a fairly large number of Coelenterates, and finally a series of four-fold dicotyledone flowers, that fully correspond to the mentioned animals, for example the fowers of Reseda.
The essential difference of these four-fold zygopleurals from the two-fold zygopleurals is based on the fact that their body consists of f o u r antimers, not of t w o antimers. However this difference is -- as has been explained above -- so far without essential significance as the relationships of the three ideal axes and their poles are the same in both cases. In both the lateral axis is equipolar, while the other two (main axis and dorso-ventral axis) are unequipolar. The difference between the 2-fold and 4-fold zygopleura becomes more apparant in the relationships of the r e a l c r o s s a x e s and the r e a l c r o s s p l a n e s that contain them, of which there are only t w o, a radial and an interradial cross plane, in the Dipleura, of which the radial one coincides with the lateral, the interradial with the median plane, while there are f o u r of them, two radial and two interradial, in the Tetrapleura of which in some cases both radial cross planes, in other cases both interradial cross planes coincide with the two directional planes (lateral and median).
It should be noted that in some Tetrapleura (interradialia) the ideal lateral plane (i.e. the lateral directional plane) does not coincide with the real lateral interradial plane, as illustrated in the next Figure by the base (or equatorial plane) of the pyramid :
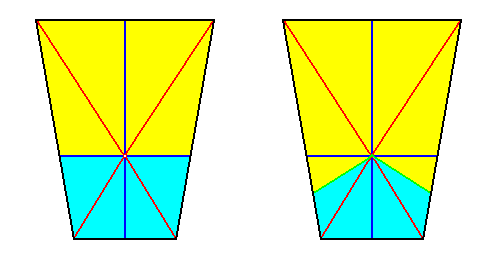
Figure 15. The basic form of the Eutetrapleura interradialia, as represented by the base of the pyramid. Their four antimers are indicated by colors : two dorsal antimers (light blue) and two ventral antimers (yellow). The two directional planes are indicated by blue lines.
Sometimes an i d e a l cross plane (i.e. a directional cross plane) does not coincide with the corresponding r e a l cross plane.
When the r e a l cross plane (under consideration) is i n t e r r a d i a l, it is (then always, and indeed by definition) the boundary surface of adjacent a n t i m e r s. In the case of the lateral real i n t e r r a d i a l cross plane, where it figures as such in the Eutetrapleura interradialia, it separates the dorsal from the (adjacent) ventral antimers. Now the lateral d i r e c t i o n a l plane, i.e. the lateral ideal cross plane, which in itself is the ideal line dividing the body into dorsal and ventral halves, and is perpendicular to the median plane, is also at the same time a r e a l (interradial) cross plane, and so not only i d e a l l y divides the body in a ventral and dorsal half, but also divides the dorsal from the ventral a n t i m e r s, as illustrated in the left Figure. However, such a coincidence of ideal and real cross axes doesn't need to be always the case : The surface that separates dorsal from ventral antimers could lie differently within the organism, namely such that it is a bent surface making angles with the lateral directional plane, angles that are equal among themselves, i.e. equal on both sides of the median plane. This is the case in the right image of the Figure. The green lines indicate (i.e. are traces of) the r e a l lateral interradial cross plane (which now is a bent plane) that separates the dorsal from the ventral antimers, while the horizontally drawn blue line is the lateral ideal cross plane (lateral directional plane), (only) i d e a l l y dividing the body into a dorsal and ventral ' half '.
In contradistinction to this, the real interradial d o r s o - v e n t r a l cross plane always coincides with the ideal dorso-ventral cross plane (the dorso-ventral directional plane).
After we will have divided the Tetrapleura into homopleural (i.e. symmetric) tetrapleurals ( E u t e t r a p l e u r a ) and heteropleural (i.e.asymmetric) tetrapleurals ( D y s t e t r a p l e u r a ), we will divide the homopleural tetrapleurals into two groups according to the quality of their d i r e c t i o n a l p l a n e s (resp. axes) :
The phenomenon of h e t e r o p l e u r a l i t y, i.e. the unequality of the left and right sides, is much more seldom in Tetrapleura as it is in Dipleura. However, where it occurs, it is so conspicuous, as in Siphonophores (social jellyfishes), that we must distinguish explicitly between the homo- and heteropleural forms : Eutetrapleura and Dystetrapleura.
The stereometric basic form of the Eutetrapleura is either a bi-isosceles pyramid or a trapezoid-pyramid (The latter can also be called an antiparallel pyramid). This stereometric form allows for 4 antimers positioned such that the whole body is symmetric with respect to the dorso-ventral directional plane, which here is the median plane of the body.
To the division of tetrapleural zygopleurals with symmetrically equal right and left body half, we first of all reckon the major part of the worms, then a large number of Coelenterates. Of the dicotyledone flowers some belong to the present group.
As has been said, we can, within the Eutetrapleura distinguish two subgroups, namely such in which the median plane coincides with a radial cross plane, and such in which it coincides with an interradial cross plane. The first subgroup will be called radial, the second interradial Eutetrapleura.
In the radial Eutetrapleura we find an unpaired dorsal and an unpaired ventral antimer, and between them two paired lateral antimers, a left one and a right one.
In the interradial Eutetrapleura on the other hand, we find a dorsal and a ventral antimer pair, each pair consisting of a left and right antimer.
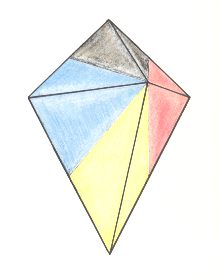
Figure 16. Oblique top view of a bi-isosceles pyramid as the basic form of the Eutetrapleura radialia. The four antimers are indicated by colors.
The Eutetrapleura radialia can be derived from orthostauric autopoles as the next Figure shows.
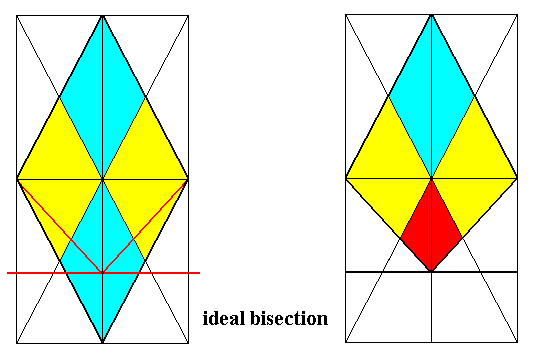
Figure 17. Derivation (shown by the bases of the pyramids) of the Eutetrapleura radialia from Autopola orthostaura (namely from the Tetraphragma radialia).
In the radial Eutetrapleurals each body half, the right one and the left one, consists of one complete and two half antimers (half the dorsal, and half the ventral antimer). The m e d i a n p l a n e is made up of a r a d i a l c r o s s p l a n e . This basic form is found for instance in many Siphonophores and in the flower of Reseda.
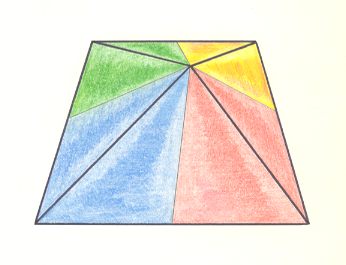
Figure 18. Oblique top view of a trapezoid-pyramid ( = antiparallelogram pyramid) as the basic form of the Eutetrapleura interradialia. The four antimers are indicated by colors.
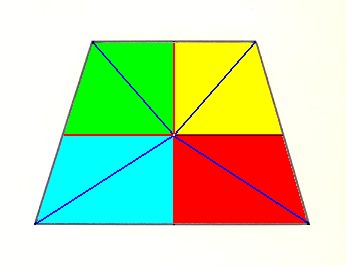
Figure 19. Base of the pyramid of Figure 18.
In that base we have indicated the (traces of the) directional planes (one horizontal and one vertical line in the drawing), and the four radii contained in the median planes of the antimers. The four antimers are indicated by colors.
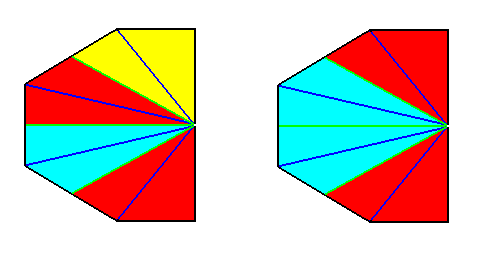
Figure 20. Result of the derivation (shown by the bisected base of a pyramid) of (a geometric body representing) the basic form of the Eutetrapleura interradialia from the Octophragma (Autopola oxystaura). The original pyramid, representing the latter, was an eight-sided amphitect pyramid having its directional planes interradial, while composed of eight antimers. Real bisection resulted in a bilateral symmetric geometric body having (or, allowing for) 4 antimers. These are indicated by colors. In the right image these colors are somewhat redistributed in order to highlight the bilateral symmetry. If we shift the center of the axial system (here drawn on the base) to the left, we obtain the configuration as depicted in the next Figure (The choice of colors, and the orientation of the object, is of course immaterial).
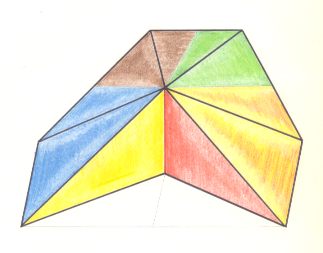
Figure 21. (Alternative) Geometrical body representing the basic form of the Eutetrapleura interradialia. We can imagine it as being derived from a possible basic form of the Octophragma, namely an eight-sided amphitect pyramid with interradial directional planes, by bisecting it, and shifting the main axis of the resulting four-fold semi-pyramid inwards along the median plane.
Figure 20 shows that the Eutetrapleura interradialia can be derived from o x y s t a u r i c autopoles (namely from Octophragma). Therefore it would seem reasonable to assess the resulting allopole, not as a zygopleural, but as an amphipleural form. The group to which it belongs should then be named "Tetramphipleura" (by reason of its having four antimers). But it differs from all other Amphipleura by the fact that it can also be derived from o r t h o s t a u r i c autopoles, as the next Figure shows.
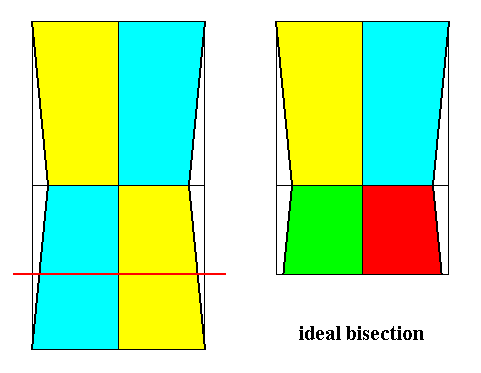
Figure 22. Derivation (as shown with the bases of the pyramids) of the Eutetrapleura interradialia from the Tetraphragma interradialia (Autopola orthostaura).
Because of this latter feature -- its derivability from o r t h o s t a u r i c autopoles, which all other Amphipleura lack -- we have sufficient reason to interpret the Eutetrapleura interradialia as belonging to the Zygopleura.
In the interradial eutetrapleural forms each body half (right and left) consists of t w o c o m p l e t e a n t i m e r s, or (as we could express it) of one pair of antimers, each such pair in turn consisting of two unequal antimers, one dorsal and one ventral. The m e d i a n p l a n e is constituted by an i n t e r r a d i a l c r o s s p l a n e. The interradial eutetrapleural forms accordingly distinguish themselves in an essential way from the radial eutetrapleural forms by the fact that their body is composed of two pairs of symmetrical equal antimers, while in the radial eutetrapleurals it is composed of one pair of symmetrically equal and one pair of (symmetrically) similar or wholly unequal antimers. Also the antimers themselves are different in the two groups. In the interradial eutetrapleural forms each antimer consists of two unequal (similar) halves and consequently itself possessing the dysdipleural form, while in the radial eutetrapleural forms this is only the case with respect to the lateral antimers. The dorsal antimer and also the ventral antimer of the radial eutetrapleurals consists of two symmetrically equal halves and so possessing the Eudipleural form.
As Eutetrapleura interradialia we must (promorphologically) interpret the majority of all worms, further some Coelenterates, and among the dicotyledone plants the flowers of some Crucifers and some others.
We have introduced the interradial eutetrapleural forms after (having dealt with) the radial eutetrapleurals, because the first, taken on the whole, appear to us as more advanced forms. They are more advanced forms because they are immediately (geometrically) connected to the Eudipleura. In both the median plane coincides with an interradial cross plane. As soon as both antimers of each lateral half of an interradial eutetrapleural body become strongly differentiated and a more rigorous centralization of the four antimers appears, the form immediately transforms into the Eudipleural form (Arthropods and Vertebrates) as the limit of such processes.
The interradial eutetrapleurals also equal the eudipleurals by the fact that in both groups the basic form of each antimer is dysdipleural.
On the other hand we must indicate that the radial eutetrapleural form is in one respect more advanced than the interradial eutetrapleural form. The radial eutetrapleural form is in most cases indeed composed of t h r e e different sorts of antimers, a dorsal, a ventral and a lateral sort (The latter sort is constituted by the two symmmetrically equal lateral antimers). In contradistinction to all this, we find in the interradial eutetrapleural form always only t w o different sorts of antimers, a dorsal and a ventral sort, each of which appears as two lateral symmetrically equal antimers. So the d i f f e r e n t i a t i o n is more strongly expressed in the radial than in the interradial eutetrapleural forms in this respect.
To see (more) real representatives of the Eutetrapleura interradialia click HERE, or scroll down to continue with the next promorphological category.
Much more seldom than the Tetrapleura with symmetrically equal lateral halves (homopleural tetrapleurals or eutetrapleurals) are those with unequal (or negatively similar) lateral halves, the heteropleurals, which we will call D y s t e t r a p l e u r a.
This form is very well expressed in some Siphonophores.
Logically the Dystetrapleura can come in two forms, the radial Dystetrapleura and the interradial Dystetrapleura. The first of these forms show their dorso-ventral directional plane to be radial, while it is interradial in the second. See the next Figures.
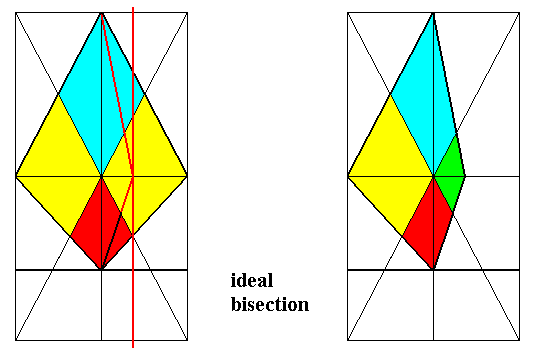
Figure 23. Derivation (as shown by the bases of the pyramids) of the Dystetrapleura radialia from the Eutetrapleura radialia. Directional axes (resp. planes) and interradial cross axes (resp. planes) are indicated.
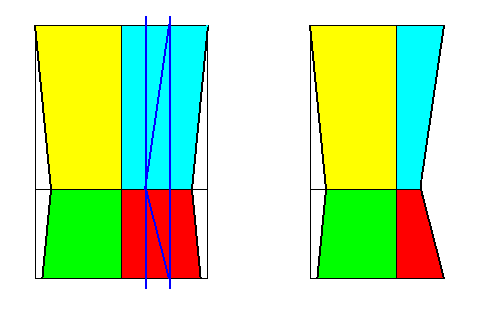
Figure 24. Derivation (as shown with the bases of the pyramids) of the Dystetrapleura interradialia from the Eutetrapleura interradialia. Directional axes (resp. planes) are indicated. For the other axes (resp. planes) See next Figure.
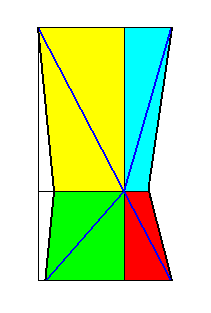
Figure 25. Dystetrapleural form (shown by the base of the pyramid) as derived in the previous Figure. The four r a d i i are indicated by blue lines.
For the time being we need not to separately deal with the Dystetrapleura radialia and Dystetrapleura interradialia. We deal with them together as Dystetrapleura.
In the Dystetrapleura we find, just like in the Dysdipleura three unequal and non-equipolar ideal axes, the main axis, the dorso-ventral axis and the lateral axis. But in the Dystetrapleura we find moreover (like in the Eutetrapleura etc.) real interradial axes (in the case of the radial dystetrapleurals, Figure 23) or real radial axes (in the case if the interradial dystetrapleura, Figure 25).
All those axes are unequal and non-equipolar. The f o u r antimers, by which the Dystetrapleurals distinguish themselves from the Dysdipleura which are composed of two antimers, often are so different that it is hardly possible to recognize them as antimers, while in other cases they are so similar that the dystetrapleural form approaches the eutetrapleural form or even the tetraphragmic or tetractinote form. Often in one and the same Siphonophore colony all transitions between these different basic forms can be observed (Haeckel, 1866).
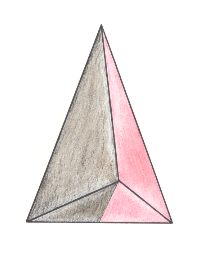
Figure 26. Oblique top view of a single isosceles pyramid as the basic form of the (Eu)dipleura. The t w o antimers are indicated by colors.
In our promorphological investigation we have finally arrived at those forms to which the equivocal term "bilateral symmetry" is most often applied, because the majority of the organisms usually called "bilateral symmetric" belongs to the present group (Dipleura), namely most Vertebrates, Arthropods and others.
For the first time we encounter basic forms that allow for only t h r e e a x e s to be drawn through their body : the Main axis, the Lateral axis and the Dorso-ventral axis. No other axes are possible. That's the reason why we can call the Dipleura -- consisting of Eudipleura and Dysdipleura -- (also) T r i a x o n i a. In the Dysdipleura these three axes are all unequal and heteropolar, and so they are equivalent.
The general properties of these two-fold Zygopleura, which we will call D i z y g o p l e u r a, or D i p l e u r a for short, are so well-known and from the contemplation of our own body so well-understood, that it is sufficient to emphasize only some of their essentials.
The body of all Dipleura consists of only t w o a n t i m e r s, a right one and a left one, united at the mid-line of the body (Planum medianum), which here is also often called s a g i t t a l p l a n e (after the course of the arrow suture (Sutura sagittalis) of the human skull). This m e d i a n p l a n e must be interpreted as the o n l y i n t e r r a d i a l p l a n e of the dipleural body, while the only r a d i a l p l a n e of that body is represented by the common median plane of both antimers, which coincides with the l a t e r a l p l a n e of the whole body. See next Figure.
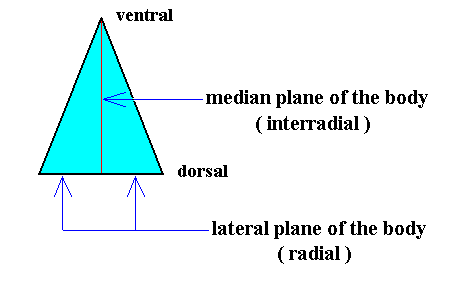
Figure 27. Base (or equatorial plane) of a single isosceles pyramid representing the basic form of the (Eu)dipleura. The left and right halves of the image in this Figure represent the two antimers. The interradial and radial cross planes are indicated.
The location of the axes and the axial center, as depicted in the above Figure, is such that it still reflects the fact that the present basic form is the result of a bisection of a Rhombic Pyramid. But after this bisection is accomplished, we could shift the axial center towards the ventral side along the interradial cross axis, till it is half-way between the dorsal and ventral ends of that axis. See the next Figure.
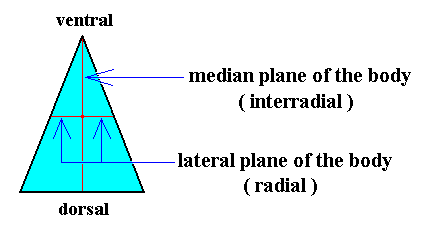
Figure 28. Base (or equatorial plane) of a single isosceles pyramid representing the basic form of the (Eu)dipleura. The left and right halves of the image in this Figure represent the two antimers. The interradial and radial cross planes are indicated. With respect to the previous Figure the axial center is shifted to the middle of the interradial cross axis.
As in the Tetrapleura, we must also in the Dipleura distinguish between two different basic forms as two subspecies, namely such where the two antimers are symmetrically equal, and such in which one body half (the right half) is more or less different from the other half (the left half), i.e. being only symmetrically similar to the other. The latter will be called D y s d i p l e u r a and the former, correspondingly, E u d i p l e u r a.
Strictly, the large majority of all Dipleura should be assigned to the heteropleural forms (Dipleura heteropleura, Dysdipleura), because indeed only in rare cases both body halves are wholly symmetrically equal in a geometric sense. It is however appropriate only to reckon those dipleurals as "asymmetric", i.e. as Dysdipleural forms, in which the inequality of the two antimers more or less conspicuously appears in the outer form, as in the Pleuronectids (flatfishes). We exclude accordingly those dipleurals from the heteropleurals, and interpret them as homopleurals, in which, it is true, the internal organs are asymmetrically patterned in the body (as is, for example, the case with our heart), but in which the external organs and the whole body shape is symmetrically developed (most Vertebrates). The strongest expression of the homopleural form within the Dipleura, internally as well as externally, we find in the Arthropods (Insects and the like).
In all Dipleura (Triaxonia) only two real cross axes (resp. cross planes) are present, and these coincide with the two ideal cross axes (resp. planes), i.e. with the two directional axes (resp. planes). One of the real cross planes is the radial plane that is identical to the median plane of both antimers (See especially Figure 28), i.e. to the lateral plane. The other real cross plane is the interradial cross plane, that coincides with the boundary plane of the two antimers, i.e. the plane that separates the latter, and which is the median plane of the whole body. In the Eudipleura two of the three unequal body axes, namely the main axis or longitudinal axis and dorso-ventral axis or axis of thickness, are heteropolar, while the third axis, the lateral axis, or axis of width, homopolar. In the Dysdipleura on the other hand all three axes are heteropolar.
As the basic form of the E u d i p l e u r a we already have indicated h a l f a R h o m b i c P y r a m i d or s i n g l e i s o s c e l e s p y r a m i d, i.e. a three-sided pyramid, the base of which is an isosceles triangle. We have once and for all determined the interpretation of its individual parts such that its base corresponds to the oral, its tip to the aboral end of the body, while of the three sides the unpaired isoscelesly triangular side is signified as the dorsal, and both paired sides (which are two non-equilateral triangles that are symmetrically congruent with respect to each other) as right and left lateral surfaces. The mid-line of the ventral surface then is that edge of the pyramid which lies opposite to the dorsal surface.
The D y s d i p l e u r a, that all are originally predispositioned as Eudipleura, and only after differentiation of both body halves have emerged from the latter, do not admit anymore of a definite stereometric basic form to be recognized. At most one could indicate their basic form as a non-equilateral pyramid, i.e. a three-fold pyramid the base of which is a non-equilateral triangle.

Figure 29. Oblique top view of a single isosceles pyramid ( = half a Rhombic Pyramid ) expressing the stereometric basic form of the Eudipleura. The two antimers are indicated by colors.
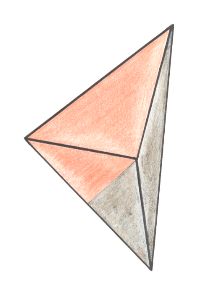
Figure 29. The same as in the previous Figure : The single isosceles pyramid from a somewhat different angle of view.
The Eudipleura or fully symmetrically equilateral and two-fold forms, can be seen as the most perfect of all organic forms. Evidently the composition of the body of only two antimers, which are symmetrically equal, is connected to a number of advantages, not shared by any other form. These advantages are mainly of a mechanical nature. They suit the free movement of the body. Indeed we see that not only most of the freely moving perfect organisms, and especially all higher animals that move around on land, are, almost without exception, built according to the eudipleural form (most Vertebrates and Arthropods), but also all artifacts built by humans for the purpose of locomotion (ships, cars and airplanes). Especially for the forward movement in a definite direction with a constant body end in front, and with a constant orientation of the poles of the dorso-ventral axis, no other basic form is as suited as is the Eudipleural form.
Apart from animals the eudipleural form is seldom encountered as basic form of higher-order form individuals. In lower-order form individuals within plants it is, on the other hand, very common, so in leaves (which are organs), including petals. Also here the eudipleural form often passes into the dysdipleural form. In Protists (which are mainly unicellular organisms) the eudipleural form is relatively seldom materialized, expressing, as it seems the lower status of such organisms. It should however be emphasized that many protists are too small to allow any strong active locomotion. Their non-eudipleural forms are probably adaptations for passive locomotion in a medium which for them (because of their smallness) is more or less viscous.
When one still wishes to use the term "bilateral symmetry", one should reserve the term for the Eudipleura, which indeed represent the bilateral-symmetric form in its strictest sense. Excluded from its content should be the Dipleura (because they also contain the Dysdipleura), Zygopleura, Centrepipeda ( = Allopola) and the Heterostaura. How essentially the eudipleural form distinguishes itself from these other basic forms, of which it is just the most special sort, is sufficiently explained in our enquiry, just like the establishment by it that the general stereometric basic form of the Eudipleura is the single isosceles pyramid or half a Rhombic Pyramid.
The Eudipleura can, if one whishes, be divided into four subgroups on the basis of axial ratios : Although the a x i a l r e l a t i o n s do not differ in all Eudipleura -- i.e. they all possess three non-equivalent axes that are perpendicular to each other and of which one axis is homopolar while the other two are heteropolar -- the a x i a l r a t i o, i.e. the ratio of the l e n g t h s of the three axes, does differ from one Eudipleural organism to another. This ratio determines general shape categories within the Eudipleura :
The Dysdipleura or the asymmetric two-fold forms could be seen as the most perfect of all organic forms, because in them, apparently, the differentiation of the axes and their poles has reached a maximum. In addition to the Diphragma (autopola) and Eudipleura, the Dysdipleura are the only forms which are constituted of only two antimers. These three basic forms share, in addition to the homotypic basic number being two, also the unequality of the three ideal axes (the main axis and both directional axes) and the unequality of the poles of the main axis. While the Eudipleura elevate themselves far above the Diphragma by their extra differentiation of the poles of their dorsoventral directional axis, the Dysdipleura go yet one step further by the fact that in them also the poles of the other directional axis (the lateral axis) are differentiated. The Dysdipleura are the only two-fold forms that distinguish themselves by three unequal and non-equipolar ideal axes, perpendicular to each other. The oral pole of the longitudinal axis is different from the aboral pole. The dorsal pole of the axis of thickness is different from the ventral pole. The left pole of the width-axis is different from the right pole. See the next Figure.
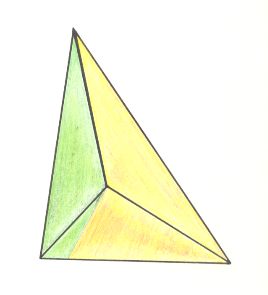
Figure 30. Oblique top view of an unequally three-sided pyramid as the basic form of the Dysdipleura. The two unequal antimers are indicated by coloration.
But while in this way the Dysdipleura can be considered in principle as representing the most advanced basic form, we see at once that with their characteristic unequality of the two lateral body halves the loss of the capacity of free movement is in some way connected, while this capacity is still present in the possessors of the eudipleural form, elevating the latter as the most perfect basic form. That's why we find the dysdipleural form only in those persons in which one body half, either the right or the left one, has a special function, a function never sustained by the other body half, or (in those persons) in which the heteropleural development of both antimers is determined by special adaptations, and connected with an essential reduction of fast locomotion. An exception are, in a sense, the flatfishes, that, although being dysdipleural, swim good enough.
The fact that the determined stereometric basic form of the isosceles pyramid, which is the basic form of the Eudipleura, cannot mathematically be demonstrated in the Dysdipleura, is already shown above. And so it could seem that a stereometric basic form cannot be found in this most differentiated form group. It rather seems that this group is connected directly to the least perfect of all form types, the absolutely irregular bodies, Anaxonia. But we must stress again that a l l D y s d i p l e u r a a r e o r i g i n a l l y s e t i n a n e u d i p l e u r a l w a y, and only secondarily became heteropleural (This is very clearly visible in the Pleuronectids which in their juvenile stage are eudipleurals), and that they display the isosceles pyramid clearly during a certain (longer or shorter) time of their life.
Indeed, above, i.e. in Figure 7 of the previous document, we derived the Dysdipleura from Eudipleura by ideal bisection (Real bisection, Figure 5, resulted in a form belonging to the Anaxonia), and the Eudipleural form was in turn derived from the basic form of the Tetraphragma interradialia (Autopola) by real bisection (Figure 2 of the previous document). When we derive the basic form of the Eudipleura not from the Tetraphragma (Autopola) but from the Diphragma (Autopola), as we did in Figure 8 of the previous document, we get a representation of the basic form of the Eudipleura in its most simple form (namely an isosceles pyramid), and then the derivation of the Dysdipleura from Eudipleura looks like that depicted in the next Figure :
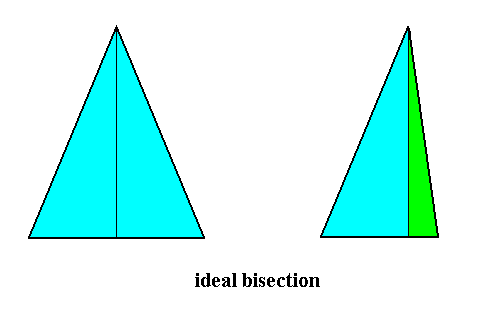
Figure 31. Derivation (by showing the bases of the pyramids) of the basic form of the Dysdipleura from that of the Eudipleura by ideal bisection.
The ideal bisection as depicted in the above Figure preserves the 2-foldness, i.e. both the eudipleural form and the derived dysdipleural form have t w o antimers. The origin of the dysdipleural basic form, from that of the Eudipleura is still evident (in that dysdipleural form), because of its 2-foldness.
We already stated that, strictly mathematically speaking, in fact the large majority of Dipleura should belong to the Dysdipleura, because the two antimers of the dipleural body are seldom wholly symmetrically equal. We only have to look to the unequality of the two halves of any human face, which in this case is more conspicuous than with respect to the other body parts. But these small deviations -- as expressed by the unequality of the two halves of the skull, or sometimes by the lopsided position of the anus, or lopsided development of the olfactory organ -- are of no determining influence on the basic form as a whole. We accordingly will consider only those dipleural forms as definitely dysdipleural forms, in which e x t e r n a l l y the unequality of the right and left body halves expresses itself in such a way that the o v e r a l l f o r m looks "a s y m m e t r i c". We say explicitly "externally", because the internal structure does show differences (And often very strong differences!) between the right and left half of most Eudipleura. But because these internal asymmetries do not exert any effect on the external appearance of the dipleural body form as a whole, we can totally ignore them.
So when we accordingly interpret only such dipleural organic forms as dysdipleural in a strict sense, in which the uneaquality of the two body halves appears in such a conspicuous way as to make the whole body as a whole asymmetric, we find this dysdipleural form in most cases only as singular exceptions in such groups of organisms, of which the general basic form is eudipleural. Of the persons in the animal kingdom we must especially mention the peculiar fish family of the Pleuronectids (flatfishes) in which the trunk is, it is true, wholly eudipleurally (developed), but in which the head is so obliquely developed, that both eyes lie on one side of their body, either on the right or on the left side. Further there is the narwal delphin in which only the left incisor has been developed into a mighty thrust tooth, while the right tooth is wholly reduced. Among Arthropods many Crustaceans are dysdipleural, for example the hermit crabs of which the soft abdomen is asymmetrically developed because they use to hide it into a spirally wounded snail shell. Correspondingly also the two pincers are very unequally developed (But this also, in a constant way, occurs in the two pincers of some other Decapoda).
Among the Lamellibranchiata dysdipleural forms can be seen where they are attached to a substrate with one valve of their shell, for example in oysters.
Among plants it is especially the eudipleural o r g a n s, which in many cases transform more or less conspicuously into the dysdipleural form. Especially among leaves, that have as their general basic form that of the Eudipleura, we very often encounter more or less clearly expressed dysdipleural forms, for instance the leaves of Begonia.
In all these cases either the embryological development or the paleontological history tells us that the unequal halves of the dysdipleural body originally were set in an eudipleural fashion, implying that the dysdipleural situation has been secondarily developed from a pure eudipleural condition. Somtimes it concerns the right, sometimes the left side, that enjoys a stronger growth (but were initially equivalent), and therefore develops at the expense of the other.
With the Dysdipleura we have come to an end of the systematic treatment of the H e t e r o p o l a h e t e r o s t a u r a, the Second Subfamily of the Stauraxonia heteropola. In the next document we append a third (and last) Subfamily of the Stauraxonia heteropola, the Heteropola gyrostaura. It comprises the gyroid pyramids, i.e. (single) pyramids with sigmoid cross axes. The group is promorphologically not very important because either none or only a few organisms show this basic form. We append it here just in order to be complete and to make room for organisms that do not possess any mirror plane but have a heteropolar main axis which is at the same time a rotational axis.
To continue click HERE to proceed further with the systematic Promorphology (Gyrostaura).
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)