Promorphology of Crystals Preparation XI

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
11

The Plane Group P31m
There are two types of two-dimensional a r r a y of motifs that involve 3-fold rotation axes and mirror lines (for example the array of red and blue discs, representing the structure of 2-D ionic crystals, considered in the previous document), that have the same total symmetry content, but must nevertheless be described by different Plane Groups. One description is in terms of the Plane Group P3m1, the other in terms of the Plane Group P31m, both of the same Point Group (symmetry Class) 3m of the 2-D "Hexagon Crystal System" which is based on the Hexagonal Net, i.e. on the 2-D Primitive Hexagonal Point Lattice. While the total symmetry content of both Plane Groups, P3m1 and P31m, is the same, the conventional location of cell edges (as defined by three crystallographic axes a₁, a₂ and a₃ ) differs by 30⁰ in the two Groups. In P3m1 the mirror lines bisect the 60⁰ angle between cell edges. In P31m the reflection lines coincide with the cell edges.
Let's take the pattern according to Plane Group P3m1, which was discussed earlier :

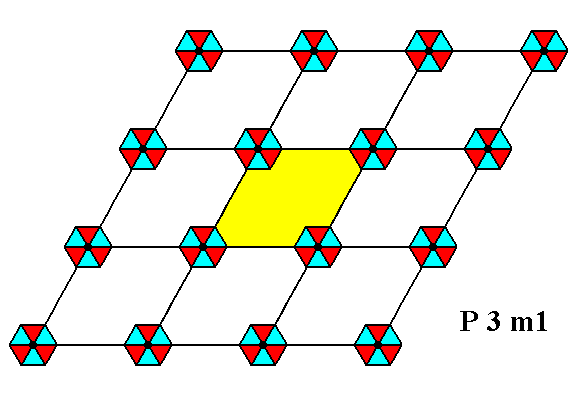
Figure 1. Periodic two-dimensional pattern according to the Plane Group P3m1. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).

and compare it with a pattern, while consisting of the same motifs s.str., is not according to the Plane Group P3m1 but to the Plane Group P31m :

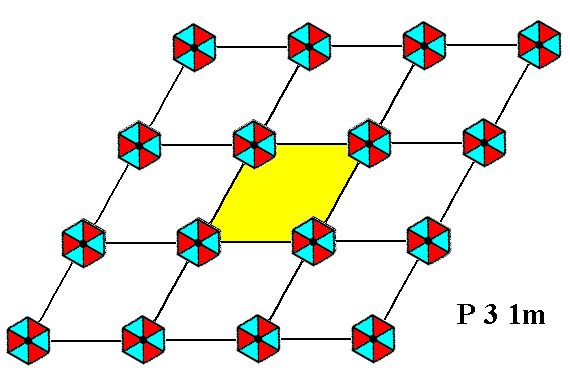
Figure 2. The above periodic two-dimensional pattern of 3m motifs can be related to (and thus described by) a hexagonal net (point lattice) with a rhomb-shaped unit cell (yellow). The net describes only one aspect of the pattern, namely the way of r e p e t i t i o n of nodes with which motifs are associated. The total symmetry of this periodic pattern can be described by the Plane Group P31m. The motifs s.str. of this pattern are identical to those of Figure 1, save that they are rotated by 30⁰ with respect to them. Also the applied point lattices are the same in both Figures. The pattern must be imagined to be extended indefinitely in 2-D space.

If we look carefully to the two patterns we see that, while both are related to the same net, the motifs s.str. of one pattern are rotated 30⁰ with respect to those of the other pattern, BUT THEIR BACKGROUND IS NOT ROTATED, i.e. the backgrounds in the one pattern have the same orientation as those in the other pattern ( For P3m1 see Figure 7r of the previous document, and for P31m click HERE ). This implies that, going from P3m1 to P31m, we have to do with a QUALITATIVE change in pattern, because the background of a motif s.str. also belongs to the motif, i.e. to the content of the pattern.
So if we want to go from P3m1 to P31m we cannot simply rotate the whole pattern to achieve this transformation. Such a simple rotation of the whole pattern -- which does not lead to a different Plane Group -- is illustrated in the next two Figures, with the ionic P3m1 pattern. This pattern has motifs s.str. that almost entirely fill all the background, so when rotating the pattern it is clear that the background (now occupied almost completely with motif s.str.) will rotate with it. And this is NOT the same as going from the pattern of Figure 1 to that of Figure 2, because there the background is not rotated. So the rotation of the entire pattern, as depicted in the next two Figures, does NOT change the pattern at all.

Figure 2a. Periodic two-dimensional pattern of 3m motifs, i.e. of motifs each having a 3m symmetry (one 3-fold rotation axis and three equivalent mirror lines at angles of 120⁰). The pattern must be described by the Plane Group P3m1.

Figure 2b. The same periodic pattern as in the previous Figure, but now 30⁰ rotated. The pattern also must be described by the Plane Group P3m1.

In discussing the Plane Group P3m1 (in the previous documents), we started with the discussion of the following motif pattern :

Figure 3. Periodic two-dimensional pattern of 3m motifs, i.e. of motifs each having a 3m symmetry (one 3-fold rotation axis and three equivalent mirror lines at angles of 120⁰).

This pattern can be related to a hexagonal net in the following way (as was done in the previous documents) :

Figure 4. The above periodic two-dimensional pattern of 3m motifs can be related to (and thus described by) a hexagonal net (point lattice) with a rhomb-shaped unit cell (yellow). The net describes only one aspect of the pattern, namely the way of r e p e t i t i o n of nodes with which motifs are associated.

When we associate a point lattice with the pattern of Figure 1 as we did in Figure 4, we can and must describe the total symmetry of that pattern with the Plane Group P3m1.
We can, however choose a different unit cell of that pattern, as the next Figure shows.

Figure 5. For the above periodic two-dimensional pattern of 3m motifs another unit cell (yellow) can be chosen as repeating unit. As can be seen, it is a centered unit cell, because it involves, in addition to its six equivalent points, a seventh equivalent point in its center.

The next Figure shows that indeed the newly chosen unit cell is a genuine repeat unit.

Figure 6. The hexagonal unit cell depicted in the above Figure is a genuine repeat unit. Four cells are highlighted.

If we interpret these hexagonal cells not as unit cells but as total motifs, i.e. as each representing the complete surroundings of the corresponding lattice point, then we can indicate again a rhomb-shaped unit cell, as the next Figure shows. This rhomb-shaped unit cell is depicted by red lines.

Figure 7. Four total motifs associated with their corresponding lattice points of another -- but still hexagonal -- net. The rhomb-shaped unit cell of this net is indicated by red solid lines. The symmetry distribution of that unit cell (and ofcourse also of the product of its repetition) seems now to be according to Plane Group P31m (while we started with a P3m1 pattern). Also the rhomb-shaped unit cell according to the Plane Group P3m1 is indicated.
The total motif contains 6x1/3+1=3 motifs s.str.
The P31m (larger) rhomb-shaped unit cell (at the corners of which are the total motifs) contains 4x1/4+2=3 motifs s.str.
The P3m1 (smaller) rhomb-shaped unit cell (at the corners of which are the motifs s.str.) contains 4x1/4=1 motif s.str.

The next Figure isolates a total motif from the pattern of the previous Figure.

Figure 8. A total motif isolated from the pattern of the previous Figure.

The repetition of this motif goes according to the net indicated by red lines in Figure 7. This net is explicitly drawn in the next Figure.

Figure 9. The net, based on the rhomb-shaped (larger) unit cell in Figure 7. This unit cell is again indicated (yellow).

So the pattern of Figure 7 is a periodic repetition of a total motif as depicted in Figure 8, and although we have nothing changed in our initial pattern (Figure 3), its seems now (also) to be (structured) according to the Plane Group P31m.
The symmetry diagram displaying the symmetry configuration of a P31m pattern, a configuration based on the edges of the rhomb-shaped unit cell coinciding with the mirror lines, is the following :

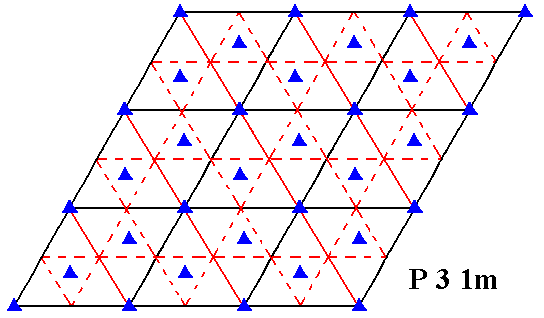
Figure 10. Symmetry content of 2-D patterns according to the Plane Group P31m. Glide lines are indicated by dashed lines. Mirror lines are indicated by red and by black solid lines, while the 3-fold rotation axes are indicated by small triangles.

Let's investigate whether the pattern of Figure 7 and 9 indeed does have (or does not have) the symmetry elements and their distribution as is indicated in the above symmetry diagram of the Plane Group P31m. All this in fact means that we must verify that the u n i t c e l l as drawn in the Figures 7 and 9 possesses the symmetry distribution as given by the symmetry diagram of Plane Group P31m.
That the 3-fold rotation axes and mirror lines are indeed present in that unit cell is easy to verify in Figure 7. :

Figure 11. In the pattern of Figure 9, the unit cell indeed has mirror lines (m) as in the symmetry diagram. Also the 3-fold rotation axes are present at their proper places : One at each corner of the unit cell (not indicated, but evident), and two in its interior (also not indicated, but evident, namely coinciding with the motifs s.str. of that interior) (A 3-fold rotation axis goes through the center of each motif s.str. of the pattern)
But, there are additional 3-fold axes (indicated as green discs) on the edges of the unit cell and two extra in its interior, not present in the symmetry diagram.

If we interpret the pattern as a repetition of the total motifs as indicated in Figure 7, then we still find extra 3-fold axes on the edges of the unit cell, not present in the symmetry diagram :

Figure 12. In the pattern of Figure 7, the unit cell indeed has mirror lines (m) as the symmetry diagram has it. Also the 3-fold rotatation axes are present at their proper places : One at each corner of the unit cell (not indicated, but evident), and two in its interior (also not indicated, they coincide the two motifs s.str. of that interior (A 3-fold rotation axis goes through the center of each motif s.str. of the pattern. But the extra 3-fold rotation axes, found above, which are not present in the symmetry diagram for the Plane Group P31m (Figure 10), are still present in the pattern (indicated as green discs).

So the pattern is not according to the Plane Group P31m, but still according to P3m1. The same result was obtained in the previous document with respect to the ionic P3m1 pattern : There we chose a similar alternative unit cell, but the pattern remained a pattern according to the Plane Group P3m1. See Figure 7h of the previous document.
Only when we interpret the motifs as indicated in Figure 7 as the total motifs of the pattern, i.e. when we do NOT interpret the motif (and all its equivalents), indicated (purple) in the next Figure, as total motif, we finally get rid of the extra 3-fold axes, and obtain a P31m pattern. And this is consequently a d i f f e r e n t pattern, different from the one we started with.

Figure 13. In order to obtain a P31m pattern from the pattern of Figure 7, we must NOT interpret the motif highligted (purple) as a genuine total motif, which means that its center (and those of all its equivalents) must not be interpreted as a lattice point. See next Figure.

Figure 14. Indication of the genuine total motifs in the pattern of Figure 7. Each, AND ALL, total motif(s) correspond(s) to a lattice point. It is the lattice corresponding with the Plane Group P31m.

By correctly interpreting the total motifs, the extra 3-fold axes have disappeared :

Figure 15. Indication of the genuine total motifs in the pattern of Figure 7. Each, AND ALL, total motif(s) correspond(s) to a lattice point. It is the lattice corresponding with the Plane Group P31m. As can be seen, the points indicated (black) are not locations of 3-fold rotation axes anymore.

The locations of the 3-fold axes are now identical to those in the symmetry diagram of the Plane Group P31m (Figure 10):

Figure 16. Location of the 3-fold rotation axes in the unit cell of the pattern of Figure 14. It complies with the symmetry diagram for the Plane Group P31m.

So the pattern of Figure 9 must be adapted in order to be compatible with the inserted net of which the directions of the cell edges with respect to the motifs are such that the structure can be described by the Plane Group P31m. See next Figure.

Figure 17. The array of motifs of Figure 9 is adapted to let the inserted net be such that it describes the pattern according to Plane Group P31m. The rhomb-shaped unit cell is indicated (yellow). Its angles are 120⁰ and 60⁰, as is also the case with the rhomb-shaped unit cell of the pattern of Figure 4 in which the inserted net allows the description of the pattern according to Plane Group P3m1. The latter pattern is however a different pattern, different from the one just obtained.

Because the non-colored motif units in the previous Figure are all equivalent and have a higer symmetry than the colored ones (i.e. they at the same time also comply with the three-fold symmetry of the colored ones), we can dispose of them all together. See the next Figure.

Figure 18. In the array of the previous Figure the non-colored motifs are erased. The resulting pattern in conjuction with the inserted net now fully complies with the Plane Group P31m, as the next Figures demonstrate.

Figure 19. In the array of Figure 18 we see that the locations of the 3-fold rotation axes comply with the symmetry diagram of Plane Group P31m in Figure 14. Only the 3-fold axes of the unit cell are indicated.

Also the mirror lines of the symmetry diagram for P31m are present, as the next Figure shows.

Figure 20. In the array of Figure 18 we see that the locations of the mirror lines comply with the symmetry diagram of Plane Group P31m in Figure 14. Only those of the unit cell are indicated.

The next Figures demonstrate that also the glide lines of the symmetry diagram for the Plane Group P31m are present.

Figure 21. In the array of Figure 18 we see that the glide lines parallel to, but not coincident with, the shorter diagonal of the unit cell are present, and thus comply with the symmetry diagram of Plane Group P31m in Figure 14. Only one such glide line (red solid line) is indicated. When we look to the unit cell just to the left and below the one indicated, we see that both glide lines to the right and to the left of the unit cell's shorter diagonal are present.

Figure 22. In the array of Figure 18 we see that the glide lines parallel to, but not coincident with, the edges of the unit cell and connecting the centers of opposite edges, are present, and thus comply with the symmetry diagram of Plane Group P31m in Figure 14. Only one such glide line (red solid line) is indicated.

Figure 22a. In the array of Figure 18 we see that the glide lines parallel to, but not coincident with, the edges of the unit cell and connecting the centers of the other pair of opposite edges, are present, and thus comply with the symmetry diagram of Plane Group P31m in Figure 14. Only one such glide line (red solid line) is indicated.

We will now determine the C o m p l e x M o t i f of the P31m pattern just established. Recall that the Complex Motif is the translation-free residue of a periodic pattern. It has the symmetry of the given Crystal Class (point symmetry). Because the glide lines of the P31m pattern, as in Figure 18, are parallel to existing mirror lines (See Figure 14), we do not have to deal with them (i.e. we do not have to eliminate the translations involved in them), the symmetry of the result will not be changed. So we can concentrate directly on the content of the unit cell. Because the Complex Motif must show all the symmetry that the given crystal has in store, we must concentrate on the most symmetric unit cell. The unit cell as chosen in Figure 18 is not the most symmetric, so we must choose another :

Figure 23. A more symmetric unit cell (in fact the most symmetric unit cell) is choosen for the P31m pattern of Figure 18.

While the rhomb-shaped unit cell of Figure 18 suggests a Complex Motif that has not the full point symmetry which the given crystal has in store (3m symmetry), the large hexagonal unit cell (which is of course not the smallest unit (cell)) suggests a hexagonal unit having the full 3m symmetry and can tile the plane, i.e. is a genuine repeating unit, and can thus serve to represent the Complex Motif. See next Figure.

Figure 24. A hexagonal repeating unit can serve as the Complex Motif, because it has all the symmetry needed to represent it.

When we isolate this hexagonal cell, we eliminate automatically all simple translations of the pattern and end up with the Complex Motif. See next Figure.

Figure 25. The Complex Motif of the P31m pattern of Figure 18.

It is interesting to compare this Complex Motif of the Plane Group P31m with that of the Plane Group P3m1. The latter can be seen by clicking HERE.
The next Figure places the Complex Motifs of the two Plane Groups side by side :

Figure 26. The Complex Motif of the P31m pattern of Figure 18 and the Complex Motif of the P3m1 pattern of Figure 1 of Part Eight. Their motif s.str. are identical, including their orientation, but their hexagonal background differs by a rotation of 30⁰.

In Figure 26 it is immediately evident that the only difference between the two Complex Motifs is the orientation of the background of the motif s.str. Equivalently we can say that the difference between the two is the ORIENTATION OF THE MOTIF S.STR. WITH RESPECT TO ITS BACKGROUND. Before we will elaborate on this further, we first consider the folowing :
With respect to the Complex Motif of the P3m1 pattern considered in Part 8, the hexagonal background had to have the orientation as it was depicted there. Here we will show that the orientation of the Complex Motif found for the P31m pattern of the present document (depicted in Figure 18) as depicted in the Figures 24 and 25, is the only orientation possible. See next Figure.

Figure 27. Motifs s.str. plus a proper hexagonal background (this background) having the orientation as depicted in the Figure, cannot as such tile the plane, and are not true repeating units, and consequently cannot represent the Complex Motif of the present P31m pattern.

So indeed the motif depicted in Figure 25 is the true Complex Motif of the P31m pattern of Figure 18. And indeed, it differs from the Complex Motif of the P3m1 pattern of Figure 1 of Part Eight by a different orientation of its hexagonal background. The orientations differ by 30⁰ (rotation). And this difference is equivalent to the following difference : The motif s.str. of the Complex Motif of the P31m pattern is rotated 30⁰ with respect to that of the P3m1 pattern. And in fact, as we will show in the next document, this is the very difference between the Plane Group P31m and the Plane Group P3m1.

To continue click HERE to further investigate the Plane Group P31m.

e-mail :