Promorphology of Crystals II

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
II

Hexagonal System
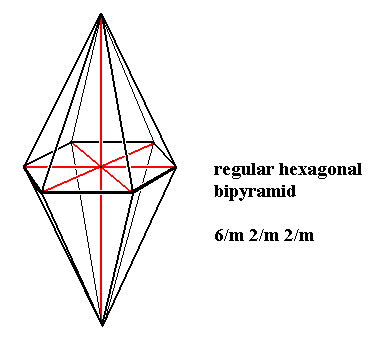
Dihexagonal-bipyramidal Class, 6/m 2/m 2/m
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Hexagonal Bipyramid (Figure 1).
This body is a regular 6-fold bipyramid.
The promorph is accordingly that of the Polypleura dodecapleura (Stauraxonia homopola isostaura) (By clicking the link you will get to the Isostaura polypleura. Some species of them are enumerated and pictured, among which the six-fold bipyramid (Figure 19), the basic form of the Polypleura dodecapleura (not mentioned by name there)).

Figure 1. A regular six-fold bipyramid, the Stereometric Basic Form of the crystals of the Dihexagonal-bipyramidal Class of the Hexagonal Crystal System.
The equatorial plane is a regular hexagon.

Dihexagonal-pyramidal Class, 6 m m
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Hexagonal Pyramid (Figure 2).
This body is a regular 6-fold pyramid.
The promorph is accordingly that of the Isopola hexactinota (Stauraxonia heteropola homostaura)

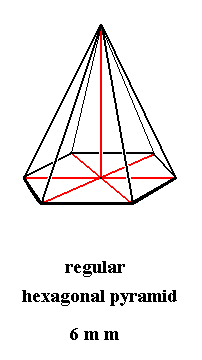
Figure 2. A regular six-fold pyramid, the Stereometric Basic Form of the crystals of the Dihexagonal-pyramidal Class of the Hexagonal Crystal System.
The base of the pyramid is a regular hexagon.

Hexagonal-bipyramidal Class, 6/m
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Regular Hexagonal Gyroid Bipyramid (Figures 3 and 4) (Versions of the gyroid bipyramid, in which the receding angles are replaced by their corresponding anti-receding angles, can occur in crystals).
The promorph is accordingly that of the Isosigmostaura sextamera (Stauraxonia homopola sigmostaura).
In the next Figure we indicate, by means of the equatorial plane, how to construct a six-fold gyroid bipyramid, as the basic form of the Isosigmostaura sextamera (Stauraxonia homopola sigmostaura).

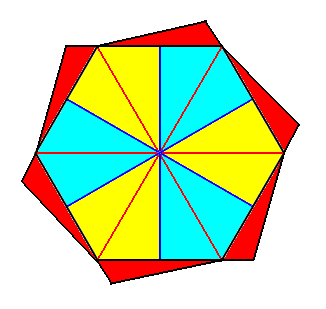
Figure 3. Construction of a regular six-fold gyroid bipyramid by means of adaptation of the equatorial plane of a regular six-fold bipyramid. Attachment of the red parts, as indicated in the Figure, causes the elimination of the mirror lines inherent in a regular hexagon. For the bipyramid this means the disappearance of all vertical mirror planes, i.e. mirror planes containing the main axis. The 6-fold rotation axis, though, remains.

The next Figure depicts the bipyramid, finally resulting from this construction.

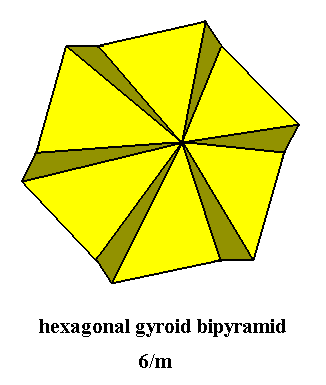
Figure 4. Regular Hexagonal (i.e. six-fold) Gyroid Bipyramid, Stereometric Basic Form of the (single) crystals of the Hexagonal-bipyramidal Class of the Hexagonal Crystal System. Because of the view direction the lower pyramid is not visible.

Hexagonal-pyramidal Class, 6
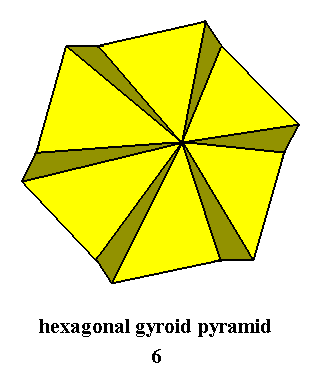
The geometric solid taken (according to the above established criteria) to represent generally the stereometric basic form (promorph) of all the crystals of this Class is the Regular Hexagonal Gyroid Pyramid (Figure 5) (Versions of the gyroid pyramid, in which the receding angles are replaced by their corresponding anti-receding angles, can as such occur in crystals).
The promorph is accordingly that of the Homogyrostaura hexamera (Stauraxonia heteropola gyrostaura).

Figure 5. Regular Hexagonal (i.e. six-fold) Gyroid Pyramid, Stereometric Basic Form of the (single) crystals of the Hexagonal-pyramidal Class of the Hexagonal Crystal System.

Hexagonal-trapezohedric Class, 6 2 2
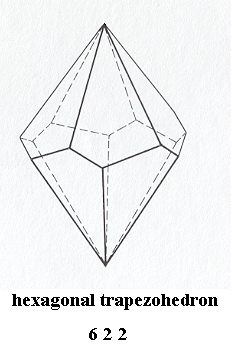
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Hexagonal Trapezohedron (Figure 6).
The promorph is accordingly that of the Scalenoidea sextamera (Stauraxonia homopola).

Figure 6. Hexagonal Trapezohedron, Stereometric Basic Form of the (single) crystals of the Hexagonal-trapezohedric Class of the Hexagonal Crystal System.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )

Ditrigonal-scalenohedric Class, 3* 2/m
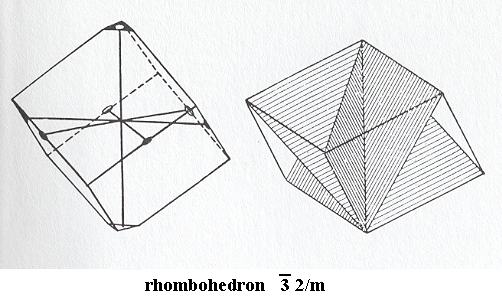
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Rhombohedron (Figure 7). The Rhombohedron can promorphologically be seen as a homopolar 3-fold bipyramid with a non-planar equatorial plane. It can be obtained by deformation of a cube in the direction of one of its axes of 3-fold rotoinversion. The Rhombohedron consists of six rhomb-shaped faces.
The promorph will be assessed as Scalenoidea rhomboedra (Stauraxonia homopola).

Figure 7. Rhombohedron, Stereometric Basic Form of the (single) crystals of the Ditrigonal_scalenohedric Class of the Hexagonal Crystal System.
Left image : Rotational axes indicated. Small triangle with hole : 3-fold rotoinversion axis. Small oval : 2-fold rotation axis.
Right image : Position of mirror planes.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )

Trigonal-rhombohedric Class, 3*
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Trigonal (3-fold) Gyroid Twisted Apical Bipyramid (Figure 11).
The promorph is accordingly Isosigmostaura pseudorhomboedra (Stauraxonia homopola sigmostaura).
In the next Figures we will construct the Trigonal Gyroid Twisted Apical Bipyramid.

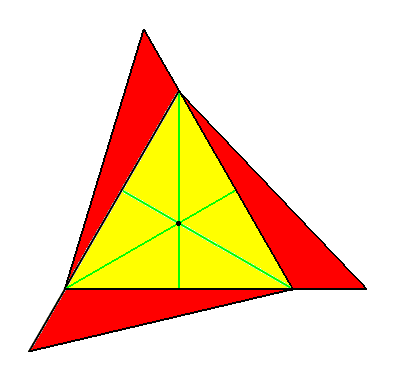
Figure 8. Construction of one of the (equal) bases of the Trigonal Gyroid Twisted Apical Bipyramid, from the base of a regular trigonal pyramid. The 3-fold rotation axis is in the center of the depicted form, as indicated.

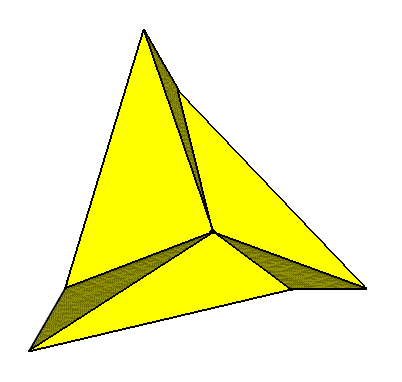
Figure 9. Slightly oblique top view of a trigonal (3-fold) gyroid pyramid. The final geometric solid to be constructed, the Trigonal Gyroid Twisted Apical Bipyramid, consists of two such pyramids, connected to each other by their tips and rotated 60⁰ with respect to each other.

By means of superimposing two bases of 3-fold gyroid pyramids, combined with a rotation by 60⁰ of one such base with respect to the other, we illustrate the construction of the Trigonal Gyroid Twisted Apical Bipyramid :

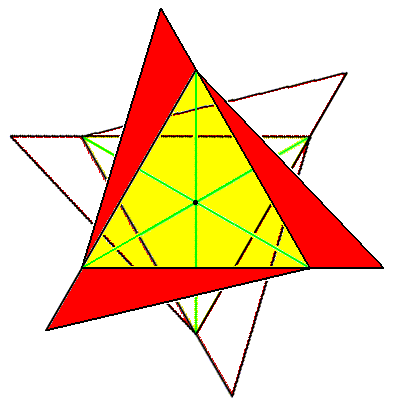
Figure 10. Superposition and rotation (60⁰) of two bases of trigonal pyramids, in order to construct the Trigonal Gyroid Twisted Apical Bipyramid.

The next Figure, finally, gives the Trigonal Gyroid Twisted Apical Bipyramid. It is the Stereometric Basic Form of all the (single) crystals of the Trigonal-rhombohedric Class of the Hexagonal Crystal System. I.e. it is the geometric solid (body) that geometrically depicts the symmetry of that Class, which here means the possession of a 3-fold rotoinversion axis as its only symmetry element.

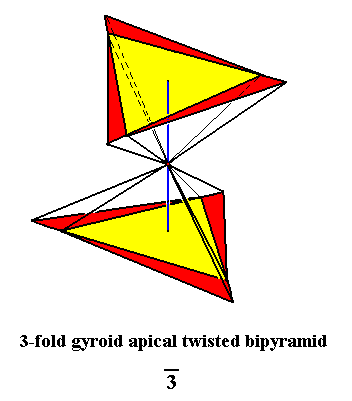
Figure 11. The Trigonal Gyroid Twisted Apical Bipyramid, the Stereometric Basic Form of all the (single) crystals of the Trigonal-rhombohedric Class of the Hexagonal Crystal System.

The symmetry of the just depicted gyroid bipyramid can be further illustrated by the following diagram representing the 3-fold rotoinversion symmetry.

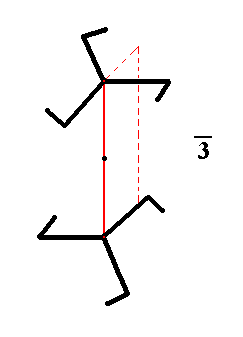
Figure 11a. The Symmetry of the Trigonal Gyroid Twisted Apical Bipyramid (Figure 11) diagrammed.

Ditrigonal-bipyramidal Class, 6* m 2
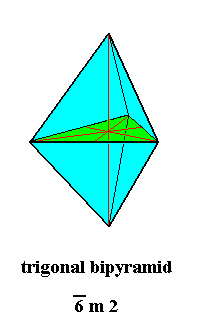
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Trigonal Bipyramid (Figure 12). The Promorph is accordingly that of the
Isostaura polypleura (hexapleura) (Stauraxonia homopola).

Figure 12. Trigonal Bipyramid, Stereometric Basic Form of the (single) crystals of the Ditrigonal_bipyramidal Class of the Hexagonal Crystal System.

Ditrigonal-pyramidal Class, 3 m
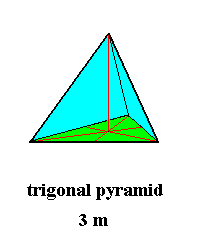
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Trigonal Pyramid (Figure 13). The Promorph is accordingly that of the
Anisopola triactinota (Stauraxonia heteropola homostaura).

Figure 13. Trigonal Pyramid, Stereometric Basic Form of the (single) crystals of the Ditrigonal-pyramidal Class of the Hexagonal Crystal System.

Trigonal-bipyramidal Class, 6*
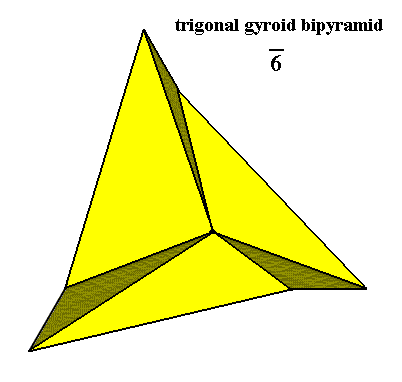
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Trigonal (3-fold) Gyroid Bipyramid (Figure 14) (Versions of the gyroid bipyramid, in which the receding angles are replaced by their corresponding anti-receding angles, can occur in crystals). The Promorph is accordingly that of the Isosigmostaura trimera (Stauraxonia homopola sigmostaura).

Figure 14. Slightly oblique top view of a Trigonal (3-fold) Gyroid Bipyramid, Stereometric Basic Form of the (single) crystals of the Trigonal-bipyramidal Class of the Hexagonal Crystal System. The lower pyramid is not visible but is present. The only mirror plane present is the equatorial plane connecting the two constituent pyramids.

The symmetry of the just depicted bipyramid can be diagrammed as follows :

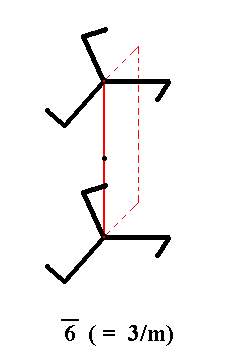
Figure 14a. Diagrammatic representation of the 6-fold rotoinversion symmetry of the gyroid bipyramid of Figure 14. This symmetry is identical to 3/m symmetry, which means a 3-fold rotation axis perpendicular to a mirror plane.

Trigonal-pyramidal Class, 3
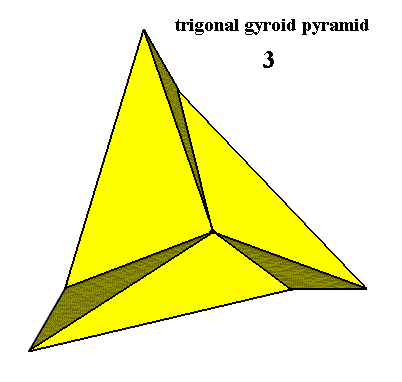
The geometric solid taken (according to the above established criteria) to represent generally the stereometric basic form (promorph) of all the crystals of this Class is the Trigonal (3-fold) Gyroid Pyramid (Figure 15) (Versions of the gyroid pyramid, in which the receding angles are replaced by their corresponding anti-receding angles, can as such occur in crystals). The Promorph is accordingly that of the Homogyrostaura trimera (Stauraxonia heteropola gyrostaura).

Figure 15. Slightly oblique top view of a Trigonal (3-fold) Gyroid Pyramid, Stereometric Basic Form of the (single) crystals of the Trigonal-pyramidal Class of the Hexagonal Crystal System. The only symmetry element present is a 3-fold rotation axis. There are no mirror planes.

Trigonal-trapezohedric Class, 3 2
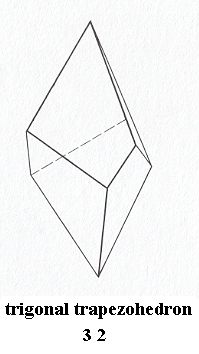
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Trigonal Trapezohedron (Figure 16). It can be seen as a trigonal bipyramid with a non-planar equatorial plane. The Promorph can, on the basis of all this, be assessed as belonging to the Scalenoidea trimera (Stauraxonia homopola).

Figure 16. Trigonal Trapezohedron, Stereometric Basic Form of the (single) crystals of the Trigonal-trapezohedric Class of the Hexagonal Crystal System. There are no mirror planes.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )

To continue click HERE to proceed with the third part of the Promorphology of Crystals.

e-mail :