e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Sequel to Infinite two-dimensional periodic patterns
Two distinct Plane Groups, P3m1 and P31m, belong to Point Group 3m. They have the same total symmetry content and shape, but the motifs differ in orientation with respect to the edges of the unit mesh (unit cell). Let's start with Plane Group P3m1.
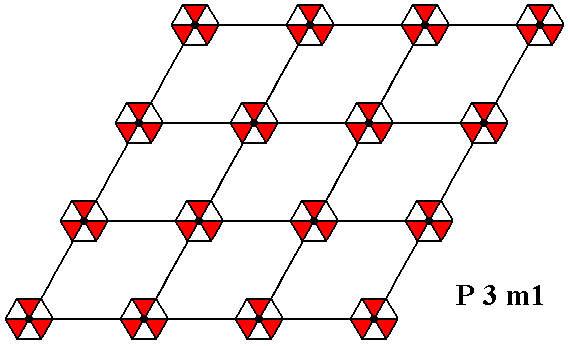
Placing motifs in a hexagonal net, but now motifs, having a point symmetry 3m -- meaning that each motif has a 3-fold rotation axis going through its center (and perpendicular to the plane of the drawing), and three equivalent mirror lines, such that their point of intersection coincides with the center of such a motif -- and oriented in the net such that their mirror lines do not coincide with the connecting lines of the net, yields a pattern (of repeated motifs) representing Plane Group P3m1. See Figure 1.
Each motif in Figure 1 is subdivided into three units. Each individual unit is still symmetric, and is, consequently not a basic motif unit. And only a basic motif unit can represent a group element, in our case an element of the group P3m1. The units as depicted in the next Figure (i.e. augmented motif units) represent subgroup and cosets of the group P3m1.

Figure 1. The insertion of motifs having 3m symmetry and oriented as described above, into a hexagonal net, leads to a periodic pattern representing Plane Group P3m1.
Each (composed) motif consists of three augmented motif units, such that the symmetry of the composed motif is 3m . Each augmented motif unit can represent a subgroup or coset of the full group.
The pattern must be conceived as extending indefinitely in two-dimensional space.
The total symmetry content of the Plane Group P3m1 is depicted in the next Figure.
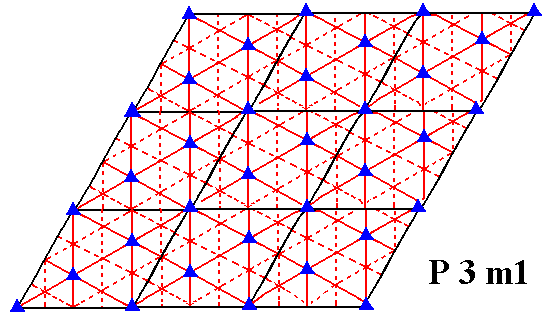
Figure 2. Total symmetry content of the Plane Group P3m1.
3-fold axes are indicated by small solid blue triangles.
Glide lines are indicated by dashed red lines.
Mirror lines are indicated by solid red lines.
For clarity we depict this same total symmetry content, but now referring only to one mesh of the net :
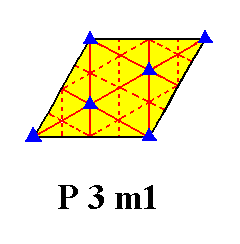
Figure 3. Total symmetry content of Plane Group P3m1, depicted for one mesh of the net. Only the red solid lines are mirror lines.
As has been said, the motif units as depicted in Figure 1 are augmented motif units. To indicate the true basic motif units, representing group elements, we should indicate the composed nature of the augmented motif units. We can do that by inserting extra lines :

or perhaps still better (i.e. a little more indicative) :

And to further highlight the basic motif units that legitimately represent group elements, we could use colors, provided we do not interpret a difference of color as an asymmetry. The two (differently colored) parts of an augmented motif unit represent different group elements, but are nevertheless symmetrically related to each other :

So now we have six basic motif units making up one composed motif of the P3m1 pattern.
To generate the full group we need one such basic motif unit to represent the identity element 1 , another basic motif unit to represent a first (of the three needed) generator, namely an anticlockwise rotation p of 1200 about a certain fixed lattice point (which we will call the point R), yet another such unit to represent a second generator, namely a reflection in the line m making an angle of 300 with the horizontal lattice connection lines, and passing through the point R, and, finally, yet another basic motif unit to represent the third generator, namely the translation t .
Let's indicate the identity element, the rotation (first generator) and the reflection (second generator) in an enlarged composed motif :
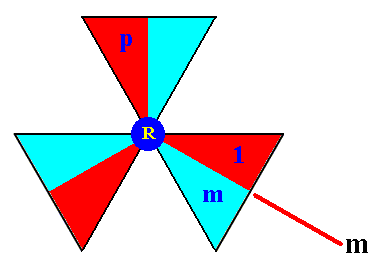
Figure 3a. The composed motif at a chosen lattice point R . As such it consists of six basic motif units representing elements of the group P3m1. One unit is chosen to be the identity element 1 , the other two are the generators p and m .
Let us now put all this in the context of the lattice. We then indicate the lattice points R and S, the identity element 1 , the generators p and m , and the generator t , which is a horizontal translation. See next Figure.
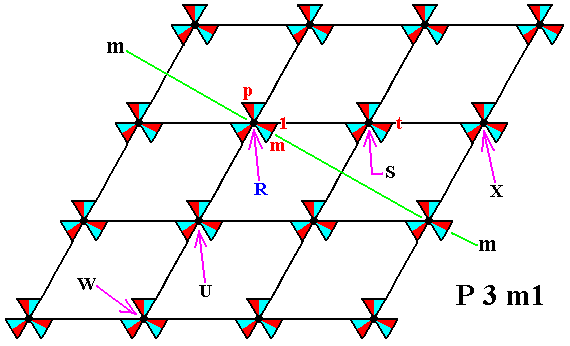
Figure 3b. Tri-radiate composed motifs are inserted into a hexagonal point lattice, such that the three mirror lines of those motifs do not coincide with the lattice lines (i.e. with the edges of the rhomb-shaped unit cell, as indicated in the Figure), resulting in a periodic pattern according to the Plane Group P3m1.
Each composed motif consists of three augmented motif units, while each augmented motif unit consists of two basic motif units (red and blue) representing elements of the group P3m1.
One such basic motif unit (of the composed motif at the lattice point R ) is chosen to represent the identity element 1 . A second basic motif unit is chosen to be the generator p , a third one is chosen to be the generator m , and a fourth basic motif unit (which is part of the composed motif at the point S ) is chosen to be the generator t .
One mirror line, the line m , is indicated.
The identity of the remaining basic motif units of the composed motif at the lattice point R can now be determined ( p3 = 1 ) :
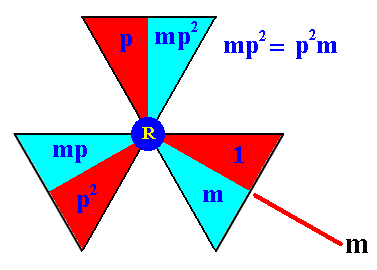
Figure 3c. The group elements of the composed motif at the point R .
Together they form the subgroup {1, p, p2 , m, mp, mp2} , having the structure of D3 .
The elements 1, p, p2 form a subgroup with the structure of C3 .
The elements 1, m form the subgroup C2 .
We will now produce the composed motif at the point S (Figure 3b). We'll do this by subjecting all the elements (basic motif units) of the composed motif at the point R to a translation t , i.e. we will form the left coset of the subgroup D3 (materialized as the composed motif at the point R) by the element t . See next Figure.
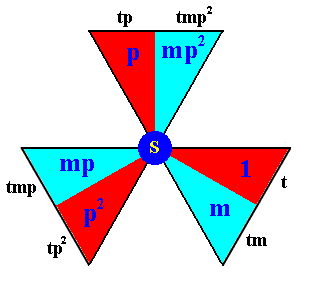
Figure 3d. The elements (basic motif units) of the composed motif at the lattice point S . They form the left coset of the D3 subgroup by the element t . The notations (i.e. identities) of the newly generated elements are placed at the perimeter of the image (i.e. outside the image).
Next we determine the elements of the composed motif at the lattice point U (See Figure 3b).
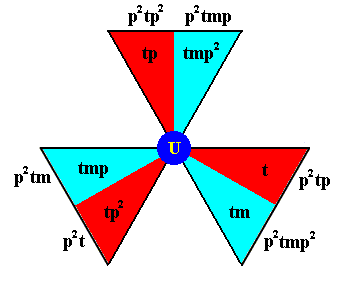
Figure 3e. Generation of the basic motif units of the composed motif at the lattice point U . The names of the newly generated elements are given at the perimeter of the image (i.e. outside the image).
The second and third row of composed motifs (Figure 3b) can now be completed by applying the translations . . . t-2, t-1, t, t2, t3, . . . etc.
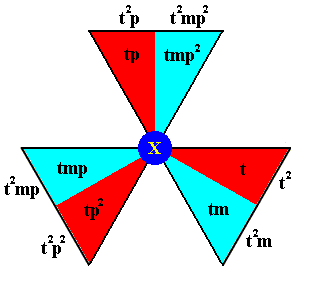
Figure 3f. Generation of the elements of the composed motif at the point X . Together they form the left coset of the subgroup D3 by the element t2 .
The notation of the newly generated elements is given at the perimeter of the image.
From this lastly obtained composed motif we can reach the fourth row (Figure 3b) of composed motifs (to be generated), by applying p2 to that lastly obtained composed motif. See next Figure.
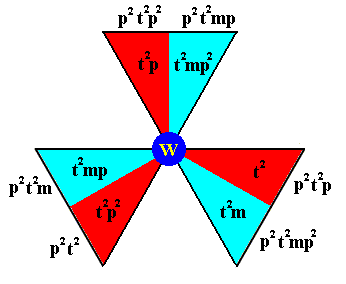
Figure 3g. Generation of the elements of the composed motif at the lattice point W . Together they form the left coset of the subgroup D3 by the element p2t2 .
The notation of the newly generated elements is given at the perimeter of the image.
The fourth row can now be completed by translations. Continuation of this procedure will generate in principle the whole group P3m1 , "in principle", because the order of the group is infinite.
Next we will generate this same group P3m1 by means of augmented motif units (instead of basic motif units as we just have done).
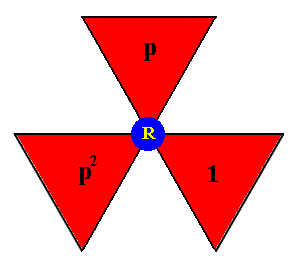
or
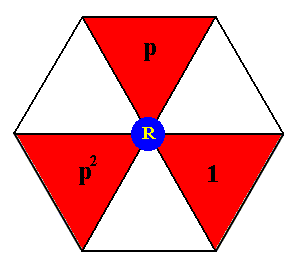
for that matter.
Because we now use augmented motif units, which themselves are symmetric, i.e. possess a mirror line, we do not need the generator m (i.e. an element resulting from a reflection of the initial element in a mirror line m ). The only generators we now need are p , which is an anticlockwise rotation of 1200 about the point R ( This generator is -- as augmented motif unit -- indicated in the above two images of the composed motif at the point R), and a (horizontal) translation t , represented by an augmented motif unit t . Also with respect to the augmented motif units, p3 = 1 holds. The augmented motif units are based on the subgroup {1, m} consisting of the basic motif units 1 and m .
Now our newly conceived motif units, the augmented motif units (consisting of two symmetrically related basic motif units), will be indicated by the same notation as was done above. The group P3m1 will then be generated by the augmented motif units p and t .
The next Figure shows the two chosen generators :
The 'element' p , represented by the augmented motif unit p , that results from the element (augmented motif unit) 1 (chosen to be the identity element, initial motif unit), by an anticlockwise rotation of 1200 about the point R .
The 'element' t , that results from the 'element' 1 by a translation t .
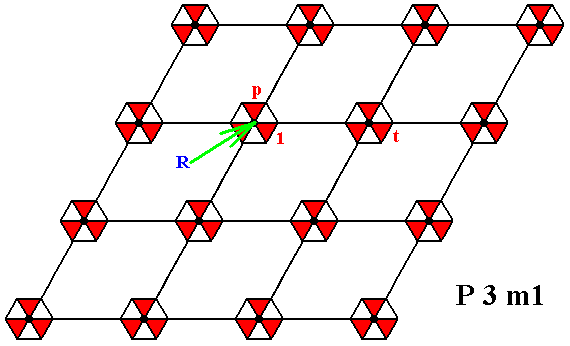
Figure 4. Two chosen generators p and t that can generate the whole P3m1 pattern.
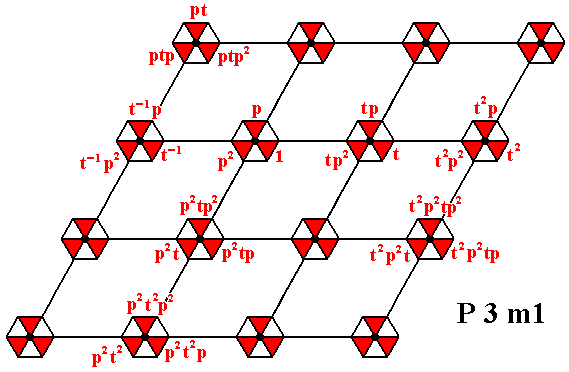
Figure 5. The whole P3m1 pattern can be produced by the generator elements p and t .
This is the last pattern of the 17 fundamental two-dimensional periodic patterns.
The motif we're now going to insert into a 2-D hexagonal lattice has the same point symmetry as the one we used for the exposition of Plane Group P3m1 above. But with respect to the connecting lines of the net our new motif is oriented differently : It is rotated 300 with respect to the one used earlier. See Figure 6.
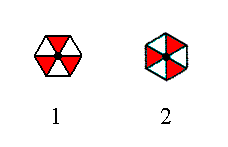
Figure 6.
(1). Orientation of the 3m motif, compatible with the Plane Group P3m1 (discussed above).
(2). Orientation of the 3m motif, compatible with the Plane Group P31m.
Both motifs (one for expressing the group P3m1, the other for expressing the group P31m) are placed in a same hexagonal net, i.e. a hexagonal net with rhomb-shaped meshes having two edges horizontally.
The 3m symmetry of both motifs corresponds to a D3 group structure.
Thus placing two-dimensional motifs with 3m symmetry into a (primitive) hexagonal net (2-D hexagonal lattice), such that the orientation of these motifs differs by 300 from that of the motifs of the Plane Group P3m1, yields a periodic pattern representing Plane Group P31m. See Figure 7.
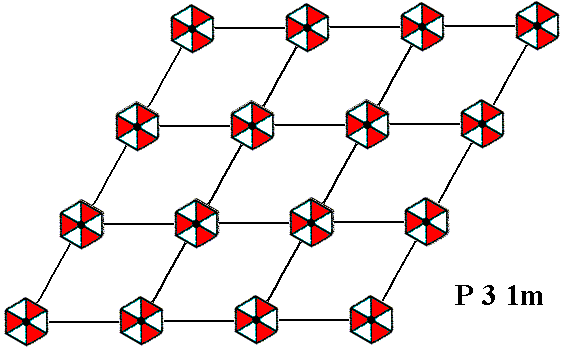
Figure 7. When motifs, having point symmetry 3m (i.e. having a 3-fold rotation axis and three equivalent mirror lines), are inserted in a (primitive) hexagonal net, in the way (i.e. the orientation) shown, a pattern of repeated motifs will emerge that represents Plane Group P31m .
Each (composed) motif consists of three augmented motif units, in such a way that the symmetry of the composed motif is 3m . Each augmented motif unit represents a subgroup or a coset.
The pattern must be conceived as extending indefinitely in two-dimensional space.
The total symmetry content of the Plane Group P31m is given in the next diagram.
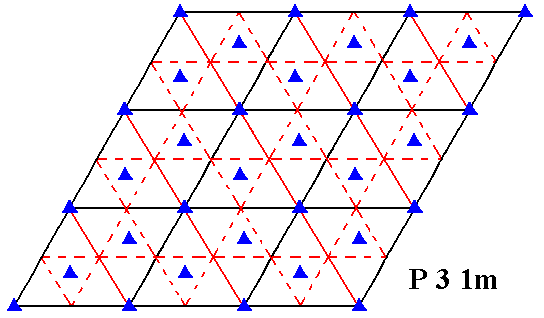
Figure 8. Total symmetry content of Plane Group P31m .
Mirror lines are indicated by solid lines (red and black).
Now we will show the generation of the group P31m by means of basic motif units that legitimately represent group elements (i.e. elements of the full group P31m). In Figure 7 we had motifs, each consisting of three units, making angles with each other of 1200, and providing the composed motif with 3m symmetry (Which is equivalent to a D3 group structure). But such a motif unit is still symmetric in itself, so in fact it is composed of still more basic motif units : It is an augmented motif unit. And indeed the basic units, as can be obtained by dividing the augmented motif units, do not have (and ought not to have) any symmetry at all. They're going to build up a symmetric pattern from scratch. They can legitimately represent group elements (i.e. elements of the full group P31m). The next image shows a composed motif, equivalent to the ones in Figure 7, but partitioned into six basic motif units.
This type of motif can perhaps be more clearly expressed as follows :

The two basic motif units composing an augmented motif unit (of which three together make up the full composed motif) can conveniently be distinguished by colors, provided we do not interpret the difference between colors as expressing an asymmetry. The two basic motif units, red and blue in the next Figures, are symmetrically related to each other :

The latter motifs we will now place in a hexagonal lattice (That lattice having the same orientation as that used for depicting the pattern of the group P3m1 ), resulting in the periodic pattern according to the group P31m. The effect is that both patterns, P31m and P3m1, have the same type of composed motif (and also of basic motif unit for that matter), but in each case those motifs are differenly orientated with respect to the lattice lines (i.e. the edges of the unit cell). This difference in orientation is 300.
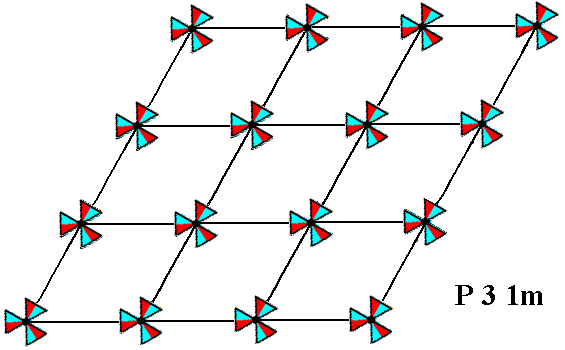
Figure 8a. Pattern according to the Plane Group P31m .
The (composed) motifs consist of six basic motif units (red and blue), each representing a group element (i.e. an element of the group P31m). The difference in color should not be interpreted as an asymmetry.
The pattern must be conceived as extending indefinitely in two-dimensional space.
The next Figure gives this same pattern. Some lattice points are marked : R, S, X, U, W. One basic motif unit (of the composed motif at point R) is chosen to be the initial motif unit, representing the identity element 1 of the group. Three other basic motif units are chosen as generators :
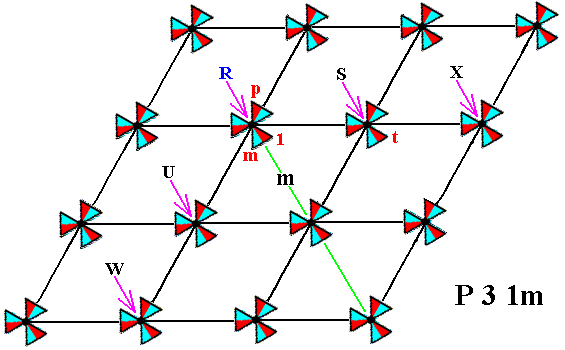
Figure 8b. Pattern according to the Plane Group P31m .
The initial motif unit, three generators and some lattice points are indicated.
The next Figure depicts an enlargement of the composed motif at the lattice point R. The initial basic motif unit, 1 , the generators p and m , and the mirror line m are indicated.
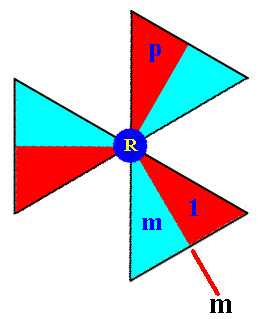
Figure 8c. Composed motif (consisting of six basic motif units) of the P31m pattern at the point R in Figure 8b.
The identity of the remaining basic motif units of the composed motif at the lattice point R can now be determined ( p3 = 1 ) :
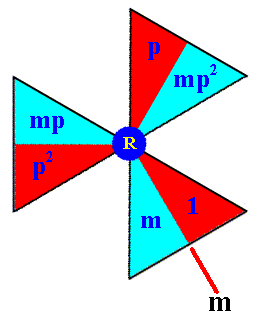
Figure 8d. The group elements of the composed motif at the point R .
Together they form the subgroup {1, p, p2 , m, mp, mp2} , having the structure of D3 .
The elements 1, p, p2 form a subgroup with the structure of C3 .
The elements 1, m form the subgroup C2 .
We will now produce the composed motif at the point S (Figure 8b). We'll do this by subjecting all the elements (basic motif units) of the composed motif at the point R to a translation t , i.e. we will form the left coset of the subgroup D3 (materialized as the composed motif at the point R) by the element t . See next Figure.
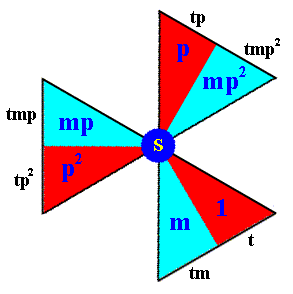
Figure 8e. The elements (basic motif units) of the composed motif at the lattice point S . They form the left coset of the D3 subgroup by the element t . The notations (i.e. identities) of the newly generated elements are placed at the perimeter of the image (i.e. outside the image).
Next we determine the elements of the composed motif at the lattice point U (Figure 8b).
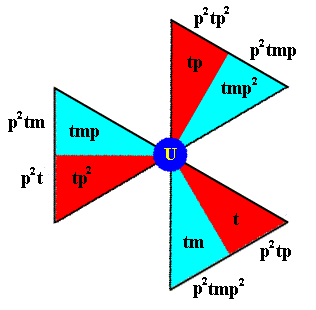
Figure 8f. Generation of the basic motif units of the composed motif at the lattice point U . The names of the newly generated elements are given at the perimeter of the image (i.e. outside the image).
The second and third row of composed motifs (Figure 8b) can now be completed by applying the translations . . . t-2, t-1, t, t2, t3, . . . etc.
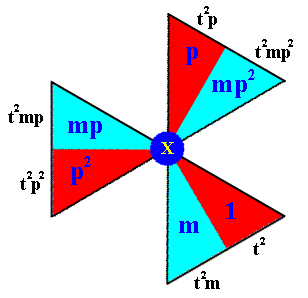
Figure 8g. Generation of the elements of the composed motif at the point X . Together they form the left coset of the subgroup D3 by the element t2 .
The notation of the newly generated elements is given at the perimeter of the image.
From this lastly obtained composed motif we can reach the fourth row (Figure 8b) of composed motifs (to be generated), by applying p2 to that lastly obtained composed motif. See next Figure.
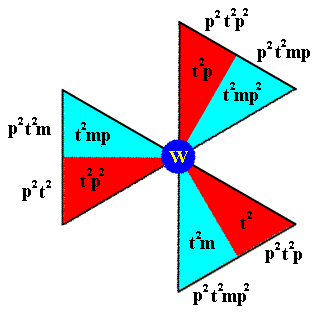
Figure 8h. Generation of the elements of the composed motif at the lattice point W . Together they form the left coset of the subgroup D3 by the element p2t2 .
The notation of the newly generated elements is given at the perimeter of the image.
The fourth row can now be completed by translations. Continuation of this procedure will generate in principle the whole group P31m , "in principle", because the order of the group is infinite.
What follows next is the generation of that same group P31m by means of augmented motif units.
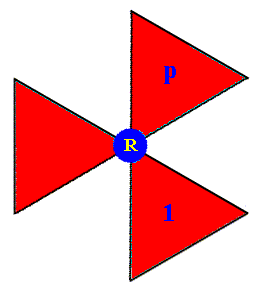
Figure 8i. Composed motif (at the lattice point R (For its position, see Figure 8b)), consisting of three augmented motif units. One is chosen to be the initial motif unit 1 , representing the identity element of the group P31m , another such augmented motif unit is chosen to be the generator p representing an anticlockwise rotation of 1200 about the lattice point R (See Figure 8b).
As a second generator we choose the horizontal translation t .
Because we now use augmented motif units to generate the group, we do not need the transformation m (reflection, see Figure 8b) anymore, so we can do it with two generators ( p and t ).
The next Figure shows the two chosen generators in the context of the lattice :
The 'element' (augmented motif unit) p , resulting from the 'element' (augmented motif unit) 1 , by an anticlockwise rotation of 1200 about the point R .
The 'element' t (augmented motif unit), resulting from the 'element' 1 by the translation t .
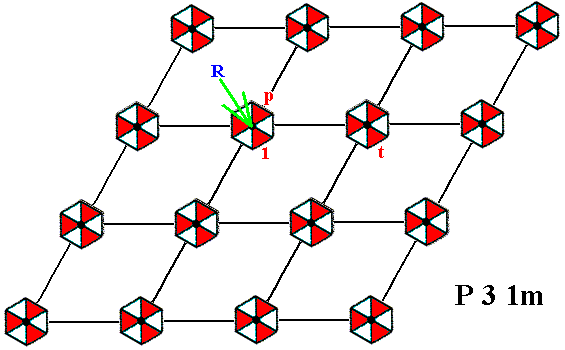
Figure 9. The two chosen generators p and t for the P31m pattern.
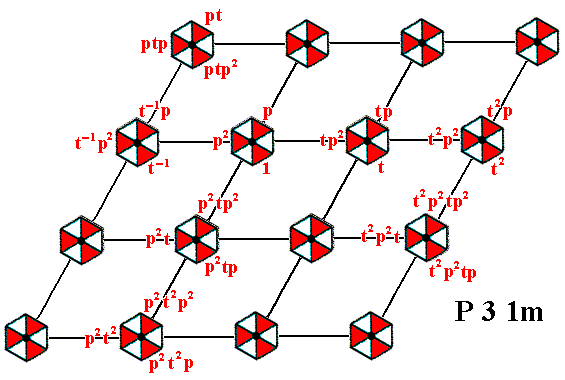
Figure 10. The whole P31m pattern can be produced by the generators p and t .
As can be seen from the above results, we can say the following :
This concludes our systematic synthetic group theoretic treatment of the 17 Plane Groups (i.e. their generation from generator elements, or from augmented motif units) describing the symmetry of two-dimensional infinite periodic patterns. Their consideration will throw much light on the symmetry of three-dimensional infinite periodic patterns, which occur in crystals, and are described by (the 230) Space Groups.
Outlook
After now having given a more or less general account of Group Theory (Part I -- XXIV), in the next document we continue this study, while (still) concentrating on the symmetry of two-dimensional patterns. First we will discuss subpatterns and subgroups of the 17 Plane Groups (all seventeen of which we have just treated globally above). Those subpatterns and subgroups will give us insight into the phenomena of layers as they occur in the growth of real (3-D) crystals, and in the phenomenon of symmetry-breaking or desymmetization (differentiation) occurring in natural processes and in (ornamental) art. But there are still more things that we should know about symmetry : The symmetry of the mentioned periodic patterns and also of their motifs, are all isometric symmetries, which means that they are transformations (in the present case transformations in the Euclidean Two-dimensional Plane E2 ) such that distances are preserved. When we generalize on that, we get the so-called similarity symmetries, in which distances are not preserved, while angles and shapes (still) are. A still further generalization leads to so-called conformal symmetries in which circles are preserved. In addition to isometric symmetries, the similarity and conformal symmetries -- which do not occur in crystals of whatever dimension, but do occur in organisms -- can provide a refinement and sophistication of quite a few Promorphological Categories, said differently, the study of the symmetries of two-dimensional patterns, including similarity and conformal symmetries, will deepen our insight in the shapes and structures of real crystals (isometries) and of organisms (isometries, similarity symmetries and conformal symmetries). With respect to organisms we will study their symmetries in the ensuing documents on Promorphology (starting after the Tectology Series).
When all this has been accomplished (i.e. the [group theoretic] study of the symmetries of two-dimensional patterns (periodic and non-periodic)), we are finally ready to embark on the symmetry theory of three-dimensional crystals, i.e. we study the pointgroups, lattices and space groups of three-dimensional (single) crystals by means of Group Theory.
When this is all done we conclude our study of three-dimensional crystals with discussions about chemical lattice types, twinning, and the thermodynamics of crystal growth. (And after this, the mentioned documents about Organic Tectology (general doctrine of structure in organisms) and (Organic) Promorphology (general doctrine of symmetry in organisms : the stereometric basic forms of organisms) follow (and which are already finished, although Promorphology must still become group theoretically refined).
The documents about the subpatterns and subgroups of two-dimensional periodic patterns, about the similarity and conformal symmetries of two-dimensional (non-periodic) patterns, and about the symmetry theory of three-dimensional crystals, are to be found by clicking the next "To continue click HERE " link. But, of course one can skip all this, and directly proceed (by using the left frame of the present document) to the documents on lattice types, twins and crystal thermodynamics (which are however not yet finished), or directly to the Tectology and Promorphology documents (which are finished, except some group theoretic polishing up).
In order not to loose track of this admittedly complicated website, we will tabulate systematically the context of the previous documents on group theory, the present documents, and the documents that follow after having clicked the To Continue link below, and, finally, what follows after those documents (The complexification of LINKING is partially due to the limited available space on the webserver, that has caused us to place a whole intermediate series of documents (concerning the sequel of two-dimensional patterns and the symmetry theory of three-dimensional crystals) on another webserver, implying that we must link to that server and than, later, back again to the present server).
So the context and order of the relevant documents on symmetry is as follows :
The next To continue --- link brings us to the Second Series of documents (second webserver) that continues the group theoretic treatment of two-dimensional patterns and the symmetry theory of three-dimensional crystals (So also the link SEQUEL TO GROUP THEORY in the left frame).
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals, with -- for the time being -- extra emphasis on two-dimensional (periodic and non-periodic) patterns.
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals
back to Part XV of the theoretical preparation to the study of 3-D crystals
back to Part XVI of the theoretical preparation to the study of 3-D crystals
back to Part XVII of the theoretical preparation to the study of 3-D crystals
back to Part XVIII of the theoretical preparation to the study of 3-D crystals
back to Part XIX of the theoretical preparation to the study of 3-D crystals
back to Part XX of the theoretical preparation to the study of 3-D crystals
back to Part XXI of the theoretical preparation to the study of 3-D crystals
back to Part XXII of the theoretical preparation to the study of 3-D crystals
back to Part XXIII of the theoretical preparation to the study of 3-D crystals