e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Sequel to Infinite two-dimensional periodic patterns

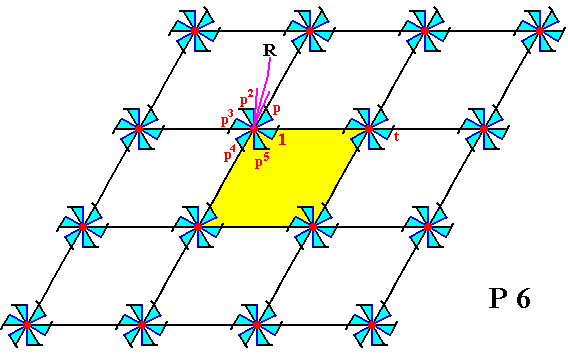
Figure 1. Inserting composed motifs, possessing point symmetry 6 , into a 2-D hexagonal point lattice, yields a periodic pattern representing Plane Group P6 .
Each motif consists of six motif units. Each motif unit is in itself asymmetric and thus can represent a group element (wherever that unit occurs in the pattern). The point R (indicated by the arrow) is the location of a 6-fold rotation axis in the pattern (there are more such axes).
The motif unit labelled 1 is chosen as the initial motif unit and as such represents the identity element of the group.
The motif unit labelled p is generated when the initial motif unit is subjected to an anticlockwise rotation of 600 about the point R . This motif unit, being a transformation, is chosen as one of the two generators of the group.
The motif unit p2 represents an anticlockwise rotation of 1200 about the point R .
The motif unit p3 represents an anticlockwise rotation of 1800 about the point R .
The motif unit p4 represents an anticlockwise rotation of 2400 about the point R .
The motif unit p5 represents an anticlockwise rotation of 3000 about the point R .
The motif unit p6 represents an anticlockwise rotation of 3600 about the point R , which is equivalent to a rotation of 00. The latter implies p6 = 1.
The motif unit labelled t represents a translation, and is chosen as the second generator.
The group P6 can be generated by the two chosen generators, p and t , i.e. they can (by combining) generate all remaining group elements, and with them all motif units that represent them.
A unit cell is indicated (yellow).
The pattern must be conceived as indefinitely extended in 2-D space.
The next Diagram depicts the total symmetry content of the Plane Group P6.
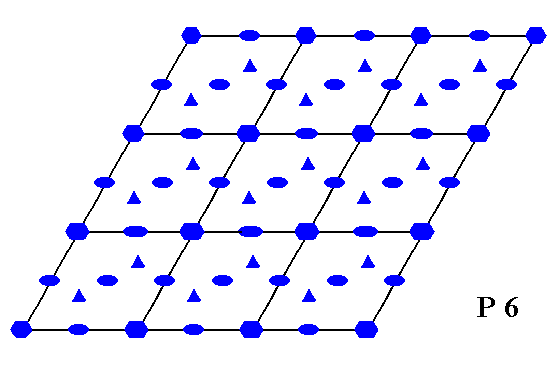
Figure 2. Total symmetry content of the Plane Group P6 .
A small solid ellipse indicates the position of a 2-fold rotation axis.
A small solid triangle indicates the position of a 3-fold rotation axis.
A small solid hexagon indicates the position of a 6-fold rotation axis.
The next Figure again gives the P6 pattern, and demonstrates the six-fold symmetry at the point R (as indicated in Figure 1).
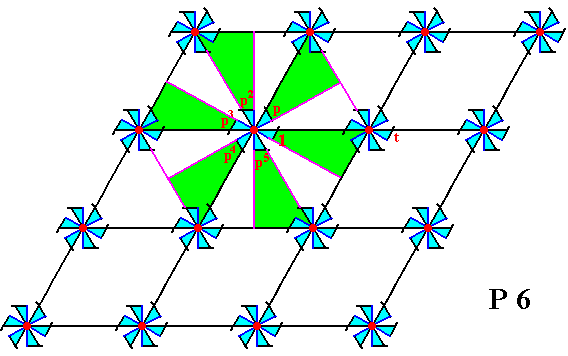
Figure 3. Six-fold symmetry of the infinite P6 pattern at the point R (There are of course many such points in the pattern).
The motif unit denoted 1 is chosen as initial motif unit, representing the identity element of the group.
The motif unit denoted p is chosen as one of the two generators of the group. The other generator is chosen to be the translation t .
The transformation p generates (from the element 1 ) the elements p , p2 , p3 , p4 and p5 . And p6 = 1.
The next Figure shows how some group elements -- represented by motif units -- are generated from the elements together representing the initial composed motif. In that composed motif the elements p2 , p3 , p4 , and p5 are produced by the generator p . And from these elements we can generate a second composed motif to the right of it, by subjecting them to the second generator of the group, the translation t . From this new composed motif we can produce yet another new composed motif by subjecting its motif units to the element p , which is an anticlockwise rotation of 600 about the point R (as indicated in Figure 1). The resulting composed motif we can see as the second one in the first row of composed motifs (See next Figure). And from this lastly obtained composed motif we can produce the other composed motifs in that first row by applying translations :
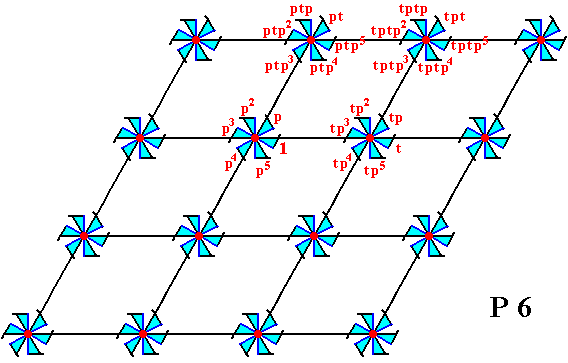
Figure 4. Generation of several composed motifs from the initial composed motif.
From the third composed motif in the second row we can produce the fourth composed motif in that same row by applying the translation t , and from this new composed motif in turn we can produce a composed motif in the fourth row (the second one in that row) by applying the transformation p4 , which is an anticlockwise rotation of 2400 about the point R (as indicated in Figure 1). This fourth row can then be completed by applying translations.
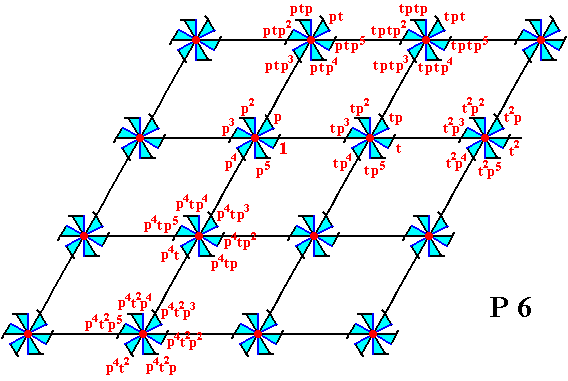
Figure 5. Generation of two more composed motifs (in addition to one obtained by a translation) of the pattern according to the Plane Group P6.
With the Plane Groups P1, P2, P3, P4 and P6, we have discussed the 'direct' plane groups, that is groups in which only rotations and translations occur.
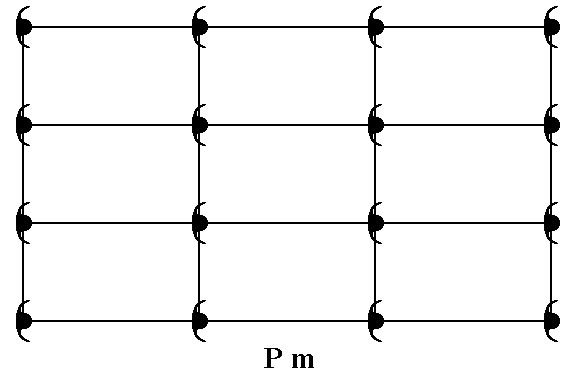
Figure 6. When we place motifs, possessing a point symmetry m, on the nodes of a primitive rectangular net, we get a pattern that represents Plane Group Pm.
The total symmetry content of the Plane Group Pm is depicted in the next Figure.
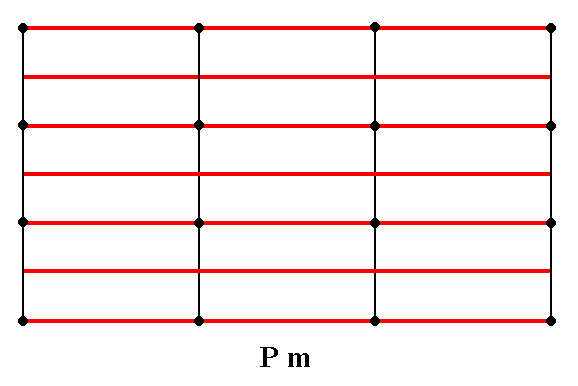
Figure 7. The total symmetry content of the Plane Group Pm.
The only symmetry elements this Group has are mirror lines parallel to the y direction. They are indicated by red lines.
For clarity the nodes of the lattice are indicated (black dots).
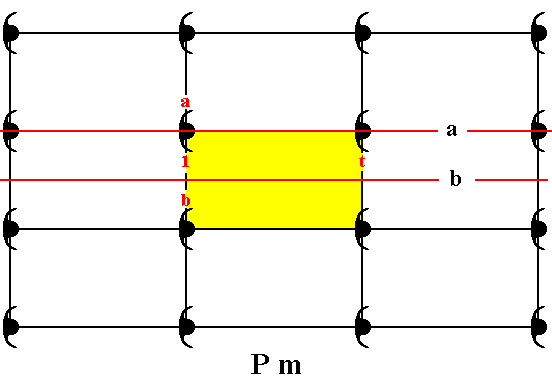
Figure 8. The Pm pattern can be generated by two parallel mirror lines, a and b , and a translation t .
In the present Figure each group element is represented by a motif unit, which is -- as before -- a comma. Two partly overlapping commas form a composed motif, that has as its only symmetry element a mirror line.
One motif unit is chosen as initial motif unit, representing the identity element of the group, denoted 1 .
Three generators are needed to produce all group elements, or, correspondingly, to produce all motif units, and thus to produce the whole Pm pattern.
The motif unit a , which is the image of the initial motif unit under the reflection a , is chosen as a generator.
The motif unit b , which is the image of the initial motif unit under the reflection b , is chosen as a second generator.
The motif unit t , which is the image of the initial motif unit under the translation t , is chosen as a third generator.
A unit cell is indicated (yellow). The pattern must be conceived as extending indefinitely in two-dimensional space.
We will now give the Pm pattern again and label some motif units such, as representing generated group elements.
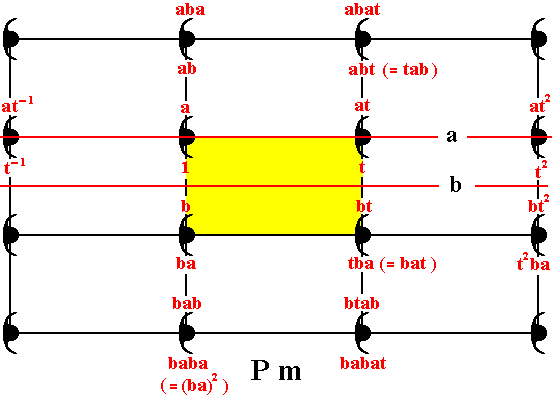
Figure 9. Generation of some group elements (represented by motif units) of the group Pm by the generators a, b and t .
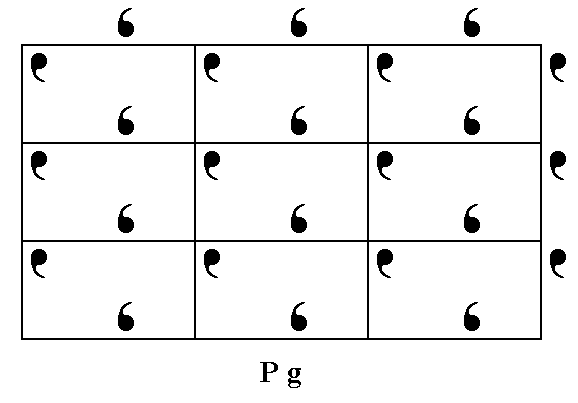
Figure 10. Assymmetric motifs (in fact motif units) placed in a primitive rectangular net, such that they alternate along the y edges (horizontal) of the meshes, produce a pattern that represents the Plane Group Pg .
The only symmetry elements the Plane Group Pg possesses, are simple translations (in the x (vertical) and y (horizontal) directions) and glide lines parallel to the y direction.
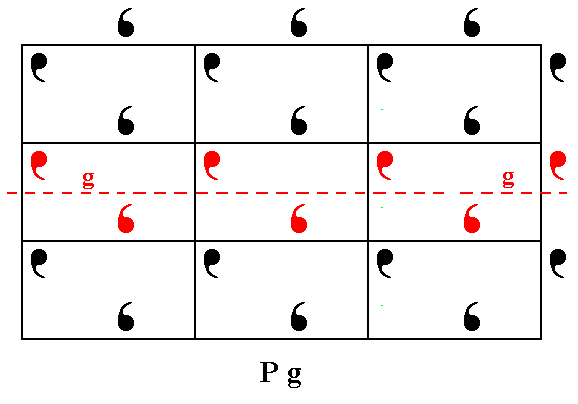
Figure 11. Patterns representing Plane Group Pg have glide lines parallel to the y direction. One of them is shown.
The total symmetry content of the Plane Group Pg is shown in the next Figure.
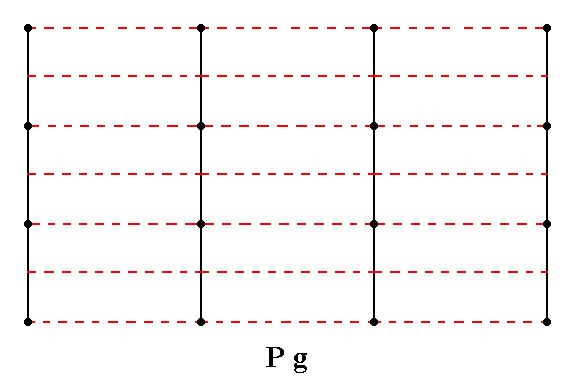
Figure 12. Total symmetry content of the Plane Group Pg.
Glide lines are indicated by red dashed lines. For clarity the nodes of the net are indicated (black dots).
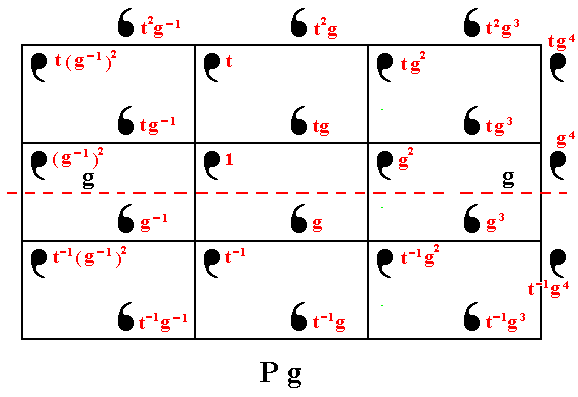
Figure 13. The pattern representing Plane Group Pg consists of motif units (commas). They can be generated from a given initial motif unit, denoted 1 , by two genrators g (a horizontal glide reflection) and t (a vertical translation).
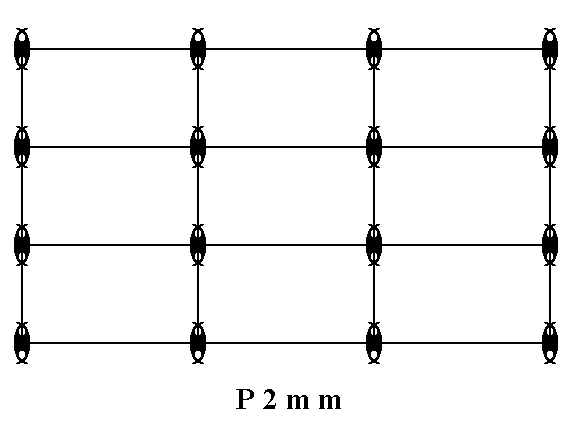
Figure 14. Placing motifs with 2mm point symmetry in a primitive rectangular 2-D lattice creates a periodic pattern of these motives representing the Plane Group P2mm. The pattern must be conceived as extending indefinitely in two-dimensional space.
The total symmetry content of this Plane Group is given in Figure 15.
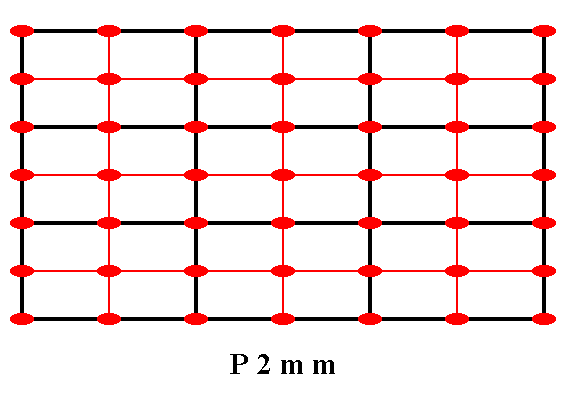
Figure 15. The total symmetry content of the Plane Group P2mm.
Solid lines (black and red) indicate mirror lines.
Small red solid ellipses indicate 2-fold rotation axes perpendicular to the plane of the drawing.
The next Figure again gives the P2mm patttern, and prepares for letting it be generated.
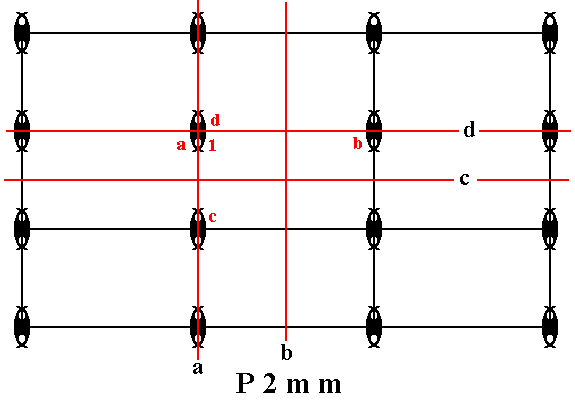
Figure 16. Each (composed) motif of our version of a P2mm pattern consists of four motif units (commas) partially overlapping, such that the symmetry of the resulting composed motif is 2mm . As before, each motif unit represents a group element.
One such motif unit is chosen to be the initial motif unit, representing the identity element of the group, and denoted 1 .
A second motif unit, denoted a , is chosen as a first generator. It is produced from 1 by the mirror line a .
A third motif unit, denoted b , is chosen as a second generator. It is produced from 1 by the mirror line b .
A fourth motif unit, denoted c , is chosen as a third generator. It is produced from 1 by the mirror line c .
Finally, a fifth motif unit, denoted d , is chosen as a fourth generator. It is produced from 1 by the mirror line d .
The next Figure shows how the motif units -- representing group elements of the group P2mm -- are generated by the generators a, b, c and d .
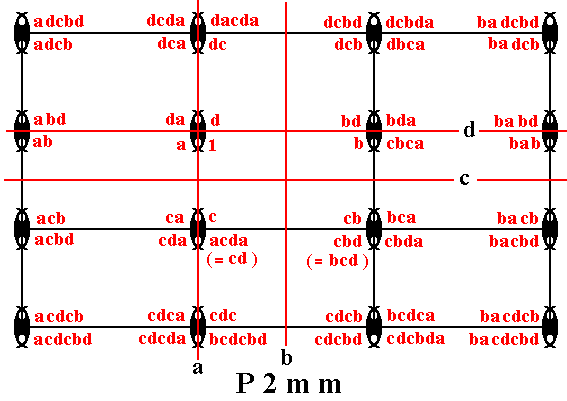
Figure 17. Generation of the group elements of the group P2mm by the generators a, b, c, d .
The primitive Rectangular Net can also accommodate motifs possessing only 2-fold rotational symmetry, i.e. motifs having a point symmetry 2. Figure 18 shows a regular array of such motifs, based on a primitive rectangular net. The pattern represents the Plane Group P2gg.
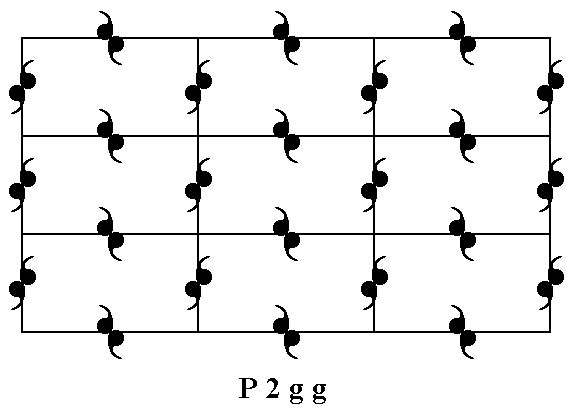
Figure 18. Motifs possessing only a 2 symmetry can be accommodated in a primitive 2-D rectangular lattice, resulting in a periodic structure. This structure must be conceived as extending indefinitely in two-dimensional space.
The total symmetry content of the Plane Group P2gg is given in the next Figure.
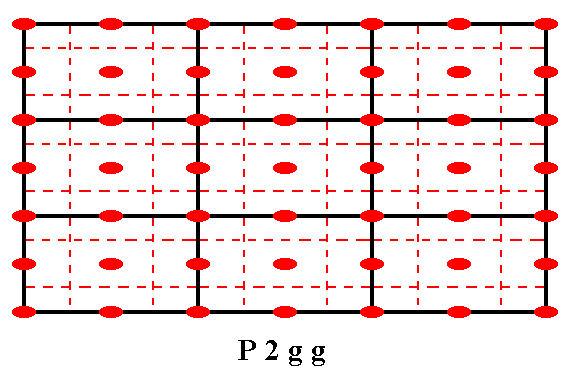
Figure 19. The total symmetry content of the Plane Group P2gg.
2-fold rotation axes perpendicular to the plane of the drawing are indicated by small solid red ellipses.
Glide lines are indicated by dashed red lines.
Mirror lines are absent.
The next Figure ilustrates one of the glide reflections present in the P2gg pattern.
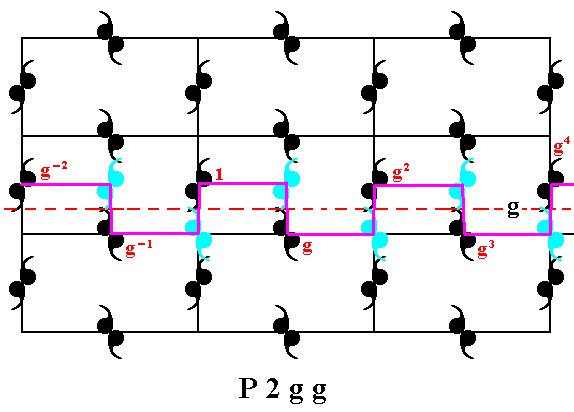
Figure 20. A glide reflection g in the P2gg pattern is indicated. Each (composed) motif consists of two motif units (commas), such that the composed motif possesses 2-fold rotational symmetry. One motif unit is chosen to figure as the initial motif unit from which the pattern is produced by (three) generators. Each motif unit represents a group element.
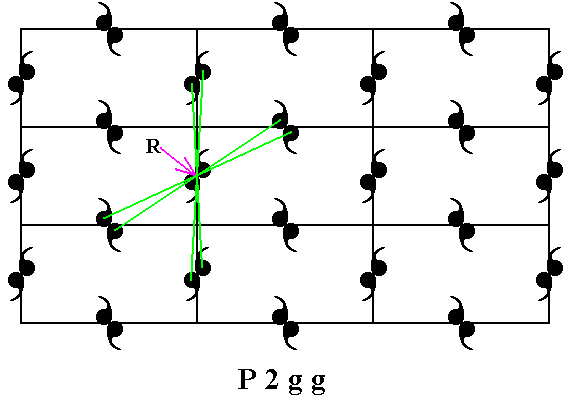
Figure 21. A 2-fold rotational symmetry is present at the point R (there are more such points). We will choose this rotation (1800 about R ) as one of the three generators of the group P2gg.
The next Figure indicates, in addittion to the one generator already chosen, the other two (chosen) generators. These three together can generate the whole pattern (and as such this repesents the generation of the group P2gg ).
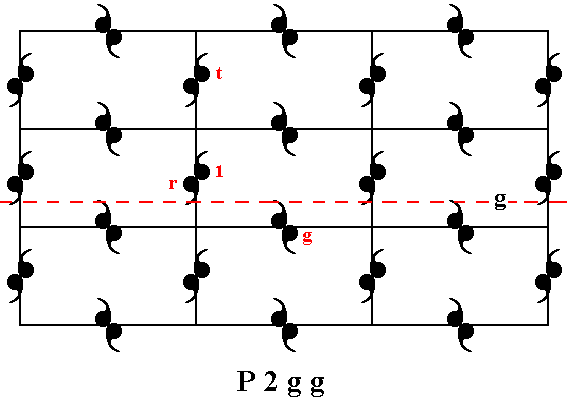
Figure 22. The three chosen generators of the group P2gg :
The glide reflection g , represented by the motif unit g , the translation (vertical) t , represented by the motif unit t and the half-turn r represented by the motif unit r .
The next Figure shows how a number of group elements (represented by motif units) can be generated by means of the three chosen generators. Eventually all elements of the group can be generated.
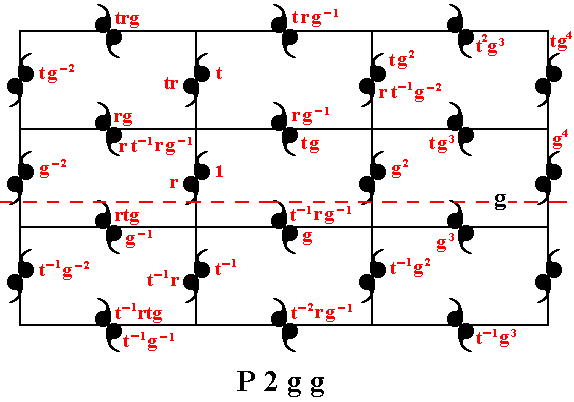
Figure 23. Generation of the P2gg pattern by using the generators g , t , r .
(For reasons of clarity of the drawing not all motif units are provided with their corresponding symbol).
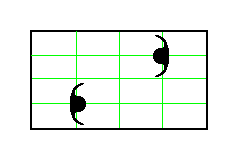
Figure 24. Two motifs, each having point symmetry m , are placed in a mesh of a primitive rectangular lattice, as indicated.
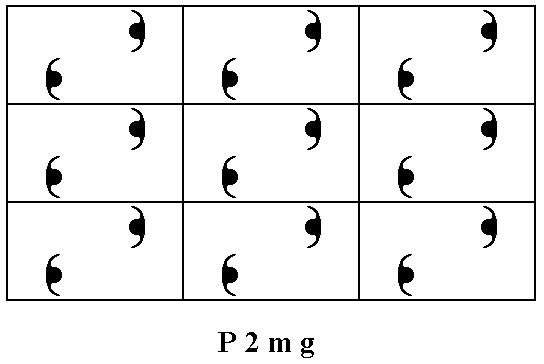
Figure 25. If we place two motifs, having a symmertry of m , in each mesh of the primitive net, as indicated in Figure 24, then we will obtain a periodic pattern of motifs representing the Plane Group P2mg. The pattern must be conceived as extending indefinitely in two-dimensional space.
The total symmetry content of Plane Group P2mg is given in the next Figure.
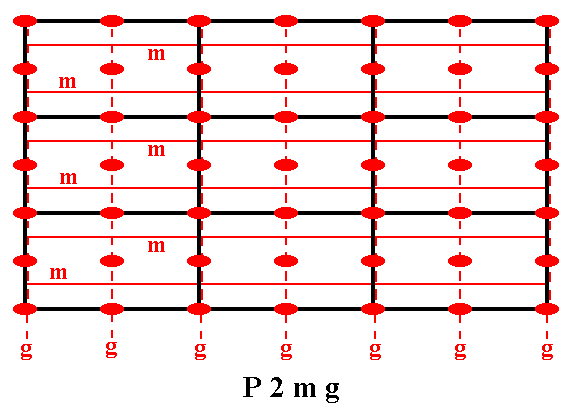
Figure 26. Total symmetry content of the Plane Group P2mg.
Solid red lines indicate mirror lines.
Small solid red ellipses indicate 2-fold rotation axes perpendicular to the plane of the drawing.
The glide lines are all parallel to the x direction, some going through the mid-line of the rectangles, others coinciding with their sides. They are indicated by red dashed lines.
The P2mg pattern, as realized in Figure 25, consists of composed motifs. Each such motif itself consists of two motif units -- commas -- which represent group elements (and each group element is a symmetry transformation of the pattern).
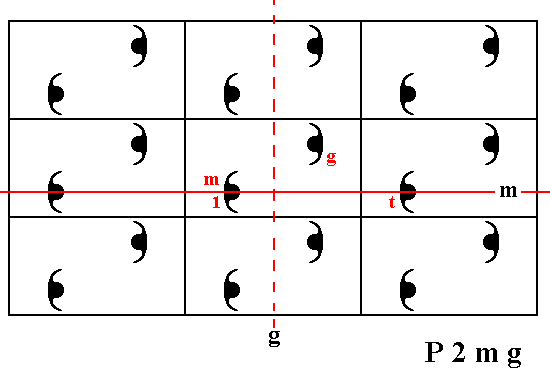
Figure 27. Three generators for the P2mg pattern are indicated.
The next Figure shows how all the group elements can be generated from the three generators g , m and t .
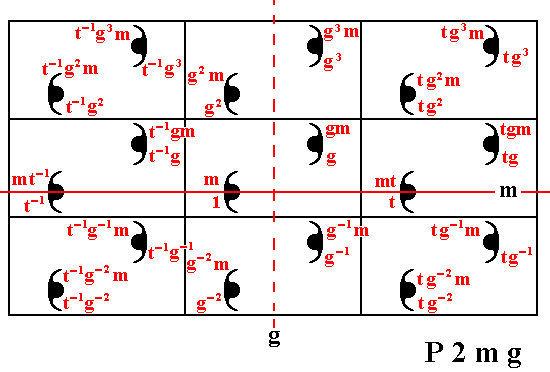
Figure 28. Generation of the P2mg pattern from the three generators.
In the next document we will continue our group theoretic study of infinite two-dimensional periodic patterns.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals
back to Part XV of the theoretical preparation to the study of 3-D crystals
back to Part XVI of the theoretical preparation to the study of 3-D crystals
back to Part XVII of the theoretical preparation to the study of 3-D crystals
back to Part XVIII of the theoretical preparation to the study of 3-D crystals
back to Part XIX of the theoretical preparation to the study of 3-D crystals
back to Part XX of the theoretical preparation to the study of 3-D crystals
back to Part XXI of the theoretical preparation to the study of 3-D crystals