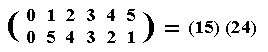
e-mail :

Sequel to Group Theory
Automorphisms of C6
To study the automorphisms of the Cyclic Group C6, let us first figure out how its group table should look like.
The Cyclic Group of order 6, C6, can be realized in several ways. We choose it to be realized in the direct symmetries of the regular hexagon, i.e. all the rotations about its center that map it onto itself. These rotations are 0 = 00, p = p1 = 600, p2 = 1200, p3 = 1800, p4 = 2400 and p5 = 3000, where p6 = 3600 = 0 (= p0). And 1 is the identity element.
The group operation will be the successive execution of two rotations.
Well if we want to know the product of, say, p3 and p2, then we must first rotate 1800 and then rotate the result by 1200, resulting in a total rotation of 1800 + 1200 = 3000 = p5.
So p3p2 = p5.
In the same way we will find that p4p3 is equal to a rotation of 2400 + 1800 = 4200 = 3600 + 600 = p6p = 0p = p (0 is the identity element).
The reader can check that in combining rotations we must add the exponents modulo 6, which means that we just add the exponents, but when the resulting exponent is 6 or above 6, we must subtract 6 and continue to subtract it till the result is smaller than 6. And this means that we can represent the elements of the Cyclic Group C6 by just the exponents of p : 0, 1, 2, 3, 4 and 5.
The set of these elements {0, 1, 2, 3, 4, 5}, together with the group operation addition modulo 6, forms the group C6. And we can now construct its group table :
| + mod 6 | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
16 = 1 + 1 + 1 + 1 + 1 + 1 = 0
56 = 5 + 5 + 5 + 5 + 5 + 5 = 30 = 0
So the period of element 1 and of element 5 is 6.
23 = 2 + 2 + 2 = 0
43 = 4 + 4 + 4 = 0
So the period of element 2 and 4 is 3.
32 = 3 + 3 = 0
So the period of element 3 is 2.
If we now want to find automorphisms of this group we must look for one or more rearragements of the elements such that the structure of the group table remains unchanged. Indeed the elements 1 and 5 can be so interchanged because they have the same period (and thus not affecting the table structure when they replace each other).
By the same reason the elements 2 and 4 can be so interchange.
Those interchanges, however, imply each other, so there is in fact only one rearrangement possible. Let us demonstrate this.
All elements of our group can be expressed in terms of the element 5 :
0 = 6 + 6 + 6 + 6 + 6 = 30 = 5 + 5 + 5 + 5 + 5 + 5 = 56.
1 = 5 + 5 + 5 + 5 + 5 = 55.
2 = 5 + 5 + 5 + 5 = 54.
3 = 5 + 5 + 5 = 53.
4 = 5 + 5 = 52.
5 = 5 = 51.
52 = 5 + 5 = 4
12 = 1 + 1 = 2
So when 5 and 1 are interchanged, so are 4 and 2.
53 = 5 + 5 + 5 = 3
13 = 1 + 1 + 1 = 3
So when 5 and 1 are interchanged, nothing happens with the position of 3.
54 = 5 + 5 + 5 + 5 = 2
14 = 1 + 1 + 1 + 1 = 4
So when 5 and 1 are interchanged, so are 2 and 4.
55 = 5 + 5 + 5 + 5 + 5 = 1
15 = 1 + 1 + 1 + 1 + 1 = 5
So when 5 and 1 are interchanged, so 1 and 5.
56 = 5 + 5 + 5 + 5 + 5 + 5 = 30 = 6 + 6 + 6 + 6 + 6 = 0
16 = 1 + 1 + 1 + 1 + 1 + 1 = 0
So when 5 and 1 are interchanged, nothing happens with the element 0.
So indeed if we interchange 5 and 1, then 2 and 4 must also be interchanged, and these are the only interchanges that will not affect the table structure, because 5 and 1 are of the same period, namely 6, while 4 and 2 are also of the same period, namely 3. So the only (extra) automorphism of the group C6 consists of the interchange of the elements 1 and 5 (and at the same time that of the elements 2 and 4). This interchange can be expressed as a permutation of six objects (in our case the six elements of the group C6), a permutation consisting of two transpositions :
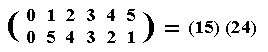
A "No rearrangement at all" can be represented by the identity permutation of the same six objects. So we have, with respect to the structure-preserving rearrangements of the elements of the group C6, two permutations in all :
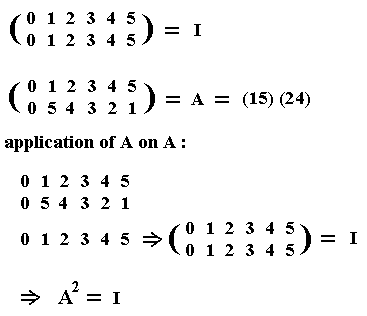
And these two permutations, representing the two automorphisms possible for C6, i.e. the permutations I (identity) and A, themselves form a cyclic group of order 2, namely C2 :
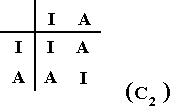
So the automorphism group of C6 is C2.
The table for the automorphism (corresponding to permutation A) of C6 is as follows :
| + mod 6 | 0 | 5 | 4 | 3 | 2 | 1 |
| 0 | 0 | 5 | 4 | 3 | 2 | 1 |
| 5 | 5 | 4 | 3 | 2 | 1 | 0 |
| 4 | 4 | 3 | 2 | 1 | 0 | 5 |
| 3 | 3 | 2 | 1 | 0 | 5 | 4 |
| 2 | 2 | 1 | 0 | 5 | 4 | 3 |
| 1 | 1 | 0 | 5 | 4 | 3 | 2 |
Let us compare the two automorphisms of C6, the one according to the identity permutation I of the elements of the group, and the other according to the permutation A of the elements:
Identity I :
| + mod 6 | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
| + mod 6 | 0 | 5 | 4 | 3 | 2 | 1 |
| 0 | 0 | 5 | 4 | 3 | 2 | 1 |
| 5 | 5 | 4 | 3 | 2 | 1 | 0 |
| 4 | 4 | 3 | 2 | 1 | 0 | 5 |
| 3 | 3 | 2 | 1 | 0 | 5 | 4 |
| 2 | 2 | 1 | 0 | 5 | 4 | 3 |
| 1 | 1 | 0 | 5 | 4 | 3 | 2 |
As one can see, the structure of the two tables is identical -- notice the positions of the identities, and the alignments of the successive elements along the NE--SW diagonal of the tables -- and so establish them as automorphisms.
Automorphisms of non-Abelian groups
When it comes to non-Abelian groups, i.e. to groups in which at least one pair of elements do not commute -- when these elements are, say, a and b, then ab is not equal to ba -- we find that they are usually much more interesting from the point of view of automorphisms. The non-Abelian group of lowest possible order (Recall that the order of a group is equal to the number of its elements) is D3 (which can be realized for instance as the group of all the symmetries -- rotations and reflections -- of the Equilateral Triangle). The table for D3 is reproduced below, with the periods of each element listed.
| 1 | p | q | a | b | c | period | ||
| 1 | 1 | p | q | a | b | c | 1 | |
| p | p | q | 1 | b | c | a | 3 | |
| q | q | 1 | p | c | a | b | 3 | |
| a | a | c | b | 1 | q | p | 2 | |
| b | b | a | c | p | 1 | q | 2 | |
| c | c | b | a | q | p | 1 | 2 |
Of course this table can be interpreted as the identity automorphism, according to the following permutation of the elements of the group (because the identity element is always the sole element with period 1, it cannot interchange with any other element, and so does not partake in the permutations expressing automorphisms) :
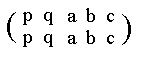
The first possibility for an automorphism, in addition to the identity automorphism, that may occur to us is the interchange of the elements p and q of period 3 (This indeed is the only automorphism for the subgroup {1, p, q}). We should find that, in order to preserve structure, the interchange of p and q would also need to be accompanied by an interchange of one pair of a, b and c (This is explained further down). For example in the case when a and c are interchanged, we obtain the automprphism :
1 -- 1
p -- q
q -- p
a -- c
b -- b
c -- a
which can be expressed by the following permutation of the elements of the group :
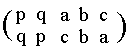
and by the table :
| 1 | q | p | c | b | a | ||
| 1 | 1 | q | p | c | b | a | |
| q | q | p | 1 | b | a | c | |
| p | p | 1 | q | a | c | b | |
| c | c | a | b | 1 | p | q | |
| b | b | c | a | q | 1 | p | |
| a | a | b | c | p | q | 1 |
We see that the structure of the two tables is identical.
There are still two other automorphisms of this group. In addition to the interchange of p and q we can interchange a and b (instead of a and c), or b and c. The first of these is according to the following permutation of the elements of the group :
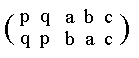
The automorphism itself is accordingly :
1 -- 1
p -- q
q -- p
a -- b
b -- a
c -- c
Its group table is :
| 1 | q | p | b | a | c | ||
| 1 | 1 | q | p | b | a | c | |
| q | q | p | 1 | a | c | b | |
| p | p | 1 | q | c | b | a | |
| b | b | c | a | 1 | p | q | |
| a | a | b | c | q | 1 | p | |
| c | c | a | b | p | q | 1 |
The other automorphism is :
1 -- 1
p -- q
q -- p
a -- a
b -- c
c -- b
which can be expressed by the following permutation :
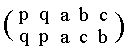
and its table is :
| 1 | q | p | a | c | b | ||
| 1 | 1 | q | p | a | c | b | |
| q | q | p | 1 | c | b | a | |
| p | p | 1 | q | b | a | c | |
| a | a | b | c | 1 | p | q | |
| c | c | a | b | q | 1 | p | |
| b | b | c | a | p | q | 1 |
Further there is of course another type of automorphism that would result from a cyclic permutation of a, b and c, namely the two permutations :
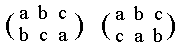
In the first of these two cases, we do not have to interchange p and q, for in the original table we have pa = b and since the automorphism replaces a by b and b by c, we get pb = c, and indeed we see in the table that pb = c (and qb is not c), so it follows that p and q must evidently be retained in their original positions.
Also in the second of these two cases we do not have to interchange p and q, for in the original table we have pb = c, and the automorphism replaces b by a, and c by b, so we get pa = b, and indeed the table says that pa = b, while qa is not b (so p and q cannot be interchanged without destroying the structure).
So the first of these automorphisms is :
1 -- 1
p -- p
q -- q
a -- b
b -- c
c -- a
which has been expressed by the permutation :
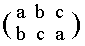
Its table is :
| 1 | p | q | b | c | a | ||
| 1 | 1 | p | q | b | c | a | |
| p | p | q | 1 | c | a | b | |
| q | q | 1 | p | a | b | c | |
| b | b | a | c | 1 | q | p | |
| c | c | b | a | p | 1 | q | |
| a | a | c | b | q | p | 1 |
The second of these two automorphisms is :
1 -- 1
p -- p
q -- q
a -- c
c -- b
b -- a
which has been expressed by the permutation :
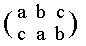
Its table is :
| 1 | p | q | c | a | b | ||
| 1 | 1 | p | q | c | a | b | |
| p | p | q | 1 | a | b | c | |
| q | q | 1 | p | b | c | a | |
| c | c | b | a | 1 | q | p | |
| a | a | c | b | p | 1 | q | |
| b | b | a | c | q | p | 1 |
So the automorphisms of the group D3 are according to (a group of) permutations of the group elements, and these permutations can be interpreted geometrically as representing all the symmetries of the Equilateral Triangle expressed as permutations of its vertices a, b and c, which means that the group of automorphisms of the group D3 is (also) D3. A reflection of this triangle across a bisector is equivalent to flipping this triangle over through the third dimension about that same bisector, and thus having 'top' and 'bottom' of the triangle, represented by p and q respectively, interchanged :
a b c p q (identity, rotation of 00 or (a multiple of) 3600))
c b a q p (reflection in the bisector through vertex b, or flip about this bisector)
b a c q p (reflection in the bisector through vertex c, or flip about this bisector)
a c b q p (reflection in the bisector through vertex a, or flip about this bisector)
b c a p q (anticlockwise rotation by 1200, vertex a goes to position b, etc.)
c a b p q (anticlockwise rotation by 2400, vertex a goes to position c, etc.)
So (the condition) pq can be interpreted as the triangle not being flipped over, while qp can be interpreted as the triangle flipped over. And when the triangle is flipped over, the directions of the rotations are reversed.
Indeed p and q can represent rotations of the equilateral triangle, namely p as an anticlockwise rotation of 1200, and q as an anticlockwise rotation of 2400. The latter is however the same as a clockwise rotation of 1200. This means that q = p-1. And in the same way p = q-1. Now it is easily seen that when we interchange p and q, we reverse the direction of rotation, but this only comes about when the triangle is reflected across one of its bisectors, i.e. when it is flipped over across one of its bisectors, and this corresponds to interchanging either a with b, or a with c, or b with c.
The highligted parts of the above permutations represent all possible permutations of three objects (here the objects a, b and c). These six permutations are, in addition to representing all the symmetries of the Equilateral Triangle, at the same time the direct symmetries of the Trigonal Bipyramid where p and q represent the apices of this bipyramid, i.e. its two tips (Recall that the direct symmetries are rotations only, while the opposite symmetries are reflections (or "enantiomorphs"). And as such it is clear that when we represent a rotation by a cyclic permutation of a b c, i.e. of the vertices of the triangle forming the equatorial plane of the trigonal bipyramid, this pyramid will not be turned over, which means that p and q will not be interchanged.
The group of automprphisms can thus be expressed as permutations in two ways (in which we now write down only the lower row of the permutation) :
a b c
c b a
a c b
b a c
b c a
c a b
or
p q a b c
q p c b a
q p a c b
q p b a c
p q b c a
p q c a b
We talked about the trigonal pyramid. It turns out that all the symmetries -- reflectional (opposite symmetries) as well as rotational (direct symmetries) -- of the equilateral triangle -- forming the group D3 -- are the same as the rotational symmetries (direct symmetries) only, of the trigonal bipyramid [The group D3 is a so-called dihedral group, in contrast to just a cyclic group as for example C3, that can be realized as the rotational symmetries of the equilateral triangle. They will be treated below]. These rotational symmetries of the trigonal bipyramid are listed just above this paragraph.
We will list them again with their proper interpretations in order that they indeed can represent the rotational symmetries of the trigonal bipyramid.
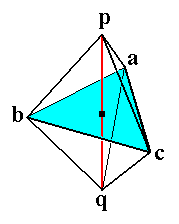
Figure 1. A Trigonal Bipyramid with its vertices marked. The 3-fold rotation axis is indicated.
p q a b c identity ( = rotation of 00).
These elements form the group D3. It can be realized in the full symmetry of the equilateral triangle, and in the rotational symmetry of the trigonal bipyramid.
The full symmetry of the trigonal bipyramid can be described by the following permutations of its vertices, starting with the rotational symmetries listed above, and followed by the reflectional symmetries :
p q a b c identity ( = rotation of 00). Period 1.
q p c b a rotation of 1800 about the bisector through b. Period 2.
q p a c b rotation of 1800 about the bisector through a. Period 2
q p b a c rotation of 1800 about the bisector through c. Period 2
p q b c a rotation of 1200 about the main axis (red). Period 3.
p q c a b rotation of 2400 about the main axis (red). Period 3.
q p a b c reflection across the equatorial plane. Period 2.
q p b c a reflection across the equatorial plane + a rotation of 1200 about the main axis. Period 6.
q p c a b reflection across the equatorial plane + a rotation of 2400 about the main axis. Period 6.
p q c b a reflection in (vertical) meridian plane containing bisector b. Period 2.
p q a c b reflection in (vertical) meridian plane containing bisector a. Period 2.
p q b a c reflection in (vertical) meridian plane containing bisector c. Period 2.
The last three permutations could suggest three more, obtained by a reflection in the equatorial plane folloerd by the mentioned reflection in the meridian planes. This would give the permutations
q p c b a
q p a c b
q p b a c
But we already have these permutations, so they are nothing new.
That a permutation like q p b c a has period 6, is easily verified. We just apply this permutation repeatedly :
p q a b c
q p b c a first application.
p q c a b second application.
q p a b c third application.
p q b c a fourth application.
q p c a b fifth application.
p q a b c sixth application.
Let's again list these 12 permutations expressing the full symmetry of the trigonal bipyramid, but now in a different order :
p q a b c
p q b c a
p q c a b
p q c b a
p q a c b
p q b a c
q p a b c
q p b c a
q p c a b
q p c b a
q p a c b
q p b a c
So we have 12 permutations, that can be interpreted as symmetry transformations. The pattern of periods over the elements is a signature of the dihedral group D6. This symmetry group is also realized in the full symmetry of the Regular Hexagon.
It is instructive to see what happens when we apply a permutation of the group elements, a permutation not in the above list (of permutations representing automorphisms).
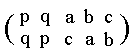
| 1 | q | p | c | a | b | ||
| 1 | 1 | q | p | c | a | b | |
| q | q | p | 1 | b | c | a | |
| p | p | 1 | q | a | b | c | |
| c | c | a | b | 1 | q | p | |
| a | a | b | c | p | 1 | q | |
| b | b | c | a | q | p | 1 |
When we look to the highlighted diagonal (green) we see that its upper part consists of the elements a c b, while its lower part consists of one and the same element only. Let us compare this with the group table in which the elements were in their original order, namely
1 p q a b c :
| 1 | p | q | a | b | c | ||
| 1 | 1 | p | q | a | b | c | |
| p | p | q | 1 | b | c | a | |
| q | q | 1 | p | c | a | b | |
| a | a | c | b | 1 | q | p | |
| b | b | a | c | p | 1 | q | |
| c | c | b | a | q | p | 1 |
In this table we see that the situation in the diagonal (green) is reversed : While its upper part consists of one and the same element only, its lower part consists of all three elements a b c. The structure of the tables is therefore not the same, and thus the element sequence
1 q p c a b is not an automorphism (of the group under consideration). Said differently, the permutation q p c a b of the elements of the group does not preserve structure, and so does not represent one of its automorphisms.
Of course the group table according to that permutation is a perfectly correct group table of our group, because we may reshuffle our elements at will (and reshuffle their products accordingly) to create a table. It is just not an automorphism of the group.
This means that from now on we read xyz as : first z, then y, and then x.
And when we must determine the product of, say, ab from the GROUP TABLE, then we first look up b in the horizontal top row enumerating the group elements, and then we look up a in the vertical left row (also enumerating the group elements).
(end Remark)
The reason for this reversal of convention is the fact that from this point onwards I will follow almost exclusively a very instructive book on Group Theory which contains extensive explanations and examples, but which follows the convention of reading products from back to front. Of course I could stick to the convention followed earlier and convert things wherever necessary, but this could cause unintended errors. The book mentioned (and referred to already earlier) is : The Fascination of Groups, by F. J. BUDDEN, 1978. At times other books will still be consulted as well, but in dealing with them we stick to BUDDEN's convention. And in all of this we, as directly as possible, head for a group theoretic understanding of the symmetry of crystals.
Inner automorphisms
We can show that the last mentioned automorphism of the group D3, according to the permutation
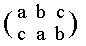
of the group elements, is a so-called inner automorphism.
Indeed, in the case of non-Abelian groups there is a systematic way of obtaining a certain class of automorphisms -- known as "inner automorphisms". We can do this by replacing the group elements by their respective conjugates or transforms, which are -- because they are products of the elements -- themselves elements of the given group. So the effect of these replacements is just a reshuffling of those elements (and this reshuffled situation represents an automorphism if the structure of the group table is preserved).
Although we will elaborate on conjugate elements of (non-Abelian) groups later on, we will already give the exact definition. Recall that the inverse of an element k -- i.e. the undoing of the element k, or, k-the-other-way-around, is indicated by the symbol k-1), and that consequently kk-1 = 1 (the identity). In this way jkk-1 = j1 = j. And also kk-1j = j. We cannot, however say that kjk-1 = j, because then we in fact say that kjk-1 = jkk-1 (supposing kj = jk), or kjk-1 = kk-1j (supposing jk-1 = k-1j), which is not necessarily the case in non-Abelian groups.
Well, here then the definition :
The element xyx-1 is called the TRANSFORM of the element y by the element x.
Also, if z = xyx-1, then y and z are called conjugate elements of the group.
Suppose x and y are any two elements of a group. Then the element xyx-1 is -- as we now know -- the transform of y by the element x, in which x can represent a transformation. And because x and y are elements of the group, as well as x-1 (because in a group the inverse of each element also belongs to that group), xyx-1, as being the product of x-1, y and x (which in fact is the product of yx-1 and x), also belongs to the group, i.e. the transform of an element of the given group by another element of that group is also an element of that same group.
If x remains fixed, while y runs through all the elements of the group, i.e. we consider the elements xy1x-1, xy2x-1, xy3x-1, ..., xynx-1, then we can show that the correspondence (i.e. a mapping) yr -- xyrx-1 constitutes an automorphism (i.e. the replacement of each element by its transform under the element x.
As has been said, the above group D3 provides an example of such an inner automorphism. Let us first reproduce the group table for D3 :
| 1 | p | q | a | b | c | period | ||
| 1 | 1 | p | q | a | b | c | 1 | |
| p | p | q | 1 | b | c | a | 3 | |
| q | q | 1 | p | c | a | b | 3 | |
| a | a | c | b | 1 | q | p | 2 | |
| b | b | a | c | p | 1 | q | 2 | |
| c | c | b | a | q | p | 1 | 2 |
Here -- in the table for D3 -- we have taken x = p. And because -- as we can check in the table -- pq = 1, q is the inverse of p, so q = p-1 = x-1. Then, letting y be equal to 1, p, q, a, b, c in turn (i.e. y1 = 1, y2 = p, y3 = q, etc.), we get (by reading off the products in the group table just given) :
p1p-1 = p1q = pq = 1
ppp-1 = p
pqp-1 = pqq = pp = q
pap-1 = paq = bq = c
pbp-1 = pbq = cq = a
pcp-1 = pcq = aq = b
And this represents the automorphism :
1 -- 1
p -- p
q -- q
a -- c
b -- a
c -- b
And this is indeed the permutation
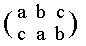
of the group elements, which had been found earlier.
Note that in the case of an Abelian group (i.e. a group in which every pair of elements commutes, which means that for every triple (a, b, c) of elements holds that if ab = c, then ba = c) xyx-1 = xx-1y = 1y = y, i.e. the transform of y by the element x is : y. So the only inner automorphism is the trivial one (i.e. the identity) which associates each element with itself.
e-mail :

To continue click HERE for further group theoretical preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals