The Total Symmetry of Three-dimensional Crystals

Part XIII
e-mail : 

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first  q, then  p, and then  a.
Sequel to Symmetry groups

In this document we will discuss some important symmetry groups in more detail, especially with respect to the five Platonic Solids (the only five possible fully regular 3-dimensional polyhedra) :
The Regular Tetrahedron,
The Regular Octahedron and Regular Hexahedron (Cube),
The Regular Icosahedron and Regular Dodecahedron.

As we have already said, the latter two cannot occur in crystals, but can occur in organisms.

Every configuration in symmetry groups as well as in all other groups whatsoever, contains the trivial symmetry group, consisting of the identity alone. It is the cyclic group of order 1, and can be denoted as C1.
The group of order 2 (which can be denoted C2 or D1) would refer to the possession of a single symmetry of period 2, but it is usual to use C2 to denote the half-turn symmetry (i.e. a rotation by 1800), and D1 to denote a bilateral symmetry. In crystallography this bilateral symmetry, as it is present as the only symmetry in the Class  m, is also indicated as the group Cs, while a center of symmetry as it is present as the only symmetry in the Class 1* , is indicated as the group Ci .
Thus the letter "S" possesses C2 symmetry, while the letter " T " possesses D1 symmetry.

If we have a group Dn representing the direct symmetries of a three-dimensional solid, in this case an n-fold bipyramid, or n-fold prism, and we now add all the enantiomorphs (reflections) ten we get the product group Dn x C2, and this is D2n only when  n  is odd (BUDDEN, p. 293).
The group of direct symmetries of the Regular Tetrahedron

Consider the direct symmetries of the Regular Tetrahedron. See next Figure.

Figure 1.  The Regular tetrahedron. Its verticed marked A, B, C, D.
Evidently there are rotations through 1200 and 2400 about each of the four axes that each pass through a corner, then goes through the center of the tetrahedron and hits the center of the triangular face lying opposite to the mentioned corner. So we have, to begin with, eight rotational symmetries of period 3 (each rotation axis of the type mentioned implies two rotations). Further we have of course the identity element. As such it might be thought that these combine to give the group C3 x C3, but this is not so, as we will see presently.
Suppose we denote by  p  the rotation which produces the cycle (BDC) of the vertices, where we rotate the whole tetrahedron, its axes included. So -- see Figure 1 -- vertex B goes to where D was, D goes to where C was, and C goes to where B was. Then p2 is represented by the cycle (BCD). Similarly  q  is (ACD), q2 is (ADC), r  is (ADB), r2 is (ABD), s  is (ABC), and s2 is (ACB).
If we translate these cycles into the corresponding permutations we get:

p = (BDC) we can say that A remains A, B becomes D, C becomes B, and D becomes C, which corresponds to the permutation
A D B C.
In the same way we can determine the permutations of the other (so far detected) group elements :
A C D B = p2
C B D A = q
D B A C = q2
D A C B = r
B D C A = r2
B C A D = s
C A B D = s2

Now consider the composition of the rotations first  p, then r2.
p  is the cycle (BDC), and this means that A remains A, B becomes D, C becomes B, and D becomes C. So  p  can be represented by the permutation A D B C.
r2 is the cycle (ABD), and this means that A becomes B, B becomes D, C remains C, and D becomes A. So r2 can be represented by the permutation B D C A.
In order to determine r2p we must execute these two permutations successively in the corresponding order :

A B C D  initial arrangement
A D B C  rearrangement according to the permutation ADBC
B A D C  rearrangement accoding to the permutation BDCA

we can see that the resulting permutation B A D C does not occur in the above list. So the set of nine permutations (including the identity permutation) so far obtained is, as it stands, not closed. This particular permutation can be written as the cycles (AB)(CD), which can be geometrically interpreted as a half-turn about an axis of rotation joining the mid-points of the edges AB and CD. Because the tetrahedron has six edges there are three such half-turns an we denote these :
a = (AB)(CD).
b = (AC)(BD).
c = (AD)(BC).

Thus we obtain a group which is different from the other groups of order 12,  C12,  D6,  C6 x C2,  and Q6.
The structure table for the Tetrahedral Group A4 is shown below.

1 a b c p p2 q q2 r r2 s s2 period
1 1 a b c p p2 q q2 r r2 s s2 1
a a 1 c b s r2 r s2 q p2 p q2 2
b b c 1 a q s2 p r2 s q2 r p2 2
c c b a 1 r q2 s p2 p s2 q r2 2
p p r s q p2 1 r2 b s2 c q2 a 3
p2 p2 s2 q2 r2 1 p c s a q b r 3
q q s r p s2 b q2 1 p2 a r2 c 3
q2 q2 r2 p2 s2 c r 1 q b s a p 3
r r p q s q2 c s2 a r2 1 p2 b 3
r2 r2 q2 s2 p2 a s b p 1 r c q 3
s s q p r r2 a p2 c q2 b s2 1 3
s2 s2 p2 r2 q2 b q a r c p 1 s 3

Table 13.1

Table of A4
Those 12 permutations of the verices (as listed above), which also provide a realization of the tetrahedral group, are known as the even permutations of the four letters.

The next Figure illustrates the direct and opposite symmetries of the Regular Tetrahedron.

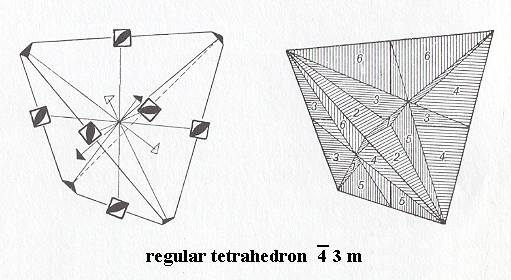
Figure 2.   Regular Tetrahedron, Stereometric Basic Form of all the (single) crystals of the Hexakistetrahedric Class of the Isometric Crystal System. Symmetry content is indicated (Small squares with solid oval :   4-fold rotoinversion axis (This axis involves a half-turn). Small triangles :   3-fold rotation axes. The right image displays the prevailing mirror planes.
In the left image we see the direct symmetries. In the right image we see the opposite symmetries.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
The Tetrahedron Group A4 (also called T) can be derived by the indirect product of the groups C3 and D2, and we write A4 = C3 semi D2. It is realized in crystals of the Tetrahedric pentagondodecahedric Class (23) of the Isometric Crystal System.

In the Promorphological System it is realized as Subendosphaerica tetartoidea (Polyaxonia subendospherica).
Matrices to represent the group of direct symmetries of the Regular Tetrahedron.

The group A4 can be represented by matrices in several ways, for example it can be represented by 4x4 permutation matrices. But for us it is more relevant to represent the group with 3x3 matrices, because they represent transformations in 3-D space. The twelve 3x3 transformation matrices that represent our group are the following :
Of these, the first one, i.e. the matrix

is the identity element :  When we post-multiply it with a point with coordinates (x, y, z), then these coordinates will not be changed :
(For matrix multiplication, see Matrices in Part I.)

The next Figure depicts a tetrahedron (red) inscribed in a cube. We have an axial system, consisting of the coordinate axes x, y and z, the origin (O) of which coincides with the center of the tetrahedron (and of the cube).
The x-axis intersects the center (U) of the tetrahedron edge AB, while U is at the same time the center of the corresponding cube face.
The y-axis intersects the center (V) of the tetrahedron edge AD, while V is at the same time the center of the corresponding cube face.
The z-axis intersects the center (W) of the tetrahedron face BD, while W is at the same time the center of the corresponding cube face.

Figure 3.  Regular Tetrahedron (red) situated within a cube (dashed lines).
The center or origin (O) of the axial system (xyz) coincides with the center of the tetrahedron (and also with that of the cube).
After BUDDEN, F. The Fascination of Groups, 1978.
The vertices of the tetrahedron are at the points A = (1, 1, -1), B = (1, -1, 1),
C = (-1, -1, -1), and D = (-1, 1, 1). It will be found that each of the twelve matrices represents a transformation which takes the tetrahedron into itself. For example, the transformation of the point A by the matrix

goes as follows :

and this means that A moves into position C.
But we can do all this in a quicker way, and find the effect of this matrix on every vertex by arranging the coordinates of the four vertices as four-column vectors to form a 3x4 matrix :

Hence the matrix

sends A, B, C, D to the positions previously occupied by C, B, D, A.
So C is replaced by A, B is replaced by B, D is replaced by C, and A is replaced by D, and this corresponds to the permutation

and since B is unchanged, it represents a rotation about OB (Figure 3) and so represents the element q2 in Table 13.1 (See also the above list of (some) permutations with respect to the direct symmetries of the Regular Tetrahedron).
This rotation takes (See Figure 3) the point
U (mid-point of AB) = (1, 0, 0) to the point
V' = (0, -1, 0),
the point
V (mid-point of AD) = (0, 1, 0) to the point
W' = (0, 0, -1), and
the point W (mid-point of BD) = (0, 0, 1) to the point
U = (1, 0, 0), as shown by the arrows in Figure 3.
The three coordinates of the image points form the columns of the transformation matrix :

This is evident from the fact that thecoordinates of initial points U, V and W togther form the identity matrix

And when we post-multiply this matrix with the transformation matrix we get our point tripel V'W'U :
The second, third and fourth of our above list of twelve transformation matrices (each of period 2) will interchange two pairs of vertices :

Indeed, the second matrix sends the point (x, y, z) to the point (x, -y, -z), and so is a half-turn about the x-axis. It swaps the vertices A and B of the tetrahedron and also C and D, and thus corresponds to the permutation B A D C, which is the cycle (AB)(CD), and this corresponds to  a  in Table 13.1 (See also HERE, where we have named the cycles).

The third matrix sends the point (x, y, z) to the point (-x, y, -z) (see below), and so is a half-turn about the y-axis. It swaps the vertices A and D, and also B and C, and thus corresponds to the permutation D C B A, and to the cycle (AD)(BC), and this corresponds to  c  in the group table given above.

The fourth matrix sends the point (x, y, z) to the point (-x, -y, z) (See below), and so is a half-turn about the z-axis. It swaps the vertices B and D, and A and C, and thus corresponds to the permutation C D A B, which is the cycle (AC)(BD), and this corresponds to b  in the group table given above.
We may also consider the direct symmetries of the tetrahedron to be the permutations of the four faces, or as permutations of the six edges. The latter will reveal A4 to be a subgroup of S6, and could be represented by 6x6 permutation matrices. The group S6 is the group of all permutations of six symbols. It contains 1x2x3x4x5x6 = 720 elements (while A4 contains 12 elements).
The full group of the Regular Tetrahedron

The full group of the Regular Tetrahedron will include not only six reflections in planes of symmetry (e.g. the reflection in a plane containing an edge of the tetrahedron and the center of the tetrahedron, which interchanges two vertices -- see right image of Figure 2), but also transformations of period 4 (indicated in the left image of Figure 2 by little squares with inscribed black ellipse), such as the one presented by the permutation

We have here the cycle (ADCB). Let's see what this geometrically is. See next Figure.

Figure 4.  The permutation DABC performed on the vertices of a regular tetrahedron (red)(inscribed in a cube). One 4* axis is indicated by a 4 with above it a small score ( = the official notation for a 4-fold roto-inversion axis).
As can be seen in the above Figure, the transformation represented by the permutation DABC rotates the vertex A first 900 anticlockwise about the 4* axis (indicated in the Figure as a 4 and above it a score) to A" (purple curved arrow) and then inverts the result through the tetrahedron's center to the vertex D (purple straight arrow). A similar transformation is at the same time implied with respect to the other vertices, B goes to A, C goes to B, D goes to C :  The whole tetrahedron is thus rotated 900 about the 4* axis indicated and then inverted through its center (and this transformation then maps the whole tetrahedron onto itself :  The image then occupies the same space as it did before, but its vertices are permuted accordingly. There are, with respect to the 4* axis indicated in the Figure, two such transformations of period 4, one (which we just discussed) in which the rotational component consists of 900 rotation, and a second of which that component consists of a rotation by 2700. Because there are three axes with repect to which we can perform such a rotation-inversion transformation, we have 3 x 2 = 6 enantiomorphs of period 4. So in addition to the above mentioned six reflections -- six enantiomorphs -- in planes of symmetry, we have the six just discovered rotation-inversion transformations -- themselves also enantiomorphs -- and thus we have now added 12 enantiomorphs to the 12 direct symmetries of the Tetrahedron resulting in the full group of the Terahedron.
Indeed, the full group of the Regular Tetrahedron contains all those 24 transformations which permute the four vertices (or faces) in any manner. Thus it is isomorphic with the group S4, the group of all permutations of four symbols (Recall that the group of the direct symmetries of the tetrahedron, A4 consists of all even permutations of the group S4 (Four the concepts of even and odd permutations see Part XI, Even and odd permutations). This group S4 is isomorphic to the Octahedral Group (BUDDEN, p. 299) O ( = D3 semi D2), the group of the direct symmetries of the Regular Octahedron and (also) of the Cube (Regular Hexahedron).

The full group of the Regular Tetrahedron, S4 ( = O ), is realized in two Crystal Classes if the Isometric Crystal System, namely in the Pentagonikositetrahedric Class (432), and the Hexakistetrahedric Class (4* 3m).
In the Promorphological System of stereometric basic forms it is realized as Subendosphaerica gyroidea (Polyaxonia subendosphaerica), and also as
Tetraedra regularia (Polyaxonia rhythmica).

Next we give the group table for S4
REMARK :  In order to distinguish clearly between the element  1  (the identity element), and the element  l  (that comes after  k ) that element (l) (coming after  k ) will be denoted as  l*.

1 a b c d f g h i j k l* m n p q r s t u v w x y per.
1 1 a b c d f g h i j k l* m n p q r s t u v w x y 1
a a 1 c b f d h g j i l* k n m q p s r u t w v y x 2
b b d 1 f a c i k g l* h j p r m s n q v x t y u w 2
c c f a d 1 b j l* h k g i q s n r m p w y u x t v 3
d d b f 1 c a k i l* g j h r p s m q n x v y t w u 3
f f c d a b 1 l* j k h i g s q r n p m y w x u v t 2
g g h m n t u 1 a p q v w b c i j x y d f k l* r s 2
h h g n m u t a 1 q p w v c b j i y x f d l* k s r 2
i i k p r v x b d m s t y 1 f g l* u w a c h j n q 3
j j l* q s w y c f n r u x a d h k t v 1 b g i m p 4
k k i r p x v d b s m y t f 1 l* g w u c a j h q n 4
l* l* j s q y w f c r n x u d a k h v t b 1 i g p m 3
m m t g u h n p v 1 w a q i x b y c j k r d s f l* 3
n n u h t g m q w a v 1 p j y c x b i l* s f r d k 4
p p v i x k r m t b y d s g u 1 w f l* h n a q c j 2
q q w j y l* s n u c x f r h t a v d k g m 1 p b i 3
r r x k v i p s y d t b m l* w f u 1 g j q c n a h 2
s s y l* w j q r x f u c n k v d t a h i p b m 1 g 4
t t m u g n h v p w 1 q a x i y b j c r k s d l* f 4
u u n t h m g w q v a p 1 y j x c i b s l* r f k d 3
v v p x i r k t m y b s d u g w 1 l* f n h q a j c 3
w w q y j s l* u n x c r f t h v a k d m g p 1 i b 2
x x r v k p i y s t d m b w l* u f g 1 q j n c h a 4
y y s w l* q j x r u f n c v k t d h a p i m b g 1 2

Table 13.2

Table of S4 (After BUDDEN, 1978)
The Cube and the Regular Octahedron

The Regular Tetrahedron is the first of the so-called five "Platonic Solids", i.e. the five fully regular polygons (Polyaxonia rhythmica). They fit into a sphere such that their vertices lie on the sphere's surface -- and thus they are endospheric polyhedra -- and moreover they consist of faces that themselves are congruent regular polygons of a kind (equilateral triangles, regular pentagons, what the case may be). So, for example the Regular Icosahedron (the fifth member of these solids) has 20 triangular faces, that are equilateral, and congruent to each other. The five Platonic Solids are :

The Regular Tetrahedron (four faces).
The Regular Hexahedron (Cube) (six faces).
The Regular Octahedron (eight faces).
The Regular Dodecahedron (twelve faces).
The Regular Icosahedron (twenty faces).

The last two of these involve 5-fold rotation axes, so they cannot occur in crystals. They do, however, occur in some organisms (as their stereometric basic form). The first three are represented in crystals as well as in organisms.

The Cube (Regular Hexahedron) and The Regular Octahedron have the same symmetry, they are dual solids :  The centers of the six faces of a cube form a regular octahedron, and the centers of the eight faces of a regular octahedron form a cube.

The simplest method of assessing the direct symmetries of the Cube (and with it, those of the Regular Octahedron) is by means of permutations of the cube's four diagonals.
Let the diagonals of the cube be called  a, b, c, d  (AA', BB', CC', DD' in the next Figure).

Figure 5.  Each direct symmetry of the cube corresponds to a permutation of its (space) diagonals.
We shall show (BUDDEN, pp. 298) that every direct transformation of the cube into itself (which is by definition a symmetry transformation) corresponds to just one of the permutations of the diagonals, and vice versa. So we have to do with the permutation of four symbols, here, diagonals, and we will show that the direct symmetries of the cube form a group that is isomorphic to the group S4, the group of all permutations of four objects. First of all there are altogether 1x2x3x4 = 24 permutations of four objects, and it is easy to see that there are also 24 direct symmetries of the cube. For consider first the symmetries of the cube which carry a particular vertex (say A) into itself. Evidently if A is invariant under a transformation, so must the other end A' of the diagonal through A, and in fact the entire diagonal  a  is not moved, because, when the vertex A is invariant, and the diagonal through A is nevertheless moved (pivoting about A), then the cube will be moved to another location (only its vertex A remaining in place) and then the cube will not be transformed into itself anymore, implying that such an operation (pivoting the diagonal  a  about A) is not a symmetry transformation of the cube. So, A being invariant, the diagonal  a  will not move, it stays where it was. The three points B, D, C' at the ends of the edges through A form an equilateral triangle. See next Figure.

Figure 6.  Symmetries of the cube which leave A invariant cause rotation of equilateral triangle BDC'.
And the only possible direct symmetries of the cube with A fixed are those which rotate about the fixed diagonal  a  through angles of 00, 1200 and 2400, and so cause the cyclic permutations of the vertices of triangle BDC' and hence a cyclic permutation of the diagonals (bdc) (the subgroup C3 ). But the point A may be mapped into any of the eight vertices of the cube, and since there are three symmetries for each of these possibilities, it follows that the total number of symmetries is 8x3 = 24, it being noted that we have not counted any of them twice. When considering the rotations about a diagonal, we, in counting the number of them, included the rotation of 00. This we must do, because, after considering the rotations about one diagonal we move the cube such that we get another diagonal right on the location where the first considered diagonal was. So the zero rotation is now combined with the transformation of one diagonal into another one, and is different from the zero rotation considered first :  there it was a zero rotation + the identity transformation of diagonals. So indeed we have 3x8 = 24 direct symmetries of teh cube, and this is the same number of elements we find in the group S4, the group of all permutations of four objects.

This still is not enough to establish the isomorphism between the direct symmetries of the cube and the group S4. We should compare the periods of the elements involved. To do so we must consider the types of movements involved in these 24 symmetries.
There are rotations of 1200 and 2400 about each of the four diagonals of the cube, so we have eight elements of period 3. To see this clearly in the case of diagonal  a  we should look to the cube exactly in the direction of this diagonal, as the next Figure shows :

Figure 7.  View of cube as seen along the diagonal AA' ( = a ).
There are six half-turns, i.e. six elements of period 2, about axes joining mid-points of opposite edges of the cube, such as shown in the next Figure.

Figure 8.  The half-turn about an axis joining mid-points of A'C, AC' (perpendicular to plane BDB'D') interchanges the faces ABCD and C'B'A'D'.
Finally there are quarter-turns and half-turns about the joins of the centers of opposite faces. And there are three such joins, one is indicated in the next Figure :

Figure 9.  One of the possible 4-fold rotation axes of the Cube is indicated.
Such a join, which is a 4-fold rotation axis, implies three non-zero rotations, 900, 1800 and 2700. The rotation of 1800 is an element of period 2, while the other two are elements of period 4.
So we have an extra 3 elements of period 2, and 3x2 = 6 elements of period 4.
Thus the group of direct symmetries of the Cube (and with it of the Regular octahedron) contains

8 elements of period 3,
9 elements of period 2,
6 elements of period 4, and the
identity.

These are the same as the numbers of elements of periods 2, 3 and 4 in the group S4 (See Table 13.2), and establishes the isomorphism, making use of the (group theoretic) result that says that two groups are isomorphic when they not only have the same number of elements, but also have the same number of elements of any specified period, provided their order is less than 27, and not 16. However, it is not difficult to prove the result independently of that theorem, though the proof needs some care :

We need to show that to every permutation of the diagonals there corresponds exactly one direct symmetry if the Cube, and vice versa, and also that products are preserved.

Note that it is not enough merely to establish a 1,1 correspondence between those symmetries and the permutations of the diagonals  a, b, c and  d. For in the case of the Regular Icosahedron (or Dodecahedron), the full group of symmetries including enantiomorphs has 120 elements (See further down). There are also 120 permutations of the five inscribed cubes (See also further down). But the full group of the Icosahedron is not S5 , but A5 x C2 .

So we need to show that products of rotations correspond to products of permutations. This follows from the fact that if r1 and r2 are rotations of the Cube, and suppose for example that r1 replaced diagonal  a  by diagonal  b, while r2 replaces  b  by  c. Then evidently r2r1 replaces  a  by  c, so that the composition of the rotations r1 followed by r2 corresponds exactly to the composition of the permutations of the diagonals.
Suppose now that it happened that two different rotations r1 and r2 were both to correspond to the same permutation  p.  Then r1r2-1 corresponds to pp-1 = the identity permutation, and clearly the only symmetry transformation of the (direct) symmetries of the Cube which retains the positions of all four diagonals is the identity [ This is not true in the full group, for the central inversion leaves all four diagonals invariant.]. Hence we get
r1r2-1 = pp-1 = 1 (the identity element), which is equivalent to
r1r2-1r2 = 1r2, and this is equivalent to
r11 = r2, and this, finally, is equivalent to
r1 = r2.
This establishes that two different rotations cannot bring about the same permutation. Moreover, it is self-evident that two different permutations cannot both correspond to the same rotation, and now the argument is complete :
The direct symmetries of the Cube (and with it of the Regular Octahedron) are as a group isomorphic to the group S4. The direct symmetries of the Cube are also called the group O. It is isomorphic to the full symmetry of the Regular tetrahedron.
The full group of the Cube and Regular Octahedron

We will arrive at the full group of the Cube (and thus including all enantiomorphs) by starting with its 24 direct symmetries.
The 24 direct symmetries of the Cube may be represented by 3x3 transformation matrices, each of which carries out the appropriate transformation. These will include, as the subgroup A4, the twelve matrices listed ABOVE. Those matrices had their (+/-) 1's in the following three positions :

And either three or one of these 1's carried a "+" sign. It will be found that the remaining twelve matrices which complete the full group of the Tetrahedron (or the group of direct symmetries of the Cube or Regular Octahedron), will have their (+/-) 1's in the three remaining possible positions :

We can still obtain 24 more matrices by, instead of letting them possess either three 1's or one 1 carrying a "+" sign, letting them have either three 1's or one 1 carrying a  minus  sign. So in all we then have 48 transformation matrices representing the 48 symmetries of the Cube, i.e. all the symmetries (direct and opposite) of the Cube (or Regular Octahedron).

That we now have all possible 3x3 matrices containing six zero's and three (+/-) 1's, where each row and each column possesses only one 1 (The typical and necessary configuration for such a matrix to represent a transformation in 3-D space), can easily be shown :
Column 1 will contain either a 1 or a -1 in one of the three places so that there are six possible ways of filling up column 1. Having done this, only two places in column 2 may contain (+/-) 1, so this column may be completed in four ways. Once column 1 and 2 are completed the only possible place in column 3 may be filled with either +1 or -1, thus two possibilities only. Thus the number of such matrices is 6x4x2 = 48.

Let us consider the matrix


This is a matrix with one of the three alternative patterns of 1's described above. It has one positive 1, so it must be an enantiomorph of the full group of the Tetrahedron, but it also occurs of course in the full set of matrices describing all 48 symmetries (direct and opposite) of the Cube. We can ask which enantiomorph is represented by this matrix. This may be decided by remembering that the points U = (1, 0, 0), V = (0, 1, 0) and W = (0, 0, 1) -- see next Figure -- are mapped into the points whose coordinates are the columns of our given matrix (because the coordinates of the initial points U, V and W, correspond to the identity matrix), namely V = (0, 1, 0), U' = (-1, 0, 0) and W' = (0, 0, -1), and then examining the geometrical interpretation of this. See next Figure.

Figure 10.  The matrix (See below) represents a quarter-turn about WOW'.
Well, going from U to V, we do in fact the following :
Rotation by 900 about the z-axis followed by inversion through the center of the cube.

(At the same time) going from V to U' is :
Rotation by 900 about the z-axis followed by inversion through the center of the cube.

(At the same time) going from W to W' is :
Rotation by 900 about the z-axis (which has no effect) followed by inversion through the center of the cube.

So what we do by the matrix

is :  Rotation of the cube about its z-axis followed by inversion through its center.

Or, alternatively (in order to find which enantiomorph is represented by the given matrix) we may write :

Now the last matrix of the above multiplication represents one of the direct symmetries of the cube, sending the points U, V, W to the points V', U, W. The point W being unchanged reveals that the line WOW' must be an axis of rotation. The above Figure shows that we have a quarter-turn about the line WOW' (the z-axis).
Furthermore the matrix


moves the point (x, y, z) to the point (-x, -y, -z), and so is the central inversion in O (the center of the cube).
Hence the matrix

represents the composition of a quarter-turn about the z-axis together with the central inversion. It can be easily verified that these two elements may be performed in either order. In fact, the central inversion commutes with every one of the remaining 47 symmetries.

The full group of the Cube or Regular Octahedron is isomorphic to S4 x C2 (And indeed, C2 can emerge by the central inversion, because the latter is an element of period 2). It is important to realize that S4 x C2 is NOT isomorphic to the group A5, because we shall see that the former is realized in crystals, while the latter cannot be so realized because it involves 5-fold rotation axes. The group A5 represents the direct symmetries of the Regular Icosahedron and Regular Dodecahedron.

Any of the 24 enaniomorphs (= opposite symmetries) of the Cube (or Octahedron) may be considered to be the product of one of the direct symmetries with the central inversion.

The full group of the Cube and Regular Octahedron, i.e. the Group S4 x C2, also called Oi, is realized in crystals of the
Hexakisoctahedric Class (4/m 3* 2/m) of the Isometric Crystal System.
In the Promorphological System it is realized as
Octaedra regularia (Polyaxonia rhythmica).
It is also realized as
Hexaedra regularia (Polyaxonia rhythmica).
In Promorphology the difference between those two lies in the number of antimers (counter parts) that are detectable in natural objects that have their symmetry according to S4 x C2.
The group A5 of the direct symmetries of the Regular Icosahedron and Regular Dodecahedron.

These two regular solids are dual solids which means that the 20 vertices of the dodecahedron correspond to the 20 faces of the Icosahedron, while the 12 vertices of the Icosahedron correspond to the 12 faces of the Dodecahedron. Their symmetry content is the same.
Said in other words, given a regular icosahedron, there is a dual regular dodecahedron whose vertices are the centers of the faces of the original solid, and vice versa.
Now for every symmetry of the Icosahedron, that is, for every transformation which carries it into itself, the inscribed Dodecahedron will also be carried into itself.
Hence, in the first place, the numbers of symmetries of the dual solids are equal. But this is not sufficient for isomorphism, which must also preserve products.
If  a, b, c  are three symmetries of the Icosahedron, such that  a  followed by  b  produces the symmetry  c,  i.e. c = ba,  and if  a', b', c'  are the corresponding symmetries induced in the Dodecahedron by the symmetries  a, b, c  of the Icosahedron (i.e. induced in the Dodecahedron by the cover operations of the Icosahedron), then  ba  induces the symmetry  b'a'  in the Dodecahedron. But  c  induces  c' in the Dodecahedron, and therefore, since  c = ba,  we must also have  c' = b'a'  :

and the isomorphism is proved.
How many elements has this group of symmetries? Imagine the dodecahedron -- which consists of 12 congruent regular pentagons -- placed on a horizontal table so that one of its pentagonal faces is fitted onto an outline on the table congruent to the face. Then for any particular face which is fitted to the external outline, there are five possible positions of the solid corresponding to the rotations of  00, 720, 1440, 2160 and 2880  about a vertical axis going through the center of the pentagonal face on which the dodecahedron sits. But any one of the twelve faces might be fitted to the external pentagonal outline, so the number of (direct) symmetries is 5x12 = 60.

We may analyse these 60 symmetries as follows (See next Figure).

Figure 11.  Rotations of the Regular Icosahedron.
Left image :  Four rotations through : 720, 1440, 2160 and 2880  about joins of opposite vertices. Total : 24.
Central image :  Two rotations through : 1200 and 2400  about joins of centers of opposite faces. Total : 20.
Right image :  Half-turns about joins of mid-points of opposite edges. Total : 15.
In analysing the symmetries we consider the case of the Icosahedron, and note that all the direct symmetries are rotations (Speaking about "the case of the Icosahedron", we mean that if we consider the 5-fold rotation axes connecting opposite vertices, the Icosahedron is automatically meant. If, on the other hand, we were to consider these axes as connecting the centers of opposite faces, then the Dodecahedron is automatically meant. Here we consider, as has been said, the symmetries of the group A5 with the Icosahedron -- as an example -- in mind)  :
  1. Rotations through multiples of 720 about lines joining opposite vertices (of the Icosahedron) (corresponding to the faces of the dodecahedron). There are four such rotations, of period 5, about each of the six space diagonals, hence we have 24 such elements (See left image of Figure 11).
  2. Rotations through multiples of 1200 about the joins of the centers of opposite faces (corresponding to the vertices of the dodecahedron). For each such axis there are two rotations (1200 and 2400), and, there being ten of these axes, this makes a total of twenty rotations of period 3 (See central image of Figure 11).
  3. Finally, there are half-turns about axes joining the mid-points of pairs of opposite edges. The number of edges is 30, so the number of such axes is fifteen, each associated with one half-turn (See the right image of Figure 11).
Hence the group contains :

An identity.
15 elements of period 2.
20 elements of period 3.
24 elements of period 5.

These figures are the same for the group of even permutations of five letters, known as the alternating group of order 60 ( A5 ) (The group S5, i.e. the group of all permutations of five letters, contains, of course, 5! = 120 permutations).
This observation does not prove that the Icosahedral Group is isomorphic with A5 , though this is in fact the case (BUDDEN, p. 304).
It is possible to inscribe five cubes in a dodecahedron. One such cube is shown in the next Figure.

Figure 12.  One of the five cubes which may be inscribed in the Regular Dodecahedron.
After BUDDEN, 1978
One edge of one of these cubes may be taken to be a diagonal (say AC) of the pentagonal face ABCDE, which is being viewed directly in the Figure. By selecting appropriate diagonals of successive adjacent faces, a cube is formed. There must be five of these cubes, since the choice of diagonal of ABCDE might have been made in five ways. Explaining in a somewhat different way, we can say :  There are 5 diagonals in a pentagonal face, so there are 12x5 = 60 face diagonals of the dodecahedron. A cube has 12 edges, so there are 60/12 = 5 cubes in all that can be inscribed in the dodecahedron.
Of the 60 symmetries of the Dodecahedron, some will cause one particular cube to be mapped onto itself. Those which do so will form a subgroup of A5 (because such a set of symmetry transformations forms a self-contained whole). Obviously, all twenty-four direct symmetries of the cube cannot be in this subgroup (i.e. despite the fact that they all map the cube onto itself). This is because of Lagrange's Theorem, since 24 is not a factor of 60. But the rotations through 1200 and 2400 about those diagonals of the dodecahedron which are also diagonals of that particular cube, will certainly be included, and there are eight of these rotations (There are four (space) diagonals in a cube, and each one of them supports two rotations). Also included will be half-turns about the joins of mid-points of opposite edges (such as ED) of the dodecahedron. Of these, there are three which take the cube into itself, being the three mutually perpendicular axes through the center and perpendicular to the faces of the cube. These eleven symmetries, together with the identity, form the group A4 (See the periods of the elements in Table 13.1). Thus we have shown geometrically that A4 is a subgroup of A5. The particular property associated with this subgroup is that it takes one particular cube into itself. Since there are five cubes, it follows that A5 has five subgroups A4.
We can interpret all the 60 direct symmetries of the Regular Dodecahedron (And at the same time those of the Regular Icosahedron) as the 60 even permutations of these five cubes (which, in the Icosahedron, tough with their vertices the centers of the Icosahedron's trianguar faces), thus as all the even permutations of five symbols, say, the letters A, B, C, D, E. And this means that the group of direct symmetries of the Icosahedron (and its dual solid) is isomorphic to the group A5. Let us identify those (even) permutations (note that we are speaking about the permutations of the five cubes, not of the permutations of the vertices of the Icosahedron or Dodecahedron). When, to begin with, we write the permutations of five letters as cycles we can easily match these cycles with the direct symmetries listed above. Apart from the identity, which is the 'cycle' (A)(B)(C)(D)(E), we have :

  1. Rotations through multiples of 720 about lines joining opposite vertices (of the Icosahedron) (corresponding to the faces of the Dodecahedron). There are four such rotations, of period 5, about each of the six space diagonals, so we have 24 such elements (See left image of Figure 11). These correspond to 24 cycles of period 5, such as (ABCDE).
  2. Rotations through multiples of 1200 about the joins of the centers of opposite faces (corresponding to the vertices of the Dodecahedron). For each such axis there are two rotations (1200 and 2400), and, there being ten of these axes, this makes a total of twenty rotations of period 3 (See central image of Figure 11). These correspond to 20 cycles of period 3, such as (ABC).
  3. Finally, there are half-turns about axes joining the mid-points of pairs of opposite edges. The number of edges is 30, so the number of such axes is fifteen, each associated with one half-turn (See the right image of Figure 11). These correspond to 15 double transpositions (period 2), such as (AB)(CD).
Let's check the numbers of these three kinds of cycles :
  1. There are indeed 24 cycles of period 5 :
    In such a cycle, for instance the cycle (ABCDE) (which is of course the same as, say, (CDEAB),
    A goes to B,
    B goes to C,
    C goes to D,
    D goes to E, and
    E goes to A.
    When the first four of these "going to's" are given, then the fifth is automatically determined. So we can choose any order of four letters, and there are 24 of them, to set up a 5-cycle.
  2. There are indeed 20 cycles of period 3 :
    Three letters, say, A, B, C, can give rise to two cycles of period 3. We can see this by imagining the three letters to represent the vertices of an equilateral triangle. Such a triangle has among its symmetry transformations two rotations of period 3, namely a rotation by 1200 and by 2400. And because with the letters A, B, C, D, E  we have, in all, 10 possible different triples, we have 10x2 = 20 cycles of period 3.
    To exhaustively determine those 10 triples, we can just as well determine the number of pairs that are possible to form with the letters A, B, C, D, E, because the number of triples must be the same. The order of the letters in the pairs does not matter, because we want just to determine what the three other letters are. These pairs can, by the way, be interpreted as single transpositions, and they are the following :

    AB, AC, AD, AE, BC, BD, BE, CD, CE, DE.

    So there are ten of them. And now we can write down the ten corresponding triples, by supplementing each pair by the three remaining letters :

    CDE, BDE, BCE, BCD, ADE, ACE, ACD, ABE, ABD, ABC.

  3. There are indeed 15 double transpositions :
    To find them, we must realize that in all cases of these double transpositions four letters are involved in those transpositions. The fifth letter does not partake in any interchange :

    A(BC)(DE)
    A(BD)(CE)
    A(CD)(BE)

    B(AC)(DE)
    B(AD)(CE)
    B(CD)(AE)

    C(AB)(DE)
    C(AD)(BE)
    C(BD)(AE)

    D(AB)(CE)
    D(AC)(BE)
    D(AE)(BC)

    E(AB)(CD)
    E(AC)(BC)
    E(BD)(AD)
We will now write examples of these three kinds of cycles as permutations of the five letters A, B, C, D, E.

  1. the cycle (ABCDE) of period 5 corresponds to the permutation

    which can be written as BCDEA.
    In it we can see that
    B is followed by A, and so contributes 1 reversal.
    C is followed by A, and so contributes 1 reversal.
    D is followed by A, and so contributes 1 reversal.
    E is followed by A, and so contributes 1 reversal.
    A contributes no reversals.

    So the permutation BCDEA involves 4 reversals. This number is even, and thus the permutation is an even permutation.

    Similarly we can determine the permutations and their parity of the remaining cycles of period 5.

  2. The cycle (ABC) of period 3 -- which is the same as (ABC)(D)(E)-- corresponds to the permutation

    which can be written as BCADE.
    In it we can see that
    B is followed by A, so contributes 1 reversal.
    C is followed by A, so contributes 1 reversal.
    A contributes no reversals.
    D contributes no reversals.
    E contibutes no reversals.

    So the permutation BCADE involves 2 reversals, so the permutation is even.

  3. The double transposition B(CD)(AE) of period 2 corresponds to the permutation

    which can be written as EBDCA.
    In it we can see that
    E is followed by B, D, C, A, so it contributes 4 reversals.
    B is followed by A, so contributes 1 reversal.
    D is followed by C, and A, so contributes 2 reversals.
    C is followed by A, and so contributes 1 reversal.
    A contributes no reversals.

    So the permutation EBDCA involves 8 reversals, and thus the permutation is even.
When we check all the cycles mentioned we will see that they correspond to 60 even permutations of five letters (A, B, C, D, E). So we have shown that we can interpret the direct symmetries of the Icosahedron (and Dodecahedron) as 60 even permutations of five letters, so this group is isomorphic with the alternating group A5 (The group S5 contains all the permutations, even and odd, 60 of each, of five letters).
The full group of the Regular Icosahedron and its dual solid the Regular Dodecahedron.

On the basis of what has been said about the group of the direct symmetries of the Regular Icosahedron and its dual solid, namely that it can be seen as the group of all (namely 60) even permutations of five letters (which can be interpreted as the five inscribed cubes), and thus being isomorphic to the alternating group A5, we could expect that the full group of the Icosahedron (and of its dual solid), i.e. now supplemented with the enantiomorphs, will be isomorphic to the group S5 of all the permutations (even and odd) of five letters, but this turns out not to be so, as we will see in due course.

We can construct this full group out of the group A5 by pairing off all the rotational symmetries of A5 with the central inversion. I.e. we perform such a rotational transformation followed by central inversion of the result (When we do this with the above mentioned 15 double transpositions (half-turns) we get the 15 mirror reflections across the 15 symmetry planes of the solid). When all the rotational symmetries are thus paired off we get the group A5 x C2.

We will, first of all consider all permutations of five letters, present in the group S5. They consist of 60 even permutations and 60 odd permutations (These 120 permutations occur in the Regular Dodecahedron as the 120 permutations of the five inscribed cubes, but, as we will see, the full group of the Dodecahedron (and of its dual solid) is not S5, but A5 x C2). The even permutations, however, we have already considered. They form the subgroup A5 of S5. So we will concentrate on the 60 odd permutations. We will first enumerate the occuring cycles and then their corresponding permutations. We will again use the five letters A, B, C, D and E.

According to BUDDEN, p. 412, the cycles, corresponding to the 60 odd permutations of the group S5, are the following :

  1. 30 cycles of period 4, such as (ABCD).

  2. 20 cycles of period 6, such as (ABC)(DE).

  3. 10 single transpositions (period 2), such as (AB)
With respect to the latter, BUDDEN had stated earlier (p. 306) that there are 15 such transpositions, but this is wrong (and indeed contradicts what is said on p. 412). ABOVE we showed that indeed there are only 10 such (single) transpositions.
We will now explain the number of the just enumerated kinds of cycles.
  1. Similarly as we argued ABOVE, we can see that there are six possible cycles of period 4 with the four letters A, B, C, D. But there are several possibilities of chosing four letters out of five. In the case of (ABCD) we left out the letter E. It is clear that there are five possible choices of leaving which letter out. So in all there are 6x5 = 30 possible cycles of four letters out of five.

  2. ABOVE we showed that there are 10 possible triples of letters to be formed out of five (disregarding the order of the letters in the triples). Each triple can be seen (just for convenience) as indicating the three vertices of an equilateral triangle. A cycle, such as (ABC) is of period 3 and can stand (still just for convenience) for a rotation of the equilateral triangle by 1200. It is clear therefore that the letters A, B, C, can involve two cycles of period 3, the other one is (ACB) which can stand for a rotation by 2400 (also of period 3).
    Now we can add to these two cycles of period 3, one transposition, and once (ABC) or (ACB) is given, we have no choice which (independent) transposition to add (out of our total of the five letters A, B, C, D, E) than the transposition (DE). So given the letters A, B, C for the cycles of period 3, we have two possible cycles of the general form (XYZ)(UV). And because we have 10 possible triples of three letters out of five, there are 10x2 = 20 possible cycles of the general form (XYZ)(UV).

  3. ABOVE we have already shown that, given five letters, there are 10 possible single transpositions.
These cycles correspond to (odd) permutations. We will show this with some examples :
  1. The cycle (ABCD) corresponds to the permutation

    which we can write as BCDAE.
    In it we see that
    B is followed by A, so contributes 1 reversal.
    C is followed by A, so contributes 1 reversal.
    D is followed by A, so contributes 1 reversal.
    A contributes no reversals.
    E contributes no reversals.

    So the permutation BCDAE involves three reversals, so the permutation is odd.

  2. The cycle (ABC)(DE) (and all the cycles of the general form (XYZ)(UV)) are of period 6, because the constituent cycle (ABC) comes back to its initial state after three repetitions, but then DE will be reversed and thus not returned to its original state. So we must run another three rounds for the whole composed cycle (ABC)(DE) to return to its original state. So only after 6 rounds this original state is again visited, and thus the period of (ABC)(DE) is 6.
    Generally we can say (BUDDEN, p. 321) :

    The period of a permutation is the Lowest Common Multiple (L.C.M) of the lengths (or periods) of its disjoint cycles.

    The composed cycle (ABC)(DE) corresponds to the permutation

    which can be written as BCAED.
    In it we see that
    B is followed by A, so it contributes 1 reversal.
    C is followed by A, so it contributes 1 reversal.
    A does not contribute any reversal.
    E is followed by D, so it contributes 1 reversal.
    D contributes no reversals.

    So the permutation BCAED involves 3 reversals, so the permutation is odd.

  3. The single transposition (AB) (which can -- in our present context -- also be written as (AB)(C)(D)(E)) corresponds to the permutation

    which can be written as BACDE.
    In it we see that
    B is followed by A, so it contributes 1 reversal.
    A does not contribute any reversal.
    C does not contribute any reversal.
    D does not contribute any reversal.
    E does not contribute any reversal.

    So the permutation BACDE involves 1 reversal, so the permutation is odd.
We now want to investigate whether with these 60 odd permutations correspond the opposite symmetries of the Regular Icosahedron and its dual solid the Regular Dodecahedron (These permutations do correspond to 60 permutations of the five cubes that can be inscribed into the dodecahedron (and mutatis mutandis also in the icosahedron)). For the even permutations this correspondence is indeed present (i.e. the correspondence with the direct symmetries of the Icosahedron or Dodecahedron) (BUDDEN, p. 304).

Indeed if we could interpret all 120 permutations of the five cubes, represented by the letters A, B, C, D and E, one by one as the 120 symmetry transformations of the Regular Icosahedron (and Regular Dodecahedron), then there would be an isomorphism between the group S5 and the full group of the Icosahedron (and Dodecahedron). We can show, however, that this is not the case :

As has been said, we can determine the enantiomorphs of the Icosahedron (and Dodecahedron) by multiplying (i.e. combining) each direct symmetry by the central inversion ( = reflection in the central point of the solid). If we combine a half-turn with central inversion, we get a reflection in a plane (mirror reflection). Well, as we saw above, there are 15 half-turns present in our solids, and when we combine each of them with central inversion ( =  rotate 1800, then invert the result through the solid's mid-point), we get 15 mirror reflections (which are thus enantiomorphs), which indeed are present in our solids.
So we have in the Icosahedron and Dodecahedron 15 elements of period 2, which should correspond to 15 odd permutations (because (all) the even permutations represent all the direct symmetries). Well, among the odd permutations we find the periods 4 and 6, and only 10 permutations of period 2. So there is no genuine correspondence between the symmetries and the permutations (of five letters), and this is equivalent to  products not being preserved  (when going from the symmetries to the permutations of five letters (standing for inscribed cubes)). And this means that the full group of the Icosahedron (Dodecahedron), which can legitimately be denoted as the product group A5 x C2, is not isomorphic to the group S5, the group of all permutations (even and odd) of five letters.
Next we give illustrations of the Regular Icosahedron and Regular Dodecahedron.

Figure 13.   The Regular Icosahedron.

Figure 14.   The Regular Dodecahedron.
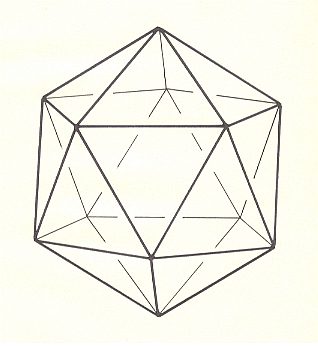
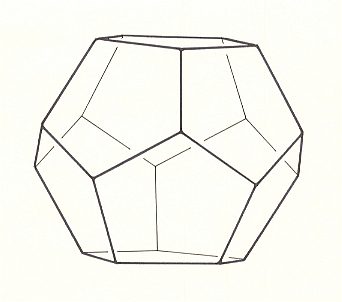
The group A5 x C2 is not, and cannot be, represented in crystals.
In the Promorphological System of basic forms it is realized as
Icosaedra regularia, and as
Dodecaedra regularia.
This concludes our exposition of the symmetry groups, their crystallography and their promorphology.
In the next document we will continue our preparatory study of Group Theory, adding some more considerations about cosets.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals

back to homepage

back to retrospect and continuation page

back to Part I of the theoretical preparation to the study of 3-D crystals

back to Part II of the theoretical preparation to the study of 3-D crystals

back to Part III of the theoretical preparation to the study of 3-D crystals

back to Part IV of the theoretical preparation to the study of 3-D crystals

back to Part V of the theoretical preparation to the study of 3-D crystals

back to Part VI of the theoretical preparation to the study of 3-D crystals

back to Part VII of the theoretical preparation to the study of 3-D crystals

back to Part VIII of the theoretical preparation to the study of 3-D crystals

back to Part IX of the theoretical preparation to the study of 3-D crystals

back to Part X of the theoretical preparation to the study of 3-D crystals

back to Part XI of the theoretical preparation to the study of 3-D crystals

back to Part XII of the theoretical preparation to the study of 3-D crystals

****************