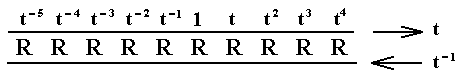
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Sequel to Cyclic Groups
In the previous documents we have discussed finite cyclic groups, i.e. cyclic groups of finite order, which means that they consist of a finite number of elements. We considered groups of prime order meaning that the number n, indicating the number of elements is a prime number, i.e. a number that is divisible by itself and by 1 only. Groups of prime order are always cyclic, and they have no subgroups. We also considered cyclic groups of composite order (i.e. where the order n is not prime). These groups have subgroups. The latter entail a lot of interesting features, like cosets, normal subgroups and homomorphisms. We have exemplified these with the cyclic group of order 12, i.e. C12.
Having seen something of cyclic groups you will be in a position to appreciate the following theorems, which are given here without proof (BUDDEN, 1978, pp. 175) :
Infinite cyclic group.
Our treatment of Group Theory is geared towards a deeper understanding of the symmetries of crystals. Especially for the symmetries of the internal order of crystals, cyclic groups of infinite order, and thus having infinitely many elements, are very important. Realized crystallographically the elements of such groups are symmetry operations, one type of them being translations. When we have some infinite pattern, and when we shift this pattern a certain distance along some direction, and when, after having done so, the pattern is precisely mapped onto itself, the pattern is said to possess translational symmetry. Such a translation can be indicated by a vector.
The set Z of integers, which is the set {..., -3, -2, -1, 0, 1, 2, 3, ...} forms a group under ordinary addition. We write (Z, +). The element 0 is the identity element, because 0 + x = x + 0 = x, for every element x of this group. And the group is infinite because repeated application of any element except the identity will never reach 0, which means that the period of every element except the identity is infinite.
This group, and isomorphic copies of it, is the cyclic group of infinite order, Cinfinite. It is infinite, because and can be generated by a single element 1 and its inverse -1 (which can also be written as 1-1).
Another way of generating Cinfinite is by means of a single translation, as in the next Figure.
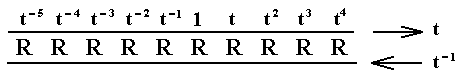
Figure 1. The symmetry group Cinfinite
The strip pattern is derived from repeated applications of the translation t applied to the letter R.
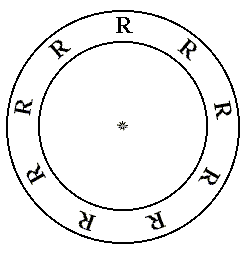
Figure 2. The symmetry group C9
The above pattern is according to the cyclic group of order 9. It is generated by a rotation through an angle of 400.
Infinite groups can also be generated by elements each of which has a finite period, for instance the reflections in two parallel mirrors, and indeed a reflection has period 2. An infinite sequence of images is generated (We are familiar with this phenomenon when we look into a mirror while having placed a second mirror behind us, parallel to the first. We then see an infinity of images of ourselves. The infinite group that is thus generated is the group Dinfinite).
The Dihedral Group
The symmetry of objects having in addition to rotational symmetries (direct symmetries) with respect to one center, also reflectional symmetries (opposite symmetries), like the regular polygons, can be described by one or another dihedral group.
The group elements of the symmetry of a regular polygon are rotations and reflections and all possible combinations of them, for instance a rotation followed by a reflection in some reflection line (mirror line). The problem is that we must decide whether such a reflection line is itself rotated by the mentioned rotation, or whether it should be considered a fixed reflection line. In order to avoid confusion we will distinguish between the vertices themselves of a polygon, and their respective positions. See next Figure, depicting the simplest regular polygon, the equilateral triangle.
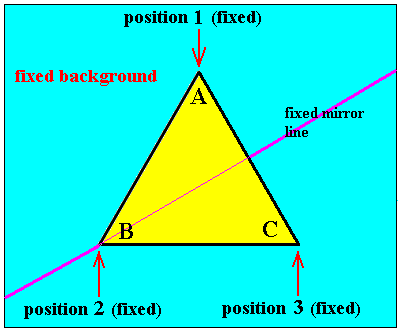
Figure 3. The equilateral triangle in its fixed background. The vertices A, B and C of the triangle can move from one position to another. The positions themselves, (1), (2) and (3), are fixed. Also the three mirror lines, supported by the triangle, are not moved (one such mirror line is depicted). The positions of the vertices as they are in this Figure will be considered as the identity transformation.
For all of the following -- concerning the equilateral triangle -- we consider the situation as depicted in Figure 3 as the initial condition :
The initial position of vertex A is position 1.
The initial position of vertex B is position 2.
The initial position of vertex C is position 3.
The triangle can be rotated by 0, 120 or 240 degrees about its mid-point effecting the triangle occupying the same patch of space again as before those operations had taken place. So the vertices -- which are parts of the triangle -- move with respect to the background. And now comes the important thing : The symmetry lines, supported by the triangle are not part of the triangle, so they are not moved when the triangle is rotated.
The next Figure illustrates an anticlockwise rotation, named p, of the triangle by 1200.
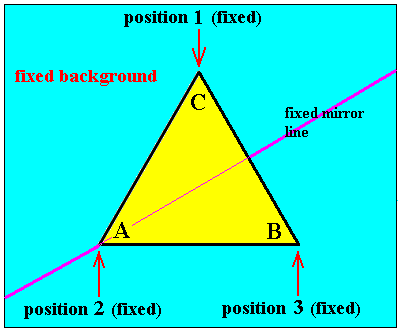
Figure 4. The equilateral triangle of Figure 3 is rotated anticlockwise through an angle of 1200. This symmetry transformation is here called p.
Well, now we do NOT say that the rotation p is a permutation
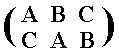
One vertex of the triangle moves from position 1 to position 2.
One vertex of the triangle moves from position 2 to position 3.
One vertex of the triangle moves from position 3 to position 1.
So we describe the rotation p by the permutation of the positions :
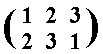
Next we will illustrate a reflection b. And that is a reflection of the triangle as it is in Figure 3, through the mirror line indicated in that figure. This mirror line has a fixed position, because it is not a part of the triangle.
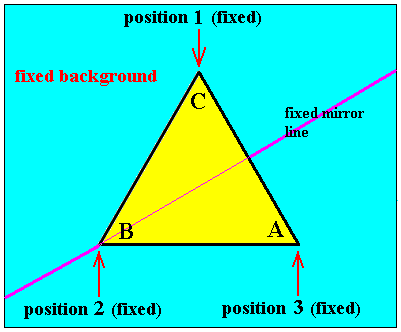
Figure 5. The equilateral triangle of Figure 3 is reflected in the mirror line indicated (This mirror line is called b).
As we see in Figure 5, reflection of the triangle in the mirror line b implies that the positions of the vertices A and C are interchanged :
Thus we will describe the reflection b as the following permutation of positions :
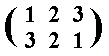
Next we will illustrate the rotation p, immediately followed by the reflection b, i.e. the symmetry transformation bp : first an anticlockwise rotation of the triangle by 1200 followed by a reflection in the fixed axis (mirror line) b, i.e. we consider the mirror line b NOT having been moved by the rotation p, because, so we could say, mirror lines do not, as a concrete part, belong to the triangle. Reflection takes place across its original position. See next Figure.
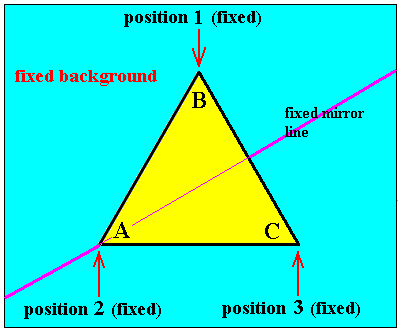
Figure 5. The equilateral triangle of Figure 3 is first rotated anticlockwise by 1200 and then reflected in the mirror line indicated (This mirror line is called b). The mirror line has not been moved by the rotation. The total symmetry transformation is bp.
So the symmetry transformation of Figure 5, namely bp, effects that
And this is equivalent to a reflection c , i.e. a reflection across a mirror line that goes through vertex C in its original position. We can indicate this symmetry transformation bp = c by the following permutation of positions :
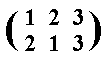
So with respect to the symmetry transformations of the lateral triangle (trigon) we have some first results :

We still have to account for a rotation by 2400 ( = p2 ) ( p3 amounts to a rotation by 3600, which is equivalent to no rotation at all, i.e. to a rotation of 00 ). Further there are two more reflections, one across the axis through vertex A-in-its-original-position, this reflection we will call a, and another across the axis through the vertex C-in-its-original-position. This reflection we will call c.
p2 is indicated in the next Figure.
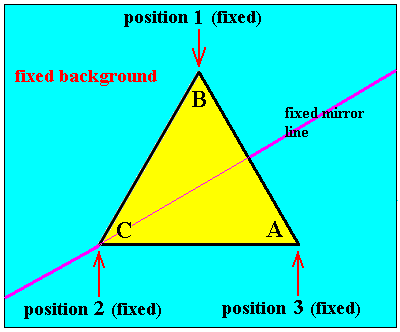
Figure 6. The equilateral triangle of Figure 3 is rotated anticlockwise by 2400. This symmetry transformation is here called p2 (i.e. applying p two times).
To express p2 correctly as a permutation we must say :
One vertex of the triangle has moved from position 1 to position 3,
One vertex of the triangle has moved from position 3 to position 2,
One vertex of the triangle has moved from position 2 to position 1.
The original positions of the vertices A, B and C (representing the identity transformation) are depicted in Figure 3, and explicitly stated below that Figure.
This rotation p2 can now be expressed as the following permutation of positions :
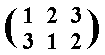
Next we have the reflection a, which is a reflection across the bisector through vertex A-in-its-original-position. See next Figure.
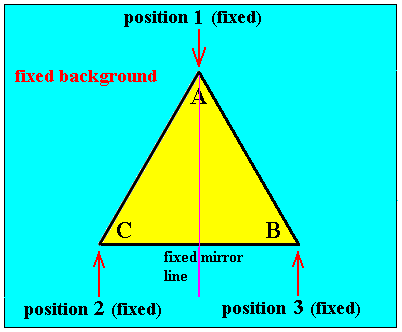
Figure 7. Reflection of the equilateral triangle of Figure 3 across the bisector through the vertex A-in-its-original-position. This symmetry transformation is here called a.
To express this transformation correctly in terms of a permutation we must say that in transformation a
So transformation a can be expressed as a permutation of positions :
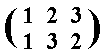
Finally, the transformation c is a reflection of the triangle across the bisector through the vertex C-in-its-original-position. See next Figure.
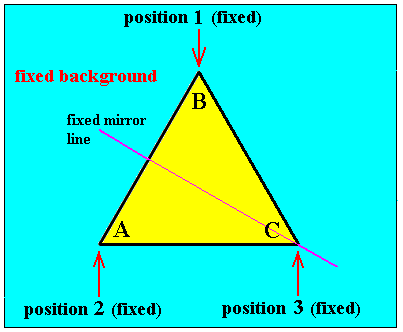
Figure 8. Reflection of the equilateral triangle of Figure 3 across the bisector through vertex C-in-its-original-position. This transformation is here called c.
To express this transformation as a permutation we must say that in transformation c
So transformation c can be expressed as the following permutation of positions :
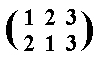
So we can now summarize all six permutations expressing the symmetry of the equilateral triangle :
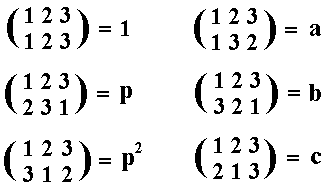
These six permutations, representing the corresponding symmetry transformations, form the dihedral group D3. When we want to construct the group table we must determine all possible binary combinations (which should turn out always to be one of the elements, 1, p, p2, a, b, c), i.e. combinations (products) such as ap (which means transformation p followed by transformation a).
We can determine these by means of the established permutations of positions. We could for instance determine ap by successively applying the corresponding permutations. In doing so we write the permutations below each other, starting with the identity, and writing down only the lower set of symbols of the relevant permutation. So the permutation p replaces 1 by 2, 2 by 3, and 3 by 1, while the permutation a replaces 1 by 1, 2 by 3, and 3 by 2.
Determining ap then goes as follows :
1 2 3
2 3 1 application of p to the identity.
3 2 1 application of a. The result is equal to the permutation b.
So ap = b.
In the same way we determine all the products :
The product pa.
1 2 3
1 3 2
2 1 3 = c
So pa = c.
We see that pa is different from ap, so the group (D3) is not commutative (non-Abelian).
The product pb.
1 2 3
3 2 1
1 3 2 = a
So pb = a.
The product pc.
1 2 3
2 1 3
3 2 1 = b
So pc = b.
The product p2a.
1 2 3
1 3 2
3 2 1 = b
So p2a = b.
The product p2b.
1 2 3
3 2 1
2 1 3 = c
So p2b = c.
The product p2c.
1 2 3
2 1 3
1 3 2 = a
So p2c = a.
The product ap2.
1 2 3
3 1 2
2 1 3 = c
So ap2 = c.
The product aa.
1 2 3
1 3 2
1 2 3 = 1 (identity). Indeed, a is a reflection, and if we perform it two times we end up with what things were, before we applied the reflections.
So aa = 1.
The product ab.
1 2 3
3 2 1
2 3 1 = p
So ab = p.
The product ac.
1 2 3
2 1 3
3 1 2 = p2
So ac = p2.
The product bp.
1 2 3
2 3 1
2 1 3 = c
So bp = c.
The product bp2.
1 2 3
3 1 2
1 3 2 = a
So bp2 = a.
The product ba.
1 2 3
1 3 2
3 1 2 = p2
So ba = p2.
bb = 1 (because b is a reflection).
The product bc.
1 2 3
2 1 3
2 3 1 = p
So bc = p.
The product cp.
1 2 3
2 3 1
1 3 2 = a
So cp = a.
The product cp2.
1 2 3
3 1 2
3 2 1 = b
So cp2 = b.
The product ca.
1 2 3
1 3 2
2 3 1 = p
So ca = p.
The product cb.
1 2 3
3 2 1
3 1 2 = p2
So cb = p2.
cc = 1, because c is a reflection.
pp2 = p2p = p3 = 1, because 1200 + 2400 = 3600 = 00 = 1 (identity).
p2p2 = p4 = pp3 = p1 = p.
On the basis of these results we can set up a group table for our group D3 :
| 1 | p | p2 | a | b | c | period | |
| 1 | 1 | p | p2 | a | b | c | 1 |
| p | p | p2 | 1 | c | a | b | 3 |
| p2 | p2 | 1 | p | b | c | a | 3 |
| a | a | b | c | 1 | p | p2 | 2 |
| b | b | c | a | p2 | 1 | p | 2 |
| c | c | a | b | p | p2 | 1 | 2 |
Table 7.1
We can see that the group admits of a homomorphic mapping to the group C2.
The group also has some subgroups, namely {1, p, p2}, {1, a}, {1, b} and {1, c}.
| 1 | p | p2 | a | b | c | period | |
| 1 | 1 | p | p2 | a | b | c | 1 |
| p | p | p2 | 1 | c | a | b | 3 |
| p2 | p2 | 1 | p | b | c | a | 3 |
| a | a | b | c | 1 | p | p2 | 2 |
| b | b | c | a | p2 | 1 | p | 2 |
| c | c | a | b | p | p2 | 1 | 2 |
Table 7.2
The group table of D3 with the subgroup {1, p, p2} ( = C3 ) highlighted (red).
| 1 | p | p2 | a | b | c | period | |
| 1 | 1 | p | p2 | a | b | c | 1 |
| p | p | p2 | 1 | c | a | b | 3 |
| p2 | p2 | 1 | p | b | c | a | 3 |
| a | a | b | c | 1 | p | p2 | 2 |
| b | b | c | a | p2 | 1 | p | 2 |
| c | c | a | b | p | p2 | 1 | 2 |
Table 7.3
The table of the group D3 with the subgroup {1, a} ( = C2 ) highlighted (red).
| 1 | p | p2 | a | b | c | period | |
| 1 | 1 | p | p2 | a | b | c | 1 |
| p | p | p2 | 1 | c | a | b | 3 |
| p2 | p2 | 1 | p | b | c | a | 3 |
| a | a | b | c | 1 | p | p2 | 2 |
| b | b | c | a | p2 | 1 | p | 2 |
| c | c | a | b | p | p2 | 1 | 2 |
Table 7.4
The table of the group D3 with the subgroup {1, b} ( = C2 ) highlighted (red).
| 1 | p | p2 | a | b | c | period | |
| 1 | 1 | p | p2 | a | b | c | 1 |
| p | p | p2 | 1 | c | a | b | 3 |
| p2 | p2 | 1 | p | b | c | a | 3 |
| a | a | b | c | 1 | p | p2 | 2 |
| b | b | c | a | p2 | 1 | p | 2 |
| c | c | a | b | p | p2 | 1 | 2 |
Table 7.5
The table of the group D3 with the subgroup {1, c} ( = C2 ) highlighted (red).
If we take, instead of the equilateral triangle (regular trigon), a regular 3-fold pyramid, i.e. a regular trigonal pyramid, we do not add or destroy any symmetry, so the symmetry of this single trigonal pyramid is also according to the group D3. And as such it is the promorph or stereometric basic form of all crystals of Ditrigonal-pyramidal Class (3m) of the Hexagonal Crystal System.
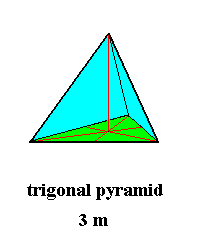
Figure 8a. The trigonal pyramid representing the promorph of all the (single non-twinned) crystals of the Ditrigonal-pyramidal Class of the Hexagonal Crystal System.
The regular trigonal pyramid belongs as promorph to the Anisopola triactinota (Stauraxonia heteropola homostaura) of the Promorphological System of Basic Forms.
Now because the reflections a, b and c can also be interpreted as half-turns (1800 rotations) of the equilateral triangle through the third dimension about the respective reflection lines, this group of six symmetry transformations is at the same time the group of direct symmetries (i.e. the rotational symmetries only) of the trigonal bipyramid, and also of the trigonal prism. The three reflections a, b and c are then half-turns about axes coinciding with the bisectors of the triangular equatorial plane of the trigonal bipyramid (or trigonal prism). See next Figure.
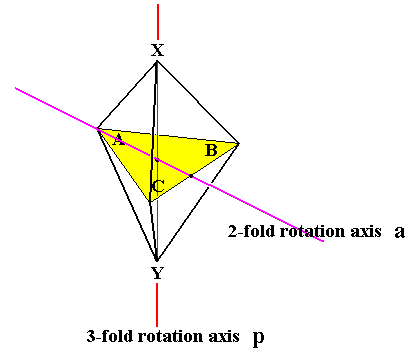
Figure 9. The trigonal bipyramid.
Its direct symmetries are according to the group D3. It has one 3-fold rotation axis, allowing for rotations of 00 (identity), 1200 (p), and 2400 (p2). Further it has three 2-fold rotation axes (one is depicted in the Figure), coinciding with the three bisectors of the triangular equatorial plane. These are equivalent to the three mirror lines of tyhe equilateral triangle.
The direct symmetries of the trigonal prism are identical to those if the trigonal bipyramid.
When we want to describe the full symmetry of the trigonal bipyramid we must add the enantiomorphs, i.e. its reflectional symmetries. These are :
A reflection across the equatorial plane. This leaves the positions of the vertices of the equilateral triangle (= the equatorial plane of the bipyramid) unchanged, but interchanges the positions of X and Y (See Figure 9).
A reflection across the equatorial plane followed by an anticlockwise rotation about the main axis of 1200.
A reflection across the equatorial plane followed by an anticlockwise rotation about the main axis of 2400.
A reflection across the (vertical) meridian plane through vertex A-in-its-original-position.
A reflection across the (vertical) meridian plane through vertex B-in-its-original-position.
A reflection across the (vertical) meridian plane through vertex C-in-its-original-position.
This effects a total of 12 symmetry transformations forming the group D6.
So the full symmetry of the trigonal bipyramid (and also of the trigonal prism) is according to the group D6.
And this group D6 is also the group of all symmetries of the regular hexagon.
In order to verify this we must examine the 12 symmetry transformations especially with respect to their periods. In order to do so we must see by what permutations they can be represented. With respect to the trigonal bipyramid we must add two more vertices X and Y, to represent the apices of the bipyramid (See Figure 9). So we now have to do with permutations of five positions that the five vertices A, B, C, X and Y could visit. We will give the permutations by their lower part only. The rotations p and p2 do not let X and Y change position. But the reflections a, b, and c can be interpreted as 'flipping-overs' of the original equilateral triangle, and thus as half-turns about the bisectors lying in the equatorial plane of the bipyramid (One such axis is indicated in Figure 9). So these half-turns (1800) do interchange the positions of the vertices X and Y. Let the initial position of vertex X be U (= up), and that of Y be D (= down). So for the direct symmetries of the trigonal bipyramid we have the following permutations and their periods :
1 = 1 2 3 U D. Period = 1
p = 2 3 1 U D. Period = 3
p2 = 3 1 2 U D. Period = 3
a = 1 3 2 D U. Period = 2
b = 3 2 1 D U. Period = 2
c = 2 1 3 D U. Period = 2
Now we have to add the above mentioned enantiomorphs (reflectional symmetries, opposite symmetries).
I. A reflection across the equatorial plane. This leaves the positions of the vertices of the equilateral triangle (= the equatorial plane of the bipyramid) unchanged, but interchanges the positions of X and Y (See Figure 9). This corresponds to the permutation 1 2 3 D U.
II. A reflection across the equatorial plane followed by an anticlockwise rotation about the main axis of 1200. This corresponds to the permutation 2 3 1 D U.
III. A reflection across the equatorial plane followed by an anticlockwise rotation about the main axis of 2400. This corresponds to the permutation 3 1 2 D U.
IV. A reflection across the (vertical) meridian plane through vertex A-in-its-original-position. This is just a reflection across a vertical plane of the trigonal bipyramid, so the positions of X and Y are not interchanged. Thuso the corresponding permutation is 1 3 2 U D.
V. A reflection across the (vertical) meridian plane through vertex B-in-its-original-position. This also is just a reflection across a vertical plane of the trigonal bipyramid, so the positions of X and Y are not interchanged. Thus the corresponding permutation is 3 2 1 U D.
VI. A reflection across the (vertical) meridian plane through vertex C-in-its-original-position. Also this, finally, is just a reflection across a vertical plane of the trigonal bipyramid, so the positions of X and Y are not interchanged.
Thus the corresponding permutation is 2 1 3 U D.
We will now determine the periods of these latter six permutations, by reatedly apply each permutation till the identity is reached.
For I :
1 2 3 U D
1 2 3 D U
1 2 3 U D
So the period of element I is 2.
For II :
1 2 3 U D
2 3 1 D U
3 1 2 U D
1 2 3 D U
2 3 1 U D
3 1 2 D U
1 2 3 U D
So the period of element II is 6.
For III :
1 2 3 U D
3 1 2 D U
2 3 1 U D
1 2 3 D U
3 1 2 U D
2 3 1 D U
1 2 3 U D
So the period of element III is 6.
For IV :
1 2 3 U D
1 3 2 U D
1 2 3 U D
So the period of element IV is 2.
For V :
1 2 3 U D
3 2 1 U D
1 2 3 U D
So the period of element V is 2.
For VI :
1 2 3 U D
2 1 3 U D
1 2 3 U D
So the period of element VI is 2.
Let us now summarize all these twelve permutations representing the symmetry transformations of the trigonal bipyramid :
1 = 1 2 3 U D. Period = 1
p = 2 3 1 U D. Period = 3
p2 = 3 1 2 U D. Period = 3
a = 1 3 2 D U. Period = 2
b = 3 2 1 D U. Period = 2
c = 2 1 3 D U. Period = 2
I = 1 2 3 D U. Period = 2
II = 2 3 1 D U . Period = 6
III = 3 1 2 D U . Period = 6
IV = 1 3 2 U D . Period = 2
V = 3 2 1 U D . Period = 2
VI = 2 1 3 U D . Period = 2
This period distribution is indeed the finger print of the dihedral group D6.
The Trigonal Bipyramid which has -- as we found out -- a D6 symmetry, is the promorph or stereometric basic form of all the (single, non-twinned) crystals of the Ditrigonal-bipyramidal Class, 6* m 2, of the Hexagonal Crystal System. This promorph belongs to the Isostaura polypleura (hexapleura) (Stauraxonia homopola) in the Promorphological System of Basic Forms .
And from here it is possible to lay the connection with the symmetry of the regular hexagon :, i.e. it is possible to bring the symmetry transformations of the trigonal bipyramid into a 1,1 correspondence and thereby preserving products. Said differently, the group of all symmetry transformations of the trigonal bipyramid is isomorph to the group of all symmetry transformations of the regular hexagon.
We will now consider the symmetry transformations of the regular hexagon and see whether it is indeed possible to set up the mentioned isomorphism.
The regular hexagon possesses the following symmetry transformations :
Rotations of 00, 600, 1200, 1800, 2400, and 3000 about the hexagon's mid-point.
Two types of reflections : reflections across lines connecting opposite vertices, and reflection across lines connecting centers of opposite sides.
The next Figure indicates those symmetries.
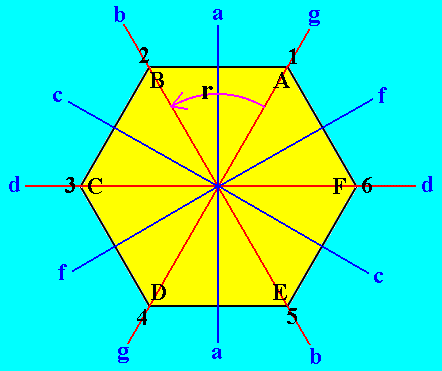
Figure 10. The Regular Hexagon and its symmetries.
There are six mirror lines, indicated as a, b, c, d, f, g, and six rotations of which one is indicated : r = 600. The other rotations are 1 (= 00, identity), r2 = 1200, r3 = 1800, r4 = 2400, r5 = 3000. The vertices A, B, C, D, E and F can move to the fixed positions 1, 2, 3, 4, 5 and 6.
The rotations of the regular hexagon will be called respectively :
Let's determine the periods of these elements :
The period of 1 (identity) is 1, because it is directly 1, without any powering.
The period of r (600 rotation) is 6, because 60 + 60 + 60 + 60 + 60 + 60 = r6 = 3600 = (effectively) 00 = 1 (identity).
The period of r2 (1200) is 3, because 120 + 120 + 120 = (r2)3 = 360 = 1 (identity).
The period of r3 (1800) is 2, because 180 + 180 = (r3)2 = 3600 = 1 (identity).
The period of r4 (2400) is 3, because 240 + 240 + 240 = 480 + 240 = 120 + 240 = 3600 = 1 (identity).
The period of r5 (3000) is 6, because 300 + 300 + 300 + 300 + 300 + 300 = 240 + 300 + 300 + 300 + 300 = 180 + 300 + 300 + 300 = 120 + 300 + 300 = 60 + 300 = 3600 = 1 (identity).
Because a, b, c, d, f, and g are reflections, their period is 2. So we can say
The period of a is 2.
The period of b is 2.
The period of c is 2.
The period of d is 2.
The period of f is 2.
The period of g is 2.
So the pattern of periods of the symmetry transformations (group elements) of the regular hexagon is :
1, 6, 3, 2, 3, 6, 2, 2, 2, 2, 2, 2
And this is indeed the finger print of the dihedral group D6.
We can now set up our isomorphism from the group of all symmetries of the trigonal bipyramid to the group of all symmetries of the regular hexagon. In this isomorphism the periods of the corresponding elements must match :
1 ---------- Period = 1 ---------- 1 (identity)
p ---------- Period = 3 ---------- r2
p2 ---------- Period = 3 ---------- r4
a ---------- Period = 2 ---------- a
b ---------- Period = 2 ---------- b
c ---------- Period = 2 ---------- c
I ---------- Period = 2 ---------- d
II ---------- Period = 6 ---------- r
III ---------- Period = 6 ---------- r5
IV ---------- Period = 2 ---------- f
V ---------- Period = 2 ---------- g
VI ---------- Period = 2 ---------- r3
By this isomorphism there are some elements related to each other which are different symmetries, for example
the element III of the group of symmetries of the trigonal bipyramid is a reflection across the equatorial plane followed by an anticlockwise rotation about the main axis of 2400. So this is an opposite symmetry. It is -- by the above isomorphism -- related to the element r5 of the group of symmetries of the regular hexagon. And this is a direct symmetry (a rotation of 3000). This relating is fully legitimate, because the respective periods are the same.
It is perhaps instructive to illustrate this with respect to the group C2. In addition to having a realization in finite arithmetics this group has three crystallographic realizations, realizations where different symmetries are involved, but whose groups are fully isomorph (i.e. group theoretically equivalent). See next group tables which are all expressing the group C2.
| + mod 2 | 0 | 1 | period |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 2 |
Table 7.6
Realization of the group C2 in finite arithmetics. The group elements are numbers.
| 1 | m | period | |
| 1 | 1 | m | 1 |
| m | m | 1 | 2 |
Table 7.7
Realization of the group C2 in crystallography. The group elements are the identity (1) and a reflection (m). As such it represents the symmetry of crystals of the Domatic Class of the Monoclinic Crystal System.
| 1 | r | period | |
| 1 | 1 | r | 1 |
| r | r | 1 | 2 |
Table 7.8
Another realization of the group C2 in crystallography. The group elements are the identity (1) and a half-turn (rotation of 1800) (r). As such it represents the symmetry of crystals of the Sphenoidic Class of the Monoclinic Crystal System.
| 1 | i | period | |
| 1 | 1 | i | 1 |
| i | i | 1 | 2 |
Table 7.9
Yet another realization of the group C2 in crystallography. The group elements are the identity (1) and an inversion ( = reflection across a point, the mid-point of the crystal) ( i ). As such it represents the symmetry of crystals of the Pinacoidal Class of the Triclinic Crystal System.
So we can now set up the group table of the dihedral group D6 using the notation that was used to indicate the symmetries of the regular hexagon. In order to do so all possible products of these symmetry transformations must be determined. We will do so for a few of them only, but nevertheless give the full table. To start with we reproduce Figure 10, depicting the regular hexagon and its possible symmetry transformations.

Figure 10 (replay). The Regular Hexagon and its symmetries.
There are six mirror lines, indicated as a, b, c, d, f, g, and six rotations of which one is indicated : r = 600. The other rotations are 1 (= 00, identity), r2 = 1200, r3 = 1800, r4 = 2400, r5 = 3000. The vertices A, B, C, D, E and F can move to the fixed positions 1, 2, 3, 4, 5 and 6.
Let us determine the product ar4.
See next Figure :
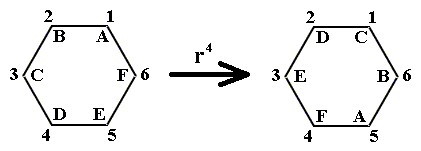
Figure 11. The transformation r4 performed on the regular hexagon.
So r4 can be represented by the permutation
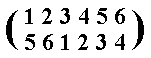
and by the cycle (153)(264).
In order to complete the transformation ar4 (i.e. the product of a and r4) we must now apply to the just obtained result the transformation a which is a reflection in the fixed axis a (Figure 10). The next Figure illustrates this completion.
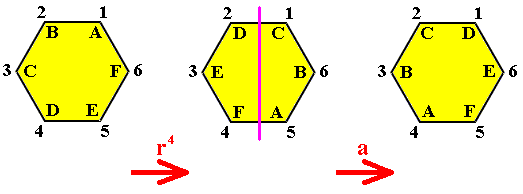
Figure 12. The complete transformation ar4 on the regular hexagon.
The movements corresponding to the transformation a are as follows :
So the permutation representing the transformation a is :
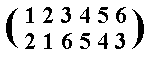
and is the cycle (12)(36)(45).
The movements corresponding to the whole transformation ar4 are then as follows :
vertex A going from position 1 to position 4,
vertex B going from position 2 to position 3,
vertex C going from position 3 to position 2,
vertex D going from position 4 to position 1,
vertex E going from position 5 to position 6,
vertex F going from position 6 to position 5.
So the permutation representing the transformation ar4 is
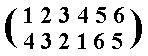
which is the cycle (14)(23)(56), which corresponds to the transformation c, which is a reflection in the axis labelled c (Figure 10). So we can say that ar4 = c (i.e. the product of the elements a and r4 is equal to the element c).
In the same way we can determine the product fb : first we perform the reflection in the axis b (Figure 10), and then the reflection in the axis f (Figure 10) :
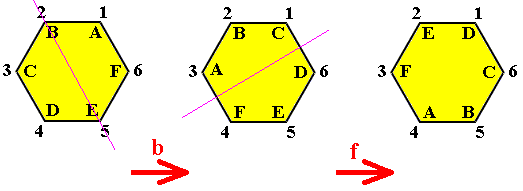
Figure 13. The transformation fb applied to the regular hexagon.
And we can see that the effect of fb is a rotation by 1800, corresponding to the transformation r3, so fb = r3.
Further we can determine the product ba. First we apply reflection in the a axis, followed by a reflection in the b axis :
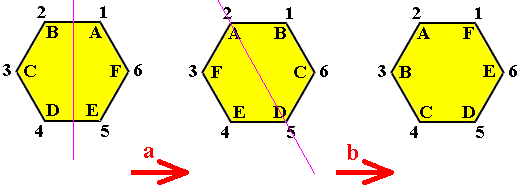
Figure 14. The transformation ba applied to the regular hexagon.
We can see that the effect of ba is a rotation of 600 anticlockwise, and thus we have ba = r.
Thus we have combined several pairs of symmetries of the regular hexagon, and this is a start towards drawing up a complete table of the group of symmetries.
The method presented, though it is instructive, is very laborious for us to obtain all the 12 x 12 = 144 possible combinations of symmetries. Instead we should, in each case, follow one particular vertex, see its starting position, and then determine its final position with respect to the relevant product. In the last example, concerning ba we know that the transformation a takes the vertex A from position 1 to position 2. Having arrived there, it will not suffer any further movement, because anything in that position remains where it was when a reflection in the axis b is applied. So, in terms of the permutation of positions, we get :
1 -- 2 and 2 -- 2, thus (as total result) 1 -- 2
Two reflections (a and b) effect a non-reflectional result, so the latter must be a rotation, and here this evidently is a rotation of 600 anticlockwise and corresponds to the transformation r.
Indeed when we have followed the fate of just one vertex we must determine whether the result is a reflectional or a rotational transformation before assessing the final result as to what it is. Let's illustrate this with the example of the product r4a. First a, then r4. By the transformation a the vertex A is taken from position 1 to position 2. Then the transformation r4 takes it to position 6. So all in all we get a shift from position 1 to position 6. This looks like a rotation of 3000, i.e. r5, but, we know that the final result must be a reflection, because there has taken place one reflection, and not a second one to make the reflectional character undone. And thus the final result is a reflection in the axis f, and so we have
r4a = f.
In this way we can determine all 144 symmetry combinations resulting in the following group table for our dihedral group D6 :
| 1 | r | r2 | r3 | r4 | r5 | a | b | c | d | f | g | period | |
| 1 | 1 | r | r2 | r3 | r4 | r5 | a | b | c | d | f | g | 1 |
| r | r | r2 | r3 | r4 | r5 | 1 | b | c | d | f | g | a | 6 |
| r2 | r2 | r3 | r4 | r5 | 1 | r | c | d | f | g | a | b | 3 |
| r3 | r3 | r4 | r5 | 1 | r | r2 | d | f | g | a | b | c | 2 |
| r4 | r4 | r5 | 1 | r | r2 | r3 | f | g | a | b | c | d | 3 |
| r5 | r5 | 1 | r | r2 | r3 | r4 | g | a | b | c | d | f | 6 |
| a | a | g | f | d | c | b | 1 | r5 | r4 | r3 | r2 | r | 2 |
| b | b | a | g | f | d | c | r | 1 | r5 | r4 | r3 | r2 | 2 |
| c | c | b | a | g | f | d | r2 | r | 1 | r5 | r4 | r3 | 2 |
| d | d | c | b | a | g | f | r3 | r2 | r | 1 | r5 | r4 | 2 |
| f | f | d | c | b | a | g | r4 | r3 | r2 | r | 1 | r5 | 2 |
| g | g | f | d | c | b | a | r5 | r4 | r3 | r2 | r | 1 | 2 |
Table 7.10
When we take, instead of the regular hexagon, the regular hexagonal pyramid (i.e. a single 6-fold pyramid) we do not add or destroy any symmetry, and thus the symmetry of the regular hexagonal pyramid is according to the dihedral group D6. And as such it is the promorph or stereometric basic form of all the crystals of the Dihexagonal-pyramidal Class (6mm) of the Hexagonal Crystal System.
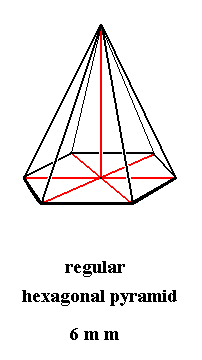
Figure 15. The hexagonal pyramid as the promorph of all the (single non-twinned) crystals of the Dihexagonal-pyramidal Class (6mm) of the Hexagonal Crystal System.
This regular hexagonal pyramid belongs as promorph to the Isopola hexactinota (Stauraxonia heteropola homostaura) of the Promorphological System of basic forms.
The group D6 also describes the direct symmetries of the regular hexagonal bipyramid (and also of the regular hexagonal prism). When we now include the opposite symmetries as well, we get the full symmetry of the hexagonal bipyramid, according to the product group D6 x C2 of order 24 (in crystallography also known as D6i ) (It is not the group D12 : If we have a dihedral group Dn representing the direct symmetries of an n-fold bipyramid, and if we then add the enantiomorphs (i.e. reflections), then we get the group Dn x C2, and this group is only D2n if n is odd (BUDDEN, p. 293)). [Product groups are explained further down (Part IX and Part XII). As such the regular hexagonal bipyramid is the promorph or stereometric basic form of all the single non-twinned crystals of the Dihexagonal-bipyramidal Class (6/m 2/m 2/m) of the Hexagonal Crystal System.
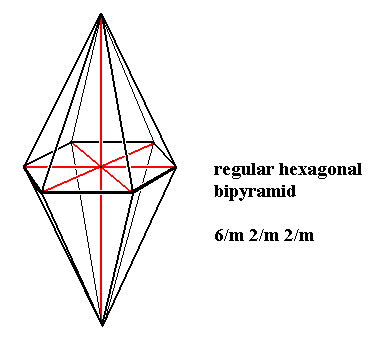
Figure 16. Regular Hexagonal Bipyramid as the promorph of all the crystals of the Dihexagonal-bipyramidal Class of the Hexagonal Crystal System.
This regular hexagonal bipyramid belongs as promorph to the Polypleura dodecapleura (Stauraxonia homopola isostaura) of the Promorphological System of Basic Forms.
The 24 symmetry transformations -- forming the group D6 x C2 -- of the regualar hexagonal bipyramid are the following :
The period distribution, visible in the above list of 24 symmetry transformations, namely 1, 6, 3, 2, 3, 6, 2, 2, 2, 2, 2, 2, 2, 6, 6, 2, 6, 6, 2, 2, 2, 2, 2, 2, is the fingerprint of the product group D6 x C2. This group can also be called D6i.
Subgroups of and Cosets in D6
In the group table of the group D6 (Table 7.10) the order (arrangement) of the elements is chosen such that the cyclic subgroup H (C6) = {1, r, r2, r3, r4, r5} and its cosets stand out clearly. Let's check these cosets.
Left and right cosets of H with respect to the element 1 :
1{1, r, r2, r3, r4, r5} = {1, r, r2, r3, r4, r5}1 = {1, r, r2, r3, r4, r5}.
Left and right cosets of H with respect to the element r :
r{1, r, r2, r3, r4, r5} = {1, r, r2, r3, r4, r5}r = (r1, rr, rr2, rr3, rr4, rr5} = {r, r2, r3, r4, r5, 1}.
Because the subgroup H is cyclic, multiplication with one of its elements does not lead us outside this subgroup, so all cosets of this subgroup with respect to elements of this subgroup are identical to the subgroup itself.
Left coset of H with respect to the element a (This coset we can easily read off from the group table).
a{1, r, r2, r3, r4, r5} = {a1, ar, ar2, ar3, ar4, ar5} = {a, g, f, d, c, b}.
Right coset of H with respect to the element a.
{1, r, r2, r3, r4, r5}a = {1a, ra, r2a, r3a, r4a, r5a} = {a, b, c, d, f, g}.
So aH = Ha.
In the same way we see that for every element x of the group (D6) the following relation holds : xH = Hx. And this means that the subgroup H = {1, r, r2, r3, r4, r5} is a normal subgroup in D6. And this in turn means that this subgroup supports a homomorphism of the whole group to the group C2, i.e. C2 is the homomorphic image group of the group D6 with respect to the subgroup H = {1, r, r2, r3, r4, r5}.
Let's demonstrate this.
In the table we can see this homomorphism clearly : The red squares contain direct symmetries only, while the green squares contain opposite symmetries only. So the two elements of the homomorphic image group of D6 could be DIRECT SYMMETRY, and OPPOSITE SYMMETRY, which we could indicate as DIRECT and OPPOSITE. Now we know that an opposite symmetry followed by another equivalent opposite symmetry results in a direct symmetry. For example, first a reflection in axis a, followed by a reflection in axis b (which is a symmetry transformation that is equivalent to a reflection in a) results in r (ba = r). And two direct symmetries -- two rotations -- being performed successively, result in a direct symmetry again. Further the successive application of a direct symmetry and an opposite symmetry always results in an opposite symmetry. So we have the group {DIRECT, OPPOSITE}, and its table looks like this :
| DIRECT | OPPOSITE | |
| DIRECT | DIRECT | OPPOSITE |
| OPPOSITE | OPPOSITE | DIRECT |
Table 7.11
So the above table depicts the homomorphic image of the dihedral group D6 with respect to the subgroup H = {1, r, r2, r3, r4, r5}, and the structure of this image is that of the cyclic group of order 2, C2.
Other subgroups of the group D6 are the ones that consist of two elements, the identity and an involute element, i.e. an element of period 2. The latter are r3, a, b, c, d, f and g. So these subgroups are {1, r3}, {1, a}, {1, b}, {1, c}, {1, d}, {1, f} and {1, g}. All these evidently have the structure of C2. The table for -- for instance -- {1, a} looks as follows :
| 1 | a | |
| 1 | 1 | a |
| a | a | 1 |
Table 7.12
There are still other subgroups of our group D6, namely those that consist of the identity, and three symmetries of period 2 that are perpedicular to each other, like for instance the rotation r3 ( = 60 + 60 + 60 = 1800), which is a rotation about an axis perpendicular to the plane of the hexagon, which means perpendicular to the mirror lines lying in that plane) together with two reflections across lines lying in the hexagon's plane and which are perpendicular to each other, like a and d (See Figure 10).
| 1 | a | r3 | d | |
| 1 | 1 | a | r3 | d |
| a | a | 1 | d | r3 |
| r3 | r3 | d | 1 | a |
| d | d | r3 | a | 1 |
The group D2 is also considered earlier (Part II).
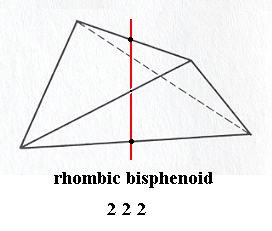
Figure 17. A Rhombic Bisphenoid, the Stereometric Basic Form of the crystals of the Rhombic-bisphenoidic Class of the Orthorhombic Crystal System.
The promorphological main axis is indicated by a red line.
This promorph belongs to the Scalenoidea duomera (Stauraxonia homopola) of the Promorphological System of Basic Forms.
The four symmetry transformations are in this case, the identity (1), and three half-turns (2a, 2b, 2c) about three perpendicular, but nevertheless equivalent, axes, a, b and c. Two half-turns about the same axis results in the identity transformation, while two half-turns about to different axes result in a half-turn about the third axis :
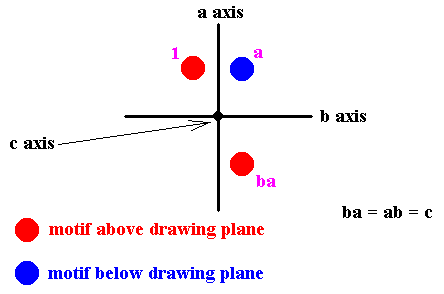
Figure 18. A half-turn about one axis, followed by a half-turn about the other axis, sends the motif to the same place as a half-turn about the third axis.
The group table, specifically for the symmetry of this Crystal Class (222) consists accordingly of the four elements 1, 2a, 2b, and 2c, and looks like this :
| 1 | 2a | 2b | 2c | |
| 1 | 1 | 2a | 2b | 2c |
| 2a | 2a | 1 | 2c | 2b |
| 2b | 2b | 2c | 1 | 2a |
| 2c | 2c | 2b | 2a | 1 |
Another crystallographic realization of the dihedral group D2 is found in crystals of the Rhombic-pyramidal Class (mm2) of the Orthorhombic Crystal System. Here the symmetry transformations are the identity, a half-turn and two mirror reflections. The promorph or stereometric basic form of all the single non-twinned crystals of this Class (mm2) is the Rhombic Pyramid. See next Figure.
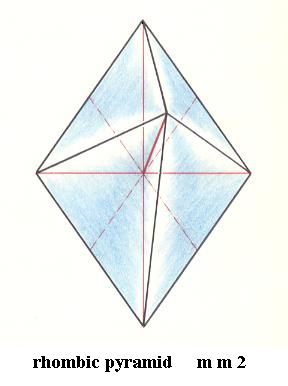
Figure 19. A Rhombic Pyramid, the Stereometric Basic Form of the crystals of the Rhombic-pyramidal Class of the Orthorhombic Crystal System.
The base is a rhombus. The three crystallographic axes are given as reddish solid lines. The one that goes to the pyramid's tip is the promorphological main axis, the other two reddish solid lines are the two promorphological radial cross axes, while the dashed lines are the two interradial cross axes.
This promorph belongs to the Tetraphragma radialia (Stauraxonia heteropola heterostaura autopola) of the Promorphological System of Basic Forms.
The group D2 in its guise of the symmetries of the just mentioned Orthorhombic Crystal Class mm2, consists accordingly of four elements, the identity (1), two mirror planes m1 and m2, perpendicular to each other, and a half-turn about a 2-fold rotation axis coinciding with the line of intersection of the two mirror planes. This half-turn will be denoted 2.
The group table then looks like this :
| 1 | m1 | m2 | 2 | |
| 1 | 1 | m1 | m2 | 2 |
| m1 | m1 | 1 | 2 | m2 |
| m2 | m2 | 2 | 1 | m1 |
| 2 | 2 | m2 | m1 | 1 |
Finally, the third crystallographic realization of the group D2 is to be found in crystals of the Prismatic Class (2/m) of the Monoclinic Crystal System. The promorph of all the single non-twinned crystals of this Class is represented by the Amphitect Gyroid Bipyramid. See next Figure.
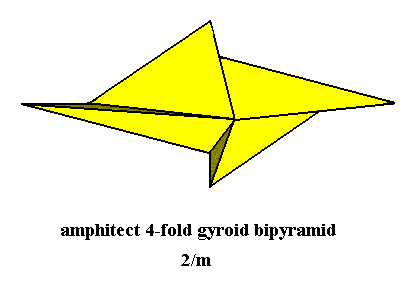
Figure 20. Slightly oblique top view of an Amphitect Gyroid Bipyramid, the Stereometric Basic Form of the crystals of the Prismatic Class of the Monoclinic Crystal System. The depicted bipyramid allows for four antimers to be recognized. The lower pyramid is not visible, but nevertheless present.
This promorph (of the Crystal Class 2/m) belongs to the Allosigmostaura quadramphimera (Stauraxonia homopola sigmostaura) of the Promorphological System of Basic Forms.
The group D2 in its guise of representing the symmetries of the just mentioned Monoclinic Class 2/m, accordingly consists of the identity (1), a half-turn (r), a mirror plane (m) perpendicular to the axis of the half-turn, and a center of symmetry (i) (The latter is a reflection in a point, namely the mid-point of the 2-fold rotation axis). These symmetry transformations are depicted in the next Figure :
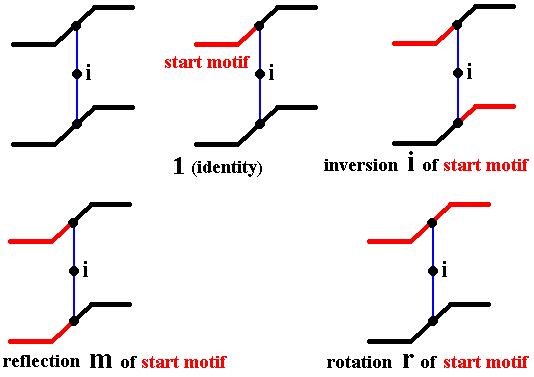
Figure 21. The symmetry transformations in crystals of the Class 2/m.
The vertical blue line is the 2-fold rotation axis.
The center of symmetry (inversion center) is indicated by i. The mirror plane goes through the center of inversion and is perpendicular to the 2-fold rotation axis.
The movement of the starting motif is indicated for the transformations 1 (identity), i (inversion in the point i), m (reflection) and r (half-turn).
From Figure 21 we can determine how these symmetries combine to form the group D2 :
ir = m
ri = m
im = r
mi = r
mr = i
rm = i
i2 = 1
r2 = 1
m2 = 1
On the basis of this we can draw the group table of this crystallographic realization (2/m) of the group D2 :
| 1 | m | r | i | |
| 1 | 1 | m | r | i |
| m | m | 1 | i | r |
| r | r | i | 1 | m |
| i | i | r | m | 1 |
In the next document we continue the study of dihedral groups.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals