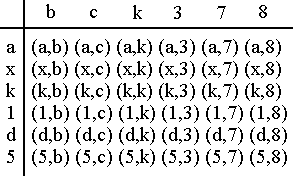
e-mail :

Group Theory
Group Theory, Symmetry, Symmetry-breaking, and Metaphysics.
As has been said, our treatment of Group Theory will almost exclusively aim at an understanding of the symmetry of crystals, it will moreover be informal (which means that we make use of some results of Group Theory found by others).
However, apart from a technical means to understand the symmetries (as an aspect of the structure) of (especially) three-dimensional crystals, Group Theory will have a much wider application within this website, not so much as a technical method but as a sort of philosophical 'unifyer'. First of all, but in a more or less 'by-the-way' sense, the Theory of the Stereometric Basic Forms of (especially) Organisms ("Promorphology"), which is considered in much detail in later documents (See HERE), will be accompanied by Group Theory. To understand the many Basic Forms, Group Theory is not absolutely necessary, but it can reveal unexpected kinships between several such Forms.
Apart from this, Group Theory will be of philosophical significance within this website in the following way :
When we think about the origin of things and features, we see that in one way or another symmetry, abstract or concrete symmetry, is involved.
At the moment of the Big Bang, i.e. at the point of origin of the Universe, there did not exist different fundamental forces, like we know them today : Electromagnetic force, Gravitational force, Strong interaction force, Weak interaction force. There was only one "Superforce". Only later, the known fundamental forces 'froze' out. So in the beginning there was a kind of homogeneity, which later evolved into some heterogeneity. The same can be expressed in different words : First there was maximal symmetry, later there was lower symmetry. We can charaterize such a process as symmetry-breaking.
In those early moments of the Universe the several kinds of atoms could not exist, but later on, when temperatures got lower, they came into existence. Also this can be considered to be a kind of symmetry-breaking.
At still lower temperatures, molecules could begin to form (by means of the chemical bonding of atoms, resulting in a huge variety of atomic configurations). From few atomic species an almost unlimited number of molecular types were generated. So those molecules 'froze' out as soon as the conditions were mild enough. Also this can be considered as a type of symmetry-breaking.
Seen from a high-level standpoint, however, a mass of molecules as such is still a random aggregation of them, not exhibiting any stable pattern, but just a dynamic chaos, that can, on that level, be considered as homogeneous, and thus of maximal symmetry.
But under certain conditions such molecules (but also ions, or single atoms) can form definite macroscopical patterns like crystals and organisms. And also this is a kind of symmetry-breaking, a transition from maximal, or near maximal, symmetry to one or another lower symmetry. Geometrically we can think of the symmetry of a sphere, which has an infinite number of mirror planes and rotations, i.e. it has maximal symmetry. When we now transform this sphere into an ellipsoid (i.e. if we stretch the sphere in one direction), we let one particular symmetry axis stand out, which causes a restriction as to where the mirror planes can lie, and also where, i.e. in what direction, rotational axes can be present. This means that the symmetry is lowered when we go from sphere to ellipsoid. This process of symmetry-breaking, which we can characterize by the ongoing differentiation of poles of symmetry axes, can go on resulting in bipyramids, pyramids, half-pyramids and so on, till total asymmetry has been reached. This total asymmetry does not mean that all features have disappeared. On the contrary, maximal differentiation has resulted : when we follow this process of symmetry-breaking in organisms (which can be seen in their individual development as well as in their evolutionary development) we can end up at, for instance, flat fishes, which in their adult state are totally asymmetric, but their body still represents a definite and stable pattern exhibiting many features. This process of symmetry-breaking, with special reference to Organisms, is described in detail in the mentioned documents on Stereometric Basic Forms (Promorphology).
And we will involve Group Theory when considering the process of symmetry-breaking. The concept of a group is very abstract, but that makes it powerful. Because of its abstractness it is general, and can crop up in many concrete situations, as we will see in the documents (on Group Theory) to come. The generality a group brings it with it that sometimes certain different symmetries fall under the same group. For instance the symmetries of the Crystal Classes m, 2 and 1*, which even divide among different Crystal Systems, are described by the same abstract group, namely the Cyclic Group of order 2. So there must be some kinship between these three diffferent symmetries.
And this leads to the idea that 'below' the 'Basic Forms', as established geometrically in the mentioned Promorphology, there are certain still more basic forms -- abstract forms -- characterized by groups. For example the symmetry of crystals of the mentioned three Crystal Classes, but also the corresponding symmetries of certain organisms, can be represented by three corresponding categories of Basic Forms ('promorphs'), namely the Zygopleura eudipleura, Heterogyrostaura tetramera, and the Anaxonia centrostigma. But they all fall under one and the same group, namely the mentioned Cyclic Group of order 2. So this group represents a still more basic form than the three mentioned. Of course such a group itself is not a form in the geometric sense anymore, it is a fully abstract basic form.
And this means that there exists some Natural System of Abstract Basic Forms that lies at the base of the System of (concrete) Basic Forms, described by Promorphology (on this website). And of course this system of abstract basic forms is somehow contained within Group Theory. Let's say a few words about this (Later it will be elaborated more fully).
Among all the existing groups there are the so-called simple groups, which are groups that have no 'telescopic images' besides the so-called point image (consisting of the identity element alone onto which every element of the given group is mapped), and the whole group itself (We will elaborate on this further down, in the actual treatment of Group Theory). These simple groups are as it were the 'fundamental particles' of finite group theory. Mathematicians set about trying to impose some form of classification on the simple groups. Several families were discovered. First of all a total of 18 infinite 'regular' families of simple groups. An infinite family consists of an infinite number of (finite) groups. The first family of this regular series is the family of all finite cyclic groups of prime order (These are cyclic groups of which the number of elements is prime), and there is an infinity of them. Besides the 18 infinite regular families of simple groups there were found a number of highly irregular 'one-off' groups (i.e. isolated single groups) that did not fit into any known pattern. They came to be called the sporadic simple groups. The smallest of these groups has 7920 elements (See for all this, DEVLIN, K., Mathematics : The New Golden Age, 1988.). The largest has 808017424794512875886459904961710757005754368000000000 elements, and is, because of this enormous number called "The Monster". The discovery of the Monster was one of the last steps in the establisment of the Classification Theorem. It is now known that the finite simple groups consist of the groups which make up the 18 regular, infinite families of groups (the first of which is the family of cyclic groups of prime order), together with the 26 sporadic groups (i.e. individual, one-off groups), and no more. This, by the way, is the result which took up 500 articles and almost 15000 pages in mathematical journals.
It is evident that especially the irregular and very large (but still finite) groups cannot represent and describe (or being able to be realized as) the symmetries of plane geometrical figures or of three-dimensional bodies (to which our discussions of symmetry will be confined). Of course there are infinite groups, i.e. groups with infinitely many elements, that can be realized as symmetries of plane or three-dimensional patterns, namely where those patterns are themselves infinite and moreover consist of a periodic repetition of a certain unit. In crystals such infinite patterns are sufficiently approximated (in the crystal's internal structure) in order for them to be described by infinite groups. And of course we can in principle imagine, say, a pyramid with 808017424794512875886459904961710757005754368000000000 equal sides which has a corresponding rotational symmetry. But the very large, and moreover sporadic groups can never be realized as the symmetry group of one or another geometric figure in two or three space dimensions. But also some modest groups are not symmetry groups, such as the group Q4, which has only eight elements. Q4 does not seem to crop up with any great frequency, i.e. it is only sparsely realized in some concrete case. And most importantly, there is no figure in either two or three dimensions whose symmetry group is Q4 (BUDDEN, F., The Fascination of Groups, 1978, p. 246/7). So only those groups, that can each be realized as a group of symmetries of one or another two- or three-dimensional figure (some finite and some infinite), can together form the System of Abstract Basic Forms. Let's call such groups symmetry groups for short.
Let's now expound the connection of all these matters of symmetry (on this website expounded in the sections on Crystallography and on Promorphology) with the metaphysical theory expounded in the first Part of this website (accessible by clicking back to homepage). There we elaborated the metaphysical concept of the Essence of a being. We found out that only genuine beings (a genuine being is a thing that is an intrinsic whole, in contradistinction to just being an aggregate) possess an essence of their own. Such an essence determines what such a thing is in and by itself, i.e. what it is necessarily. It is the intrinsic whatness of such a thing. It is moreover the thing's intrinsic cause. In the first Part of this website this intrinsic cause or essence is generally identified as follows :
The E s s e n c e or intrinsic cause of a real and genuine being or thing is the D y n a m i c a l L a w of that Dynamical System that generated that thing. This dynamical law is inherent in the system elements, but exists there in a dispersed manner. As essence it exists in the thing generated.
Genuine beings are, for example, individual crystals, and organisms. They are the products of certain dynamical systems each governed by a certain dynamical law. Well, the action of such a dynamical law, when generating such a genuine being, causes the necessary symmetry-breaking of an initially more ore less homogeneous medium, consisting of an unstructured mass of system elements, a mass having maximal or high symmetry. This we clearly see when a crystal is formed from a melt, or when an organism is developed from a fertilized egg cell. But also in the evolutionary process of differentiation of the organic (animal or plant) body we see this process of symmetry-breaking. Symmetry-breaking is equivalent to the origin of more or less stable features, differences, differentiations, functions and forms, out into the world.
So it will be clear that the concept of symmetry is paramount for our undertaking on this website. And that's where Group Theory comes in, because its symmetry groups lie at the basis of all symmetry.
REMARK :
Sets and their Cartesian Product
A set is a collection of objects -- elements -- which all differ from each other (within one and the same set). In Mathematics these elements normally are numbers, functions, matrices, permutations, and so on.
The notation is as follows :
X = {a, x, k, 1, d, 5} denotes the set X consisting of the elements a, x, k, 1, d and 5.
The order of the elements in the above notation for sets is immaterial.
In addition to being finite, a set can be infinite, i.e. can consist of infinite elements, for example the set N = {1, 2, 3, 4, ... }, i.e. the set of all natural numbers.
It is possible to combine two sets in different way. One such combination is very important for our purposes, namely the Cartesian Product of two sets :
The cartesian product of two sets S and T -- denoted as S x T -- is the set of all possible ordered pairs, each pair consisting of an element of S and an element of T. The number of elements in set S must equal the number of elements of T.
For example if we have the set X = {a, x, k, 1, d, 5} and the set Y = {b, c, k, 3, 7, 8} then we can form the cartesian product X x Y in the following way :
The set consisting of all these ordered pairs is the carthesian product of the set X and the set Y (X x Y) It is evident that any cartesian product AxB is not necessary equal to the cartesian product BxA. This is in fact what was meant by "ordered pairs".
A subset S of a set K is a set either containing all elements of the set K and nothing else, or some elements of the set K and nothing else. In the latter case we have to do with a proper subset of K.
Mappings
A mapping form one set to another (or to the same set) is the setting up of corresponding between the elements of the two sets.
A mapping of set A into the set B is a correspondence of elements of set A to a definite elements of set B :
Let us have the sets A = {a, k, c, d} and B = {1, 2, 3, 4, 5, 6}, then a mapping from set A into set B could be the following :
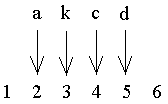
To a (element of X) is definitely assigned 2 (element of Y).
To k (element of X) is definitely assigned 3 (element of Y).
To c (element of X) is definitely assigned 4 (element of Y).
To d (element of X) is definitely assigned 5 (element of Y).
Sometimes a simple prescription suffices, like in the following mapping form X into Y :
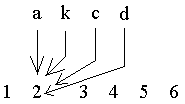
The prescription for this mapping could read :
Assign to each element of the set A, the element 2 of set Y.
Groups
A set, in itself, is just a collection of elements. It has no structure.
We can, however, introduce structure into a set.
One way of doing this is to define a binary operation -- let us call it " * " -- on the elements of a given set S. Such an operation means that to any ordered pair of elements of that set we assign a definite element of that same set. In fact this means that we first take the cartesian product of that set with itself : S x S. We then have the set of all ordered pairs, such that each pair consists of an element of S and another (or the same) element of S :
So with the set A = {a, k, c, d} we take A x A which is the following set : {(a,a),(a,k),(a,c),(a,d),(k,a),(k,k),(k,c),(k,d),(c,a),(c,k),(c,c),(c,d),(d,a),(d,k),(d,c),(d,d)}
When we now assign to each elements of A x A, i.e. to each of the above ordered pairs, a definite element of the set A, then we have defined a mapping from A x A into A, or, differently said, we have defined a binary operation in the set A, and have thus provided the set A with structure.
The set, onto which we have imposed such a structure, i.e. in which we have defined a binary operation, then is a Group if that operation satisfies the following conditions :
An example of an (infinite) Group is the set Z of integers Z = {... -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6,...} under the operation of conventional addition :
When we add whatever two numbers from Z together, we always get a number also belonging to Z, for example 12 + 5 = 17. So the operation " + " is closed for Z.
When we add two numbers from Z, and add to the result a third number from Z, the same result is obtained when we first add the second and third number, and add the result to the first number. For example (3 + 2) + 6 = 3 + (2 + 6) = 11. So the operation " + " is associative.
For every element of our set holds that when it is added to 0, or when 0 is added to it, the result will always be that same element. For example 0 + 3 = 3 = 3 + 0. So we have an identity element ( i = 0 ).
Every element of Z has an inverse under the operation " + ", namely that same element, but of opposite sign. Adding an element to its inverse, or adding the inverse to its corresponding element, always results in the identity element. For example 3 + (-3) = 0 = (-3) + 3.
So the set Z, together with the binary operation +, forms a group, and we write : Z,+.
Another example, this time of a finite Group, is our ordinary clock and its short hand indicating the hours. The dial of such a clock reads from 1 to 12. After 12 comes 1. All this implies that we have the set CLK = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. So when we add two numbers, say 3 and 4, we get 7 (to the ordered pair (3,4), which is element of the carthesian product CLK x CLK, the element 7 of CLK is assigned).
The operation (addition) is closed, because there is not any product of two elements of CLK which brings us outside the set : 10 + 5 = 3, 11 + 1 = 12, etc.
The operation is associative, for example (10 + 6) + 3 = 10 + (6 + 3) = 7, etc.
There is an identity element present, namely 12 : 5 + 12 = 5 = 12 + 5, etc.
Every element has an inverse. When we have an element of our set CLK, say 5, then its inverse will be obtained by 'undoing' 5, which means that we shift the hand of the clock -- starting at position 12 (= the 'having-still-not-anything-done-position') -- 5 positions backwards (the undoing-5 movement), resulting in its new position 7. So 7 is the inverse of 5. We can write 7 = 5-1. And indeed 7 + 5 = 12 (where 12 is the identity element). The inverse of 11 can be obtained in a similar way : Perform the undoing-11 movement from the start position (12). When we do this we will end up at position 1. So 1 is the inverse of 11, or equivalently 1 = 11-1. And indeed 11 + 1 = 12.
Consequently our clock forms a Group under addition (+). The latter is, as we have seen, not in all respects an ordinary addition. It is an addition such that it is closed within the set CLK = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. While the hand of the clock moves (i.e. when we add numbers), it eventually passes 12 and visits 1 again, the 2, etc., i.e. it cycles through the elements of the set over and over again. That's why we call such a Group a cyclic group.
If all the elements of a Group commute under the group operation, i.e. if for every pair (a,b) of elements a * b = b * a holds, in which * is the operation of the Group, then we call the Group commutative or abelian.
If there is at least one pair of elements which does not commute, then the Group is called non-commutative or non-abelian.
Group Table, Period (or order) of an element.
When a Group is finite, we can express exhaustively all the possible combinations of its elements according to the group operation. This we can conveniently do by means of a Group Table. For our Clock Group, (CLK, +), considered above we can construct such a table as follows (in which we adopt the convention of placing the identity element -- which in our case is the element 12 -- always at the first position of the enumeration of the elements at the upper and left sides of the table) :
The elements of the set CKL = {12, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} are lined up horizontally and vertically. The order in which we line up those elements is immaterial, though some oderings can turn out to be very convenient.
The identity element (12) is highlighted. The distribution of the identity element tells us something about the structure of the given group table.
To read the table, i.e. to determine what a product, say, 3 + 4, is (We will call generally a combination of two elements of a group according to its group operation a "product", no matter what that group operation is like), we look up the first element in the left column (left of the line) and the second element in the upper row (above the line). We then will find the product in the position of the intersection of the horizontal line from the (looked up) first element and the vertical line from the (looked up) second element. And so we will find 3 + 4 = 7, i.e. to the ordered pair (3,4) of the carthesian product CLK x CLK is assigned the element 7 of the set CLK.
In our Group the element 6 in fact means +6. If we perform '+6' from our starting position -- which is 12 -- we get 12 + 6 = 6. If we now perform this once again on the result, we get 6 + 6 = 12, i.e. after two times applying +6 we arrived at the identity (element). When we apply +6 again on the last obtained result we get 12 + 6 = 6, and if we again apply +6 to the last result we get 6 + 6 = 12. So after four times applying +6 we again arrive at the identity. These results can be denoted as follows :
62 (= two times applying +6) = 12, or, if we indicate the identity element as i, 62 = i. Further we found 63 = 6, and 64 = i.
Now we are ready to state a definition.
Definition : The period of an element x is the smallest positive integer m such that xm = i (identity). When no such integer exists, x is said to have 'infinite period'.
So the period of element 6 in our clock group is 2.
Let's now try to determine the periods of the other elements of our group.
The identity is always -- i.e. in any group whatsoever -- of period 1, because one performance of this element directly yields the identity. So in our case the period of element 12 is 1.
The element 1 must evidently be repeated twelve times in order to reach the identity for the first time :
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 12 (= i ), so 112 = i, and thus the period of element 1 is 12.
The element 2 must be repeated six times in order to reach 12, the identity, for the first time :
2 + 2 + 2 + 2 + 2 + 2 = 12 = i.
So 26 = i, i.e. the period of the element 2 is 6.
The element 3 must be repeated four times in order to reach the identity for the first time :
3 + 3 + 3 + 3 = 12 = i.
So 34 = i, i.e. the period of the element 3 is 4.
The element 4 must be repeated three times in order to reach the identity for the first time :
4 + 4 + 4 = 12 = i.
So 43 = i, i.e. the period of element 4 is 3.
The element 5 must be repeated 12 times in order to reach the identity for the first time :
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 12. This is so because, only when we reach 60, that result divides by 12 without remainder :
5 + 5 = 10, 10 + 5 = 3, 3 + 5 = 8, 8 + 5 = 1, 1 + 5 = 6, 6 + 5 = 11, 11 + 5 = 4, 4 + 5 = 9, 9 + 5 = 2, 2 + 5 = 7, 7 + 5 = 12 = i.
So 512 = i, implying that the period of the element 5 is 12.
The element 7 must be repeated 12 times before reaching the identity for the first time :
When we start at the identity and begin adding 7 we get :
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84. And 84 divides by 12 for the first time.
So 712 = i, implying that the period of the element 7 is 12.
The element 8 must be repeated 6 times for it to reach the identity :
8, 16, 24, where 24 divides by 12 for the first time.
So 83 = i, implying that the period of the element 8 is 3.
The element 9 must be repeated four times in order to reach the identity for the first time :
9, 18, 27, 36, in which 36 for the first time divides by 12.
So 94 = i, implying that the period of the element 9 is 4.
The element 10 must be repeated six times in order to reach the identity for the first time :
10 + 10 + 10 + 10 + 10 + 10 = 12 = i.
So 106 = i, implying that the element 10 has period 6.
The element 11 must be repeated 12 times before reaching the identity for the first time :
When we start at the identity, 12, and begin adding repeated 11, we get the following sequence :
11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132. And, indeed only when we arrive at 132 we get something that divides by 12, so that 132 = 12 = i. Thus 1112 = i, implying that the element 11 has period 12.
Summarizing the elements of our group and their periods gives the following :
Element Period 12 1 1 12 2 6 3 4 4 3 5 12 6 2 7 12 8 3 9 4 10 6 11 12The order of a group is the number of its elements.
A group can be taken as just an abstract structure, defined by the structure of its table, or, in the case of infinite groups, by certain defining relations.
Such an abstract group can have many realizations, one of which is the above group table, where the elements of the group are (twelve) integers and the operation, manipulating those number, an addition modulo 12 [which means that all numbers are reduced to remainders after division by 12 (but where -- to preserve the analogy to the clock -- we have called the element 0 (= no remainder) "12"].
Another realization of our group C12 can be in terms of permutations of twelve objects (See for permutations also Part One). These objects can be the twelve numbers used earlier. The order of those numbers can be changed in many ways, in fact in 1x2x3x4x5x6x7x8x9x10x11x12 = 12! (twelve faculty) = 479001600 ways. The group, consisting of all these permutations is called S12. Our present group is only a subgroup of S12, consisting of just 12 permutations of 12 symbols (figures).
When we look to the group table above we can interpret the identity element (12) as the permutation :
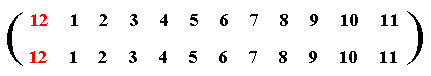
This means that 12 is replaced by 12, 1 is replaced by 1, 2 is replaced by 2, etc., which of course means that the order of the numbers will not be changed. So our identity element can (also) be represented by this particular permutation.
Now, generally, every permutation of n objects can be written down in the form just presented, namely a top row of these n objects according to a determined original order, and a bottom row indicating the swapping of those objects dictated by the given permutation.
The element 1 of our table can be represented as a permutation by its corresponding row, such that that row represents the bottom row, while the top row is constituted by these same numbers but in their original order :
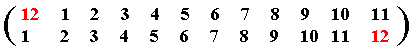
In this permutation, representing element 1, 12 is replaced by 1, 1 is replaced by 2, 2 is replaced by 3, 3 is replaced by 4, ......., 10 is replaced by 11, 11 is replaced by 12.
The element 2 can, in the same way, be represented by the permutation (as characterized by the element 2's corresponding row) :
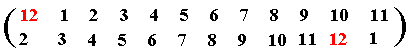
In this permutation 12 is replaced by 2, 1 is replaced by 3, 2 is replaced by 4, ........, 10 is replaced by 12, 11 is replaced by 1.
In this way we can interpret each element of our group as a permutation of twelve numbers, resulting in twelve such permutations.
When we indeed want to study our group C12 in terms of permutations it is more convenient to replace the numbers by letters, i.e. the twelve objects which are permuted are now letters :
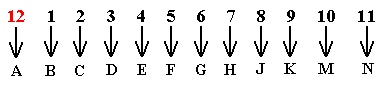
So in this way we can represent the twelve elements of our group C12 as twelve different permutations of twelve letters :
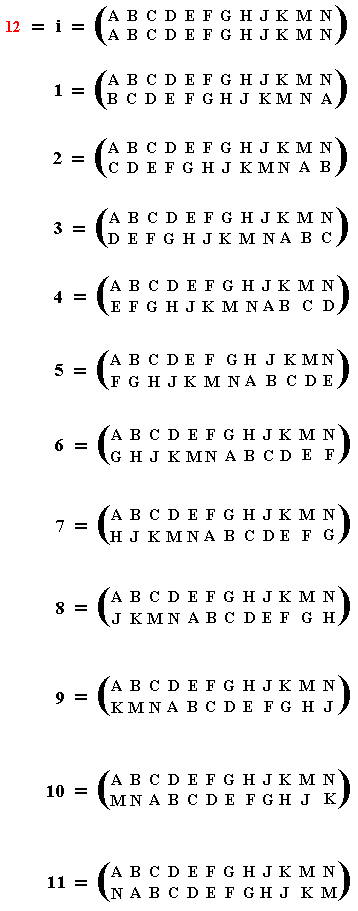
These permutations should be read in the same way as we did above when the objects were represented by numbers. So, for example, the last permutation should be read :
A is replaced by N
B is replaced by A
C is replaced by B
D is replaced by C
E is replaced by D
F is replaced by E
G is replaced by F
H is replaced by G
J is replaced by H
K is replaced by J
M is replaced by K
N is replaced by M
All the permutations now constituting the elements of our group C12, imply cycles.
We will denote such a cycle as follows :
The cycle (ABC) means : A is replaced by B, B is replaced by C, and C is replaced by A.
In the permutation
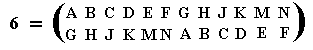
representing element 6 of our group, we can detect the following cycles :
A becomes G
G becomes A
B becomes H
H becomes B
C becomes J
J becomes C
D becomes K
K becomes D
E becomes M
M becomes E
F becomes N
N becomes F
The remaining cycles we already have :
G becomes A
A becomes G
H becomes B
B becomes H
J becomes C
C becomes J
K becomes D
D becomes K
M becomes E
E becomes M
N becomes F
F becomes N
So this permutation consists of the six following cycles :
(AG)(BH)(CJ)(DK)(EM)(FN)
These cycles are all of period 2.
For example (AG) :
First application of the cycle : A becomes G.
Second application of the cycle to the result : G becomes A again.
In the same way we can determine the cycles of all the remaining permutations :
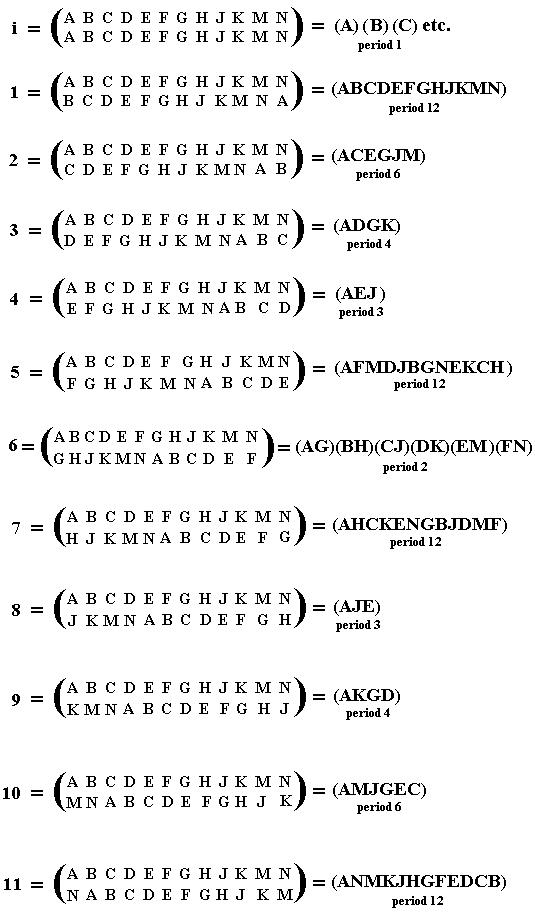
Of course we get the same periods as we had determined earlier for the elements 12, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11 of our "clock interpretation' of the group C12.
We can now say that the numbers in our Group Table represent all the above permutations, so when we want to determine the product of, say,
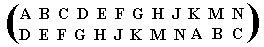
and
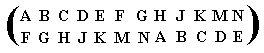
we can obtain that product by first executing the first permutation, and execute the second permutation on the result :
A B C D E F G H J K M N
D E F G H J K M N A B C (first permutation)
The second permutation lets A to become F, B to become G, C to becom H, etc. We will apply that to the just obtained result :
D E F G H J K M N A B C (first permutation)
J K M N A B C D E F G H (application of second permutation)
So the result is :
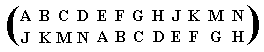
which corresponds to the element 8 of our group table.
The first permutation corresponded to the element 3 and the second permutation corresponds to the element 5 of the table. And indeed 3 + 5 = 8 according to that table.
Because in writing down a permutation of objects the top row always depicts the original sequence of those objects -- in our permutations that was the sequence A B C D E F G H J K M N -- it is (as long as the original sequence is known) sufficient to give only the bottom row, when indicating the permutation. So, say, the first permutation (figuring in the just given product) can be indicated by D E F G H J K M N A B C.
The permutations 4 = E F G H J K M N A B C D 8 = J K M N A B C D E F G H combine to give the permutation A B C D E F G H J K M N = 12 = i, which means that the second permutation is the inverse if the first, and vice versa. Indeed 4 + 8 = 12 = i. So we have the permutations
A B C D E F G H J K M N = 12
B C D E F G H J K M N A = 1
C D E F G H J K M N A B = 2
D E F G H J K M N A B C = 3
E F G H J K M N A B C D = 4
F G H J K M N A B C D E = 5
G H J K M N A B C D E F = 6
H J K M N A B C D E F G = 7
J K M N A B C D E F G H = 8
K M N A B C D E F G H J = 9
M N A B C D E F G H J K = 10
N A B C D E F G H J K M = 11
which form one of the realizations of the cyclic group C12.
Now, to make all this more concrete, and moreover to delve more deeply into the matter, we can interpret the above permutations of letters, as the permutations of the twelve vertices -- indicated by those letters -- of a regular dodecagon, i.e. a regular 12-gon, a regular 2-dimensional closed figure with twelve equal sides and twelve equal angles obtained between those sides.
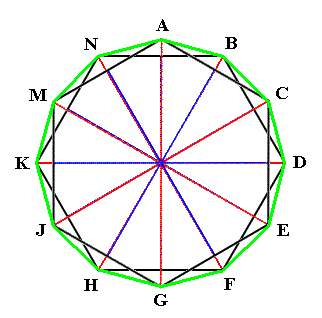
Figure 1. Regular Dodecagon, indicated by the green line. The vertices (corners) are indicated by the letters A, B, C, D, E, F, G, H, J, K, M and N.
The regular dodecagon has several symmetries, rotations and reflections. The latter are normally called opposite symmetries while the former are called direct symmetries.
A rotation of 00 leaves everything unchanged. It is the identity element, and corresponds to the permutation
A B C D E F G H J K M N = i = 12 (of our C12 group table).
A clockwise rotation of 300 sends vertex A to B, B to C, C to D, D to E, E to F, F to G, G to H, H to J, J to K, K to M, M to N and N to A.
It thus corresponds to the permutation (of vertices)
B C D E F G H J K M N A = 1 (of the group table).
A clockwise rotation of 600 sends vertex A to C, B to D, C to E, D to F, E to G, F to H, G to J, H to K, J to M, K to N, M to A and N to B. So it corresponds to the permutation
C D E F G H J K M N A B = 2.
A clockwise rotation of 900 sends vertex A to D, B to E, C to F, D to G, E to H, F to J, G to K, H to M, J to N, K to A, M to B and N to C. So it corresponds to the permutation
D E F G H J K M N A B C = 3.
A clockwise rotation of 1200 sends the vertex A to E, B to F, C to G, D to H, E to J, F to K, G to M, H to N, J to A, K to B, M to C and N to D. So it corresponds to the permutation
E F G H J K M N A B C D = 4.
A clockwise rotation of 1500 sends vertex A to F, B to G, C to H, D to J, E to K, F to M, G to N, H to A, J to B, K to C, M to D and N to E. So it corresponds to the permutation
F G H J K M N A B C D E = 5.
A clockwise rotation of 1800 sends vertex A to G, B to H, C to J, D to K, E to M, F to N, G to A, H to B, J to C, K to D, M to E, and N to F. So it corresponds to the permutation
G H J K M N A B C D E F = 6.
A clockwise rotation of 2100 sends vertex A to H, B to J, C to K, D to M, E to N, F to A, G to B, H to C, J to D, K to E, M to F and N to G. So it corresponds to the permutation
H J K M N A B C D E F G = 7.
A clockwise rotation of 2400 sends vertex A to J, B to K, C to M, D to N, E to A, F to B, G to C, H to D, J to E, K to F, M to G and N to H. So it corresponds to the permutation
J K M N A B C D E F G H = 8.
A clockwise rotation of 2700 sends the vertex A to K, B to M, C to N, D to A, E to B, F to C, G to D, H to E, J to F, K to G, M to H and N to J. So it corresponds to the permutation
K M N A B C D E F G H J = 9.
A clockwise rotation of 3000 sends the vertex A to M, B to N, C to A, D to B, E to C, F to D, G to E, H to F, J to G, K to H, M to J and N to K. So it corresponds to the permutation
M N A B C D E F G H J K = 10.
Finally, a clockwise rotation of 3300 sends the vertex A to N, B to A, C to B, D to C, E to D, F to E, G to F, H to G, J to H, K to J, M to K, and N to M. So it corresponds with permutation
N A B C D E F G H J K M = 11.
All these rotations can also be generated by repeated application of 300, which means that we can express all the rotations, except the identity, in terms of that rotation by 300.
When we call this rotation element p (= p1), then the rotation of 600 is equal to two times applying the 300 rotation, and it can be denoted by p2. In the same way 900 rotation can be achieved by three times applying the rotation of 300, and can be denoted by p3, etc. And even the identity could be expressed by p0. We prefer however to call it 1.
This means that we can rename the elements of our group as follows :
1, p, p2, p3, p4, p5, p6, p7, p8, p9, p10 and p11, where p12 = 1.
The group table of our cyclic group C12 would then be as follows :

Instead of by permutations the group elements are now given in terms of the one generator p. And the defining relation is p12 = 1.
Subgroups.
Definition :
A subgroup of a group is a subset which is itself a group under the group operation.
In order to show some subgroups we recapitulate the group C12 and its realization in terms of the nimbers of a clock :

Recall that the element 12 is the identity.
From this table we can recognize several subgroups :
First of all {12, 6}.
That this is really a subgroup (not just a subset) can directly be deduced by its table :

An element with period 2, as our element 6, is called an involute element. In all cases such an element can, to gether with the identity, form a group of order 2 (i.e. a group consisting of two elements). In the present case it is a subgroup (C2) of a larger group (C12).
Another subgroup of C12, namely C3, is {12, 4, 8}. We can check its table whether this is so :

Yet another subgroup, namely C4 is {12, 3, 6, 9}. We can check its group table :

Again, another subgroup, namely C6 is {12, 2, 4, 6, 8, 10}. Let's see its table :

If we denote the order of a group G, i.e. the number of elements of the group G, as order(G), then we can state (without proof) an important result in Group Theory :
Lagrange's theorem
If H is a subgroup of a group G, and if order(G) = n (n is finite), order(H) = m, then m is a factor of n.
So the order of a subgroup must divide the order of the group.
Abstract Groups, Isomorphism.
In his book The Fascination of Groups, 1978, F. J. BUDDEN, p.131, relates the following :
"Daddy, I know a good joke : Why do white sheep eat more than black sheep?"
"I've no idea."
"Because there are fewer black sheep than white sheep!"
If Daddy had wished to 'repeat' this joke in his club, he would probably have altered it :
"Any of you chaps know why Americans drink more whisky than Scotsmen ...?"
Here we have an example of what we might call isomorphic jokes : They are really the same joke, but placed into a different context. So it is with groups .... .
A group of order four in many different situations
Indeed, the 'same' group may appear in many different guises, for example the group table for the group D2
| 1 | X | Y | Z | |
| 1 | 1 | X | Y | Z |
| X | X | 1 | Z | Y |
| Y | Y | Z | 1 | X |
| Z | Z | Y | X | 1 |
can stand for the rotations through half a revolution about three perpendicular axes in space, and thus represent the symmetry of the Crystal Class 222 (Rhombic-bisphenoidic Class of the Orthorhombic Crystal System).
In finite arithmetics we can find multiplication tables all with an identical structure as the one above :
Multiplication modulo n (X mod 8) means multiplication of whole positive numbers, but only retaining the remainder after division by n.
So, for example 3 x 5 (mod 8) = 7 (i.e. 15 - 8).
Let's show some multiplication tables of finite arithmetics ( that all -- as it turns out -- form the group D2 ) :
| x mod 8 | 1 | 3 | 5 | 7 |
| 1 | 1 | 3 | 5 | 7 |
| 3 | 3 | 1 | 7 | 5 |
| 5 | 5 | 7 | 1 | 3 |
| 7 | 7 | 5 | 3 | 1 |
| x mod 12 | 1 | 5 | 7 | 11 |
| 1 | 1 | 5 | 7 | 11 |
| 5 | 5 | 1 | 11 | 7 |
| 7 | 7 | 11 | 1 | 5 |
| 11 | 11 | 7 | 5 | 1 |
| x mod 15 | 1 | 4 | 11 | 14 |
| 1 | 1 | 4 | 11 | 14 |
| 4 | 4 | 1 | 14 | 11 |
| 11 | 11 | 14 | 1 | 4 |
| 14 | 14 | 11 | 4 | 1 |
| x mod 16 | 1 | 7 | 9 | 15 |
| 1 | 1 | 7 | 9 | 15 |
| 7 | 7 | 1 | 15 | 9 |
| 9 | 9 | 15 | 1 | 7 |
| 15 | 15 | 9 | 7 | 1 |
As can be seen, all these tables have the same structure, despite the fact that they represent different realizations of the same group, namely the abstract group D2.
We say that these groups are isomorphic.
Now we can prepere for the definition of isomorphism.
We can indicate a group by a pair of symbols, of which the first member signifies the set of elements of the group, while the second symbol signifies the group operation, i.e. the way how any two elements of the group can be combined.
So with the group (X, *) we mean a group, having as its set of elements the set X, while the elements of that set combine according to the operation *.
The same goes for the group denoted by (Y, o).
Suppose we have a theatre with seats. And suppose every visitor has found his or her seat. And suppose further that no empty seats are left. Then we have a 1,1 correspondence between the set of visitors and the set of seats.
Definition :
Two groups (X, *) and (Y, o) are said to be ISOMORPHIC if :
(a) It is possible to set up a 1,1 correspondence between the elements of X and those of Y, i.e. such that, for each element x of X there corresponds a unique element y of Y, and vice versa, and also
(b) If x1 and x2 are two elements of X, and y1, y2 are the two corresponding elements of Y, and if :
x1 * x2 = x3 and y1 o y2 = y3,
then x3 and y3 are also corresponding elements.
Also (b) might have been re-stated : if x1 and y1 are a pair of mates, and x2 and y2 are a pair of mates, then x1 * x2 and y1 o y2 are also a pair of mates.
Briefly, therefore, we may describe isomorphism as a 1,1 correspondence which preserves structure, or which preserves products.
So when we speak about the 'same' group, what we really mean is that in all the widely differing situations (much more than exemplified above), a group table results which has an identical pattern, except that perhaps different letters have been used, and they have had different meanings in the different cases. In every case, the structure of the table has had 1's along the leading diagonal (indicated red in the tables above, and again indicated in the general table below),
| 1 | a | b | c | |
| 1 | 1 | a | b | c |
| a | a | 1 | c | b |
| b | b | c | 1 | a |
| c | c | b | a | 1 |
This means that a2 = b2 = c2 = 1, and bc = cb = a, ca = ac = b, ab = ba = c.
When we are not particularly concerned with what a, b, c, ... represent, but only with the ways in which they combine, we have then abstracted superfluous considerations, and the table shows the abstract group which describes anyone of the various concrete situations. The word 'realization' is the one chiefly used of the reverse process, e.g. the half-turns about three mutually perpendicular axes are one realization of the abstract group showed in the above general table, and alternatively described by the defining relations, a2 = b2 = 1, ab = ba. Thus the word 'realization' is, in the group sense, the inverse of the word 'abstraction'.
Thus groups which have the same structure are called isomorphic. The above group is called the Klein four-group. The code name for the Klein four-group is either D2, or C2xC2, or D1xD1.
Two essentially different groups of order four.
How many groups exist of order four? You may try re-arranging the order of the elements in D2, but you will find that the pattern of the table is thereby unchanged. Does this mean that there is only one abstract group of order four? Certainly not, because there exist the following counter examples drawn from finite arthmetics (the identity element is highlighted by red, + is addition, x is multiplication) :
| + mod 4 | 0 | 1 | 2 | 3 |
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
| x mod 5 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 1 | 3 |
| 3 | 3 | 1 | 4 | 2 |
| 4 | 4 | 3 | 2 | 1 |
Now it looks as if we have produced two further different groups of oeder 4. But a little consideration may convince you that, in spite of the apparent dissimilarity (observe the different pattern of the identity element in each case), there are encouraging similarities.
In the first table there is one element (2) of period 2 (2 + 2 = 22 = 0 (identity)), and two (1,3) of period 4 (14 = 1 + 1 + 1 + 1 = 2 + 1 + 1 = 3 + 1 = 0, and 34 = 3 + 3 + 3 + 3 = 2 + 3 + 3 = 1 + 3 = 0).
In the second table we find one element (4) of period 2 (4 x 4 = 42 = 1 (identity), and two (2,3) of period 4 (24 = 2 x 2 x 2 x 2 = 4 x 2 x 2 = 3 x 2 = 1, and 34 = 3 x 3 x 3 x 3 = 4 x 3 x 3 = 2 x 3 = 1).
This suggests that we should rearrange the elements in the second table so that the two elements of period 4 become separated in either of the two following ways :
| x mod 5 | 1 | 2 | 4 | 3 |
| 1 | 1 | 2 | 4 | 3 |
| 2 | 2 | 4 | 3 | 1 |
| 4 | 4 | 3 | 1 | 2 |
| 3 | 3 | 1 | 2 | 4 |
| x mod 5 | 1 | 3 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 3 | 3 | 4 | 2 | 1 |
| 4 | 4 | 2 | 1 | 3 |
| 2 | 2 | 1 | 3 | 4 |
And now we see that both new tables have the same structure as that for (0, 1, 2, 3}, + mod 4 (notice the distribution of the identity element, and also the fact that the same elements are aligned along a NE--SW diagonal of the group table). This group (now visible in the above four guises) is the Cyclic Group of order 4, C4, and it is different from the group D2 considered above.
D2 and C4 are the only possible abstract groups of order 4.
Of order 6 there are also only two possible abstract groups, namely D3 and C6 (BUDDEN, 1978, op. cit., p. 140).
Automorphism.
Let us give the general table for the group C4, i.e. the cyclic group of order four. With "general table" we mean the abstract group (i.e. the group table without any interpretation as to what the elements stand for).
| 1 | p | a | q | |
| 1 | 1 | p | a | q |
| p | p | a | q | 1 |
| a | a | q | 1 | p |
| q | q | 1 | p | a |
Now we have seen several metamorphoses of this table, but the following redrafting of it bears a remarkable similarity to the one just given :
| 1 | q | a | p | |
| 1 | 1 | q | a | p |
| q | q | a | p | 1 |
| a | a | p | 1 | q |
| p | p | 1 | q | a |
This is so because it is merely the original table with p and q interchanged, i.e. the table has been subjected to the transposition (pq).
[a two-fold cycle, for instance p becomes q, and q becomes p, is called a transposition].
Thus we have an isomorphism of the group (1, p, a, q} on to itself {1, q, a, p} by the correspondence
1 ---- 1
p ---- q
a ---- a
q ---- p
Such an isomorphism of a group onto itself is called an automorphism, and you may appreciate an automorphism as a re-labelling of the elements of the group.
Automorphisms of the Klein four-group, D2
In the case of the group D2, we have more scope for automorphism, since there are three elements of period 2. Using the notation 1, a, b, c, with a2 = b2 = c2 = 1, a = bc, b = ca, c = ab, it is evident that any permutation may be applied to the elements a, b and c to produce an automorphism, because they all give 1 when multiplied with themselves, and each of them is equal to the product of the two others.
For instance the permutation
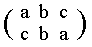
(a becomes c, b remains b, c becomes a, i.e. a and c are interchanged) takes the original table
| 1 | a | b | c | |
| 1 | 1 | a | b | c |
| a | a | 1 | c | b |
| b | b | c | 1 | a |
| c | c | b | a | 1 |
into the form :
| 1 | c | b | a | |
| 1 | 1 | c | b | a |
| c | c | 1 | a | b |
| b | b | a | 1 | c |
| a | a | b | c | 1 |
We see that the structure of the table is preserved, which means that not only all the relations between the elements are the same in both tables, but that also the pattern is identical in the two tables, one such 'pattern feature' is for instance the identity elements being lined up along the main diagonal.
While preserving pattern, both tables have :
a2 = 1, b2 = 1, c2 = 1,
ab = ba = c, ac = ca = b, bc = cb = a,
and it is evident that in addition to the applied cycle (ac) as represented by the above permutation, also the other five cycles will produce an automorphism.
Let's enumerate all of them :
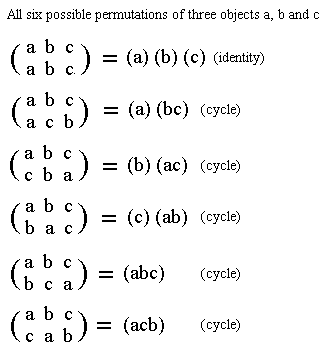
Any one of these six cycles (including the identity) produces an automorphism of this group (D2). These six permutations themselves form a group. In fact there is a theorem that the automorphisms of any group themselves form a group.
Let us give all six automorphisms of our present group, i.e. the Klein four-group (D2), preceded by its corresponding permutation of the group elements indicated by the cycle involved (And you can check, and will indeed find, that the table pattern and the relations stated above between the group elements remain the same in these six tables) :
| 1 | a | b | c | |
| 1 | 1 | a | b | c |
| a | a | 1 | c | b |
| b | b | c | 1 | a |
| c | c | b | a | 1 |
| 1 | a | c | b | |
| 1 | 1 | a | c | b |
| a | a | 1 | b | c |
| c | c | b | 1 | a |
| b | b | c | a | 1 |
| 1 | c | b | a | |
| 1 | 1 | c | b | a |
| c | c | 1 | a | b |
| b | b | a | 1 | c |
| a | a | b | c | 1 |
| 1 | b | a | c | |
| 1 | 1 | b | a | c |
| b | b | 1 | c | a |
| a | a | c | 1 | b |
| c | c | a | b | 1 |
| 1 | b | c | a | |
| 1 | 1 | b | c | a |
| b | b | 1 | a | c |
| c | c | a | 1 | b |
| a | a | c | b | 1 |
| 1 | c | a | b | |
| 1 | 1 | c | a | b |
| c | c | 1 | b | a |
| a | a | b | 1 | c |
| b | b | a | c | 1 |
You can check that all six tables have
As has been said, these six groups form a group, namely the group of automorphisms of D2.
The group D2 {1, a, b, c} has the automorphism group D3, these automorphisms corresponding to every possible permutation of the elements a, b, and c between themselves, and there are six such permutations in all (They are given above). Obviously the group operation of this (and any) automorphism group is the successive execution of permutations (two at a time).
The group D2 may be realized as the group of the symmetries of the rectangle :
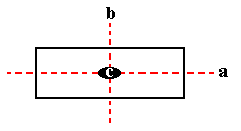
Figure 2. The symmetries of a rectangle.
Two mirror lines (a and b), and one 2-fold rotation axis (c).
Here we have three elements a, b and c (Figure 2), all of period 2, thus a2 = 1 (identity), b2 = 1 and c2 = 1.
e-mail :

To continue click HERE to proceed further with Group Theory
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals