e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Direct Product Groups
It is possible to multiply two (or more) groups such that the result is also a group.
| 1 | i | -1 | -i | |
| 1 | 1 | i | -1 | -i |
| i | i | -1 | -i | 1 |
| -1 | -1 | -i | 1 | i |
| -i | -i | 1 | i | -1 |
Table 9.1
The group table for the group {1, r, r2} (C3) is as follows :
| 1 | r | r2 | |
| 1 | 1 | r | r2 |
| r | r | r2 | 1 |
| r2 | r2 | 1 | r |
Table 9.2
We will now form the direct product C4 x C3 of the groups {1, i, -1, -i} (C4) and
| e = (1, 1) | a = (i, 1) | b = (-1, 1) | c = (-i, 1) |
| d = (1, r) | f = (i, r) | g = (-1, r) | h = (-i, r) |
| j = (1, r2) | k = (i, r2) | n = (-1, r2) | m = (-i, r2) |
In order to turn this set of ordered pairs (i.e. all possible ordered pairs formed from the elements of the two groups) into a group, we must define a group operation for this new type of group, a group operation valid for all possible product groups. And with "valid" we mean of course that it always must turn the set into a group.
Well, on our set of ordered pairs we define the general operation * such that to every pair of pairs from our set of ordered pairs another pair, also from our set, is assigned (analogous to the fact that we, in ordinary multiplication assign to two numbers, say 5 and 7, a third number, namely 35, which we call the product of 5 and 7).
We will call a general element of the first group x, while a general element of te second group wil be called y.
So let's define the operation * assigned to the above set of ordered pairs.
(x1, y1) * (x2, y2) = (x1x2, y1y2).
For example (now omitting * and using juxtaposition), we have :
jh = (1, r2) (-i, r) = (-i, 1) = c.
k2 = (i, r2)2 = (i, r2) (i, r2) = (-1, r) = g.
The resulting ordered pair P always consists of (1) a product of two elements of the first group, and that product is also is element of that first group, and (2) a product of two elements of the second group, and that product is also an element of that second group. So the resulting ordered pair P also consists of two members of which the first one comes from the first group, and the second one from the second group. THe product does not bring us outside our set of ordered pairs. So the set of ordered pairs as listed above is closed under the operation *.
Associativity, i.e.
[(x1, y1) * (x2, y2)] * (x3, y3) = (x1, y1) * [(x2, y2) * (x3, y3)]
is evident, because the definition of the operation * only contains ordinary multiplications which are themselves associative.
The identity element is (1, 1).
Finally each element of our new set has an inverse :
Let x be an element of the first group, that is the group {1, i, -1, -i} , and y be an element of the second group, that is the group {1, r, r2}, then 1 / x is the inverse of x [ because the operation in that group is ordinary multiplication which implies that x times 1 / x = x / x = 1 ], and 1 / y is the inverse of y for the same reason with respect to the second group. And because we have to do with groups, the inverses 1 / x and 1 / y belong to these respective groups, and thus the pair (1 / x, 1 / y) automatically belongs to the set of ordered pairs.
Now (x, y) (1 / x, 1 / y) = (x / x, y / y) = (1, 1) (which is indeed the identity element of our set of ordered pairs), so that the inverse of ( i, r2), for example, is (1 / i, 1 / r2) = (-i, r),
i.e. k-1 = h.
Let's show that 1 / i is indeed equal to -i.
1 / i = 1/Sqr(-1) = Sqr(-1) / -1 = -Sqr(-1) = -i.
Let's also show that 1 / r2 = r.
1 / r2 = r2 / r4 = r2 / (r3r) = r2 / r = r.
Thus the twelve elements form a group.
Note that in the array of elements (ordered pairs) as listed above, the top row is the subgroup C4, and the first column is the subgroup C3.
Now,
f = (i, r).
f 2 = (-1, r2) = n.
f 3 = (-i, 1) = c.
f 4 = (1, r) = d.
f 5 = (i, r2) = k.
f 6 = (-1, 1) = b. And in the same way we can cintinue :
f 7 = h.
f 8 = j.
f 9 = a.
f 10 = g.
f 11 = m.
f 12 = e.
Hence element f is of period 12, it generates all the elements of the group, and thus the group must be C12.
We are now ready to give a formal (and general) definition of the direct product of two groups :
(gp, gq') (gr, gs') = (gp * gr , gq' *' gs')
is a group of order nn', and is called the Direct Product Group of G and G', and is abbreviated G x G'.
Sometimes instead of the term "Direct Product", the term "Direct Sum" is used.
Because gp and gr belong to the first group, their product ( gp* gr ) also belongs to that group.
And because gq' and gs' belong to the second group, their product ( gq' *' gs' ) also belongs to that group.
And thus the pair (gp * gr , gq' *' gs') belongs to the set of ordered pairs generally denoted by (gp, gq'), which means that in all cases the set of ordered pairs is closed under the defined operation.
In the example above, what we have done is to form the direct product of C4 and C3, and we have shown that the direct product group so obtained is in fact the familiar C12.
If we were to rewrite the elements of C4 and C3 in terms of generators, thus C4 { i0, i1, i2, i3 } and C3 { r
| e = (i0, r0) | a = (i1, r0) | b = (i2, r0) | c = (i3, r0) |
| d = (i0, r1) | f = (i1, r1) | g = (i2, r1) | h = (i3, r1) |
| j = (i0, r2) | k = (i1, r2) | n = (i2, r2) | m = (i3, r2) |
and in applying the product rule, for example,
jh = (i0, r2) (i3, r1) = (i3, r3) = (i3, r0) = c, and
k2 = (i1, r2) (i1, r2) = (i2, r4) = (i2, r1) = g,
it is clear that we are adding the indices modulo 4 and modulo 3 respectively, so that, if we represent our ordered pairs by depicting only the indices, thus :
| e = (0, 0) | a = (1, 0) | b = (2, 0) | c = (3, 0) |
| d = (0, 1) | f = (1, 1) | g = (2, 1) | h = (3, 1) |
| j = (0, 2) | k = (1, 2) | n = (2, 2) | m = (3, 2) |
we may now write
jh = (0, 2)(3, 1) = ((0 + 3)mod 4, (2 + 1)mod 3) = (3, 0) = c, and
k2 = (1, 2)(1, 2) = (1 + 1)mod 4, (2 + 2)mod 3) = (2, 1) = g,
and so on.
So the group C4 x C3 is seen in a new guise, as the set of oredered pairs (x, y) with x being an element of {0, 1, 2, 3}, and y being an element of {0, 1, 2}, combined according to the composition rule
(x1, y1) (x2, y2) = ((x1 + x2)mod 4, (y1 + y2)mod 3).
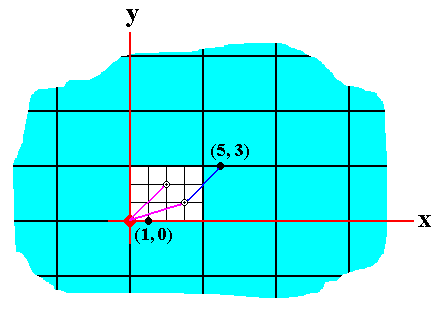
This adding of the corresponding members of ordered pairs also takes place in the case of vector addition in 2-dimensional space, albeit without applying a finite modulus. So then, with respect to the pairs (0, 2) and (3, 1) we get the vector addition
(0, 2)(3, 1) = (0, 2) + (3, 1) = ((0 + 3), (2 + 1)) = (3, 3), and
(3, 1)(2, 2) = (3, 1) + (2, 2) = ((3 + 2), (1 + 2)) = (5, 3).
But in the case being considered above, the x-coordinates have been reduced modulo 4, and the y-coordinates reduced modulo 3, and this implies working within a confined area, as the next Figure illustrates (after BUDDEN, F. J., 1978, The fascination of Groups, p. 256/7).

Figure 1. Vector addition with modular arthmetic.
In non-modular arithmetic the vectors (3, 1) and (2, 2) would add to give the vector (5, 3), but in that modular arithmetic which is isomorphic with our product group C4 x C3, the two vectors add up to ((3 + 2)mod 4, (1 + 2)mod 3) = (1, 0).
A one-dimensional integer space can be seen as points on a line representing the whole numbers (..., -3, -2, -1, 0, 1, 2, 3, ...) and is indicated by the set Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}. A corresponding two-dimensional integer space can be represented as an infinite array of points in two dimensions and consists of pairs of integer coordinates.
h(x1, y1) =
((x1)mod 4, (y1)mod 3).
h(x2, y2) =
((x2)mod 4, (y2)mod 3).
h(x1, y1) + h(x2, y2) =
((x1)mod 4, (y1)mod 3) + ((x2)mod 4, (y2)mod 3) =
([(x1)mod 4 + (x2)mod 4]MOD 4, [(y1)mod 3 + (y2)mod 3]MOD 3) =
((x1 + x2)mod 4, (y1 + y2)mod 3).
h[(x1, y1) + (x2, y2)] =
h[(x1 + x2, y1 + y2] =
((x1 + x2)mod4, (y1 + y2)mod 3).
So h[(x1, y1) + (x2, y2)] = h(x1, y1) + h(x2, y2), and thus h is a homomorphism from Cinfinite x Cinfinite to C12, according to the definition of homomorphism.
The direct product of C4 x C3 may also be illustrated as the product of the cyclic permutations of two independent sets {A, B, C, D} and {P, Q, R}. These permutations can themselves be illustrated by the rotations of a square and an equilateral triangle respectively :
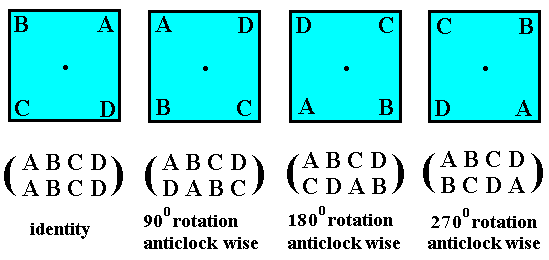
Figure 2. The cyclic permutations of the four symbols A, B, C, and D. They can be interpreted as the rotations of a square (regular tetragon).
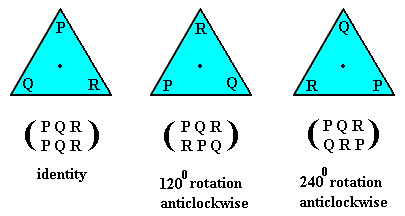
Figure 3. The cyclic permutations of three symbols P, Q, and R. They can be interpreted as the rotations of an equilateral triangle.
Let's try to identify these 12 permutations with the set of ordered pairs established above, where we discussed the direct product of the group {1, i, -1, -i} (C4) and {1, r, r2} (C3) -- and where we have let the indices (powers) of the elements to be represented by the members of the mentioned ordered pairs. Recall that these ordered pairs were the following :
| e = (0, 0) | a = (1, 0) | b = (2, 0) | c = (3, 0) |
| d = (0, 1) | f = (1, 1) | g = (2, 1) | h = (3, 1) |
| j = (0, 2) | k = (1, 2) | n = (2, 2) | m = (3, 2) |
The permutations for A, B, C, D, and for P, Q, R, as established above, can now be combined such that the first part, consisting of the letters A, B, C, and D, corresponds to the first member of the mentioned pairs, while the second part, consisting of the letters P, Q, and R, corresponds to the second member of those pairs. The result is 12 permutations of seven symbols, A, B, C, D, P, Q, R. In the list below we will only list the lower part of each permutation, for example the permutation
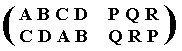
Let's now list the 12 permutations accordingly :
A B C D P Q R
D A B C P Q R
C D A B P Q R
B C D A P Q R
A B C D R P Q
D A B C R P Q
C D A B R P Q
B C D A R P Q
A B C D Q R P
D A B C Q R P
C D A B Q R P
B C D A Q R P
When we look to the part of the permutations played by the letters A, B, C, D, we see that the order of the letters is always according to the alphabetical sequence A, B, C, D, if we read them, starting with A and when arrived at the right-hand end, continue with the left-hand end, reading to the right.
The effect of the second permutation of those four letters is that they are shifted one place to the right.
The effect of the third permutation of those four letters is that they are shifted two places to the right.
The effect of the fourth permutation of those four letters is that they are shifted three places to the right.
After this the original places of the letters are restored again (A is again at the first place).
Well, the first members of the above pairs e = (0, 0), a = (1, 0), b = (2, 0), etc. must be added modulo 4, and thus they correspond exactly with the cyclic permutations of the four letters A, B, C, and D. So we can specify the respective positions of A, as 0 (this is the case in the permutation A B C D, which is the identity permutation), 1 (this is the case in the permutation D A B C), 2 (this is the case in the permutation C D A B), etc.
Precisely the same we can do with the permutations of P Q R. They correspond to the second member of every pair, i.e. the pairs e = (0, 0), a = 1, 0), b = 2, 0), etc.
Also there we see that the alphabetical sequence of the letters P, Q, and R is preserved. When we start reading with P and go to the right, till the end, and then continue at the left-hand end, always reading to the right, we will always encounter P Q R, in this (alphabetical) order.
And also here we see that
the effect of the second permutation of those three letters is a shift of one place to the right,
the effect of the third permutation of those three letter is a shift of two places to the right,
while a fourth permutation would restore the letters in their original places.
Well, the second member of the pairs e = (0,0), a = (1, 0), b = (2, 0), etc. must be added modulo 3, and so they correspond exactly with the just mentioned cyclic permutations of the three letters P, Q, and R.
So we can specify the respective positions of P as 0 (this is the case in the permutation P Q R (the identity permutation)), 1 (this is the case in the permutation R P Q ), and 2 (this is the case in the permutation Q R P).
And indeed, when we accordingly denote any particular permutation of the above list by an ordered pair specifying the position of the letters A and P, calling the positions in the cycles respectively 0, 1, 2, 3 and 0, 1, 2, then, for example h, which is (3, 1), comes to correspond with the permutation B C D A R P Q, since A occurs in the final position (of 0 1 2 3) and P in the middle position (of 0 1 2).
In this way we have set up a full correspondence between the 12 permutations and the 12 ordered pairs.
We know how to write a permutation as one or more cycles, for example the permutation BCDARPQ means that
A becomes B
B becomes C
C becomes D
D becomes A
P becomes R
Q becomes P
R becomes Q
In the cycle notation we then write (ABCD)(PRQ), we thus have a 4-cycle and a 3-cycle.
What is the overall period of this set of two cycles?
After four shifts (A becomes B, B becomes C, etc.) we are back at A again, but then the second cycle has also performed four shifts, which implies that it effectively has performed one shift : after it has returned to P (P becomes R, R becomes Q, and Q becomes P) (three shifts), it goes one step further (a total of four shifts) : P becomes R.
After a second round of four shifts (totalling eight shifts) it is clear that the cycle (PRQ) still has not returned to P, because this only will happen after three, or a multiple of three shifts. And indeed a third round of four shifts (totalling 12 shifts) will not only bring the cycle (ABCD) back to its starting position, but also the cycle (PRQ). In (ABCD) this happened for the third time, while in (PRQ) this happened for the fourth time.
So in this way we can write down the above permutations as cycles and determine their overall period (from the periods of the individual cycles which are contained in such a permutation). This determination of the overall period from the periods of the individual cycles can now be stated as follows :
The period of a combination of cycles is equal to the Lowest Common Multiple (L.C.M) of the periods of the individual cycles.
We can, in the same way determine the periods of the ordered pairs e = (0, 0), a = (1, 0), b = (2, 0), etc. The first members of which must be added modulo 4, the second members must be added modulo 3.
The periods of the first members are :
0 = 0, Period(0) = 1
1 + 1 + 1 + 1 = 0, Period(1) = 4
2 + 2 = 0, Period(2) = 2
3 + 3 + 3 + 3 = 0, Period(3) = 4
The periods of the second members are :
0 = 0, Period(0) = 1
1 + 1 + 1 = 0, Period(1) = 3
2 + 2 + 2 = 0, Period(2) = 3
The period of an ordered pair is now equal to the L.C.M. of the periods of the individual members :
e = (0, 0), (Period 1, Period 1), implying overall period of 1.
a = (1, 0), (Period 4, Period 1), implying overall period of 4.
b = (2, 0), (Period 2, Period 1), implying overall period of 2.
c = (3, 0), (Period 4, Period 1), implying overall period of 4.
d = (0, 1), (Period 1, Period 3), implying overall period of 3.
f = (1, 1), (Period 4, Period 3), implying overall period of 12.
g = (2, 1), (Period 2, Period 3), implying overall period of 6.
h = (3, 1), (Period 4, Period 3), implying overall period of 12.
j = (0, 2), (Period 1, Period 3), implying overall period of 3.
k = (1, 2), (Period 4, Period 3), implying overall period of 12.
n = (2, 2), (Period 2, Period 3), implying overall period of 6.
m = (3, 2), (Period 4, Period 3), implying overall period of 12.
Now we will determine the periods of the 12 permutations by considering their cycle notation :
A B C D P Q R = (A) (B) (C) (D) (P) (Q) (R). Period = 1
D A B C P Q R = (ADCB) (P) (Q) (R). Period = 4
C D A B P Q R = (AC) (BD) (P) (Q) (R). Period = 2
B C D A P Q R = (ABCD) (P) (Q) (R). Period = 4
A B C D R P Q = (A) (B) (C) (D) (PRQ). Period = 3
D A B C R P Q = (ADCB) (PRQ). Period = 12
C D A B R P Q = (AC) (BD) (PRQ). Period = 6
B C D A R P Q = (ABCD) (PRQ). Period = 12
A B C D Q R P = (A) (B) (C) (D) (PQR). Period = 3
D A B C Q R P = (ADCB) (PQR). Period = 12
C D A B Q R P = (AC) (BD) (PQR). Period = 6
B C D A Q R P = (ABCD)(PQR). Period = 12
And now we can set up the correspondence between the 12 ordered pairs and the 12 permutations :
e --- ABCD PQR
a --- DABC PQR
b --- CDAB PQR
c --- BCDA PQR
d --- ABCD RPQ
f --- DABC RPQ
g --- CDAB RPQ
h --- BCDA RPQ
j --- ABCD QRP
k --- DABC QRP
n --- CDAB QRP
m --- BCDA QRP
Because there is at least one element with period 12 (and the group is of order 12) we can identify our direct product group as (isomorphic with) C12.
Thus we can say that C4 x C3 is isomorphic with C12.
We will now consider another direct product group, namely C6 x C2.
A B C D E F P Q (A) (B) (C) (D) (E) (F) (P) (Q), Period = 1
F A B C D E P Q (AFEDCB) (P) (Q), Period = 6
E F A B C D P Q (AEC) (BFD) (P) (Q), Period = 3
D E F A B C P Q (AD) (BE) (CF) (P) (Q), Period = 2
C D E F A B P Q (ACE) (BDF) (P) (Q), Period = 3
B C D E F A P Q (ABCDEF) (P) (Q), Period = 6
A B C D E F Q P (A) (B) (C) (D) (E) (F) (PQ), Period = 2
F A B C D E Q P (AFEDCB) (PQ), Period = 6
E F A B C D Q P (AEC) (BFD) (PQ), Period = 6
D E F A B C Q P (AD) (BE) (CF) (PQ), Period = 2
C D E F A B Q P (ACE) (BDF) (PQ), Period = 6
B C D E F A Q P (ABCDEF) (PQ), Period = 6
We see that there is no element of period 12, so our new group is definitely not C12. The underlying reason for this is, of course, that 2 is a factor of 6, so that when either of the twelve permutations has been performed six times, the letter P and Q are the right way round again, and the order of the whole set is restored. So no element can be of period greater than 6, and thus we do certainly not have to do with C12. In fact, C6 x C2 (or C2 x C6) is a new group of order 12 which is not isomorphic with either C12, or D6 or Q6 (This last one is the quaterion group of order 12). In D6, which can be realized in the symmetries of the Regular Hexagon, there are 7 elements of period 2, while in our present group there are only 3 of them. In the group A4, which is also of order 12, and which can be realized as the direct symmetries of the Regular Tetrahedron, has no elements of order 6, so our present group cannot be isomorphic with A4.
Of the five groups of order 12, D6, Q6, and A4 are all non-Abelian, whereas C12 and C6 x C2 are Abelian.
For us it is important that C6 x C2 has a crystallographic realization, namely in crystals of the Hexagonal-bipyramidal Class (6/m) of the Hexagonal Crystal System. Such crystals have one mirror plane, coinciding with the equatorial plane. No other mirror planes are present. Perpendicular to the equatorial plane is a 6-fold rotation axis. In this realization the group C6 x C2 is called C6i .
Indeed we can interpret the above 12 permutations as the symmetry transformations of the crystals of this Class (6/m). These symmetries are rotations about the main axis and reflection across the equatorial plane.
Let us first list and name those symmetry transformations :
1 = identity (00 rotation).
r = rotation by 600.
r2 = rotation by 1200.
r3 = rotation by 1800.
r4 = rotation by 2400.
r5 = rotation by 3000.
a = reflection in equatorial plane.
ar = ra = reflection in equatorial plane followed by a rotation of 600.
ar2 = r2a = reflection in equatorial plane followed by a rotation of 1200.
ar3 = r3a = reflection in equatorial plane followed by a rotation of 1800.
ar4 = r4a = reflection in equatorial plane followed by a rotation of 2400.
ar5 = r5a = reflection in equatorial plane followed by a rotation of 3000.
We can now let these symmetries to be corresponded to the above twelve permutations :
A B C D E F P Q = 1. Period = 1
F A B C D E P Q = r. Period = 6
E F A B C D P Q = r2. Period = 3
D E F A B C P Q = r3. Period = 2
C D E F A B P Q = r4. Period = 3
B C D E F A P Q = r5. Period = 6
A B C D E F Q P = a. Period = 2
F A B C D E Q P = ar = ra. Period = 6
E F A B C D Q P = ar2 = r2a. Period = 6
D E F A B C Q P = ar3 = r3a. Period = 2
C D E F A B Q P = ar4 = r4a. Period = 6
B C D E F A Q P = ar5 = r5a. Period = 6
We can now construct the group table for the group C6 x C2 with the notation and interpretation of its twelve elements geared to the description of the group of symmetries of crystals of the Class 6/m :
| 1 | r | r2 | r3 | r4 | r5 | a | ar | ar2 | ar3 | ar4 | ar5 | period | |
| 1 | 1 | r | r2 | r3 | r4 | r5 | a | ar | ar2 | ar3 | ar4 | ar5 | 1 |
| r | r | r2 | r3 | r4 | r5 | 1 | ar | ar2 | ar3 | ar4 | ar5 | a | 6 |
| r2 | r2 | r3 | r4 | r5 | 1 | r | ar2 | ar3 | ar4 | ar5 | a | ar | 3 |
| r3 | r3 | r4 | r5 | 1 | r | r2 | ar3 | ar4 | ar5 | a | ar | ar2 | 2 |
| r4 | r4 | r5 | 1 | r | r2 | r3 | ar4 | ar5 | a | ar | ar2 | ar3 | 3 |
| r5 | r5 | 1 | r | r2 | r3 | r4 | ar5 | a | ar | ar2 | ar3 | ar4 | 6 |
| a | a | ar | ar2 | ar3 | ar4 | ar5 | 1 | r | r2 | r3 | r3 | r5 | 2 |
| ar | ar | ar2 | ar3 | ar4 | ar5 | a | r | r2 | r3 | r4 | r5 | 1 | 6 |
| ar2 | ar2 | ar3 | ar4 | ar5 | a | ar | r2 | r3 | r4 | r5 | 1 | r | 6 |
| ar3 | ar3 | ar4 | ar5 | a | ar | ar2 | r3 | r4 | r5 | 1 | r | r2 | 2 |
| ar4 | ar4 | ar5 | a | ar | ar2 | ar3 | r4 | r5 | 1 | r | r2 | r3 | 6 |
| ar5 | ar5 | a | ar | ar2 | ar3 | ar4 | r5 | 1 | r | r2 | r3 | r4 | 6 |
Table 9.3
The group C6 x C2 looks like the group D6, but we see a different period distribution over the group elements, so the groups are different. Compare with Table 7.10 in Part VII.
As has been said, the group C6 x C2 is crystallographically realized in crystals of the Hexagonal-bipyramidal Class (6/m) of the Hexagonal Crystal System. The promorph or stereometric basic form of all the single non-twinned crystals of this Class (6/m) is the Regular Hexagonal Gyroid Bipyramid, and it belongs to the Isosigmostaura sextamera (Stauraxonia homopola sigmostaura) of the Promorphological System of Basic Forms. See next Figure.
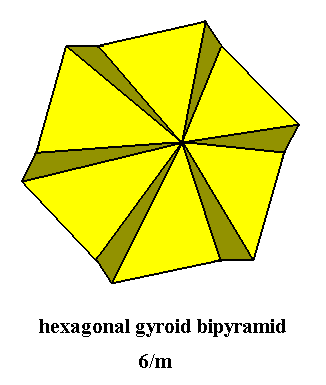
Figure 4. Regular Hexagonal (i.e. six-fold) Gyroid Bipyramid, Stereometric Basic Form of the (single) crystals of the Hexagonal-bipyramidal Class of the Hexagonal Crystal System. Because of the view direction the lower pyramid is not visible.
Associativity and Commutativity of Direct Product
We will demonstrate that the direct product of groups is commutative as well as associative. We will derive these properties from the definition of the direct product. Let's give this definition again :
(gp, gq') (gr, gs') = (gp * gr , gq' *' gs')
is a group of order nn', and is called the Direct Product Group of G and G', and is abbreviated G x G'.
When we reverse the order of the two (general) groups G and G' of the definition, the order within the ordered pairs are reversed. We get for G' x G :
(gq', gp) (gs', gr) = (gq' *' gs' , gp * gr).
To establish the isomorphy between G x G' and G' x G we first show that between the elements of G and G' there is a 1,1 correspondence (blue arrow) :
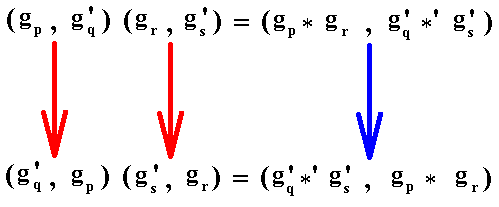
What we now have to do (in order to prove the isomorphism) is to show that products are conserved (which it self is a prof for homomorphy) :
Call the 1,1 mapping from G to G' the mapping h. Then we have :
h [(gp * gr , gq' *' gs') (ga * gc , gb' *' gd')] =
h [(gp * gr ) * (ga * gc) , (gq' *' gs') *' (gb' *' gd')] =
((gq' *' gs') *' (gb' *' gd') , (gp * gr ) * (ga * gc))
In words : The image of the product [i.e. (the image under h of) the product of two elements (both are ordered pairs) of the group G x G'] is a new ordered pair, and is calculated as follows : first we determine the product, and this results in a pair of which the first member consists of the product (*) of the first members of the initial two ordered pairs to be multiplied, and of which the second member consists of the product (* ') of the second members of the initial two ordered pairs to be multiplied. Then, to obtain the image under h, we reverse the members of the obtained ordered pair.
h [(gp * gr , gq' *' gs')] = (gq' *' gs' , gp * gr ).
h [(ga * gc , gb' *' gd')] = (gb' *' gd' , ga * gc).
In words : The image under h of the first element of G x G' is obtained by the reversal of the two members of that pair that constituted that first element. The image of that element is an element of G' x G.
The image under h of the second element of G x G' is obtained by the reversal of the two members of that pair that constituted that second element. The image of that element is also an element of G' x G.
h [(gp * gr , gq' *' gs')] h [(ga * gc , gb' *' gd')] =
(gq' *' gs' , gp * gr ) (gb' *' gd' , ga * gc) =
((gq' *' gs') *' (gb' *' gd') , (gp * gr ) * ( ga * gc)).
Thus we have demonstrated that
h [(gp * gr , gq' *' gs') (ga * gc , gb' *' gd')] =
h [(gp * gr , gq' *' gs')] h [(ga * gc , gb' *' gd')].
Or in words : The image (under h ) of the product is equal to the product of the images, which means that products are preserved in the mapping h from G x G' to G' x G. So the mapping h is a homomorphism. And because it is a 1,1 homomorphism (bijective homomorphism) it is an isomorphism. It is an isomorphism between the groups G x G' and G' x G, so the commutativity of the direct product is demonstrated.
Associativity of the direct product, i.e. that (A x B) x C = A x (B x C), where A, B and C are groups, can also be proved from the definition of direct product. Moreover it can be demonstrated that the elements of A x B x C may be taken to be ordered triples of the form (a, b, c) where a is element of A, b is element of B, and c is element of C. The rule for the composition of such triples can be worked out from the rule of the composition of ordered pairs.
Thus we may write A x B x C without ambiguity, and, moreover, the letters may be permuted in any manner A x B x C is isomorphic with B x C x A, etc. For example,
C2 x C6 is isomorphic with C6 x C2, and since C6 is isomorphic with C3 x C2 (because the L.C.M. of 3 and 2, i.e. elements of period 3 to be combined with elements of period 2, is 6), we may also write C2 x C6 is isomorphic with C2 x (C2 x C3) is isomorphic with C2 x C2 x C3 is isomorphic with C3 x C2 x C2, etc.
We will shortly show that C2 x C2 is isomorphic with D2, and then we can say :
C2 x C6 is isomorphic with D2 x C3.
This means that the group C2 x C6 may be realized by the product of two disjoint sets of permutations one being those permutations of four letters A B C D, which give the group D2, the other being the cyclic permutations of P Q R.
D2 can be represented by the permutations
1 = A B C D = (A)(B)(C)(D), implying this element to be of period 1.
a = B A D C = (AB) (CD), implying this element to be of period 2.
b = C D A B = (AC) (BD), implying this element to be of period 2.
ab (ba) = D C B A = (AD) (BC), implying this element to be of period 2.
and C3 by the permutations
1 = P Q R = (P) (Q) (R), implying this element to be of period 1.
p = R P Q = (PRQ), implying this element to be of period 3.
p2 = Q R P = (PQR), implying this element to be of period 3.
Hence the group D2 x C3 is the group of the set of twelve permutations obtained by combining these (i.e. by combining the just listed permutations), such as
pab is : first permutation b, then permutation a, and then permutation p.
The permutation b is then
C D A B P Q R
While the permutation a is
B A D C P Q R
So the permutation ab is
D C B A P Q R
The permutation p is
A B C D R P Q
So the permutation pab is
D C B A R P Q.
Now we will demonstrate that C2 x C2 is isomorphic with D2.
The group C2 is a cyclic group consisting of two elements, the identity (1), and one element of period 2 (let us call it h, and thus hh = 1) (for example a rotation by 1800). The group can thus be denoted by {1, h}. So in order to form the product C2 xC2, we must form all the possible ordered pairs (i.e. the cartesian product) of the two sets {1, h} and {1, h}. These pairs are :
(1, 1), (1, h), (h, 1), (h, h).
We will now investigate how these pairs behave under multiplication according to the definition of a direct product.
(1, 1) (1, 1) = (1.1, 1.1) = (1, 1)
(1, 1) (1, h) = (1.1, 1.h) = (1, h)
(1, 1) (h, 1) = (1.h, 1.1) = (h, 1)
(1, 1) (h, h) = (1.h, 1.h) = (h, h)
(1, h) (1, 1) = (1.1, h.1) = (1, h)
(1, h) (1, h) = (1.1, h.h) = (1, 1)
(1, h) (h, 1) = (1.h, h.1) = (h, h)
(1, h) (h, h) = (1.h, h.h) = (h, 1)
(h, 1) (1, 1) = (h.1, 1.1) = (h, 1)
(h, 1) (1, h) = (h.1, 1.h) = (h, h)
(h, 1) (h, 1) = (h.h, 1.1) = (1, 1)
(h, 1) (h, h) = (h.h, 1.h) = (1, h)
(h, h) (1, 1) = (h.1, h.1) = (h, h)
(h, h) (1, h) = (h.1, h.h) = (h, 1)
(h, h) (h, 1) = (h.h, h.1) = (1, h)
(h, h) (h, h) = (h.h, h.h) = (1, 1)
We clearly see that the set {(1, 1), (1, h), (h, 1), (h, h)} is closed under the operation of the multiplication of ordered pairs according to the definition of the direct product.
In order to show that these four pairs, (1, 1), (1, h), (h, 1), (h, h), i.e. the elements of the group C2 x C2, behave according to the group D2, we will rename these elements as repectively 1, X, Y, and Z. Thus :
(1, 1) = 1
(1, h) = X
(h, 1) = Y
(h, h) = Z
So we can translate the above multiplications accordingly :
(1, 1) (1, 1) = (1, 1) is equivalent to 1.1 = 1
(1, 1) (1, h) = (1, h) is eqquivalent to 1.X = X
(1, 1) (h, 1) = (h, 1) is equivalent to 1.Y = Y
(1, 1) (h, h) = (h, h) is equivalent to 1.Z = Z
(1, h) (1, 1) = (1, h) is equivalent to X.1 = X
(1, h) (1, h) = (1, 1) is equivalent to X.X = 1
(1, h) (h, 1) = (h, h) is equivalent to X.Y = Z
(1, h) (h, h) = (h, 1) is equivalent to X.Z = Y
(h, 1) (1, 1) = (h, 1) is equivalent to Y.1 = Y
(h, 1) (1, h) = (h, h) is equivalent to Y.X = Z
(h, 1) (h, 1) = (1, 1) is equivalent to Y.Y = 1
(h, 1) (h, h) = (1, h) is equivalent to Y.Z = X
(h, h) (1, 1) = (h, h) is equivalent to Z.1 = Z
(h, h) (1, h) = (h, 1) is equivalent to Z.X = Y
(h, h) (h, 1) = (1, h) is equivalent to Z.Y = X
(h, h) (h, h) = (1, 1) is equivalent to Z.Z = 1
We can now construct a group table of these products :
| 1 | X | Y | Z | |
| 1 | 1 | X | Y | Z |
| X | X | 1 | Z | Y |
| Y | Y | Z | 1 | X |
| Z | Z | Y | X | 1 |
From the yable we can see that, except the identity all elements are of period 2 :
Let's now consider the direct product D3 x C2. Since D3 is not Abelian (i.e. not commutative), we do not expect the direct product group to be Abelian. Using permutations, we need to combine the full set of six permutations of three letters, A, B, C (because they express the structure of D3) with the transpositions of two letters, P, Q. Because the full group of six permutations of three letters (i.e. all possible permutations of three letters) is in fact (also called) the group S3, and all the possible permutations of two letters consitute the group S2, the product might as well be called S3 x S2 (Sn is the group of permutations (i.e. all possible permutations) of n symbols).
D3 expresses the symmetry of the equilateral triangle, and at the same time the symmetry of the regular trigonal pyramid (i.e. a single pyramid with an equilateral triangle as its base). If we now add a second trigonal pyramid, congruent with the first one, such that the two pyramids are attached to each other by their bases, then we have the regular trigonal bipyramid. In fact we now have combined the D3 symmetry with a 'flip-flop' symmetry, or, in other words, we have combined the elements of D3 with a new element of period 2. And this combination yields six more elements (i.e. six more symmetry transformations).
Further down we will list all these elements as named permutations of the letters A, B, C, P, Q.
In the mentioned trigonal bipyramid
The upper apex of this pyramid is called P,
The lower apex is called Q,
The vertices at the triangular equatorial plane are called A, B, and C.
See next Figure.
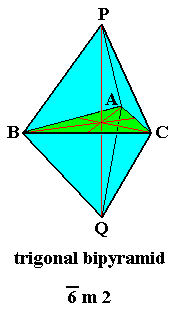
Figure 5. The Trigonal Bipyramid, its vertices named A, B, C, P, Q.
Equatorial plane indicated (green). The three cross axes lying in the equatorial plane are indicated (red).
In the permutations to follow we will recognize the symmetry transformations of the trigonal bipyramid :
| 1 | A | B | C | P | Q | Identity | d | A | B | C | Q | P | eq. refl. | |||
| p | C | A | B | P | Q | rot. 1200 | dp | C | A | B | Q | P | 1200+eq.refl. | |||
| p2 | B | C | A | P | Q | rot. 2400 | dp2 | B | C | A | Q | P | 2400+eq.refl. | |||
| a | A | C | B | P | Q | refl. in a | da | A | C | B | Q | P | refl. in a + eq.refl. | |||
| b | C | B | A | P | Q | refl. in b | db | C | B | A | Q | P | refl. in b + eq.refl. | |||
| c | B | A | C | P | Q | refl. in c | dc | B | A | C | Q | P | refl. in c + eq.refl. |
We can now determine the periods of these 12 elements :
ABC PQ = (A) (B) (C) (P) (Q). Period = 1
CAB PQ = (ACB) (P) (Q). Period = 3
BCA PQ = (ABC) (P) (Q). Period = 3
ACB PQ = (A) (BC) (P) (Q). Period = 2
CBA PQ = (AC) (B) (P) (Q). Period = 2
BAC PQ = (AB) (C) (P) (Q). Period = 2
ABC QP = (A) (B) (C) (PQ). Period = 2
CAB QP = (ACB) (PQ). Period = 6
BCA QP = (ABC) (PQ). Period = 6
ACB QP = (A) (BC) (PQ). Period = 2
CBA QP = (AC) (B) (PQ). Period = 2
BAC QP = (AB) (C) (PQ). Period = 2
The distribution of periods among the 12 elements is the finger print of the group D6, thus we have demonstrated that D3 x C2 is isomorphic with D6. So the full symmetry of the trigonal bipyramid and also that of the regular hexagon as well as that of the regular hexagonal pyramid (single pyramid), is according to the group D6, which is isomorphic with D3 x C2.
In the next document we will continue the study of some more product groups, especially those with crystallographical realizations.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals