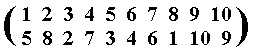
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Conjugate elements and normal subgroups
In group theory we often encounter the combined operation xyx-1.
This is a very important operation, and it is useful to point directly to its equivalent that can be derived from it :
z = xyx-1 is equivalent to
zx = xyx-1x, and this is equivalent to
zx = xy, (which is of course equivalent to xy = zx)
We shall now call this operation by name, and study it further.
The element xyx-1 is called the t r a n s f o r m of the element y by the element x.
Also, if z = xyx-1 (equivalent to zx = xy), then y and z are called conjugate elements of the group.
The term "conjugate" implies that the relationship between conjugate elements is 'reciprocal', 'mutual', 'two-way', or 'symmetric' -- if z is conjugate to y, then one has a right to expect that y will be conjugate to z.
Let's see.
z = xyx-1 implies zx = xy, and this implies x-1zx = x-1xy = y.
Hence y = x-1zx, so that y is the transform of z by the element x-1, and the symmetric nature of the relationship is proved. It would be possible to distinguish xyx-1 and x-1yx by describing them as 'right' and 'left' conjugates of y by x. However, in the absence of any specification, we shall normally mean the former, i.e. xyx-1.
The equations y = x-1zx and z = xyx-1 are indeed equivalent, because both are equal to xy = zx (xy = xx-1zx, resp. zx = xyx-1x).
Note that in an Abelian group (i.e. a group in which all elements commute, in the sense of ab = ba for all elements a, b of the group) the whole concept of the transform of an element becomes trivial, for in this case, xyx-1 = xx-1y = y, and so each element is its own transform.
In a non-Abelian group, xyx-1 will generally be different from the transformed element y, though it will have some features in common with it. If, however, by chance xyx-1 does equal y, then we have xyx-1x = yx, which is equivalent to xy = yx, so that the two elements commute, though the group as a whole may be non-Abelian.
Conjugate elements have the same period
One of the features which conjugate elements have in common is that they have the same period.
If yk = 1 (which means that the period of the element y is k), then
(xyx-1)k = (xyx-1)(xyx-1)(xyx-1) . . . (xyx-1) ( k factors) =
xy(x-1x)y(x-1x)y . . . y(x-1x)yx-1 = xyyyy . . . yyx-1 = xykx-1 = x1x-1 = 1, and k is the least integer for which this is true, because xykx-1 only becomes 1 as soon as yk = 1, and y only becomes 1 until it is repeated k times, and not earlier. So xyx-1 must be repeated k times before it becomes 1.
Hence xyx-1 is also of period k.
Conjugate elements as similar permutations
We illustrate xyx-1 from a group of permutations (BUDDEN, p. 364).
Let
y represent the product of cycles (1 5 3 2 8)(4 7 6)(9 10),
x represent the product of cycles (5 6 8 9)(2 7)(3 10),
so that
x-1 represents the product of cycles (10 3)(7 2)(9 8 6 5).
We will consider the effect of xyx-1. But before doing that we will determine to what permutations those products of cycles correspond.
The product of cycles (1 5 3 2 8)(4 7 6)(9 10) means a reshuffling of the numerals 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. And, specifically, this particular product of cycles means :
1 becomes 5
5 becomes 3
3 becomes 2
2 becomes 8
8 becomes 1
4 becomes 7
7 becomes 6
6 becomes 4
9 becomes 10
10 becomes 9
(It is clear, by the way, that the cycle, say, (4 7 6) is identical to (7 6 4)).
On the basis of this we can now write the permutation implied by this product of cycles :
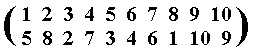
Which can also be written as 5 8 2 7 3 4 6 1 10 9.
In the same way we can determine the corresponding permutations of the other products of cycles.
Further it is clear that when some element does not occur in such a product of cycles, it will not become another element, but stays the same. For example in the product of cycles x = (5689)(27)(3 10) the 1 does not occur, so here 1 'becomes' 1.
When we, in the following write, say,
1 -- (x-1) -- 1 -- (y) -- 5 -- (x) -- 6,
we mean the following :
The symbol 1, subjected to the operation x-1, becomes (i.e. stays) 1, this result, subjected to the operation y becomes 5, and this result subjected to the operation x becomes 6. And this in turn means that when we apply the combined operation xyx-1 to the symbol 1 we get the symbol 6.
Let us now consider the effect of xyx-1 ( = first perform the operation x-1 on the number sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, then, on the result, the operation y, and finally the operation x ) (The operations x, x-1 and y are specified above -- as permutations of symbols indicated as products of cycles) :
1 -- (x-1) -- 1 -- (y) -- 5 -- (x) -- 6
6 -- (x-1) -- 5 -- (y) -- 3 -- (x) -- 10
10 -- (x-1) -- 3 -- (y) -- 2 -- (x) -- 7
7 -- (x-1) -- 2 -- (y) -- 8 -- (x) -- 9
9 -- (x-1) -- 8 -- (y) -- 1 -- (x) -- 1
So we obtain the cycle (1 6 10 7 9).
2 -- (x-1) -- 7 -- (y) -- 6 -- (x) -- 8
8 -- (x-1) -- 6 -- (y) -- 4 -- (x) -- 4
4 -- (x-1) -- 4 -- (y) -- 7 -- (x) -- 2
So we obtain the cycle (2 8 4).
3 -- (x-1) -- 10 -- (y) -- 9 -- (x) -- 5
5 -- (x-1) -- 9 -- (y) -- 10 -- (x) -- 3
So we obtain the cycle (3 5 ).
Threfore xyx-1 contains the cycles (1 6 10 7 9)(2 8 4)(3 5). We have here an example of a general theorem :
The transform of a given permutation by another permutation will contain cycles of the same lengths as the given permutation.
In the above case, the cycles were of lengths 5, 3, and 2 both for y and for xyx-1. So in addition to the fact that conjugate elements are of the same period, we have here discovered a second resemblance of an element and its conjugate. The permutations y and xyx-1 are often described as similar permutations.
Furthermore we observe that
y = (1 5 3 2 8)(4 7 6)(9 10),
xyx-1 = (1 6 10 7 9)(4 2 8)(5 3) ((428) = (284), and (53) = (35)),
and the symbols in each cycle of y are replaced according to the permutation x which, as implied by the given product of cycles, is :
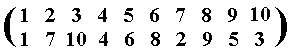
And this permutation should be applied not to the permutation y, but to the symbols 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, as they are arranged in the three constituent cycles together representing the permutation y. So the permutation x, must be applied to 1 5 3 2 8 4 7 6 9 10.
All this is illustrated by the following diagram :
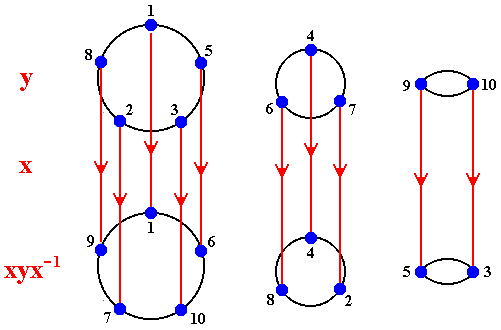
In the diagram we can follow the action of xyx-1, taking a symbol to another symbol, by first applying x-1, then y then x :
Reflection in a moved axis
In the next diagram let m and m* denote the operations of reflecting in the lines labelled m and m*, where the second mirror line is obtained from the first by a rotation r about a certain point O. Now consider the effect of reflecting a motif (F) in the moved (*) mirror line. This same effect can, however, be obtained in another way, by using reflection in the mirror line in its original position : Apply the inverse rotation, r-1, to the motif, taking it back to the position r-1(F), then reflect in the original position of the mirror, so obtaining
mr-1(F), then apply the rotation r to carry this image, with the mirror, into its final position, rmr-1(F).
Hence we obtain m* = rmr-1,
i.e. the operation of reflecting in the rotated mirror is the transform by the rotation, of the operation of reflection in its original position.
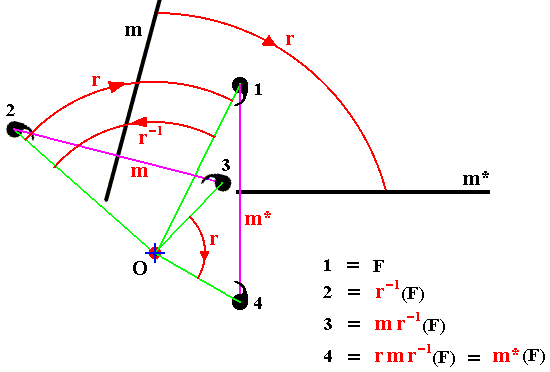
Figure 2. Reflection in the rotated mirror is the conjugate of m by r,
i.e. m* = rmr-1.
The black straight lines are the mirror (m), and the rotated mirror (m*).
The operations r, m, and r-1 and m* are applied to a comma motif.
All the rotations are about the point O.
In the above diagram we can see that when we subject the motif F (position 1) to the operation r-1 (which here is an anticlockwise rotation of 750) we move it to position 2, and can indicate it as r-1(F). When we now subject this result to the operation m (which is a reflection in the original mirror line), the motif ends up in position 3, and we can indicate this as mr-1(F). When, finally, we subject this result to the operation r (which is a clockwise rotation of 750, the motif ends up at position 4.
It is instructive to illustrate this in the case of the symmetries of a figure. Consider the group D4 as the group of symmetries of the Square or Regular Tetragonal Pyramid.
Let us first give the table of D4 (in which the elements are denoted by different letters, i.e. not in terms of generators).
| 1 | a | b | c | d | f | g | h | period | |
| 1 | 1 | a | b | c | d | f | g | h | 1 |
| a | a | 1 | h | g | f | d | c | b | 2 |
| b | b | f | 1 | h | g | a | d | c | 2 |
| c | c | g | f | 1 | h | b | a | d | 2 |
| d | d | h | g | f | 1 | c | b | a | 2 |
| f | f | b | c | d | a | g | h | 1 | 4 |
| g | g | c | d | a | b | h | 1 | f | 2 |
| h | h | d | a | b | c | 1 | f | g | 4 |
Table 15.1
With the notation of the above group table we may let f denote an anticlockwise rotation through 900, f 2 = g, f -1 = h (because f h = 1). The reflections are shown in the next Figure, these axes being fixed in space.
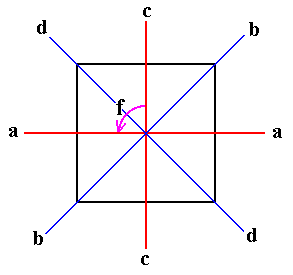
Figure 3. Symmetries of the Square (or Regular Tetragonal Pyramid).
b = fdf -1. d = fbf -1.
df -1 = dh = a
b = fdf -1
bf -1 = bh = c
fc = d, so
d = fbf -1
We see that b and d are conjugate elements. So reflection in one diagonal is conjugate, under a quarter-turn, to reflection in the other diagonal, and this is precisely because the quarter-turn transforms one diagonal into the other (because f is -- as stated above -- an (anticlockwise) rotation of 900).
In the particular example of Figure 2 above, we used r to denote a rotation of the mirror, but it might have represented any transformation. The above statement m* = rmr-1 (also expressed verbally) may thus be generalized thus :
The operation of reflecting in the transformed mirror is equivalent to applying the inverse transformation (i.e. first taking the mirror back to its original position), reflecting in the original position, and finally applying the transformation (to restore the final position).
Symbolically : m* = tmt-1, where t is any transformation of the mirror axis.
Transformed operations in general
Consider next a rotation r through angle THETA about P and a translation t represented by the vector PQ. See next Figure.
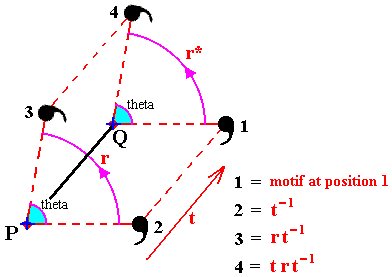
Figure 4. Rotation transformed by a translation.
Let us find out what is the significance of the operation r transformed by t , i.e. the significance of trt-1. The diagram makes it clear that the combined operation trt-1 is equivalent to a single rotation about Q (i.e. the new position of P transformed by the operation t, which carries P to Q). This is also apparent from other considerations : for the effect of trt-1 on the point Q itself is to leave it where it is :
trt-1(Q) = tr(P) (since t-1(Q) = P)
= t(P) (since r(P) = P)
= Q.
And since the combined operation which consists of a parallel movement, a rotation through THETA, and then another parallel movement, is intuitively equivalent to a single rotation through THETA, it is evident that trt-1 is a rotation through THETA about Q ( = r* ), so r* = trt-1.
The above discussion may be summarized and generalized by reference to the following diagram illustrating s = trt-1.
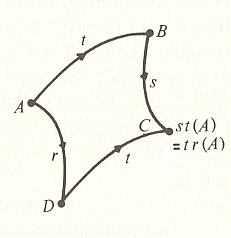
A point A is transformed by t into the point B, i.e. B = t(A). B is then transformed by s into C, so that C = s(B) = st(A). On the other hand, A is transformed by r into D, so D = r(A), while C = t(D) = tr(A). Hence we have st(A) = tr(A), or st = tr, which is equivalent to stt-1 = trt-1, which in turn is equivalent to s = trt-1. The point of the diagram is to show that to go from B to C (operation s ), one may go via A and D, performing the operations t-1, r, and t consecutively. Or, looking at it another way, the transformation s (the conjugate of r under t ) is obtained from r by replacing each point and its image under r (e.g. A and D) by their images under t (i.e. B and C).
Next we give some informal illustrations of the operation xyx-1.
Conjugacy classes
If, for two elements y and z of a group, it is possible to find an x in the group such that z = xyx-1 (or that y = x-1zx, or that zx = xy, or that x-1z = yx-1), then, as we have seen, y and z are described as a pair of conjugate elements. If y and z are both given, there may not exist in the whole group a single element x such that zx = xy, and in this case, y and z are not conjugate. Thus conjugacy is a relation between elements of a group. It is evidently reflexive, since there is always an element in the group that transforms a given element into itself, namely the identity : y = 1y1-1, and we have already shown that it is a symmetric relation which justifies the name "conjugate". To show that it is also transitive (which then finally would establish the relation 'is conjugate to' to be an equivalence relation), suppose that the relation 'is conjugate to' is denoted 'R'. Then if yRz and zRw , we require to demonstrate that yRw.
Suppose we have a group G.
Now yRz implies yx1 = x1z for some x1 in G.
And zRw implies zx2 = x2w for some x2 in G.
From zx2 = x2w we can deduce zx2x2-1 = x2wx2-1, an this implies z = x2wx2-1.
Making use of this we can now say yx1 = x1x2wx2-1, so that yx1x2 = x1x2wx2-1x2, which implies yx1x2 = x1x2w.
Thus if x1x2 = x3 (the group G being closed), we have yx3 = x3w, and therefore yRw.
We have thus proved that conjugacy is an equivalence relation.
We may now proceed to set up equivalence classes.
For a fixed element y, all those elements z1, z2, z3, . . . which are conjugate to y will be in the same equivalence class with y. We can state the concept of a conjugacy class in a different but equivalent way : Those elements which belong to the same conjugacy class may be transformed into each other.
Note that in an Abelian group (in which all elements commute) the question of conjugacy is trivial : The only element which is conjugate to y is y itself, so each element is the sole member of its particular conjugacy class.
In all groups, including non-Abelian groups, it is obvious that the identity is going to be in a class on its own -- it cannot be 'transformed into' another element of the group because it has a different nature from all the others. Indeed, it is the only element of period 1, and since we have seen that the period of an element is unchanged by conjugation by any other element, it is clear that no other element of the group can possibly be conjugate to the identity.
An element is said to be self-conjugate when it commutes with every element of the group, i.e. belongs to the center (See later for the concept of center). For if xy = yx for all y in the group, then x = yxy-1 for all y, i.e. x is transformed into itself by all the elements of the group -- no other element of the group is conjugate to it -- its conjugacy class contains it alone.
Finding conjugacy classes
Let us show how we can find conjugacy classes in a given group.
Now it is evidently going to be a very long and tedious process to work out xyx-1 for every possible pair of values of x and y (for a group of order twelve up to 144 such computations would be necessary). But the work can be greatly reduced. To begin with, we may easily find pairs of conjugate elements as follows : find any element p in row x (say p = xy). Next find p in column x, so that p = zx. Then p = xy = zx, so that yRz. This is a suitable procedure only when the transforming element x is given. It becomes a different matter when we want to know whether two given elements are conjugates.
Suppose we are trying to discover whether or not two given elements y and z are conjugate. See next Figure.
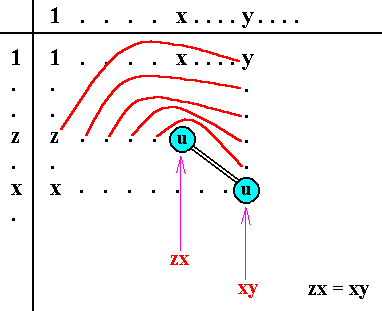
Figure 6. Finding out whether the two elements z and y are conjugates.
This means that we are seeking an x in the group such that zx = xy = u (say). The element u will occur in row z, column x, and also in column y, row x. To find it, we look along row z and down column y at each element in turn, thus in such a way that we compare elements which find themselves every time at the same location in row z and in column y : We first compare the first element of row z with the first element in column y, and if they are not identical we compare the second element of row z with the second element in column y, etc. (See diagram above), till we find a pair the same (i.e. two identical elements). In the diagram it is supposed that the first five elements in row z and column y disgree till we reach the sixth, which are both u's (The corresponding elements that are being compared are linked by red lines in the diagram). This common element u has the property that it lies in row z, column x (say), and also in column y, row x, so that zx = xy, or z = xyx-1 and zRy (It would also be possible to have used column z in conjunction with row y, since zRy is equivalent to yRz ).
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | period | |
| 1 | 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | 1 |
| a | a | 1 | c | b | s | r2 | r | s2 | q | p2 | p | q2 | 2 |
| b | b | c | 1 | a | q | s2 | p | r2 | s | q2 | r | p2 | 2 |
| c | c | b | a | 1 | r | q2 | s | p2 | p | s2 | q | r2 | 2 |
| p | p | r | s | q | p2 | 1 | r2 | b | s2 | c | q2 | a | 3 |
| p2 | p2 | s2 | q2 | r2 | 1 | p | c | s | a | q | b | r | 3 |
| q | q | s | r | p | s2 | b | q2 | 1 | p2 | a | r2 | c | 3 |
| q2 | q2 | r2 | p2 | s2 | c | r | 1 | q | b | s | a | p | 3 |
| r | r | p | q | s | q2 | c | s2 | a | r2 | 1 | p2 | b | 3 |
| r2 | r2 | q2 | s2 | p2 | a | s | b | p | 1 | r | c | q | 3 |
| s | s | q | p | r | r2 | a | p2 | c | q2 | b | s2 | 1 | 3 |
| s2 | s2 | p2 | r2 | q2 | b | q | a | r | c | p | 1 | s | 3 |
Table 15.2
Now one way in which the work can be reduced is that we know that yRz implies that y and z have the same period (as we found out ABOVE). Therefore it is a waste of time even to make the above check for elements of different periods. In the group A4, we begin by checking whether or not aRb, i.e. whether the element a is conjugate to the element b (note : both a and b are of period 2). The best way to do this is to take row a, and column b, and write the latter horizontally below the former. Above these we will place the group elements as they are arranged along the top of the group table (as well as along its left side) (As such this top row does not belong to the group table proper) :
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | |
| Row a | a | 1 | c | b | s | r2 | r | s2 | q | p2 | p | q2 |
| Column b | b | c | 1 | a | s | q2 | r | p2 | q | s2 | p | r2 |
How must we read and interpret this diagram?
We know that a product xy must be read off from a group table as follows :
Look in row x, and then in column y, and see what element we find at the intersection. On the other hand, if we want to know the factors of a product z, given somewhere in the group table, we determine first the row in which that product is, say that it is row x, and then we determine the column in which that product is, say it is y. And now we know that z = xy. When we want to know whether a is conjugate to b, we look into row a and column b, which we align horizontally as done above, and see whether there are two identical elements (products) which are situated at corresponding locations of the row and column (for example both at the third entry), i.e. whether we can find in the above diagram identical products one precisely on top of the other, one upper product and one lower product. If we have found two such products then we know that a and b are conjugated.
So when we want to identify -- in our present example -- the factors of the upper product s (which is in row a ) we see that it is at the same time in column p, so we have s = ap. If, on the other hand, we want to determine the factors of the lower product s (present in column b, ) we must now interpret the arrangement of group elements, written down on top of the above diagram, as the headers of the twelve rows. In this way we find that the lower product s is in row p, while it is at the same time in column b, and so we find s = pb.
So from the above diagram we see that
ap = pb = s, so app-1 = pbp-1, and this is equivalent to a = pbp-1, which means that a and b are conjugates, that is aRb.
As has been said, this is sufficient for establishing aRb, but it is instructive to analyse the above diagram further.
In it we see that there are some more identical products (elements) at corresponding locations of the row and column. On the basis of this we can establish that
aq = qb = r (also implying aRb)
ar = rb = q (also implying aRb)
Although we already know that aRb = bRa, we can check it out by using, instead of row a and column b, row b and column a :
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | |
| Row b | b | c | 1 | a | q | s2 | p | r2 | s | q2 | r | p2 |
| Column a | a | 1 | c | b | r | s2 | s | r2 | p | q2 | q | p2 |
The identical elements at corresponding positions are indicated (red). They are : s2, r2, q2, p2.
From this we can see that
bp2 = p2a = s2 (implying bp2(p2)-1 = p2a(p2)-1, which is equivalent to b = p2a(p2)-1, meaning bRa ).
Further we see that
bq2 = q2a = r2 (also implying bRa).
br2 = r2a = q2 (also implying bRa).
bs2 = s2a = p2 (also implying bRa).
In the same way we can verify aRc :
In order to do so we take row a and column c of the group table of the group A4 :
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | |
| Row a | a | 1 | c | b | s | r2 | r | s2 | q | p2 | p | q2 |
| Column c | c | b | a | 1 | q | r2 | p | s2 | s | p2 | r | q2 |
From this we can see that
ap2 = p2c = r2 (implying aRc).
aq2 = q2c = s2 (implying aRc).
ar2 = r2c = p2 (implying aRc).
as2 = s2c = q2 (implying aRc).
And we know that cRa.
In the same way we can find that bRc, and of course cRb.
And now we know that a, b, and c are each others conjugate (and we will see that they are not conjugates of any other element of the group A4), so we have the conjugacy class {a, b, c} (we will continue to find more conjugacy classes of the group A4 in due course).
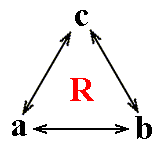
Figure 7. The conjugate class {a, b, c} of the group A4 . In addition to being conjugate to each other, these elements are also conjugate to themselves (not expressed in the Figure).
Now it so happens that this class contains all the elements of period 2. But do not imagine that just because two elements have the same period they are bound to be conjugate. For instance, consider p and q2, both of period 3. In order to find out whether they are conjugates we investigate row p and column q2.
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | |
| Row p | p | r | s | q | p2 | 1 | r2 | b | s2 | c | q2 | a |
| Column q2 | q2 | s2 | r2 | p2 | b | s | 1 | q | a | p | c | r |
Here we do not see the same products at corresponding locations in the row and the column, so we conclude that p and q2 are not conjugate elements, despite the fact that they have the same period.
On the other hand, p and q are conjugate, there being three occasions for detecting it as we go along row p and column q.
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | |
| Row p | p | r | s | q | p2 | 1 | r2 | b | s2 | c | q2 | a |
| Column q | q | r | p | s | r2 | c | q2 | 1 | s2 | b | p2 | a |
From this we can see that
pa = aq = r (implying pRq ).
pr = rq = s2 (also implying pRq ).
ps2 = s2q = a (also implying pRq ).
It turns out that pRqRrRs, giving a conjugacy class {p, q, r, s}, and also -- which can be verified in the same way -- that p2Rq2Rr2Rs2, giving the class {p2, q2, r2, s2}.
The group A4 is therefore partitioned into the following conjugacy classes :
{1}
{a, b, c}
{p, q, r, s}
{p2, q2, r2, s2}
The identity element is always transformed into itself : for any element y of whatever group we have : y1y-1 = yy-1 = 1.
The results obtained above (i.e. the discovering of all the conjugacy classes of the group A4) should be interpreted in the context of the direct symmetries of the Regular Tetrahedron. We have seen that p, q, r and s are in one class, and p2, q2, r2 and s2 in another. Interpreted as symmetries of the Regular Tetrahedron, these conjugate elements represent rotations through 1200 (which implies a period of 3), one class being clockwise and the other class anticlockwise. Those which belong to the same conjugacy class (e.g. p, q, r, s) may be transformed into each other, each being a rotation about an altitude of the tetrahedron in the same sense [Note, however, that, while in A4 the elements of period 3 fall into two classes, in S4 ( = the group, consisting not only of all even permutations of four symbols -- as is the case in A4 -- but also of all odd permutations of those four symbols) these eight elements are all in the same class].
More generally, it is true that rotations of the same magnitude and sense about different axes are conjugate if an operation exists in the group which would map one axis into the other. Thus, in A4 for example, p and q are conjugate with xpx-1 = q, and the transforming element x is one which maps the directed altitude p into the directed altitude q of the tetrahedron. But there is no element in the group which transforms p into q2, in other words, there is no operation in the group which transforms the p-altitude into the q-altitude and reverses its sense (rotating backwards about the q-altitude is the operation q2).
Before we continue to discuss the conjugacy of group elements, and especially say some more about the transforming elements, we will explain two important group theoretical concepts, namely "center" and "centralizer".
Center of a non-Abelian group
Sometimes, in a non-Abelian group, we find an element (say) k, which commutes with every element of the group. Elements of the group which have this property form a special subset known as the center of the group. It is clear that the identity always belongs to the center, because it commutes with every element of the group : 1y = y1, where y is any element of the group (In an Abelian group all elements commute with all the others, so there the center is the whole group itself).
We shall now demonstrate that this set of elements which commute with every element of the group do in fact form a subgroup. To establish this we only need to demonstrate closure.
Now suppose that H is the center of the group G, i.e. it is the set of all those elements of G which commute with every element of G. We note first that the center of every group is non-empty, since we saw that the identity element commutes with every element of a group (A group whose center consists of the identity only is described as having a trivial center).
Suppose that h1 and h2 are any two elements of H. Now we must prove that h1h2 also belongs to H, i.e. that H is closed under the group operation and consequently is a subgroup of G. Let x be any element of G.
Then, h1 being an element of H, implies h1x = xh1 ,
h2 being an element of H, implies h2x = xh2 .
Then (h1h2)x = h1(h2x) = h1(xh2) = (h1x)h2 = (xh1)h2 = x(h1h2).
Thus h1h2 commutes with x ( = any element of G), and so h1h2 is an element of H, by definition. Therefore the center H is a subgroup of G, and is, of course, an Abelian subgroup.
Although a group such as Q6 is a group of order 12, it has a very small center (consisting of the identity and one more element, i.e. it is of order 2). There are some groups whose center contains only the identity. It can be proved for example, that the center of Sn ( = group of all permutations of n symbols) is merely the identity, for all n greater than 2, and this may be surprising. Another way of saying this is that there is no permutation of n symbols, other than the identity, which commutes with every other permutation, or, that for any given permutation, one can always find a permutation which does not commute with it (BUDDEN, p. 218).
Normalizers and centralizers
If we select one particular element a of a group G, and write down the set of all elements which commute with the given element, i.e. the set {x : ax = xa, where x is element of G} (meaning the set of all elements x such that ax = xa), this set is called the centralizer (or normalizer) of a, and we can prove that it is bound to be a subgroup. For, if x1 and x2 are in the centralizer of a, then ax1 = x1a and also ax2 = x2a. Hence,
(x1x2)a = x1(x2a) = x1(ax2) = (x1a)x2 = (ax1)x2 = a(x1x2).
Thus x1x2 also commutes with the given element a, and so is in the normalizer of a. So closure is established, and with it that the centralizer is a subgroup. Similarly, of, course, x2x1 is also in the centraliser (because now we know that the centralizer is a group), but note that x1x2 is not necessarily equal to x2x1, so that one should not expect the centralizer to be Abelian.
Now we shall contrinue our discussion concerning conjugates.
The transforming elements
Now when we were looking for conjugacy classes in the group A4 , we did not bother to check, say, row p against column p, because we know that pRp (i.e. conjugacy is reflexive, which means that there is always some element, namely the identity, that transforms p into itself : 1p1-1 = 1p1 = p1 = p).
It would be interesting to note which elements of a group can transform an element into itself. In the case of p in the group A4 we have :
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | |
| Row p | p | r | s | q | p2 | 1 | r2 | b | s2 | c | q2 | a |
| Column p | p | s | q | r | p2 | 1 | s2 | c | q2 | a | r2 | b |
We can see that
p1 = 1p = p (implying p11-1 = 1p1-1, and this is equivalent to p = 1p1-1, and this means pRp ).
pp = pp = p2 (implying ppp-1 = ppp-1, and this is equivalent to p = ppp-1, and this means pRp ).
pp2 = p2p = 1 (implying pp2(p2)-1 = p2p(p2)-1, which is equivalent to p = p2p(p2)-1, and this means pRp ).
Hence p is transformed into itself by the elements 1, p, and p2. Or xpx-1 = p when x = 1, x = p or x = p2.
Again, consider the values of x for which c = xcx-1 :
| 1 | a | b | c | p | p2 | q | q2 | r | r2 | s | s2 | |
| Row c | c | b | a | 1 | r | q2 | s | p2 | p | s2 | q | r2 |
| Column c | c | b | a | 1 | q | r2 | p | s2 | s | p2 | r | q2 |
From this we see that
c1 = 1c = c (implying c = 1c1-1, which means cRc ).
ca = ac = b (implying c = aca-1, which means cRc ).
cb = bc = a (implying c = bcb-1, which means cRc ).
cc = cc = 1 (implying c = ccc-1, which means cRc ).
So c is self-conjugate under transformation by the elements 1, a, b and c. But cp = r, and pc = q, so cp is not equal to pc, which implies that c is not equal to pcp-1, which means that c is not transformed into itself by the element p. So c is self-conjugate only with respect to certain transforming elements. Only if it would be transformed into itself by all the elements of the group, it would be truly self-conjugate (see BUDDEN, p. 374/5).
You will realize that, for a given element y of any group, if y is self-conjugate under transformation by an element x so that y = xyx-1, then this means that yx = xy, in other words that x will commute with y. All those elements which do commute with the given element y constitute what we have described as the centralizer or normalizer of y, and we saw that the centralizer is a subgroup. Confirmation of this is seen in the case of A4 by noting that the centralizer of p is the subgroup {1, p, p2} (See row p and column p above, where we see the elements x of the group (A4), namely 1, p, and p2, such that xpx-1 = p, which is equivalent to xpx-1x = px, which in turn is equivalent to xp = px). The centralizer of c is the subgroup {1, a, b, c} (See row c and column c above).
Indeed we can see in the group table of A4 ABOVE that
pp = p2
pp2 = 1
p1 = 1p = p
p21 = 1p2 = p2
p2p2 = p
11 = 1
So all possible products of the subset (1, p, p2} are again elements of this subset, so this subset is a subgroup.
For the set {1, a, b, c} it is directly evident from the group table that it is a subgroup.
Conjugacy classes and cosets
Now cosets of a group only exist in relation to some pre-selected subgroup. Nevertheless, cosets seem somehow to be emerging in the considerations concerning conjugacy even though no subgroups are identified (apart from what we did in the last paragraph). With respect to the group A4 we can see that those elements which transform r into p by the relations
pb = br = s
pq2 = q2r = b
ps = sr = q2
are b, s and q2. Now {b, s, q2} is in fact one of the cosets in A4 , being a left coset of {1, r, r2} :
(b, s, q2} = b{1, r, r2} = s{1, r, r2} = q2{1, r, r2},
or a right coset of {1, p, p2} :
{b, s, q2} = {1, p, p2}b = {1, p, p2}s = {1, p, p2}q2.
All this can be verified by consulting the group table of A4.
Now just as subgroups arise from a consideration of centralizers, so their cosets arise in an analogous way from a consideration of conjugacy classes. We now proceed to investigate this more fully (BUDDEN, pp. 380).
Now we will expound the relationship between coset, centralizer and conjugation.
When we have a centralizer H of an element x in a group G, then each element h of the centralizer transforms x into itself, because xh = hx, which implies xhh-1 = hxh-1, which is equivalent to x = hxh-1. And when we take, as transforming element an element z, not in H, then x will not necessarily be transformed into itself, i.e. zxz-1 is not necessarily equal to x. Let us say it is y.
And when we take as transforming elements the elements of the left coset of H by the element z, i.e. zH, then all these elements will transform x into y.
So given the coset zH, where H is the centralizer of x, all the elements of this coset will transform the element x into a same element, namely y, when indeed zxz-1 = y.
And conversely, if we have kxk-1 = y = zxz-1, then k is an element of zH, i.e. of the left coset of H by the element z.
Thus we reason from coset to conjugation, and then from conjugation to coset.
Well, let us now prove all this.
Let a be a fixed element of a group G, and let H be the centralizer of a, i.e. the set H = {1, h1, h2, h3, . . . } such that ah = ha for all h element of H (which implies a = hah-1, meaning that all elements h of H transform the element a into itself). Now let b be a second fixed element of G which is not in H, and let bab-1 = c. Consider the transform of a by any element bh of the left coset bH :
(bh)a(bh)-1
= bhah-1b-1 (because (bh)-1 = h-1b-1)
= b(hah-1)b-1
= bab-1 (because, since h is an element of H, hah-1 = a )
= c.
Hence all elements of the left coset bH transform a into c.
For example, in A4 (See the group table of A4 ABOVE), the centralizer of r is the subgroup {1, r, r2} and its left coset by b is b{1, r, r2} = {b, s, q2} (which can be read off from the group table), and each of these three elements transforms r into p :
brb-1 = brb = p (because b2 = 1, which is equivalent to bb = 1, implying b = b-1. Further, rb = q, bq = p ),
srs-1 = srs2 = p,
q2r(q2)-1 = q2rq = p (because (q2)-1 = q, so q2r(q2)-1 = q2rq = q2s2 = p.
We have shown (above the example just given) that in the general case, all the elements of the left coset bH transform a into bab-1 ( = c).
We shall also prove the converse, that if xax-1 = c, then x is an element of bH, where H is the centralizer of a.
For c = bab-1 = xax-1 (given) so that ab-1 = b-1xax-1, which implies a = b-1xax-1b = (b-1x)a(b-1x)-1 (because genrally (ab)-1 = b-1a-1). This means, by definition, that b-1x lies in the centralizer of a, i.e. b-1x is an element of H, so finally x is an element of bH (because b-1x being an element of H is equivalent to bb-1x being an element of bH, which in turn is equivalent to x being an element of bH ), which was what we wished to prove.
We may add that, since all the cosets of a particular subgroup contain the same number of elements, it follows that the number of elements which will transform a given element a alike (i.e. every time into the same element) is equal to the order of the centralizer of a.
The transform of a given subgroup : conjugate subgroups
When H is a given subgroup of a group G, we now consider the transform of H by a fixed element a of G (not in H). This will be denoted aHa-1, and refers to the set {a1a-1, ah1a-1, ah2a-1, ah3a-1, . . . }, where 1, h1, h2, h3, . . . are the elements of H. We shall demonstrate that this new set is also a subgroup of G, and to do this (in the case of finite groups) it will only be necessary to establish closure.
Well, if ahra-1 and ahsa-1 are any two elements of aHa-1, then
(ahra-1)(ahsa-1) = ahr(a-1a)hsa-1 = ahrhsa-1 (because a-1a = 1).
But hr and hs are in the subgroup H, and thus also their product hrhs, and we can call this product ht. And now we know that ahta-1, which is equal to the product
(ahra-1)(ahsa-1), is undoubtedly one of the elements of aHa-1.
Thus aHa-1 is a subgroup of G. It will be of the same order as H provided there are no repetitions of elements. This possibility is ruled out by the fact that ahra-1 = ahsa-1 would imply that hr = hs. because (applying the cancellation law two times) :
ahra-1 = ahsa-1 is equivalent to
a-1ahra-1 = a-1ahsa-1, which implies
hra-1 = hsa-1, which is equivalent to
hra-1a = hsa-1a, implying
hr = hs.
Therefore H and aHa-1 are subgroups of the same order, and the group aHa-1 is called the conjugate subgroup of the group H (both subgroups of G) by the element a.
The remaining question is : Are they the same subgroup?, Well, they're generally not. For instance, in the group A4 (See Table 15.2), we have the subgroup {1, p, p2}. Calling this H, then pHp-1 = {p1p-1, ppp-1, pp2p-1} = {1, p, pppp-1} = {1, p, pp} = {1, p, p2} = H. However, aHa-1 = {1, q, q2}, and this is not the subgroup H.
( That aHa-1 is indeed equal to {1, q, q2} can be seen as follows :
aHa-1 = {a1a-1, apa-1, ap2a-1}, and because a2 = 1 (See table), we can say a-1 = a. Therefore we have
aHa-1 = {a1a, apa, ap2a}, which is (See table) equal to {1, q, q2} ).
We now prove that conjugate subgroups are isomorphic.
Suppose we have a group G with H being one of its subgroups. Suppose further that k is an element of G. Then the conjugate of the subgroup H by the element k is the subgroup kHk-1. Above we have established that the order of H and its conjugate is the same. So we can set up a 1,1 (one-to-one) correspondence between their respective elements. Let this 1,1 correspondence be the mapping PHI from H to kHk-1, where PHI means that we assign to each element of H the conjugate (by the element k ) of that element, and that conjugate is an element of aHa-1. Let p and q be any two elements of H. Then
PHI(p) = kpk-1, and
PHI(q) = kqk-1.
Now (PHI(p)) (PHI(q)) = (kpk-1)(kqk-1) = kp(k-1k)qk-1 = kpqk-1 = PHI(pq), which means that products are preserved when we go from H to kHk-1, and establishes the isomorphism between them.
Clearly, in the general case, a subgroup H is transformed into itself by any of its own elements, i.e. hHh-1 = H, when h is an element of H :
For if hr, hs are any two elements of H, then, because H is a group, hs-1, the inverse of hs, must also be an element of H, and so is the product hshrhs-1. Thus the subgroup H contains all the transforms (by the element hs) of its elements, implying that the operation hsHhs-1 transforms H into itself.
However, one may ask whether there are any elements of G, not in H, which transform H into itself? The answer is that this may well be possible, as we can see, for instance, when we take H to be the subgroup {1, a, b, c} of the group A4.
Consider pHp-1.
p is an element of the group, but not of the subgroup H. In the table of A4 we can see that pp2 = 1, which means that p-1 = p2, so pHp-1 = pHp2 = {p1p2, pap2, pbp2, pcp2} = {1, pap2, pbp2, pcp2} = (See table) {1, c, a, b} = H.
Again, consider r2H(r2)-1. To determine (r2)-1 we must find (in the table of A4 ) the inverse of r2, i.e. we must find the element which, when multiplied with r2, yields the identity. We find that this is the element r. So r2H(r2)-1 = r2Hr = {r21r, r2ar, r2br, r2cr} = {1, r2ar, r2br, r2cr} = {1, b, c, a} = H.
Note that the transform of H, by p, and also by r2 produces H, but with the elements rearranged, and this is an automorphism of H (it is not an inner automorphism of H, because the transforming elements p and r2 do not belong to H). When H is the whole group G, we get xGx-1, and we obtain the various inner automorphisms of G by the various elements x.
Why does this happen in some cases and not in others?
We may write the relation aHa-1 = H in another way, namely aH = Ha, because :
aHa-1 = H is equivalent to
aHa-1a = Ha, which is equivalent to
aH = Ha.
And this can be interpreted in terms of cosets : every element of the left coset aH is an element of the right coset Ha.
Note that this does not require that ah = ha for every element h in H. It does require that the elements of aH, i.e. a, ah1, ah2, ah3, . . . , are (just) a rearrangement of the elements of Ha, i.e. a, h1a, h2a, h3a, . . . . For example, taking H to be {1, a, b, c} in the group A4, we have pH = {p, r, s, q} and Hp = {p, s, q, r} -- the elements turn up in a different order. But the order in which they turn up does not concern us here -- we are only interested in the set (i.e. that the two cosets are equal), and (interested only) in, which particular elements it contains (and those sets contain the same elements).
Normal subgroups
Now the requirement aH = Ha, that the left and right cosets of H by the element a are the same, endows the subgroup H with the vastly important property of being a normal subgroup, provided it is true for all elements a in G. It may not be generally realized by students that if aH = Ha for some particular a in G, there may yet exist another element b for which the left and right cosets are different, i.e. aH = Ha does not imply bH = Hb. For instance, in the group D6 (See Part VIII, Table 8.1), we have the subgroup H = {1, u}.
Now xH = x{1, u} = {x, a}
while Hx = {1, u}x = {x, a}
so xH = Hx.
But vH = v{1, u} = {v, p}
and Hv = {1, u}v = {v, p2}
so vH is not equal to Hv.
and so {1, u} is not a normal subgroup.
A normal subgroup is also called self-conjugate subgroup, and also invariant subgroup.
There are several methods making it possible to decide whether a given subgroup is normal or not. We will not go over all those methods. However two of them we shall briefly expound.
Another method to find out whether a given subgroup is normal or not is of a geometric nature and can especially be applied to groups of symmetry operations.
We give two examples, one with repect to the Regular Hexagon (or Regular Hexagonal Pyramid for that matter), the other with respect to the Cube.
Consider the group D6, as describing all the symmetries of the Regular Hexagon (and also, as has been said, those of the Regular Hexagonal Pyramid), in the notation as we had it in Table 7.10 (Part VII). There we have the subgroup H = {1, a}. Is it a normal subgroup in D6?
Let x be any of the symmetries of the group. Then xHx-1 = x{1, a}x-1 = {x1x-1, xax-1} = {1, xax-1}. Well, H = {1, a} is a normal subgroup in D6 when xH = Hx for all elements x of the group. We would then have xH = {x, xa}, and Hx = {x, ax}, where {x, xa} would be equal to {x, ax}, implying that xa = ax, which is equivalent to xax-1 = axx-1, which is equivalent to xax-1 = a. So if H is a normal subgroup, then a = xax-1. But, as we saw earlier in this document, xax-1 is a reflection in the new position of the reflection axis a to which that axis is moved by the operation x. If xax-1 is to be equal to a, therefore, x must preserve the axis of a in its original position ( x stands for all elements of the group). Since all the operations of the group (D6) (other than 1, a, and r3) do in fact move the axis of a, it follows immediately that {1, a} is not a normal subgroup in D6. On the other hand, {1, r3} is a normal subgroup, for this time the rotation axis of the half-turn r3 is invariant under all the operations of the group, because the axis of r3 is perpendicular to the hexagon (and also perpendicular to the base of the regular hexagonal pyramid), and stays where it is under all operations of the group (rotations and reflections).
Now we turn our attention to the rotation group of the Cube, i.e. the group of all direct symmetries of the Cube or Regular Hexahedron. Suppose that H = {1, r1, r2, . . . } is a normal subgroup, and s is an operation of the group not in H. Then sHs-1 = {1, sr1s-1, sr2s-1, . . . }, and contains rotations about the axes of the rotations r1, r2, . . . in the new positions to which they have been moved by s. Therefore, if H is to be a normal subgroup, the system of rotation axes must be invariant under any operation of the group : i.e. when H is normal, then sH = Hs for any s, which implies sHs-1 = Hss-1, implying sHs-1 = H, where H is the system of rotation axes 1, r1, r2, . . . . . Note that when H is normal in the group, then sHs-1 = H, but that does not necessarily mean that r1 = sr1s-1, r2 = sr2s-1, etc., but only that the result is a swapping of those same elements, resulting in H staying the same, i.e. being invariant, under the operation sHs-1.
We consider two examples of subgroups (of the group of direct symmetries of the Cube).
First C3, containing rotations through +/- 1200 about one of the diagonals of the cube. This sole axis is moved to a new position by most of the symmetry operations of the rotation group, so clearly the subgroup is not normal, and neither is any of the four subgroups of order 3 (i.e. the four C3's corresponding to the four 3-fold rotation axes of the cube, the four space diagonals). Note, that the whole set of the four 3-fold rotation axes of the cube remains invariant, because the cube is transformed into itself by any of its symmetry operations, but a particular C3 subgroup is associated with one particular 3-fold rotation axis, and such an individual axis is not invariant under all symmetry operations of the cube.
Next, we consider the half-turns about the three axes through the center of the cube and parallel to the edges, which form the subgroup D2 (The elements of this subgroup thus are : the identity, a half-turn about the first axis, a half-turn about the second axis, and a half-turn about the third axis). This time we find that any one of the remaining symmetry operations of the cube leaves this set of three axes invariant. For example, a quarter-turn about one of them will interchange the other two. A third-turn about a diagonal will permute them cyclically, and so on. Here, then, we have geometrical evidence of the fact that the subgroup is normal.
The above method may evidently be extended to cover the investigation of the invariance of any subgroup of symmetries in a group of symmetry operations which may include reflections and central inversion ( = reflection in a point), and may be extended still further to cover the case of infinite groups connected with patterns, which will include translations, and possibly glide reflections. Briefly the method (of determining whether a given subgroup is normal or not) is to consider the system of reflection axes, rotation centers and glide axes of the subgroup (the "symmetry chart" of the subgroup, as it is called) and decide what happens to this system under the operations of the rest of the group. If all the symmetry operations of the group map the framework on to itself, then the subgroup is normal in the symmetry group. Much light can be thrown on the subgroups of plane patterns by adopting a system of coloring. Those elements of the subgroup under consideration are colored alike, and each coset is given its own color (so that the number of colors is equal to the index of the subgroup). If the subgroup is not normal, the coloring of the left cosets will produce a different aspect from the coloring of the right cosets. If it is normal, the two colored patterns will be indistinguishable (BUDDEN, p. 390).
Normal subgroups and cosets (BUDDEN, p. 392)
It is instructive to realize that aHa-1 may be thought of as a post-multiplication by a-1 of the set aH, which is the left coset of H by a.
One could generalize this concept by forming a set xHy from any subgroup H by any pair of selected elements x and y not in H.
For example, in A4 (See its group table), we have the subgroup H = {1, p, p2}, from which we can form sets of the form xHy :
aHb = a{1, p, p2}b = {a, s, r2}b = {c, p, s2},
aHr2 = a{1, p, p2}r2 = {a, s, r2}r2 = {p2, b, r}.
(All this can be read off from the group table).
Each of the sets obtained is a coset of a different subgroup, i.e. different from {1, p, p2} ( = H ), the first being c{1, r, r2} (a left coset of the subgroup {1, r, r2}), or {1, q, q2}c (a right coset of the subgroup {1, q, q2}), and the second being b{1, s, s2} (a left coset of the subgroup {1, s, s2}) or {1, q, q2}b (a right coset of the subgroup {1, q, q2}).
It is interesting to pursue these discoveries in the cases of other subgroups, and to find what comes out. When the subgroup selected is a normal subgroup, we find that xHy will always turn out to be a coset of H itself, and not of a different subgroup as happened in the examples given above. For instance, if H = {1, a, b, c} in A4, then pHr2 =
(pH)r2 = {p, q, r, s}r2 = {c, a, 1, b} = H (which can be seen as the left (or right) coset of H by the element 1), while pHr =
(pH)r = {p, q, r, s}r = {s2, p2, r2, q2} = p2H = Hp2 ( = left and right coset of H ).
That this is bound to happen is an immediate consequence of the property of normal subgroups, that all their left and right cosets contain the same elements. For then we see that, since xH = Hx for every x in the group,
therefore xHy = Hxy = H(xy) = (xy)H = Hz = zH, the coset of H by the element z = xy.
This concludes our exposition of conjugation in groups.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals