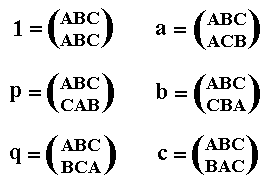
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Homomorphism, Quotient groups and Normal subgroups ( A working-over of BUDDEN's Chapter 21 on Homomorphism, pp. 396, in The Fascination of Groups, 1978 )
Let us consider the isomorphism between the group (Z, +), i.e. the group of integers with the group operation of ordinary addition, and the group ({10n},x) [where n is element of the set Z of all integers], i.e. the group of integer powers of 10, with the group operation of ordinary multiplication (indicated by "x" ). The isomorphism is the assignment to each integer k the number 10k. For example to the number 6 is assigned the number 106. So in the group (Z, +) we have -1 + 6 = 5, and the corresponding result in the second group, the group ({10n}, x), is 10-1 x 106 = 105, and we remind you that the elements of the two groups can be put into a one-to-one correspondence in such a way that products are preserved, the result being that, whether the groups are finite or infinite, their structure is identical. In the above example, the structure of both groups was Cinfinite. What we were really doing in the above case was mapping from the integers on to their antilogarithms (base 10).
Homomorphic mappings
Suppose that, instead of base 10, we had used base i ( = the square root of minus one [ sqrt(-1) ] ), That is, suppose we had performed the mapping
n ---> in
i.e. a mapping from the integers to the powers of i.
If we execute powers of i we shall see that we have to do with a cyclic state of affairs, which can be seen when we produce a number of images under the mapping defined above ( Recall that i = sqrt(-1) ) :
1 ---> i1 = sqrt(-1) = i
2 ---> i2 = (sqrt(-1))2 = -1
3 ---> i3 = (sqrt(-1))3 = i2i = -i
4 ---> i4 = (sqrt(-1))4 = i2i2 = 1
5 ---> i5 = i4i = i
6 ---> i6 = i4i2 = i2 = -1
7 ---> i7 = i4i3 = i3 = -i
etc.
So the (total) image of the mapping will be expected to be the set {1, i, -i, -1}, which forms a group under ordinary multiplication, and as such is one of the possible realizations of the cyclic group of order 4, i.e. C4.
So all those integers which divide exactly by 4 will map into the number 1, for i-8 = i-4 = i0 = i4 = i8 = . . . . = 1.
The set {. . . -3, 1, 5, 9, . . . } will map into i.
The set {. . . -6, -2, 2, 6, . . .} will map into the number -1.
And the remaining integers, {. . . -5, -1, 3, 7, . . . } map into the number -i.
Indeed, the image of the set Z under this mapping consists therefore of four complex numbers only, {1, i, -1, -i}.
A complex number is a number of the form a + bi, where a and b are real numbers [ = ordinary numbers, including fractions and also irrational numbers like sqrt(2) ], and i = sqrt(-1). The real numbers are special cases of complex numbers, they are the numbers where b = 0. Whereas real numbers are located on a continuous infinite line, the complex numbers occupy an infinite plane, containing the line of real numbers.
The correspondence is no longer one-to-one, but many-to-one, in fact infinitely many-to-one in this case. Nevertheless, products are still preserved, i.e. a product in the first group corresponds with a product in the second (in the first group the numbers are added, while in the second group these numbers appear as exponents of i, and are also added, because multiplication of powers of some number must be done by addition of the respective exponents). For example
-1 + 6 = 5 in (Z, +) induces the result :
i-1 x i6 = i5,
or, (using i4 = 1)
because i-1 = i-1i4 = i3, and
i6 = i4i2 = i2, and
i5 = i4i1 = i1,
i3 x i2 = i1,
that is, because i3 = -i, and i2 = -1,
(-i) x (-1) = i in the image group ({1, i, -1, -i}, x) (in which "x" means multiplication).
We have here an example of a Homomorphic Mapping from the group (Z, +) on to the smaller group ({1, i, -1, -i}, x).
In earlier documents (from Part V onwards) we already discussed homomorphic mappings using examples from finite groups. There we called the (smaller) group in which the original group was mapped, the telescopic image.
The properties of a homomorphism are similar to those of an isomorphism -- strictly speaking, an isomorphism is a special type of homomorphism -- namely that products are preserved, but the difference is that in a homomorphism, many elements of the original set may be mapped into a particular element of the image set, that is to say, while structural properties are preserved, the individuality of the elements is destroyed.
If the mapping, or function, n ---> in, is denoted by PHI, we have in the case above :
PHI(-4) = 1
PHI(0) = 1
PHI(4) = 1
etc.
PHI(-1) = -i
PHI(6) = -1
PHI(1) = i
and so on.
In fact we may say : PHI{. . . -8, -4, 0, 4, 8, . . .} = 1, that is to say, the homomorphism carries the whole set of integers divisible by 4 into the number 1, which is the identity of the group ({1, i, -1, -i}, x). That subset which is mapped into the identity element of the image group is called the Kernel of the homomorphism.
Now the group ({1, i, -1, -i}, x) is isomorphic to the group ({0, 1, 2, 3}, + mod 4), and we can also map the group (Z, +) homomorphically on to the latter realization of the group C4 by placing the set Z into four equivalence classes, namely the residue classes modulo 4. If the homomorphism function is again denoted PHI, we have
PHI{. . . -8, -4, 0, 4, 8, . . . } = 0
PHI{. . . -7, -3, 1, 5, 9, . . . } = 1
PHI{. . . -6, -2, 2, 6, 10, . . . } = 2
PHI{. . . -5, -1, 3, 7, 11, . . . } = 3
Many-to-one mappings in general
Indeed, the partitioning of a set into equivalence classes by an equivalence relation induces a homomorphism of the whole set on to the set of equivalence classes. We can see this in the relation of genus to species, and also of species to individuals. For example all individual dogs belong to the species Canis domesticus, and all individual lions belong to the species Leo leo. So all the dogs are mapped into the one class Canis domesticus, and all lions are mapped into the one class Leo leo. It is true that neither the set of all dogs, nor of all lions is a group in the grouptheoretical sense, and also the set of all animal species is not a group, so we are not mapping a group on to another group but a set with no (algebraic) structure on to another amorphous set (And indeed, BUDDEN, reports, some mathematicians would object to the term homomorphism being stretched to cover cases when no operation is involved). The correct term is many-to-one mapping. However, homomorphisms are not necessarily many-to-one mappings, since they include isomorphisms as a special case. The principle is the same, however, that we have a homomorphic mapping PHI which maps Fido (your dog) into the element Canis domesticus of the set of animal species : PHI(Fido) = Canis domesticus.
An example of a homomorphism in a finite group
In previous documents (from Part V onwards) we already discussed homomorphisms of finite groups. Here is yet another example.
Consider the set of permutations of three letters
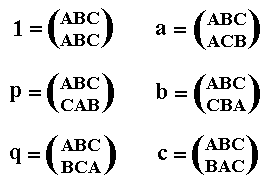
which form the group S3 ( = D3 ). This group we know already well from previous documents, see for instance Part VII. Now the first three of these are even permutations, and the last three are odd permutations (See for even and odd permutations, HERE in Part XI).
Consider the function PHI such that :
PHI(1) = I
PHI(p) = I
PHI(q) = I
PHI(a) = X
PHI(b) = X
PHI(c) = X
This means that we are making no distinction between the permutations ABC, CAB and BCA -- they lose their individuality -- but are placing them all in a class I, and likewise the odd permutations are placed into the class X. We may now say that I2 = I = X2, and XI = IX = X, meaning that the composition of two even permutations or of two odd permutations is an even permutation, while the product of an odd with an even permutation is an odd permutation. This may be summarized in the table
| I | X | |
| I | I | X |
| X | X | I |
which has the structure of the 2-group. Here, then, we have a homomorphic mapping of the group S3 onto the smaller group C2 ( = S2 ).
If one thinks of an equilateral triangle, and interprets the above permutations as permutations of its vertices, then the even permutations correspond to the movements of the triangle which do not turn it over (i.e. the rotations only), while the odd permutations correspond to those symmetries in which the opposite face of the triangle is exposed (i.e. flip through the third dimension, which is equivalent to reflection in a line -- a bisector of the triangle).
The homomorphism may be summarized in the following two group tables, one of the group D3 ( = S3), the other of its homomorphic image, the group C2 :
| 1 | p | q | a | b | c | |
| 1 | 1 | p | q | a | b | c |
| p | p | q | 1 | b | c | a |
| q | q | 1 | p | c | a | b |
| a | a | c | b | 1 | q | p |
| b | b | a | c | p | 1 | q |
| c | c | b | a | q | p | 1 |
| I | X | |
| I | I | X |
| X | X | I |
The symmetry operations of the triangle belong to the two Classes I and X as follows :
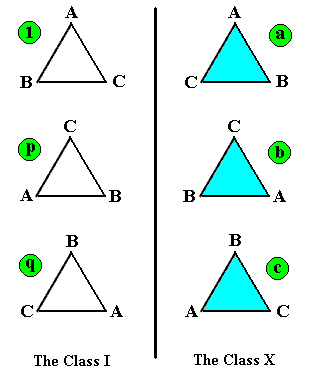
Figure 1. The symmetries of the Equilateral Triangle and their distribution among the two classes I and X, which are elements of the homomorphic image under the mapping PHI.
The kernel of a homomorphism
An important theorem is that,
if a group G is mapped homomorphically onto a group G', then the kernel K of the homomorphism is a normal subgroup of G.
For example, the kernel of the group S3 above is the set of even permutations {1, p, q}, for these map into the identity I of the image group (They map into I, according to the above definition of PHI, and then this I turns out to be the identity of the image group). These three elements do in fact form a normal subgroup of S3.
To prove this in general, we must first show that the kernel is a subgroup, which means that we must demonstrate :
Well, let us have a group G, and let the kernel K contain the elements {k1, k2, k3, . . . } so that, if the homomorphic function is PHI and the identity of the image group is I, we have
PHI(k1) = I, PHI(k2) = I, etc., and PHI(kr) = I for all r.
Now, PHI(krks) = PHI(kr)PHI(ks) [ because products are preserved by a homomorphic mapping ] = ( I )( I ) = I,
and this means that krks also maps into I. Hence kr , ks being (general) elements of K implies that krks (the product) is also element of K, and closure is established.
We cannot yet be sure that K contains the identity element 1 of G, so suppose PHI(1) = X. Then if k is any element of K, then k1 = k [because 1 is the identity of the group G], so that PHI(k1) = PHI(k) = I [because k is any element of K].
But PHI(k1) [ where 1 is the identity of G] = PHI(k)PHI(1) [because products are preserved in a homomorphic mapping] = IX [ because we supposed PHI(1) = X ] = X.
So we have PHI(k1) = I, and PHI(k1) = X, so we have X = I, and this implies PHI(1) = I, which means that the identity element 1 of G is mapped into the identity element I of the image group and this in turn means that the identity element 1 of G belongs to K. So we have until now established that the set K is closed under the group operation (of the group G), and that it contains the identity element of G.
Finally, to show that K contains the inverse of every element of K, i.e. to show that k being an element of K implies that k-1 also belongs to K, we have
PHI(kk-1) = PHI(1) [ because kk-1 = 1 ] = I [as proved above].
But PHI(kk-1) = PHI(k)PHI(k-1) = I(PHI(k-1)).
So we have
PHI(kk-1) = I, and
PHI(kk-1) = I(PHI(k-1)),
hence I(PHI(k-1)) = I, so PHI(k-1) = I, which means that k-1 belongs to K, and the inverse of each element k of K is contained in K.
Therefore K is a subgroup (Associativity is already guaranteed because we have to do with the same group operation).
To show that K is moreover a normal subgroup, we must demonstrate that the left and right cosets of K coincide, i.e. that if x is any element whatsoever in G, then xK = Kx, or, equivalently, xKx-1 = K.
Well, xKx-1 is the set {xk1x-1, xk2x-1, xk3x-1, . . . . }, where k1, k2, k3, . . . are elements of K, and we must now show that this set is equal to K (in which it is not necessarily so that k1 = xk1x-1, k2 = xk2x-1, etc.), we must show that any of these elements are contained in K, i.e. that xkr x-1 is element of K. And we do this by showing that xhr x-1 is mapped by PHI in the element I of the image group. In other words we must show that for any element kr in K, the transform of kr by the element x, that is xkr x-1, is mapped by PHI in I, and so must also be in K.
Now : PHI(xkr x-1) = PHI(x)PHI(kr )PHI(x-1) (properties of homomorphism).
But PHI(kr ) = I since kr is element of K.
Hence PHI(xhr x-1) = PHI(x)(I)PHI(x-1) = PHI(x)PHI(x-1) = PHI(xx-1) (property of homomorphism) = PHI(1) = I (as proved above). So PHI(xhr x-1) = I, which indeed means that xhr x-1 belongs to K, which establishes that xKx-1 = K, and thus that xK = Kx, for every element x of G, and consequently we have shown that the kernel K is a normal subgroup of the parent group.
Normal subgroups, groups of cosets, quotient groups
In previous documents we have seen that when it is possible to partition the group table of a group G in a certain way, a homomorphism is possible from G to the sets that are represented by those partitions. We will show under what conditions such partitions are possible, and thus under what conditions a homomorphism is possible.
Let us consider a group of even order, 2n, which has a subgroup of order n, for example the dihedral group D4, which has 8 elements, and which has a subgroup of order 4, namely C4 :
| 1 | r | r2 | r3 | a | b | c | d | |
| 1 | 1 | r | r2 | r3 | a | b | c | d |
| r | r | r2 | r3 | 1 | b | c | d | a |
| r2 | r2 | r3 | 1 | r | c | d | a | b |
| r3 | r3 | 1 | r | r2 | d | a | b | c |
| a | a | d | c | b | 1 | r3 | r2 | r |
| b | b | a | d | c | r | 1 | r3 | r2 |
| c | c | b | a | d | r2 | r | 1 | r3 |
| d | d | c | b | a | r3 | r2 | r | 1 |
Table 16.1
The subgroup C4 is {1, r, r2, r3}.
| K | A | |
| K | K | A |
| A | A | K |
where K denotes the subset {1, r, r2, r3} and A denotes the set {a, b, c, d}. The reason why the elements of D4 can be so arranged such that this overall structure becomes directly apparent, is because of the Latin Square Property of all finite groups. It can be proved that :
The structure table for any finite group is always a Latin Square, that is to say, each row and each column contains all the elements of the set with no repetitions.
This does not mean, however, that a table in the form of a Latin Square is necessarily a group table : Associativity will usually fail somewhere along the line.
But when a table is a group table (of a finite group) then it possesses the Latin Square Property.
Since the top left-hand square of the table of D4 contains the subgroup {1, r, r2, r3}, each of its four rows must be a permutation of these four elements (because multiplications of the elements with each other always result in elements of that same subgroup).
And if an element x of any subgroup is multiplied with two different elements of that subgroup the result is always two different elements :
For if
xy = u, and
xz = u, then we have
xy = xz, which is equivalent to
x-1xy = x-1xz, which is equivalent to
y = z, and this is contrary to the supposition, namely that they are different. So xy and xz always result in the production of different elements.
So no row connected with the subgroup {1, r, r2, r3} contains repetitions, and we see the Latin Square Property at work.
Therefore, for the whole group, since each of the first four rows must be a permutation of all eight elements (Latin Square Property), it follows that the remaining four elements of each row must be drawn from {a, b, c, d}, and thus the whole of the top right-hand block must consist of a's, b's, c's and d's.
A similar consideration of the Latin Square Property applied to the first four columns convinces us that the bottom left-hand block must also consist entirely of a's, b's, c's and d's. Finally, the remaining four elements of the last four rows (or columns) are bound to be 1, r, r2 or r3 -- again by the Latin Square Property.
In previous documents we already showed several examples of group tables revealing their overall C2 structure (for example with respect to the group D6 in Part VII, Table 7.10).
We may say that the group has been mapped on to the group C2 by a homomorphism which takes the elements of the subgroup K into the identity element of C2 , while the elements of its coset are carried into the other element of C2. In all this we can interpret the whole subgroup K (which itself is its right or left coset by the identity element) as one element of the image group, and also the whole coset of K as the other element.
It is obvious that this arrangement can always succeed when the order of the subgroup K is one half of the order of the group G, i.e. when the index of the subgroup is 2.
Normal subgroups of index 3
We next ask the question : if the index of the subgroup is 3, will it always be possible to map the group onto the group C3 in a similar way as is done in the next table where the group is A4 and the subgroup D2 ? Here A4 is mapped homomorphically by the function -- let us again call it -- PHI onto the group C3 by the correspondence :
{1, a, b, c} ---> K
{p, q, r, s} ---> P
{p2, q2, r2, s2} ---> Q.
Table 16.2
| K | P | Q | |
| K | K | P | Q |
| P | P | Q | K |
| Q | Q | K | P |
We now attempt to do the same sort of thing in the case of the subgroup {1, b, c, g} (C4 ) of the group Q6. The table of this group is shown below :
| 1 | a | b | c | d | f | g | h | j | k | l* | m | |
| 1 | 1 | a | b | c | d | f | g | h | j | k | l* | m |
| a | a | l* | 1 | d | f | g | h | j | c | m | k | b |
| b | b | 1 | m | j | c | d | f | g | h | l* | a | k |
| c | c | j | d | k | l* | a | 1 | b | m | g | h | f |
| d | d | c | f | m | k | l* | a | 1 | b | h | j | g |
| f | f | d | g | b | m | k | l* | a | 1 | j | c | h |
| g | g | f | h | 1 | b | m | k | l* | a | c | d | j |
| h | h | g | j | a | 1 | b | m | k | l* | d | f | c |
| j | j | h | c | l* | a | 1 | b | m | k | f | g | d |
| k | k | m | l* | g | h | j | c | d | f | 1 | b | a |
| l* | l* | k | a | f | g | h | j | c | d | b | m | 1 |
| m | m | b | k | h | j | c | d | f | g | a | 1 | l* |
Table 16.3
In trying to find a partition of the group table (of Q6) on the basis of the subgroup H = {1, b, c, g} in the same way as was accomplished above (with the group A4), we rearrange the elements of Q6, as given in the above group table, such that we get the subgroup {1, b, c, g} in the top left-hand corner of the (new) group table. All this should lead to the establishing of a homomorphism of the group Q6 onto a smaller group (isomorphic to C3 ). Well, let's try.
| 1 | b | c | g | a | l* | j | f | d | h | k | m | |
| 1 | 1 | b | c | g | a | l* | j | f | d | h | k | m |
| b | b | 1 | g | c | l* | a | f | j | h | d | m | k |
| c | c | g | b | 1 | j | f | l* | a | k | m | h | d |
| g | g | c | 1 | b | f | j | a | l* | m | k | d | h |
| a | a | l* | d | h | ||||||||
| l* | l* | a | h | d | ||||||||
| j | j | f | k | m | ||||||||
| f | f | j | m | k | ||||||||
| d | d | |||||||||||
| h | h | |||||||||||
| k | k | |||||||||||
| m | m |
Now the right coset of H ( = {1, b, c, g}) by the element a, i.e. Ha, is {1, b, c, g}a = {a, l*, j, f} (where l* means the letter l -- to distinguish it from the identity element symbolized by the numeral 1 ), so we place these elements next in order across the top margin of the new table, and complete the row with d, h, k and m. Everything goes smoothly for the first four rows (Recall that all the products are determined according to the structure of the group Q6 displayed in Table 16.3 given above), but when we come to rows a, l*, j, f we run up against trouble, for the left-hand block of the second super-row contains not only the elements a, l*, j and f, but also four (different) alien elements (indicated by red coloring in the above table), d, h, k and m. It is clear that the reason the above case 'does not work' is precisely because {1, b, c, g} is not a normal subgroup of Q6 : the left coset a{1, b, c, g} = {a, l*, d, h} is different from the right coset {1, b, c, g}a = {a, l*, j, f}, and it is from this left coset that two of these new 'alien' elements d and h have come. The other two, k and m appearing in the left cosets j H and f H.
Homomorphic images of Abelian groups
Now every subgroup of an Abelian group is obviously normal :
Every element x of an Abelian group commutes with every other, so we have ab = ba, for every two elements of such a group. This implies abb-1 = bab-1, which gives a = bab-1 for any two elements of the group. And this implies bHb-1 = H for any subgroup. So for any subgroup of an Abelian group we have bHb-1b = Hb, which gives bH = Hb for any element b of the group, which in turn means that for any subgroup of an Abelian group its left and right cosets are the same, meaning that those subgroups are normal in the group.
And so it is always possible to produce homomorphic images of an Abelian group of composite order (groups of prime order do not have subgroups at all), whereby any subgroup may be mapped into the identity of the homomorphic image group, and thus can serve as kernel for a particular homomorphism. We have shown this in the case of the cyclic group C12, where all its subgroups induce subdivisions of the group table and so allow for homomorphisms (See Parts V and VI ).
Another case of failure when subgroup is not normal
Before drawing together the threads of the foregoing discussions, let us give one more example to demonstrate the failure of a group to yield a homomorphic image by a non-normal subgroup, by considering {1, p, p2} in the group A4 (See Table 16.2 above).
The left cosets are
{1, p, p2}
{a, s, r2}
{b, q, s2} and
{c, r, q2}.
The right cosets are
{1, p, p2}
{a, r, s2}
{b, s, q2} and
{c, q, r2}.
Let us derive two of these cosets, namely the left and right cosets of our subgroup by the element a :
a{1, p, p2} = {a, ap, ap2} = (reading off from the group table) {a, s, r2}.
{1, p, p2}a = {a, pa, p2a} = {a, r, s2}.
So we have one example of the non-equality of a right and left coset of {1, p, p2} by a same element (a), and this is sufficient for this subgroup not to be a normal subgroup.
Now we can show that the system of cosets with respect to our subgroup is not closed under set multiplication, which implies that that system does not form a group, that is to say, it cannot figure as a homomorphic image of our group A4 (a quotient group cannot be formed on the basis of this particular subgroup -- we spoke about quotient groups in earlier documents, and will return to them in due course).
| a | s | r2 | |||||
| c | b | q | s2 | ||||
| r | p | p2 | 1 | ||||
| q2 | r2 | a | s | ||||
Because the subgroup {1, p, p2} has three (different) elements, every coset of this subgroup therefore has three different elements. The system of these cosets to be closed means that any product of any two of these cosets (according to set multiplication) must yield another coset, also belonging to set of cosets of {1, p, p2}. Well, when we multiply the cosets {c, r, q2} and {a, s, r2} (both cosets of our subgroup) the result is (see table above) the set {b, q, s2, p, p2, 1, r2, a, s}, and this is a set consisting of nine different elements, so it cannot be any coset of {1, p, p2}, and thus is the set of cosets of {1, p, p2} not closed, and is therefore not a group, and consequently cannot figure as a homomorphic image of our group A4.
In contrast we see in the Table of A4 that the cosets of the subgroup {1, a, b, c} are perfectly orderly, which we can see when we look to the (colored) squares in the table representing these cosets : each square consists of four (different) elements only (the same number as the number of elements of the subgroup {1, a, b, c}). For example if we multiply the coset {p, q, r, s} -- which is the left coset of {1, a, b, c} by the element p (as well as by the elements q, r, s ) -- with the coset {p2, q2, r2, s2} -- which is the right coset of {1, a, b, c} by the element p2 (as well as by the elements q2, r2, s2 ) -- we get the square containing only the four elements 1, a, b, c.
Products of cosets of normal subgroups -- general theory
We will now prove that the system of cosets of a normal subgroup forms a group.
For this we must show :
So if K is a normal subgroup of the group G, and aK and bK are any two of its (left) cosets, then we have bK = Kb. Hence the product set (determined by the multiplication of sets on the basis of how the individual elements combine according to the group table of G)
aKbK = aKKb. But KK = K (as K is a subgroup, the mutual multiplication of its elements always yields elements of that same subgroup)
Therefore aKbK = aKb = abK = (ab)K, and this is one of the (left) cosets of K.
Hence the system of cosets is closed under the operation of the formation of product sets.
Further, we see that K (which itself is also a coset, namely 1K) is an identity element within the system of cosets, because for every element x of G we have (xK)K = xKK = xK (because KK = K), and K(xK) = KxK = KKx (because K is a normal subgroup) = Kx = xK.
Finally, because we have already supposed a to be an element of G (and figuring as such in the coset aK), a-1 must also be an element of G. And so there exists also a coset a-1K of K. And because (a-1K)(aK) = a-1KKa = a-1Ka = a-1aK = K ( = the identity element of the closed set of cosets), we can say that a-1K is the inverse of aK under set multiplication, and we already know that this inverse is a genuine coset of K (because a-1 is an element of G). So every coset of the set of cosets of the normal subgroup K has an inverse which is one of the elements of that set of cosets.
So now we have proved that the set of cosets of a normal subgroup is a group (in which the group operation is the set multiplication of those cosets). And this group of cosets we call the quotient group (or factor group) G/K ("G slash K") of the group G with respect to the normal subgroup K. And this quotient group is a homomorphic image of the group G.
The above important proof can also be given in an expanded form. We shall give it with respect to closure :
First a preliminary remark : We make use of the property of K being a normal subgroup of G as follows : When kx is an element of K, and p is an element of G, then this means that pkx is an element of the left coset pK of the subgroup K by the element p. But K is a normal subgroup, which means that this left coset of K by the element p, pK, is equal to the right coset Kp of K by that same element p. So the element pkx of pK is equal to some element kyp of Kp. We write pkx = kyp.
The product set aKbK means the set of all elements such as akrbks , in which kr and ks are elements of K. Now we know that bks is in bK, but then, since bK = Kb, it is also in Kb, so bks = ktb for some element kt of K. Hence a typical element of aKbK is akrbks = akrktb = akub (because K is a subgroup, the product of two of its elements -- kr and kt -- is another element of it, and we call this element ku ). But again, we require the 'normal' property of K to be able to say that kub = bkv for some element kv in K. Hence a typical element of aKbK is abkv , and this is an element of the left coset of K by the element ab, i.e. of (ab)K.
So any product of two (left) cosets of K results in some (other) (left) coset of K, which means that the set of cosets of the normal subgroup K is closed under set multiplication.
In Part XIV where we discussed the products of sets, we stated without proof that only when two cosets of a normal subgroup of order m are used to form products, do we get a product set containing m elements only, and thus can be a coset of that normal subgroup. The illustrations there were all drawn from the group Q6. We have now generalized the result, examined the theory behind it and provided the proof.
Quotient groups, or factor groups
When H is a normal subgroup of a group G, we shall write H $ G (In the literature, instead of $ a small triangle is used).
We now return to the question of the mapping of a group G which contains a normal subgroup K of index m ( meaning order(G) / order(K) ) onto a smaller group of order m, as we already have seen on many occasions. As has been said, the group of cosets is called the Quotient Group, or the Factor Group, and is indicated G/K. Thus, for example, when G is A4 and K is D2 , the quotient group G/K is C3 (See Table 16.2). Again, when G is C4xC2 , and K is C4 , the quotient group G/K is C2 (See Table 10.4 in Part X), and it is this latter sort of example which probably accounts for the name 'quotient'. But the name, and the notation, are somewhat unfortunate, for if the quotient group of G by the normal subgroup K is a group H (i.e. G / K = (isomorphic) H ), the notation strongly suggests that G = KxH (i.e. K and H multiplied), but this is not always so. Thus, A4 / D2 = C3 is not equivalent to A4 = D2xC3 , i.e. A4 is not the direct product of the groups D2 and C3 , since in any case, the latter ( i.e. D2xC3 ) is Abelian, whereas A4 is not.
In Table 5.3 of Part V and Table 6.5 of Part VI we can see that C12 / C2 = C6 , and C12 / C6 = C2 , yet C12 is different from C6xC2 (See HERE in Part IX ).
Again, S4 / A4 = C2 , but S4 is not the direct product of A4 and C2 .
More remarkable is that both C6 / C3 and D3 / C3 give the same quotient group, C2 .
However, it may be proved (BUDDEN, p. 407) that if
A $ G, B $ G, and the sets A and B have only the element 1 in common, and
oder(A)order(B) = order(G), then
G = (isomorphic) AxB. (Where $ means "is a normal subgroup of")
Which means that if A and B are two normal subgroups of a group G which have only the identity in common and the order of A multiplied with the order of B is equal to the order of G, then the group G is the direct product of A and B.
Quotient groups of direct product groups
We have noted that C / A = B does not imply that C = (isomorphic) AxB.
One may wander, however, whether the converse is true :
If C = AxB, is it true that C / A = B?
Before we can answer this question, it is first necessary to discover whether A is a normal subgroup of C, otherwise C / A is meaningless.
Suppose A is the group {1, a1, a2, a3, . . . } and B is the group {1, b1, b2, b3, . . . }.
The elements of the direct product group AxB are :
| (1, 1) | (a1, 1) | (a2, 1) | (a3, 1) | . | . | . | subgroup A |
| (1, b1) | (a1, b1) | (a2, b1) | (a3, b1) | . | . | . | |
| (1, b2) | (a1, b2) | (a2, b2) | (a3, b2) | . | . | . | |
| (1, b3) | . | . | . | . | . | . | |
| subgroup B |
Note that we here have to do with the (direct) product of two g r o u p s. We should not confuse this with the product of two subsets of one and the same group ( See Part XIV, Multiplication of subsets, and for the direct product of groups, see Part IX, Direct product groups ).
Because C is the direct product of the groups A and B, A and B are subgroups of the group C.
Now the first row of this array constitutes an isomorphic image of the group A, i.e. it can represent this group (and also its coset by the element 1) as a subgroup of C, while the successive rows are the cosets by the elements (1, b1), (1, b2), etc. For instance, the left coset of A by the element (1, b1) is :
(1, b1){(1, 1), (a1, 1), (a2, 1), (a3, 1), . . . }, which is the set {(1, b1), (a1, b1), (a2, b1), (a3, b1), . . . }, and this is the second row of the array. So every row of the above array is a coset of A, and they are all the cosets of A (The corresponding left and right cosets are here always the same, which we shall demonstrate below). We shall explain why they are all the cosets of A (where A is represented in the product group by its isomorphic image {(1, 1), (a1, 1), (a2, 1), (a3, 1), . . . }). At first sight we could note that the rows of the array only represent cosets of A by the elements (1, 1), (1, b1), (1, b2), (1, b3), etc. But of course every element of our group C (of which the elements are enumerated in the above array) can form a coset of A. So let us form a (left) coset of A by the element (a2, b1) :
(a2, b1){(1, 1), (a1, 1), (a2, 1), (a3, 1), . . . } =
{(a21, b1), (a2a1, b1), (a2a2, b1), (a2a3, b1), . . . }
We see a set of ordered pairs and we focus on the first member of each pair. Such a first member is a product of a2 with an element of A, i.e. with the elements 1, a1, a2, a3, etc. These latter elements are all the elements of the group A. But a2 (the element with which each element of A -- the first member of the original pairs -- is multiplied) is also an element of A. And because A is a group the resulting products (the first members of the resulting set of pairs) must all be elements of A again. And because all the enumerated elements of A are different elements, multiplying each of them with a same element, namely a2 , the result will be as many elements as we had before, and again different elements, which means that we get all the elements of A back again. So all the first members of the above resulted pairs are just elements of A again, while the second member being b1 . This means that the resulting set of pairs must be equal to the second row of the above array, so no new coset is produced by the multiplication of the element (a2, b1) with the set {(1, 1), (a1, 1), (a2, 1), (a3, 1), . . . }. The same reasoning can be applied to all the other elements of the row from which we took the pair (a2, b1), by taking those other elements and multiplying each of them in turn with the set {(1, 1), (a1, 1), (a2, 1), (a3, 1), . . . }. In this way we can handle all rows of the above array, and discover that no new cosets are being produced.
From all this we can see that the rows of the above array represent all (left) cosets of A ( where A is represented by {(1, 1), (a1, 1), (a2, 1), (a3, 1), . . . }).
We will now show that the left cosets are identical to the corresponding right cosets, since in any case, we have
(ar, 1)(1, bs) = (1, bs) (ar, 1) = (ar, bs) for all r and s, which indeed means that the left coset is identical to the corresponding right coset. We are therefore certain that A (and especially its isomorphic image {(1, 1), (a1, 1), (a2, 1), (a3, 1), . . . }) is a normal subgroup of C, and so C / A is meaningful, and we now need to know whether C / A has the structure of B (Recall that we are investigating the question that if C = AxB, is it true that C / A = B?).
Suppose the rows of the above array are denoted A, B1, B2, B3, . . . (i.e. they are all the cosets of A (and of its isomorphic image), so that Br denotes the set of ordered pairs {(1, br), (a1, br), (a2, br), (a3, br), . . . }. Consider the product of the cosets BrBs : letting (ai, br) be any element of Br and (aj, bs) be any element of Bs , we have (fully in the context of multiplying sets, which here means multiplication of their respective elements -- these being ordered pairs) :
(ai, br)(aj, bs) = (aiaj, brbs) = (ak, bt),
Because ai and aj are elements of the group A = {1, a1, a2, a3, . . . }, their product aiaj is also belonging to A, so we can call this product ak . Similarly, br and bs are elements of the group B = {1, b1, b2, b3, . . . }, so their product brbs is also an element of B, so we can call it bt . Therefore the product of any two elements of Br and Bs is an element of Bt (which we can see regarding the structure of the last term (ak, bt) of the above relation), and we may express this : BrBs = Bt . The behavior of the cosets of A (or of its isomorphic image) in the direct product group therefore exactly mimics the behavior of the elements of the group B itself. For, the group B = {1, b1, b2, b3, . . . }, we can say :
brbs = bt , which indeed mimics BrBs = Bt . This means that the group of cosets C / A is isomorphic to the group B.
Hence it is true that, C / A = B, which is equivalent to (AxB) / A = B.
And, because the group B is not different in status from the group A, we can also state : (AxB) / B = A.
Chains of normal subgroups
We have seen that D2 $ A4 (meaning that D2 is a normal subgroup of A4 ) (See Table 16.2), the subgroup consisting of {1, a, b, c} in the case of the group table just referred to. But D2 is Abelian, so any of its subgroups is normal to it, e.g. {1, a} $ {1, a, b, c}. See next group table.
| 1 | a | b | c | |
| 1 | 1 | a | b | c |
| a | a | 1 | c | b |
| b | b | c | 1 | a |
| c | c | b | a | 1 |
So we have C2 $ D2 $ A4 , a 'chain' of normal subgroups. We may extend the chain one stage further to the left by including the identity 1 as a trivial (normal) subgroup of C2 . See next tables.
| 1 | a | |
| 1 | 1 | a |
| a | a | 1 |
| 1 | |
| 1 | 1 |
Table 16.6 depicts the group consisting of the identity element alone.
C1 $ C2 $ D2 $ A4 $ S4
Note the curious fact that, though C2 $ D2 $ S4 , yet C2 is not normal in S4 . Referring to the group table for S4 (See Table 13.2, Part XIII), we have the normal subgroup {1, h, r, y}. Though each of the subgroups {1, h}, {1, r}, {1, y} is normal in D2 , neither of them is normal in S4 . This must be so, because if {1, h} is to be normal in a group, h must commute with every element of the group (only true for subgroups of order 2). This we can show as follows : If {1, h} is a normal subgroup in G, then for any element x in G we have x{1, h} = {1, h}x, which is equivalent to {x, xh} = {x, hx}, which implies that xh = hx for every element x of G. And this in turn means that h belongs to the center. But it can be proved that the center of S4 consists of the identity alone. This counter-example illustrates that $ is not a transitive relation between groups.
In the chain C1 $ C2 $ D2 $ A4 $ S4 , the respective quotient groups are (where "=" means "is isomorphic with") :
C2 / C1 = C2
D2 / C2 = C2
A4 / D2 = C3
S4 / A4 = C2.
These quotient groups are called composition factors of the chain, and a group which resolves into a succession of cyclic quotient groups in this way is called a soluble group. So S4 is a soluble group.
Infinite groups
Normal subgroups, and the resulting quotient groups of cosets, occur in infinite groups as well as in finite groups. We may find the subgroup and the induced factor group to be both infinite, or only one of these may be an infinite group. For example, consider the group (Z , +) which has the structure Cinfinite , and take the subgroup H = {. . . -15, -10, -5, 0, 5, 10, 15, . . . } which is isomorphic to (5Z , +) (where 5Z is the set of multiples of 5 ). And products are thus formed by addition of the elements. Then the cosets are :
H + 1 : {. . . -14, -9, -4, 1, 6, 11, . . . }
H + 2 : {. . . -13, -8, -3, 2, 7, 12, . . . }
H + 3 : {. . . -12, -7, -2, 3, 8, 13, . . . }
H + 4 : {. . . -11, -6, -1, 4, 9, 14, . . . }
(The subgroup itself is at the same time its (left, or right) coset by the element 0, which is the identity element : 0 is added to each element of the subgroup leaving it unchanged).
These are the residue classes modulo 5, and we may use the least positive residue as a representative of each class, and denote the classes 0, 1, 2, 3, 4. The next table shows the addition of these cosets : when we say that 4 + 2 = 1, we mean that any number selected from the coset 4 added to a number from the coset 2 will give a number in the coset 1.
| + | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
Table 16.7
The group of table 16.7 is the quotient group (Z , +) / (5Z , +), which we can -- thereby indicating the structure of its 'components' -- also denote as Cinfinite / C5. This quotient group is at the same time a homomorphic image of the group (Z , +). This homomorphism accordingly maps the set of all integers onto the set {0, 1, 2, 3, 4}.
The above casts a new light on the finite arithmetic tables of earlier documents. We now see the group ({0, 1, 2, 3, . . . , n-1}, + mod n) as the quotient group in the group (Z , +) formed by the cosets of the subgroup consisting of multiples of n, these cosets being the residue classes which we might denote 0, 1, 2, 3, . . . n-1. Thus when H is the normal subgroup (nZ , +), consisting of multiples of n, we see that the quotient group (Z , +) / H is the group Cn .
Another example is provided by (Q\0, x) (where Q\0 means the set of rationals -- integers and fractions -- excluding zero, and "x" means ordinary multiplication), a normal subgroup of which is (Q+, x), i.e. all the positive rationals under multiplication. There are just two cosets, being the partition of the rationals in positive and negative rationals. Let us explain.
The subgroup (Q+, x) is the set {. . . 1/4, . . . 1, . . . 3/2, . . . 5/2, . . . 20/3, . . . }. When we form a left or right coset of it, by a positive rational, then we in fact form a coset by multiplying the elements of this subgroup by one of its own elements (and so for every one of its own elements). And because there is no smallest rational, the result will be the subset itself, i.e. the set of all positive rationals. If, on the other hand, we form a left or right coset of this same subgroup by an element not in this subgroup, then this element is a negative rational (It cannot be zero, because zero is absent in the group (i.e. it is absent in the group (Q\0, x) of which (Q+, x) is a normal subgroup). When we now multiply such a negative rational with the elements of the subgroup, then the elements of the resulting coset are negative rationals. And of course the left coset is identical to the right, because ordinary multiplication is commutative.
These cosets combine according to the next table :
| x | + | - |
| + | + | - |
| - | - | + |
So the quotient group is C2 .
We may not interpret the group ({1, 2, 3, . . . , n-1}, x mod n) (where "x" means multiplication) in quite a comparable way, since (Z , x) (where "x" again means multiplication) itself is not a group : If we take for example the element 3 of (Z, x), we see that its inverse is 1/3 (When you make something 3 times as big , to undo this you must take one third of the result), but this element does not occur in (Z, x), so the latter is not a group. However, (taking n = 5 as an example), when we say that 4 x 3 = 2 (mod 5), this may be interpreted in terms of product sets. To do this let us first consider the following three sets :
{ . . . -1, 4, 9, 14, . . . }, where we can see that
-1 = -1 x 5 + 4, meaning that -1 is equal to a multiple of 5 with a residue of 4.
4 = 0 x 5 + 4, meaning that 4 is equal to a multiple of 5 with a residue of 4.
9 = 1 x 5 + 4, meaning that 9 is equal to a multiple of 5 with a residue of 4.
14 = 2 x 5 + 4, meaning that 14 is equal to a multiple of 5 with a residue of 4.
{ . . . -2, 3, 8, 13, . . . }, where we can see that
-2 = -1 x 5 + 3, meaning that -2 is equal to a multiple of 5 with a residue of 3.
3 = 0 x 5 + 3, meaning that 3 is equal to a multiple of 5 with a residue of 3.
8 = 1 x 5 + 3, meaning that 8 is equal to a multiple of 5 with a residue of 3.
13 = 2 x 5 + 3, meaning that 13 is equal to a multiple of 5 with a residue of 3.
{. . . -3, 2, 7, 12, . . . }, where we can see that
-3 = -1 x 5 + 2, meaning that -3 is equal to a multiple of 5 with a residue of 2.
2 = 0 x 5 + 2, meaning that 2 is equal to a multiple of 5 with a residue of 2.
7 = 1 x 5 + 2, meaning that 7 is equal to a multiple of 5 with a residue of 2.
12 = 2 x 5 + 2, meaning that 12 is equal to a multiple of 5 with a residue of 2.
Now when we say that 4 x 3 = 2 (mod 5), this may be interpreted (using the three sets above) in terms of product sets as follows :
Any number in the set { . . . -1, 4, 9, 14, . . . } multiplied by
any number in the set { . . . -2, 3, 8, 13, . . . } gives
a number in the set {. . . -3, 2, 7, 12, . . . }, and if these sets are
indicated by the least positive residue in bold type, this abbreviates to 4 x 3 = 2.
The group table for multiplying these sets, as represented by the residue classes modulo 5, is the following :
| x | 1 | 2 | 3 | 4 | period |
| 1 | 1 | 2 | 3 | 4 | 1 |
| 2 | 2 | 4 | 1 | 3 | 4 |
| 3 | 3 | 1 | 4 | 2 | 4 |
| 4 | 4 | 3 | 2 | 1 | 2 |
Table 16.9
Indeed this is the group C4 .
| x | 1 | 2 | 4 | 3 | period |
| 1 | 1 | 2 | 4 | 3 | 1 |
| 2 | 2 | 4 | 3 | 1 | 4 |
| 4 | 4 | 3 | 1 | 2 | 2 |
| 3 | 3 | 1 | 2 | 4 | 4 |
Table 16.10
Let us check the periods of its elements, i.e. with respect to an element y (we must find) the least integer p such that yp = 1 (the identity element of the group). The group operation is multiplication modulo 5.
Interpreted in terms of rotations we can say that
Element 1 (identity) corresponds to a rotation of 00.
Element 2 corresponds to a rotation of 900.
Element 4 corresponds to a rotation of 1800.
Element 3 corresponds to a rotation of 2700.
So we have a mapping of (Z , x) to the four residue classes which we have named 1, 2, 3, 4. Every product in (Z , x) corresponds to a product of residue classes, so products are preserved. But, (Z , x) is not a group, and consequently we have no group homomorphism, but only a set homomorphism.
Some general remarks, and a brief summary of the present document on homomorphism, quotient groups and normal subgroups (BUDDEN, p. 417)
The substance of the present document is of enormous importance (So BUDDEN relates to us) if you are going more deeply into the theory of groups. Indeed, it is no exaggeration to say that, in studying a particular group, those properties which are of chief interest to the mathematician are first : which normal subgroups does the group possess, and second, what quotient groups do these normal subgroups produce, i.e. what homomorphic images does the group admit? For note that every single normal subgroup partitions the group into cosets, and these form the quotient group peculiar to that particular subgroup, so that there is a homomorphic image of a group relative to each one of its normal subgroups. This is known as a 'Natural Homomorphism' of the group.
Let us now give a brief summary of the present document.
We discussed instances of groups which may be mapped into (smaller) groups by a homomorphism. The meaning of homomorphism is expressed as a mapping which preserves products (but which does not necessarily demand a one-to-one correspondence between the elements of the original group and those of the image group). Those elements in the given group G which map into the identity of the image group constitute the kernel K, and this is a normal subgroup of G.
Next we saw how the cosets of a normal subgroup themselves form a group under the product set law of composition. We gave examples from finite groups with the quotient group 'displayed' by 'division' of the group table, this division being indicated by colors. We also showed how an attempt to divide the group will fail if the subgroup is not normal. We then proved (A x B) / B to be isomorphic to A, and warned that there is no valid converse of this result, i.e. the following is not always true :
G / K = (isomorphic) H implies G = K x H.
Finally, quotient groups derived from infinite groups were considered.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals
back to Part XV of the theoretical preparation to the study of 3-D crystals