
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of the previous document, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Cyclic Groups
Definition
n! ("n-faculty") is a number that is equal to 1 x 2 x 3 x 4 x ... x n-1 x n.
For example 4! = 1 x 2 x 3 x 4 = 24.
An important theorem is Cayley's Theorem, which we will give without proof :
Any finite group of order n (in which n is accordingly finite) is isomorphic to a subgroup of the group Sn of permutations of n objects.
This group Sn (or Pn) is the full group of all n! permutations of n objects (symbols, letters, numbers, etc.). The order of the group Sn is therefore n!, and it is called the Symmetric Group, so that the full group of permutations of four letters, is denoted S4 or P4, and is of order 24.
In the foregoing we have already referred to cyclic groups, for example to C12, inspired by a clock. The name "cyclic" derives from the fact that such groups appear whenever we have a set of cyclic permutations of a number of objects.
If we have for example the cycle p = (01234), meaning
0 becomes 1,
1 becomes 2,
2 becomes 3,
3 becomes 4, and
4 becomes 0 again,
we can derive three other cycles from it by following (01234) but taking only every second number :
0 becomes 2,
2 becomes 4,
4 becomes 1,
1 becomes 3, and
3 becomes 0 again.
So we have the cycle (02413), which is in fact an application of the cycle two times, i.e. p2.
In the same way we can derive the cycles (03142) = p3 and (04321) = p4. If we, starting from the first cycle p = (01234), and pick out every fifth number, then we get
0 becomes 0,
1 becomes 1,
2 becomes 2,
3 becomes 3,
4 becomes 4.
And this is of course the identity.
These five cycles can be expressed as the following five cyclic permutations :
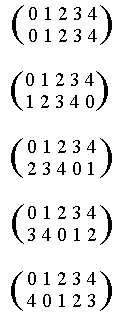
These five permutations can also be written down as follows :
| 1 | p | p2 | p3 | p4 | period | |
| 1 | 1 | p | p2 | p3 | p4 | 1 |
| p | p | p2 | p3 | p4 | 1 | 5 |
| p2 | p2 | p3 | p4 | 1 | p | 5 |
| p3 | p3 | p4 | 1 | p | p2 | 5 |
| p4 | p4 | 1 | p | p2 | p3 | 5 |
For 1 (identity) we could write p0, and for p we could write p1.
In this way we can see that all the elements of this group (C5) can be expressed in terms of a single element p, namely p0, p1, p2, p3, p4, i.e. all the possible distinct 'powers' of p. This is true of all cyclic groups :
The cyclic group of order n (denoted Cn) has elements {1, x, x2, x3, x4, ..., xn-1} with x satisfying the relation xn = 1.
(xm is not 1 when m is equal to or greater than 1, but smaller than n).
Cyclic groups may be divided into two kinds : those for which the order is prime, and those for which it is composite.
A prime number is an integer that can only be divided by 1 and by itself (like 1, 2, 3, 5, 7, 11, etc). All other integers are called composite numbers (like 4, 6, 8, 9, 10, 12, etc.
Cyclic groups of which the order is prime, like the above group, C5, are in most repects less interesting, chiefly because they have no subgroups.
While the group C5 does not occur in crystals, other cyclic groups do, for instance the Cyclic Group C6 (which is, consequently, a group of composite order), of which the abstract table (i.e. a table without its elements being interpreted as permutations, numbers, symmetry transformations or whatever) is :
| 1 | p | p2 | p3 | p4 | p5 | period | |
| 1 | 1 | p | p2 | p3 | p4 | p5 | 1 |
| p | p | p2 | p3 | p4 | p5 | 1 | 6 |
| p2 | p2 | p3 | p4 | p5 | 1 | p | 3 |
| p3 | p3 | p4 | p5 | 1 | p | p2 | 2 |
| p4 | p4 | p5 | 1 | p | p2 | p3 | 3 |
| p5 | p5 | 1 | p | p2 | p3 | p4 | 6 |
This abstract table (abstract group) can show many realizations, in terms of permutations, numbers (for instance the complex sixth roots of unity), mechanical devices, or whatever.
The possible realizations of an abstract group should not be confused with the possible automorphisms of the group. The latter are just rearrangements of the symbols of the elements while retaining the same table structure.
We will concentrate on the interpretation (realization) of the abstract group C6 in terms of symmetry transformations.
C6 is, among others, realized in the promorph or stereometric basic form of crystals of the Class 6, i.e. crystals possessing a 6-fold rotation axis as their only symmetry element (concerning its point symmetry, i.e. its non-translational symmetry). This symmetry element contains six possible rotations. See Figure 1.
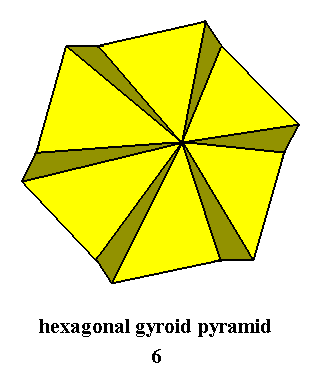
Figure 1. The Regular Hexagonal Gyroid Pyramid as the Stereometric Basic Form (belonging to the Homogyrostaura hexamera, [Stauraxonia heteropola gyrostaura]) of crystals belonging to the Hexagonal-pyramidal Class (Class 6) of the Hexagonal Crystal System. Its symmetry content consists of a 6-fold rotation axis.
The just mentioned "stereometric basic form" (or "promorph") of a given crystal is the geometric solid that geometrically (i.e. purely geometrically, and not also in chemical or physical terms) represents the point symmetry of that crystal (a single, i.e. non-twinned, ideally grown crystal, representing a certain chemical substance or mineral). It is treated of extensively (concerning crystals as well as organisms) in the documents on Promorphology.
Realized as the symmetries of the mentioned gyroid pyramid, we can now interpret the individual elements of the group C6 :
1 is the identity element of the group, i.e. a rotation about the main axis of the gyroid pyramid by 00, or, equivalently, 3600 or a multiple thereof. Its period is 1, i.e. 11 = 1 = identity.
p is an (by convention) anticlockwise rotation about the main axis by 600. Its period is 6, i.e. p6 = 6 x 60 = 3600 = 1 = identity.
p2 is an anticlockwise rotation of 1200, i.e. it is two times the (transformation) p. Its period is 3, i.e. (p2)3 = 3 x 120 = 3600 = 1 = identity.
p3 is an anticlockwise rotation of 1800, i.e. it is three times the (transformation) p. Its period is 2, i.e. (p3)2 = 2 x 180 = 3600 = 1 = identity.
p4 is an anticlockwise rotation of 2400 (or a clockwise rotation of 1200, i.e. the inverse of p2), i.e. it is four times the (transformation) p. Its period is 3, i.e. (p4)3 = 3 x 240 = 720 = 1 = identity.
p5 is an anticlockwise rotation by 3000 (or a clockwise rotation of 600, i.e. the inverse of p, i.e. five times the (transformation) p. Its period is 6, i.e. (p5)6 = 6 x 300 = 1800 = 5 x 3600 = 1 = identity.
The Cyclic Group C3 also occurs in crystals, namely in crystals of the Class 3, i.e. the Trigonal-pyramidal Crystal Class, of the Hexagonal Crystal System. The promorph or stereometric basic form of such crystals is the geometric solid that geometrically expresses their symmetry content. This solid is the Regular 3-fold Gyroid Pyramid, and is depicted in the next Figure (Versions of the gyroid pyramid, in which the receding angles are replaced by their corresponding anti-receding angles, can occur in crystals).
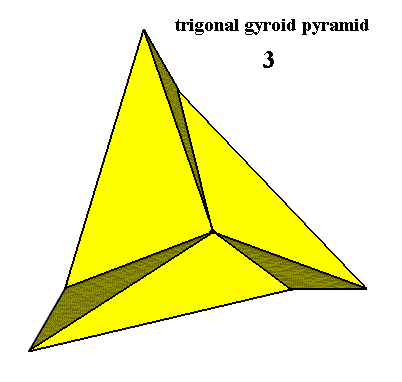
Figure 2. Regular Trigonal Gyroid Pyramid, as the Stereometric Basic Form of Crystals of the Trigonal-pyramidal Class of the Hexagonal Crystal System. This specific basic form belongs to the ( promorphological category of the ) Homogyrostaura trimera (Stauraxonia heteropola gyrostaura). Its symmetry content consists of one 3-fold rotation axis.
Although crystals of this Class 3 can occur as regular trigonal pyramids and appear to have the symmetry of the Ditrigonal-pyramidal Class (3m) with three vertical symmetry planes, they in fact have a lower symmetry (namely 3) which can be revealed by chemical or physical features.
| 10 | p1 | p2 | period | |
| 10 | 10 | p1 | p2 | 1 |
| p 1 | p 1 | p2 | 10 | 3 |
| p2 | p2 | 1 0 | p 1 | 3 |
The elements in this table are interpreted as follows :
1 is the identity, namely a rotation of 00 about the gyroid pyramid's main axis.
p is an anticlockwise rotation of 1200 about the mentioned axis.
p2 is an anticlockwise rotation of 2400. It is equivalent to a clockwise rotation of 1200.
Although in handling Group Theory only insofar as we need it for the description of crystal symmetries, it is instructive to realize that groups can have many realizations. So our cyclic group C3 can be realized in finite arithmetics as a table of multiplication modulo 14
(x mod 14) :
| x mod 14 | 8 | 2 | 4 | period |
| 8 | 8 | 2 | 4 | 1 |
| 2 | 2 | 4 | 8 | 3 |
| 4 | 4 | 8 | 2 | 3 |
The multiplication modulo 14, is like ordinary multiplication but in the results only retaining the remainders after division by 14. It is commutative because ordinary multiplication is commutative. So 2 x 8 (mod 14) = 8 x 2 (mod 14) = 16 = 16 - 14 = 2. Further we see that 4 x 8 (mod 14) = 4, and 8 x 8 (mod 14) = 8, and this means that 8 is the identity element. We see that the table has the same structure as the previous table.
Next we consider the Cyclic Group C4, which also shows a realization in crystals. It is realized in crystals of the Tetragonal-pyramidal Class (i.e. Class 4) of the Tetragonal Crystal System. The geometric solid, representing generally the symmetry of such crystals entirely geometrically, is the Regular Tetragonal Gyroid Pyramid, which as such is the promorph or stereometric basic form of all (single, i.e. non-twinned) crystals of this Class (Versions of the gyroid pyramid, in which the receding angles are replaced by their corresponding anti-receding angles, can occur in crystals). The Regular Tetragonal Pyramid is given in the next Figure.
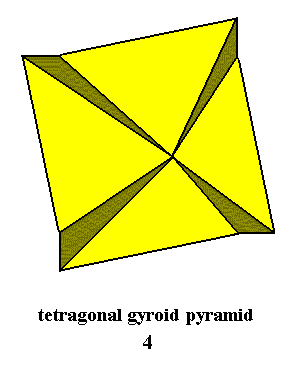
Figure 3. The Regular Tetragonal Gyroid Pyramid as the general promorph of crystals of the Class 4, as such belonging to the (promorphological category of the) Homogyrostaura tetramera (Stauraxonia heteropola).
The group table for the Cyclic Group C4 is the following :
| 10 | p1 | p2 | p3 | period | |
| 10 | 10 | p1 | p2 | p3 | 1 |
| p 1 | p 1 | p2 | p3 | 10 | 4 |
| p2 | p2 | p3 | 1 0 | p 1 | 2 |
| p3 | p3 | 1 0 | p 1 | p2 | 4 |
With respect to the symmetries of crystals we can interpret the elements of the table just given as follows :
1 is the identity element. It is a rotation of 00, or, equivalently, of 3600 or a multiple thereof.
p is an anticlockwise rotation of 900 (about the main axis of the gyroid pyramid). Its period is 4, because p4 = 90 + 90 + 90 + 90 = 3600 = 00 = identity = 1.
p2 is an anticlockwise rotation of 1800. Its period is 2, because (p2)2 = 180 + 180 = 3600 = 00 = identity = 1.
p3 is an anticlockwise rotation of 2700. It is equivalent to a clockwise rotation of 900. Its period is 4, because (p3)4 = 270 + 270 + 270 + 270 = 1080 = 360 + 360 + 360 = 0 + 0 + 0 = 0 = identity = 1.
The Cyclic Group of order two, C2, is also realized in crystals : It is realized in three Crystal Classes (which means that it forms the common abstract group of those three Classes) : The Sphenoidic Class -- i.e. the Class 2 -- of the Monoclinic Crystal System, The Domatic Class -- i.e. the Class m -- also of the Monoclinic Crystal System, and, finally, The Pinacoidal Class -- i.e. the Class 1* -- of the Triclinic Crystal System.
In the Crystallographic literature the asterisk is replaced by a horizontal score above the relevant numeral (indicating a rotation axis). So 1* indicates a rotation of 00 about the axis 1 immediately followed by an inversion across a point on that axis. Analogously 3* indicates an anticlockwise rotation of 1200 about an axis labelled 3 immediately follwed by an inversion across a point on that axis.
See for "inversion across a point" the first Part of this website -- accessible by back to homepage -- and there in the document "The Morphology of Crystals".
So we see the Cyclic Group C2 crystallographically realized in the Classes 2, m, and 1*. And we see that the abstract group (C2) crosses the boundary between two different Crystal Systems.
The group table of the group C2 is as follows :
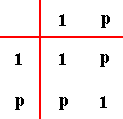
Here the element 1 is the identity element (Its period is, like all identity elements, 1).
The element p has period 2, because p2 = 1. This element can be crystallographically realized either as a rotation of 1800, and then we have to do with the Sphenoidic Crystal Class of the Monoclinic System, or as a reflection across a mirror plane, and then we have to do with the Domatic Crystal Class of the Monoclinic System, or a point inversion, and then we have to do with the Pinacoidal Class of the Triclinic System.
Realization of C2 in Crystal Class 2.
The geometric solid generally representing geometrically the symmetry of crystals of the Sphenoidic Class (i.e. Class 2) of the Monoclinic Crystal System is the Amphitect Gyroid Pyramid. It is the promorph or stereometyric basic form of all the crystals of this Class and as such belongs to the (promorphological category of the) Heterogyrostaura tetramera (Stauraxonia heteropola gyrostaura). See next Figure.
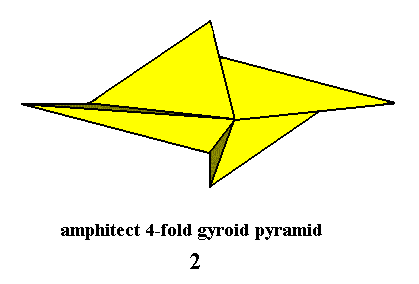
Figure 4. The Amphitect Gyroid Pyramid as the promorph of all the crystals of the Sphenoidic Class of the Monoclinic Crystal System. The tip of the pyramid is pointing to the beholder. Its only symmetry element (not to be confused with group element) is a 2-fold rotation axis going from the pyramid's tip to its base.
When the number of antimers (counterparts) (assessible by the morphological analysis of the translation-free chemical motif -- " Complex Motif ") is two instead of four, the promorph is that of the Heterogyrostaura dimera, and the ggeometric solid, generally expressing the symmetry and this number of antimers, is the same as for the dimera.
Realization of C2 in Crystal Class m.
The geometric solid generally representing geometrically the symmetry of crystals of the Domatic Class (i.e. Class m) of the Monoclinic Crystal System is Half a Rhombic Pyramid. It is the promorph or stereometyric basic form of all the crystals of this Class and as such belongs to the (promorphological category of the) Zygopleura eudipleura (Stauraxonia heteropola heterostaura allopola). See next Figure.
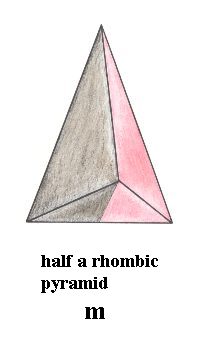
Figure 5. Half a Rhombic Pyramid as the promorph of all the crystals of the Domatic Class of the Monoclinic Crystal System. The tip of the pyramid is pointing to the beholder. Its only symmetry element (not to be confused with group element) is a mirror plane as the median plane of the pyramid.
Realization of C2 in Crystal Class 1*.
The geometric solid generally representing geometrically the symmetry of crystals of the Pinacoidal Class (i.e. the Class 1*) of the Triclinic Crystal System is a Triclinic Bipyramid or Oblique Rhombic Bipyramid. It is the promorph or stereometric basic form of all the crystals of this Class and as such belongs to the Anaxonia centrostigma (Anaxonia). See next Figure.
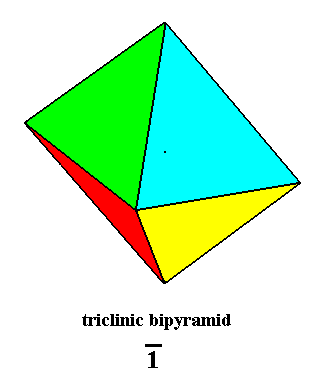
Figure 6 Triclinic Bipyramid, Stereometric Basic Form of the Pinacoidal Class of the Triclinic Crystal System.
The angle between the equatorial plane and the main axis is different from 900.
The next Figure depicts this same bipyramid, but now with the triclinic axial system inserted.
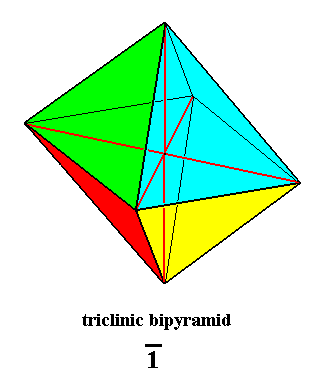
Figure 7. Triclinic Bipyramid, Stereometric Basic Form of the Pinacoidal Class of the Triclinic Crystal System.
The angle between the equatorial plane and the main axis is different from 900. Triclinic axial system inserted. The three axes do not involve angles of 900.
The next Figure depicts the equatorial plane of the Triclinic Bipyramid. It is not a square, nor a rectangle, and especially, not a rhombus.
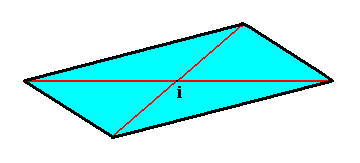
Figure 8. Equatorial plane of a Triclinic Bipyramid, as seen from a direction perpendicular to that plane (and thus not seen along the direction of the bipyramid's main axis).
The angle between the equatorial plane and the main axis is different from 900. Two triclinic axes inserted (red), they meet in the bipyramid's center of symmetry ( i ).
In order to make matters more clear, the next Figures depict a parallelopipedum which is a geometric body also possessing only a center of symmetry. But because we can divide this body such that the resulting parts are still parallelopipeda (each still possessing a center of symmetry), in other words, because this body is idem specie divisible, it cannot serve as the geometric body that represents the 1* symmetry geometrically, as we had established in Part One of The Promorphology of Crystals.
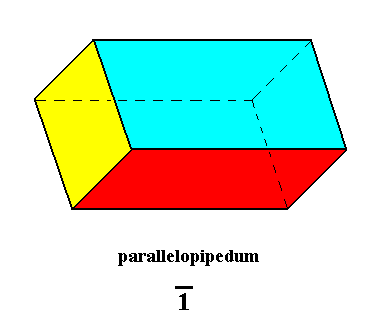
Figure 9. Parallelopipedum, having the symmetry of the Pinacoidal Class of the Triclinic Crystal System. All angles are different from 900. There are no symmetry axes, nor mirror planes.
One could, while looking at the parallelopipedum, be persuaded that it should have, in addition to a center of symmetry, at least some 2-fold rotational symmetry axes. But this is not so, as the next Figure illustrates :
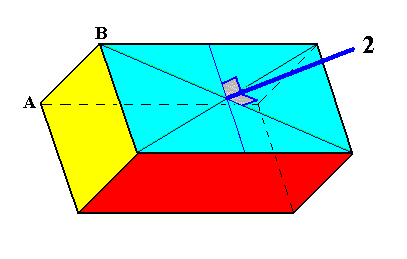
Figure 10. Parallelopipedum, having the symmetry of the Pinacoidal Class of the Triclinic Crystal System. All angles are different from 900. There are no symmetry axes, nor mirror planes. When we nevertheless try out a 2-fold rotation axis, we see that such an axis will map the face (of the parallelopipedum) on which it is perpendicular, indeed onto itself. But such an axis will not map the whole parallelopipedum onto itself, because that axis is not perpendicular to the opposite face (it is not parallel to AB). This opposite face will not be mapped onto itself by an oblique 2-fold rotation axis.
The Cyclic Group C1 finally, is also realized in crystals. It is so realized in the Asymmetric Class (i.e. the Class 1) of the Triclinic Crystal System. The geometric solid generally representing geometrically the symmetry of this Class (which has no symmetry whatsoever) is Half a Triclinic Bipyramid. Such a bipyramid has, because of this division, of course become a single pyramid. The promorph or stereometric basic form is accordingly that of the Anaxonia acentra (Anaxonia), i.e. irregular bodies possessing no genuine promorphological axes, nor symmetry axes, and no mirror planes. See next Figures.
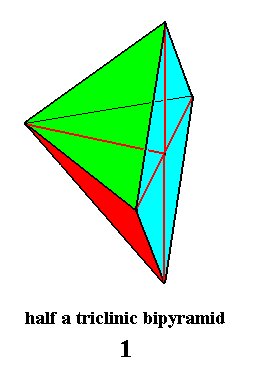
Figure 11. Half a Triclinic Bipyramid, the Stereometric Basic Form of the crystals of the Asymmetric Class of the Triclinic Crystal System. The depicted geometrical solid is (in fact) a single pyramid : a totally irregular pyramid.
The next Figure gives the equatorial plane of half a triclinic bipyramid.
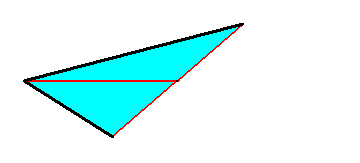
Figure 12. Equatorial plane of Half a Triclinic Bipyramid.
The group table of the Cyclic Group of order 1, i.e. the group C1, only consists of the identity element :
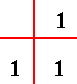
The Cyclic Group C1 has only one element, the identity. This element can be interpreted as a rotation of 00 about any axis of the given solid.
So the (abstract) cyclic groups realized in (single non-twinned) crystals are accordingly : C1, C2, C3, C4 and C6.
Cyclic Groups of Prime Order
Cyclic Groups having a number of elements which is prime, we already met : C1 and C3.
We will now discuss a cyclic group of order 7 (which is also prime), C7, realized in finite arithmetics as addition modulo 7 :
| + mod 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 0 | 1 | 2 | 3 | 4 | 5 |
The period of the identity element is (as it is always) 1.
The period of all other elements of the group (C7) is 7.
Another way of saying this is that any element of the group may be used to generate the whole group.
In the above table we used the element 1 to generate the group. We did this by successively applying the element 1 :
1 + 1 = 12 = 2 gave the element 2.
1 + 1 + 1 = 13 = 3 gave the element 3.
1 + 1 + 1 + 1 = 14 = 4 gave the element 4.
1 + 1 + 1 + 1 + 1 = 15 = 5 gave the element 5.
1 + 1 + 1 + 1 + 1 + 1 = 16 = 6 gave the element 6.
finally, 1 + 1 + 1 + 1 + 1 + 1 + 1 = 17 = 7 = 0 (mod 7), which is the identity element.
(1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 18 = 8 = 1 (mod 7), etc.).
While the generator element was 1, we've now generated the elements 2, 3, 4, 5, 6 and 0, i.e. we now have all the elements of the group.
But we can, alternatively, use the element 3 to generate the same group :
So, given the generator element 3, the rest of the elements can be generated as follows :
3 + 3 = 32 = 6.
3 + 3 + 3 = 33 = 9 = 2 (mod 7).
3 + 3 + 3 + 3 = 34 = 12 = 5 (mod 7).
3 + 3 + 3 + 3 + 3 = 35 = 1 (mod 7).
3 + 3 + 3 + 3 + 3 + 3 = 36 = 4 (mod 7).
3 + 3 + 3 + 3 + 3 + 3 + 3 = 37 = 21 = 0 (mod 7), which is the identity.
(3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 38 = 24 = 3 (mod 7)).
(3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 39 = 27 = 6 (mod 7), etc.).
Starting with 0, then 3, and then the generated elements in the above order gives us one of the automorphisms of C7, i.e. instead of the original order of elements
0 1 2 3 4 5 6
We have now :
0 3 6 2 5 1 4
Indeed when we construct the table for this latter sequence we see that the structure is preserved :
| + mod 7 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 0 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 | 0 |
| 6 | 6 | 2 | 5 | 1 | 4 | 0 | 3 |
| 2 | 2 | 5 | 1 | 4 | 0 | 3 | 6 |
| 5 | 5 | 1 | 4 | 0 | 3 | 6 | 2 |
| 1 | 1 | 4 | 0 | 3 | 6 | 2 | 5 |
| 4 | 4 | 0 | 3 | 6 | 2 | 5 | 1 |
We can interpret this table also geometrically, namely as a tour of the vertices of the star heptagon :
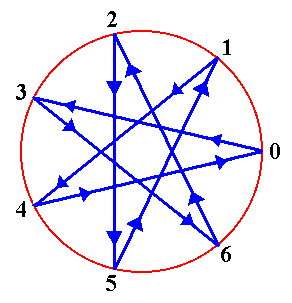
The vertices are visited in the order of the cycle (following the arrowed lines), 0, 3, 6, 2, 5, 1, 4, and back to 0 again. The fact that every vertex is visited in turn corresponds to the fact that, if you change your socks every (say) three days, then whichever day you start on, you must make a subsequent change on every possible day of the week, i.e. there will be some monday on which you change your socks, but also some tuesday on which you do that, some wednesday, some thursday, some fryday, some saturday and some sunday. Here we are dealing with the modulo 7 arithmetic, and this statement about changing socks would remain true if 3 were replaced by 1, 2, 4, 5, 6, or for that matter by any number not divisible by 7. That's why cyclic groups of prime order do not have subgroups (i.e. there is no subcycle that restricts its visits to just a part of the vertices).
If we were dealing with a composite modulus, e.g. modulo 12, it would be a different story. If receive (and pay) your telephone bill once a quarter, and the first account is received in February, then subsequent payments will be due in May, August, November, February, ... and you will never receive the bill in any other month.
Automorphisms of C7
The fact that every element in C7, except the identity element, is primitive, i.e. each of them can generate the whole group, because they each have a period of 7, and may be used as a generator, means that here we have a system in which all the elements (apart from the identity element) are of equal status - every member of this 'democracy' is just as good as every other, except the identity, who is a sort of president. This means that the group C7 has six automorphisms :
If we take the element 1 as generator, a certain sequence of the group elements results, let us call it the original sequence.
If we take instead of 1, the element 2 as generator, another sequence of the group elements will result. This other sequence will, however, preserve structure, i.e. with respect to the original sequence : products are preserved, which in turn means that a product in a group table based on the original sequence of group elements, corresponds exactly to a product in a group table based on the second sequence of group elements. Such an alternative sequence of group elements, in which structure is preserved, is called an automorphism of the group.
If we take the element 3 as generator, yet another sequence will result, which constitutes yet another automorphism, and so on, with respect to the remaining elements of the group. The original sequence of group elements we call the identity automorphism. So the following replacements of the original generator by another generator
1 -- 1
1 -- 2
1 -- 3
1 -- 4
1 -- 5
1 -- 6
result in six different but structure preserving generated sequences of group elements, i.e. six reshufflings of group elements, and that means : six automorphisms. These specific reshufflings are based on the fact that we can generate the whole group either with element 1, or with 2, or with 3, or 4, or 5, or 6. We already have done so with element 1 and with element 3, resulting in two different, but structure preserving, element sequences -- autmorphisms.
Each of such an automorphism thus is a permutation (reshuffling) of the group elements (These are in our case the elements 0, 1, 2, 3, 4, 5 and 6), for example the automorphism resulting from the replacement of the generator 1 by the generator 3 ( The automorphism thus being an element sequence generated by the element 3 ) can be expressed by the following permutation of the group elements :
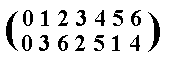
Let us systematically derive all six automorphisms of C7 :
The elements in the sequential order 0 1 2 3 4 5 6 means that the group elements are successively generated by the element 1 :
1 + 1 (mod 7) gives element 2.
1 + 1 + 1 (mod 7) gives element 3.
1 + 1 + 1 + 1 (mod 7) gives element 4.
1 + 1 + 1 + 1 + 1 (mod 7) gives the element 5.
1 + 1 + 1 + 1 + 1 + 1 (mod 7) gives the element 6.
1 + 1 + 1 + 1 + 1 + 1 + 1 (mod 7) gives the element 0.
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 (mod 7) gives the element 1 again.
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 (mod 7) gives the element 2 again.
etc.
When we place the element 0 in front [We are allowed to do so, because the element 0 does not partake in the permutations generating automorphisms -- it cannot do so because its period is different from that of the other ones], the resulting sequence of the (generated) elements is :
0 1 2 3 4 5 6. This corresponds to the permutation (of the group elements) :
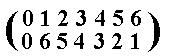
The corresponding group table is (as given earlier) :
| + mod 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 0 | 1 | 2 | 3 | 4 | 5 |
In the same way the element 2 generates all the elements of the group :
2 + 2 (mod 7) gives the element 4.
2 + 2 + 2 (mod 7) gives the element 6.
2 + 2 + 2 + 2 (mod 7) gives the element 1.
2 + 2 + 2 + 2 + 2 (mod 7) gives the element 3.
2 + 2 + 2 + 2 + 2 + 2 (mod 7) gives the element 5.
2 + 2 + 2 + 2 + 2 + 2 + 2 (mod 7) gives the element 0 .
So placing again the element 0 in front we get the sequence
0 2 4 6 1 3 5. This corresponds to the permutation :
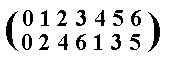
The corresponding group table is :
| + mod 7 | 0 | 2 | 4 | 6 | 1 | 3 | 5 |
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 | 0 |
| 4 | 4 | 6 | 1 | 3 | 5 | 0 | 2 |
| 6 | 6 | 1 | 3 | 5 | 0 | 2 | 4 |
| 1 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
| 3 | 3 | 5 | 0 | 2 | 4 | 6 | 1 |
| 5 | 5 | 0 | 2 | 4 | 6 | 1 | 3 |
We can clearly see that the table structure of this group table is the same as the previous one (corresponding to the identity permutation).
With the element 3 we can generate the group elements as follows :
3 + 3 (mod 7) gives the element 6.
3 + 3 + 3 (mod 7) gives the element 2.
3 + 3 + 3 + 3 (mod 7) gives the element 5.
3 + 3 + 3 + 3 + 3 (mod 7) gives the element 1.
3 + 3 + 3 + 3 + 3 + 3 (mod 7) gives the element 4.
3 + 3 + 3 + 3 + 3 + 3 + 3 (mod 7) gives the element 0.
So placing the element 0 in front, we get :
0 3 6 2 5 1 4.
This corresponds to the permutation :
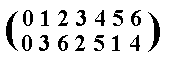
The corresponding table (as given earlier) is :
| + mod 7 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 0 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 | 0 |
| 6 | 6 | 2 | 5 | 1 | 4 | 0 | 3 |
| 2 | 2 | 5 | 1 | 4 | 0 | 3 | 6 |
| 5 | 5 | 1 | 4 | 0 | 3 | 6 | 2 |
| 1 | 1 | 4 | 0 | 3 | 6 | 2 | 5 |
| 4 | 4 | 0 | 3 | 6 | 2 | 5 | 1 |
Also here the structure has remained the same.
With the element 4 we can generate the group elements as follows :
4 + 4 (mod 7) gives the element 1.
4 + 4 + 4 (mod 7) gives the element 5.
4 + 4 + 4 + 4 (mod 7) gives the element 2.
4 + 4 + 4 + 4 + 4 (mod 7) gives the element 6.
4 + 4 + 4 + 4 + 4 + 4 (mod 7) gives the element 3.
4 + 4 + 4 + 4 + 4 + 4 + 4 (mod 7) gives the element 0.
So placing the element 0 in front, we get :
0 4 1 5 2 6 3.
This corresponds to the permutation :
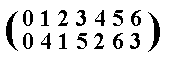
The corresponding table is :
| + mod 7 | 0 | 4 | 1 | 5 | 2 | 6 | 3 |
| 0 | 0 | 4 | 1 | 5 | 2 | 6 | 3 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 | 0 |
| 1 | 1 | 5 | 2 | 6 | 3 | 0 | 4 |
| 5 | 5 | 2 | 6 | 3 | 0 | 4 | 1 |
| 2 | 2 | 6 | 3 | 0 | 4 | 1 | 5 |
| 6 | 6 | 3 | 0 | 4 | 1 | 5 | 2 |
| 3 | 3 | 0 | 4 | 1 | 5 | 2 | 6 |
Also here the structure is unchanged.
With the element 5 we can generate the group elements as follows :
5 + 5 (mod 7) gives the element 3.
5 + 5 + 5 (mod 7) gives the element 1.
5 + 5 + 5 + 5 (mod 7) gives the element 6.
5 + 5 + 5 + 5 + 5 (mod 7) gives the element 4.
5 + 5 + 5 + 5 + 5 + 5 (mod 7) gives the element 2.
5 + 5 + 5 + 5 + 5 + 5 + 5 (mod 7) gives the element 0.
So when placing the element 0 in front we get the sequence :
0 5 3 1 6 4 2.
The corresponding permutation is :
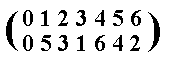
And the table is :
| + mod 7 | 0 | 5 | 3 | 1 | 6 | 4 | 2 |
| 0 | 0 | 5 | 3 | 1 | 6 | 4 | 2 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 | 0 |
| 3 | 3 | 1 | 6 | 4 | 2 | 0 | 5 |
| 1 | 1 | 6 | 4 | 2 | 0 | 5 | 3 |
| 6 | 6 | 4 | 2 | 0 | 5 | 3 | 1 |
| 4 | 4 | 2 | 0 | 5 | 3 | 1 | 6 |
| 2 | 2 | 0 | 5 | 3 | 1 | 6 | 4 |
Also here the structure is fully preserved.
Finally, with the element 6 we can generate the group elements as follows :
6 + 6 (mod 7) gives the element 5.
6 + 6 + 6 (mod 7) gives the element 4.
6 + 6 + 6 + 6 (mod 7) gives the element 3.
6 + 6 + 6 + 6 + 6 (mod 7) gives the element 2.
6 + 6 + 6 + 6 + 6 + 6 (mod 7) gives the element 1.
6 + 6 + 6 + 6 + 6 + 6 + 6 (mod 7) gives the element 0.
So when placing element 0 in front we get the sequence :
0 6 5 4 3 2 1
This corresponds to the permutation :
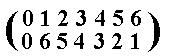
And the table is :
| + mod 7 | 0 | 6 | 5 | 4 | 3 | 2 | 1 |
| 0 | 0 | 6 | 5 | 4 | 3 | 2 | 1 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 5 | 5 | 4 | 3 | 2 | 1 | 0 | 6 |
| 4 | 4 | 3 | 2 | 1 | 0 | 6 | 5 |
| 3 | 3 | 2 | 1 | 0 | 6 | 5 | 4 |
| 2 | 2 | 1 | 0 | 6 | 5 | 4 | 3 |
| 1 | 1 | 0 | 6 | 5 | 4 | 3 | 2 |
Also here the structure is preserved.
Writing down all six automorphisms as permutations of the six mentioned elements, while writing down only the lower part of the permutation symbol, we get :
0 1 2 3 4 5 6 (identity)
0 2 4 6 1 3 5
0 3 6 2 5 1 4
0 4 1 5 2 6 3
0 5 3 1 6 4 2
0 6 5 4 3 2 1
It is perhaps instructive to show a case -- i.e. a permutation of the group elements -- that does not yield an automorphism. We try the permutation:
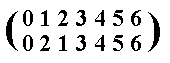
The table would be accordingly :
| + mod 7 | 0 | 2 | 1 | 3 | 4 | 5 | 6 |
| 0 | 0 | 2 | 1 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 3 | 5 | 6 | 0 | 1 |
| 1 | 1 | 3 | 2 | 4 | 5 | 6 | 0 |
| 3 | 3 | 5 | 4 | 6 | 0 | 1 | 2 |
| 4 | 4 | 6 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 6 | 1 | 2 | 3 | 4 |
| 6 | 6 | 1 | 0 | 2 | 3 | 4 | 5 |
We see clearly that the structure is not preserved (not only with respect to the pattern of identity elements, but also with respect to the NE--SW diagonals). So if we depart from the sequence 0 1 2 3 4 5 6 of the group elements, then this last (departure) that we've just tried out, is not a automorphism of the group C7.
Let's try yet another case, namely the permutation :
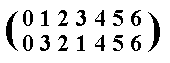
The table is then :
| + mod 7 | 0 | 3 | 2 | 1 | 4 | 5 | 6 |
| 0 | 0 | 3 | 2 | 1 | 4 | 5 | 6 |
| 3 | 3 | 6 | 5 | 4 | 0 | 1 | 2 |
| 2 | 2 | 5 | 4 | 3 | 6 | 0 | 1 |
| 1 | 1 | 4 | 3 | 2 | 5 | 6 | 0 |
| 4 | 4 | 0 | 6 | 5 | 1 | 2 | 3 |
| 5 | 5 | 1 | 0 | 6 | 2 | 3 | 4 |
| 6 | 6 | 2 | 1 | 0 | 3 | 4 | 5 |
The structure is again totally different.
Above we found out that the following permutations yielded automorphisms of the group C7. They should themselves form a group, the automorphism group of the group C7, notated Aut(C7) :
0 1 2 3 4 5 6 (identity)
0 2 4 6 1 3 5
0 3 6 2 5 1 4
0 4 1 5 2 6 3
0 5 3 1 6 4 2
0 6 5 4 3 2 1
The 0 element does not partake in the permutations, so in fact we have the permutations :
1 2 3 4 5 6 (identity)
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
5 3 1 6 4 2
6 5 4 3 2 1
i.e. six permutations of 6 symbols.
Let's look to the periods of those six permutations.
The period of the identity permutation is of course 1.
We now will apply the second permutation repeatedly till we arrive at the identity :
1 2 3 4 5 6
2 4 6 1 3 5 (1)
4 1 5 2 6 3 (2)
1 2 3 4 5 6 (3)
So the period of the second permutation is 3.
Now the third permutation :
1 2 3 4 5 6
3 6 2 5 1 4 (1)
2 4 6 1 3 5 (2)
6 5 4 3 2 1 (3)
4 1 5 2 6 3 (4)
5 3 1 6 4 2 (5)
1 2 3 4 5 6 (6)
So the period of the third permutation is 6.
Now the fourth permutation :
1 2 3 4 5 6
4 1 5 2 6 3 (1)
2 4 6 1 3 5 (2)
1 2 3 4 5 6 (3)
So the period of the fourth permutation is 3.
Now the fifth permutation :
1 2 3 4 5 6
5 3 1 6 4 2 (1)
4 1 5 2 6 3 (2)
6 5 4 3 2 1 (3)
2 4 6 1 3 5 (4)
3 6 2 5 1 4 (5)
1 2 3 4 5 6 (6)
So the period of the fifth permutation is 6.
Finally, the sixth permutation :
1 2 3 4 5 6
6 5 4 3 2 1 (1)
1 2 3 4 5 6 (2)
So the period of the sixth permutation is 2.
Summarizing those periods gives :
1, 3, 6, 3, 6, 2
and we will show that this is the 'signature' of the group C6, i.e. the cyclic group of order 6. Its elements are here represented by the above permutations (of the elements of the group C7). We will give these permutations 'names', i.e. indicate them by letters :
1 2 3 4 5 6 = i
2 4 6 1 3 5 = a
3 6 2 5 1 4 = b
4 1 5 2 6 3 = c
5 3 1 6 4 2 = d
6 5 4 3 2 1 = f
These elements are indeed generated by an element of period 6, for example the element
5 3 1 6 4 2 which we can now call d (The other element is b).
The repeated application of d yielded -- as we saw above -- the following permutations :
1 2 3 4 5 6 = i
5 3 1 6 4 2 = d
4 1 5 2 6 3 = c
6 5 4 3 2 1 = f
2 4 6 1 3 5 = a
3 6 2 5 1 4 = b
So we have an element -- the permutation d -- which generates all the other elements, so these permutations must form a cyclic group of order six (C6).
So we can say that the automorphism group of the group C7 is the group C6, i.e. Aut(C7) = C6.
Let's analyze this automorphism group further. Its elements are the permutations i, a, b, c, d and f. These six permutations can be seen as the six permutations of the vertices of a regular hexagon under rotation of the latter, i.e. they can be seen as the direct symmetries of the Regular Hexagon, i.e. its rotational symmetries only. The next Figure depicts this hexagon and the appropriate labelling of its vertices in order for to express the permutations.
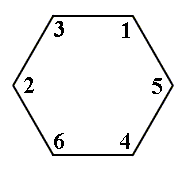
Figure 13. A regular hexagon with marked vertices. As such it represents the identity permutation 1 2 3 4 5 6 = i ( i.e. 1 remains 1, 2 remains 2, etc.) of the six (non-identity) elements of the group C7 , forming the group C6 ( = Aut(C7 ). This identity permutation is equivalent to a rotation of the hexagon (and thus its vertices) of 00 about the hexagon's mid-point.
The next Figure depicts an anticlockwise rotation of the vertices of this hexagon by 600 about the hexagon's mid-point. It turns out that this is conform the third permutation
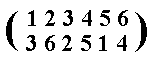
which we had called b above.
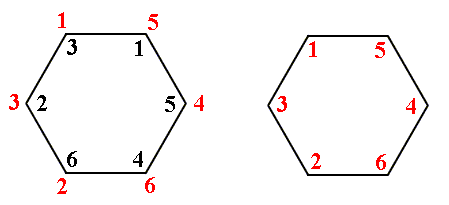
Figure 14. Anticlockwise rotation of the regular hexagon of Figure 13 by 600, according to permutation b.
We must read this rotation as follows :
1 goes to position 3.
2 goes to position 6.
3 goes to position 2.
4 goes to position 5.
5 goes to position 1.
6 goes to position 4.
The result of this rotation is depicted in the right image.
The permutation
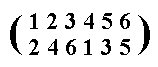
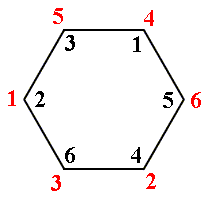
Figure 15. Anticlockwise rotation of the hexagon of Figure 13 by 1200, according to the permutation a. We must read this as follows :
1 goes to position 2
2 goes to position 4
3 goes to position 6
4 goes to position 1
5 goes to position 3
6 goes to position 5
The permutation
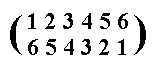
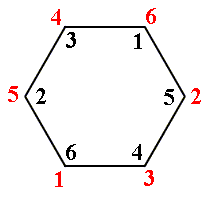
Figure 16. Anticlockwise rotation of the hexagon of Figure 13 by 1800, according to the permutation f. We must read this as follows :
1 goes to position 6
2 goes to position 5
3 goes to position 4
4 goes to position 3
5 goes to position 2
6 goes to position 1
The permutation
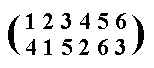
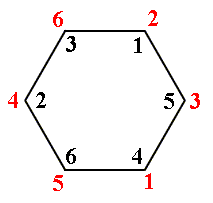
Figure 17. Anticlockwise rotation of the hexagon of Figure 13 by 2400, according to the permutation c. We must read this as follows :
1 goes to position 4
2 goes to position 1
3 goes to position 5
4 goes to position 2
5 goes to position 6
6 goes to position 3
Finally, the permutation
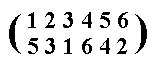
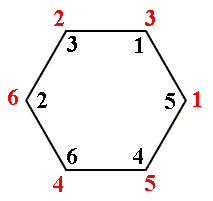
Figure 18. Anticlockwise rotation of the hexagon of Figure 13 by 3000, according to the permutation d. We must read this as follows :
1 goes to position 5
2 goes to position 3
3 goes to position 1
4 goes to position 6
5 goes to position 4
6 goes to position 2
Let us now write down our six permutations represented by their corresponding letters as given above, and indicate their periods (as found out above) :
i period 1, rotation of 00.
b period 6, rotation of 600.
a period 3, rotation of 1200.
f period 2, rotation of 1800.
c period 3, rotation of 2400.
d period 6, rotation of 3000.
In order to make a group table it is convenient to express the just mentioned elements i, b, a, f, c and d in terms of a generator. In our case element b, which is of period 6, can function as generator.
We will call element i element 1. And if we call the element b (600 rotation) r, then the element a (1200 rotation) will be r2, element f (1800) will be r3, etc. In this way we get the following renaming :
i -- 1
b -- r
a -- r2
f -- r3
c -- r4
d -- r5
We will now give the table for this automorphism group (C6), i.e. the table for Aut(C7) :
| 1 | r 1 | r2 | r3 | r4 | r5 | |
| 1 | 1 | r1 | r2 | r3 | r4 | r5 |
| r1 | r1 | r2 | r3 | r4 | r5 | 1 |
| r2 | r2 | r3 | r4 | r5 | 1 | r 1 |
| r3 | r3 | r4 | r5 | 1 | r 1 | r2 |
| r4 | r4 | r5 | 1 | r 1 | r2 | r3 |
| r5 | r5 | 1 | r 1 | r2 | r3 | r4 |
So this table depicts the automorphism group (C6) of the group C7, in terms of the generator r, which (generator) can be interpreted as a rotation of 600 of a regular hexagon about its center.
We will now explain what precisely is meant by "(while) preserving structure" when we say that a certain permutation of the elements of the group C7 preserves structure and thus is an automorphism of the group.
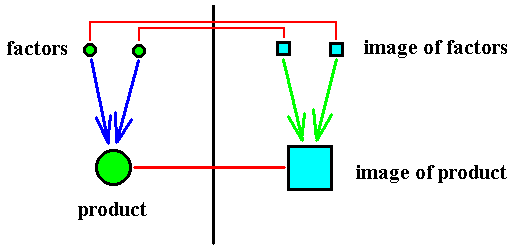
Figure 19. Diagram illustrating preservation of products.
The image of the product is identical to the product of the images of the factors, implying that to the original factors and product there not only correspond images, but also that those images themselves relate to each other as factors and product.
This alternative sequence of group elements -- being a particular permutation of the group elements -- then is an automorphism of the group. Generally, an automorphism is an isomorphism of the group with itself. An isomorphism between two groups G and H means that there can be found a one-to-one correspondence between the elements of G to those of H such that products are preserved. In the present case, the case of automorphism, it concerns a one-to-one correspondence between the elements of the group with the elements of that same group. Of course a group is isomorphic to itself : the identity correspondence between its elements naturally preserves products. But if we can find additional one-to-one correspondences, also from the elements of the group to those of the same group, which also preserve products, then we have found automorphisms of the group (the original identity one-to-one correspondence can then be seen as the identity automorphism).
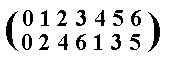
So according to this permutation each element of the group corresponds with a certain (other) element of that same group :
0 ==> 0
1 ==> 2
2 ==> 4
3 ==> 6
4 ==> 1
5 ==> 3
6 ==> 5
This is a function from the group to itself. Let us call this function PHI.
Then the image of (say) 2, under the function PHI, is 4. In short : PHI(2) = 4.
The group operation is addition modulo 7. And "2 + 4 = 6" we call a product of the elements 2 and 4. These latter two elements are then the factors. We could also write : 2.4 = 6, (2)(4) = 6, or 24 = 6, for that matter.
Let us now consider the product 3 + 5 = 1, in which 3, 5 and 1 are elements from the original sequence 0 1 2 3 4 5 6 of group elements. So here 1 is the product. Then we can say :
PHI(1) = 2 (image of the product)
PHI(3) = 6 (image of factor)
PHI(5) = 3 (image of factor), then
PHI(3) PHI(5) = 6 + 3 = 9 = 2 (because 9 mod 7 = 2) (product of the images of factors)
So the image of the product is equal to the product of the images, which means that that particular product is exactly reflected in the alternative sequence of elements according to the function PHI. And this in turn means that that particular product is preserved. When this holds for all possible products, we have an automorphism of the group.
Let us now prove that in any sequence of group elements, generated by one of the possible generators of the group C7, namely the generators 1, 2, 3, 4, 5 or 6, resulting in the above listed six permutations of group elements, products are preserved , and thus these sequences representing automorphisms of the group C7 :
The sequence of group elements generated by the element 1 can be written as
0, 1, 12, 13, 14, 15, 16
in which, generally, 1y, in the present case, means 1 + 1 + 1 + . . . , where this sequence contains y 1's. For example 14 is equal to 1 + 1 + 1 + 1 = 4 (Recall that the group operation is addition modulo 7 ).
Let's now choose a different generator out of the remaining possible generators 2, 3, 4, 5, 6 ( all of the same period, namely 7 ), namely the generator x. It will generate the sequence
0, x, x2, x3, x4, x5, x6
in which, for instance, x3 = x + x + x = 3x, and which is a new sequence of group elements of the group C7 , i.e. a permutation of those group elements. The correspondence of the elements of the original sequence with those of the new sequence can be indicated by the function THETA, and is the following one-to-one correspondence between the elements of our group :
0 ==> 0
1 ==> x
12 ==> x2
13 ==> x3
14 ==> x4
15 ==> x5
16 ==> x6
A product of elements of the original sequence could be, for instance, 1214 = 16 (which means 2 + 4 = 6 ), or, generally, 1a1b = a1 + b1 = a + b. And a + b is certainly an element of the group, let us call it c, which is equal to 1c. So the product of 1a and 1b is equal to 1c, or, equivalently, a + b = c. Now we can say :
1a1b = 1c (product)
THETA(1c ) = xc = cx ( image of the product )
THETA(1a ) = xa ( image of factor )
THETA(1b ) = xb ( image of factor ), then
THETA(1a ) THETA(1b ) = xaxb = ax + bx = (a + b)x = cx ( = xc ) (product of images of factors).
So, now we have proved, generally for the group C7 , that the image, under the general function THETA, of any product is equal to the product of the images of the factors, which means that for all six permutations of the group elements (of the group C7 ), resulting from an alternative choice of generator, products are preserved, so that these six permutations (including the identity permutation) are indeed as many automorphisms of the group C7 .
Because there are six equally valid and independent generators of the group C7 , we get six automorphisms.
Generally we can say that a cyclic group Cp , where p is prime, has p-1 equally valid generators, and thus it has p-1 automorphisms, so the order of the automorphism group (i.e. the group of all automorphisms) of Cp is p-1.
The set of automorphisms is a set of permutations of group elements, and these particular permutations preserve products. That this set is itself a group is readily appreciated :
In every one such permutation a generator is replaced by another (one generator by one other, in cyclic groups), and the remaining elements are then generated by this new generator. So a general element xa becomes ya, where the generator x is substituted by the generator y. When we now apply another permutation (again one that substitutes a generator) on the result, say a replacement of the generator y by the generator z, then the general element becomes za. So the successive application of two permutations (each replacing a generator) effects xa ==> za, and this involves yet another replacement of generators, namely x being replaced by z, resulting in yet another automorphism of the group Cp . So the set of automorphisms is closed under the operation of successive application.
The set also contains an identity element, namely the identity permutation, i.e. the identity automorphism.
Further, the inverse of every automorphism is itself an automorphism : Suppose we have the automorphism in which the generator x is replaced by y. Then the inverse consists of a replacement of the generator y by the generator x.
Finally, associativity is guaranteed by the fact that the successive application of permutations is always associative :
For three permutations named S, T, U, we have (ST)U = S(TU), because for a general element s of S, a certain element t of T, and a certain element u of U, we have :
(s ==> t) ==> u = s ==> (t == > u)
because when we first replace s by t, and then t by u, we in fact have replaced s by u. And when, on the other hand, we replace s by the (result of the) replacement of t by u, we also have in fact replaced s by u.
So the set of automorphisms of a group is indeed itself a group.
We now will demonstrate that the automorphism group of a cyclic group of prime order is also a cyclic group.
In order to do that, let's first again consider the group C7 . Because the group is of prime order, every non-identity element is a potential generator, i.e. every such element can generate all other elements of the group. So the generator x, where x7 = the identity element, generates the following sequence of non-identity elements : x, x2, x3, x4, x5, x6. The generator x2 generates the sequence x2, x4, x6, x, x3, x5. And so on.
In this way six sequences of all the non-identity elements of the group are generated :
| x | x2 | x3 | x4 | x5 | x6 |
| x2 | x4 | x6 | x | x3 | x5 |
| x3 | x6 | x2 | x5 | x | x4 |
| x4 | x | x5 | x2 | x6 | x3 |
| x5 | x3 | x | x6 | x4 | x2 |
| x6 | x5 | x4 | x3 | x2 | x |
These six sequences are six permutations (of six objects), and it is obvious that we can represent them just as well by the indices ('powers') :
| 1 | 2 | 3 | 4 | 5 | 6 | cycle | period |
| 2 | 4 | 6 | 1 | 3 | 5 | (1 2 4) (3 6 5) | 3 |
| 3 | 6 | 2 | 5 | 1 | 4 | (1 3 2 6 4 5) | 6 |
| 4 | 1 | 5 | 2 | 6 | 3 | (1 4 2) (3 5 6) | 3 |
| 5 | 3 | 1 | 6 | 4 | 2 | (1 5 4 6 2 3) | 6 |
| 6 | 5 | 4 | 3 | 2 | 1 | (1 6) (2 5) (3 4) | 2 |
So here we have again six permutations, their inherent cycles and periods. Together they (as do the equivalent permutations above) form the group C6 , isomorphic to the automorphism group of the group C7. That this automorphism group is indeed cyclic, is appreciated
by realizing that -- as has been said -- in a cyclic group of prime order every non-identity element can be a generator of the whole group. And because of this, looking to the list of permutations directly above -- permutations that came to be created by the generation of the group elements by the successive generators -- we see that the first row (being the identity permutation) of that list is just the natural number sequence 1 2 3 4 5 6. In the second row all numbers have been replaced by another number (but always taken from the set {1, 2, 3, 4, 5, 6}). And in all the other rows this is also the case. This is because of the fact that each row is generated by another generator. Every permutation from the above list replaces every symbol of the initial sequence by another symbol, and this means that all the listed permutations can be interpreted as rotations of some two-dimensional figure, and this in turn implies that the group is cyclic.
All of this can easily be generalized to all cyclic groups of prime order :
Each and every non-identity element of such a group can generate all elements of such a group. The resulting sequences of group elements are each produced by a different generator. The first is generated by x, the second by x2, the third is generated by x3, and so on. Sequences produced by such generators will not show overlaps, and thus are permutations that can potentially represent rotations of some figure. And because all sequences must represent rotations, the group they form must be cyclic.
In the case of the automorphism group of the group C7 , we can show -- with the aid of the representation of them by cycles (as indicated in the above list) -- that, and in what way, the five non-identity permutations (being elements of Aut(C7)) can represent rotations. See next Figure.
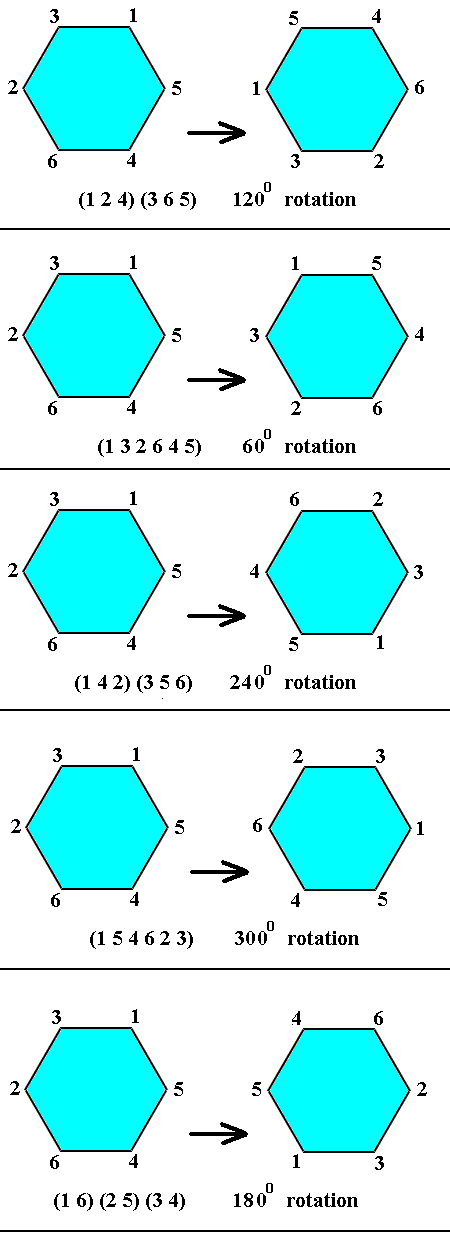
Figure 20. The five non-identity autmorphisms of the group C7 interpreted geometrically as (anticlockwise) rotations.
In Part XVII, Part XVIII and Part XIX, we will deal more thoroughly with the concept of automorphism.
We now summarize some results concerning cyclic groups :
In a cyclic group of prime order p, every element (except the identity) is of period p. (BUDDEN, p. 170)
There exists only one type of group of prime order, namely the cyclic group. (BUDDEN, p. 170)
Aut(Cp) is isomorphic to Cp-1 when p is prime, i.e. the automorphism group of a cyclic group of prime order has an order that is one lower than that of the original group. (BUDDEN, p. 423)
In the next document we will study cyclic groups of composite order.
e-mail :

To continue click HERE for further group theoretical preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals