e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Sequel to Direct Product Groups
Groups of order eight
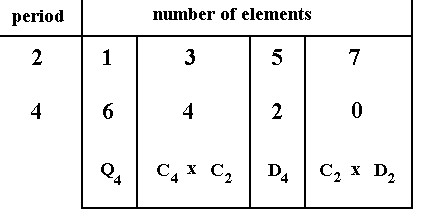
The groups C8 (cyclic group of order 8), D4 (dihedral group of order 8), and Q4 (quaternion group of order 8) all are of order 8.
By means of product groups we can form still two more of order 8, namely C4 x C2, and D2 x C2 or, equivalently, C2 x C2 x C2. These are both Abelian groups, so that there are three Abelian groups of order 8 (The third one is C8). These, with the two non-Abelian groups D4 and Q4 exhaust all the possible groups of order 8. The truth of this statement may be easily verified in the folowing way. If a group of order 8 has an element of period 8, then it is C8. If not, then by Lagrange's theorem, it may have elements of period 2 and 4 only (these elements generate subgroups).
But the number of elements of period 4 must be even, because they occur in inverse pairs (for example a rotation r = 900 anticlockwise, and r-1 = 2700 anticlockwise). The maximal number of elements of a period other than that of the identity element is of course 7 (for groups of order 8). So the number of elements of period 8 is 0, 2, 4, or 6. The number of elements of period 2 must be odd, because of the following : If the number of reflections is even (as in the regular 2n-gons, i.e. polygons with an even number of sides, f.i. a regular hexagon), then there exists necessarily a rotation of 1800, and so the number of elements with period 2 is odd. If the number of reflections is odd, as in all (2n+1)-gons, f.i. the regular pentagon, then there is no rotation of 1800 present, and thus is the number of elements of period 2 again odd. All this means that in groups of oeder 8 the number of elements of period 2 is 1, 3, 5 or 7.
So we have the following possibilities for groups of order 8 :

The number of elements of period 2 plus the number of elements of period 4 must be 7 in all cases (The 8th element is the identity).
This shows briefly that there are only five possible groups of order 8.
We often identified groups by considering the order of the group and the distribution of the periods over its elements. Well, a self-evident truth is the following :
If two finite groups are isomorphic, then not only they have the same number of elements, but also they each have the same number of elements of any specified period (BUDDEN, 1978, p. 143).
The converse, which might be thought to be true is, in fact true only of order less than 27, but not true of order 16 (BUDDEN, 1978, p. 143).
It is this converse we had often used : same number of elements and same period distribution : groups are isomorphic.
If two groups disagree in the matter of numbers of elements of a given period, then they are certainly not isomorphic.
The above demonstration that there are only five groups of period 8, rests on the theorem just given.
Of the five groups of order eight, C8, Q4, C4 x C2, D4, and C2 x C2 x C2 ( = D2 x C2), only the last three have crystalligraphic realizations. That of the dihedral group D4 has already been considered earlier.
The product group C4 x C2 has its crystallographic realization in crystals of the Tetragonal-bipyramidal Class (4/m) of the Tetragonal Crystal System. The group is also called C4i. The promorph or stereometric basic form (representing the (4/m) symmetry fully geometrically) of all the single non-twinned crystals of this Class is the Tetragonal Gyroid Bipyramid (See next Figure), and as promorph it belongs to the Isosigmostaura quadrimera (Stauraxonia homopola) of the Promorphological System of Basic Forms.
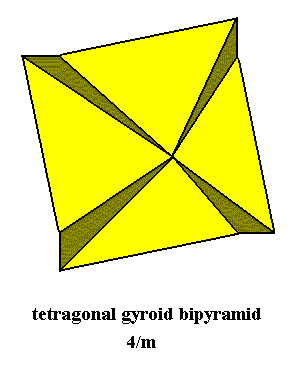
Figure 1. Oblique top view of the Tetragonal (4-fold) Gyroid Bipyramid, Stereometric Basic Form of all the (single) crystals of the Tetragonal-bipyramidal Class of the Tetragonal Crystal System. Because of the view direction the lower pyramid is not visible.
We must still demonstrate that the group describing the symmetry, 4/m, is indeed the product group C4 x C2. We begin with describing the symmetry transformations inherent in the above depicted Tetragonal Gyroid Bipyramid. A side view of such a pyramid looks as follows :
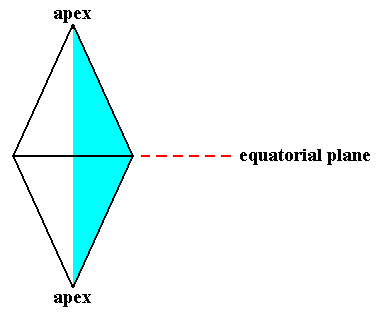
Figure 2. Side view of (a representative of) the Tetragonal Gyroid Bipyramid, expressing the 4/m symmetry. The coloration indicates the absence of vertical mirror planes, which implies that there are no 2-fold rotation axes perpendicular to the bipyramid's main axis.
The symmetry transformations of this gyroid pyramid are :
And this complies with the period distribution in the group C4 x C2.
Having demonstrated the fact that the 4/m symmetry can be fully described by the direct product group C4 x C2, it is nevertheless instructive to work it all out comprenensively.
So let us first give the group table of C4, in which we interpret the element r as a rotation of 900, r2 as a rotation of 1800, and r3 as a rotation of 2700 :
| 1 | r | r2 | r3 | period | |
| 1 | 1 | r | r2 | r3 | 1 |
| r | r | r2 | r3 | 1 | 4 |
| r2 | r2 | r3 | 1 | r | 2 |
| r3 | r3 | 1 | r | r2 | 4 |
Table 10.1
So we have given here the group C4 as {1, r, r2, r3}.
| 1 | m | |
| 1 | 1 | m |
| m | m | 1 |
So we have given here the group C2 as {1, m}.
In order to determine the product of C4 and C2, we are going to form the cartesian product of the elements, i.e. we are forming all possible ordered pairs of elements, pairs of which the second member is an element of C4, while the first member is an element of C2 (And this is nothing else than following the definition of product groups) (Recall that the direct product of two groups is commutative, i.e. A x B is isomorphic with B x A) :
| 1 | r | r2 | r3 | |
| 1 | (1, 1) | (1, r) | (1, r2) | (1, r3) |
| m | (m, 1) | (m, r) | (m, r2) | (m, r3) |
Next we will investigate whether these pairs, when combined according to the definition of direct product groups, behave as the symmetry transformations of the above depicted Tetragonal Gyroid Bipyramid, which has 4/m symmetry. To accomplish this we must determine all possible products of these pairs, for instance
| x | (1, 1) | (1, r) | (1, r2) | (1, r3) | (m, 1) | (m, r) | (m, r2) | (m, r3) |
| (1, 1) | (1, 1) | (1, r) | (1, r2) | (1, r3) | (m, 1) | (m, r) | (m, r2) | (m, r3) |
| (1, r) | (1, r) | (1, r2) | (1, r3) | (1, 1) | (m, r) | (m, r2) | (m, r3) | (m, 1) |
| (1, r2) | (1, r2) | (1, r3) | (1, 1) | (1, r) | (m, r2) | (m, r3) | (m, 1) | (m, r) |
| (1, r3) | (1, r3) | (1, 1) | (1, r) | (1, r2) | (m, r3) | (m, 1) | (m, r) | (m, r2) |
| (m, 1) | (m, 1) | (m, r) | (m, r2) | (m, r3) | (1, 1) | (1, r) | (1, r2) | (1, r3) |
| (m, r) | (m, r) | (m, r2) | (m, r3) | (m, 1) | (1, r) | (1, r2) | (1, r3) | (1, 1) |
| (m, r2) | (m, r2) | (m, r3) | (m, 1) | (m, r) | (1, r2) | (1, r3) | (1, 1) | (1, r) |
| (m, r3) | (m, r3) | (m, 1) | (m, r) | (m, r2) | (1, r3) | (1, 1) | (1, r) | (1, r2) |
Table 10.3
Now we determine the periods of the elements of the above table :
Element (1, 1) evidently is the identity element. Its period is 1.
(1, r)4 = (1, r) (1, r) (1, r) (1, r) = (1, r2) (1, r2) = (1, r4) = (1, 1).
So the period of (1, r) is 4.
(1, r2)2 = (1, r2) (1, r2) = (1, r4) = (1, 1).
So the period of (1, r2) is 2.
(1, r3)4 = (1, r3) (1, r3) (1, r3) (1, r3) = (1, r2) (1, r2) = (1, r4) = (1, 1).
So the period of (1, r3) is 4.
(m, 1)2 = (m, 1) (m, 1) = (m2, 1) = (1, 1).
So the period of (m, 1) is 2.
(m, r)4 = (m, r) (m, r) (m, r) (m, r) = (1, r2) (1, r2) = (1, 1).
So the period of (m, r) is 4.
(m, r2)2 = (m, r2) (m, r2) = (1, 1).
So the period of (m, r2) is 2.
(m, r3)4 = (m, r3) (m, r3) (m, r3) (m, r3) = (1, r2) (1, r2) = (1, 1).
So the period of (m, r3) is 4.
Thus the period distribution of the elements of the above table (Table 10.3) is the following :
1, 4, 2, 4, 2, 4, 2, 4
Now we can legitimately interpret the elements of (Table 10.3) as the symmetry transformations of the Tetragonal Gyroid Bipyramid ( = promorph of the Crystal Class 4/m ), and rename them accordingly :
(1, 1) ---- Identity ---- 1.
(1, r) ---- rotation of 900 ---- r.
(1, r2) ---- rotation of 1800 ---- r2.
(1, r3) ---- rotation of 2700 ---- r3.
(m, 1) ---- reflection in equatorial plane ---- m.
(m, r) ---- rotation of 900 followed by a reflection in the equatorial plane (These two constituent transformations in reverse order makes no differrence) ---- mr.
(m, r2) ---- rotation of 1800 followed by a reflection in the equatorial plane ---- mr2.
(m, r3) ---- rotation of 2700 followed by a reflection in the equatorial plane ---- mr3.
We can now set up the group table for the product group C4 x C2 in terms of the two (independent) generators r and m :
| 1 | r | r2 | r3 | m | mr | mr2 | mr3 | period | |
| 1 | 1 | r | r2 | r3 | m | mr | mr2 | mr3 | 1 |
| r | r | r2 | r3 | 1 | mr | mr2 | mr3 | m | 4 |
| r2 | r2 | r3 | 1 | r | mr2 | mr3 | m | mr | 2 |
| r3 | r3 | 1 | r | r2 | mr3 | m | mr | mr2 | 4 |
| m | m | mr | mr2 | mr3 | 1 | r | r2 | r3 | 2 |
| mr | mr | mr2 | mr3 | m | r | r2 | r3 | 1 | 4 |
| mr2 | mr2 | mr3 | m | mr | r2 | r3 | 1 | r | 2 |
| mr3 | mr3 | m | mr | mr2 | r3 | 1 | r | r2 | 4 |
Table 10.4
This concludes our discussion of the direct product group C4 x C2.
The group C2 x C2 x C2
In the previous document we had shown that C2 x C2 is isomorphic with D2. So indeed C2 x C2 x C2 can be written as D2 x C2.
Now D2 contains elements of period 1, 2, 2, 2 {1, a, b, ab}, and C2 contains elements of period 1, 2 {1, c}. We will give the group tables of both groups :
| 1 | a | b | ab | |
| 1 | 1 | a | b | ab |
| a | a | 1 | ab | b |
| b | b | ab | 1 | a |
| ab | ab | b | a | 1 |
| 1 | c | |
| 1 | 1 | c |
| c | c | 1 |
Next we determine the periods of the elements of the product group D2 x C2, on the basis of the Lowest Common Multiple of the combined periods of the two constituent groups (D2 and C2) :
| L.C.M. | 1 | 2 | 2 | 2 |
| 1 | 1 | 2 | 2 | 2 |
| 2 | 2 | 2 | 2 | 2 |
This table of the periods shows that C2 x C2 x C2 ( = D2 x C2) contains the identity and seven elements all of period 2. We can form ordered pairs as follows :
| 1 | c | |
| 1 | (1, 1) | (1, c) |
| a | (a, 1) | (a, c) |
| b | (b, 1) | (b, c) |
| ab | (ab, 1) | (ab, c) |
The next group table shows how these pairs behave when they are combined ('multiplied') according to the definition of product groups :
| (1, 1) | (a, 1) | (b, 1) | (ab, 1) | (1, c) | (a, c) | (b, c) | (ab, c) | |
| (1, 1) | (1, 1) | (a, 1) | (b, 1) | (ab, 1) | (1, c) | (a, c) | (b, c) | (ab, c) |
| (a, 1) | (a, 1) | (1, 1) | (ab, 1) | (b, 1) | (a, c) | (1, c) | (ab, c) | (b, c) |
| (b, 1) | (b, 1) | (ab, 1) | (1, 1) | (a, 1) | (b, c) | (ab, c) | (1, c) | (a, c) |
| (ab, 1) | (ab, 1) | (b, 1) | (a, 1) | (1, 1) | (ab, c) | (b, c) | (a, c) | (1, c) |
| (1, c) | (1, c) | (a, c) | (b, c) | (ab, c) | (1, 1) | (a, 1) | (b, 1) | (ab, 1) |
| (a, c) | (a, c) | (1, c) | (ab, c) | (b, c) | (a, 1) | (1, 1) | (ab, 1) | (b, 1) |
| (b, c) | (b, c) | (ab, c) | (1, c) | (a, c) | (b, 1) | (ab, 1) | (1, 1) | (a, 1) |
| (ab, c) | (ab, c) | (b, c) | (a, c) | (1, c) | (ab, 1) | (b, 1) | (a, 1) | (1, 1) |
Table 10.7
Now we can rename the elements as follows :
1 = (1, 1)
a = (a, 1)
b = (b, 1)
c = (1, c)
d = (b, c)
f = (a, c)
g = (ab, 1)
h = (ab, c)
We see that
bc = (b, 1) (1, c) = (b, c) = d.
cb = (1, c) (b, 1) = (b, c) = d.
So bc = cb = d.
ac = (a, 1) (1, c) = (a, c) = f.
ca = (1, c) (a, 1) = (a, c) = f.
So ac = ca = f.
ab = (a, 1) (b, 1) = (ab, 1) = g.
ba = (b, 1) (a, 1) = (ba, 1) = (ab, 1) = g.
So ab = ba = g.
(The fact that ab = ba is evident from the table of the group D2 (See Table 10.5), and D2 is a subgroup of D2 x C2, which is evident from Table 10.7).
abc = (a, 1) (b, 1) (1, c) = (ab, 1) (1, c) = (ab, c) = h.
The group C2 x C2 x C2 needs three (independent) generators. We can choose them from the seven non-identity elements of the group. The above relations show that if we choose as generators the elements a, b and c, then f, g, and h are determined. And if we now set up the group table for the group C2 x C2 x C2 (= D2 x C2) in terms of the generators a, b, and c, we should use the following renamings of the ordered pairs :
1 = (1, 1) = 1
a = (a, 1) = a
b = (b, 1) = b
c = (1, c) = c
d = (b, c) = bc
f = (a, c) = ac
g = (ab, 1) = ab
h = (ab, c) = abc
On the basis of this we can reconstruct Table 10.7 as follows :
| 1 | a | b | ab | c | ac | bc | abc | |
| 1 | 1 | a | b | ab | c | ac | bc | abc |
| a | a | 1 | ab | b | ac | c | abc | bc |
| b | b | ab | 1 | a | bc | abc | c | ac |
| ab | ab | b | a | 1 | abc | bc | ac | c |
| c | c | ac | bc | abc | 1 | a | b | ab |
| ac | ac | c | abc | bc | a | 1 | ab | b |
| bc | bc | abc | c | ac | b | ab | 1 | a |
| abc | abc | bc | ac | c | ab | b | a | 1 |
Table 10.8
Table of D2 x C2 ( = C2 x C2 x C2). The D2 subgroup {1, a, b, ab} stands out clearly.
Now since the group is the direct product of three groups, C2 x C2 x C2, we could just as well obtain it as a set of ordered triples, each component taken from a group C2, for instance ((+1, -1}, x). This version of C2 has the following group table :
| x | 1 | -1 |
| 1 | 1 | -1 |
| -1 | -1 | 1 |
In this case the elements would be :
(1, 1, 1)
(-1, 1, 1)
(1, -1, 1)
(1, 1, -1)
(1, -1, -1)
(-1, 1, -1)
(-1, -1, 1)
(-1, -1, -1)
From this the elements might also be represented by 3 x 3 matrices, such as :
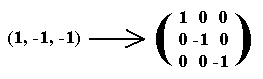
The importance of the matrix representation is that each of these matrices may be interpreted as a transformation matrix, and these transformations (of three-dimensional space) link up with our realization (below) of the group in terms of the symmetries of the Cuboid or Rhombic Bipyramid. Later, when we will consider in a systematic way the symmetries of crystals in terms of Group Theory, we will derive all these transformation matrices expressing the symmetry transformations that occur in crystals.
The group C2 x C2 x C2 is realized in crystals of the Rhombic-bipyramidal Class (2/m 2/m 2/m) of the Orthorhombic Crystal System. This 2/m 2/m 2/m symmetry can be geometrically expressed in several ways, namely as the Cuboid ( = Rhombic Prism) or as the Rhombic Bipyramid. The latter is chosen as representing the promorph or stereometric basic form of all the single non-twinned crystals of the Class 2/m 2/m 2/m. This promorph belongs to the Allostaura octopleura (Stauraxonia homopola) of the Promorphological System of Basic Forms. See next Figure.
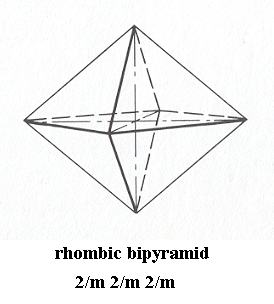
Figure 1. A Rhombic Bipyramid or Rhombic Octahedron, the Stereometric Basic Form of the crystals of the Rhombic-bipyramidal Class of the Orthorhombic Crystal System.
The equatorial plane is a rhombus.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
The symmetries of this bipyramid can be best illustrated by the Cuboid (which has the same symmetries as the rhombic bipyramid). There are three mirror planes perpendicular to each other. And normal (i.e. perpendicular) to each mirror plane there is a 2-fold rotation axis (All this is expressed by the symbol 2/m 2/m 2/m). See next Figure.
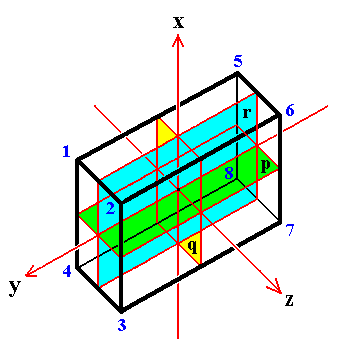
Figure 2. The Cuboid or Rhombic Prism.
Its three mirror planes are indicated : p (green), q (yellow), and r (blue).
Three 2-fold rotation axes are indicated : x, y, and z.
The vertices are numbered 1, 2, 3, 4, 5, 6, 7, and 8.
We will now work out the symmetry transformations of the Cuboid (and with it of the Rhombic Bipyramid), by means of consulting the permutations of its verices. The group C2 x C2 (which is isomorphic with D2) describes the direct symmetries of the Cuboid. Now we'll include the enantiomorphs as well (i.e. we add the reflectional symmetries). In addition to the reflections in the planes p, q and r, there is inversion which we call i. This symmetry transformation interchanges the opposite vertices (17)(28)(35)(46) (See Figure 2). So in total we have eight summetry transformations :
The symmetry transformation p is a reflection in the plane p. It can be represented by the permutation
which means that (See Figure 2)
vertex 1 goes to where vertex 4 originally was,
vertex 2 goes to where vertex 3 originally was,
vertex 3 goes to where vertex 2 originally was,
vertex 4 goes to where vertex 1 originally was,
vertex 5 goes to where vertex 8 originally was,
vertex 6 goes to where vertex 7 originally was,
vertex 7 goes to where vertex 6 originally was,
vertex 8 goes to where vertex 5 originally was.
This permutation 43218765 can also be written as cycles :
(14)(23)(58)(67)
And this element is clearly of period 2.
Let's now write down all the permutations of the vertices of the Cuboid (See Figure 2) :
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| r | 2 | 1 | 4 | 3 | 6 | 5 | 8 | 7 |
| y | 3 | 4 | 1 | 2 | 7 | 8 | 5 | 6 |
| p | 4 | 3 | 2 | 1 | 8 | 7 | 6 | 5 |
| q | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 |
| x | 6 | 5 | 8 | 7 | 2 | 1 | 4 | 3 |
| i | 7 | 8 | 5 | 6 | 3 | 4 | 1 | 2 |
| z | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
These permutations combine in the following way, forming the group C2 x C2 x C2 :
| 1 | r | y | p | q | x | i | z | |
| 1 | 1 | r | y | p | q | x | i | z |
| r | r | 1 | p | y | x | q | z | i |
| y | y | p | 1 | r | i | z | q | x |
| p | p | y | r | 1 | z | i | x | q |
| q | q | x | i | z | 1 | r | y | p |
| x | x | q | z | i | r | 1 | p | y |
| i | i | z | q | x | y | p | 1 | r |
| z | z | i | x | q | p | y | r | 1 |
Table 10.9
Table of D2 x C2 ( = C2 x C2 x C2). The D2 subgroup {1, r, y, p} stands out clearly.
It is instructive to compare the above group table (Table 10.9) with the list of permutations given earlier (These permutations are the elements of the group table). We then see that each of these permutations coresponds with a row of the group table, i.e. that row is itself that same permutation. For example the row headed by p in the group table is p y r 1 z i x q, and this can be interpreted as a reshuffling of the sequence headed by 1 in the group table, namely 1 r y p q x i z. So the sequence headed by p in the group table is itself the following permutation of the eight symbols, 1, r, y, p, q, x, i and z :
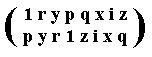
So in this permutation
the first symbol becomes the fourth symbol,
the second symbol becomes the third symbol,
the third symbol becomes the second symbol,
the fourth symbol becomes the first symbol,
the fifth symbol becomes the eighth symbol,
the sixth symbol becomes the seventh symbol,
the seventh symbol becomes the sixth symbol,
the eighth symbol becomes the fifth symbol.
This corresponds to the permutatation headed by p = 4 3 2 1 8 7 6 5 in the above list of permutations. The same can be found out with respect to all the rows in the group table. Indeed we see that the structures of the list of permutations is the same as that of the corresponding group table.
So even without interpreting the individual group elements 1, r, y, p, q, x, i, z as permutations, the rows in the group table are themselves permutations of the group elements. And this indicates clearly Cayley's Theorem, saying that any finite group of order n is isomorphic to a subgroup of the group Sn of permutations of n objects. So in the present case our group C2 xC2 x C2 is a subgroup of S8 (The group of all permutations of 8 objects).
Further we recognize in the group table, as given in Table 10.9, the normal subgroup {1, r, y, p}, which has the structure of D2.
This group table is isomorphic to that of Table 10.8, and the isomorphism is immediately evident, because the structure of both tables is identical. Both have the subgroup D2 in the top left-hand corner. But of course the group table of Table 10.8 can appear in a reshuffled form like the following version :
| 1 | a | b | c | bc | ac | ab | abc | |
| 1 | 1 | a | b | c | bc | ac | ab | abc |
| a | a | 1 | ab | ac | abc | c | b | bc |
| b | b | ab | 1 | bc | c | abc | a | ac |
| c | c | ac | bc | 1 | b | a | abc | ab |
| bc | bc | abc | c | b | 1 | ab | ac | a |
| ac | ac | c | abc | a | ab | 1 | bc | b |
| ab | ab | b | a | abc | ac | bc | 1 | c |
| abc | abc | bc | ac | ab | a | b | c | 1 |
Table of D2 x C2 ( = C2 x C2 x C2), in terms of the generators a, b, c, where those three generators are placed next to each other. The consequence of this reshuffling of the group elements is that the D2 subgroup {1, a, b, ac} does not stand out clearly (but is of course nevertheless present).
And in this case the isomorphism is not immediately obvious because in the latter version the elements are arranged in the order 1, a, b, c, bc, ac, ab, abc, where a, b, and c are generators, whereas in the former versions, we had the subgroup D2, {1, a, b, ab}, and {1, r, y, p} respectively in the top left-hand corner of the group table, with p = ry (So in fact we have 1, r, y, ry, as elements of the subgroup which we recognize as D2, like we saw it as {1, a, b, ab}). The subgroup D2 {1, a, b, ab} is of course present in the version depicted in Table 10.10, but it doesn't stand out. In Table 10.9 p, q, and r would serve as generators, because we can express all elements in terms of p, q, r :
A possible isomorphism that can be set up between the elements of the group table of Table 10.10 and those of Table 10.9 is the following :
1 --- 1
a --- x
b --- y
ab --- z
c --- p
ac --- i
bc --- r
abc --- q
The number of possible reshufflings of the eight elements of our group are determined as follows :
For putting in place one of the sequence of the eight elements we can choose out of 8 elements.
Then for putting in place two (after having put one element in place one) of the sequence of the eight elements we can choose out of 7 elements.
Then for putting in place three (after having put one element in place one and one element in place two) of the sequence of the eight elements we can choose out of 6 elements.
Then for putting in place four of the sequence of the eight elements we can choose out of the 5 elements left.
Then for putting in place five of the sequence of the eight elements we can choose out of the 4 elements left.
Then for putting in place six of the sequence of the eight elements we can choose out of the 3 elements left.
Then for putting in place seven of the sequence of the eight elements we can choose out of the 2 elements left.
Then, finally, for putting in place eight of the sequence of the eight elements we can choose out of the 1 element left.
This means that we have 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 8! (pronounce "eight faculty"), and this is equal to 40320.
When we now want to establish the number of possible isomorphisms between, say, the group table of Table 10.10 and that of Table 10.9, i.e. the number of possible 1,1 correspondences between the elements of the one table with those of the other, we will encounter certain restrictions. Firstly the identity element of the first table must correspond to the identity of the other table, because the identity is always unique in a group (it is the only element with period 1). So we have only seven elements left to choose from. But there is a further restriction : Having corresponded three elements of the first table with three elements of the other table, the remaining correspondences are then fixed. For example if we have made the three correspondences
x --- a
y --- b
p --- c, then
q is fixed, because xyp = q, and this means that q = abc,
i is fixed, because xp = i, and this means that i = ac,
r is fixed, because yp = r, and this means that r = bc,
z is fixed, because yx = z, and this means that z = ba (Recall that our present group is Abelian).
So when we (after having let to correspond the respective identity elements) take the second element of the first table, then we can choose from seven elements of the second table one element to correspond with that second element.
And when we then take the third element of the first table we can choose out of six elements of the second table one element to correspond to it.
And when we then take the fourth element of the first table we can choose out of five elements of the second table one element to correspond with it.
So, apart from the identities, we have now made three correspondences. The other correspondences are now fixed. So in all we have 7 x 6 x 5 = 210 possible isomorphisms between the tables mentioned.
If we, alternatively, let the elements a, b, c correspond with the elements r, y, p, i.e. with elements within the subgroup (1, r, y, p}, then also the other correspondences are fixed, because :
q = abc, x = rq = aabc = bc, i = ac, z = pq = cabc = ab.
The seven elements, i.e. all the elements apart from the identity, are completely group theoretically equivalent. There are three generators necessary, and it doesn't matter which three elements we take to be the generators of the group.
Automorphisms of the group C2 x C2 x C2.
With this group having seven elements all of period 2, it is evident that there is going to be a large group of automorphisms. But, though we may reshuffle those seven elements in 7! ( = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040) ways, there will certainly not be as many automorphisms as all that. Indeed, in the foregoing we saw that one's 'freedom of movement' is surprisingly restricted.
When we, in reshuffling the group elements of our group, as it is, say, depicted in Table 10.9, want the table structure to be fully preserved, which is equivalent to establising the possible automorphisms of the group, then the only interchanges we can make is between generator triples. So in seeking automorphisms, we are certainly free to replace any pair of elements by any other as generators (i.e. two of three generators). This is possible in 7 x 6 = 42 ways (See further down for an example) :
The first generator which we take to be replaced can be chosen from the seven non-identity elements of the group. For the second generator there are still 6 elements to choose from. When we now want to choose a third generator to be replaced, we cannot of course take one of the already chosen two generators. But we, moreover, cannot select an element (to represent the third generator) which is the product of the two generators already chosen, because the generators must be independent. So from the seven elements there are only 7 - 2 - 1 = 4 to choose from, and that makes 7 x 6 x 4 = 168 possibilities, which means that our group C2 x C2 x C2 has 168 automorphisms, and they form a group of order 168. This automorphism group is, in fact, a particular interesting group, having a peculiar rare property of being what is called 'simple'. This property is shared by the group A5 ( which is the Icosahedral Group) of order 60, and by no other groups of order less than 168 (Apart from the cyclic groups of prime order which have no subgroups at all). It means that the group has no normal subgroups.
The icosahedral group A5 , cannot be realized in crystals. The full group (i.e. including the enantiomorphs) A5 x C2 is realized in the promorphological categories of the Icosaedra regularia and the Dodecaedra regularia (See at the Polyaxonia rhythmica, in the Promorphological System of Basic Forms).
Above we explained generally why there are 42 ways to interchange a pair of elements of the group C2 x C2 x C2 with another pair present in that group. Now we will give an example.
Suppose our seven elements (i.e. all non-identity elements of our group C2 x C2 x C2 ) were named 1, 2, 3, 4, 5, 6, and 7. And suppose further that we want to know how many, and what pairs can replace the pair 1 2, i.e. can be interchanged with the pair 1 2. Well, together with the identical replacement, i.e. that the pair 1 2 is replaced by the pair 1 2, there are indeed 42 such pairs :
| 1 2 | 2 1 | 3 1 | 4 1 | 5 1 | 6 1 | 7 1 |
| 1 3 | 2 3 | 3 2 | 4 2 | 5 2 | 6 2 | 7 2 |
| 1 4 | 2 4 | 3 4 | 4 3 | 5 3 | 6 3 | 7 3 |
| 1 5 | 2 5 | 3 5 | 4 5 | 5 4 | 6 4 | 7 4 |
| 1 6 | 2 6 | 3 6 | 4 6 | 5 6 | 6 5 | 7 5 |
| 1 7 | 2 7 | 3 7 | 4 7 | 5 7 | 6 7 | 7 6 |
In spite of the fact that all seven of the elements of period 2 are of 'democratically equal status' in the group, it would appear from the realization as the group of symmetries of the Cuboid that this is not so. For p, q and r (See Figure 2) appear to be in a class of their own, namely that of reflections, x, y and z are half-turns, whereas i is an odd man out being, apparently, a different sort of transformation altogether. To see that this is an illusion (from a group theoretic standpoint), consider the group as that of the permutations of the vertices, as listed above (Above Table 10.9). When we now renumber the vertices we will see that the permutations now represent altogether different kinds of symmetries. Therefore it is an illusion, dependent on the particular method of numbering the vertices, that the elements of the group seem to differ from each other in character. But of course, geometrically they do differ, and divide among plane reflections, rotations and a point inversion ( = central inversion).
In the next document we'll continue and finish the study of the direct product of groups.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals