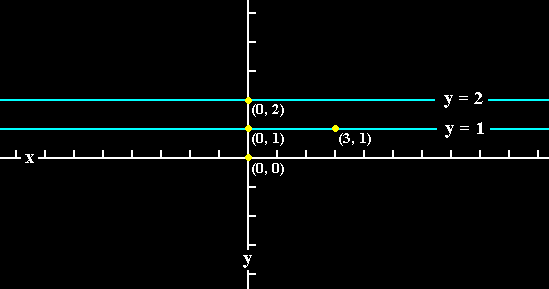
e-mail : 

Sequel to Group Theory

The general idea of a direct product embodied in the definition applies just as well to infinite groups. A simple example is the direct product of the group (Z, +) with itself. This gives us ordered pairs of integers which are added by the ordinary 'vector rule' :  (a, b) + (c, d) = (a + c, b + d), where  a, b, c, d  are elements of Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}. Note that the direct product has added another dimension by providing us with two-dimensional entities, which we may regard as displacements, or vectors. Thus we have constructed a new infinite group which may be designated C_infinite x C_infinite .

It is also possible to have the direct product of an infinite group with a finite group. For example, the positive reals (R⁺) form a group under multiplication (x), and so also the set {-1, +1}. The direct product of these two groups would consist of ordered pair such as (a, -1), (b, +1), etc. They combine according to the law

(a₁, b₁) (a₂, b₂) = (a₁a₂, b₁b₂).

So we can get

(a, 1) (b, 1) = (ab, 1)
(a, 1) (b, -1) = (ab, -1)
(a, -1) (b, -1) = (ab, 1)
(a, -1) (b, 1) = (ab, -1)

and the direct product group would in fact be isomorphic to the whole set of reals, positive and negative (0 excluded), under multiplication, i.e.

(R⁺, x) x ({-1, +1}, x) is isomorphic to (R\{0}, x). The correspondence being :
(a, 1)  ---  +a
(a, -1)  ---  -a

The elements (0, 1) and (0, -1) are excluded.

Again, if we take the groups (R, +) (i.e. all real numbers under addition), and ({0, 1, 2}, + mod 3) (i.e. the set {0, 1, 2} under addition modulo 3), we shall have ordered pairs of the form (x, y) where  x  is element of R and  y = 0, 1, or 2. The elements (x, 0) (x element of R) form the subgroup (R, +). The elements (0, 0), (0, 1) and (0, 2) form the subgroup C₃. See next Figure.

Figure 1.  The coordinate system of two-dimensional space.
In it we see the real number line, which is the  x-axis, and the points (0, 0), (0, 1), (0, 2). The product of these two groups, (R, +) and ({0, 1, 2}, + mod 3) consists of all the points of the x-axis, of the line y = 1, and of the line y = 2.
A point (3, 1) (as an element of the product set) is indicated.

The group C_infinite x C₂ is an important special case. The group may be realized by taking C_infinite as the integers under addition, i.e. the group (Z, +), and C₂ as the group ({0, 1}, + mod 2), i.e. the set {0, 1} under addition modulo 2. Or we may think of two generators of the product group, r  (of infinite period), and  a  (of period 2). The first group then contains the elements ... r^-2, r^-1, 1, r, r² ..., and the second group consists of the elements 1 and  a.  The product group will then contain elements

When we now consider the product of the elements, say, (r^-2, 1) and (r, a), the result is
(r^-1, a), and this behavior is precisely mimicked by
(r^-2) (ra) = r^-2ra = r^-1a,  where we set  a² = 1.
So we can rename the elements accordingly :
.
.
.
(r^-2, 1) --- r^-2
(r^-1, 1) --- r^-1
(1, 1) --- 1
(r, 1) --- r
(r², 1) --- r²
(r^-2, a) --- r^-2a
(r^-1, a) --- r^-1a
(1, a) --- a
(r, a) --- ra
(r², a) --- r²a
.
.
.

To show that the above correspondences (which form an isomorphism) are well-founded, we check the periods of the elements :

The element (r^-2, 1).
(r^-2, 1)² = (r^-4, 1),
(r^-2, 1)³ = (r^-6, 1), etc.
So the period of (r^-2, 1) is infinite. But the period of just  r^-2  is also infinite.

The element (r^-1, 1).
(r^-1, 1)² = (r^-2, 1),
(r^-1, 1)³ = (r^-3, 1), etc.
So also this element has an infinite period, and so has  r^-1.

The element (1, 1).
(1, 1)² = (1, 1). But because (1, 1) not only gives the identity element when raised to the power of two, but is already itself equal to the identity element (which is (1, 1)), its period is 1. But also the corresponding element  1  has period 1.

The element (r, 1).
(r, 1)² = (r², 1),
(r, 1)³ = (r³, 1), etc.
So the period of (r, 1) is infinite, and so is that of  r.

The same applies to the elements (r², 1), (r³, 1), etc.

The element (r^-2, a).
(r^-2, a)² = (r^-4, 1),
(r^-2, a)³ = (r^-6, a),
(r^-2, a)⁴ = (r^-8, 1), etc.
So the period of the element (r^-2, a) is infinite, and so is that of  r^-2a :  When r^-2 and  a  commute, then (r^-2a)² = r^-2ar^-2a = r^-2aar^-2 = r^-2r^-2 (because aa = 1) = r^-4, and (r^-2a)³ = r^-4r^-2a = r^-6a, etc. The period is thus infinite.  And when r^-2 and  a  do not commute we get :  (r^-2a)² = r^-2ar^-2a,  and (r^-2a)³ = r^-2ar^-2ar^-2a,  and so on, in which case the period is thus also infinite.

The element (r^-1, a).
(r^-1, a)² = (r^-2, 1),
(r^-1, a)³ = (r^-3, a),
(r^-1, a)⁴ = (r^-4, 1), etc.
So the period of the element (r^-1, a) is infinite, and so is that of  r^-1a.

The element (1, a).
(1, a)² = (1, 1),
So the period of element (1, a) is 2, and so is that of  a.

The element (r, a).
(r, a)² = (r², 1),
(r, a)³ = (r³, a),
(r, a)⁴ = (r⁴, 1), etc.
So the period of element (r, a) is infinite, and so is that of  ra.

The element (r², a).
(r², a)² = (r⁴, 1),
(r², a)³ = (r⁶, a),
(r², a)⁴ = (r⁸, 1), etc.
So the period of element (r², a) is infinite, and so is that of  r²a.

This product group C_infinite x C₂ can be seen more vividly on a Cayley diagram. Let us explain briefly what such a diagram is all about.
All groups may be represented by a network or graph known as a Cayley diagram. Each element of the given group is represented by a point, and the directed links between points represent generators of the group. Each link connecting the points represents the operation expressed by the given generator. Sometimes we need two kinds of links, for example to exppress two generators, say, r, where rⁿ = 1 and where  n  is greater than 2, represented by an arrowed link, and, say, a, where a² = 1, which means that a^-1 = a, so the link representing  a  is not a directed link, and can be represented in the Cayley diagram by just a line (i.e. it needs not to be arrowed). By following the arrowed and non-arrowed lines we generate the group elements one by one, till the job is done.

The group C_infinite x C₂ with elements as given above can now be represented as the following Cayley diagram :

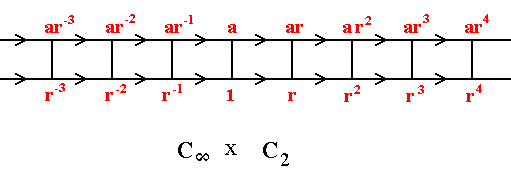
If we start at  1  in the above Cayley diagram and apply  ar, we first perform  r, and then on the result  a. See next diagram.

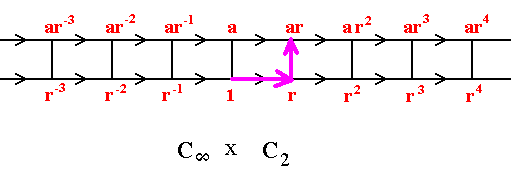
And when we want to assess  ra  (instead of ar), we first perform  a  (on  1), and then apply, on the result,  r. We then end up in the same place as before, which means that  ar = ra. See next diagram.

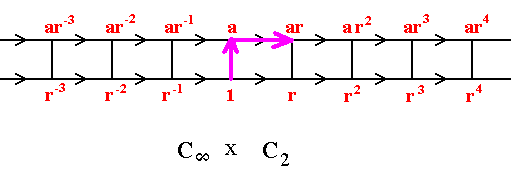
The following Cayley diagram looks much like the one depicted above, but differs in the fact that the direction of the upper horizontal links is reversed :

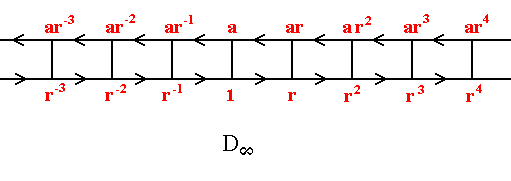
Here we can again perform  ar, by first applying  r, and then  a :

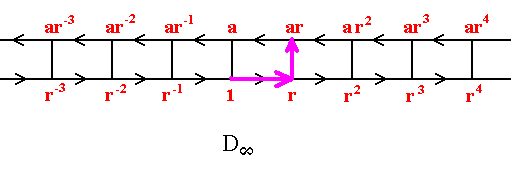
When we want, however, to assess  ra  (instead of ar), we first apply  a, and then  r, but must go in the direction of the arrows (for they indicate the generation of the group) :

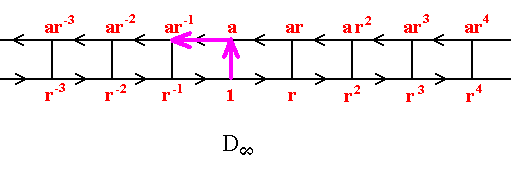
We end up at  ar^-1, and not at  ar, which means that  ra is not equal to ar, but to   ar^-1.
So we have to do with an altogether different infinite group. Indeed it is the group D_infinite. While the group considered above, C_infinite x C₂, needs, it is true, two generators (in contradistinction to cyclic groups, including infinite cyclic groups), but is commutative, as we 'll see shortly), the group indicated by the last mentioned Cayley diagrams is not commutative (as we just saw), and needs two generators, and is consequently a dihedral group.

A very realistic interpretation, or representation, of the group C_infinite x C₂ may be seen by letting  r  denote a translation (i.e. a shift), which has an infinite period, and  a  a geometric transformation of period 2, such as a mirror image in a line, or a half-turn about a point :

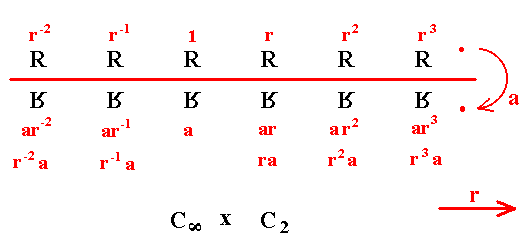
Here  a  represents a reflection in the central axis of the strip pattern. Note that  ar  is a glide reflection (See next diagram), and if  ar = g ( = ra), then this element itself generates the group
C_infinite {... g^-1, 1, g, g², ...}, which is a subgroup of Gp(a, r), i.e. of our group C_infinite x C₂, generated by the elements  a  and  r.

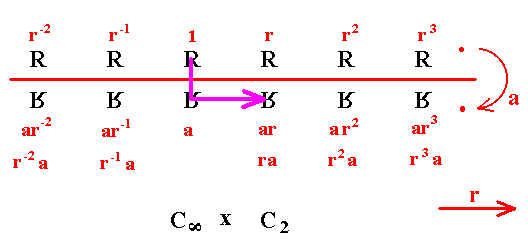
In the above pattern of the group C_infinite x C₂, we see that if we go from  1  to  ra, we first perform  a, which is a reflection, and then  r, which is a translation along the line of reflection. Such a combined transformation is called a glide reflection.

We observe that both Gp(r), i.e. the group generated by the element  r, and Gp(g), i.e. the group generated by the glide reflection, are subgroups of C_infinite x C₂, each being isomorphic to C_infinite . The group Gp(g) accounts for a part of the pattern of R's depicted above, and this part is depicted below :

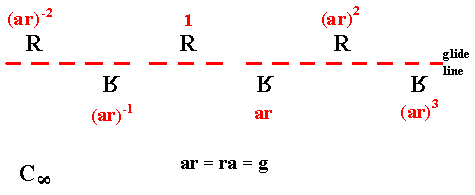
The group Gp(r) corresponds to the upper half of the original pattern. And of course we have the subgroup C₂ {1, a} which accounts for just two of the positions of the motif. See next diagram.

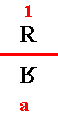
We may extend the possibilities for patterns by including further generators in the group. We will return to patterns later on.

We have already seen on many occasions that a group can be expressed as a set of permutations under the group operation of successive application of permutations. A permutation of a set of objects, placed in an initial sequence, means a replacement of one or more of those objects by objects from that same set, such that no two or more objects are replaced by the same object, a replacement resulting in a different sequence of those objects, i.e. different from the initial sequence. We can also say that a permutation of a set of objects is a swapping of one or more pairs of those objects, i.e. when a pair consists of the objects X ... Y situated in the total sequence of objects, then the swapping results in Y ... X.  The objects can be letters (which themselves can stand for, say, vertices of a geometric figure, or whatever). Suppose we have a set of four letters {A, B, C, D}, then (the following pattern)

,

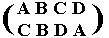means that
A is replaced by C.
B is replaced by B (i.e. nothing has happened to B.
C is replaced by D.
D is replaced by A.

or, alternatively, that we have the following cycles :
(ACD)(B), or, again alternatively, that we can produce this permutation by successive application of the swapping of A and C, and the swapping of A and D :
ABCD -- swapping of AC -- CBAD -- swapping of AD -- CBDA.

So far so good. But in group theory one discriminates between even and odd permutations (and for us this important for understanding a certain symmetry group realized in crystals). But what is an even permutation of  n  symbols (or objects)?
Consider n = 4 (the first interesting case). Take again the four symbols, the letters A, B, C, D. In alphabetic order these letters form a 'word', ABCD. By repeatedly swapping pairs of letters it is possible to rearrange these four letters into any one of 4 x 3 x 2 x 1 = 24 different 'words' (or orders). And, as we already know, any such arrangement is called a permutation of ABCD.
It is an even permutation if it is obtained by an even number of swappings, an odd permutation if the number of swaps is odd. For instance the permutation given above, CBDA, is an even permutation because it can be obtained by two successive swappings :

First a swapping of A and C :
ABCD becomes CBAD, then a swapping of A and D :
CBAD becomes CBDA.

So the number of swappings needed to obtain the given permutation is two and that is an even number.
BACD is an odd permutation, being arrived at from ABCD by swapping just the single pair A and B.

This phenomenon of permutations being even or odd can be expounded in a somewhat different but equivalent way as follows :
Consider the permutation of the numbers

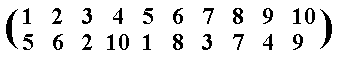
We count up how many pairs are out of their natural order. For instance, in the natural order, 6 comes after 3, but in this permutation, the order of 3 and 6 is reversed, so we have here what is known as an inversion of order, or a reversal. We want to enumerate all such reversals. The best way is to tale each digit in turn, and count up the number of reversals as follows :

5 is followed by 2, 1, 3, and 4, so it contributes to
    4 reversals.
6 is followed by 2, 1, 3, 4, so contributs to
    4 reversals.
2 is followed by 1, so contributes
    1 reversal.
10 is followed by 1, 8, 3, 7, 4, 9, so contributes
    6 reversals.
1 contributes
    no reversals.
8 is followed by 3, 4, 7, so contributes
    3 reversals.
3 contributes
    no reversals.
7 is followed by 4, so contributes
    1 reversal.
9 contributes
    no reversals.

The total number of reversals thus is 19. This number is odd, and so this particular permutation is described as being an odd permutation. Or we may say that the parity of the permutation is odd.

Let us next determine the effect on the parity of the above permutation, namely

as a consquence of a single swap, say of the numbers  2  and  7. In the first place, the interchange of these two numbers themselves causes a change in the parity, for there is now a new reversal, (7 2). So when we replace 2 by 7, and 7 by 2, then the numbers that originally (i.e. in the original permutation) were before 2 -- and thus also before 10, 1, 8, 3, 7, 4 and 9 -- are still before 2, 10, 1, 8, 3, 7, 4, and 9. The same can be said about the numbers that came after 7 in the original permutation -- and thus after 5, 6, 2, 10, 1, 8, 3, 7 :  they still come after those numbers. So when assessing the effect on the parity we do not have to check those numbers that were before 2 in the original permutation, and after 7 in the original permutation. So only the numbers that were between 2 and 7 must be investigated. The latter now are placed 7 ...... 2, and we must see whether there are numbers between them that are smaller than 7 and at the same time greater than 2, because these numbers cause extra reversals. When those numbers are only smaller than 7, or only greater than 2, they cause one new reversal but eliminate another, and so do not contribute extra reversals. So in the present example the only number which could cause any alteration in parity is the number 3, and the new reversals are (7 3) and (3 2). So apart from the (7 2) reversal we have two additional ones, and the final effect of the interchange, therefore, is to cause three reversals, (7 2), (7 3) and (3 2). Consult for this the change from

... 2 10 1 8 3 7 ...   to
... 7 10 1 8 3 2 ...

Next suppose (in another case) that there are several numbers lying between the pair which are being switched, whose numerical value lies between them. To be definite, suppose we interchange the numbers  12  and  58, resulting in ... 58...12..., and that there are  r  numbers lying between them which are greater than 12 and at the same time less then 58. For example one of them might be  49 :

... 12 ... 49 ... 58 ...  becomes
... 58 ... 49 ... 12 ...

The effect of the switch -- so far as the number 49 is concerned -- is to cause two extra reversals to appear (We had (58 12), and now also (58 49) and (49 12)), and the same will happen for every one of the  r  numbers mentioned, because every number between 12 and 58, not having their numerical value between the latter (and thus not counted to determine  r ) do not contribute any extra reversal as an effect of the reversal of 12 and 58. Thus we get  2r  extra reversals -- an even number -- on account of these  r  intermediate numbers. The third reversal is of course the reversal of 12 and 58 themselves. Thus, altogether an odd number of reversals have appeared, namely 2r + 1.
And when we interchange two numbers of which the larger one is on the left, an odd number of reversals is lost.
We see therefore that in all cases, an interchange of two symbols ( = one transposition) changes the parity of the permutation, because
EVEN + (or -) ODD = ODD ( = change of parity), and
ODD + (or -) ODD = EVEN ( = change of parity).

Consider again the permutation

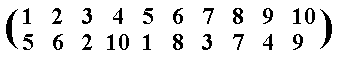
which also can be expressed by

5  6  2  10  1  8  3  7  4  9.

Starting from the numbers in their natural order, we may obtain this permutation by successive swaps of pairs of numbers, or transpositions :

We may start with the transposition (1 5), which brings the number 5 into the desired position :
5 2 3 4 1 6 7 8 9 10.  Next, since we require 6 in the second position, we make the transposition (2 6), obtaining the order :
5 6 3 4 1 2 7 8 9 10.  Next, since we require 2 in the third position, we make the transposition (3 2), obtaining the order :
5 6 2 4 1 3 7 8 9 10. Next, since we require 10 in the fourh position, we make the transposition (4 10), obtaining the order :
5 6 2 10 1 3 7 8 9 4. Next, since we require 1 in the fifth position, we make the transposition (5 1). But this transposition we had already made. Next, since we require 8 in the sixth position, we make the transposition (3 8), obtaining the order :
5 6 2 10 1 8 7 3 9 4. Next, since we require 3 in the seventh position, we make the transposition (7 3), obtaining the order :
5 6 2 10 1 8 3 7 9 4.  Next, we require 7 in the eighth position, and indeed it is already there.  Next, since we require 4 in the ninth position we make the transposition (9 4), obtaining the order :
5 6 2 10 1 8 3 7 4 9.  Finally, we require 9 in the tenth position, and indeed it is already there.

So we can build our permutation by seven successive swappings (transpositions) (and we note that this number is odd). Thus we see that the permutation may be 'resolved' into a finite number of transpositions. It is clear that the method may be extended to cover any permutation of any number of objects. It should also be evident that we may always achieve the desired permutation by not more than  n-1  moves (because, arrived at the one but last number to be put in its place, the last number is then automatically placed in its proper location), less than this if we are lucky. However it is not the number of moves that is important, but the parity of that number (i.e. whether it is even or odd). In the above case, the number of transpositions was seven, and this was an odd permutation with nineteen reversals. We will see that any odd permutation (i.e. having an odd number of reversals) is the result of transpositions the number of which will always be odd. Similarly an even permutation will decompose (in an unlimited variety of ways) into transpositions, the number of which is bound to be even. This theorem follows immediately from the Interchange Theorem established above, namely the fact that every single transposition changes the parity of the permutation. Starting from the natural order, suppose that a given permutation is built up from  k  transpositions. Then, since each transposition changes the parity of the permutation, and since the parity of the original order is even (The number of reversals is then zero, which is an even number), it follows that the parity of the resulting permutation is equal to the parity of  k  : An even number of transpositions will restore the parity to even, while an odd number will cause the final permutation to be odd.

We can verify that of the 24 permutations of four symbols (these are all the permutations possible : 4 x 3 x 2 x 1 = 24), there are 12 even and 12 odd. The number of even and odd permutations of five symbols are also equally balanced. We will, without proof state the following theorem (where  n!  is 1 x 2 x 3 x ... x (n-1) x n) (where  x  means multiplied by).

Of the  n!  permutations of  n  objects, there are an equal number of odd and even permutations.

The even permutations of a group are closed under successive application, because combining two even permutations, consisting of (i.e. constructible by) respectively  2p and 2q transpositions, yields a permutation consisting of 2p + 2q transpositions, which is equal to 2(p + p) transpositions and which is an even number. Therefore these even permutations form a group, and this is the alternating group A_n.
The odd permutations are not closed under successive application because (2p + 1) + (2q + 1) = 2p + 2q + 2 = 2(p + q + 1), which is even, and thus we are brought outside the set of odd permutations.

e-mail : 

back to homepage

back to retrospect and continuation page

back to Part I of the theoretical preparation to the study of 3-D crystals

back to Part II of the theoretical preparation to the study of 3-D crystals

back to Part III of the theoretical preparation to the study of 3-D crystals

back to Part IV of the theoretical preparation to the study of 3-D crystals

back to Part V of the theoretical preparation to the study of 3-D crystals

back to Part VI of the theoretical preparation to the study of 3-D crystals

back to Part VII of the theoretical preparation to the study of 3-D crystals

back to Part VIII of the theoretical preparation to the study of 3-D crystals

back to Part IX of the theoretical preparation to the study of 3-D crystals

back to Part X of the theoretical preparation to the study of 3-D crystals