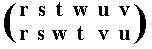
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Sequel to Automorphisms
At the end of the previous document we were (still) investigating on the automorphisms of the group Q4 . First we determined the inner automorphisms. After that we started with the process of determining all automorphisms (inner and outer) of this group, by means of finding alternative generator pairs, and determine what sequence of group elements they imply. Sequences found in that way are automorphisms of the group.
After again giving all the twenty-four alternative pairs of generators, found in the previous document, and repeating a small paragraph from the end of that same document, we continue to determine all the 24 automorphisms of the group (Q4).
| rt | rw | ru | rv | st | sw |
| su | sv | tu | tv | wu | wv |
| tr | ts | wr | ws | ur | us |
| ut | uw | vr | vs | vt | vw |
Our initial generator pair was set to be (r t), and (in the previous document) we replaced that pair by (w u), and obtained a new sequence of group elements, namely w, t, u, v, s, r, representing one of the group's automorphisms. Apart from obtaining one of the automorphisms, the objective was to lay out the procedure to find all automorphisms of the group. We will now -- while following this procedure -- derive all automorphisms of the group Q4 , by considering the replacement of the generator pair r t successively by the pairs from the above table.
The initial pair (r t) being replaced by (to begin with) the pair (r w) effects the following :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| r | r-1 | w | w-1 | wr | rw |
| r | s | w | t | v | u |
First row : The original sequence of relevant group elements.
Second row : The elements expressed in terms of r and t.
Third row : Replacement of generators.
Fourth row : Expressing the elements of the resulting sequence by single symbols, according to the Group Table of Q4 as given in the previous document (Click link).
So the resulting permutation accordingly is
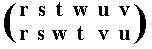
which corresponds to the cycle (t w) (u v), which is of period 2.
It can represent an automorphism of the group Q4 , and this in turn corresponds to the full sequence 1 a r s w t v u of group elements. This automorphism is yet another element of the automorphism group of Q4.
Next we replace the initial generator pair (r t) by the generator pair (r u) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| r | r-1 | u | u-1 | ur | ru |
| r | s | u | v | w | t |
The resulting permutation accordingly is
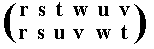
corresponding to the cycle (t u w v), which is of period 4.
Next we replace the initial generator pair (r t) by the generator pair (r v) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| r | r-1 | v | v-1 | vr | rv |
| r | s | v | u | t | w |
The resulting permutation accordingly is
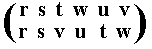
and it corresponds to the cycle (t v w u) which is of period 4.
Next we replace the initial generator pair (r t) by the generator pair (s t) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| s | s-1 | t | t-1 | ts | st |
| s | r | t | w | v | u |
The resulting permutation accordingly is
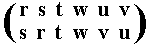
corresponding to the cycle (r s) (u v), which is of period 2.
Next we replace the initial generator pair (r t) by the generator pair (s w) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| s | s-1 | w | w-1 | ws | sw |
| s | r | w | t | u | v |
The resulting permutation accordingly is
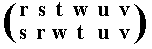
corresponding to the cycle (r s) (t w), which is of period 2.
Next we replace the initial generator pair (r t) by the generator pair (s u) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| s | s-1 | u | u-1 | us | su |
| s | r | u | v | t | w |
The resulting permutation accordingly is
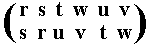
corresponding to the cycle (r s) (t u) (w v), which is of period 2.
Next we replace the initial generator pair (r t) by the generator pair (s v) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| s | s-1 | v | v-1 | vs | sv |
| s | r | v | u | w | t |
The resulting permutation is accordingly
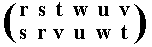
corresponding to the cycle (r s) (t v) (w u), which is of period 2.
Next we replace the initial generator pair (r t) by the generator pair (t u) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| t | t-1 | u | u-1 | ut | tu |
| t | w | u | v | r | s |
The resulting permutation is the following
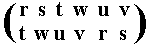
corresponding to the cycle (r t u) (s w v), which has period 3.
Next we replace the initial generator pair (r t) by the generator pair (t v) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| t | t-1 | v | v-1 | vt | tv |
| t | w | v | u | s | r |
The resulting permutation accordingly is
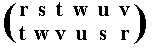
corresponding to the cycle (r t v) (s w u), which has period 3.
Next we replace the initial generator pair (r t) by the generator pair (w u) (In the previous document this was already done, serving as example of procedure.) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| w | w-1 | u | u-1 | uw | wu |
| w | t | u | v | s | r |
The resulting permutation is accordingly
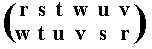
corresponding to the cycle (r w v) (s t u), which is of period 3.
Next we replace the initial generator pair (r t) by the generator pair (w v) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| w | w-1 | v | v-1 | vw | wv |
| w | t | v | u | r | s |
The resulting permutation accordingly is
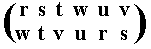
corresponding to the cycle (r w u) (s t v), which is of period 3.
Next we replace the initial generator pair (r t) by the generator pair (t r) (Recall that the initial pair is replaced successively by the generator pairs (found and) summarized in the TABLE ABOVE) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| t | t-1 | r | r-1 | rt | tr |
| t | w | r | s | v | u |
The resulting permutation accordingly is
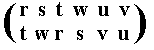
corresponding to the cycle (r t) (s w) (u v), which is of period 2.
Next we replace the initial generator pair (r t) by the generator pair (t s) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| t | t-1 | s | s-1 | st | ts |
| t | w | s | r | u | v |
The resulting permutation accordingly is
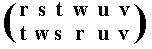
corresponding to the cycle (r t s w), which is of period 4.
Next we replace the initial generator pair (r t) by the generator pair (w r) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| w | w-1 | r | r-1 | rw | wr |
| w | t | r | s | u | v |
The resulting permutation accordingly is
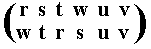
coresponding to the cycle (r w s t), which is of period 4.
Next we replace the initial generator pair (r t) by the generator pair (w s) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| w | w-1 | s | s-1 | sw | ws |
| w | t | s | r | v | u |
The resulting permutation accordingly is
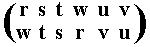
corresponding to the cycle (r w) (s t) (u v), which is of period 2.
Next we replace the initial generator pair (r t) by the generator pair (u r) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| u | u-1 | r | r-1 | ru | ur |
| u | v | r | s | t | w |
The resulting permutation accordingly is
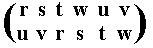
corresponding to the cycle (r u t) (s v w), which has period 3.
Next we replace the initial generator pair (r t) by the generator pair (u s) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| u | u-1 | s | s-1 | su | us |
| u | v | s | r | w | t |
The resulting permutation accordingly is
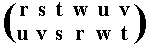
corresponding to the cycle (r u w) (s v t), which is of period 3.
Next we replace the initial generator pair (r t) by the generator pair (u t) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| u | u-1 | t | t-1 | tu | ut |
| u | v | t | w | s | r |
The resulting permutation accordingly is
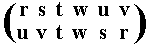
corresponding to the cycle (r u s v), which is of period 4.
Next we replace the initial generator pair (r t) by the generator pair (u w) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| u | u-1 | w | w-1 | wu | uw |
| u | v | w | t | r | s |
The resulting permutation accordingly is
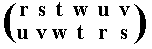
corresponding to te cycle (r u) (s v) (t w), which is of period 2.
Next we replace the initial generator pair (r t) by the generator pair (v r) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| v | v-1 | r | r-1 | rv | vr |
| v | u | r | s | w | t |
The resulting permutation accordingly is
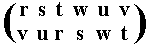
corresponding to the cycle (r v t) (s u w), which is of period 3.
Next we replace the initial generator pair (r t) by the generator pair (v s) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| v | v-1 | s | s-1 | sv | vs |
| v | u | s | r | t | w |
The resulting permutation accordingly is
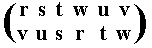
corresponding to the cycle (r v w) (s u t), which is of period 3.
Next we replace the initial generator pair (r t) by the generator pair (v t) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| v | v-1 | t | t-1 | tv | vt |
| v | u | t | w | r | s |
The resulting permutation accordingly is
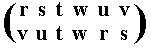
corresponding to te cycle (r v s u), which is of period 4.
Finally, we replace the initial generator pair (r t) by the generator pair (v w) and determine the implied permutation of the elements r, s, t, w, u, v, which corresponds to yet another automorphism of the group Q4 :
| r | s | t | w | u | v |
| r | r-1 | t | t-1 | tr | rt |
| v | v-1 | w | w-1 | wv | vw |
| v | u | w | t | s | r |
The resulting permutation accordingly is
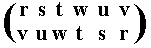
corresponding to the cycle (r v) (s u) (t w), which is of period 2.
We have now determined all 24 automorphisms of the group Q4 . Let's now summarize the total result. We've found 24 permutations of group elements. Of each of these permutations we have determined the cycles they represent, and by means of these cycles we could determine the periods of those permutations. In the next table we will summarize these cycles and the determined periods in order to identify the group they form, i.e. to identify the automorphism group of the group Q4 (The identity element of this automorphism group is of course the identity permutation having period 1, and is one of the 24 automorphisms) :
| cycle | period |
| identity | 1 |
| (t w) (u v) | 2 |
| (r s) (u v) | 2 |
| (r s) (t w) | 2 |
| (r s) (t u) (w v) | 2 |
| (r s) (t v) (w u) | 2 |
| (r t) (s w) (u v) | 2 |
| (r w) (s t) (u v) | 2 |
| (r u) (s v) (t w) | 2 |
| (r v) (s u) (t w) | 2 |
| (r t u) (s w v) | 3 |
| (r t v) (s w u) | 3 |
| (r w v) (s t u) | 3 |
| (r w u) (s t v) | 3 |
| (r u t) (s v w) | 3 |
| (r u w) (s v t) | 3 |
| (r v t) (s u w) | 3 |
| (r v w) (s u t) | 3 |
| (t u w v) | 4 |
| (t v w u) | 4 |
| (r t s w) | 4 |
| (r w s t) | 4 |
| (r u s v) | 4 |
| (r v s u) | 4 |
So we have found
one element of period 1,
nine elements of period 2,
eight elements of period 3, and
six elements of period 4.
And this leaves no doubt that the full group of automorphisms of Q4 (i.e. Aut(Q4 ) is S4 , the inner automorphisms being the normal subgroup with structure D2 (as we had found out in the previous document). The group table of the group S4 was depicted in Part XIII, and can be seen by clicking HERE.
The first four cycles in the above list correspond to the inner automorphisms.
The way in which the group S4 arises may be seen in another way (BUDDEN, p. 426). For the three pairs of elements of period 4 may be likened to the three pairs of opposite faces of a cube. If we label these faces r s t w u v in opposite pairs, each of the twenty-four rotations of the cube will correspond to exactly one of the permutations in the list of automorphisms of Q4 . These rotations are :
identity
(t w) (u v)
(r s) (u v)
(r s) (t w)
And above we interpreted r s t w u v as pairs of opposite faces of a cube. Well, in this interpretation the three transpositions just given do in fact interchange opposite pairs of faces. Each one of them interchanges two pairs of opposite faces, so they must each correspond to a rotation of 1800 about an axis connecting the two remaining opposite faces of the cube. So we now have a geometrical interpretation of the four (including the identity) inner automorphisms of the group Q4 . Indeed there are three such rotations, i.e. three rotations of 1800 of the cube that interchange two pairs of opposite faces.
The interest in all this lies in the fact that, though the group Q4 is not the symmetry group of any geometrical figure, yet it has this curious association with the Cube (or Octahedron).
This concludes our discussion concerning the automorphism group of the group Q4 .
Now Q6 is also a group with six elements of period 4, and one might expect that its automorphisms would also number twenty-four. This is not so, because one's freedom of choice is now more restricted in the following way (See next table, and what follows).
| 1 | a | b | c | d | f | g | h | j | k | l* | m | period | |
| 1 | 1 | a | b | c | d | f | g | h | j | k | l* | m | 1 |
| a | a | l* | 1 | d | f | g | h | j | c | m | k | b | 6 |
| b | b | 1 | m | j | c | d | f | g | h | l* | a | k | 6 |
| c | c | j | d | k | l* | a | 1 | b | m | g | h | f | 4 |
| d | d | c | f | m | k | l* | a | 1 | b | h | j | g | 4 |
| f | f | d | g | b | m | k | l* | a | 1 | j | c | h | 4 |
| g | g | f | h | 1 | b | m | k | l* | a | c | d | j | 4 |
| h | h | g | j | a | 1 | b | m | k | l* | d | f | c | 4 |
| j | j | h | c | l* | a | 1 | b | m | k | f | g | d | 4 |
| k | k | m | l* | g | h | j | c | d | f | 1 | b | a | 2 |
| l* | l* | k | a | f | g | h | j | c | d | b | m | 1 | 3 |
| m | m | b | k | h | j | c | d | f | g | a | 1 | l* | 3 |
Table 19.1
The group contains two elements of period 6 (a and b in the notation used in the above group table of Q6 ), and two of period 3 ( l* and m ). It is essential that an automorphism shall either leave each of these pairs alone, or else interchange them (i.e. interchanges the members of such a pair). Thus, for example, dg = a, while fc = b, So an automorphism which replaces d by f and g by c is feasible because then two elements of the same period (a and b, both of period 6) are interchanged. And indeed one of the automorphisms of Q6 is (c g) (d f) (h j). But since, for example, jh = m, we do not have an automorphism which replaces d by j and g by h, because then elements of different periods (a, which is of period 6, and m, which is of period 3) would be interchanged, resulting, obviously, in products not being preserved.
Automorphisms of S4
Finally, we consider the automorphisms of S4 , and, using the notation of the group table as it is given HERE in Part XIII, we may take two of the elements of period 4 (out of the subset {j, k, n, s, t, x}) to be generators of the whole group so long as they are not inverses. We are therefore in a similar position to the one we were in when obtaining the automorphisms of Q4 , and the group of these is of order 24. Not unexpectedly, its structure (i.e. the structure of Aut(S4)) is (isomorphic to) S4 , but what is surprising is that all the automorphisms are inner. This may be seen by considering the effect of conjugation upon the subset {j, k, n, s, t, x} (Recall that the sequential order of elements of a set is immaterial), as the next table shows (Note that in every case, the period of the transforming element is equal to the period of the induced permutation). Recall that the conjugate or transform of an element p of a group G by an element q of that same group is qpq-1, where q is the transforming element. So -- as we also did on other occasions -- in the following table we transform every element, generally denoted by X, of the mentioned set, by each group element in turn. And what we will see is that we get 24 inner automorphisms, and, knowing that the total number of automorphisms of the group S4 is 24, we see that all the automorphisms of this group are inner automorphisms. We show the resulting permutations (representing the automorphisms), their corresponding cycles, and the implied period of those permutations (evident from the cycles) :
| conjugation |
permutation of elements of period 4 |
cycle | period |
| 1X1-1 | j t k n s x | -- | 1 |
| aXa-1 | k n j t x s | ( j k) (t n) (s x) | 2 |
| bXb-1 | s x n k j t | ( j s) (t x) (k n) | 2 |
| cXc-1 | x s t j k n | ( j x n) (t s k) | 3 |
| dXd-1 | n k s x t j | ( j n x) (t k s) | 3 |
| fXf-1 | t j x s n k | ( j t) (k x) (n s) | 2 |
| gXg-1 | n k t j x s | ( j n) (t k) (s x) | 2 |
| hXh-1 | t j n k s x | ( j t) (k n) | 2 |
| iXi-1 | k n x s t j | ( j k x) (t n s) | 3 |
| jXj-1 | j t s x n k | (k s n x) | 4 |
| kXk-1 | x s k n j t | ( j x t s) | 4 |
| l*Xl*-1 | s x j t k n | ( j s k) (t x n) | 3 |
| mXm-1 | x s j t n k | ( j x k) (t s n) | 3 |
| nXn-1 | s x k n t j | ( j s t x) | 4 |
| pXp-1 | t j s x k n | ( j t) (k s) (n x) | 2 |
| qXq-1 | n k x s j t | ( j n s) (t k x) | 3 |
| rXr-1 | j t n k x s | (k n) (s x) | 2 |
| sXs-1 | k n t j s x | ( j k t n) | 4 |
| tXt-1 | j t x s k n | (k x n s) | 4 |
| uXu-1 | k n s x j t | ( j k s) (t n x) | 3 |
| vXv-1 | s x t j n k | ( j s n) (t x k) | 3 |
| wXw-1 | x s n k t j | ( j x) (t s) (k n) | 2 |
| xXx-1 | n k j t s x | ( j n t k) | 4 |
| yXy-1 | t j k n x s | ( j t) (s x) | 2 |
In the above table we see that the permutations (representing automorphisms) are such that
It will readily be seen that the six elements of period 4 may be associated with the six faces of a cube, and that the automorphism may be thought of as a re-labelling of the six quarter-turns : When we rotate the cube about one axis connecting two opposite faces, we can rotate by 900, 1800, and 2700 (as being three symmetry operations). Two of these rotations, namely 900 and 2700, are of period 4, and both can be denoted as quarter-turns, the former anti-clockwise, the latter clockwise. And because the cube has three such axes, there are six quarter-turns. These quarter-turns can then be labelled j, t, k, n, s, x, i.e. corresponded to the six period 4 elements of the group S4. The automorphisms then constitute swappings of these labels.
Proof that the inner automorphisms are a normal subgroup of the full group of automorphisms.
Finally we give the proof (BUDDEN, p. 428) that the inner automorphisms of any group are a normal subgroup of all the automorphisms of that group.
An automorphism of a group G is a permutation of the group elements of G, i.e. a swapping of all, or some non-identity elements of G, such that products are preserved. So in such a permutation a general element pr is replaced by a general element ps (which could be the same element or a different element). Such a permutation, that is to say such an automorphism, we will (in the proof to be outlined) indicate by a capital letter. And such an automorphism is an element of the corresponding automorphism group of the group G.
The elements of the group G itself we will indicate by small letters (with or without subscript). That the inner automorphisms are a subgroup of the group of automorphisms, has already been proved in the beginning of Part XVIII (Click HERE to see it). We now must show that (in all cases) they are a normal subgroup of the group of automorphisms.
If a subgroup K of a group is a normal subgroup of a group G, then for all elements x of G the following must hold : xK = Kx, which means that for every element the left coset is equal to the right coset. But xK = Kx is equivalent to xKx-1 = Kxx-1, and this is equivalent to xKx-1 = K. And this means that when whatever element of K is transformed by any element of G, the result will be an element of K. So, generally, when K is a subgroup of G, and if xKx-1 = K, then K is a normal subgroup of G.
We are now ready to give the proof that the group of inner automorphisms of any group is a normal subgroup of the full group of automorphisms.
Suppose that X is any outer automorphism of a group G, and Y is any inner automorphism of that same group. So X, as well as Y are a permutation of the group elements of the group G. From the foregoing it is clear that in order to prove that the inner automorphisms are a normal subgroup (of the full group of automorphisms), it is sufficient to show that XYX-1 is an inner automorphism. To understand this, keep in mind that X, Y, as well as XYX-1, are elements of the group of automorphisms. So "XYX -1 is an inner automorphism" means that any element Y of the subgroup of inner automorphisms will be transformed by any element X of the full group of automorphisms into an element XYX-1 of the subgroup of inner automorphisms (And when this is indeed shown to be the case, this subgroup of inner automorphisms is a normal subgroup of the full group of automorphisms).
Let Y ( = any inner automorphism of G) be produced by conjugation by the element y of G, i.e. Y is the resulting sequence of group elements of G after transforming each element by the transforming element y, so that with respect to a general element x of G we have : x ==> yxy-1. And suppose that X ( = any outer automorphism of G) has the effect (which is : the swapping of elements of the group G) shown below :
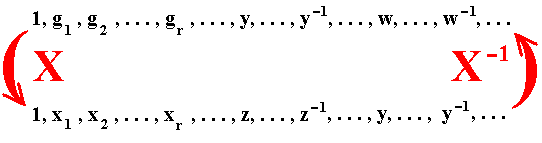
that is, the general element gr is changed by X into xr , y is changed into z, and w into y. The inevitable consequence of the latter is that y-1 is changed into z-1, and w-1 into y-1.
Now, we know that X is a certain permutation of the elements of G, and X-1 is the reverse permutation of those same elements, as indicated above. Further we know that Y also is a certain permutation of the group elements of G. But then, for example, XY is also a certain permutation of the group elements of G, namely that one resulting from first performing the permutation Y, and then performing, on that result, the permutation X. And because X and Y are moreover automorphisms (i.e. permutations in which products are preserved), the permutation XY is also an automorphism (because the set of automorphisms form a group under successive application of the corresponding permutations). Further we can denote, say, X(gr) as being the effect of the permutation X on the particular element gr , and XY(gr) as the effect of the permutation XY on that particular element gr . And the same goes for XYX-1(xr).
Now we have :
XYX-1(xr) (where xr may be regarded as any selected element of G) = XY(gr) = X(ygry-1) = X(y) X(gr) X(y-1) (in view of the fact that X is an automorphism, and so preserves products) = zxrz-1.
So XYX-1(xr) = zxrz-1 , which means that the effect of the permutation XYX-1 on the element xr is to transform the element xr into the element zxrz-1. Hence XYX-1 is that automorphism which is brought about by transforming the elements of the group, each in turn, by z. It is therefore an inner automorphism, so the subgroup of inner automorphisms is invariant under conjugation by X (Recall that X, X-1, Y, and XYX-1 are elements of the automorphism group of the group G). Seeing that X was any outer automorphism -- and seeing at the same time that when Y is transformed by Y we get as a result an inner automorphism anyway, because YYY-1 = Y --- it follows that the inner automorphisms are an invariant subgroup, which means that it is a normal subgroup of the automorphism group of the group G (Again, when we denote such a subgroup by K, then the invariance is expressed as xKx-1 = K (where x is any (outer) automorphism), which is equivalent to xKx-1x = Kx, which in turn is equivalent to xK = Kx, indicating that K is a normal subgroup of the full group of automorphisms of the group G ).
This concludes our long discussion (which took three documents) about automorphism.
The next document will expand group theory into the symmetry of 2-dimensional periodic patterns (as the gateway to an understanding of the structure of three-dimensional crystals).
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals
back to Part XV of the theoretical preparation to the study of 3-D crystals
back to Part XVI of the theoretical preparation to the study of 3-D crystals
back to Part XVII of the theoretical preparation to the study of 3-D crystals
back to Part XVIII of the theoretical preparation to the study of 3-D crystals