e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Sequel to Dihedral Groups
In the previous document we studied the dihedral group D6 and some of its subgroups. We found a C6 subgroup, C2 subgroups, and D2 subgroups. But there exist still more subgroups of D6, namely one C3 = {1, r2, r4} (i.e. the identity, a rotation of 1200, and a rotation of 2400), and two D3 namely {1, r2, r4, a, c, f} and 1, r2, r4, b, d, g} subgroups.
Let's start with the latter two.
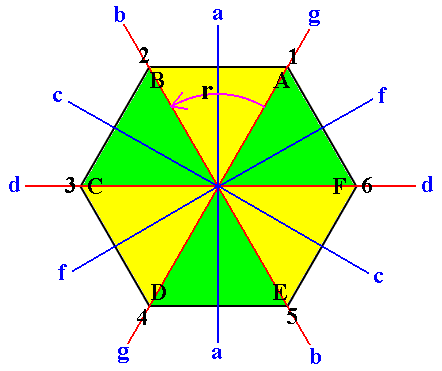
In the next Figure we depict a hexagon with its symmetry transformations, rotations and reflections. As such the full symmetry of the hexagon is, as we know, according to the dihedral group D6, it has full 6-fold symmetry. But in that same Figure we see that also a 3-fold symmetry is involved as a subgroup.

Figure 1. Implied 3-fold symmetry in the regular hexagon.
When we isolate this 3-fold symmetry we get :
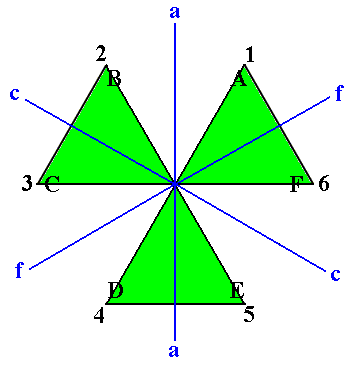
Figure 2. The implied 3-fold symmetry in the regular hexagon isolated.
The symmetry transformations of the object we now have are then :
And in addition to this three-fold subgroup thre is another one, as the next Figures illustrate :
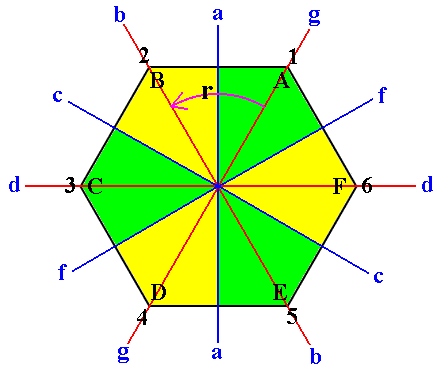
Figure 3. A second implied 3-fold symmetry in the regular hexagon.
If we isolate this 3-fold substructure we get :
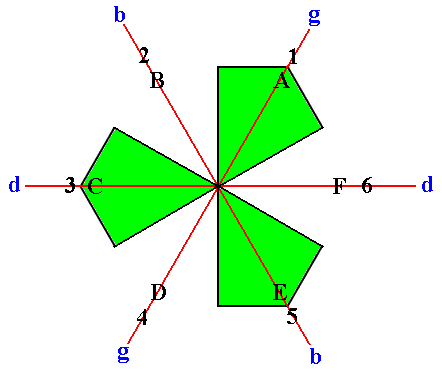
Figure 4. The second implied 3-fold symmetry in the regular hexagon isolated.
The symmetry transformations involved in this 3- fold substructure are then :
And of course a subgroup of both D3's just detected is {1, r2, r4}, which is isomorphic to the cyclic group of order 3, i.e. C3, and of course this C3 is at the same time a subgroup of the whole group, that is to say to the group D6.
This subgroup {1, r2, r4} supports an interesting homomorphism : The set of all cosets of this subgroup (which includes the subgroup itself) form a group that is isomorphic to the dihedral group D2 (The mapping of the set of group elements of the parent group (in our case that is the group of all symmetries of the regular hexagon) onto the set of elements of the mentioned D2 image group is a homomorphism in the strict sense, because it is a many-to-one mapping, while the mapping of the mentioned cosets onto the elements of the D2 image group is an isomorphism). In order to clearly see this homomorphism from our group G of symmetries of the regular hexagon to the mentioned D2 image group, we will change the notation the elements of our group G as follows :
| old notation | 1 | r2 | r4 | a | c | f | r3 | r5 | r | d | g | b |
| new notation | 1 | p | p2 | a | b | c | x | y | z | u | v | w |
In spite of them now being indicated by other symbols, we let those elements still combine according to the original group table of D6 as depicted in the previous document Table 7.10, otherwise we would not have to do with the same group anymore.
The new group table of the ('old') group D6, with this new notation of elements is as follows :
Table 8.1
In the above group table we recognize a possible homomorphism, supported by the subgroup U = {1, p, p2} of our D6 group G. Let's go a little deeper into these matters.
What the table clearly shows is that the group is partioned into four subsets {1, p, p2}, {a, b, c}, {x, y, z} and {u, v, w}. This is done by a so-called equivalence relation, E, which performs a sort of abstraction of the group elements, resulting in equivalence classes in the same way that we classify all vertebrate animals in to the five classes Fishes, Amphibians, Reptiles, Birds and Mammals. So a lot of animals are, although they are different among each other, are placed in the class birds In this way we abstract from all kinds of differences between them, and look only to one specific set of features which they have in common, like the possession of feathers.
Thus by the equivalence relation E our group elements are placed into several classes. In our case the equivalence relation concerns the proper assignment of a group element to a certain coset. So we can say that those elements of our group G that belong in the same coset of U as the element a does are equivalent under the equivalence relation E. Clearly, element b belongs in that coset, and also element c. So the elements a, b and c are equivalent to each other (despite their differences). We can write this down as : aEb, aEc, bEc. Together they form the equivalence class [a]. So there is a correspondence of the elements a, b and c on the one hand, to the equivalence class [a], on the other.
In the same way we can say that those elements of our group G that belong to the same coset of U as the element x does are equivalent and form the equivalence class [x]. And this class contains the elements x, y and z.
And, again, we can say that those elements of G that belong to the same coset of U as the element 1 does are equivalent and form the equivalence class [1], and this class contains the elements 1, p, and p2.
Finally we can say that those elements of G that belong to the same coset as the element u does are equivalent. They form the equivalence class [u], which contains the elements u, v and w.
So the equivalence relation E splits up the set of group elements into the four equivalence classes [1], [a], [x] and [u].
Generally, if q is element of mU, we can say that, because m is also an element of U (we find it there as m1 = m), qEm ( = q is equivalent to m). But q being element of mU means that there is an element x such that mx = q, in which x is element of U, and thus also mm-1x = qm-1, and thus x = qm-1. And so we know now that qm-1 is an element of U. So now we have two statements saying the same : qEm and qm-1 element of U. The set G / U of all right (left) cosets of the subgroup U can now be seen as the quotient set G / E ( U brings about the equivalence relation E ), and because its elements (the cosets of U) form a group, it can be called the quotient group (sometimes called factor group) of G to U.
In this way we can, because of the mentioned correspondence of elements to certain classes, set up a mapping or transformation k from G to G / U, defined by q --- [q] = qU ( = Uq in our case) for every element q of G, for example a --- [a], b -- [a], x --- [x], y --- [x], etc., i.e. to every element of G a definite class is assigned, but of course several elements can be assigned to the same class. And this mapping k is called the canonical transformation.
After we have mapped the elements of G onto the set of cosets of U -- according to the canonical transformation k -- we can in turn map this set (which is a group) into some other appropriate group G*, by an injective mapping g (going both ways, but hitting only a subset of G*). It can be proved that this subset of G* which (subset) is the image under the mapping g, is a subgroup of G*.
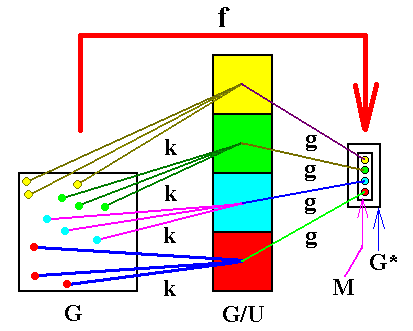
If we now perform yet another mapping f from our group G directly into the group G* in such a way that the image of f, i.e. f(G), coincides with the just mentioned subset of G*, and further in such a way that the images of the elements of G under f coincide with the images under the above (mentioned) mapping g from G / U to G*, then we can say that f is a homomorphism from G to G*. And this transformation f ( i.e. the homomorphism f from G to G* ) can also be obtained by first performing the canonical transformation k from G to G / U (which itself is also a homomorphism), and then the mapping g from G / U to G*.
The set G / U (which is a group) is illustrated in the above group table. The group G* to which the homomorphism (finally) goes will be illustrated in due course (in fact its subgroup which is the image f(G) of the homomorphism will be considered). From the table we can see that the structure of G / U is that of the group D2 :
The elemnts of the group G / U are the cosets of U = {1, p, p2}, now forming the classes [1] ( = {1, p, p2}), [a] ( = {a, b, c}), [x] ( = {x, y, z}, and [u] ( = {u, v, w}.
Let's consider some products. We can see that
[1][1] = [1], but because [1] alone is already [1], its period is 1.
[1][a] = [a].
[1][x] = [x].
[1][u] = [u].
[a][a] = [1], so the period of [a] is 2.
[x][x] = [1], so the period of [x] is 2.
[u][u] = [1], so the period of [u] is 2.
In this all we recognize the structure of D2, i.e. the group G / U is isomorph to D2. This implies that the structure of the image of G / U under the mapping g also must have this structure. This image is a subgroup M of G*, and we will illustrate this subgroup, which has the structure of D2, by means of one of its crystallographic realizations, namely the symmetries occurring in the Prismatic Class (2/m) of the Monoclinic Crystal System.
Our mapping g from the quotient group G / U to the subgroup M of G* will correspond their elements as follows :
[1] --- 1 (identity transformation)
[a] --- m (reflection)
[x] --- r (rotation by 1800)
[u] --- i (inversion in a point)
Now we can give the group table of M (subgroup of G*, and equal to g(U / U)) :
| 1 | m | r | i | |
| 1 | 1 | m | r | i |
| m | m | 1 | i | r |
| r | r | i | 1 | m |
| i | i | r | m | 1 |
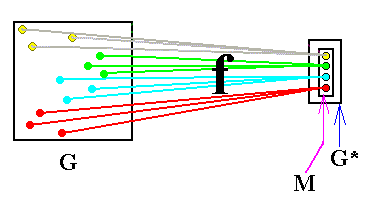
And of course the homomorphism f maps our group G directly into G* and onto M.
Having all this in mind we can summarize and elaborate further the important concept of homomorphism (See DEVLIN, K, Mathematics : The New Golden Age, 1988) :
One of the primary aims of science is to identify and study the basic objects from which all other objects are constructed, like the cells in biology, the atoms in chemistry, or the most fundamental particles in physics. So too in many branches of mathematics, for example in number theory where the prime numbers are the basic building blocks. So the basic objects of such fields (i.e. theories) are structurally simple, in the sense that, from the point of view of the theory, they cannot be decomposed into smaller entities of the same kind.
The fundamental building blocks in group theory are the simple groups. To explain just what these are, and how any given (finite) group can be split into component simple groups we require the concept of a homomorphic image of a group. Such an image is in fact a telescopic image of a given group. Roughly speaking, when you make a telescopic image of a group G (like we did above, and on severeal earlier occasions), what you get is a sort of 'scaled-down' version of G. The group operation of G is reflected in the telescopic image, though in a reduced form. It being reflected means that products are conserved when we go from the original group to the image group. It is a bit like looking at an object through the wrong end of a telescope : The main features of the object are preserved, but it appears smaller and many features may no longer be distinguishable.
To be a little more precise, if you start with a group G, then to form the homomorphic image, G', of G you have to associate with each element a of G an element a' of G' (called the image of a ) in such a way that for any pair of elements a, b of G with images a', b', respectively, the product of a' and b' in G' (according to the group operation of G') has to be the image of the element ab in G (i.e. ab is the product of a and b according to the group operation of G). When we call the homomorphism h, we can indicate this succinctly as :
h(ab) = h(a) h(b)
I.e. the image of the product is the product of the images.
Thus G' preserves the structure of G. And as we saw above, there is nothing to prevent several elements of G having the same image in G', and indeed it is this 'collapsing' or 'coalescing', or abstraction as we said above, of the elements that accounts for the reduction in size when you go from G to G'. In the example above we went, according to the homomorphism f, from the group D6, possessing 12 elements, to the group D2, which has only four elements. The group D2 is a telescopic image, or homomorphic image of the group D6.
Every group G has at least two telescopic images. On of these is G itself, where each element of G is its own image. This situation trivially satisfies the requirements for being a telescopic image (products are preserved), though it is clearly an extreme case. The other telescopic image which any group G possesses lies at the other extreme. It is the point image of G, namely the group which has only one element, the identity element (let us call it) e. Indeed the general definition of a group allows for an identity element to form a group of its own, albeit a rather trivial one. Its multiplication table (group table) is as follows :
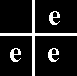
In the point image, every element of G has the same image, namely e, so in this case also the requirements of a telescopic image are satisfied : If we call this homomorphism i, then we have, for any two elements a, b of G :
i(a) = e
i(b) = e
i(ab) = e
i(a) i(b) = ee = e
Thus i(ab) = i(a) i(b),
and the condition for the preservation of products is satisfied.
A nice example of a homomorphic mapping ( = forming a telescopic image) other than the two extremes just mentioned, is the conversion of time from the 24-hour clock to the 12-hour clock :
Let G be a clock of order 24, i.e. the cyclic group C24, and let G* be the clock of order 12, i.e. the cyclic group C12. For G the identity element is 24, while for G* it is 12.
Now we can set up a homomorphism h from G to G*. For each number n from 1 to 12 in G, its image h(n) is n itself, while for n between 13 and 24 (inclusive) h(n) is n-12. So the homomorphism h is defined by the following assignments of the elements of G to those of G* :
1 --- 1
2 --- 2
3 --- 3
4 --- 4
5 --- 5
6 --- 6
7 --- 7
8 --- 8
9 --- 9
10 --- 10
11 --- 11
12 --- 12
13 --- 1
14 --- 2
15 --- 3
16 --- 4
17 --- 5
18 --- 6
19 --- 7
20 --- 8
21 --- 9
22 --- 10
23 --- 11
24 --- 12
We see that the identity of G which is 24, is mapped onto the identity of G* which is 12. But also the element 12 of G is mapped onto the identity of G*.
So the elements
1 and 13 of G are mapped onto 1 of G*
2 and 14 of G are mapped onto 2 of G*
3 and 15 of G are mapped onto 3 of G*
4 and 16 of G are mapped onto 4 of G*
5 and 17 of G are mapped onto 5 of G*
6 and 18 of G are mapped onto 6 of G*
7 and 19 of G are mapped onto 7 of G*
8 and 20 of G are mapped onto 8 of G*
9 and 21 of G are mapped onto 9 of G*
10 and 22 of G are mapped onto 10 of G*
11 and 23 of G are mapped onto 11 of G*
12 and 24 of G are mapped onto 12 of G*
The subset {12, 24} of the group G, which is mapped onto the identity element of the group G*, is called the kernel of the homomorphism and is a normal subgroup in G :
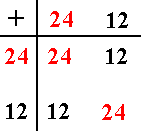
Now we can say that
h(7) = 7
h(18) = 6
h(7 + 18) = h(1) = 1 in G*.
h(7) + h(18) = 7 + 6 = 1 in G*.
So the image of the product 7 and 18 is equal to the product of the images of 7 and of 18, which means that this particular product is preserved.
We can check that this preservation is the case for all possible products in G and in G*.
Observe that in the example just given it was important that 12 (the order of G*) divides 24 (the order of G). A clock group of prime order has no telescopic images other than itself and the point image. This provides a family of examples of simple groups :
A simple group is a group whose only telescopic images are itself and the point image, which implies that it does not have a normal subgroup.
By means of telescoping, every finite group may be split into a unique set of simple groups in much the same way that a composite number is decomposed into its prime factors (In Part V we determined the homomorphic images of the group C12, and found the groups C6, C4, C3 and C2. The last two of these are groups of prime order so they do not have proper subgroups and thus do not have homomorphisms besides the two trivial ones mentioned above (the whole group, and its point image), so they are simple groups. The first two (C6 and C4) do have subgroups (for example {0, 3} and {0, 2} respectively, and because both groups are Abelian, i.e. commutative, these subgroups are normal subgroups, which in turn means that they support homomorphisms other than the trivial ones, and thus C6 and C4 are not simple groups.
Indeed the analogy of simple groups and prime numbers goes further : The number of elements in each of these simple-group components is a factor of the number of elements of the original group, and the product of all these numbers is equal to the number of elements in the original group. There, however, the analogy stops. For one thing, the simple-group components of a group may contain a composite number of elements (The rotational symmetries of the regular dodecahedron -- which form a group isomorphic with A5 -- are a simple group of order 60). Also, whereas the product of all the prime numbers in a given set is a unique number, a given set of simple groups can often be combined in different ways to form quite distinct groups. (DEVLIN, 1988, p. 120).
The dihedral group D4, the symmetries of the Square.
The group D4 can be generated by two reflections in mirrors intersecting at an angle of 450. It represents the full symmetry of the square (regular tetragon) :
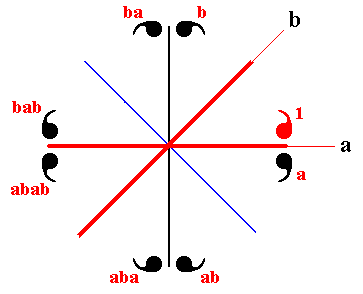
Figure 5. Generation of the dihedral group D4 by successive reflections in two mirrors (red) inclined at 450 to each other.
The pattern of motifs or operands (comma's) has a D4 symmetry. It is generated by a given initial motif (red comma). The identity transformation applied to this initial motif gives this motif (and its position) itself, so this (initial) motif is indicated by 1. The pattern is then generated as follows :
Reflection of the initial motif in the mirror a yields the motif (position and orientation) a.
Reflection of the initial motif in the mirror b yields the motif (position an orientation) b.
Reflection of the motif a in the mirror b yields the motif ba.
Reflection of the motif ba in the mirror a yields the motif aba.
Reflection of the motif aba in the mirror b yields the motif baba, which is not as such indicated in the Figure, but which is the same as the motif abab as we will see shortly.
Reflection of the motif b in the mirror a yields the motif ab.
Reflection of the motif ab in the mirror b yields the motif bab.
Reflection of the motif bab in the mirror a yields the motif abab.
The group table for the group D4 is the following :
| 1 | r | r2 | r3 | a | b | c | d | period | |
| 1 | 1 | r | r2 | r3 | a | b | c | d | 1 |
| r | r | r2 | r3 | 1 | b | c | d | a | 4 |
| r2 | r2 | r3 | 1 | r | c | d | a | b | 2 |
| r3 | r3 | 1 | r | r2 | d | a | b | c | 4 |
| a | a | d | c | b | 1 | r3 | r2 | r | 2 |
| b | b | a | d | c | r | 1 | r3 | r2 | 2 |
| c | c | b | a | d | r2 | r | 1 | r3 | 2 |
| d | d | c | b | a | r3 | r2 | r | 1 | 2 |
Table 8.3
In the above table for the dihedral group D4 we clearly see the normal subgroup C4 {1, r, r2, r3}, and its two cosets, namely itself and the set {a, b, c, d}. The table is divided into four blocks of which the top left-hand corner is the (table of the) subgroup {1, r, r2, r3}, and it will be seen that the bottom right-hand block also consists entirely of the elements of that subgroup. The remaining two squares are entirely filled with elements from the coset {a, b, c, d}, so that the table possesses the broad overall structure of the C2 group :
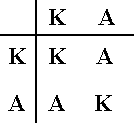
This is the telescopic image (homomorphic image) of our group D4, where K denotes the kernel of the homomorphism, i.e. the set of all elements of our original group that are mapped by the homomorphism onto the identity element of the image group, and A denotes the set {a, b, c, d}.
The group D4 can be realized as the group of the full symmetry of the Square, and at the same time of the Tetragonal Pyramid. These symmetries of the square are indicated in the next Figure.
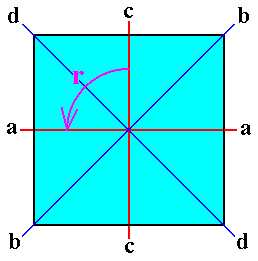
Figure 6. The full symmetry of the Square (regular tetragon).
r --- anticlockwise rotation of 900 (r 2 then is 1800, and r 3 2700).
a, b, c, and d are reflecion lines.
The complete symmetry of the Square is equal to the complete symmetry of the Regular Tetragonal Pyramid (as the Egyptian pyramids indeed are). As such it is the promorph or stereometric basic form of all the single non-twinned crystals of the Ditetragonal-pyramidal Class (4mm) of the Tetragonal Crystal System, and belongs to the Isopola tetractinota (Stauraxonia heteropola homostaura) of the Promorphological System of Basic Forms.
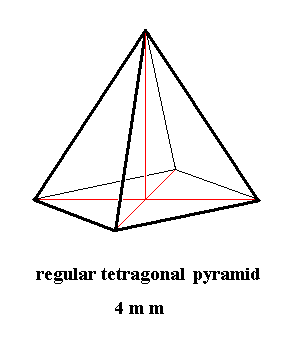
Figure 7. Regular Tetragonal Pyramid, Stereometric Basic Form of all the (single) crystals of the Ditetragonal-pyramidal Class of the Tetragonal Crystal System.
The particular symmetry transformations of this Crystal Class (4mm) are :
Identity,
900 rotation about the pyramid's main axis,
1800 rotation about the pyramid's main axis,
2700 rotation about the pyramid's main axis,
reflection in meridian plane containig cross axis a (See also Figure 6),
reflection in meridian plane containing cross axis b,
reflection in meridian plane containing cross axis c, and
reflection in meridian plane containing cross axis d.
As such we see these symmetry transformations in Table 8.3.
The group D4 is also realized in two other Classes of the Tetragonal Crystal System, namely in 4*m2 and in 422 (In the crystallographic literature the asterisk is replaced by a horizontal score above the 4.) :
The promorph or stereometric basic form of all the single non-twinned crystals of the Class 4*m2, i.e. the Tetragonal-scalenohedric Class, is the Tetragonal Bisphenoid or Tetragonal Tetrahedron. See next Figure.
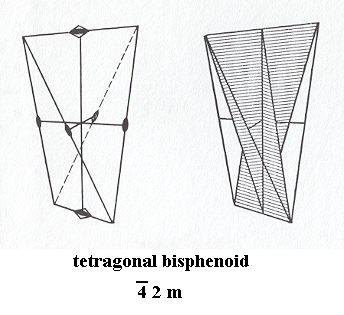
Figure 8. Tetragonal Bisphenoid, Stereometric Basic Form of all the (single) crystals of the Tetragonal-scalenohedric Class of the Tetragonal Crystal System.
Left image : The position of the rotational axes. Small square with solid oval indicates a 4-fold rotoinversion axis. Small oval indicates a 2-fold rotation axis.
Right image : The position of the two mirror planes.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
As such this promorph belongs to the Scalenoidea dimera (Stauraxonia homopola) of the Promorphological System of Basic Forms.
The symmetry transformations of this Class (4*2m) are the following :
One element of period 1 (identity).
Two elements of period 4 (900 rotation + inversion, and 2700 rotation + inversion).
Five elements of period 2 :
(1802 rotation + inversion,
1800 rotation about cross axis,
1800 rotation about other cross axis,
Reflection in plane containing main axis and bisector, and
Reflection in plane containing main axis and other bisector).
So the elements of Table 8.3 (This table expressing the symmetries of the Square or Regular Tetragonal Pyramid) need only be properly renamed and reinterpreted to obtain the group table of the Class 4*2m (Tetragonal-scalenohedric Class).
Finally, the dihedral group D4 is realized in the symmetry of crystals of the Class 422, i.e. the Tetragonal-trapezohedric Class (of the Tetragonal Crystal System). The promorph or stereometric basic form of all the single non-twinned crystals of this Class is represented by the Tetragonal Trapezohedron. See next Figure.
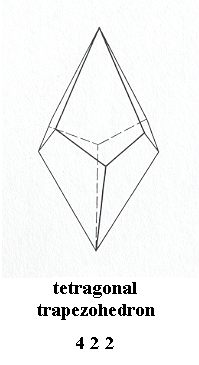
Figure 9. Tetragonal Trapezohedron, Stereometric Basic Form of all the (single) crystals of the Tetragonal-trapezohedric Class of the Tetragonal Crystal System.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
This promorph belongs to the Scalenoidea quadrimera (Stauraxonia homopola) of the Promorphological System.
The symmetry transformations (forming the dihedral group D4) of the Class 422 (Tetragonal-trapezohedric Crystal Class) are :
One element of period 1,
Two elements of period 4, and
Five elements of period 2.
If we rename and re-interpret the elements of Table 8.3 properly, we get the particular group table for crystals of the Class 422.
The abstract symmetry group D4 thus applies to the Square, the Regular Tetragonal Pyramid, the Tetragonal Bisphenoid and the Tetragonal Trapezohedron. It also applies to the direct symmetries of the Tetragonal Bipyramid. If we now add to these direct symmetries all the opposite symmetries (enantiomorphs) of that bipyramid we obtain the product group D4 x C2. [ It is not D8, because when we have the group Dn as the direct symmetries of a solid (The n-fold bipyramid) it is, when the enantiomorphs are added, only D2n when n is odd (BUDDEN, p. 293)]. The elements of the group D4 x C2 will be :
The Regular Tetragonal Bipyramid, while possessing the above listed symmetry transformations, which form the group D4 x C2, is the promorph or stereometric basic form of all the single non-twinned crystals of the Ditetragonal-bipyramidal Class (4/m 2/m 2/m) of the Tetragonal Crystal System. See for this promorph the next Figure.
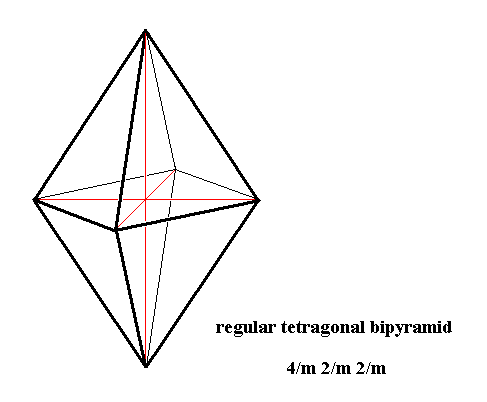
Figure 10. Tetragonal Bipyramid, Stereometric Basic Form of all the (single) crystals of the Ditetragonal-bipyramidal Class of the Tetragonal Crystal System.
This promorph belongs to the Isostaura octopleura (Stauraxonia homopola) of the Promorphological System.
The group D4 x C2 is also called D4i.
The derivation of new groups out of the product of two (or more) groups, and then obtaining groups like D4 x C2, is discussed and explained further down (For the direct product, as in the latter case, See the next document, while for the indirect product (also called semidirect product), see Part XII).
The dihedral group D5
The dihedral group of order ten, D5, can be illustrated with the Regular Pentagon. See next Figure.
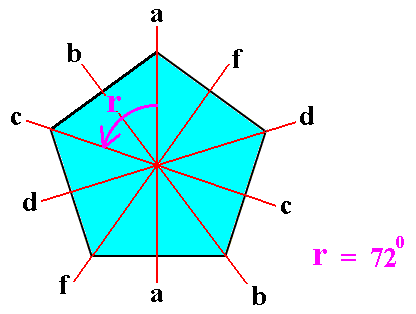
Figure 11. The Regular Pentagon, illustrating the dihedral group D5. Its five interradial axes, a, b, c, d, and f, are mirror lines.
r indicates an anticlockwise rotation of 720 about the center of the pentagon.
The symmetry transformations of the Regular Pentagon, forming the group D5, are as follows (See Figure 11) :
The distribution of the periods over the elements thus is :
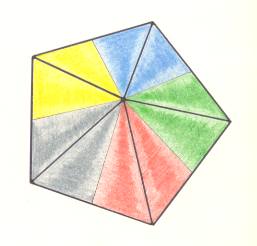
Figure 12. Slightly oblique top view of a five-fold regular pyramid as the basic form of the Pentactinota. The five antimers are indicated by colors.
The group Dinfinite
The next Figure shows a pattern produced by reflections in two mirrors inclined at 200.
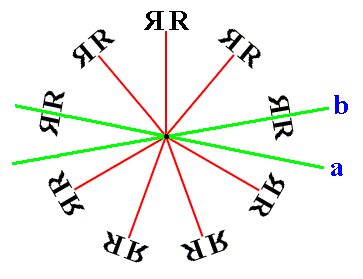
Figure 13. Pattern generated by reflecting a motif in two mirrors making an angle of 200. The symmetry of the pattern is according to the dihedral group D9 .
If we now reduce the angle between the two mirror lines in Figure 13 and magnify the pattern, the circle would become larger and larger, and we get groups like D100, D1000, D10000, etc. (as long as the angles involved are genuine fractions of 3600). When, in the limit, the mirror lines are finally parallel we get a strip pattern of an infinite number of motifs, representing the dihedral group Dinfinite , as the next Figure shows.
Figure 14. The group Dinfinite generated by two reflections a and b performed on the operand (motif) R.
The generators a and b generate an infinity of group elements. Note that these two generators are both of finite period, namely 2. But ab and ba are inverse translations, and each of these has infinite period. ab is a translation through twice the distance between the mirror to the left, and ba is the translation through this distance to the right. And how often we repeat such a translation, it will never bring the motif back to where it started to be. In the above diagram, the operations which produce the respective images are shown in each case.
If a group is generated by two elements of period 2, it is dihedral.
This means that we can also generate Dinfinite when the two generators a and b are, say, half-turns about two points. In this case ab is a translation, and we get the pattern generated as in the next Figure :
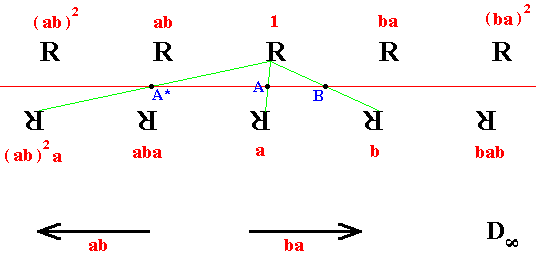
Figure 15. Infinite strip pattern generated by half-turns about two points A, B.
The pattern is according to the group Dinfinite
Note that if A* = ab(A), i.e. when the point A is shifted by the translation ab, then a half-turn about the point A* (call this operation a*) is given by
a* = (ab) a (ab)-1
Earlier we defined that the element xyx-1 of a group G is the transform of the element y in G by the element x in G.
So (ab)a(ab)-1 is the transform of the element a in our present infinite group by the element ab in that same group. We can show that this transform a* = (ab)a(ab)-1 is in fact the element (ab)2a.
Before we do this we will first in general show that the inverse of a product is the product of the factors, but with their order reversed :
(xy)-1 (xy) = 1. (identity) [because by definition pp-1 = p-1p = 1 (identity)].
(xy)-1(xy)y-1 = y-1.
(xy)-1x = y-1.
(xy)-1xx-1 = y-1x-1.
(xy)-1 = y-1x-1.
In our present group a and b are half-turns and their period is 2.
Thus aa = a2 = 1, bb = b2 = 1. This means that a = a-1, and b = b-1.
Now we wil show that the transform of element a by the element ab , i.e. a* = (ab)a(ab)-1, is in fact the element (ab)2a.
a* = (ab)a(ab)-1 =
abab-1a-1 = ababa = (ab)2a.
If, on the other hand, the two generators a and b of period 2 (generators for the group Dinfinite) are a reflection (in a line a) and a half-turn about the point B, then we shall get an infinite group so long as B is not on the axis of reflection. See next Figure.
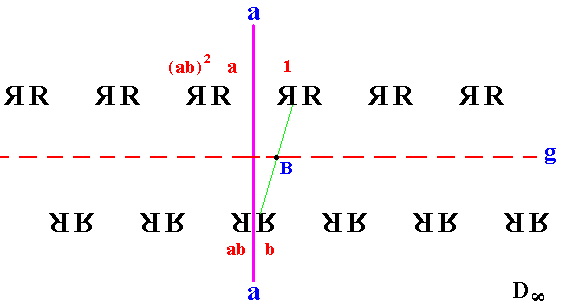
Figure 16. Infinite strip pattern generated by half-turn about B and reflection in mirror a.
It will be seen from the Figure that ab is a glide reflection g in the line through B perpendicular to the mirror, and that its inverse g-1 is ba. (A glide reflection in a line g is a reflection in that line, followed by a translation.) Naturally this glide reflection must itself generate an infinite group, and in fact Gp(g), i.e. the group generated by the element g, is the infinite cyclic group (Cinfinite), which of course is a subgroup of Dinfinite. This subgroup consists of the elements ab, (ab)2, (ab)3, (ab)4, (ab)5, etc. See for this glide reflection the next two Figures.
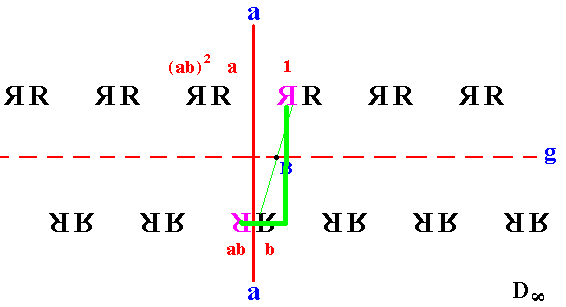
Figure 17. Infinite strip pattern generated by half-turn about B and reflection in mirror a. The glide line (g) is indicated by the red dashed line, while the corresponding glide operation is indicated by the thick green hooked line going from 1 to ab. The vertical part of this green line is a reflection in the red dashed line. The second part is a translation parallel to the dashed line.
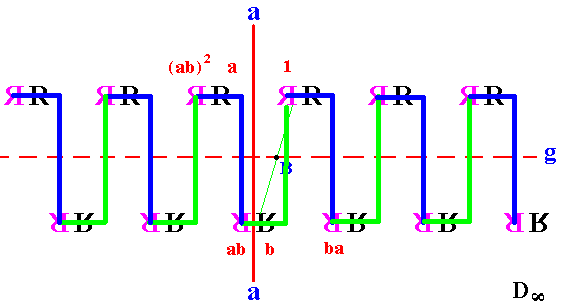
Figure 18. The glide reflection g and its inverse g-1 generate the subgroup Cinfinite .
The element (ab)2 is a translation t ( = g2), which also generates an infinite cyclic group (also Cinfinite). This group then consists of the elements (ab)2, ((ab)2)2, ((ab)2)3, ((ab)2)4, ((ab)2)5, etc., or equivalently, of the elements t, t2, t3, t4, t5, etc. The images which belong to this subgroup Gp(t), i.e. the group generated by t) consist of all those R's which are the right way up : R.
 , form the subgroup Gp(b, t), and consist of those images which result from transformations containing an even number of reflections. This is because t = (ab)2 = abab, containing two reflections (a), and a repetition of (ab)2 will keep the number of reflections even. The element b is just a rotation.
, form the subgroup Gp(b, t), and consist of those images which result from transformations containing an even number of reflections. This is because t = (ab)2 = abab, containing two reflections (a), and a repetition of (ab)2 will keep the number of reflections even. The element b is just a rotation.
This group is clearly an infinite cyclic group totally isomorph with the group (Z, +) of all integers, and has the same number of elements (This can be demonstrated by the fact that we can correspond to each interger a multiple of 10). Moreover (with respect to Dinfinite being a subgroup of Dinfinite), Dn is a subgroup of D2n (as we can see in regular 2n-gons with their inscribed n-gons). So we have D100 is a subgroup of D200, and this remains true however large the order of the dihedral group.
We continue with the pattern depicted in the Figures 16 -- 18, i.e. the infinite pattern generated by a reflection in a line a, and a half-turn about the point B. The next Figure shows how the element b(ab)3 = b a b a b a b is generated (starting from element 1) according to the following steps (executing the sequence from back to front) :
b a b a b a b.
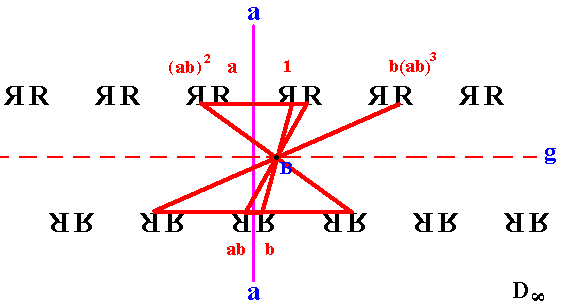
Figure 19. Generation of the element b(ab)3 of the Dinfinite pattern of the prevoius Figures.
The next Figure depicts the generation of the element (ab)2a = ababa by the following successive steps :
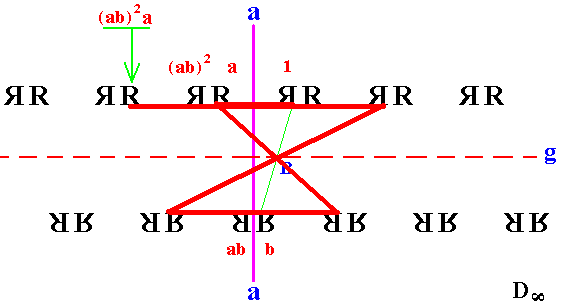
Figure 20. Generation of the element (ab)2a.
When B, the point about which the half-turn takes place in the previous Figures, lies on the mirror line a, we now have ab = ba, so that ab has period 2 :
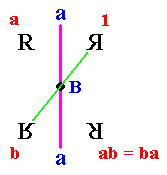
Figure 21. Finite pattern generated by a reflection in a line and a half-turn about the point B on that line. The group D2 is generated.
Because the group D2 is finite we can draw the (complete) group table for the pattern of Figure 21 :
| 1 | a | b | ab | |
| 1 | 1 | a | b | ab |
| a | a | 1 | ab | b |
| b | b | ab | 1 | a |
| ab | ab | b | a | 1 |
Table 8.4
This concludes our exposition of dihedral groups.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals