

e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Symmetry groups
The relevance of Group Theory for the Theme of the present website
In the introduction to Group Theory in Part Two we expounded the relevance of this theory not only for understanding the structure (especially the aspect of symmetry) of three-dimensional crystals, but also for the general theme of this website (Its first Part [ accessible by clicking on back to homepage ], as well as its present (second) Part). The general theme concerns pattern formation in the natural world. And this is linked up with the origin of real genuine beings, inorganic as well as organic. Such a real genuine being or thing is a being in the full sense, it is an intrinsic whole like a crystal or an organism, which originates at the occasion of certain extrinsic conditions it is true, but, once the process has initiated develops according to intrinsic causes. This in contradistinction to an aggregate, which has all its causes being extrinsic, and so does not appear as a stable repeatable pattern. And also quantum entities -- like electrons -- cannot be considered as real genuine beings, they are, according to me, deficient beings, not full-fledged real beings.
In ancient philosophy (Greek and Medieval philosophy) one tried to locate the very cause of a thing-as-it-is-in-itself. In other words, one was looking for the thing's essence that would account for the thing's intrinsic whatness (i.e. what the thing is in and for itself, and not what it is for us), for its stability and repeatability, in fact its lawfulness.
The great philosopher Plato (4th century B.C.) -- who invented metaphysics, i.e. the theory of being insofar being -- conjectured that the 'intrinsic' cause of a genuine being or thing, in the sense of the very essence of the thing, lies nevertheless, in a way, outside the thing itself. It resided in a non-material world of Ideas, or in other words, the essence of a thing was considered to be 'transcendent' with respect to the thing. Concrete things, as they are visible in our material world, were just more or less imperfect images of the pure transcendent Ideas.
His great pupil, on the other hand, Aristotle, thought otherwise. For him the essence of a real genuine (material) being lies in the thing itself, it is not transcendent but immanent. It is the very core of that thing, a stable core that dictates what the thing intrinsically is. It does not alter under accidental changes of the thing : Socrates remains Socrates, and with it remains a human being, whether he is occasionally tanned by the summer sun, or not so, namely during the winter months. The condition of being tanned is purely accidental with respect to Socrates being Socrates, and Socrates being a human being.
This metaphysical theory of Aristotle was worked out further by St Thomas Aquinas in the 13th century. Especially St Thomas' work on that subject is expounded in the first Part of this website (Classical Series of documents). But in that same first Part of our website (Non-Classical Series of documents) we wanted to go further with this theory (i.e. we were not contented to limit ourselves to just presenting a historical account of it). We wanted to see whether this theory, this "Substance-Accident Metaphysics" (Substance is often more or less equated with Essence), to which only a few contributions came after St Thomas, could still stand today, especially in the light of the many discoveries done by Natural Science. This investigation is indeed carried out in the first part of this Website, and the conclusion is that the theory still stands, beit with some amendments. And what is very significant -- and is substantial for the just mentioned claim -- the theory is worked out fully, i.e. we created a detailed account of it, using a lot of findings of modern science insofar as these findings were relevant, more or less certain, and of sufficient generality. So in the website's first Part we were trying to precisely locate the essence or intrinsic cause of a real genuine being. We first of all found out that it is immanent, not transcendent. So we went along the lines of Aristotle and St Thomas Aquinas. Secondly we found out that modern Dynamic Systems Theory was holding the key for the solution of our problem (The precise location and nature of the essence of a thing). This Theory of Dynamical Systems and its metaphysical relevance is introduced in that same first Part of our website. The main conclusion, in a succinct form, about the location and nature of the essence of a true being (given already earlier at the introduction to Group Theory) is as follows :
The E s s e n c e or intrinsic cause of a real and genuine being or thing is the D y n a m i c a l L a w of that Dynamical System that generated that thing. This dynamical law is inherent in the system elements, but exists there in a dispersed manner. As essence it exists in the thing generated.
So real things, real beings, originate in the context of certain dynamical systems. Such a true being is an intrinsic whole, completey unified, a genuine individuum, which is a totality of essental features co-generated by the original dynamical system. Such a dynamical system I call a totality-generating system, in contrast to systems that do not create a Totality, but only rearrange the elements of such a system without organizing them into a coherent whole or pattern. When a dynamical system generates a multitude of Totalities, a multitude of new true beings, we concentrate on just one of them. The dynamical law of a dynamical system, and especially that of a totality-generating system is immanent in the system elements. So its existence is dispersed over the participating system elements, which means that it is present in an abstract version or condition. Initially the dynamical system consists just of the individual system elements which form a more or less homogenic mass. In this condition the system has maximal symmetry. As soon as the system begins to organize its elements a definite pattern begins to appear, eventually resulting in the origin of the Totality or genuine being. With this the symmetry of the whole system is generally lowered, a phenomenon that is called symmetry-breaking. In Group Theory symmetry-breaking means the transition from a given group to one of its subgroups. Symmetry-breaking in fact means the origin of features in the sense of differentiations, directedness (i.e. a definite orientation of parts), functions, etc. The initially high symmetry of the system is lowered to some intermediate symmetry or even to total asymmetry. We can see this process in the origin of a crystal and in the individual development of an organism. When such a stable unified pattern with intrinsic boundaries has originated from the more or less homogeneous mass of system elements, we say that the very essence of that pattern (with intrinsic boundary), which we can now call a Totality, or genuine being or thing, is the dynamical law that governed the dynamical system that generated that Totality. As such this dynamical law, this essence, although immanent in the thing generated, has still a more or less abstract existence. Its way of being is not that of a concrete thing, it is implicit rather then explicit. We say that the essence resides in the 'genotypical domain' of the thing. But the very features that are generated by the dynamical system (governed by the mentioned dynamical law) are explicit, concrete (i.e. not abstract). The new being is a genuine totality of its intrinsic but concrete features and properties. We say that these features and properties exist in the 'phenotypical domain' of the thing. In addition to such intrinsic and stable features, there are also the 'accidental features'. They are mainly generated by extrinsic and external agents (extrinsic and external with respect to the given thing or true being). And such accidental features can be replaced by others while the intrinsic features remain constant. The latter are generated and maintained by the dynamical law of the initial system, which as essence resides in the thing generated. While the essence of a thing is generally not directly evident and easily described or formulated, because it is only implicitly present in the thing, the features and properties it has generated are directly evident (after they have been distinguished from accidental features) and susceptible to description and formulation. Of course there are many many such features and properties, but they all, in a way, represent the one essence of the given thing. So in studying this more or less hidden, and abstract essence we must direct our attention to the features and properties produced by it, because they are directly observable. On this website we cannot of course study all those (intrinsic) features, but will concentrate on some of them, especially STRUCTURE, PATTERN, SYMMETRY and FORM, which are of course closely related to each other. The most important of these is SYMMETRY. And the various symmetries we encounter in real beings are the results of symmetry-breaking processes. The dynamical law of a totality-generating dynamical system brings about such a symmetry-breaking process, which leads to the ongoing differentiation of the poles of the imaginary axes of a body, be it a crystal or an organism. This process of differentiation, the transition from homopolar to heteropolar body axes is extensively described in our documents on Promorphology in the present part of our website (See H E R E to see where it begins). This Promorphology discusses the basic symmetries of Organisms and also of Crystals, resulting in a Promorphological System of Stereometric Basic Forms, yielding a great many "promorphological categories" or promorphs, which are representations of the basic symmetry of the relevant organisms or crystals in purely geometric terms, resulting in the presentation of geometric bodies such as spheres, ellipsoids, cones, pyramids, which themselves represent the symmetry of organisms and crystals. With respect to organisms these are often the result of idealizing, because of the strong variability generally present in the organic world. We have tried to be as less arbitrary as we possibly could in establishing the Stereometric Basic Form (or promorph) of a given organism. In the case of crystals the symmetry generally is clear-cut, but there also we indicate the Stereometric Basic Form wholly in geometric terms (instead of partly physical terms).
And all this, finally, is where Group Theory comes in, the subject of the present series of documents.
The central concept in Group Theory is a GROUP. This is a very abstract concept, which implies that it can crop up in many disparate concrete cases, one of these are the cases of concrete symmetry. And even within symmetry it is general, resulting in the fact that it can reveal unexpected kinships between several distinct symmetries. We gave an example in the introduction to Group Theory in Part II of the present Series of documents. A Group is a type of algebraic structure. It is a set of elements, and for the combining of those elements there is defined one operation (This group operation can be different for different groups, but every group has only one such operation defined for the combination of the group elements) (There are other algebraic structures which possess two such operations, but these are for that reason no groups). This group operation must be such that it be associative, and admits of an identity element to be present. Furher every group element must have its inverse also within the group. In this way a group is a self-contained unity.
Among the very many existing groups there are groups of a special type, namely the so-called simple groups. These are groups that have no proper telescopic images, i.e. they cannot be mapped onto a smaller group (the telescopic image) that has the same basic structure, more precisely, in which products are preserved. In the foregoing documents we have encountered many such telescopic images. The corresponding mappings are called homomorphisms, and the telescopic images that are being produced are called homomorphic images. Absence of the possibility of homomorphisms means that such groups do not have normal subgroups. So simple groups do not admit of homomorphic images and do not possess normal subgroups.
Finite simple groups are generally regarded as the "fundamental particles" of finite group theory, so they are of considerable theoretical importance. The way we must imagine such groups to be fundamental constituents of group structures is that we must see them as that what remains after we have completely telescoped a given (non-simple) group, i.e. when we have formed its telescopic images, and when these are not already themselves simple groups we have to form telescopic images of them in turn, until we end up with groups that do not admit anymore of creating homomorphic images [apart from those special homomorphic images consisting either of the group itself or its point image -- the latter is the group formed by the identity element alone], and which are then consequently simple groups. Indeed, by means of telescoping, every finite group may be split into a unique set of simple groups in much the same way that a composite number is decomposed into its prime factors (DEVLIN, 1988, p. 120. See below).
So the simple groups are in some significant sense fundamental, and therefore they must play an important part in the classification of groups. In fact mathematicians set out, and finally succeeded, in classifying all simple groups. A very interesting and accessible account of the efforts of classifying all simple groups is given by DEVLIN, K. Mathematics : The New Golden Age, 1988. For our purposes it is important to get an idea of the existence of the several types of groups, in order to give some relief to the symmetry groups describing geometrical symmetries.
Classification of finite simple groups.
Only by the year 1980 one succeeded in classifying all existing finite simple groups.
First of all we must distinguish between commutative groups and non-commutative groups (Abelian, respectively non-Abelian groups as they are also called). In an Abelian group we have a * b = b * a for all elements a, b whatsoever of the group, where * represents the group operation. But if at least one pair of elements does not comply with this, then the group is non-Abelian. This distinction applies to simple as well as to non-simple groups.
Further we have among groups (simple as well as non-simple) the so-called cyclic groups, which we have learned to know in the foregoing documents. These are groups that need only a single generator to produce all the group elements. They all are Abelian. Moreover they are (a type of) symmetry groups, describing for example the rotational symmetries of regular polygons or pyramids. Of these 'clock groups' only the ones which have a prime number of elements (i.e. are of prime order) are simple groups (cyclic groups of composite order are not simple groups) (Recall that a prime number is a number only divisible by 1 and by itself, like the numbers 1, 2, 3, 5, 7, 11, 13, 17, etc.).
We now have identified the first (regular) family of simple (finite) groups, the cyclic groups of prime order. Of course there are infinitely many such groups, so the family itself is infinite.
The second family of (finite) simple groups are among the alternating groups discussed in the previous document. Alternating groups are special subgroups of permutation groups. A permutation group Sn is a set of all possible permutations of n symbols (which could be letters, numbers, or whatever), under the group operation of successive application of permutations. Now it is proved that any finite group of order n is isomorphic to a subgroup of the permutation group Sn (Cayley's Theorem). (Isomorphic means that the two groups can be mapped onto each other by a 1,1 correspondence of their elements, and that the mapping preserves products, i.e. preserves structure.). Now, as we saw in the previous document, any permutation group consists of an equal number of even and odd permutations. While the odd permutations cannot form a (sub)group, because they are not closed under the operation of successive application, the even permutations do form a (sub)group of their own, and such a group is called an alternating group.
Now let us look to the permutation group S2, i.e. the group of all permutations of two symbols, say A and B (which is isomorphic to the group C2). It consists of only two elements, namely the identity permutation AB (which means that A remains A, and B remains B), and the permutation BA (which means that A becomes B, and B becomes A, and thus going from the sequence AB to the sequence BA). The identity permutation needs zero transpositions (swappings) and thus is an even permutation. The permutation BA needs one transposition to be accomplished, so this permutation is odd. So the alternating group formed out of S2 consists of the identity permutation only. And because it obviously does not admit of any telescopic image it is a simple group, be it a trivial one.
Now let us look to the permutation group S3, i.e. the group of all permutations of three symbols. It consists of six permutations, half of them are even. These even permutations are with respect to the symbols A, B, and C :
ABC (the identity permutation), BCA, and CAB. Indeed BCA can be obtained by two transpositions, namely (A B) and (A C) :
ABC --- BAC --- BCA. So the permutation BCA is even.
CAB can also be obtained by two transpositions, namely by the transpositions (A C) and (A B) :
ABC --- CBA --- CAB. So the permutation CAB is even.
So the permutations ABC, BCA and CAB together form the alternating group S3, and this group is isomorphic to the cyclic group of order 3, because the elements BCA and CAB are both of period 3, while the element ABC is of period 1, and this is the fingerprint of the cyclic group of order 3. Let's check the periods of the two non-identity elements :
A B C
B C A
C A B
A B C
So indeed the period of the permutation BCA is 3.
A B C
C A B
B C A
A B C
So indeed the period of the permutation CAB is 3.
So we have shown that the alternating group, formed from the permutation group S3, is isomorphic to the group C3, i.e. to the cyclic group of order 3. And because this is a cyclic group of which the order is prime, it is a simple group, and as such (and as being commutative) it belongs to the first family of finite simple groups. This family consists of all commutative, i.e. Abelian, finite simple groups. All other simple groups are non-commutative (non-Abelian).
If we now look to the permutation group S4, i.e. the group of all permutations of four symbols, then we can deduce the alternating group A4, consisting of all even permutations of S4. This group, however, turns out not to be simple (This we will show in due course).
When, finally, we look to all alternating groups An where n is greater than 4, then it has turned out that all of them are simple (non-commutative) groups, and they represent the second (regular) family of (finite) simple groups. Of course this family also contains an infinite number of (alternating) groups, so we say the family is infinite.
In addition to these two regular infinite families of simple groups, 16 other such families are found, making a total of 18 regular infinite families of simple groups.
Also found were a number of highly irregular one-off groups that did not fit into any known pattern. One of these sporadic simple groups, as they came to be called, has 7920 elements, another has 244823040 elements, and yet another has 175560 elements. All in all 26 sporadic simple groups were discovered. The largest of them has 808017424794512875886459904961710757005754368000000000 elements.
It is now known that the finite simple groups consist of the groups which make up the 18 regular, infinite families of groups, together with the 26 sporadic groups, AND NO MORE.
So the ultimate groups, the simple groups, are definitively classified.
In the following we will concentrate on symmetry groups, with respect to the description of two- or three-dimensional finite or infinite figures and patterns. We can find them among simple groups, for instance the Icosahedral Group A5, which is the alternating group of order 60 , and which represents the rotational symmetries of the Regular Dodecahedron or Icosahedron [ It does not, and cannot, occur in crystals, but does occur (as subgroup) in (the promorph of) certain organisms ], further, the whole family of cyclic groups of prime order, all being simple groups, are symmetry groups (of which some occur in crystals (C1, C2 and C3 ), and some in organisms [ There, in addition to C1, and -- at least as a subgroup -- C2 and C3, we will also find (as subgroup) C7, but especially C5 (also as subgroup) ], but (we find symmetry groups) also among non-simple groups, for instance the Tetrahedral Group A4, which is the alternating group of order 12, and which represents the rotational symmetries of the Regular Tetrahedron, and does occur in crystals as well as in organisms (but in the latter probably as subgroup only). Further the cyclic groups of composite order (i.e. non-prime order) are symmetry groups, some occuring in crystals (C4 and C6 ), and many in organisms (especially, and at least as subgroups, C4, C6, C8, and occasionally C9 ). Also among the Dihedral Groups, like D2, D3, etc. we find symmetry groups, representing the symmetry of two- or three-dimensional figures or patterns, and which are non-simple groups. Some of them occur in crystals, more of them occur in organisms (where the corresponding cyclic groups, mentioned just above, occur as subgroups).
Note that being a simple group is a rare property. We find them as cyclic groups of prime order, we find it in the group A5 of order 60, and in the group of all automorphisms of the product group C2 x C2 x C2, where this automorphism group is of order 168. Apart from these there are no other simple groups of order less than 168.
With respect to finite cyclic groups of order n, whether they be subgroups of, say dihedral groups, or standing on their own, and when interpreted geometrically for two- or three dimensional figures, the whole group can be generated by one element. These elements can be written as 1, r, r2, r3, ..., rn-2 and rn-1. And in all these cases rn = 1. The number n must be a whole number. Applied to a regular polygon, we must say that the polygon has rotational symmetries according the group Cn which means that when we draw lines from the center of the polygon to its vertices (corners), the angles between these lines are all equal to 3600 / n.
When we add the polygon's mirror symmetries (its 'enantiomorphs') we get the dihedral group Dn with twice as many elements. In it the corresponding rotations then form a subgroup of the dihedral group. Further, the symmetry content, and therefore the group, is the same for a polygon and for its corresponding (single) pyramid erected on it (with its apex right above the polygon's center) :
The regular 6-fold twisted hexagon (See next Figure) and the corresponding regular twisted pyramid (having its apex right above the center of the twisted hexagon) both have a symmetry according to the group C6, while the regular hexagon and the regular 6-fold pyramid (having its apex right above the center of the hexagon) both have a symmetry according to the group D6.
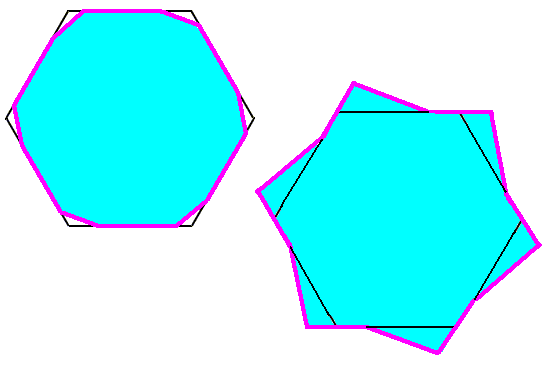
Figure 1. Two examples of (regular) Twisted Hexagons (derived from normal hexagons).
Left : With convex angles, as they occur in crystals.
Right : With concave (i.e. receding) angles, as such not occurring in single non-twinned crystals.
In crystals only 1-, 2-, 3-, 4-, and 6-fold rotational symmetries can occur, because of their periodic structure. In organisms also others can occur, and indeed, 5-fold rotational symmetry is very common, as we see it in the regular Echinoderms (starfishes and some sea-urchins) and in many (regular 5-fold) flowers.
In addition to cyclic groups we find symmetry groups among the dihedral groups, like D2, D3, both occurring in crystals, and D5, occurring in organisms (full symmetry of regular Echinoderms).
Further we find symmetry groups among direct product groups, like C2 x C2 x C2, which occurs in crystals.
Also among alternating groups we find symmetry groups, like A4, which occurs in crystals, and A5, which occurs (as subgroup) in some organisms (namely some Radiolarians).
When we add to A5 the enantiomorphs we get the direct product group A5 x C2 of order 120 (as such occurring in the mentioned Radiolarians). This is the highest finite order that can occur among symmetry groups describing the symmetry of two- or three-dimensional finite patterns. So all the finite groups of order higher than 120 (i.e. having more than 120 group elements) are not symmetry groups that describe the symmetry of 2- or 3-dimensional finite patterns.
When we consider groups of infinite order, then there are some that can decribe finite as well as infinite 2- or 3-D patterns. Finite patterns according to infinite groups are for example the circle, the cone, the egg, the cylinder, the bicone, the spheroid, etc. The first three are realizations of the group Dinfinite (with subgroup Cinfinite), while the last three possess an additional mirror plane, and are described by the direct product group Dinfinite x C2.
In addition to finite patterns that can be described by infinite groups, we have infinite patterns that can also be described by infinite groups. These are the periodic patterns as we encounter them in all crystals. In such patterns a basic morphological unit is periodically repeated (in 3 directions with respect to 3-D crystals, in 2 directions with respect to (the imaginary) 2-D crystals). Of course in crystals these periodic patterns are not really infinite, but they can be considered to be so, because the period of some group element is very high indeed, and infinite for all intents and purposes. When a crystal lattice, supplied with motifs, is group theoretically described, it will be seen as being infinitely extended and valuated accordingly. The obtained results will then approximate quite closely the situation as it occurs in real crystals. The elements of the infinite groups describing the periodic patterns are translations, glide reflections and screw axes, all with an infinite period. In addition to these there can be reflections and rotations of finite period.
In the following we enumerate some finite groups, among them several symmetry groups, and refer to the Crystal Classes where they are realized. For these Crystal Classes (and Crystal Systems), see the first Part of the website (accessible by clicking on back to homepage), and there : Special Series, where you can first consult the document on The Morphology of Crystals for general information, and then (after perhaps skipping the Derivations) consult the documents on The Isometric Crystal System, The Tetragonal Crystal System, and so on.
With respect to GROUPS, a particular order, i.e. a particular number of group elements, can often sustain more than one different groups (simple groups as well as non-simple groups) :
Order 1 can sustain only one group, namely the cyclic group C1. Its only element is of period 1, and it is the identity element. It is a symmetry group. The group C1 is realized in Crystals of the Asymmetric Class (1) of the Triclinic Crystal System.
In the Promorphological System of Stereometric Basic Forms it is realized as
Anaxonia acentra.
Order 2 can sustain one group, namely the cyclic group C2 (also called D1). It is a symmetry group.
In the Promorphological System the group C2 is realized as
Heterogyrostaura tetramera (Stauraxonia heteropola gyrostaura) (When there are just two antimers present then : dimera), as
Zygopleura eudipleura (Stauraxonia heteropola heterostaura allopola), and as
Anaxonia centrostigma in the Promorphological System of Stereo metric Basic Forms.
Order 3 can sustain one group, namely the cyclic group C3 (isomorphic to the alternating group A3 ). It is a symmetry group.
In the Promorphological System it is realized as the Homogyrostaura trimera (Stauraxonia heteropola gyrostaura).
Order 4 can sustain two groups, namely C4 and D2 ( = C2 x C2 ).
In the Promorphological System it is realized as
Homogyrostaura tetramera (Stauraxonia heteropola), and as
Allosigmostaura pseudobisphenoidea (Stauraxonia homopola sigmostaura).
D2 is realized in three Crystal Classes, namely the
Rhombic-bisphenoidic Class (222) of the Orthorhombic Crystal System, the
Prismatic Class (2/m) of the Monoclinic Crystal System, and the
Rhombic-pyramidal Class (mm2) of the Orthorhombic Crystal System.
In the Promorphological System the group D2 is realized as
Scalenoidea duomera (Stauraxonia homopola), as
Allosigmostaura quadramphimera (Stauraxonia homopola sigmostaura) (When there are just two antimers present then : duamphimera), and as
Tetraphragma radialia (Stauraxonia heteropola heterostaura autopola), if we assume four antimers to be present (The geometric rhombic pyramid as such has four (geometrical) antimers.
Order 5 can sustain one group, namely C5.
Order 6 can sustain two groups, namely C6 and D3 (The latter is isomorphic to S3, the group of all permutations of three symbols).
In the Promorphological System the group C6 is realized as
Homogyrostaura hexamera (Stauraxonia heteropola gyrostaura), as
Isosigmostaura pseudorhomboedra (Stauraxonia homopola sigmostaura), and as
Isosigmostaura trimera (Stauraxonia homopola sigmostaura).
The dihedral group D3 is realized in two Crystal Classes of the Hexagonal Crystal System, namely the
Trigonal-trapezohedric Class (32), and the
Ditrigonal-pyramidal Class (3m).
In the Promorphological System the group D3 is realized as as
Scalenoidea trimera (Stauraxonia homopola), and as
Anisopola triactinota (Stauraxonia heteropola homostaura).
Order 7 can sustain one group, namely the cyclic group C7.
Order 8 can sustain five groups, namely
The cyclic group C8 cannot be realized in crystals.
In the Promorphological System it can potentially be realized as a species of the Gyrostaura homogyrostaura (Stauraxonia heteropola).
The group C4 x C2 is realized in crystals of the Tetragonal-bipyramidal Class of the Tetragonal Crystal System.
In the Promorphological System it is realized as Isosigmostaura quadrimera (Stauraxonia homopola).
The group C2 x C2 x C2 is realized in the Rhombic-bipyramidal Class of the Orthorhombic Crystal System.
In the Promorphological System it is realized as Allostaura octopleura (Stauraxonia homopola).
The group D4 is realized in three Classes of the Tetragonal Crystal System, namely the
Tetragonal-trapezohedric Class (422), the
Ditetragonal-pyramidal Class (4mm), and the
Tetragonal-scalenohedric Class (4*2m).
In the Promorphological System D4 is realized as
Scalenoidea quadrimera (Stauraxonia homopola), as
Isopola tetractinota (Stauraxonia heteropola homostaura), and as
Scalenoidea dimera (Stauraxonia homopola).
The dicyclic group Q4, finally, does not represent the symmetries of any geometric 2-dimensional figure or any 3-dimensional body, and is consequently not a symmetry group (BUDDEN, 1978, p. 246/7).
Order 9 can sustain two groups, namely
The group C3 x C3 cannot be realized in crystals. It has one element of period 1 (the identity element) and 8 elements of period 3, and is Abelian. I guess it does not represent a 2-D or 3-D finite geometric pattern.
Order 10 can sustain two groups, namely C10 and D5.
The group D5 cannot be realized in crystals.
In the Promorphological System it is realized as
Anisopola pentactinota (Stauraxonia heteropola).
Order 11 can sustain one group, namely C11.
Order 12 can sustain five groups, namely
The cyclic group C12 cannot be realized in crystals.
In the Promorphological System it is potentially realized as a species of the
Gyrostaura homogyrostaura (Stauraxonia heteropola).
The group C6 x C2 is realized in crystals of the Hexagonal-bipyramidal Class (6/m) of the Hexagonal Crystal System.
In the Promorphological System it is realized as
Isosigmostaura sextamera (Stauraxonia homopola sigmostaura).
The group D6 is realized in four Crystal Classes of the Hexagonal Crystal System, namely
Hexagonal-trapezohedric Class (622),
Ditrigonal-scalenohedric Class (3* 2/m),
Dihexagonal-pyramidal Class (6mm), and
Ditrigonal-bipyramidal Class (6* m2).
In the Promorphological System the group D6 is realized as
Scalenoidea sextamera (Stauraxonia homopola), as
Scalenoidea rhomboedra (Stauraxonia homopola), as
Isopola hexactinota (Stauraxonia heteropola homostaura), and as
Isostaura polypleura (hexapleura) (Stauraxonia homopola).
The group Q6, cannot, as far as I know, represent the symmetries of any two- or three-dimensional finite pattern, and so is not a symmetry group.
The Tetrahedron Group A4, which is the alternating group of order 12, representing the even permutations of the permutation group S4, is realized in crystals of the
Tetrahedric-pentagondodecahedric Class (2 3) of the Isometric Crystal System.
In the Promorphological System it is realized as
Subendosphaerica tetartoidea (Polyaxonia subendospherica).
Order 13 can sustain one group, namely C13.
All cyclic groups of still higher order cannot occur in crystals. And also the corresponding dihedral groups (which then have a subgroup C7 or higher) cannot be realized in crystals. And when we look to organisms, we see that forms with 7 or more antimers, and certainly with 10 or more antimers -- forms that would have their symmetry according to cyclic groups C7 and higher, or to dihedral groups D7 or higher -- become less constant. The number of rays (radii, antimers) varies within the organic species, and so does not represent a natural occurring stable pattern.
Order 15 In spite of the fact that 15 is a composite number, there is only one group of order 15, namely C15 (BUDDEN, 1978, p. 291).
Order 16 sustains several groups, among which the cyclic group C16 and the direct product group D4 x C2.
C16 cannot be realized in crystals.
In the Promorphological System it can, like C15, potentially be realized, but in organisms such many-radiate forms are not represented in a stable and constant way.
D4 x C2 is realized in crystals of the Ditetragonal-bipyramidal Class (4/m 2/m 2/m) of the Tetragonal Crystal System. [ It is not D8 (because n of Dn is even), but is denoted by D4i ].
In the Promorphological System it is realized as Isostaura octopleura (Stauraxonia homopola).
Order 24 can sustain 15 groups. In addition to the group C24, we can have the groups
The group A4 is the group of direct symmetries (i.e. the rotational symmetries only) of the Regular Tetrahedron, and is also called T. It is isomorphic to the group of all even permutations of four symbols.
The full group (i.e. now the enantiomorphs -- reflections -- included) of the Tetrahedron is isomorphic to the group S4 (BUDDEN, 1978, p. 297), i.e. to the group of all (i.e. even and odd) permutations of four symbols, and is isomorphic to the Octahedral Group O, i.e. the group of direct symmetries of the Regular Octahedron and also of its dual solid the Cube. It can be obtained by the indirect product (explained later) of D3 and D2, and is realized in two Classes of the Isometric Crystal System, namely
Pentagonikositetrahedric Class (432), and
Hexakistetrahedric Class (4* 3m).
In the Promorphological System the group O is realized as
Subendosphaerica gyroidea (Polyaxonia subendospherica), and as
Tetraedra regularia (Polyaxonia rhythmica).
The group D6 x C2 is realized in crystals of the
Dihexagonal-bipyramidal Class (6/m 2/m 2/m) of the Hexagonal Crystal System.
In the Promorphological System it is realized as
Polypleura dodecapleura (Stauraxonia homopola isostaura) (By clicking the link you will get to the Isostaura polypleura. Some species of them are enumerated and pictured, among which the six-fold bipyramid (Figure 19), the basic form of the Polypleura dodecapleura (not mentioned by name there)).
The group Ti is realized in crystals of the
Duakisdodecahedric Class (2/m 3*) of the Isometric Crystal System (not to be confused with the Class 3* 2/m of the Hexagonal Crystal System!).
In the Promorphological System it is realized as
Subendosphaerica pyritoidea (Polyaxonia subendosphaerica).
Order 48 sustains (among others), in addition to the group C48, the group Oi , which can be obtained by O x C2 ( = S4 x C2 ) (BUDDEN, p. 302).
Order 120 sustains (among others -- f.i. C120) the group S5, i.e. the group of all permutations of five symbols, and the important group A5 x C2. The group A5, the Icosahedral Group, is a subgroup of A5 x C2, and is moreover a simple group. Its order is 60. The icosahedral group can be realized as the group of direct symmetries of the Regular Icosahedron (a regular solid consisting of 20 congruent equilateral triangles as its sides), and of its dual solid (that can be inscribed in it) the Regular Dodecahedron (a regular solid with 12 faces that are congruent regular pentagons).
The orders which produce the highest numbers of groups tend to be those which have many factors, particularly high powers of prime factors. For example there are fourteen groups of order 16, and no fewer than 267 of order 64, and 238 of order 160 (BUDDEN, p. 291).
There are some more groups that can describe the symmetry of the shape of solids, namely some groups that have infinitely many elements :
Order Infinity sustains (among others -- ) the group O(2) i.e. the Orthogonal group in two dimensions : A circle can be thought of as a regular polygon with infinitely many sides. But, adding one more dimension, a Cone has precisely the same symmetry content as the circle has. The symmetry group of the Cone consists of all rotations about its main axis, together with all reflections in planes that contain that main axis. The symbol for the group is O(2), the orthogonal group in two dimensions (STEWART & GOLUBITSKY, Fearful symmetry, p. 49).
It cannot be realized in crystals.
In the Promorphological System it is realized as
Diplopola monepipeda (Monaxonia).
Another infinite group describing the shape of some solids is the group O(3), the Orthogonal Group in three dimensions. It is the symmetry group of the Sphere. It consists of all rotations about the sphere's center, and all reflections in planes that pass through that center (STEWART & GOLUBITSKY, p. 49).
It cannot be realized in crystals.
In the Promorphological System it is realized as
Homaxonia.
Further there are the 230 Space Groups, infinite groups, that describe the internal symmetry of periodic structures such as crystals.
The indirect product of groups
As we have seen, some groups can be characterized as direct products of two or more other groups. Such a product is in fact a group structure imposed on the carthesian product of sets of elements, where these sets were themselves groups. It is the definition of direct product which definitely assigns to each two elements of the mentioned carthesian product set a third element, that imposes the group structure on the carthesian product set. The direct product of the groups G and F was notated as G x F. Because the direct product has itself a group structure, such a product is a means to deduce new groups from given groups, and this is of course significant for the derivation of, say, all crystallographically realized groups from some given starting groups, like C1, C2, C3, etc. It has, however, turned out that the direct product does not exhaust all possibilities for deriving new groups. So in addition to the direct product one has established a second type of product, to cover more cases. And that is the indirect product of groups. It is also called semidirect product. Also this product, however, together with the direct product, does still not exhaust all possibilities for deriving new groups, but they do exhaust all possibilities with respect to the derivation of all crystallographic point groups (i.e. all the groups which describe the symmetry of all 32 Crystal Classes).
So on the carthesian product of two sets (that are groups) we will impose yet another definition, a definition that assigns to each two elements of that carthesian product set a third element in a different way than has been established for the direct product. This is the mentioned indirect product. And because this new type of product also imposes a group structure on the carthesian product, it also is a means of deriving new groups.
Indeed above we characterized some groups by means of the indirect product of two other groups.
In order to define the indirect product we need to briefly recapitulate some involved concepts.
An isomorphism i between two groups G and F means that there exists a mapping ( i ) such that there is a 1,1 correspondence between the elements of both groups, and that in the image of that mapping the products are preserved. The latter can be expressed as follows :
i(ab) = i(a) i(b), for all elements a, b of G, and where i is an isomorphism.
In words : The image of a product (of any two elements of G) is equal to the product of the images of those two elements.
A homomorphism h between two groups is the same as an isomorphism between them, but the correspondence between the elements does not necessarily to be a 1,1 correspondence, which means that the image group is generally a smaller group, i.e. smaller than the original group. But, also here products are preserved :
h(ab) = h(a) h(b), for all elements a, b of G, and where h is a homomorphism.
An automorphism alpha on a group G is an isomorphism from G to itself, such that products are again preserved :
alpha(ab) = alpha(a) alpha(b), for any elements a, b of G, where alpha is an automorphism.
An automorphism of a group G, just means that two or more elements of the group are swapped while preserving the structure of the group table, or, equivalently, while preserving products. And the set of all possible automorphisms of G, (and this set) under the operation of successive application of automorphisms of the group (i.e. successive application of swapping elements of G) turns out to form a group, and this group is called the automorphism group of the group G, and is denoted Aut(G).
We will now introduce the indirect product formally, later followed by an illuminating example (taken from BURZLAFF & ZIMMERMANN, 1977, p. 237--239).
Let G and H be groups.
Let the indirect product be a multiplication (according to the definition of the indirect product) of the elements of G x H.
Further, let Aut(H) be the automorphism group of H.
And further, let phi be a mapping, in fact a homomorphism, from G to Aut(H), which we write phi(g) = gphi = an element of Aut(H), which means that the homomorphism phi assigns to the element g of of the group G a certain automorphism from the group of automorphisms of the group H. Thus gphi is a certain automorphism of H. Such an automorphism thus is a certain permutation of the elements of H. So when we apply the automorphism gphi to an element of H, we get an other element of H.
g1, g2 are elements of the group G.
h1, h2 are elements of the group H.
(g, h) is an element of the carthesian product set G x H.
One now defines on the set G x H a multiplication of its elements as follows :
(g1, h1) (g2, h2) = ( g1g2, g2phi (h1) h2 ).
So when this multiplication rule is imposed on the set G x H we have the indirect product of the groups G and H, which we can denote as G semi H.
We can verbally read the above defined multiplication rule as follows :
If we multiply two elements (g1, h1) and (g2, h2) of the carthesian product set G x H according to the indirect product of G and H, then the outcome is as follows :
The first member, g1, of the pair that constitutes the first multiplication factor is multiplied (according to the group operation of the group G) with the first member, g2, of the pair that constitues the second multiplication factor. This product then forms the first member of the pair that constitutes the outcome of the product of the two factors according to the rule to be defined. The second member of that pair is formed as follows : The automorphism g2phi, which is the image of g2 -- the first member of the pair that constitutes the second multiplication factor -- under the homomorphism phi, is applied to h1, i.e. to the second member of the pair that constitute the first multiplication factor. And the result (of the application of the automorphism) is multiplied -- according to the group operation of the group H -- with h2 , i.e. with the second member of the pair that constitutes the second multiplication factor.
When this multiplication rule is imposed on the set G x H, it forms a group, and, as has been said, we write G semi H, which means the indirect product of the groups G and H, yielding the new group G semi H.
For this new group indeed to be a group, we must prove that (1) the defined multiplication of the elements of the (general) set G x H is associative, (2) that it has an identity element, and, (3) that every element of G x H has an inverse within that set. Indeed this can be proved for the general case (BURZLAFF & ZIMMERMANN, p. 237).
When we write the indirect product (also called semiproduct) of the groups G and H as G semi H, we should also indicate which homomorphism from G to Aut(H) is actually used, when this is not evident at the outset, because different homomorphisms define different indirect products. We should then write G semi (phi) H.
We will now give the promised illustrative example of the application of the indirect product of two groups.
The example explains the indirect product G = C2 semi C4.
We will show with this example that the group D4 can be obtained by the indirect product of the groups C2 and C4.
So we consider the indirect product G = C2 semi C4.
The cyclic group C2, the first factor of the (indirect) product can be given as {1, y}, while the group C4, the second factor of the product, can be given as {1, a, a2, a3}. In the latter group the identity element 1 is of course of period 1, the element a is of period 4 (we can think of a rotation by 900), the element a2 is of period 2 (1800 rotation), and the element a3 is again of period 4 (2700 rotation).
In order to determine the indirect product we must know first of all the automorphism group of the second factor, i.e. of the group C4.
Because in every automorphism the identity element must be mapped onto itself, because it cannot be swapped with any other element (In automorphisms only elements of the same period can be swapped, i.e. can be mapped onto each other), the automorphic mapping (a permutation of the elements of the group C4) can only consist in the interchange of the elements a and a3, because they are both of period 4, while a2 is of period 2. a4 = 1, and (a3)4 = 1. So only two automorphisms are possible, namely the identity permutation (of the elements of C4, let us call this automorphism e , and the permutation that swaps the elements a and a3, let us call that automorphism f.
So the automorphism group Aut(C4) is {e, f} (and is, by the way, (consequently) a cyclic group of order 2).
Because by a homomorphism phi : from C2 to Aut(C4) -- i.e. a homomorphic mapping from the first factor C2 of the indirect product to the automorphism group Aut(C4) of the group C4, the second factor of the indirect product -- the identity element 1 of C2 = {1, y} must be mapped onto the automorphism e, there are, for the homomorphism phi, only two possibilities : either the element y (of C2) is mapped onto the automorphism e, and then one obtains the direct product (explained below), or y is mapped onto the automorphism f, and one obtains the indirect product.
So we have, when choosing for the indirect product :
1 phi = e
which means that the element 1 is mapped according to the homomorphism phi onto the automorphism e.
y phi = f
which means that the element y is mapped according to the homomorphism phi onto the automorphism f.
The elements of the group G, i.e. the elements of the carthesian product set C2 x C4, which is now the indirect product group C2 semi C4, are all the possible pairs of which the first member consists of an element of C2, and the second member of an element of C4.
So these elements are :
e' = (e, e)
a' = (e, a)
a'2 = (e, a2)
a'3 = (e, a3)
b' = (y, e)
c' = (y, a2)
f ' = (y, a)
d' = (y, a3).
These elements must now be multiplied with each other according to the rule of the indirect product (being indicated by "."), for instance :
a'.c' = (e, a).(y, a2) = (ey, yphi(a) a2) = (y, f(a) a2) = (y, a3 a2) = (y, a5) = (y, a) = f '.
To grasp the above multiplication one must see that ey = y.
Further we can see that f(a) means the automorphism f applied to the element a. And this means that the element a is interchanged for the element a3.
Further we see that a5 = a4a = 1a = a.
Indeed, if the element y of C2 were mapped onto the automorphism e instead of on the automorphism f, we would get e(a) instead of f(a), which means that the automorphism e is now applied to the element a, and this means that the result is a again, i.e. e(a) = a.
The above multiplication would then run as follows :
a'.c' = (e, a).(y, a2) = (ey, yphi(a) a2) = (y, e(a) a2) = (y, aa2) = (y, a3), which is exactly according to the rule for the direct product. In this case we accordingly would get a'.c' = d' (instead of a'.c' = f ' ).
In this way, i.e. by determining all products, according to the rule of the indirect product, one will obtain the group table for C2 semi C4 :
| e' | a' | a'2 | a'3 | b' | c' | d' | f ' | period | |
| e' | e' | a' | a'2 | a'3 | b' | c' | d' | f ' | 1 |
| a' | a' | a'2 | a'3 | e' | d' | f ' | c' | b' | 4 |
| a'2 | a'2 | a'3 | e' | a' | c' | b' | f ' | d' | 2 |
| a'3 | a'3 | e' | a' | a'2 | f ' | d' | b' | c' | 4 |
| b' | b' | f ' | c' | d' | e' | a'2 | a'3 | a' | 2 |
| c' | c' | d' | b' | f ' | a'2 | e' | a' | a'3 | 2 |
| d' | d' | b' | f ' | c' | a' | a'3 | e' | a'2 | 2 |
| f ' | f ' | c' | d' | b' | a'3 | a' | a'2 | e' | 2 |
Table 12.1
Indeed this group G = C2 semi C4 turns out to be the dihedral group D4, which crystallographically is realized as the Classes 422, 4mm and 4*2m.
To round off this document it would be appropriate to give, without proof, an important result :
Cn, Dn, A4, S4, A5
for rotation groups. To these may be added :
Cn x C2, Dn x C2, A4 x C2, S4 x C2, A5 x C2
when opposite symmetries are included.
A4 can represent :
The rotational symmetries of the Regular Tetrahedron.
All even permutations of four symbols.
S4 can represent :
The full group of the Regular Tetrahedron (BUDDEN, p. 297).
The direct symmetries of the Cube and Regular Octahedron (BUDDEN, p. 299).
All permutations of four symbols.
A5 can represent :
The direct symmetries of the Regular Icosahedron and Regular Dodecahedron.
All even permutations of five symbols.
S4 x C2 can represent
The full group of the Cube and Regular Octahedron (BUDDEN, p. 302).
A5 x C2 can represent
The full group of the Regular Icosahedron and Regular Dodecahedron.
It is important to know that the full group of the Regular Icosahedron (and Dodecahedron) is not S5 (BUDDDEN, p. 300, note).
In the next document we will actually consider the symmetry groups that have not yet, or only cursorily, been treated in previous documents.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals