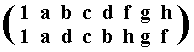
of the group elements, and which can be expressed as the cycle (b d) (f h).
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Automorphisms
In Part II, Part IV and Part X we already considered automorphism, and in Part III also inner automorphisms. An automorphism is an isomorphism of a group with itself. The formal definition goes as follows :
PHI(g1g2) = PHI(g1)PHI(g2).
Inner and outer automorphisms
With respect to non-Abelian groups there are two types of automorphism, inner and outer.
An i n n e r a u t o m o r p h i s m of a group is obtained by selecting an element from the group (say the element p ), and conjugating every element of the group by it. That is, the general element g of the group is transformed into pgp-1.
If the group is of order n, then there are n possible inner automorphisms (because we can use each element in turn to figure as transforming element), but some of these may well overlap. Note that with respect to the formation of an inner automorphism we are forming the transforms, by a certain element of the group, of all elements of the group, and because the transforming element, as well as its inverse, and also the element that is being transformed, all belong to the group, the transform must also belong to the group, and this means that the result is just the same set of all the group elements, but now (generally) in a different order, i.e. a permutation of the original sequence of the group elements.
That the set of transforms of (all) the elements of a group is indeed always a genuine automorphism, we can prove as follows :
Suppose x and y are elements of a group G. Suppose further that xy = z, where z is also an element of G. Suppose further that b is yet another element of G.
Let us call the transform function by the element b, PHI. Then we have :
PHI(z) = bzb-1 ( = image of the product of x and y )
PHI(x) = bxb-1 ( = image of factor)
PHI(y) = byb-1 ( = image of factor)
PHI(x)PHI(y) = bxb-1byb-1 = bx(b-1b)yb-1 = bxyb-1 = bzb-1.
So the image of the product is equal to the product of the images (of the factors), and thus the isomorphism between the group G and itself in the case of conjugation of all elements by a general element b is proved, and thus the automorphism is proved.
Let us illustrate this for the group D4 , as given by the following group table :
| 1 | a | b | c | d | f | g | h | period | |
| 1 | 1 | a | b | c | d | f | g | h | 1 |
| a | a | 1 | h | g | f | d | c | b | 2 |
| b | b | f | 1 | h | g | a | d | c | 2 |
| c | c | g | f | 1 | h | b | a | d | 2 |
| d | d | h | g | f | 1 | c | b | a | 2 |
| f | f | b | c | d | a | g | h | 1 | 4 |
| g | g | c | d | a | b | h | 1 | f | 2 |
| h | h | d | a | b | c | 1 | f | g | 4 |
Table 17.1
On the basis of the above group table we will now form the transforms of all the elements by, successively, the transforming elements 1, a, b, c, d, f, g and h (all the elements of the group).
Generally, to compute xyx-1 we first take x-1, multiply it by y, and then multiply the result with x.
When the transforming element is 1 -- the identity -- we get for a general element y of the group the following : 1y1-1 = y11-1 = y. So all the elements of the group remain the same under conjugation by the element 1. The resulting automorphism is consequently the identity automorphism.
When the transforming element is a, we get the following :
a1a-1 = aa-1 = 1. So 1 becomes 1.
aaa-1 = a. So a becomes a.
aba-1 = af = d. So b becomes d.
aca-1 = ag = c. So c becomes c.
ada-1 = ah = b. So d becomes b.
afa-1 = ab = h. So f becomes h.
aga-1 = ac = g. So g becomes g.
aha-1 = ad = f. So h becomes f.
All this amounts to a first (determined) inner automorphism of the group D4, that can be represented by the permutation
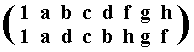
of the group elements, and which can be expressed as the cycle (b d) (f h).
So with this automorphism the new sequence of group elements is :
1 a d c b h g f
When we interpret the group D4 geometrically, i.e. as the symmetries of the Square or of the Regular Tetragonal Pyramid , this automorphism can be seen as an interchange of the mirrors b and d, together with an interchange of the rotations of 900 and 2700, i.e. of f h ( The latter two both of period 4 -- See Table 17.1 ). The next Figure illustrates the relabelling of the mirrors according to the present automorphism.
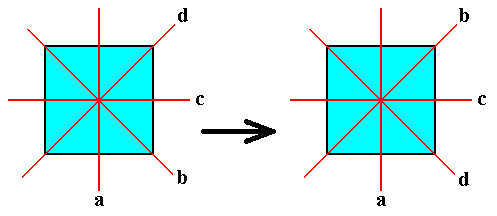
Figure 1. The interchange of the mirrors b and d of the Square.
We now shall see how the group table (of D4 ) will look like with this new sequence of its elements. To construct this new group table we will multiply the elements according to our first table of D4 , where the group is once and for all defined, i.e. all the products set fixed. Our new table, representing the first inner automorphism of the group D4 -- having used the element a as the transforming element -- will be the following (Some elements are colored differently to highlight structure) :
| 1 | a | d | c | b | h | g | f | |
| 1 | 1 | a | d | c | b | h | g | f |
| a | a | 1 | f | g | h | b | c | d |
| d | d | h | 1 | f | g | a | b | c |
| c | c | g | h | 1 | f | d | a | b |
| b | b | f | g | h | 1 | c | d | a |
| h | h | d | c | b | a | g | f | 1 |
| g | g | c | b | a | d | f | 1 | h |
| f | f | b | a | d | c | 1 | h | g |
Table 17.2
For comparison we again give the group table of D4 with the original sequence of its elements, which as such represents the identity automorphism :
| 1 | a | b | c | d | f | g | h | |
| 1 | 1 | a | b | c | d | f | g | h |
| a | a | 1 | h | g | f | d | c | b |
| b | b | f | 1 | h | g | a | d | c |
| c | c | g | f | 1 | h | b | a | d |
| d | d | h | g | f | 1 | c | b | a |
| f | f | b | c | d | a | g | h | 1 |
| g | g | c | d | a | b | h | 1 | f |
| h | h | d | a | b | c | 1 | f | g |
Table 17.3
As we can see, the structure of both group tables is identical, so indeed the one represents an (inner) automorphism of the other, i.e. an isomorphism between D4 and itself.
When the transforming element is b, we get the following :
This amounts to the second inner automorphism of D4 and is represented by the permutation
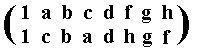
of the group elements, and which can be expressed by the cycle (a c) (f h).
So with this automorphism the new sequence of group elements is :
1 c b a d h g f
Geometrically this automorphism can be interpreted as an interchange of the mirrors a and c, together with an interchange of the rotations by 900 and 2700, i.e. of f and h.
Our new table, representing the second inner automorphism of the group D4 -- having used the element b as the transforming element -- will be the following (Some elements are colored differently to highlight structure) :
| 1 | c | b | a | d | h | g | f | |
| 1 | 1 | c | b | a | d | h | g | f |
| c | c | 1 | f | g | h | d | a | b |
| b | b | h | 1 | f | g | c | d | a |
| a | a | g | h | 1 | f | b | c | d |
| d | d | f | g | h | 1 | a | b | c |
| h | h | b | a | d | c | g | f | 1 |
| g | g | a | d | c | b | f | 1 | h |
| f | f | d | c | b | a | 1 | h | g |
Table 17.4
Also here we see that the structure of the table is unchanged.
When the transforming element is c, we get the following :
This amounts to the third inner automorphism of D4 and is represented by the permutation
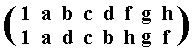
of the group elements, and which can be expressed by the cycle (b d) (f h). And this inner automorphism we already had earlier.
When the transforming element is d, we get the following :
This amounts to the fourth inner automorphism of D4 and is represented by the permutation
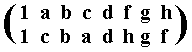
of the group elements, and which can be expressed by the cycle (a c) (f h). And also this inner automorphism we already had earlier.
When the transforming element is f, we get the following :
This amounts to the fifth inner automorphism of D4 and is represented by the permutation
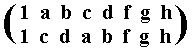
of the group elements, and which can be expressed by the cycle (a c) (b d). And this is a new inner automorphism not yet encountered before. So with this automorphism the new sequence of group elements is :
1 c d a b f g h
Geometrically this (inner) automorphism can be interpreted as an interchange of the mirrors a and c together with an interchange of the mirrors b and d.
The new group table of D4, with the elements in the just determined sequence according to the inner automorphism obtained by the transforming element f, reads as follows :
| 1 | c | d | a | b | f | g | h | |
| 1 | 1 | c | d | a | b | f | g | h |
| c | c | 1 | h | g | f | b | a | d |
| d | d | f | 1 | h | g | c | b | a |
| a | a | g | f | 1 | h | d | c | b |
| b | b | h | g | f | 1 | a | d | c |
| f | f | d | a | b | c | g | h | 1 |
| g | g | a | b | c | d | h | 1 | f |
| h | h | b | c | d | a | 1 | f | g |
Table 17.5
Also here we see that the structure of the table is unchanged.
When the transforming element is g, we get the following :
This amounts to the identity automorphism (sixth inner automorphism).
When, finally, the transforming element is h, we get the following :
This amounts to the seventh (determined) inner automorphism of D4 and is represented by the permutation
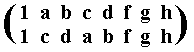
of the group elements, and can be expressed by the cycle (a c) (b d). This automorphism was already encountered earlier.
So all in all we have found four different inner automorphisms of the group D4, represented by the cycles
(1) (a) (b) (c) (d) (f) (g) (h) (identity automorphism).
(b d) (f h).
(a c) (f h).
(a c) (b d).
So the inner automorphisms of D4 constitute four permutations (of the elements), one of period 1 (identity permutation), and three of period 2. So they form the group D2 (And this group will turn out to be a normal subgroup of the full group of automorphisms (inner and outer)).
In addition to the four inner automorphisms, D4 also admits of four outer automorphisms. To find these, we look to all elements of period 2, except the element g which is unique, because it commutes with all elements of the group. To show this we repeat the group table of D4 and highlight this special status of the element g :
| 1 | a | b | c | d | f | g | h | period | |
| 1 | 1 | a | b | c | d | f | g | h | 1 |
| a | a | 1 | h | g | f | d | c | b | 2 |
| b | b | f | 1 | h | g | a | d | c | 2 |
| c | c | g | f | 1 | h | b | a | d | 2 |
| d | d | h | g | f | 1 | c | b | a | 2 |
| f | f | b | c | d | a | g | h | 1 | 4 |
| g | g | c | d | a | b | h | 1 | f | 2 |
| h | h | d | a | b | c | 1 | f | g | 4 |
Table 17.6
ab = h
Indeed, apart from the identity, only the element g commutes with every element of the group, so the center of the group is {1, g}. This means that of the non-identity elements, g has a unique status and cannot be interchanged by any other element of the group and at the same time preserve the structure of the group table.
So with respect to period 2 elements, we are left with the set {a, b, c, d}. Geometrically the elements of this set represent the four mirrors of the Square or of the Regular Tetragonal Pyramid. In some of the inner automorphisms some of them were interchanged (See for instance Figure 1, above). There are still some possible interchanges left for these mirrors, namely (expressed as cycles) :
(a b c d), and its inverse (a d c b).
(a b) (c d), and (a d) (b c).
According to BUDDEN, p. 421, these latter two "have the effect of interchanging f and h". I cannot figure out what he means by this, because an interchange solely of f and h can -- according to me -- only be accomplished by interchanging b and d, as Figure 1 illustrates. There, as a result of the interchange of b and d, the figure is flipped over, resulting in the two rotations of period 4 (900 and 2700), i.e. f and h (which are each other's inverses), being interchanged. We will look into the matter shortly (The final solution of this problem is stated HERE, i.e. much further down , and was found by systematically deriving all the automorphisms of the group D4 by means of considering the substitution of generators. This consideration starts a little further down).
(a b c d) renames the mirrors in anticlockwise direction, while (a d c b) renames them in clockwise direction.
The effect of (a b) (c d) is illustrated in the next Figure.
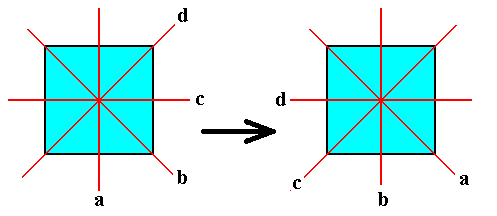
Figure 2. Effect of (a b) (c d) -- expressing a permutation of the elements a, b, c and d of the group D4 . This permutation is one of D4's outer automorphisms. The interchange is between the two types of mirrors.
Let us summarize the eight automorphisms of the group D4. We'll give the cycle, the corresponding permutation (of the group elements) and their periods. The permutations will be given by their lower part only.
Inner automorphisms
(1)(a)(b)(c)(d)(f)(g)(h) = 1 a b c d f g h period 1.
(b d) (f h) = 1 a d c b h g f period 2.
(b d) (a c) = 1 c d a b f g h period 2.
(a c) (f h) = 1 c b a d h g f period 2.
They accordingly form the group D2.
Outer automorphisms
(a b c d) = 1 b c d a f g h period 4.
(a d c b) = 1 d a b c f g h period 4.
(a b) (c d) = 1 b a d c f g h period 2.
(a d) (b c) = 1 d c b a f g h period 2.
Together, these inner and outer automorphisms of the group D4 form the full automorphism group, and this group has the structure of D4, as the distribution of the periods indicates. So we can write
Aut( D4 ) = D4 . The inner automorphisms form the group D2, and this is a normal subgroup of the full automorphism group.
An alternative way of deriving the eight automorphisms of the group D4
It is possible to express the elements of the group D4 in terms of generators. Two such generators (independent generators) are needed, because D4 contains a subgroup, C4, which can be generated by a single element, but then we do not get outside this subgroup, and consequently cannot generate the remaining elements of the full group. So we need another generator in addition to one that generates the subgroup. To generate the subgroup we can take the element f, which has a period of 4 (corresponding to a rotation of 900). However, we prefer to call this element "r". The other generator we will call "a".
Now, in terms of these generators the group D4 has as defining relations
r4 = 1
a2 = 1
ar = r3a
(BUDDEN, p. 290)
The first relation implies that the period of r is 4.
The second relation implies that the period of a is 2.
The third relation says that a rotation r followed by a reflection a has the same result as a reflection a followed by three times a rotation r.
The next Figure shows the interpretation of the third defining relation in terms of the symmetries of the Square :
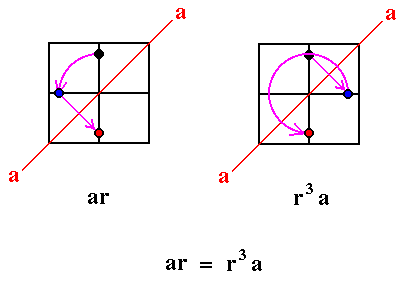
Figure 3. To show geometrically that ar = r3a. It is valid for all mirror lines of the Square.
An automorphism of the group D4 can be found by choosing an alternative and equally valid pair of generators (a pair, because this group requires two generators), and then generate the sequence of group elements. We then obtain one permutation of the elements such that the table structure is preserved, i.e. we have found an automorphism. Then we choose another possible pair of generators and generate another sequence of the group elements, and obtain yet another permutation representing a second automorphism.
| 1 | r | r2 | r3 | a | period | ||||
| 1 | 1 | r | r2 | r3 | a | 1 | |||
| r | r | r2 | r3 | 1 | 4 | ||||
| r2 | r2 | r3 | 1 | r | 2 | ||||
| r3 | r3 | 1 | r | r2 | 4 | ||||
| a | a | 2 | |||||||
But r and a generate a new element, namely ra, so this element must be added :
| 1 | r | r2 | r3 | a | ra | period | |||
| 1 | 1 | r | r2 | r3 | a | ra | 1 | ||
| r | r | r2 | r3 | 1 | ra | 4 | |||
| r2 | r2 | r3 | 1 | r | 2 | ||||
| r3 | r3 | 1 | r | r2 | 4 | ||||
| a | a | 2 | |||||||
| ra | ra | 2 | |||||||
But the elements r and ra generate a new element again, namely r 2a, so this new element must be added :
| 1 | r | r2 | r3 | a | ra | r2a | period | ||
| 1 | 1 | r | r2 | r3 | a | ra | r2a | 1 | |
| r | r | r2 | r3 | 1 | ra | r2a | 4 | ||
| r2 | r2 | r3 | 1 | r | 2 | ||||
| r3 | r3 | 1 | r | r2 | 4 | ||||
| a | a | 2 | |||||||
| ra | ra | 2 | |||||||
| r2a | r2a | 2 | |||||||
Finally, the element r and the element r 2a produce again a new element, namely r 3a. So we must add this element to the table (We will see that we now have generated all elements of the group, i.e. by subsequent multiplications no new elements will be created anymore).
| 1 | r | r2 | r3 | a | ra | r2a | r3a | period | |
| 1 | 1 | r | r2 | r3 | a | ra | r2a | r3a | 1 |
| r | r | r2 | r3 | 1 | ra | r2a | r3a | 4 | |
| r2 | r2 | r3 | 1 | r | 2 | ||||
| r3 | r3 | 1 | r | r2 | 4 | ||||
| a | a | 2 | |||||||
| ra | ra | 2 | |||||||
| r2a | r2a | 2 | |||||||
| r3a | r3a | 2 |
We must now complete the group table (of D4 , in terms of the generators r and a ).
On the basis of the above given defining relations we can compute the remaining entries of the table. Let us complete the first four rows :
| 1 | r | r2 | r3 | a | ra | r2a | r3a | period | |
| 1 | 1 | r | r2 | r3 | a | ra | r2a | r3a | 1 |
| r | r | r2 | r3 | 1 | ra | r2a | r3a | a | 4 |
| r2 | r2 | r3 | 1 | r | r2a | r3a | a | ra | 2 |
| r3 | r3 | 1 | r | r2 | r3a | a | ra | r2a | 4 |
| a | a | 2 | |||||||
| ra | ra | 2 | |||||||
| r2a | r2a | 2 | |||||||
| r3a | r3a | 2 |
Now we're going to compute the last four rows of the table, (still) making use of the defining relations
r4 = 1
a2 =1
ar = r 3a
The second element of the fifth row (headed by a ) is ar. But this is not a new element, because according to the third defining relation we see that
ar = r 3a. And this element we have already found earlier. We now generate the remaining elements of this fifth row :
ar 2 = arr = r 3ar = r 3r 3a = r 6a = r 4r 2a = r 2a , and this, indeed, is again not a new element. We can put it in its right place in the table, as the third element of the fifth row.
ar 3 = arrr = r 3arr = r 3r 3ar = r 4r 2ar = r 2ar = r 2r 3a = r 5a = r 4ra = ra. We place this result in the appropriate location of the table.
The next element is aa, and this is equal to 1.
Then the next element of the row is ara, and this can be reduced as follows :
ara = r 3aa = r 3.
In the same way we compute all the remaining elements of the fifth row, and then all the elements of the last three rows.
The resulting c o m p l e t e group table (of D4 , in terms of the generator pair r and a ) is given below :
| 1 | r | r2 | r3 | a | ra | r2a | r3a | period | |
| 1 | 1 | r | r2 | r3 | a | ra | r2a | r3a | 1 |
| r | r | r2 | r3 | 1 | ra | r2a | r3a | a | 4 |
| r2 | r2 | r3 | 1 | r | r2a | r3a | a | ra | 2 |
| r3 | r3 | 1 | r | r2 | r3a | a | ra | r2a | 4 |
| a | a | r3a | r2a | ra | 1 | r3 | r2 | r | 2 |
| ra | ra | a | r3a | r2a | r | 1 | r3 | r2 | 2 |
| r2a | r2a | ra | a | r3a | r2 | r | 1 | r3 | 2 |
| r3a | r3a | r2a | ra | a | r3 | r2 | r | 1 | 2 |
Table 17.7
In this group table the sequence of elements is :
1 r r 2 r 3 a ra r 2a r 3a
This sequence is generated by the generators r (period 4) and a (period 2).
In order to find automorphisms we replace the original generators by two others, also of periods
4 respectively 2 (only elements of the same period can be interchanged with each other).
The elements of period 4 are :
r
r 3
The elements of period 2 are :
r 2
a
ra
r 2a
r 3a
So the element r 3 of period 4 can replace r.
The elements r 2 , ra, r 2a and r 3a can replace a.
But when we replace a by r 2 (period 2), we will duplicate this element, because it already occurs at the third place of the row of group elements. So we will not use this particular replacement. The remaining elements of period 2 can be interchanged with a, without duplicating elements.
On the basis of this we can now determine all the possible alternative pairs of generators :
| r | a |
| r | ra |
| r | r2a |
| r | r3a |
| r3 | a |
| r3 | ra |
| r3 | r2a |
| r3 | r3a |
We will now determine the possible sequences of group elements, generated by the alternative pairs of generators as given above. We begin with the original sequence of elements (generated by the pair r and a ), and consider the generator pair r and ra : In the original sequence we replace r by r, wherever it occurs (changing nothing of course), and we replace a by ra, wherever it occurs. We then will obtain a new sequence of elements, i.e. a permutation of them, and thus we find an automorphism.
Next we consider the generator pair r and r 2a , and replace every r in the original sequence by r (which doesn't change anything), and we replace every a in the original sequence by r 2a, and so obtain yet another sequence of group elements, i.e. another permutation, and thus another automorphism.
We continue to do so with respect to the remaining possible pairs of generators, and we then will obtain the following eight permutations of the group elements and thus all the eight automorphisms (inner and outer) of the group D4 :
| 1 | r | r2 | r3 | a | ra | r2a | r3a |
| 1 | r | r2 | r3 | ra | r2a | r3a | a |
| 1 | r | r2 | r3 | r2a | r3a | a | ra |
| 1 | r | r2 | r3 | r3a | a | ra | r2a |
| 1 | r3 | r2 | r | a | r3a | r2a | ra |
| 1 | r3 | r2 | r | ra | a | r3a | r2a |
| 1 | r3 | r2 | r | r2a | ra | a | r3a |
| 1 | r3 | r2 | r | r3a | r2a | ra | a |
Each row of the above array represents a permutation of the group elements of the group D4 , these elements being expressed in terms of r and a (And these permutations must of course correspond to the permutations found earlier).
We found these permutations by interchanging pairs of independent generators, and, for example with respect to the second row, we have let r the same, while replacing a by ra. We then substituted every a in the first row by ra, and obtained the new sequence of elements.
This procedure can also be outlined in a slightly different but fully equivalent way :
When we start with the elements 1, r, r 2, and r 3 -- which can be generated from the element r -- , and when we now add the element ra, then 1(ra) gives ra, so nothing new is produced. But if we now determine r(ra), which is r2a, we have a new element. And when we now determine r(r2a), which is r3a, we have again a new element. And when we in turn determine r(r3a), which is a, we have again a new element. When, finally, we determine r(a), which is ra, we have found an element which we already have.
So the generated sequence of group elements found in this way is :
1, r, r 2, r 3, ra, r2a, r 3a, a
And this is indeed equal to the second row of the above array.
Let us determine the periods of these permutations (i.e. the permutations depicted in the above array).
Thereby we let the first row of the above array represent the identity permutation :
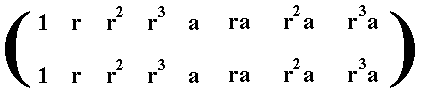
which can also be written as just
1 r r 2 r 3 a ra r 2a r 3a
To find the periods of the permutations ( that of the identity permutation is of course 1 ), we will express them as cycles :
The second permutation of the above array is :
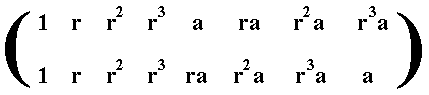
We see that a is replaced by ra, ra is replaced by r 2a, r 2a is replaced by r 3a, r 3a, finally, is replaced by a. So the cycle is :
( a ra r 2a r 3a ). And this cycle is clearly of period 4. So the second permutation of the above array is of period 4.
In the same way we determine the periods of the remaining six permutations (of the above array), providing us with the following overall result (first we give the permutation, then its expression as a cycle, and then its period) :
| 1 | r | r2 | r3 | a | ra | r2a | r3a | 1 | |
| 1 | r | r2 | r3 | ra | r2a | r3a | a | ( a ra r2a r3a ) | 4 |
| 1 | r | r2 | r3 | r2a | r3a | a | ra | ( a r2a ) ( ra r3a ) | 2 |
| 1 | r | r2 | r3 | r3a | a | ra | r2a | ( a r3a r2a ra ) | 4 |
| 1 | r3 | r2 | r | a | r3a | r2a | ra | ( r r3 ) ( ra r3a ) | 2 |
| 1 | r3 | r2 | r | ra | a | r3a | r2a | ( r r3 ) ( a ra ) ( r2a r3a ) | 2 |
| 1 | r3 | r2 | r | r2a | ra | a | r3a | ( r r3 ) ( a r2a ) | 2 |
| 1 | r3 | r2 | r | r3a | r2a | ra | a | ( r r3 ) ( a r3a ) ( ra r2a ) | 2 |
From the distribution of the periods over the eight permutations we can deduce that the automorphism group of the group D4 has the structure of D4.
So Aut(D4) = D4 , where "=" means "is isomorphic to".
We can now correspond the determined permutations of the elements of D4 expressed with r and a, with the permutations of the elements of the same group (these elements) expressed (as was done alternatively) by the symbols 1, a, b, c, d, f, g and h, according to :
| 1 | r | r2 | r3 | a | ra | r2a | r3a |
| 1 | f | g | h | a | b | c | d |
According to this scheme we will replace the symbols of the above list of permutations. The result is the following :
| 1 | f | g | h | a | b | c | d |
| 1 | f | g | h | b | c | d | a |
| 1 | f | g | h | c | d | a | b |
| 1 | f | g | h | d | a | b | c |
| 1 | h | g | f | a | d | c | b |
| 1 | h | g | f | b | a | d | c |
| 1 | h | g | f | c | b | a | d |
| 1 | h | g | f | d | c | b | a |
The next array adds the cycles and periods.
| 1 | f | g | h | a | b | c | d | 1 | |
| 1 | f | g | h | b | c | d | a | (a b c d) | 4 |
| 1 | f | g | h | c | d | a | b | (a c) (b d) | 2 |
| 1 | f | g | h | d | a | b | c | (a d c b) | 4 |
| 1 | h | g | f | a | d | c | b | (f h) (b d) | 2 |
| 1 | h | g | f | b | a | d | c | (f h) (a b) (c d) | 2 |
| 1 | h | g | f | c | b | a | d | (f h) (a c) | 2 |
| 1 | h | g | f | d | c | b | a | (f h) (a d) (b c) | 2 |
So here we have again the automorphism group ( isomorphic to D4 ) of the group D4.
We can now compare these results with those that were found above when we just started with the search for automorphisms in the group D4 .
As can be seen, the results fully comply with the results obtained EARLIER. There we had all those permutations, and among them (a b) (c d) and (a d) (b c). Referring to these two latter permutations (expressed as cycles) BUDDEN, p. 421, stated that they "have the effect of interchanging f and h ", which rather puzzled us. We now know what he meant : Each of those two cycles are accompanied by the transposition (f h), so in fact the full permutations are : (f h) (a b) (c d), and (f h) (a d) (b c). So the problem is solved.
It is perhaps instructive to show a case of interchanging elements in the group D4, such that the general 'look' of the resulting group table is the same, but that nevertheless products are not preserved.
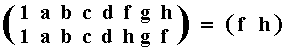
| 1 | a | b | c | d | h | g | f | |
| 1 | 1 | a | b | c | d | h | g | f |
| a | a | 1 | h | g | f | b | c | d |
| b | b | f | 1 | h | g | c | d | a |
| c | c | g | f | 1 | h | d | a | b |
| d | d | h | g | f | 1 | a | b | c |
| h | h | d | a | b | c | g | f | 1 |
| g | g | c | d | a | b | f | 1 | h |
| f | f | b | c | d | a | 1 | h | g |
Table 17.8
Table of D4 , in which the elements f and h are interchanged with respect to the sequence of elements as we have it in Table 17.1.
This table is of course a correct table, as such defining the group D4, but it is not isomorphic to the table bearing the original sequence of the elements :
fd = a (as can be read off from the original table)
PHI(a) = a ( = image of the product)
PHI(f) = h ( = image of factor)
PHI(d) = d ( = image of factor)
Then
PHI(f) PHI(d) = hd = c (as can be read off from the image group table).
So the image of the product is not equal to the product of the images (of the factors).
This one counter-example of products not being preserved is sufficient for G' not to be isomorphic with G, and thus the permutation (given by the cycle (f h)) does not express an automorphism of the group D4.
But of course G and G' are isomorphic because, although the particular one-to-one correspondence between their elements (expressing the alleged automorphism)
1 ---> 1
a ---> a
b ---> b
c ---> c
d ---> d
f ---> h
g ---> g
h ---> f
does not preserve products, there can be found a one-to-one correspondence between the elements of G and G' that does preserve products, namely
1 ---> 1
a ---> a
b ---> b
c ---> c
d ---> d
f ---> f
g ---> g
h ---> h
Let us call this correspondence THETA, and let us now try out the above product of the element f and the element d.
According to the original group table we again have
fd = a, then
THETA(a) = a ( = image of the product)
THETA(f) = f ( = image of factor)
THETA(d) = d ( = image of factor)
THETA(f) THETA(d) = fd = (reading off from the alternative group table) a .
So we see that the image of the product is equal to the product of the images (of the factors). Thus the product fd = a in the original group is preserved in the image group. The isomorphism is of course only established when this holds for all products. So let us generally prove this.
Let x, y, and z be any three elements of our group G, and let xy = z.
Further let PSI be the one-to-one correspondence from the group G to the group G'. Then we have :
PSI(z) = z
PSI(x) = x
PSI(y) = y, then
PSI(x) PSI(y) = xy
But because in the table of G' the products are the same as in the original table (because we have constructed the new table -- with the elements f h interchanged -- according to the products of the original table), we can say
PSI(x)PSI(y) = xy = z, so indeed the image of the product is equal to the product of the images, and thus the isomorphism is established.
It is instructive to give yet another example of a permutation of the elements of the group D4 which is not an automorphism of this group :
We show how the group table looks, when the elements of the group are interchanged according to the following permutation :
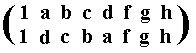
which can be expressed as the cycle (a d) (b c)
| 1 | d | c | b | a | f | g | h | |
| 1 | 1 | d | c | b | a | f | g | h |
| d | d | 1 | f | g | h | c | b | a |
| c | c | h | 1 | f | g | b | a | d |
| b | b | g | h | 1 | f | a | d | c |
| a | a | f | g | h | 1 | d | c | b |
| f | f | a | d | c | b | g | h | 1 |
| g | g | b | a | d | c | h | 1 | f |
| h | h | c | b | a | d | 1 | f | g |
Table 17.9
Table of D4 , in which the elements are interchanged according to the cycle (a d) (b c), with respect to the sequence of elements as we have it in Table 17.1.
In the original table (Table 17.1) we can see that
So we see that the image of the product is not equal to the product of the images (of the factors). And this one counter-example of products not being preserved is sufficient for stating that there is no isomorphism, i.e. that the one-to-one correspondence set up according to the cycle (a d) (b c) does not preserve products and is therefore not an automorphism of the group D4.
In the next document we continue our investigation into the phenomenon of automorphism in groups.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals
back to Part XV of the theoretical preparation to the study of 3-D crystals
back to Part XVI of the theoretical preparation to the study of 3-D crystals