3-D Crystals XXIII

The Total Symmetry of Three-dimensional Crystals

Part XXIII

e-mail :

Sequel to Group Theory

We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.

Sequel to Infinite two-dimensional periodic patterns

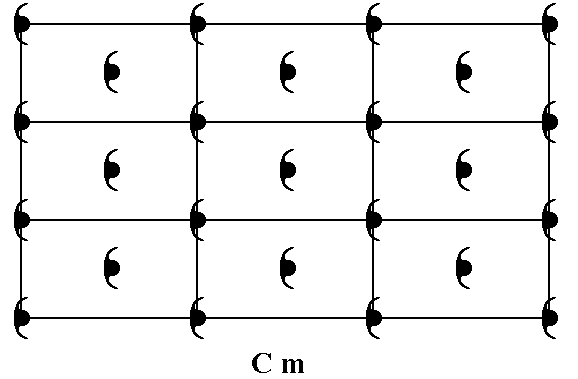
The pattern according to the Plane Group Cm

Figure 1. Placing symmetric motifs in a centered rectangular net, such that each lattice node is associated with such a motif, yields a pattern representing Plane Group Cm. The pattern must be conceived as extending indefinitely in two-dimensional space.

In the pattern representing Plane Group Cm as depicted in Figure 1, we have (composed) motifs, each consisting of two motif units -- commas --, such that the composed motif has point symmetry m (i.e. it has a mirror line as its only symmetry element). The motif units represent group elements.

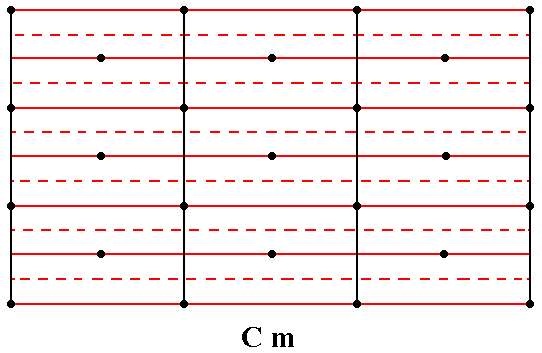
The total symmetry content of the Plane Group Cm is shown in the next Figure.

Figure 2. Total symmetry content of the Plane Group Cm.
Glide lines are indicated by red dashed lines.
Mirror lines are indicated by red solid lines.
All the glide lines and mirror lines are parallel to the y direction.
For clarity the nodes of the net are indicated (black dots).

The next Figure shows a set of two chosen generators :
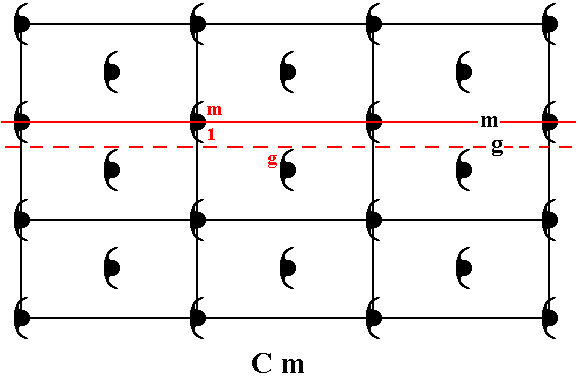
The element g (represented by the corresponding motif unit), which results from the chosen initial motif unit 1 (representing the identity element), by (the action of) the glide reflection g .
The element m (represented by the corresponding motif unit), which results from the initial motif unit (representing the identity element), by a reflection in the line m .

Figure 3. The two chosen generators of the group Cm .

These two generators together can generate the whole pattern :

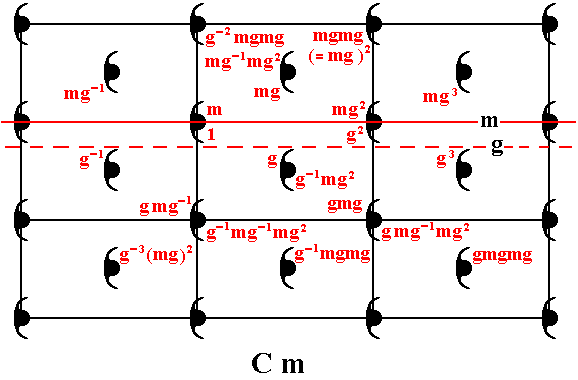
Figure 4. For a number of motif units their generation is indicated.
Continuing this process will yield the whole Cm pattern.

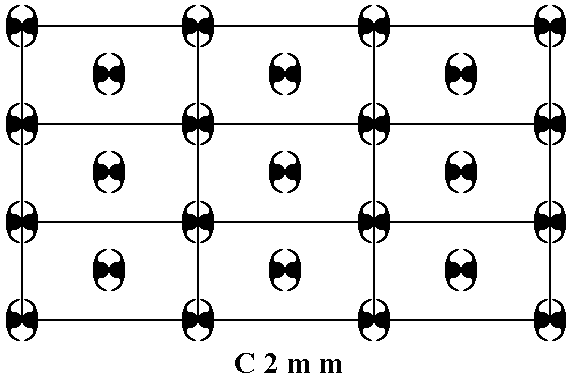
The pattern according to the Plane Group C2mm

Figure 5. Placing motifs with point symmetry 2mm in a centered rectangular net, yields a periodic array of motifs representing Plane Group C2mm.
In our representation each (composed) motif consists of four motif units (commas), such that the composed motif has 2mm symmetry (Two mirror lines and one 2-fold rotation axis). Each motif unit represents a group element.
As in all cases the pattern must be imagined to be extended indefinitely across the two-dimensional plane.

The total symmetry content of any pattern representing Plane Group C2mm is given in the next Figure.

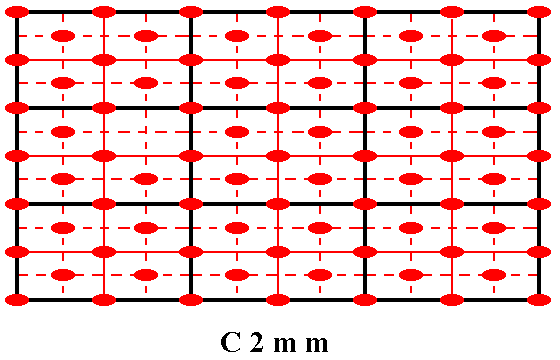
Figure 6. Total symmetry content of Plane Group C2mm.
2-fold rotation axes perpendicular to the plane of the drawing are indicated by small solid red ellipses.
Mirror lines are indicated by solid lines (black, and red).
Glide lines are indicated by red dashed lines.

The next Figure shows three generators that can generate the whole pattern :
The element a that results from the element 1 (chosen to represent the identity element) by a reflection in the line a .
The element b that results from the element 1 by a reflection in the line b .
The element s that results from the element 1 by a half-turn about the point S .
These three generators together can produce all other group elements (each such element may be represented by a motif unit).

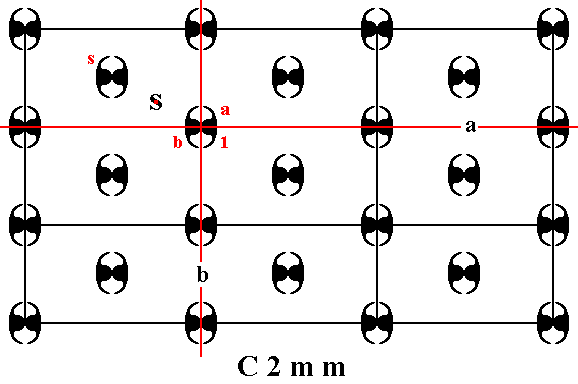
Figure 7. The three chosen generators for the C2mm pattern.

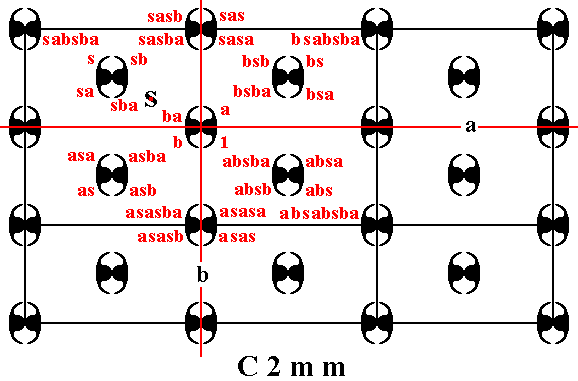
Figure 8. The C2mm pattern can be generated by the elements a, b and s .
The right part of the pattern can be reached as follows :
From the generated element absabsba (lower right) we can generate a new element by rotating it 180⁰ about the point S . This new element is situated to the left of the part of the pattern depicted (i.e. it lies outside the depicted part of the pattern). When we now reflect this new element (represented by a motif unit) in the reflection line b , we will obtain yet another new element (motif unit) that lies far to the right again, while relection in the line a will yield a motif unit further down. It is clear therefore that the whole pattern can be produced from these three generators.

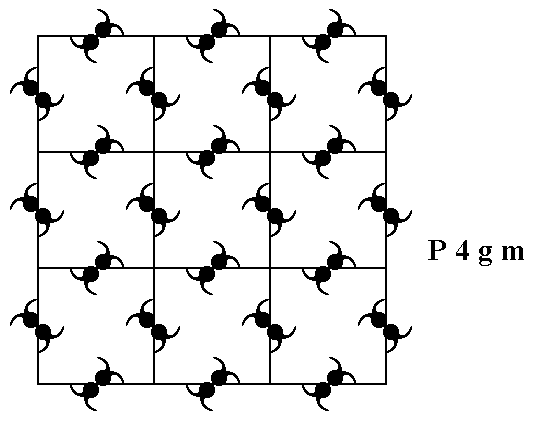
The pattern according to the Plane Group P4gm

Figure 9. A periodic pattern of motifs based on a 2-D square lattice (net). This particular pattern represents the Plane Group P4gm. It must be imagined to extend indefinitely over the 2-D plane. In the present representation each (composed) motif consists of four motif units (commas), such that the symmetry of the composed motif is 2mm . Each motif unit represents a group element.

In the next Figure we depict the total symmetry content of patterns representing the
Plane Group P4gm.

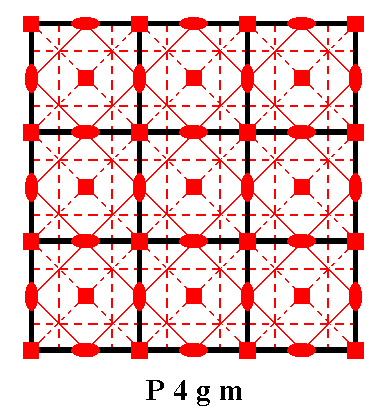
Figure 10. Total symmetry content of the Plane Group P4gm.
Glide lines are indicated by red dashed lines.
Mirror lines are indicated by red solid lines.
4-fold rotation axes are indicated by small red solid squares.
2-fold rotation axes are indicated by small red solid ellipses.

The next Figure depicts two chosen generators :
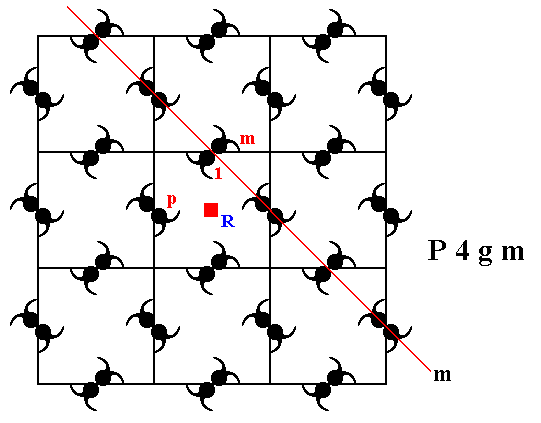
The element (motif unit) m resulting from the element 1 (chosen to represent the identity element), by reflecting it in the mirror line m .
The element (motif unit) p resulting from the element 1 , by rotating it 90⁰ anticlockwise about the point R .

Figure 11. The two chosen generators of the group P4gm (and with it of the corresponding pattern, where the generated group elements are represented by motif units).

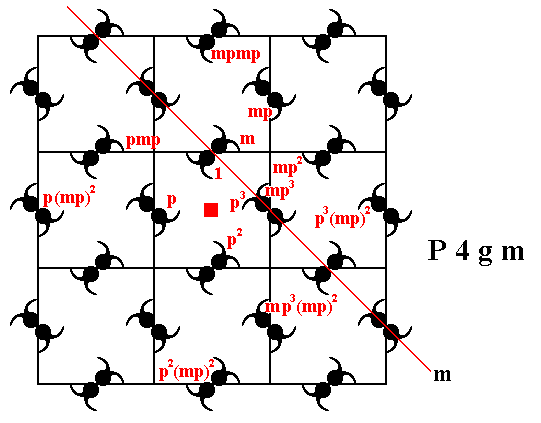
Figure 12. The P4gm pattern can be generated by the two elements m and p.

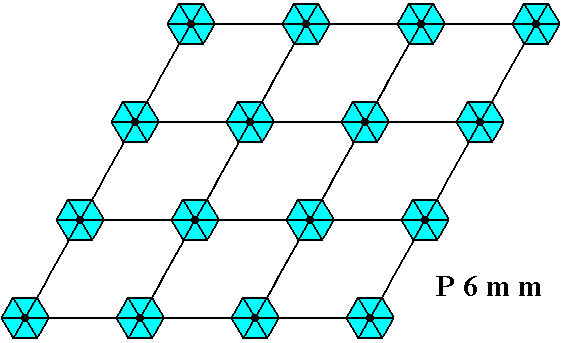
The pattern according to the Plane Group P6mm

Figure 13. When motifs, having point symmetry 6mm (i.e. having a 6-fold rotation axis and two types of mirror lines), are inserted into a (primitive) hexagonal net, a pattern of repeated motifs will emerge that represents Plane Group P6mm.
Also here the unit mesh is rhomb-shaped with angles of 60⁰ and 120⁰.
In the present representation each (composed) motif consists of six motif units, together making up a composed motif with 6mm symmetry. The pattern must be conceived to be extended indefinitely in two-dimensional space.

The total symmetry content of Plane Group P6mm is depicted in Figure 14.

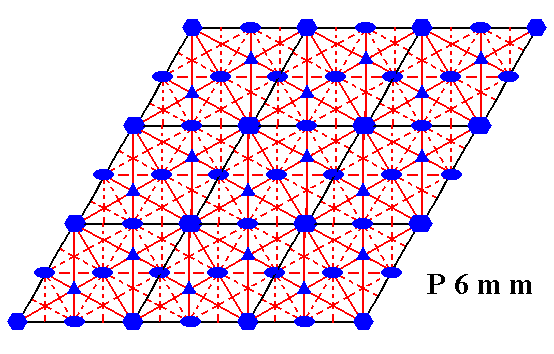
Figure 14. Total symmetry content of the Plane Group P6mm.
All rotation axes are perpendicular to the plane of the drawing.
6-fold rotation axes are indicated by small blue solid hexagons.
3-fold rotation axes are indicated by small blue solid triangles.
2-fold rotation axes are indicated by small blue solid ellipses.
Glide lines are indicated by red dashed lines.
Mirror lines are indicated by solid lines (red and black).
(One should not worry about the small discrepancies at some places in the drawing.)

Figure 13 gives an accurate representation of the Plane Group P6mm. All the symmetries of the group are present in the image of that Figure. So for analytic purposes (analytic group theoretic approach) the representation is appropriate.
However, for a synthetic group theoretical approach, the figure is, in a way, not detailed enough. In it we see a composed motif consisting of six motif units :

But we also see that each motif unit itself is still composed, namely (composed) out of two symmetrical halves. So such a symmetrical motif unit cannot represent a group element, it represents already two group elements. The genuine motif unit, representing a group element, is therefore half the motif unit as set initially. This means that each whole composed motif, as depicted above (and in Figure 13), consists not of six, but of twelve genuine motif units. And these newly conceived motif units are indeed asymmetric, that is to say they cannot be further divided anymore. And they indeed can represent the group elements :

To highlight these genuine motif units more clearly, we can use colors, provided we do not interpret the difference in color to represent an asymmetry : one motif unit (red or blue) is asymmetric. Two of them together (one red and one blue) make up a symmetric entity (representing not a group element but a subgroup of the full group), and twelve of them (six red, six blue) make up the full composed hexagonal motif :

The next Figure has such motifs be placed in a hexagonal net (point lattice) :

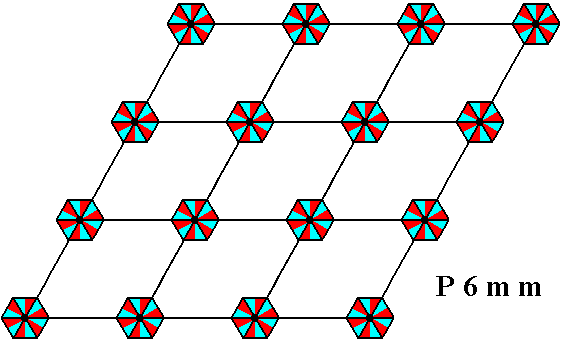
Figure 14a. A representation of a P6mm pattern, in terms of genuine basic motif units (red and blue). Here the difference in color should not be interpreted as asymmetry, it only serves to indicate the basic motif units (making up the hexagonal composed motifs). Each such composed motif is supposed to have 6mm symmetry, i.e. it has D₆ structure (not C₆ structure). It has therefore six rotations and six reflections. Each (genuine) motif unit (either red or blue) represents a group element of the Plane Group P6mm .

In order to generate the P6mm pattern, which means to generate the Plane Group P6mm, which in turn means to generate all group elements, we choose one motif unit to be the initial motif unit and as such to represent the identity element, denoted 1 , and three others to represent generator elements :

A generator element m , resulting from a reflection of the initial motif unit in a mirror line m .
A generator element p , resulting from a 60⁰ anticlockwise rotation of the initial motif unit about the point R (See next Figure).
A generator element t , resulting from a horizontal translation t of the initial motif unit.

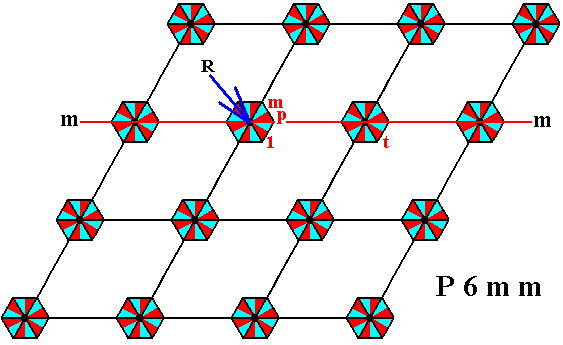
Figure 14b. Three generators, m, p and t , represented by motif units, and one initial motif unit, representing the identity element, are chosen. The motif unit p results from a 60⁰ anticlockwise rotation of the initial element 1 about the point R . The motif unit t results from a horizontal shift of the initial motif unit to the right.

For clarity we enlarge the region around the point R :

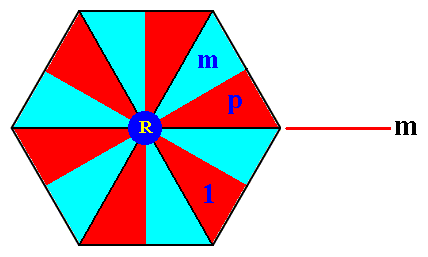
Figure 14c. The composed motif (enlarged) from the P6mm pattern of the previous Figure at the point R . It consists of twelve true motif units (red and blue), representing group elements. The difference in color should (here) not be interpreted as representing asymmetry.
The motif units 1 , m, p and the mirror line m are indicated.

The other motif units of the composed motif of Figure 14c are then automatically implied :

Figure 14d. The composed motif and its twelve constituent basic motif units, at the point R of Figure 14b. These basic motif units represent the group elements 1, m, p, mp, mp², mp³, mp⁴, mp⁵, p², p³, p⁴ and p⁵ . They form the subgroup D₆ of the group P6mm . The elements 1, p, p², p³, p⁴, p⁵ also form a subgroup (of the group P6mm as well as of the subgroup D₆ ) with structure C₆ .

In order to further generate the pattern (and with it the group elements) we can subject the elements of the subgroup D₆ (Figure 14d) to a translation t resulting in 12 new group elements (represented by 12 basic motif units). A few of these new elements are indicated in the next Figure.

Figure 14e. Some new group elements resulting from the translation t are indicated. Also some points, bearing composed motifs, of the lattice are indicated (R , Q , U, W).

The next Figure shows the composed motif next to the right of the one at point R, with the group elements (represented by basic motif units) indicated, as they were produced by the translation t with respect to the composed motif at the point R.

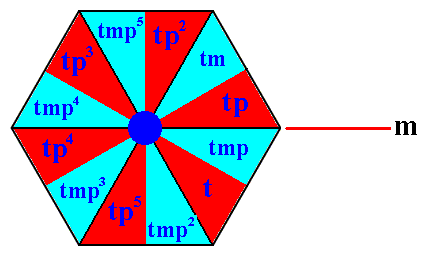
Figure 14f. The composed motif next to the right of the one at the point R .

The red motif units in Figure 14f together form the left coset of the subgroup {1, p p², p³, p⁴, p⁵ } (with structure C₆ ) (See Figure 14d) by the element t .
All the twelve elements (red and blue in Figure 14f ) together form the left coset of the D₆ subgroup (See Figure 14d) by the element t .

Next we're going to generate the composed motif at the point Q in Figure 14e. It can be obtained by rotating the previously generated composed motif (the motif next to the one at point R) 300⁰ anticlockwise (or, which is the same, 60⁰ clockwise) about the point R, which means that we subject all elements of the previously generated composed motif to the action of p⁵ .
The next Figure gives this new composed motif. Inside the image we have left the notations for the elements as they were in the motif next to R, while the identities of the newly generated group elements are given at the perimeter of the image :

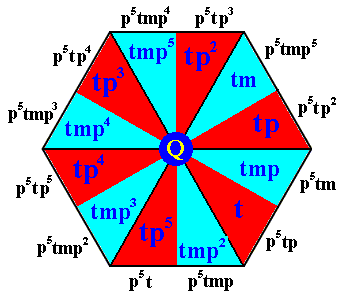
Figure 14g. The newly generated composed motif at lattice point Q (as indicated in Figure 14e). The names of the new elements are given at the perimeter of the image (i.e. outside the image).

All the elements in Figure 14g (red and blue) together form the left coset of the D₆ subgroup (See Figure 14d) by the element p⁵t .

The third row (Figure 14e) of composed motifs can now be completed by means of applying to this lastly obtained composed motif the translations . . . t^-3, t^-2, t^-1, t, t², t³ . . . . And along the same lines we can complete row 2 of the pattern.

In order to reach the fourth row we first determine the composed motif at the point U by applying t² ( = 2 times applying the translation t ) to the elements of the composed motif at the point R :

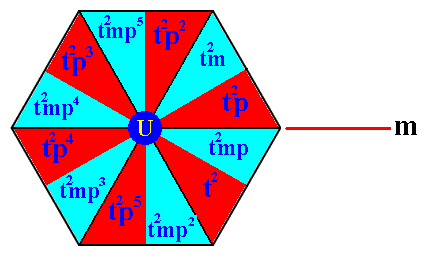
and then rotate it 300⁰ anticlockwise about the point R, i.e. applying p⁵ :

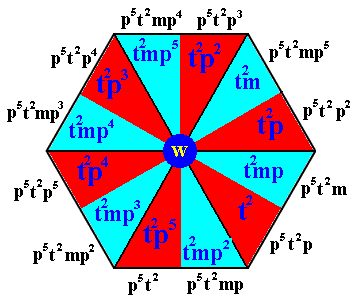
Figure 14h. The composed motif at the point W (Figure 14e) is completed, by applying p⁵ to the composed motif at the point U . The original element notations as they were at point U have been put inside the image, while at its perimeter we have put the notations of the newly generated elements of the composed motif at the point W.

The six red motif units of the above Figure (Figure 14h) together form the left coset of the subgroup {1, p, p², p³, p⁴, p⁵} (with structure C₆ ) by the element p⁵t² .
This fourth row can now be completed by means of translations.

The same P6mm pattern can be generated by an augmented motif unit, which could be, for instance, two symmetrically related basic motif units :

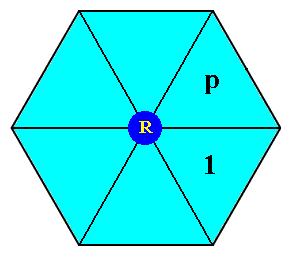
Figure 14i. Composed motif (of the P6mm pattern) consisting of six symmetric motif units. Two of them are provided with a notation. Each such motif unit in fact consists of two symmetrically related basic motif units. These non-basic motif units cannot represent group elements. The one denoted by 1 is in fact the subgroup {1, mp} (in the notation above [See Figure 14d ], referring to basic motif units), which has the structure of C₂ ( The element mp is of period 2, which can easily be verified in Figure 14d ).

We will now generate the P6mm pattern by means of the non-basic motif units established in Figure 14i. We will use the same notation as we did with respect to the basic motif units. Because we now use symmetrical motif units (which, as has been said, consists of two symmetrically related basic motif units), we do not need the generator m anymore. We can do it with the generators p (rotation) and t (translation). So now to begin with we can generate the other elements of the composed motif (representing the subgroup D₆ ) :

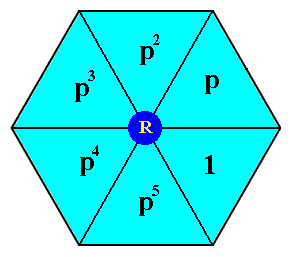
Figure 14j. By the generator p the remaining elements of the subgroup D₆ are generated : Given 1 (initial element) and p (generator), the element p² results after two times applying p to the initial element. The element p³ results from three times applying p , etc., while p⁶ = 1 , where p is an anticlockwise rotation of 60⁰ about the point R .

The next Figure summarizes the two chosen generators, as represented by non-basic motif units (augmented motif units), that can generate the whole group P6mm :
The element (augmented motif unit) p , resulting (as just established) from the element 1 (which is chosen to represent the identity element), by an anticlockwise rotation of 60⁰ about the point R .
The element (augmented motif unit) t resulting from element 1 in virtue of the translation t .
We must realize that, although speaking about "elements", they are not true elements of the group, but subgroups or cosets.
If we were to insist that they are true group elements, then we would not in fact have to do with the group P6mm anymore, but with the group P6 instead, i.e. with a subgroup of P6mm, because repeated rotation (there where p⁶ = 1) and translation of some initial entity results in the group structure of P6 (See the beginning of the previous Part, where P6 is indeed generated from a rotation and a translation).

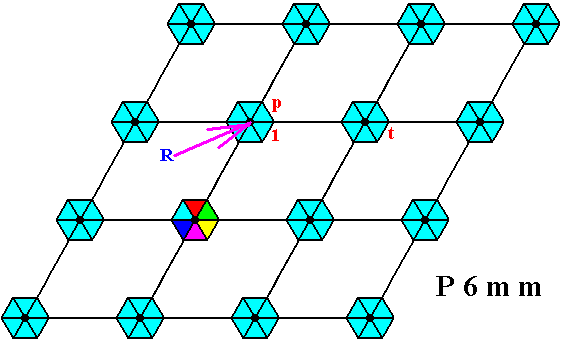
Figure 15. Two chosen generators, p and t for the P6mm pattern.
In one of the composed motifs (which are of course all identical) its composition out of six (augmented) motif units is indicated by colors.

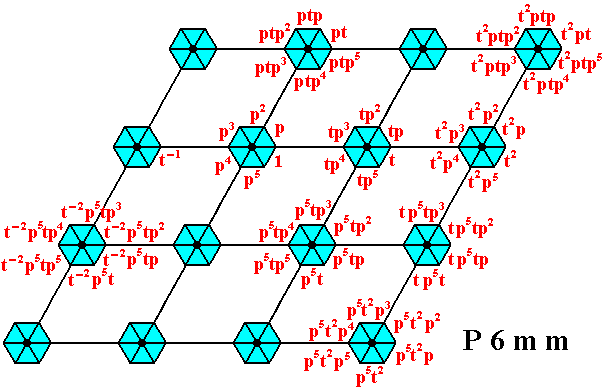
Figure 16. Generation of the group P6mm by the generators p and t . See also next Figures.

The next Figures explain some of the generative relations between some group 'elements' (augmented motif units) established by applying the generator p five times to a particular (already generated) augmented motif unit. Five times applying p means applying p⁵ , which in turn means an anticlockwise rotation of 5 x 60 = 300⁰ about the point R (as indicated in Figure 15). In the ensuing Figures augmented motif units and their images under p⁵ are indicated by coloring.

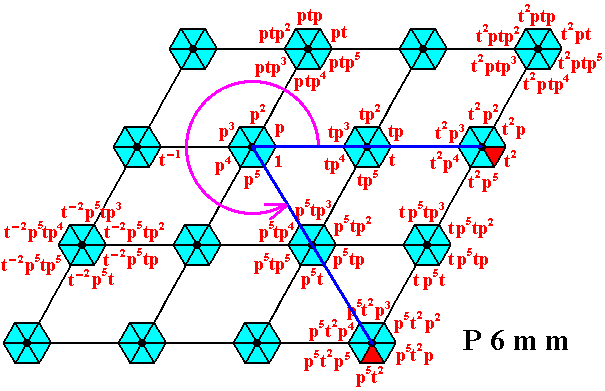
Figure 17. Image p⁵t² -- under (the action of) p⁵ -- of the augmented motif unit representing the group 'element' t² .
The action of p⁵ is indicated by the circular arrow.

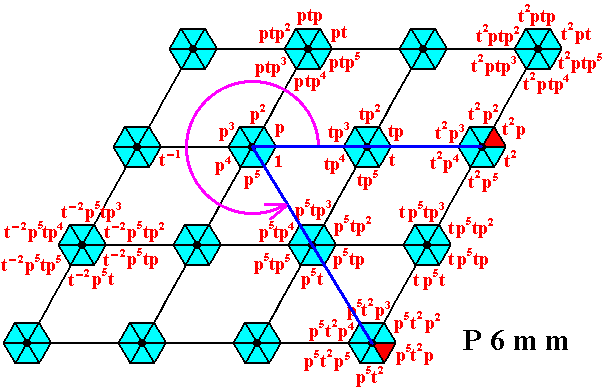
Figure 18. Image p⁵t²p -- under (the action of) p⁵ -- of the augmented motif unit representing the group 'element' t²p .
The action of p⁵ is indicated by the circular arrow.

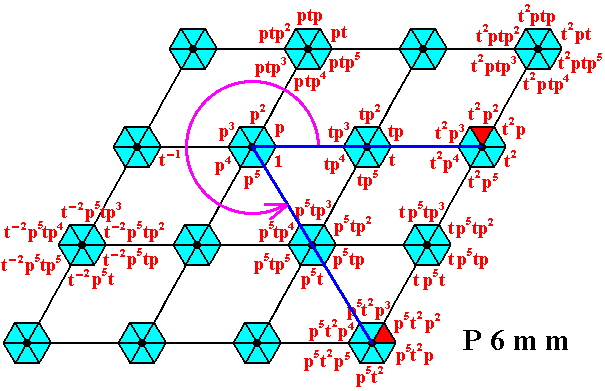
Figure 19. Image p⁵t²p² -- under (the action of) p⁵ -- of the augmented motif unit representing the group 'element' t²p² .
The action of p⁵ is indicated by the circular arrow.

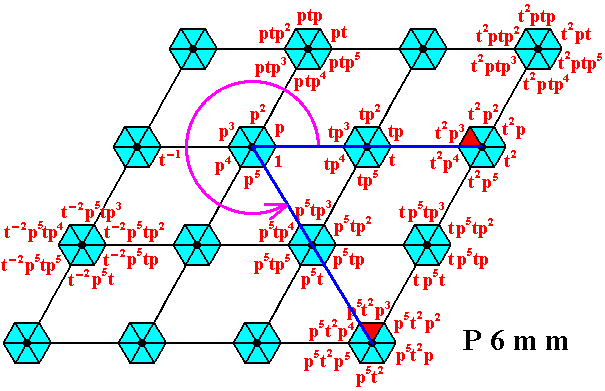
Figure 20. Image p⁵t²p³ -- under (the action of) p⁵ -- of the augmented motif unit representing the group 'element' t²p³ .
The action of p⁵ is indicated by the circular arrow.

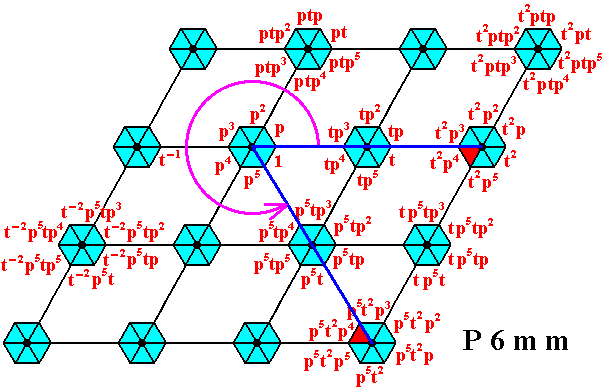
Figure 21. Image p⁵t²p⁴ -- under (the action of) p⁵ -- of the augmented motif unit representing the group 'element' t²p⁴ .
The action of p⁵ is indicated by the circular arrow.

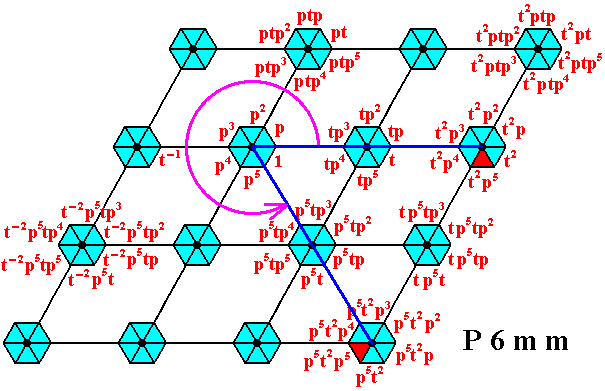
Figure 22. Image p⁵t²p⁵ -- under (the action of) p⁵ -- of the augmented motif unit representing the group 'element' t²p⁵ .
The action of p⁵ is indicated by the circular arrow.