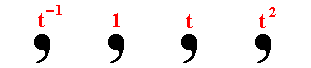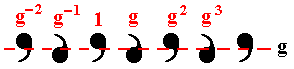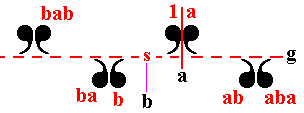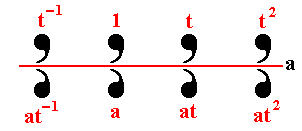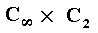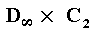The Total Symmetry of Three-dimensional Crystals
Part XXI
e-mail : 
Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Sequel to Infinite two-dimensional periodic patterns
In the previous document we began the study of 2-D periodic patterns along a synthetic approach, which means that we investigate the symmetry of such patterns by building them up, using generators. This implies that we generate the group -- underlying the pattern -- by successively generating its elements. Every such group element is then represented by the location and orientation of a basic motif unit with respect to an initial such basic motif unit. But because the pattern contains infinitely many of such motif units, the number of group elements is infinite, so the process of generating the group will never be concluded. But from a certain point onwards it's becoming clear that no new generators will be needed and the pattern can be extended as far as we please. Such patterns are periodic, which means that we can detect a certain unit which is repeated in two directions while preserving its orientation. In crystallography (including also that of imaginary 2-dimensional crystals) such a unit is called a unit-cell.
The concept of unit-cell, in relation to certain point nets (two-dimensional point lattices), the symmetry of these point nets, and the the symmetry that results when motifs are placed into such point nets, is extensively treated in the first part of this website. The latter is accessible by the following link back to homepage, and the analytical approach with respect to studying the symmetry of two-dimensional periodic infinite patterns can be found in the Special Series, where the relevant documents (beginning after the documents on Crystal Systems) are named Internal Structure of Crystals (Part I -- XX).
In the previous document we generated a pattern according to the P4mm Plane Group. We did this by using four generators, acting on an asymmetric basic motif unit (a comma). This does not mean, however, that the minimum number of generators is necessarily four. By chosing other, appropriate, generators we can do the job with a minimum of three generators.
In order to understand two-dimensional periodic patterns (and through them, three-dimensional periodic patterns -- real crystals -- ) we must direct our attention to one-dimensional periodic patterns, which are patterns consisting of a unit that is repeated, while preserving its orientation, in one direction only (and within that direction, backwardly and forewardly repeated). Such patterns are called frieze patterns or strip patterns. As has been said, such patterns extend to infinity in one dimension. Because of the demand of periodicity there are only 7 types of such patterns, i.e. seven distinct patterns (for two dimensions there are 17 such patterns -- described by plane groups -- , and for three dimensions we have 230 such patterns -- described by space groups).
In the next table we show these seven distinct one-dimensional patterns, using again as motif unit the comma. The group elements they contain can be half-turns, mirror lines, translations and glide lines.
A half-turn is indicated by s ,
a mirror line is indicated by a red solid line,
a translation is evident from the pattern itself, and
a glide line (glide reflection) is indicated by a red dashed line.
In a second column we indicate some possible sets of generators, and in a third column we indicate the group theoretical structure of the pattern.
|
Pattern |
Generators |
Structure |
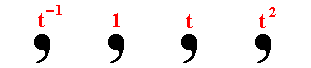 |
1 translation
t |
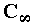 |
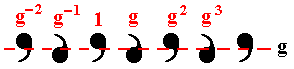 |
1 glide
g |
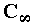 |
 |
2 reflections
a and b
or
reflection and translation
(t = ba) |
 |
 |
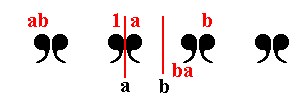
2 half-turns
a and b
or
half-turn and translation
(t = ba) |
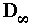 |
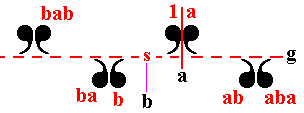 |
1 reflection (a) and
1 half-turn (b)
(g = ab) (t = (ab)2 ) |
 |
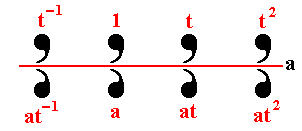 |
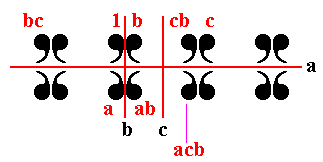
1 reflection (a) and
1 translation (t)
or
reflection and glide
(g = at) |
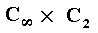 |
 |
3 reflections (a) (b) and (c).
Other sets of generators
may include
t = cb
g = acb, etc. |
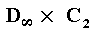 |
The seven frieze (strip) patterns.
With the frieze patterns, seven groups are involved as realizations of four abstract groups : Cinfinite , Dinfinite , Cinfinite x C2 , and Dinfinite x C2 . This means that some of these patterns have identical distributions of periods (over their group elements), while these periods are represented by different symmetries, for example, instead of two reflections (involving a period of 2) : two half-turns (also involving a period of 2).
The groups Cinfinite x C2 and Dinfinite x C2 can also be called respectively Cinfinite x D1 and Dinfinite x D1, because C2 is isomorphic to D1 (BUDDEN, p. 290).
The seven strip patterns will also be encountered as parts of two-dimensional periodic patterns.
The two-dimensional periodic patterns
We will now discuss the 2-D periodic patterns ('wall-paper patterns'). One of these, P4mm, we already spoke about earlier.
There are, as we have stated earlier, exactly seventeen distinct plane patterns for a given choice of motif. These plane patterns must contain translations in two different directions, and may also contain reflections, glide reflections and rotations. There are only five of the seventeen patterns in which the motifs are not 'turned over', i.e. which contain only translations and rotations. This is a consequence of a theorem, known as Barlow's theorem, which states that the only possible periods of rotation in such patterns are 2, 3, 4 and 6 (and of course the trivial rotation, the identity, which has period 1). These periods of rotation correspond to the possible presence of only 2-fold, 3-fold, 4-fold, 6-fold, or 1-fold rotation axes in such patterns, where with "such patterns" is meant infinite periodic patterns.
Let's take a closer look to these rotation axes.
A 2-fold rotation axis implies a rotation of 1800, which is of period 2.
A 3-fold rotation axis implies rotations of 1200 and 2400, both of period 3.
A 4-fold rotation axis implies rotations of 900 and 2700, both of period 4 (Moreover it implies a rotation of 1800 which is of period 2).
A 6-fold rotation axis implies rotations of 600 and 3000, both of period 6 (Moreover it implies a rotation of 1200 and of 2400, both of period 3, and a rotation of 1800, which is of period 2).
A 1-fold rotation axis is a rotation of 00 or of 3600, which are of period 1 (Recall that these rotations are not just any rotations, they are cover operations (cover transformations) resulting in the object that is being rotated to occupy the same space as it did before it was rotated. Only such transformations (including reflections and other cover operations) describe the symmetry of the given object).
A proof that this is all there is -- with respect to rotations -- in plane periodic patterns, as well as in three-dimensional periodic patterns, is given in the first part of our website accessible by back to homepage, and there within the Special Series in the document Derivation of Crystal Classes I.
We will now look at the 17 basic periodic plane patterns from a synthetic viewpoint, which, as has been explained earlier, means that we consider the building up of them by generating the group elements from two or more possible generators (Recall that the consideration of them from an analytic viewpoint was already done in the first part of our website, in the documents on the Internal Structure of Crystals (Part I -- XX) in the Special Series of documents). The groups describing the symmetry of such patterns are called plane groups. Each such pattern consists of an imaginary point lattice (indicated by lines, the intersections of which are the points) in which motifs have been placed.
A letter P in the plane group symbol means that the underlying (imaginary) point lattice is primitive, which means that the unit cell (the unit that is periodically repeated) contains motifs only at its corners, while in a centered (2-D) point lattice there is also a motif in its center. Plane groups of patterns that are underlied by such a centered point lattice have the letter C in their symbols. In all the 2-D patterns that we will show, we can detetect a unit cell, which is outlined by the auxiliary lines indicating the point lattice (net), i.e. a single mesh of that net. It is a unit that indicates the periodicity of the pattern : The area of the unit cell is repeated throughout the pattern without (that area) being turned.
The pattern according to the Plane Group P1.
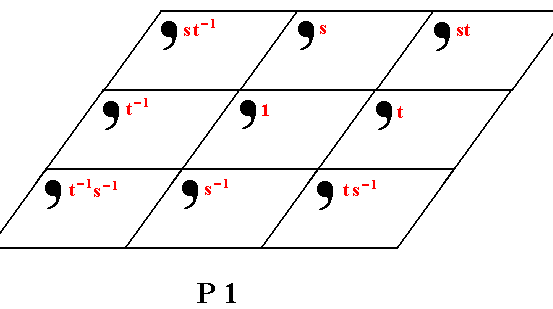
Figure 1. Placing 2-D motifs with point symmetry 1 into an oblique 2-D point lattice yields a pattern that represents the Plane Group P1. This is not the generation of the pattern, but a description. The synthetic approach considers the generation of such a pattern by (chosen) generators. Such generators are given group elements (symmetry transformations) that generate all the other group elements (geometrically represented by the position and orientation of motifs, in all cases of symmetry groups).
By the generators s and t (both translations) all other group elements (represented by the position and orientation of the motifs) of the group P1 can be generated from the initial element 1. Some of those are shown (for example st, ts-1, etc.).
The pattern must be considered as (becoming to be) indefinitely extending in 2-D space.
( The angle between the auxiliary lines need not necessarily be the (particular) one that has been used in the Figure, it can be any angle, i.e. the angle between the two translations can be any angle.)
The total symmetry content of Plane Group P1 is given in the next Figure.
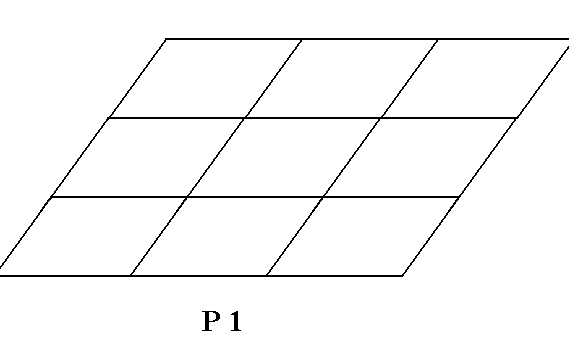
Figure 1a. Total symmetry content of Plane Group P1.
The only symmetry present is : simple translation.
The pattern according to the Plane Group P2.
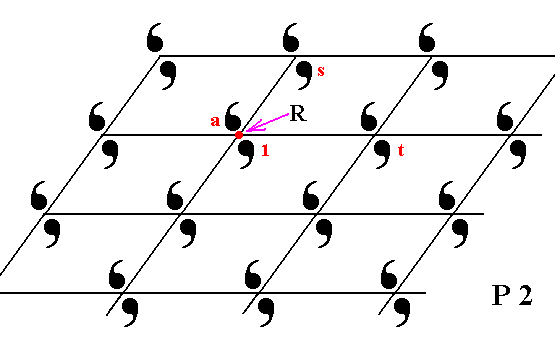
Figure 2. Placing 2-D motifs with point symmetry 2 into an oblique 2-D lattice yields a pattern that represents the Plane Group P2. The pattern must be viewed as extending indefinitely in 2-D space.
To generate such a P2 pattern from an initial motif, i.e. to generate the group P2 , we choose three transformations to be the generators :
Rotation by 1800 about the point R ,
A translation s and a translation t .
In the next Figure we give the total symmetry content of the Plane Group P2.
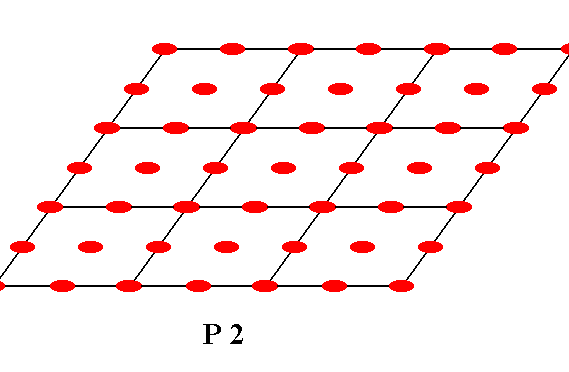
Figure 2a. The total symmetry content of the Plane Group P2 : simple translation (two translation vectors), 2-fold rotation axes.
The next Figure shows that the pattern as a whole will return as it was before (i.e. occupy the same (patch of) space as it did before) after a half-turn about the point R , meaning that the point R indicates a symmetry axis of the pattern.
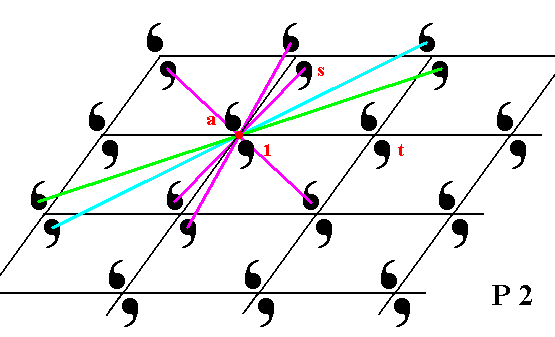
Figure 3. The point R marks a two-fold rotation axis to be present in the P2 pattern. There are of course many such axes, but this particular one is chosen to be one of the generators of the pattern from an initial motif, (the latter) indicated by the numeral 1. The other generators needed are two translations.
The next Figure shows how the P2 pattern can be generated from the three chosen generators. And this is equivalent to the generation of the group P2.
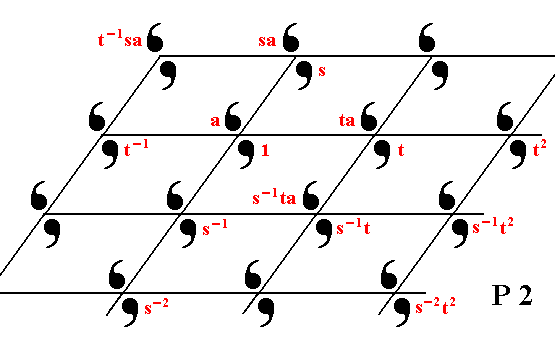
Figure 4. The pattern -- and with it the group elements -- can be generated by two translations s and t , and the half-turn a.
The pattern must be viewed as becoming to extend indefinitely in 2-D space.
The pattern according to the Plane Group P3.
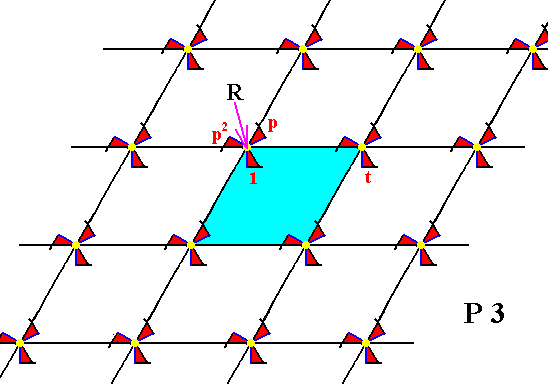
Figure 5. Arranging motifs with point symmetry 3 in a hexagonal 2-D lattice yields a pattern that represents Plane Group P3. The pattern must be conceived as to be indefinitely extended in two-dimensional space.
A unit cell, outlined by the hexagonal net, is indicated (light blue).
Each motif consists of three motif units. One such unit is considered as the initial motif unit, and is indicated by the numeral 1.
As generators, for building up this pattern, we choose a (horizontal) translation t and an anticlockwise rotation of 1200, denoted by p about the point R .
So from the initial motif unit 1 (representing the identity element of the group) the motif unit p is generated (which represents the group element p ). And when -- on the initial motif unit -- the rotation p is twice applied, we get the motif unit p2, and with it the corresponding group element p2. Three times applying p yields the identity element, so p3 = 1.
Wherever we have some (already generated) motif unit (representing a group element), we can generate a new motif unit (representing a new group element) by rotating it 1200 about the point R . Another new motif unit can be produced by shifting it according to the translation t. (See Figure 6).
The total symmetry content of the Plane Group P3 is given in the next Figure.
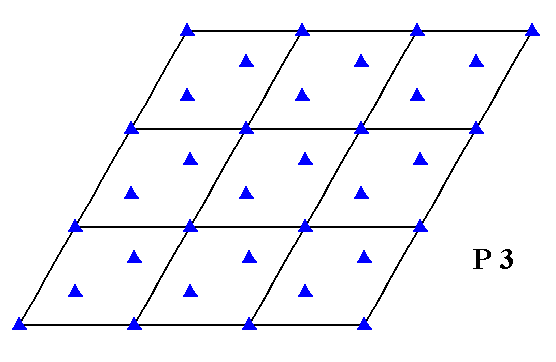
Figure 5a. Total symmetry content of the Plane Group P3.
There are no mirror lines and also no glide lines. The Plane Group only possesses 3-fold rotation axes and translations.
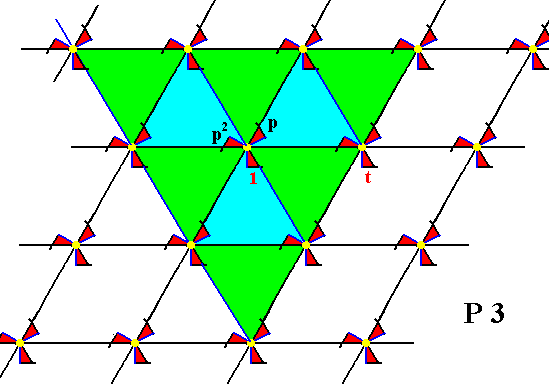
Figure 6. This Figure shows the tri-radiate nature of the P3 pattern with respect to the point R . ( That point is explicitly indicated in the previous Figure). The whole pattern returns as it was before (i.e. occupies the same space as it did before), when we rotate it 1200 about R . The point R is not the only point with this property : There are many such points. But the rotation about the specific point R by 1200 anticlockwise, is chosen as a generator of the group. Any already existing motif unit (representing a group element) of the pattern yields a new motif unit (representing a new group element), when it is subjected to rotation of 1200 or of 2400 about the point R . In addition to this particular generator a second generator is needed, which is chosen to be a horizontal translation to the right (and implying also such a translation to the left). By this translation the motif units (representing group elements) t-1, t , t2, etc. are generated from the initial motif.
The next Figures show the generation of the P3 pattern. A number of motif units are provided with the indication of how they can be generated by means of the two generators p (rotation of 1200 about the point R (indicated in Figure 5)), and t (translation horizontally to the right).
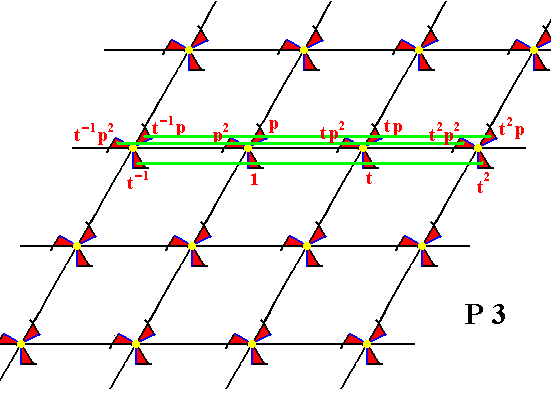
Figure 7.
From the element 1 the elements t-1 , t, t2 , etc. are generated by the element t .
From the element 1 is generated the element p by applying the transformation p , which is an anticlockwise rotation by 1200.
From the element p is generated the element p2 by (again) applying p .
From the element p are generated the elements t-1p , tp , t2p , etc. by applying t .
From the element p2 are generated the elements t-1p2 , tp2 , t2p2 , etc. by the element t .
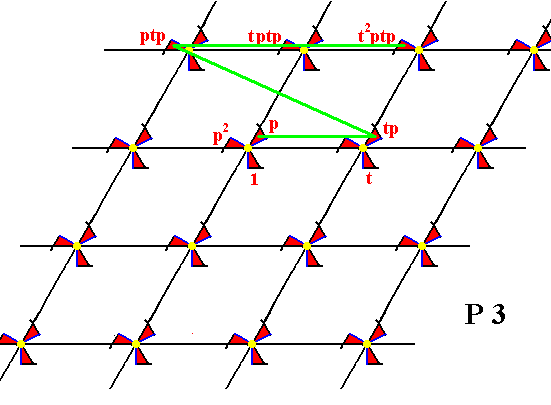
Figure 8.
From the element p the element tp is generated by applying t , and from tp the element ptp is generated by applying p , i.e. an anticlockwise rotation of 1200 about the point R (as indicated in Figure 5).
From the element ptp the elements tptp , t2ptp , etc. are generated by applying t .
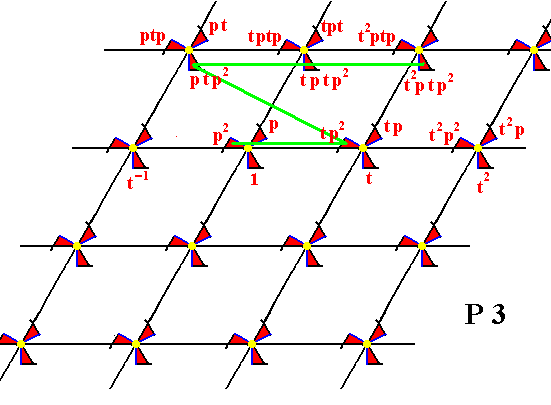
Figure 9.
From the element p2 the element tp2 is generated by applying t , and from tp2 the element ptp2 is generated by applying p (rotation of 1200 anticlockwise about R ), and from ptp2 the elements tptp2 , t2ptp2 , etc. are generated by t .
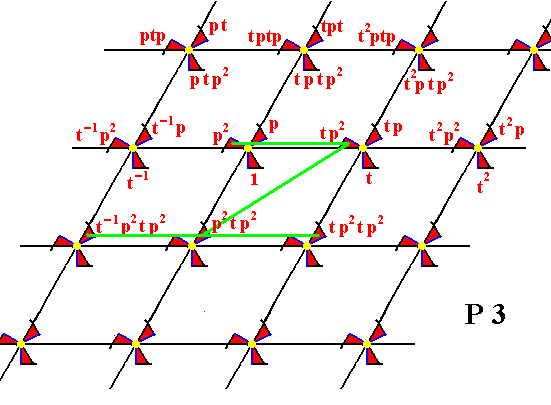
Figure 10.
From the element p2 the element tp2 is generated by applying t , and from the element tp2 the element p2tp2 is generated by applying p2 (A rotation of 2400 anticlockwise about the point R (As given in Figure 5).
From p2tp2 are generated the elements t-1p2tp2 , tp2tp2 , etc. by applying t .
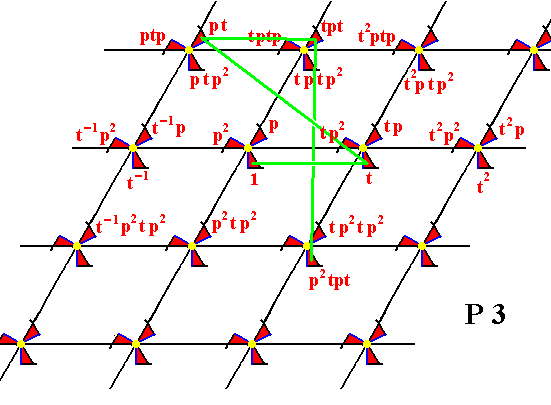
Figure 11.
From the element 1 the element t is generated by applying the translation t , and from the element t the element pt is generated by applying the rotation p about the point R (see Figure 5), and from the element pt the element tpt is generated by applying the translation t . From the element tpt the element p2tpt is generated by applying the rotation p2 (about the point R ).
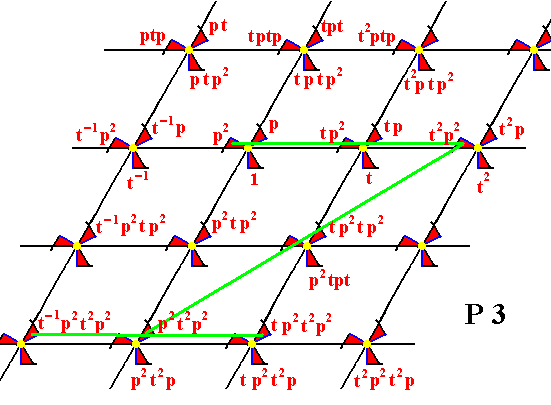
Figure 12.
From the element p2 the element t2p2 is generated by applying the translation t2 , and from the element t2p2 the element p2t2p2 is generated by the rotation p2 . And from the element p2t2p2 the elements t-1p2t2p2 , t p2t2p2 , etc. are generated by applying the translation t .
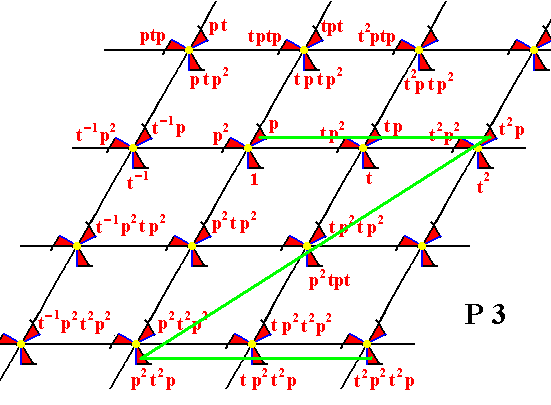
Figure 13.
From the element p the element t2p is generated by applying the translation t2 (i.e. applying the translation t two times), and from the element t2p the element p2t2p is generated by the rotation p2 . And from the element p2t2p the elements t p2t2p , t2 p2t2p , etc. are generated by applying the translation t .
The next Figure shows the overall result. In fact the generation of ever new group elements must be conceived to go on indefinitely.
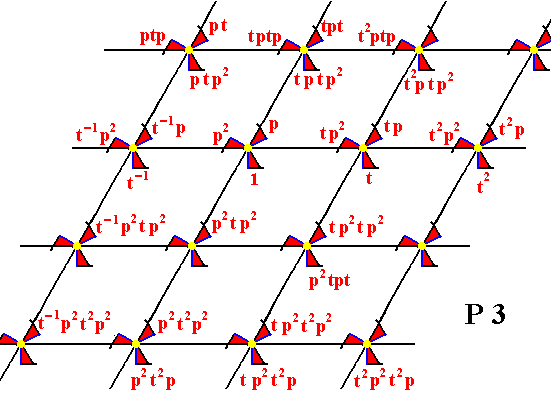
Figure 14. The P3 pattern, generated by the transformations p and t .
( The pattern must be conceived as becoming to be extended indefinitely in 2-D space)
The pattern according to the Plane Group P4.
Here we give a two-dimensional periodic pattern with motifs at the nodes of a square lattice. Each motif consists of four motif units -- commas, as used above -- such that the whole (composed) motif has a point symmetry 4 , i.e. a motif having a 4-fold rotation axis as its only symmetry element. It admits of four rotations : 00, 900, 1800 and 2700.
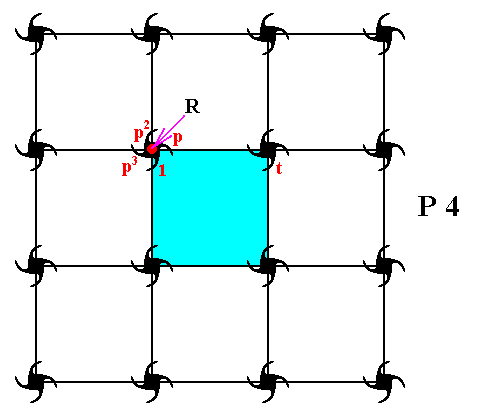
Figure 15. When we place four-fold motifs (in the present case motifs, each consisting of four partly overlapping commas) at the nodes of a square point lattice (square point net), we obtain a pattern according to the Plane Group P4 . A unit cell is indicated (light blue). The point R is the location of a four-fold rotation axis (There are more such axes). The element p is obtained by an anticlockwise rotation of 900 about the point R and is chosen as a generator of the group. A second generator is needed. We choose it to be the translation t. See Figure 16.
The next Figure shows the total symmetry content of the Plane Group P4.
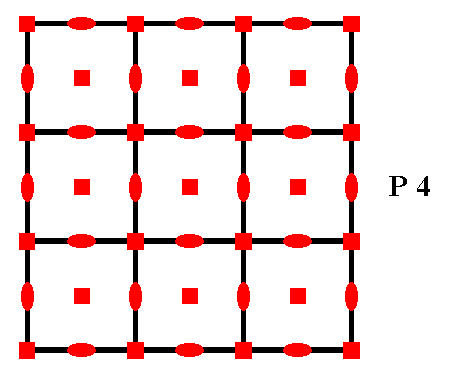
Figure 15a. The total symmetry content of any pattern representing Plane Group P4. There are neither mirror lines, nor glide lines present.
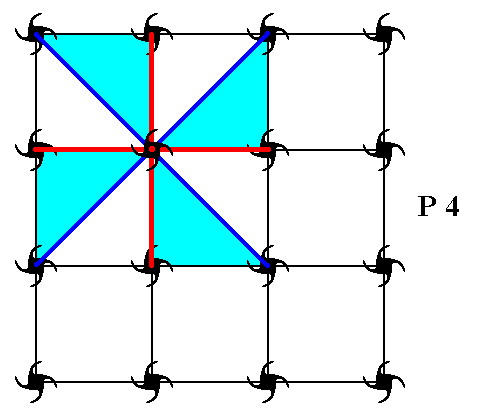
Figure 16. This Figure shows the four-fold symmetry at the point R , which means that the whole pattern returns as it was before (i.e. it will occupy the same space as it did before) after it has been anticlockwise rotated either by 900, 1800, or 2700 about the point R (indicated in the previous Figure). The group element representing a 900 rotation about this point R of the initial element 1 (See previous Figure) is denoted by p (See previous Figure) and is chosen as a generator of the group (in addition to this generator a second one is needed). A 1800 rotation (about R ) of the initial element generates the group element p2 (See previous Figure), while a 2700 rotation (about R ) generates the element p3 (See previous Figure). Finally a 3600 rotation about R is equivalent to 00 rotation, which means that we can say : p4 = 1.
As the second generator we have chosen the translation t (See previous Figure).
We will now show how the P4 pattern -- and with it the group P4 -- is generated by the generators p and t. This means that, given the identity element (and its representation as an initial motif unit) and the elements p and t (represented by the position and orientation of corresponding motif units with respect to those of the initial motif unit), we can in principle generate all other elements of the group, and with it all motif units (commas in our case) of the pattern (and thus generate the pattern itself), by combining the elements p and t . Again we shall show this in several stages. We follow the transformations of each of the four individual motif units (commas) of a composed motif, and connect the latter with the resulting composed motif (also consisting of four motif units) by a (i.e. one) green line. So such a line represents the transformation of a whole composed motif into another whole composed motif.
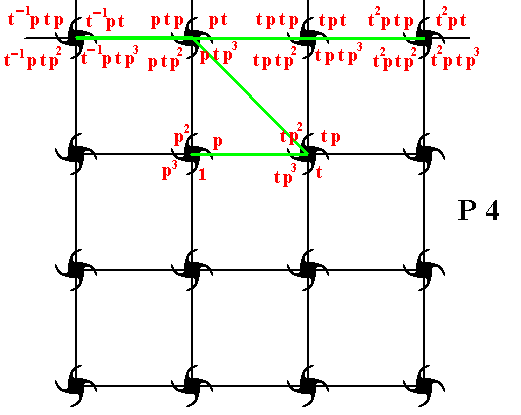
Figure 17. Generation of five new motifs (each one is a composed motif, consisting of four motif units), from the initial motif (which also consists of four motif units : the initial motif unit, and the motif units p, p2, p3 ).
Our initial motif consists, as has been said, of four motif units :
- The initial motif unit, denoted by 1 .
- The motif unit p , formed as an image of 1 under anticlockwise rotation of 900 about the point R .
- The motif unit p2 , formed as an image of 1 under anticlockwise rotation of 1800 about the point R .
- The motif unit p3 , formed as an image of 1 under anticlockwise rotation of 2700 about the point R .
We will now follow in detail the generation of (the above mentioned) five new (comnposed) motifs, by considering what happened to each of the four components of our initial image (See Figure 17 above) :
Our intitial composed motif consists of the four motif units 1 , p , p2 and p3 . If we produce the coresponding images of these under the translation t (which is a shift to the right along a certain fixed distance), then we get respectively t , tp , tp2 , tp3 , which form a new composed motif to the right of the initial composed motif (See Figure 17).
We're now going to produce the image of this new composed motif under an anticlockwise rotation of 900 about the point R , i.e. we subject it to the transformation p . This means that
t becomes pt
tp becomes ptp
tp2 becomes ptp2
tp3 becomes ptp3
In this way we have obtained yet another new composed motif consisting of pt , ptp , ptp2 , ptp3 , which we can find as the second composed motif of the top row in Figure 17.
When we now subject this last found composed motif to successively the translations t-1 , t , and t2 , we get the following :
pt becomes t-1pt
ptp becomes t-1ptp
ptp2 becomes t-1ptp2
ptp3 becomes t-1ptp3
An this yields yet another new composed motif, which we can see as the first one in the top row of Figure 17.
pt becomes tpt
ptp becomes tptp = (tp)2
ptp2 becomes tptp2
ptp3 becomes tptp3
This yields the third composed motif in the top row of Figure 17.
pt becomes t2pt
ptp becomes t2ptp
ptp2 becomes t2ptp2
ptp3 becomes t2ptp3
And this yiels the fourth composed motif in the top row of Figure 17.
So we now have indeed generated five new composed motifs from the initial composed motif.
Next we shall generate still more composed motif of our P4 pattern :
The third row of composed motifs can be generated along the same lines as we did it for the first row. The difference is that we now use an (anticlockwise) rotation (about the point R (As it is denoted in Figure 15 )) by 2700 (instead of 900) of the earlier obtained composed motif, the motif at the right of the initial composed motif. See next Figure.
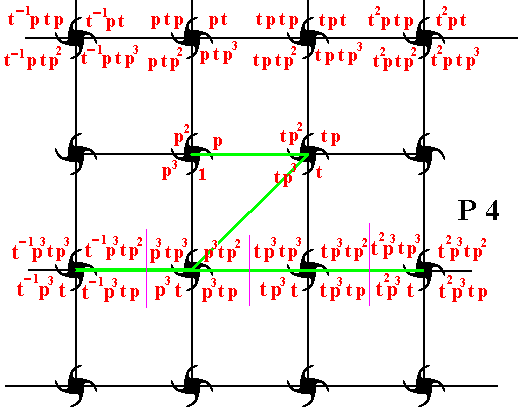
Figure 18. To the composed motif to the right of the initial motif the transformation p3 is applied, resulting in a new composed motif (second of the third row). From this new composed motif three other composed motifs are generated repectively by the transformations t-1 , t , t2 .
Next we generate the rest of the second row of composed motifs by applying respectively the translations t-1 and t2 to the initial composed motif :
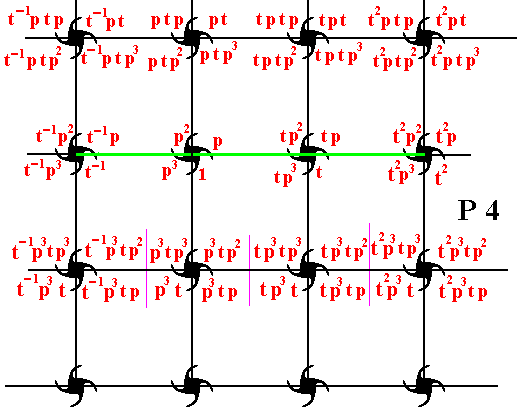
Figure 19. Two more composed motifs of the second row are generated by the translations t-1 and t2 .
To generate composed motifs of the fourth row, we start from the last one of the second row, subject it to the transformation p3 , which is an anticlockwise rotation of 2700 about the point R (as indicated in
Figure 15 ). This results in a new composed motif (the second one in the fourth row). From this new composed motif we can the generate the rest of the composed motifs of that row by applying translations :
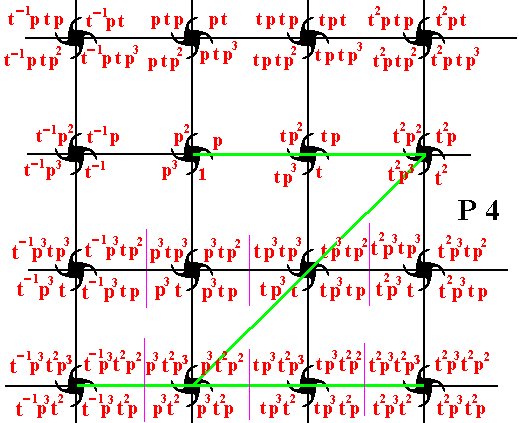
Figure 20. The fourth row of composed motifs can be generated from the fourth composed motif of the second row, using the transformations p3 , t-1 , t and t2 .
Of course one should continue this process indefinitely, because the group is infinite. However, it is by now clear how to generate the pattern, and with it the group governing its symmetry.
In the next document we will continue our exposition of the synthetic approach to the 17 two-dimensional periodic patterns.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to homepage
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals
back to Part XV of the theoretical preparation to the study of 3-D crystals
back to Part XVI of the theoretical preparation to the study of 3-D crystals
back to Part XVII of the theoretical preparation to the study of 3-D crystals
back to Part XVIII of the theoretical preparation to the study of 3-D crystals
back to Part XIX of the theoretical preparation to the study of 3-D crystals
back to Part XX of the theoretical preparation to the study of 3-D crystals
****************