e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III, a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns
Now we will discuss group theory as we find it in infinite two-dimensional periodic patterns. Evidently this will throw some light on infinite three-dimensional patterns, which are much harder to understand, but which are one of our objectives enabling us to better understand and discuss the internal structure of real crystals. Crystals consist of an internal pattern of microscopic chemical units that are repeated periodically in three different directions. This structure can be seen as a three-dimensional periodic point grid or point lattice in which the points are occupied by certain chemical motifs. Because a crystal consists of a huge number of such chemical motifs it can be considered as to possess an infinite periodic pattern.
Generally a pattern can be conceived as a basic motif that is regularly repeated. This can occur in two basic ways. In the first way the basic motif is repeated radially about some axis of rotation, or it is repeated by way of reflection about a point, line or plane. It can be proved that those plane patterns (and the same will be the case with three-dimensional patterns) in which the motif appears only a finite number of times must have a fixed point, i.e. that each symmetry operation leaves at least one point in place, and that their groups are either cyclic (such as, for example, C6 , C7 , etc.) or dihedral (such as D3 , D6 , etc.) (BUDDEN, p. 505). Such groups, i.e. groups involving a fixed point, are called point groups in crystallography. As we know from the first part of this website -- accessible via back to homepage -- in (three-dimensional) crystals there are precisely 32 such point groups, representing the 32 crystal classes of crystallography. In the two-dimensional realm such a point group can be realized, for example, by the Square ( D4 ) (and all other images having the same symmetry), the Equilateral Triangle ( D3 ), etc., while in three dimensions it can be represented by, for example, the Cube (Oi ) (and all other images having the same symmetry), the Tetrahedron (S4 ), and also the Regular Tetragonal Pyramid ( D4 ) and the Regular Trigonal Pyramid ( D3 ), etc.
However, as soon as symmetry operations, containing translations, are included in a pattern, not a single point is fixed anymore, because a translation, or translational component, shifts the whole pattern. Patterns that have such symmetry operations included, resulting in periodic patterns, are based upon, what we could call translational groups, as such contrasting with point groups.
In the present document we will be concerned with such translational groups, limiting ourselves, however, to two-dimensional translational groups, underlying infinite two-dimensional periodic patterns (As has been said, they will support the understanding of three-dimensional periodic patterns as they occur in real crystals). The groups that describe such patterns are called plane groups (groups describing three-dimensional periodic infinite patterns are called space groups).
There are two ways to discuss infinite two-dimensional periodic patterns, the analytic approach and the synthetic approach.
Let's begin with saying something about the analytical approach.
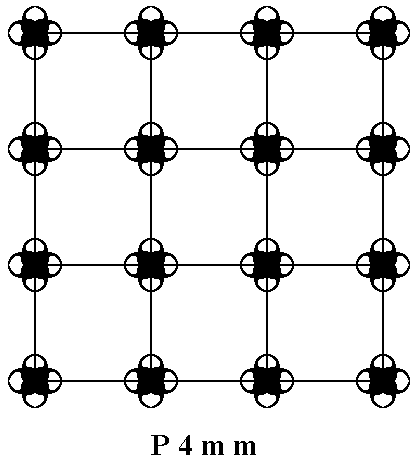
Figure 1 depicts part of an infinite periodic two-dimensional pattern according to the plane group P4mm, while figure 2 analyses its symmetry :

Figure 1. Placing 2-dimensional motifs with point symmetry 4mm into a square 2-dimensional point lattice yields a pattern that represents the Plane Group P4mm. The pattern must be conceived as extending indefinitely in two-dimensional space.
The total symmetry content of the Plane Group P4mm consists of simple translations, gline lines, 4-fold rotations and two types of mirror line. See Figure 2.
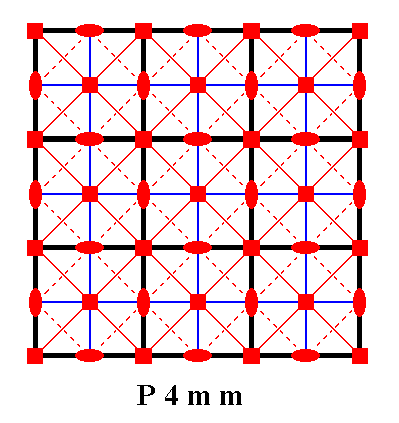
Figure 2. Total symmetry content of the Plane Group P4mm.
All continuous lines, including those that represent (the lines connecting the nodes of) the net, are mirror lines. There are two types of them, diagonal and non-diagonal. Dashed lines signify glide lines, small solid ellipses signify 2-fold rotation axes perpendicular to the plane of the drawing, and small solid squares signify 4-fold rotation axes perpendicular to the plane of the drawing.
The analytic approach is extensively treated in the first part of this website. The latter is accessible by the following link back to homepage, and the analytical approach with respect to studying the symmetry of two-dimensional periodic infinite patterns can be found in the Special Series, where the relevant documents (beginning after the documents on Crystal Systems) are named Internal Structure of Crystals (Part I -- XX). In those documents the two-dimensional periodic patterns are treated as representing imaginary two-dimensional crystals, as a prelude to the study of three-dimensional crystals. And because their analysis is so extensively treated there, we will dwell on it no further, and we will right away continue with the synthetic approach to those two-dimensional periodic infinite patterns.
In the synthetic approach we will actually build up the pattern from a basic motif unit. What we then actually do is generating the group, underlying that pattern, by means of its generators.
In the foregoing documents we had several occasions of generating a finite group. There we saw that after some new different elements had been formed by combining other elements, no further new elements are being formed anymore, which was a signal that all the elements of the group had indeed been generated.
With respect to infinite groups matters are different. How ever far we prolong our generating procedure, new elements keep coming. This means that we in fact cannot stop the process, because if we did, the result would be a set of elements which is not closed (under the operation of combining the elements already present), and thus such a result will not constitute a group. So the process of generating elements must be conceived as having been extended all the way to infinity. Only after we conceive for ourselves as having produced the infinite number of elements, we can consider the resulting set as being a group. It seems to be that here the concept of group is a little bit strained and tied up with the pecularities of the concept of infinity, which is certainly not without philosophical problems. In crystals, the symmetry of the internal structure is described by such infinite groups, but the actual structure of those crystals corresponds only to a finite number of symmetry transformations, i.e. to a finite number of group elements. But, as has been said, the number of them is huge (because of the very small distances between the conceived lattice points), so inconceivably huge, that it can, for all practical purposes, be considered to be infinite.
So in generating the group we encounter new elements all the time. These elements are group elements, and in patterns they represent symmetry transformations, in fact, symmetry transformations applied to a certain basic motif. When we have, for example, a mirror line, and a motif at some distance from that line, then a second motif will be produced at the opposite side of that mirror line, resulting in a total figure -- the two motifs taken together -- having bilateral symmetry. But when we only had this mirror line no further motifs (in addition to the two just described) will be generated. As soon as a translational symmetry operation (which is a shift over a certain distance) is introduced, new motifs will be produced without this process (of producing new elements) ever to stop. We will never produce a motif that was already in place somewhere in the pattern. Indeed it is the location and orientation of a motif with respect to some initial (and given) motif, which corresponds to the symmetry transformation that had produced it (from the initial motif), and thus which corresponds to the relevant group element. So a (i.e. any) group element of an infinite group can be represented by the position and orientation of some basic motif (unit) with respect to some intially given motif (unit).
Let us now begin with building up the pattern of Figure 1, little by little. As has been said, building up the pattern corresponds to generating the group underlying that pattern. Our basic motif unit is a comma, which in itself has no symmetry whatsoever :
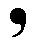
As such it will be our initial (given) motif. We will now subject this motif to a translation t (We have chosen this translation to be substantially smaller in length than the corresponding translation inherent in the pattern of Figure 1. The eventually resulting pattern will accordingly be more dense, but this is of course theoretically immaterial) :
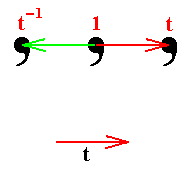
Figure 3. A translation t and its reverse t-1 applied to the intial motif (1).
So in the above Figure we generated two new group elements, t and t-1, represented by two new locations of the basic motif. It is clear that these two new elements do not have a finite period, because however often they are repeated, they will never end up to be the identity element (represented by the position of the initial motif (1)), so the period is equal to infinity. Indeed, when we repeat the (action of the) two elements -- one of them is a translation t to the right, while the other is that same translation, but directed to the left, indicated by t-1 -- we get the following pattern :
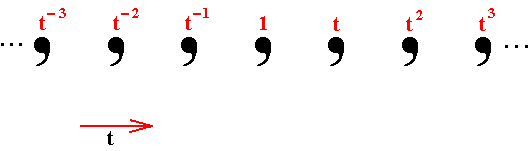
Figure 4. repeated application of the translation t and t-1, generating new motifs, representing new group elements. By constantly reapeating the mentioned translations, an infinite sequence of motifs will appear, forming a one-dimensional pattern, of course still not being the pattern of Figure 1.
The translation t can be seen as a generator of the group, i.e. one of the generators of the group which will -- when fully generated -- underly the symmetry of the pattern of Figure 1.
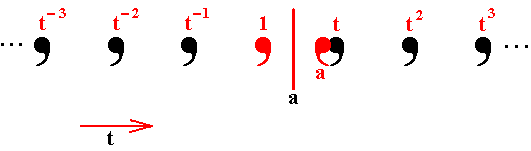
Figure 5. A second generator -- the mirror reflection a -- is added (to be the next stage in the built-up of the pattern of Figure 1).
The initial motif is reflected in the mirror line a thereby creating yet another motif representing yet another group element a.
But at the same time a combines with t , i.e. the motif, representing the group element t , is reflected in the mirror line a and creates yet another motif which represents the group element at , which means first apply t and then apply (to the result) a. See next Figure.
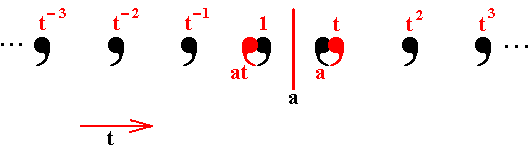
Figure 6. Also the motif representing the group element t is reflected in the mirror line a , generating a new motif representing the group element at.
Of course the other elements -- . . . t-3, t-2, t-1, t2, t3 . . . -- are also reflected in the mirror line a , thereby generating still more motifs representing still more group elements. See next Figure.
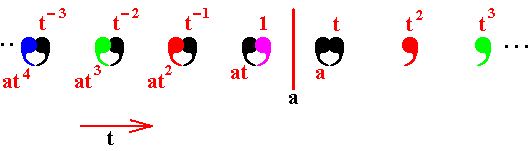
Figure 7. The motifs . . .t4, t3, t2. . . also being reflected in a.
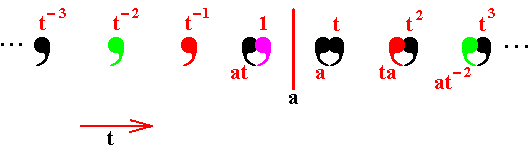
Figure 8. The motifs . . .t-3, t-2, t-1. . . also being reflected in a where ta = at-1 .
All this results in the following (infinite) pattern :
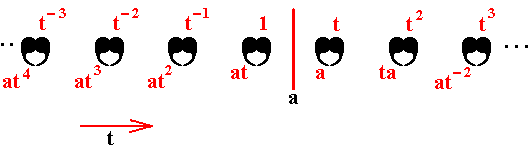
Figure 9. The total result of combining the translation t and the reflection a.
It is a one-dimensional infinite pattern. Not yet, however, the pattern of Figure 1.
In this intermediary result we can already detect a subgroup, namely { 1, at }.
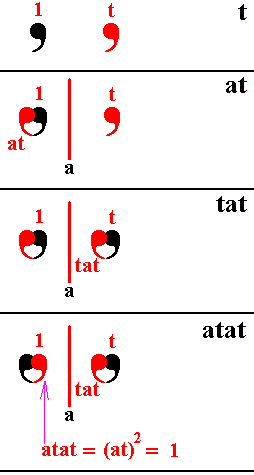
Figure 10. The operation (at)2.
t is a translation. a is a reflection in the line a.
If we first apply the operation t on the intial motif (1), and then on the result apply a , then on this result in turn t , and, finally, on the latter result the operation a , we will end up at the initial motif again.
All this clearly shows that (at)2 = 1, which means that the period of the element at is 2.
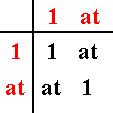
Figure 11. The subgroup { 1, at } as we find it in the infinite pattern sofar generated.
But the pattern of Figure 1 is not yet generated, which means that we need yet another generator to be introduced. This will be a horizontal mirror line denoted b , placed just above the motifs such that the string of motifs as we have it in Figure 9 will be reflected :
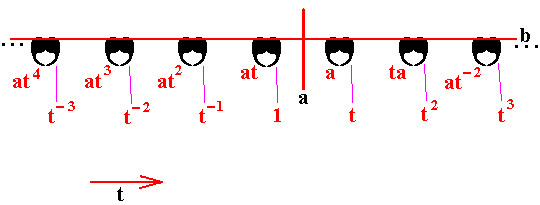
Figure 12. A third generator, the mirror line b is added.
The motifs will all be reflected in the newly added mirror line b :
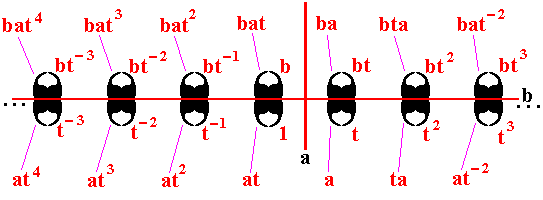
Figure 13. The new mirror line b reflects the motifs, and so creating as many new motifs, which represent as many new group elements.
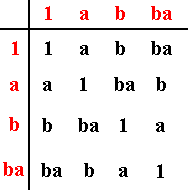
A second subgroup can now be detected : { 1, a, b, ba }. Let's check this.
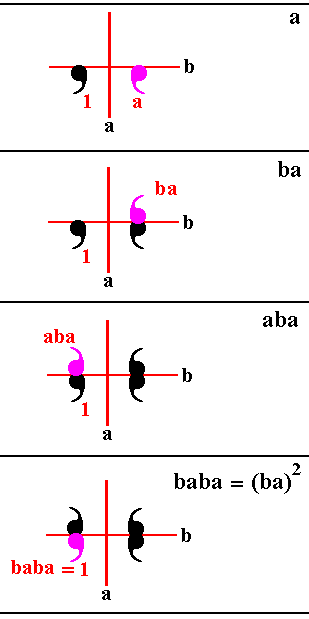
Figure 14. The action of (ba)2. It turns out that we end up at the initial motif again. So (ba)2 = 1.
From the above Figure it is clear that the period of the element ba is 2. And this means that all the elements of the set {1, a, b, ba}, except the identity element 1, are of period 2.
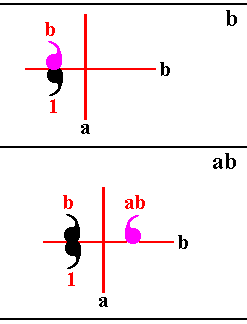
Figure 15. ba = ab . Compare with ba in the previous Figure.
All in all we have the set {1, a, b, ba}, with defining relations a2 = b2 = (ba)2 =1, and ba = ab.
So the structure of the set {1, a, b, ba} is clearly that of the group D2 :
Along the same line we can detect yet another subgroup with D2 structure, namely
Still we haven't yet produced the pattern of Figure 1. So a fourth generator is needed (at least in the path we've chosen to follow in generating the final pattern). This new generator will be the glide line g passing through the point of intersection of the two existing mirror lines, while bisecting the 900 between them :
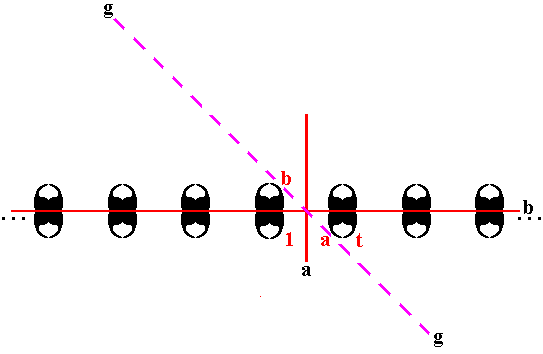
Figure 16. A fourth generator, the glide line g is added, indicated by a purple dashed line, passing through the intersection of the two mirror lines already in place, and bisecting the 900 angle between those mirror lines.
We spoke about, and explained, glide lines -- as being one of the translational symmetries occurring in 2-D periodic patterns -- in the first part of out website (accessible by back to homepage) in the Special Series : Part I of the subseries Internal Structure of Crystals. So here it is enough to reproduce one Figure explaining what a glide line is :
A glide line is a combination of a translation and a reflection with respect to a line parallel to the translation. If the translational aspect is removed we end up with a mirror line.
See Figure 17.
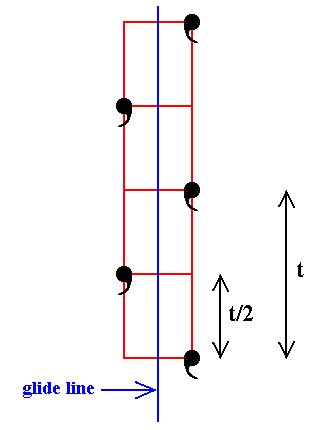 |
Figure 17. The operation of a glide line performed on a motif. The initial motif is translated by the vector t/2 parallel to the glide line, immediately followed by a reflection with respect to that glide line. The shortest translational distance between motifs in the direction of the glide line is t. |
In the above Figure the glide line is indicated by a solid line, but normally we indicate it by a dashed line (as we did in Figure 16), as to distinguish it from a mirror line.
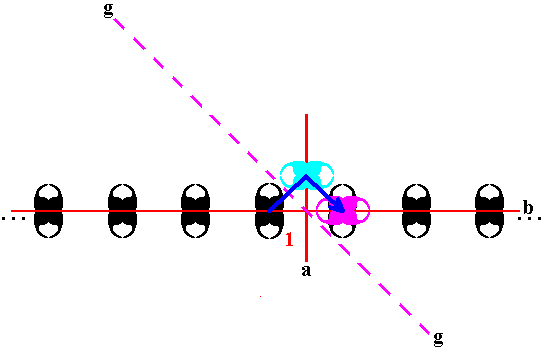
Figure 18. Effect of the operation g (glide reflection) on a composed motif. The latter is first relected in the (glide) line, resulting in just a transient motif (light blue), and then translated along that same line. The resulting new (composed) motif (purple), representing four new group elements, is differently orientated then the motifs produced so far. It combines with an existing (composed) motif to form the ultimate composed motif as we see it in Figure 1.
Taking into account the direction of the translation involved in this glide reflection we could denote the latter as g-1 .
So the resulting pattern is the following :
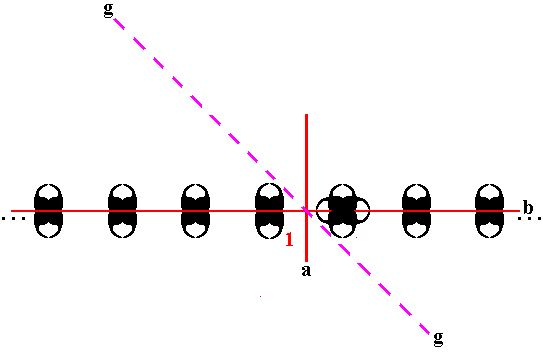
Figure 19. Ultimate effect of the glide reflection g on one particular composed motif.
If we concentrate just on what happens to the initial basic motif -- the single comma we started with, denoted by 1 -- we see the new motif unit appear, representing the new group element g-1 :
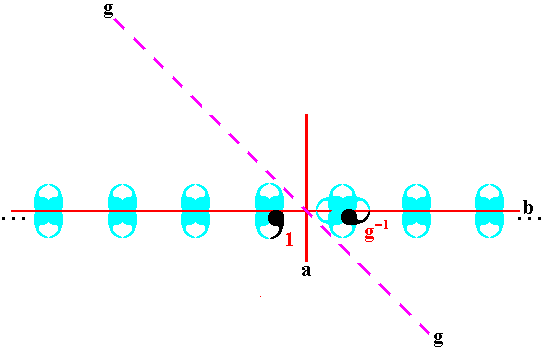
Figure 20. The element g-1 generated by the glide reflection, from the element 1 .
If we concentrate just on what happens to the motif unit representing the group element b , we see a new motif appear, representing the group element g-1b :
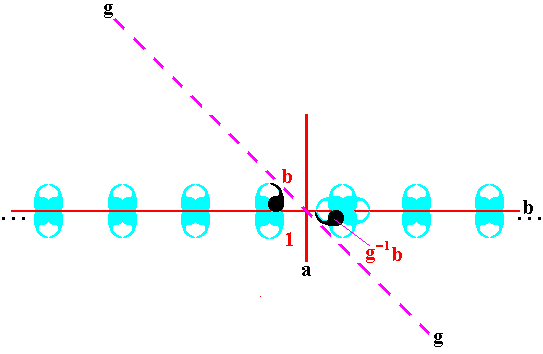
Figure 21. The element g-1b generated by the glide reflection, from the element b .
If we concentrate just on what happens to the motif unit representing the group element bat , we see a new motif appear, representing the group element g-1bat :
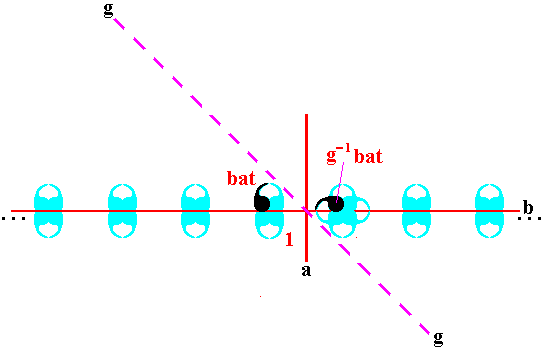
Figure 22. The element g-1bat generated by the glide reflection, from the element bat .
If we, finally, concentrate just on what happens to the motif unit representing the group element at , we see a new motif appear, representing the group element g-1at :
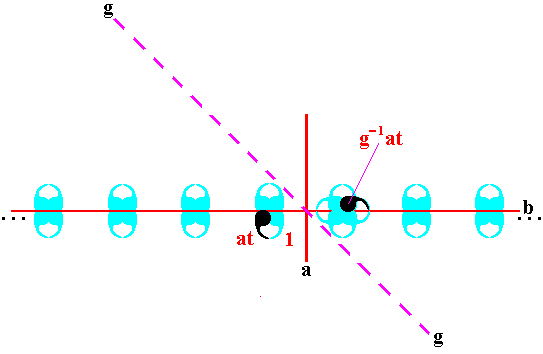
Figure 23. The element g-1at generated by the glide reflection, from the element at .
The next Figure shows the generation of still more composed motifs by the action of the glide reflection on the initially generated composed motif (Figure 19). Both directions are taken into account ( g-1 and g ) :
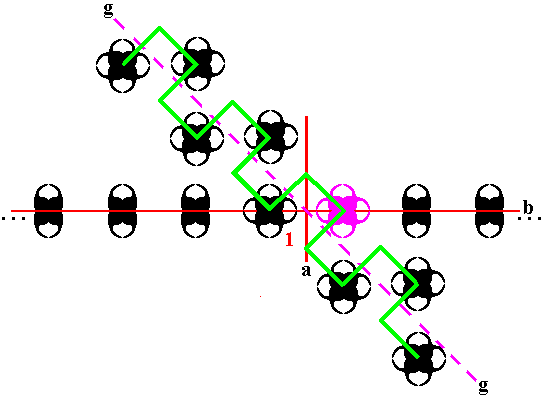
Figure 24. The action of the glide reflection (glide line) g on the initially generated composed motif produces more such composed motifs, and with it many more group elements.
Next we consider the effect of the mirror line b on the whole of the pattern produced so far :
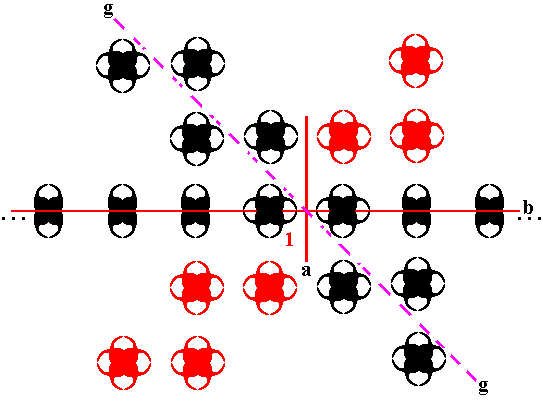
Figure 25. The pattern so far obtained is reflected in the mirror line b resulting in the appearance of still more motifs and correspondingly many new group elements.
The glide line g produces yet another composed motif. See next Figure.
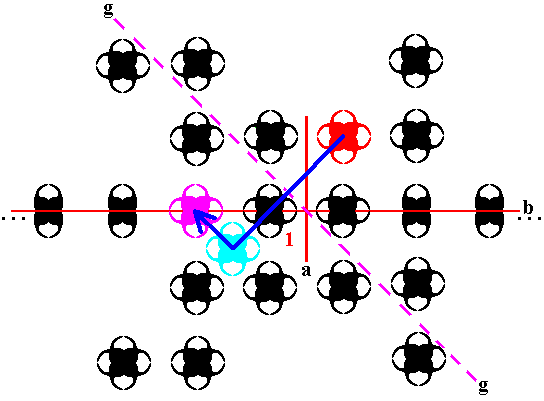
Figure 26. A new composed motif (purple) produced from one already present (red) (the light blue 'motif' is not a new motif, it is just a intermediate state of the action of the glide reflection).
This new motif is then reflected in the mirror line a :
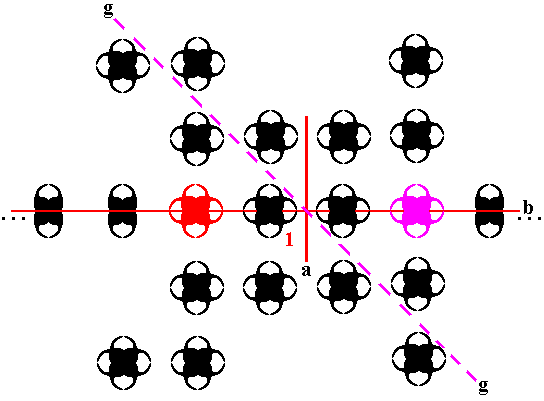
Figure 27. The new (composed) motif (red) generated in the previous Figure is reflected in the mirror line a and produces yet another (composed) motif (purple).
Yet another composed motif can be produced by the glide reflection g from an already existing composed motif :
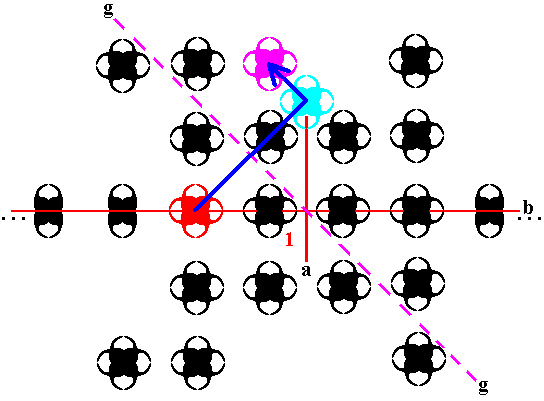
Figure 28. A new composed motif (purple) is generated by the glide reflection g from an already existing composed motif (red).
And this new (composed) motif can be reflected in the mirror line a producing yet another (composed) motif :
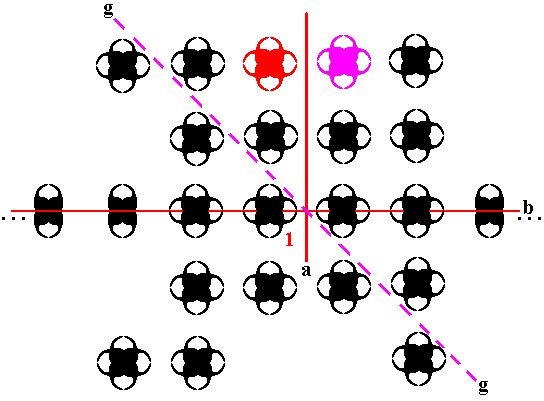
Figure 29. A new composed motif (purple) generated by a reflection in a , from an already existing composed motif (red).
The glide reflection produces yet another composed motif :
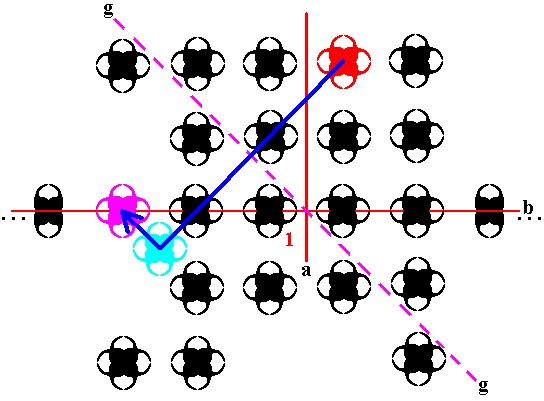
Figure 30. A new composed motif (purple) is generated by the glide line g , from an already existing composed motif (red).
Thus the pattern, so far produced, is the following :
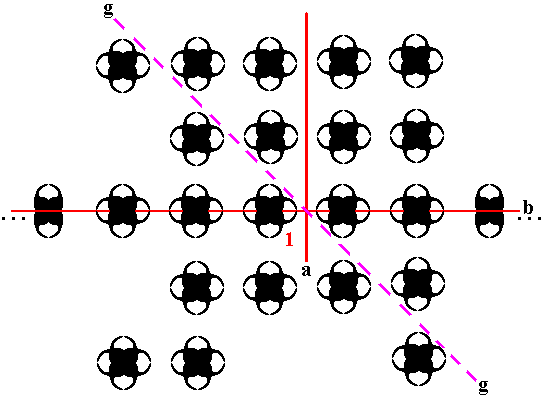
Figure 31. The pattern, so far produced by the generators t, a, b, and g.
It is clear that we can produce the whole pattern -- as it was (partially, and with a somewhat different length of the translation) given in Figure 1 -- i.e. we can go on indefinitely to extend the pattern as far as we please, without needing further new generators (i.e. no new generators, in addition to the four mentioned, are needed). And while extending in this way the pattern we thereby automatically generate more and more group elements. Indeed we have to do with an infinite group.
In the next document we continue our group theoretic study of (other) two-dimensional periodic patterns.
e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals
back to retrospect and continuation page
back to Part I of the theoretical preparation to the study of 3-D crystals
back to Part II of the theoretical preparation to the study of 3-D crystals
back to Part III of the theoretical preparation to the study of 3-D crystals
back to Part IV of the theoretical preparation to the study of 3-D crystals
back to Part V of the theoretical preparation to the study of 3-D crystals
back to Part VI of the theoretical preparation to the study of 3-D crystals
back to Part VII of the theoretical preparation to the study of 3-D crystals
back to Part VIII of the theoretical preparation to the study of 3-D crystals
back to Part IX of the theoretical preparation to the study of 3-D crystals
back to Part X of the theoretical preparation to the study of 3-D crystals
back to Part XI of the theoretical preparation to the study of 3-D crystals
back to Part XII of the theoretical preparation to the study of 3-D crystals
back to Part XIII of the theoretical preparation to the study of 3-D crystals
back to Part XIV of the theoretical preparation to the study of 3-D crystals
back to Part XV of the theoretical preparation to the study of 3-D crystals
back to Part XVI of the theoretical preparation to the study of 3-D crystals
back to Part XVII of the theoretical preparation to the study of 3-D crystals
back to Part XVIII of the theoretical preparation to the study of 3-D crystals
back to Part XIX of the theoretical preparation to the study of 3-D crystals