e-mail : 

Sequel to Group Theory

When we come to groups of composite order -- and in the present document first of all to cyclic groups of composite order -- things are getting much more interesting. This is because groups of composite order -- in contrast to groups of prime order -- have SUBGROUPS. And many features of groups are directly associated with subgroups (The cyclic groups C₄ and C₆, both of composite order, have already been considered (previous Part) with respect to their crystallographic realizations).

Let us start with a rather large cyclic group of order twelve (C₁₂), and discover its features. C₁₂ can be realized in several ways. If we let it be realized as the numbers  0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11  under addition modulo 12, and if we arrange those numbers according to their natural sequence (as we had just presented them, namely 0, 1, 2, 3, etc.) then the following table will emerge (Recall that addition modulo 12 is just addition, but only retaining the remainders after division by 12) :

Table 5.1

This is because the element  1 has period  12.
Also each other element of period  12 will generate the whole group by repeated application.

But if we try to generate the whole group with the element  6, which has period 2, then we get by repeated application of  6 :
6² = 6 + 6 = 12 mod 12 = 0.
6³ = 6 + 6 + 6 = 18 mod 12 = 6.
So only the elements  0  and  6  are generated. And this means that the set {0, 6} is a subgroup of our group {0, 1, 2, 2, 4, 5, 6, 7, 8, 9, 10, 11}, + mod 12  ( = C₁₂). now, as we've said, with subgroups are connected some important features. In order to show these features we will rearrange the group elements in such a way that the subgroup {0, 6} stands out clearly, resulting in the next group table version of C₁₂ :

Table 5.2

The next group table of again C₁₂ has the same arrangement of elements as in version b, but now we highlight the different SUBSETS as we see them appear in the table, including the subset that is the subgroup {0, 6}. Every subset consists of two different group elements (two 'individuals' of each sort), for example

2 8
8 2

which should be written as the set {2, 8}.

Table 5.3

Table 5.4

So when, in our present example, we 'multiply' the subgroup {0, 6} with the element  1 of our group, then we either get 1{0, 6} (left coset by the element 1), or {0, 6}1  (right coset by the element 1). Let us work out these multiplications (which are here, remember, addition modulo 12).
1{0, 6} = {1 + 0 (mod 12) = 1, 1 + 6 (mod 12) = 7}, which is the set {1, 7} and which is the left coset of {0, 6} by the element  1. This set is indicated in light blue in the above group table.
{0, 6}1 = (0 + 1 (mod 12) = 1, 6 + 1 (mod 12) = 7, which is the set {1, 7} and which is the right coset of {0, 6} by the element  1. This set is indicated green in the above group table.
So the left and right cosets of the subgroup {0, 6} by the element  1 are equal : 1{0, 6} = {0, 6}1, or, when we indicate the subgroup {0, 6} by H, we get 1H = H1.

From that table we can verify that the left and right cosets of our subgroup H ( = {0, 6}) by the element  7  are both {7, 1}, i.e. 7H = H7 = {7, 1}. And these cosets are equal to 1H and to H1 [Recall that for sets to be equal, the arrangements of their elements does not matter, thus the set {1, 7} is equal to the set {7, 1}]. 
So 1H = H1 = 7H = H7.

The left coset of H by the element  2, i.e. the set 2H, is 2{0, 6}, which is 2 + 0 (mod 12) = 2, 2 + 6 (mod 12) = 8} which is the set {2, 8}, brown in the above table.
The right coset of H by the element  2, i.e. the set H2, is {0, 6}2, which is {0 + 2 (mod 12) = 2, 6 + 2 (mod 12) = 8} which is the set {2, 8}, dark green in the above table.
So 2H = H2 = {2, 8}.

The left and right cosets of H by the element  8  both are also {8, 2} ( = {2, 8}), so 2H = H2 = 8H = H8 = {2, 8}.

In the same way we can see that
3H = H3 = 9H = H9 = {3, 9}.
4H = H4 = 10H = H10 = {4, 10}.
5H = H5 = 11H = H11 = {5, 11}.
0H = H0 = 6H = H6 = {0, 6}.

We see that for every element  x  of our group G  xH = Hx, which means that H is a normal subgroup in  G.

Homomorphic image of a group
In Table 5.3 we see that these cosets are repeated throughout the group table.
In fact we see that these cosets are multiplied with each other (according to the group operation which is addition modulo 12), as is illustrated in the next Table (still of our group G = {0, 1, 2, 3, ..., 11}, + mod 12,   C₁₂).

Table 5.5

In Table 5.3 we see all the possible products of the cosets, and also see that multiplication of these cosets does not bring us outside the set of cosets (of the subgroup H = {0, 6}):

{0, 6} = 0H = H0 = 6H = H6
{1, 7} = 1H = H1 = 7H = H7
{2, 8} = 2H = H2 = 8H = H8
{3, 9} = 3H = H3 = 9H = H9
{4, 10} = 4H = H4 = 10H = H10
{5, 11} = 5H = H5 = 11H = H11

So multiplication of the cosets of the subgroup H of our group G is closed.
There is also a coset that functions as an identity element, namely the coset 0H = H0 = H = {0, 6}, i.e. the left (or right) coset of our subgroup by the element  0, which is the subgroup {0, 6} itself. See Table 5.2 where we can see it be distributed in the same way as we see it in cyclic groups. Indeed we see that multiplication of {0, 6} with any coset X results in coset X again. And in that same Table 5.2 we can see that for every coset X there is a coset X^-1, such that XX^-1 = H. So in our set of cosets for every coset there is an inverse coset. The multiplication of these cosets is associative, which means that (XY)Z = X(YZ) for every three cosets in our set of cosets.
All this implies that the set of cosets of the subgroup H of our group G = {0, 1, 2, 3, ..., 11}, + mod 12,  is itself a group.

If we look to the cosets of H -- which include H itself, which is the left or right coset by the element  0, or by the element  6 -- we see that in all cases the difference between the two elements is 6, so we could represent these cosets by, say, the smallest element, because then the other element is already determined. So we can rename these cosets as follows :

{0, 6} --   0
{1, 7} --   1
{2, 8} --   2
{3, 9} --   3
{4, 10} -- 4
{5, 11} -- 5

In fact this is a mapping of the cosets onto the set {0, 1, 2, 3, 4, 5}, which we will call B. Said differently :
The elements 0 and 6 of group G are mapped onto element 0 of B.
The elements 1 and 7 of group G are mapped onto element 1 of B.
The elements 2 and 8 of group G are mapped onto element 2 of B.
The elements 3 and 9 of group G are mapped onto element 3 of B.
The elements 4 and 10 of group G are mapped onto element 4 of B.
The elements 5 and 11 of group G are mapped onto element 5 of B.

And if we now replace all the cosets in our above tables by these numbers, i.e. if we actually carry out the above mapping of group G onto the set B, we get the following table, which is -- as we found out above -- a group table :

Table 5.6

{0, 6} --   0
{1, 7} --   1
{2, 8} --   2
{3, 9} --   3
{4, 10} -- 4
{5, 11} -- 5

Next we summarize this homomorphic mapping of G onto B :

+ mod 12	0	6	1	7	2	8	3	9	4	10	5	11
0	0	6	1	7	2	8	3	9	4	10	5	11
6	6	0	7	1	8	2	9	3	10	4	11	5
1	1	7	2	8	3	9	4	10	5	11	6	0
7	7	1	8	2	9	3	10	4	11	5	0	6
2	2	8	3	9	4	10	5	11	6	0	7	1
8	8	2	9	3	10	4	11	5	0	6	1	7
3	3	9	4	10	5	11	6	0	7	1	8	2
9	9	3	10	4	11	5	0	6	1	7	2	8
4	4	10	5	11	6	0	7	1	8	2	9	3
10	10	4	11	5	0	6	1	7	2	8	3	9
5	5	11	6	0	7	1	8	2	9	3	10	4
11	11	5	0	6	1	7	2	8	3	9	4	10

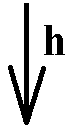
+ mod 6	0	1	2	3	4	5
0	0	1	2	3	4	5
1	1	2	3	4	5	0
2	2	3	4	5	0	1
3	3	4	5	0	1	2
4	4	5	0	1	2	3
5	5	0	1	2	3	4

h(xy) = h(x) h(y)

This in turn means that to the product  xy  in G₁ corresponds the product  h(x)h(y) in G₂.

In the same way, when two groups G₁ and G₂ are connected by the isomorphism  i, then for any two elements  x  and  y  of G₁ the following relation (expressing the preservation of products) holds :

i(xy) = i(x) i(y)

Also here the product  xy  in G₁ corresponds to the product i(x)i(y) in G₂.

e-mail : 

back to homepage

back to retrospect and continuation page

back to Part I of the theoretical preparation to the study of 3-D crystals

back to Part II of the theoretical preparation to the study of 3-D crystals

back to Part III of the theoretical preparation to the study of 3-D crystals

back to Part IV of the theoretical preparation to the study of 3-D crystals