e-mail : ( Please write in  ' Subject '  entry :  ' METAPHYSICS ',  in order for me to be able to distinguish your mail from spam )

Arguments in favor of the discreteness of space (in contrast to its alleged continuity), i.e. the discreteness of the extensive aspect of the Explicate Order (= the whole of material space-time reality) will, in the sequel, be presented. These arguments are largely based on those of  PETRONIEVICS, 1904, but supplemented by me. But before we do so we will already describe how discrete material reality will look like. So in these preliminaries we will speak about "quality-points", "negation-acts", "discrete space", etc., without having them demonstrated. Only in the long section about INFINITY this will be done.

All this, opens the way to see the Explicate Order as the developing result of the execution of an "overall cellular automaton rule" (or set of rules) transforming a previous spatial configuration of primitive quality-points into the next configuration of such points as to their qualitative content. These configurational changes macroscopically result in higher-level sequences of changes as we observe them in the Explicate Order where they are described by means of concepts like "projection", "causality", "behavior", "chemical reaction", "motion", etc.
The formation of Substances, namely atoms, molecules, crystals, and organisms, takes place within the overall cellular automaton (CA) rule.

In what follows (in these preliminaries and subsequent arguments) we will lay down a theory holding that ultimate reality, i.e. reality at its lowest level, is not a genuine continuum but a discretum. It is a lattice of quality-points, a lattice that, as lattice, is determined by a geometrically minimum non-zero distance of geometric points (= quality-points considered as to their pure geometrical aspect).
This theory provides a certain boost for the crystal analogy (crystals-organisms) as it was presented in Fourth Part of Website (see link at the end of the document). Organisms are, it is true, not crystals, but may, as to their general morphology and thermodynamics, be well understood from a consideration of dendritic crystals.

In our documents on Unimol, it was held by its author Oskar Müller, 1959, that crystallinity is in fact avoided in the constitution of organisms. We still hold to that position, but here "crystallinity" should be understood as it is at a macroscopic level, where it is indeed absent in organisms. As to organisms "crystallinity" is only present at reality's lowest level and there not confined to organisms. And it may be that the great morphological potential of crystallinity, as we see it in dendritic crystals (such as ice-flowers) (not considered by Petronievics), is, in the case of organisms, in some way passed on from the ultra-ultra-microscopic "crystalinity" of ultimate material reality to the macroscopic constitution of the organismic body, without rendering that body itself crystalline. So, macroscopic crystallinity will surely inhibit favorable morphological development in organisms (it stops short in dendritic crystals).

So, as to the discrete nature of the extensional aspect of material reality, for the reader it may be wise to first consult the (final) document on the crystal analogy in Fourth Part of Website.

The lowest level in material reality (the Explicate Order) definitely known to us is the quantum level. It is described and investigated by quantum mechanics. Energy, radiation, and perhaps matter too, come in smallest indivisiblle packets. Quantum mechanics is a branch of natural science, and that means that results of observation speak the last word. And also here, constant relationships between physical magnitudes (relationships that are supposed to be uncovered) are theoretically set up and finally tested in experiment and observation.
In natural philosophy things are somewhat different. While accepting the conclusions of natural science if these are logically consistent, it tries to press on down along the chain of ever more fundamental "why" questions to its absolute end, i.e. to the very bottom of reality. It doesn't stop at the observational end, but considers also things (possibly) existing, but principally not observable, insofar as the existence of such things can sufficiently be reasoned. Our realistic theory of knowledge forbids us to say that "what is principally not observable does not exist". And even natural science presupposes (often without knowing it) things that cannot be observed.
Anyway, here in the present document, in our series on natural philosophy, we investigate whether reality still further extends below the level of even quantum mechanics. And again, this attempt is not physics but natural philosophy, and here its procedure almost entirely consists of thinking and reasoning, in the present case mainly on the logical status of infinity, because here the nature of space, insofar as it is spatial, is conceptually investigated in order to indeed reach the very bottom of material reality.

If we conceptually "vertically" drill through several places (points) in any given region of material reality (the Explicate Order) with a fine "needle", we encounter in every individual drilling a qualitative local state or condition (i.e. a quality not necessarily of something, of a substrate, but just a content, a qualitative content). We hit, so to say, a "quality point" of that region (i.e. one of its many quality points). Many of these points will be qualitatively the same but also many of them will be different. So we may, for the time being, suppose that material reality is ultimately constituted of so-called quality points. But even when we consider not just (complex) qualities but  elementary  qualities (whatever these may be), we must admit that a point, a true point, that is, a qua size, mathematical point, cannot have or be a quality because such a point has no extension and cannot therefore contain anything. But in order to nevertheless assign to every such point, apart from its position in space, something definite we must have recourse to an analogy :  Instead of the "quality content" of such a point we take that content to be a letter of the alphabeth. Indeed, we may say that any larger part or spatial region of reality "tells its story". It does so, analogically, by way of one or more "sentences" consisting of "words" which in turn consist of "letters". And so every point in material reality is a letter, the smallest indivisible unit of words and sentences. Indeed, earlier (see Theoretic Intermezzo (two documents) in present Part of Website) we have theorized that the Implicate Order is the domain of ontologically-taken natural numbers. In it there are embedded certain subsystems, also consisting of natural numbers but coding for states in the Explicate Order, that is, upon "projection" (into the Explicate Order) (analogically being the process of unfolding of the meaning of the relevant numbers) these numbers (describing for instance organic strategies) appear as material entities in the Explicate Order. So already such numbers tell a story and already are a text, and this text is subsequently decoded in (and by) the Explicate Order (we can also say that the Explicate Order materially simulates certain immaterial entities themselves residing in the Implicate Order). Well, accepting this, we may suppose that the very lowest level of material reality is still, like in the Implicate Order, a text, but now one with corresponding letters (instead of numbers) i.e. a pattern of words and sentences. And, of course immediately "higher up" it is our familiar world of material things and processes precisely corresponding to this "text". And so in this way our fine needle drilling in some location of a given region of material reality hits on a letter of this "text". And as long as we keep this in mind we may still call these points (found by the needle) "quality points".

We can now say something more about a material Substance, "Substance" here in the metaphysical sense, that is, a true self-contained being (such as a free atom, a molecule, a crystal, or an organism). A being of which the cause ultimately is immanent, i.e. residing in the Substance itself as its Substantial Form (the efficient, material, and final cause can all be reduced to the formal cause). Now this Substantial Form, as determining Prime Matter, is, as is the Substance itself, a true unity, meaning that it has no actual parts (but only virtual parts)  (See the Section on Aristotelian metaphysics in previous document). Now in terms of letters, words, and sentences, as described above, we may hold that a true Substance is at the lowest level of material reality a coherent "tekst" describing a true being. But then this text is composed of individual letters, rendering the Substantial Form itself be composed, i.e. itself having parts. And true parts have ontological priority over the whole they constitute, so that then Substance would not be the ultimate being, it would not be the primary instance of being in the material world. So if we take Substance to be such a primary instance it cannot consist of parts, at least not of actual parts. But, as we had explained in the mentioned Section of the previous document, a part of a true whole is only a part when it is, as it were, cut out from that true whole. But then it is something all by itself, something different from the whole out of which it was dissected. Indeed, the same is true of a single letter considered by itself, a letter taken from some "story". When such a letter is dissected from the text it no longer has its proper meaning (if it has a meaning at all!). Its meaning or content is only something definite when it is fully integrated into the text. It acquires content in virtue of the text and only with that text, which itself is a true unity. So also in our idea of material reality ultimately consisting of quality-points, "letters", and thus every material Substance, every Substantial Form, consisting of "letters", of parts, really doesn't consist of parts or letters, but is one entity entirely. When such "parts" are dissected (by us) out of the text they may perhaps tell us a little about this text, but very little indeed, if not, nothing at all. So, as to a true Substance, the letters only appear upon analysis (dissection). Having this in mind, we may happily keep on speaking about "letters" or "quality-points" together "composing" Substances and with them material reality. So the Explicate Order may, at its very bottom, be a pattern of quality-points. And this brings us to the constitution and status of material space in its aspect of extensivity (including also the extensionality of material bodies). Are these quality-points touching each other, or are they somehow separated from each other, and if so, by what? Are these quality-points forming a regular or irregular network or wicker-work? What exactly is the status of a "point" of an extensive medium like material space, or mathematical space for that matter?
All these issues will form the subject of our long subsequent discussion involving space, continuity, discreteness, infinity, etc. And they will eventually result in a theory of discrete material reality acting as a kind of universal cellular automaton (CA) (for cellular automata, see the document about them in First Part of Website, click HERE to see it). Let us now then proceed to develop this theory.

We will prove that space (= the aspect of extensionality of material things) is discrete. Is it really discrete, then space is already geometrically quantified at least at the subatomic level. This might mean that geometrically quantified space, i.e. the discrete nature of the extensional, lies at the root of the quantum structure of the subatomic world (not visible at the macroscopic level). However, the subatomic world (as described by quantum mechanics) already is a high-level phenomenon as compared to the discrete geometric ultra-ultra-structure of space (i.e. of the spatial, the extensional). And in turn, the macroscopic phenomena would then be high-level phenomena of the subatomic world of quantum mechanics. As to the quantified condition of the world, see Ph. BALL, "Designing the molecular world", 1994, p.91-92. And of course the macroscopic world is the more so a high-level phenomenon if compared (all the way down) with discrete space consisting of quality-points.

The universal point-lattice of explicate reality.
Much of what follows as to the discreteness of space is inspired by a book called  "Principien der Metaphysik", written (two volumes) in 1904 (first volume) and 1912 (second volume), by B. Petronievics. Large parts of his philosophy of ultimate reality we cannot accept, especially when he, more or less, attributes consciousness to the ultimate points of the discrete network of reality. According to us, consciousness is a high-level phenomenon occurring in certain organisms, and absent at the lower structural levels of that same organism (brain-cells cannot think). Of course primitive analogues or traces of it may exist in lower, and even the lowest, animals, but that is about all. Ideas about consciousness as in Petronievics stem from the conviction that the ultimate and most basic and most elementary data about the constitution of reality are to be found in human consciousness only. Perhaps these data came into it from outside, but the only thing we have to our disposal in this respect is our consciousness. Or, there even isn't something like an objective world at all, but only consciousness, or at least the existence of such an objective world cannot be demonstrated. This view of knowledge and of things is opposite to our own view which is the so-called realistic theory of knowledge :  Our knowledge of things is directly of and from things. These things exist independently of being known, and we can in principle know them as they are in themselves, not merely as they have become as a result of them being known.
Nevertheless, much in Petronievics is worth reading and worth considering (despite its ancientry, because much of it is either metaphysical or mathematical namely the mathematics dealing with finiteness versus infinity). He has presented various proofs of the logical impossibility of the "actual infinite", while the "potentional infinite" is merely "undetermined (unfixed) finiteness". Applying all this to space (i.e. to the extensional aspect of material reality), he is able to describe it as a discrete point-net and set up a discrete geometry of this space. We ourselves think that the lattice nature of ultimate material reality may be, or may imply, a form-generation potential (for macroscopic objects), as we have explained it in the case of dendritic crystals (as an analogy). Further, such a discrete nature may have consequences of what "motion" in fact is, and what it is not. And, finally, such a nature may point to the possibilty that the Explicate Order at its lowest level is something like a cellular automaton display window, driven by rules residing in the Implicate Order. We'll see. In what follows, it is thematically important to keep in mind what was, above, said about "quality-points".

In what, later, further down, follows, we prove -- following Petronievics, 1904 -- the discreteness of space. The latter then consists of space-points that always are kept separate from each other by a so-called negation-act itself not residing in space. This negation-act extends [i.e. draws apart from one another] every two space-points such that they come to lie at an indivisible simple unit-distance from each other. The entitative content, the qualitative, resides, in its elementary form in these extended space-points. Each space-point is the location of one or another primitive quality (which we above took to be a letter) (all qualities known to us are secondary, are composed). As to their quality, every space-point is continually updated resulting in either the same or in another primitive quality. This generates the universal flow of time. So we now have the following :  The world, reality (material + immaterial), is a gigantic cellular automaton (CA), and the material world in particular is its display window, while the rules reside in the immaterial Order of reality. The pattern of quality-points accordingly continually changes as to the quality of these (in themselves stationary) points. These points and their updating cannot be observed (because they are mere points). What we observe are statistical means of (the qualities of) very large numbers of such points. Among the resulting macroscopic (= observable) quality-patterns there are some that, seen after the fact, remain  constant  within a rather wide range of external conditions and are thus stable. And these are the "Substances" (in the metaphysical sense). Other patterns also, it is true, always appear when certain conditions are satified, but their possibility of existence is confined to very narrow conditions. So, for example, the structure of (a) granite (pebble) -- the spatial pattern (taken generally) of quartz, biotite, and feldspar crystals -- originates, it is true, under a rather wide range of physical conditions and is then as 'frozen pattern' fairly stable also after its formation (i.e. after the volcanic magma has been cooled down), but the particular  structure  (now not considering it merely generally as a "granite" anymore), considered insofar as it is a particular pattern of spatial distribution and mutual sizes of the individual crystals of the three mentioned minerals and their proportional contribution in a given granite, [this paricular] structure is as such determined by very narrow conditions of formation, and will be different in different conditions. So such a particular spatial pattern is not so stable after all (during its formation).
All this, in contradistinction to, for example, a(n) (free) atom, a molecule, a crystal, or an organism. Their internal pattern will persist in rather different conditions of formation and conditions subsequent to formation. Their particular internal pattern is stable, especially in atoms and molecules. But already in crystals and organisms we have to do with large objects, and here the distinction appears between "essential" structure and "accidental" features (accidental with respect to the what-is-it of a given thing, a given Substance). Here it is the stability (in conditions of formation and subsequent conditions) of the essential structure (which structure tells us what the thing is in itself) rendering these things to be Substances (in the metaphysical sense). So a granite is, despite its 'typical general structure', just a mere aggregate (of Substances), whereas atoms, molecules, crystals, and organisms are genuine Substances. Let us concentrate for a while on the nature of such Substances (Of course, on this website much has already been said about what a Substance is supposed to be, but it is nevertheless instructive to speak about it again in the present context of discrete material reality).
The investigation of HOENEN, 1947 (See  Parts 15e and 15f  of the present Series of documents), has made it clear that the composing parts and particles of such a Substance could just as well be described as qualities of that particular Substance, without having to give up the relevant results of natural science concerning such Substances :  For instance, the periodic structure, discovered by natural science, in crystals (and the possible and impossible crystal symmetries to be derivable from it) remains exactly the same when we either describe this structure in terms of the particles constituting the crystal or in terms of local qualities of, and in, such a crystal. Accordingly, the pattern of the (various) constituent) particles is equivalent to a corresponding pattern of (various) qualities in one and the same crystal (here, in one and the same species of crystal).
And if such equivalence (now taken generally as the equivalence of (1) constituent parts or particles and (2) qualities of a given thing) would  exclusively  occur in those beings that we call, by different reasons but with conviction, "Substances" (in the metaphysical sense), and if it moreover occurs in all Substances, then it would constitute a precise delimitation distinguishing true Substances from mere aggregates (of Substances). Hoenen demonstrates this equivalence (in description) in otherwise evident Substances ( he especially demonstrates it in molecules and crystals. He also attributes it to organisms, but doesn't demonstrate it, because his book is about inorganic nature). This equivalence in description between (constituent) particles and qualities, forces us to investigate what then precisely are the constituents of true Substances :  are they (1) material individual particles or parts constituting the Substance, or (2) are they the qualities of such a Substance? See for this also our metaphysical description of holistic beings (Substances) ("Wholeness and Aristotelian metaphysics") HERE  in previous document. If they are qualities, then the thing of which they are qualities is one single whole thing, without composing material parts or particles, and this means that such a thing is holistically constituted (whereas if constituted of material particles it would not be holistically constituted). And accordingly, the holistic constitution (found out in some other way) of a thing may point to it being a true Substance, and thus could legitimately point to the fact that the heterogeneity of such a thing is the result of, not its being made up of parts or particles, but being the result of a pattern of qualities of that particular thing. Now this is demonstrated by Hoenen for the atom, i.e. the atom behaves holistically and thus it is not a mere aggregate but a true Substance. And it is indeed here, in the atom, that its constitutive 'particles' do not behave as true particles but as something like "standing waves" (especially the electrons of the atom). Accordingly, these 'particles' would not be particles but qualities of the atom. However convincing this is for the atom, we cannot, without qualification, generalize on this, i.e. applying it to molecules, crystals, and organisms. This means that the assertion that in these Substances the constituting particles and parts are in fact qualities of these Substances remains a hypothesis  ( This hypothesis, though, gains support from the fact that the chemical bond in molecules renders these molecules to be similar to (free) atoms (in fact molecules are atoms with more than one nucleus) because also the chemical bond is, just like the atom itself, subjected to quantum conditions rendering them non-mechanical and thus holistic. And as to organisms, the hypothesis becomes more plausible if the Unimol view (one-molecule view), as presented in the previous four documents, turns out to be correct). Of course, the equivalence of description remains demonstrated (certainly for atoms, small molecules, and crystals).
So far, so good. We may then say that Hoenen has demonstrated that for atoms, molecules, and crystals, their constituent particles can also be described as constituent qualities, and, if organisms qua Substance are equivalent to atoms, molecules, and crystals (and organisms to be equivalent to molecules is rendered probable by the Unimol view), then their parts (such as organs and parts of them) may also be described as qualities of these organisms. In short, in true Substances (in the metaphysical sense) their composing parts or particles may also be described as qualities of these Substances.
But suppose that this equivalence-in-description turns out to hold  also  in those things that we take, by whatever reason, to be mere aggregates (and thus not Substances). Then this equivalence would no longer be a criterion of distinction between Substance and aggregate. Unfortunately this possibility or impossibility is not investigated by Hoenen. But if it indeed turns out that no longer we have this criterion (but still some other criteria) to distinguish Substance and aggregate, then the phenomenon itself, i.e. the phenomenon that in all cases (in Substance and in aggregate) the composing parts or particles can be described as qualities still is an interesting discovery. It is especially interesting because it as such is a support for the view of "the world as network of quality-points", points, that, as to their quality, are being constantly updated, and so a support of the idea of "the world as gigantic cellular automaton", in which the "cells" are the quality-points. All patterns in the (material) world are then purely qualitative patterns, and their real distinction from one another, their separateness ( = the prevention of their coincidence, especially of points with the same quality) is accomplished in the Explicate Order as a result of spatial extension (in the sense of keeping them spatially apart from one another) of these quality-points from one another by so-called negation-acts, which are not of a spatial nature themselves.

All material things in the Universe are Substances (in the metaphysical sense), even aggregates ultimately are aggregates of Substances. And so all qualities found in material reality are qualities of Substance. But Substances are individuals. These individuals must be separate from one another by "not-Substance".
If we now view the elements of every true mixtum (= Substance) as qualities of such a Substance, then in the CA display window (i.e. the output window of the world-cellular automaton) there is no clear distinction between regions where "to-be-a-Substance" reigns and regions where "not-to-be-a-Substance" reigns, because every reality-point is a quality-point, whether it lies in or outside a Substance. The solution of this problem is our exposition of the Substance-Accident Structure of things (see in previous document).
A second solution of this problem is the aether of Lorentz. This eather (see for it Part XVa of the present Series), this imponderable aether, penetrates all the ponderable and vice versa. Every point of the universal network of quality-points contains an "aether-element", i.e. has something eather-like, has an imponderable aspect, whereas many (not all) points have, in addition, in them, a ponderable aspect, i.e. a primitive quality of ponderable matter. Well, accordingly, every net-point (at the given moment) of which the content now consists exclusively of a "not-ponderable" primitive quality, i.e. having in it exclusively the aether-aspect, at that very moment belongs to the non-substantial (the not-ponderable substantial) background. Together such points constitute the 'empty space' between (ponderable) Substances, and in this way accentuate (ponderable) Substance against this background (at that given moment) of the non-ponderable substantial, or, said differently, the, at the given moment present, not-ponderable substantial aspect of material reality renders true Substances to be qualitatively (and then also quantitatively) separate from one another, i.e. being thus separated with respect to every net-point of them.
If we represent a net-point only carrying the aether-aspect (solid white) by , and a net-point carrying in addition also a 'ponderable' primitive quality (solid black) by , then we can represent 'motion' of a point of a Substance (and thus either of the whole Substance itself or a region of it) 'through' the aether as follows :

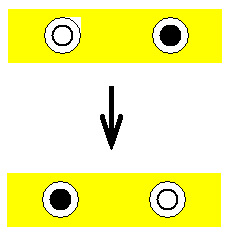
Here the 'ponderable' Substance-point has 'moved' to the left. The arrow indicates Time.
So, with the help of the earlier accepted aether of Lorentz (as a universal medium of localization) we now also clarify the fact of the empirically so conspicuous distinction between true Substances and the non-substantial (in fact between the ponderable substantial and the non-ponderable substantial), i.e. the separation of individual Substances from one another :  All of them are immersed in an imponderable aether, the aether of Lorentz, and they can 'move' in it.

Further specification of the Universal Cellular Automaton (CA).
In the above given description of "motion" we may say that the content of certain consecutive (but) stationary net-points, 'cells' of the universal cellular automaton display-window, has changed, according to certain rules, the CA rules. The changed points together form the "trajectory" of the motion in question. The macroscopic effect of the application of these rules is as such not visible. It is only visible (in the Explicate Order) indirectly as cause and effect in things, summarized by science in so-called physical laws.
In fact, all findings in natural science, i.e. all natural laws (of course only insofar as they are correctly formulated by it), all regularities in chemical behavior, regularities in biological; behavior, etc., that is, all the scientific effort, ultimately is the mapping-out of the universal CA-law (or set of CA-transformation-rules).
This law refers to forms in the Implicate Order, which [forms] as such are already adapted to in principle exist in the Explicate Order, and thus be able to in-form Prime Matter. So this CA-law is solely about the dynamics of "projection" and "injection" (retraction) of such forms, among which also are those forms that are "strategies", existential strategies, appearing in the Explicate Order as organisms. Thus, the CA-law is not about the actual formation (generation, derivation) of such strategies, and also not about the generation of any other immaterial form in the Implicate Order. In particular, the transformation of (immaterial) forms into (initially still immaterial) strategies takes place, in the Implicate Order, as a result of the aspiration of all immaterial forms to their ontological completion, i.e. to their becoming material. And to-be-material can only be the case in the Explicate Order, so they must be able to (materially) exist and persist in that Order.
From one moment of Time to the next, the universal CA-law determines the qualitative-content of net-points in the real discretum (the CA display window, the Explicate Order). For cellular automata (CA's) in general, see the document about them in First Part of Website :  click HERE  for consulting it. After having (later) derived the discrete nature of ultimate material reality, by demonstrating the logical impossibility of the extensive (in contra-distinction to intensive) continuum, i.e. after having demonstrated the discrete nature of the extensive aspect of material reality, we shall further elaborate on the universal cellular automaton.

Difference in quality-points.
The quality of a net-point always is an absolutely primitive quality, and such quality-points together can then constitute the complex (secondary) qualities as they are known to us, such as color, pressure, temperature, musical note, etc.
If we descend all the way down to the fundamental bottom of material reality, i.e. to the basic point-net of space (i.e. of the extensional aspect of all material things), then we have to do with two fundamental relations, viz., the relation of identity and the relation of non-identity, and these ultimately only within (i.e. along) two dimensions, the extensive and the intensive dimensions. The relation of identity as such is in fact not a relation because it has only one relatum (point of reference) (A = A) :  spatial and temporal identity, that is, numerical identity, results in coincidence. Qualitative identity is only possible in numerical difference and then is a relation of equality (not absolute identity). So as genuine relations we only have either qualitative difference and/or numerical difference.
Now, numerical difference of qualities (i.e. spatially separate 'individuals' of quality) may be specified by the spatial distance between them, and this distance may decrease all the way down to the spatially touching of those qualities (qualities in one single thing or in, say, two different things), spatially touching, that is, not qualitatively touching). And then we have the absolute unity (in the sense of minimal distance of separation) of numerical difference. For the preservation of the spatial separation of every two identical primitive qualities (neighboring individual same-quality-points) an "extensive negation-act" is necessary (which act itself is not spatial). Qualitatively different points cannot, when approaching one another, coincide. No negation-act is then needed. All this is clear by considering the nature of the objective spatial.
Now Petronievics, 1904 (in his book on discrete material reality), tries to demonstrate the same as to qualitative difference. For him the content of consciousness is the primarily given - (not for us, though, because we adhere to the so-called "realistic theory of knowledge" according to which objects outside consciousness are directly intended by logical intentions such as concepts, propositions and arguments (see for "Intentional Logic" Fifth Part of Website, from that particular document onwards)) - from it, i.e. from consciousness, all true fundamental data are supposed to be obtained (together with non-fundamental data). But while he, with respect to numerical difference, doesn't make explicit use of our experiencing of such differences (i.e. the presence of them in consciousness), he does do this as to qualitative difference. And then he concludes that also this type of difference (difference of primitive qualities we would say) is accomplished (in order to prevent coincidence) by negation-acts. We, however, consider consciousness as an aspect of existential strategy and so not being adapted to necessarily represent all original data of reality :  Consciousness is not an extensive, but intensive medium (and particularly a secondary intensive medium, because the primary intensive medium is the Implicate Order). So admitting that two identical qualities as such may not possibly be given in consciousness (because it is an intensive medium), they can as such (i.e. as two identical (copies of) qualities) exist in an extensive medium (which evidently is present also, viz., observable material reality), namely if they differ numerically (in different places in space, or in the same place at different times). So, for keeping apart (from one another) quality-points having the same or different quality in the extensive medium (and thus objective material reality) no special negation-acts are necessary. Negation-acts, effecting extension are already sufficient. And so we arrive at our real discretum consisting of quality-points together constituting a spatial net.
In an  intensive medium  things are different. There, there is no extension  ( In a medium that supports the extensional aspect of things, an "extensive medium", parts can be outside one another), and thus qualitatively equal net-points must be kept separate by qualitative negation-acts. This may possibly be the case in the Implicate Order which we take to be the primary intensive medium (in which parts of things can coincide). Consciousness is secondarily intensive, it is 'simulating' primary intensivity, it is an emergent high-level phenomenon in the Explicate Order (there it, accordingly, appears only at a high organizational level of organic matter and thus only in very complex organisms).
Every relation of difference, in fact every logically genuine relation, if it truly can be taken as a really existing relation, must be taken as an absolutely simple unit, which as such then demands the simplicity of relata-points (points of reference). And then it is clear that a continuous transition of the one quality into the other is not possible :  The points of reference are simple (i.e. not composed), and between them there reigns one simple (i.e. not gradated) relation as to the qualitative content of these points. If in the intensive medium two qualities approach each other qualitatively (i.e. become more and more similar), then they, in the end, will qualitatively touch one another and thus coincide. A qualitative negation-act must prevent this. The two qualities, becoming more and more similar, never will, in the intensive medium, become completely equal, the negation-act keeps them apart from one another rendering their difference then to be an indivisible minimum (i.e. a difference that cannot be further diminished anymore). Therefore, between qualities, separated by a negation-act (qualities that are different but up to this point have approached one another qualitatively), there is nothing, meaning that these in-the-limit-qualitatively-approached-to-each-other qualities oppose one another, in the sense that the one is not the other (they do not grade into one another). So in the Implicate Order (which is the primary intensive medium) the qualities -- there present in coded form -- are indeed separated by qualitative negation-acts, while in the Explicate Order the extensive negation-acts are sufficient for that.
Every quality (primitive quality) has, in the Implicate Order, its own dimension of intensity. So in the Implicate Order there are in fact two chief dimensions :

• The intensive quality dimension (one for each quality), the 'scale' along which the intensity of the quality can vary.
• The quality-dimension-proper, in which the various primitive qualities are being kept apart by qualitative negation-acts. It is the dimension of qualitative difference.

The discrete net-work of quality-points as compared with a continuum containing qualities.
In the discrete net-work of quality-points, and this seen as CA display window, true motion is impossible :  the points of the net are rigidly connected-and-separated with one another by negation-acts. Only the qualitative content of such a stationary net-point can change :  the one primitive quality is replaced by another (according to the CA-rule). Motion is nothing more than a directed successive change of quality of stationary quality-points lying on a 'trajectory' :

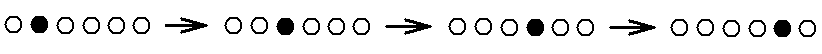
This means that the net-work of points is not compressible and also cannot be stretched. Quality-regions in that net-work cannot be contracted, compressed, or stretched too, because also their points are rigidly connected to one another, but these points together can perfectly well simulate compression or stretching of those regions :

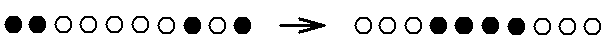
And because such quality-regions (in the point-network) are not really compressible or stretchable, they are as such favorable to the constancy of qualitative patterns and the preservation of relatively high (plane) symmetries (high promorphs, high stereometric basic forms) (being perturbed may result in a lower plane-symmetry of a thing). In organisms this is often 'disturbed' by the biological demand of the functionality of shapes and structures, but nevertheless many organisms or their parts (such as flowers) have fairly high promorphs. In (solid) minerals we generally find high promorphs, here they are not 'disturbed' by functionality, but only depend on thermodynamic stability. On the other hand, the parts in supposed  continuous  reality are compressible, etc., because continuous space is without points, it is elastic. Here there is no restriction.

Space is not a particular entity in which things may find their place. Neither is space an a priori subjective condition for observing placed things. Space is no more than the simple being-together of the real things themselves, thus just a relation between them. Not the real thing is placed into a pre-existing space, but the spatial place is only determined by the real things (namely by their relations of contact (one thing between and touching two others)). Spatial location or position is nothing more than the expression of the fact that the things -- of which each one is a numerical unit -- are given together (= adjacent to one another, touching one another).

Because we cannot observe last indivisible space units (in the case of time we can do it, there they are the NOW-moments), the finiteness or infinity of space towards the inside (i.e. the finiteness or infinity within (within space, towards the small)) must  logically  follow from the (meaning of the) concept of space.
We will find out whether the concept "infinity of space within" is logically consistent. If it is not consistent (also not in further qualification), then it contains one or more intrinsic contradictions, and when these are real, then "infinity-within of space" must be rejected, meaning that space is finite within (in turn meaning that space ultimately must consist of indivisible units, preventing further division of space). This finiteness-within surely must then be further qualified in order not itself turn out to be inconsistent.

The argument that infinity-within of space is logically impossible is given by Petronievics, 1904, pp.186.  In RUCKER's book "Infinity", 1982, we do not find such an argument (or its refutation). There, the actual infinite is happily assumed to be consistent and really existing in Nature and in mathematics. Perhaps we find it in the Intuistionistic Mathematics of the school of  BROUWER (not mentioned in Petronievics (because it appeared a little later)).
In what follows, we shall first summarize and subdivide the long and difficult text (in German) of Petronievics, 1904, pp.186 on the impossibility of infinity-within of space.

Petronievics sees, to begin with, three basic contradictions (Grundwidersprüche) in the idea of  "actual infinity"  [On the other hand, "potential infinity", as Aristotle defines it, does not contain intrinsic contradictions, because potential infinity in fact is :  undetermined finiteness :  the series continues without ever reaching an end, in which continuing it remains finite wherever it is at the moment (where the "wherever" is an asserted, but justifiable, extrapolation into the unknown). Here, finiteness-within as well as finiteness-without (i.e. finiteness to the small and to the great, for example finiteness to the left and to the right of a straight line) is seen as the result of counting of units (points, or still extended but indivisible units) (for finiteness-within we in fact count the number of divisions until we reach the indivisible unit). If we do this counting by means of natural numbers (how could we do differently?), then, in counting (1, 2, 3, 4, ...), every last natural number (reached where the counting is concluded) indicates the number of members of the counted series. Through thus setting up a one-to-one correspondence of natural numbers with members of a series to be counted, we can in principle count every set of things (whatever they are) and thus also the (set of) points or extensive units of a line-segment, and in this way consider the finiteness-within or without or infinity-within or without. The same holds for the counting of parallel lines in a plane and parallel planes in a solid. But we cannot do so in the case of so-called "real numbers" (integers together with fractions and irrational numbers) because we cannot set up the mentioned one-to-one correspondence (with natural numbers), i.e. the series of real numbers is uncountable infinite, whereas the series of natural numbers itself is countable infinite. As long as we view these infinities as potential infinities, there are no intrinsic contradictions. And of course the set of points in a line segment (in any line segment) is uncountable infinite if it is true that we cannot indicate the next point of a given point. But in asserting that no next point can be indicated, the infinity-within is already assumed to be the case (and is the cause of this impossibility), so the impossibility in principle to indicate the true next point of a given point of a line segment should be demonstrated. But however that will turn out, as long as (countable or uncountable) infinity is taken to be  potential  infinity there are no contradictions.].

Here, thus, it is about the logical consistency or inconsistency of the actual countable infinite. Now, this latter concept contains, as has been said, according to Petronievics at least three basic contradictions (and then let alone the uncountable infinite) :

1. Contradiction in the trans-finite number.

2. Contradiction of the absolute finiteness of every infinite entity.

3. Contradiction of the leap from the finite into the infinite.

At the end of the treatment of the First Contradiction we insert three geometrical arguments given in favor of space as an absolute continuum (and thus with actual infinity-within). And these arguments are refuted.

If the actual infinite is intrinsically contradictory, then also space, toward within as well as toward without, is not actually infinite. If space is discrete, it is, within, also [i.e. together with actually] not  potentially  infinite, beause we then [i.e. if space is discrete] after a finite number of divisions, bump onto a last indivisible space unit.

The indivisible arithmetic basic unit is undoubtedly the number  1  [all true fractions, irrational numbers, and imaginary numbers (such as pi) evidently make no sense in arithmetic because they presuppose the divisibility of the true unit, the 1, which is impossible. In genuine arithmetic it is about numbers as a result of counting, and thus about natural numbers with the indivisible unit 1.]. And because we do not have original experience (meaning that we have not and cannot observe[ed] it or find [found] it) of a  spatial  unit, we must take an analogue which is directly evident, namely the 1 of arithmetic, and thus meaning that we must consider the infinity-without (i.e. the infinity towards the great) of the set N of natural numbers (as we do in counting things with them) in order to see how things go in counting spatial parts originating in continuous division or continued spatial extension of a given space volume (or surface, or length).

The concept of number.
Before we begin with expounding the contradictions of the infinite, we must, as to "number", distinguish between the numerical unit and the number as a result of synthesis of such units. The numerical unit is given in experience only in Time, namely in the NOW-moment. Although the number-synthesis is not given to us in Time, because there only the NOW's and their transition to the past are accessible to us, it [the numerical synthesis] is given to us in the spatial series. There we can count macroscopic things (taking such composed things as non-composed, indivisible units to be counted) because a great many of them are always simultaneously available. So although the true numerical unity (the true spatial indivisible unit of counting) is not given to us, we surely can count composed units (in the spatial world) and in this way accomplish the numerical synthesis (but a synthesis not of true units).
Basing ourselves on the concept of number, we shall now investigate whether space-within is finite or infinite, through counting spatial parts (or number of divisions) by mapping them onto the natural numbers which themselves are syntheses of the true arithmetic unit, the 1.

First contradiction :  the contradiction in the transfinite number.

Infinity or finiteness (finitude) of time and space can, as has been said, only be investigated and proved from the number-series rendering counting of spatial and temporal units possible :  1, 2, 3, 4, . . .
That the past does not stretch out into infinity follows from the fact that the NOW has actually been reached. If the beginning of Time were to lay infinitely far back, the series of consecutive time units never would have reached the present. So Time is towards the past certainly finite (it is also finite within, with its indivisible unit, the now-moment). Toward the future, Time is undetermined finite (= potentially infinite), because every NOW-moment is followed by the next, while the old NOW-moment disappears in the past. But because there always does exist only a single NOW-moment, we neeed the number-series in order to conclude of the undetermined finiteness (potenial infinity) of Time towards the future.
The proof of the finitude or infinity of space and time must be based upon the number of elementary space-points and time-points respectively, not upon composed spatial and temporal units (if infinity-within is to be investigated). But before considering it, we first investigate whether the number of numerical units (composed or not) must necessarily be infinite. And in this way we arrive at the first contradiction in the concept of (actual) infinity, the contradiction of the transfinite number.

If one holds that the series {1, 2, 3, 4, . . .} is infinite, then the last number of this series (indicating the number of members of this series) must be infinitely large. Yet, nevertheless, whatever number of the series we consider is finite, and so the series itself -- up to then -- is always finite. [In matters like these we necessarily always must extrapolate to the, strictly taken, unknown. This extrapolating is expressed by "whatever number of the series", and terms like "always", "all", "every", etc.]

The contradiction then is :  If the series is infinite, then the truly last number must be transfinite, i.e. infinitely large. But it must nevertheless be finite because the series (1, 2, 3, 4, ...) is such that the last number resulting from counting the series' members (here accomplished by simply visiting the members one after another) is the up-to-now number of those members, and the truly last number of the series must be finite because it is generated by continually adding a unit (1) to previous finite numbers [Here also the "continually" brings us into, in fact, admittedly unknown territory. It is not demonstrated whether very large (but still finite) numbers still arithmetically behave in the same way as do the smaller numbers familiar to us.]. And adding a finite number, here 1, to an initially finite number can never result in an infinite number.

The contradiction of the transfinite number seems, however, to be resolvable by the mentioned extrapolation into the unknown :
Every number, considered to be the last one in a  finite  series [here "every" is not such an extrapolation] at the same time indicates the number-up-to-now of members of the series. The high-lighted condition -- finite series -- we must take into account, because we still do not know anything about the number of numbers (members) of a series lacking an end, an infinite series. In an  infinite series  there is, by definition no last member, thus in our series, 1, 2, 3, 4, ..., no last number. Therefore, to such a series, as to its number of members, not necessarily the same applies as it does to a finite series (so for such a series does not hold :  last number = number of members, because there is no last number in such an infinite series). If we now posit that the number of numbers of our infinite series is OMEGA (where OMEGA is supposed to be a transfinite number), then, to this OMEGA, not a priori that does apply what applies to the number that, in a finite series, indicates the number of members, implying that OMEGA, does not necessarily have to be a member of the series, and thus it does not necessarily follow that OMEGA must be  finite. So here we do not have :  the infinite is finite. Therefore, there is no contradiction. Of course all this under the supposition that an infinite series in certain respects behaves differently from a finite series, in such a degree different, for example, that the total number of members of an infinite series is not indicated by one of its members (but by an entity outside such a series).
But, if we suppose that an infinite series behaves differently from a finite series (i.e. that actual infinity is something fundamentally different -- not merely different in degree -- from finiteness), then with that the possibility of the actual infinite is presupposed :  If there is something as the actual infinite, then it is fundamentally different (in a numerical sense) from the finite. So the existence of the actual infinite is nothing else than a hypothesis, moreover a hypothesis which is not urged by anything.
And if this hypothesis is accepted, then OMEGA lies outside the series, i.e. outside 1, 2, 3, 4, .... As such it would say something about something else, namely about the series 1, 2, 3, 4, ..., namely that this series contains infinitely many members. But if OMEGA is the first transfinite number appearing  after  the series 1, 2, 3, 4, ... (in whatever sense of "after"), then the series itself doesn't contain any transfinite number (indicating the number of members), and thus, if we stay inside this series, the series is  finite. It is finite, in spite of the fact that this series has no last member, thus in spite of the fact that the series is  infinite (as asserted by OMEGA). So we see that the contradiction persists.

This contradiction cannot be removed by adding to the transfinite number OMEGA yet more units (in order to make the "infinite" which had turned out to be finite, truly infinite), because then we get infinitely many (i.e. not halting somewhere) transfinite numbers of the form  OMEGA + 1,  OMEGA + 2,  OMEGA + 3, ... ,  2.OMEGA, ... ,  3.OMEGA,  4.OMEGA, ... ,  OMEGA², ... ,  OMEGA³, ... ,  OMEGA⁴, ... ,  OMEGA^OMEGA, ... ,  OMEGA^OMEGA  + 1,  OMEGA^OMEGA  + 2, ... , etc.  And we then in fact have to do with the same situation as with the not-ending series 1, 2, 3, 4, ... . Ineed, if we, as we did in the series 1, 2, 3, 4, ..., OMEGA,  place every transfinite number of the series (such as the first OMEGA,  and then also all OMEGA's  in  OMEGA+1, OMEGA+2,  2.OMEGA,  (2.OMEGA)+1,  3.OMEGA, etc.) outside the series, then we are no longer  counting  anymore, i.e. we then are not uninterruptedly carrying on counting anymore (we then 'count' :  1, 2, 3, 4, ... , 1, 2, 3, 4, ... , 1, 2, 3, 4, ... , etc.), and moreover, the whole series (and its parts) has then become finite.
Addition of space units must proceed in the same way as in 1, 2, 3, 4, ... , because precisely that is the counting of space units. From this certainly follows the potential infinity of space toward the great (i.e. as to the successive expansion of space)  if  we model space, as to the degree of its extention, after the series 1, 2, 3, 4, ... , which must be so, because we are counting. [We accept the potential infinity (= undetermined finiteness) of space because a physical end of space would be purely coincidental. A  curved  space (a space returning onto itself, biting its own tail) is, it is true, finite (but without boundary), but implies the existence of, ultimately, a non-curved space (straight space) one dimension higher, in which the curved space is embedded (every curved space necessarily presupposes a space in which it is curved), and this non-curved space is again potentially infinite (not having a boundary).]. And  if  we thus model space, as to its finiteness or infinity after the number series 1, 2, 3, 4, ... ,  then from the existence of an absolutely indivisible unit of counting in that number series, it follows that also space possesses an absolutely indivisible unit, i.e. just like the number series, a smallest indivisible unit, which, just like the unit of the number series, can be summed up (i.e. the units added together) without resulting in the coincidence of these units (and thus without space collapsing in to one single point), and then space, towards its inside, is finite :  We can divide space into progressively smaller parts until we arrive at this smallest space unit.

Before we continue with the other two contradictions of infinity, we first discuss three geometric arguments against any discreteness of space.

Introduction

There are, however, put forward three geometric reasons in favor of the infinity-within of space. They are geometric reasons which allegedly militate against the logical possibility of indivisibe points as space constituents. So they are three arguments in favor of space as absolute continuum, i.e. space without (actual) points. In today's literature one often speaks of the "continuum of the real numbers", this because the set of so-called "real numbers" (integers, fractions, rationals, and irrationals) can be mapped onto a line segment, i.e. onto the  points  of such a line segment. This line segment, viewed in this way, is, however, not a genuine continuum, but one of the several possible or impossible forms of a void-less discretum (i.e. a discretum without gaps, holes, or interruptions). What it is about in these geometric arguments (involving the existence or non-existence of geometric points) is the possibility of an  absolute spatial continuum, and thus an extensum without points (and this possibility is refuted by Petronievics (pp.202)). It is important to realize that the three contradictions of the concept of infinity (of which we have treated the first already) are not implied by the absolute continuum (spatial or non-spatial), because such a continuum, as to answer questions about its finiteness/infinity, is not, and cannot be, modeled with the number series 1, 2, 3, 4, ... , because in such a continuum, being without points, we cannot count anything.
The three geometric arguments in favor of the absolute continuum, and thus arguments against a constitution of space (by anything), i.e. of space as pure extensum (or qua extensum) are first given concisely by Petronievics (p. 202) :

• According to the first geometric argument, the simple (i.e. not composed) point as part of space is impossible because the size of such a point is zero, and from merely zero's an extensive magnitude cannot be formed (the points with zero-size would coincide, and space would be contracted into one single point). [And Petronievics then holds that in analogy with the number series of counting numbers -- natural numbers -- with which space, as to its finiteness or infinity, is judged, a space point must have the value 1].
• According to the second geometric argument, the simple point is impossible because two (adjacent) of such points must immediately touch one another (not involving empty space-parts), and they cannot do so because necessarily there must exist a simple point between them separating them (otherwise they were not  two  points). So the points would never be able to touch one another because there always must be a point between them. [And Petronievics explains how points may nevertheless be able to touch one another.]
• Finally, according to the third geometric argument, the simple point as constituent of space is impossible, because these points must be able to touch one another which would, however, result in the (geometric) disintegration of those simple points into still more fundamentally simple points [The points will, when touching one another, either partly overlap, and thus implying complexity of the simple points, or touch one another with a certain 'region' of them, also implying complexity instead of simplicity of these points. But, as Petronievics explains, the 1 as the value of a point cannot be divided, and the points are, according to Petronievics, kept apart by the earlier mentioned negation-acts].

We shall now discuss these geometric arguments one by one and demonstrate their failure.

That a simple space point as such is impossible because its size is  necessarily  zero, and from merely zero's no extensive magnitude can be generated, is an assertion whose untenability can easily be shown.
In the time-series the absolute indivisible unit is the NOW-moment. So, such an indivisible unit is conceptually possible. As to the number-series, 1, 2, 3, 4, ... ,  an indivisible unit not only is possible but even necessary. And it is clear that that simple (i.e. not composed) moment of time forms the substrate-in-experience of this simple unit of number. And this unit is not zero, but 1. And therefore the absolute indivisible unit of space (of spatial extension) is surely possible.
That the numerical unit must be 1 is necessary by the following :  Suppose, we can divide the 1, then we get 1/2.  In this genuine fraction (thus not, say, 4/2, 5/1, etc.) the denominator itself evidently is a number and signifies the sum of two units (1 + 1), which as such are indivisible. For if we think of such a unit as being in turn composed of two parts (1/2 + 1/2 + 1/2 + 1/2), then things will repeat with respect to the 2, and so on and so on. In considering things this way, we cannot count, because there is no counting unit anymore :  That unit has become undetermined, it is 1, but nevertheless 1/2 + 1/2, but this is in fact :

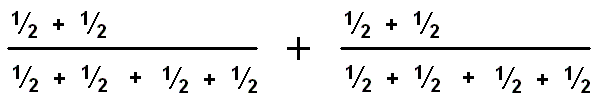
but this is . . . ,  etc., etc.

And, consequently, 1 is indivisible.

So the first geometric argument which views the simple point as part of space (as constituent of the extensum qua extensum) to be impossible is false. The simple point is in any case conceptually possible. As having the value 1 the space point can now by addition generate all extensivity. It can be the unit of extension, at least conceptually.

Also here the impossibility of the simple space-point is allegedly demonstrated. Such points must touch one another, but in order to remain separate there must be a point between them. But between such a point and the original points there must again be a point, etc., ad infinitum. Touching thus is impossible, and so space consisting solely of points.
If it is now assumed that all space-points are of the same nature, then the argument is valid and compelling. And indeed it is so assumed. And this is only correct if the first geometric argument would be correct :  that all points are zero's (because then they all are of the same nature). However, it certainly is conceptually possible to distinguish between a real space-point filled with content and an irreal point not filled with content separating two real points from one another. The irreal point then is not a space-point, it is non-spatial, not geometric, but is a negation-act, effecting as it were from without the extensional nature of space, by holding apart from one another the members of every pair of real space-points 'touching' each other, i.e. keeping separate the members of such a pair from one another.
Everything what lies between the members of such a pair of 'touching' real space-points (or including also the 'first' point of such a pair) we can take to be the smallest and indivisible unit of extension, i.e. the unit of space (unit of spatial extension).
And taking things in this way, i.e. admitting that there may exist at least two different 'sorts of points' in the spatial, this second geometric argument (against a discretum) breaks down, because now (real) space-points can 'touch' one another without coinciding. This 'touching' means to be separated by the smallest possible (unit of) extension.

Also this argument militates against the punctual composition of the extensional, and it is refuted by demonstrating that extension-without-points is not a logical necessity. The argument says that the simple space-point is impossible as unit of extension because the points must touch one another resulting in the disintegration of these points into parts of them (namely as a result of  partial overlap or touching with  parts  of them) rendering these points not to be the ultimate indivisible units. If such units are  composed (instead of simple) then touching one another means that they touch one another with parts of them, for example solids (bodies) with (parts of) their faces, faces with one or more of their lines, and lines with their points. But this case of touching is different from the touching of  simple  units with one another :  Between two touching  composed  units (i.e. things considered as units) there is  nothing (that, in fact, is what touching is) :  They touch one another with some of their parts, but that's it. Their touching defines parts of them [ So in fact only entities that have (potential or actual) parts can directly touch one another, and if true units are not composed, they must be points, and these completely coincide upon touching one another, because their only 'part' (by which they would touch) is themselves]. Only when we assume an intermediate point between every two touching real points (a negation-act which itself is not a space-point) that separates them from one another the difficulty of the impossibility of touching of simple space-points vanishes (they then do not coincide upon touching one another), because now there is not absolutely nothing between two mutually touching real space-points. It is the irreal space-point (the negation-act) which separates them. The mutually touching real space-points do not coincide anymore, and no parts of them are being defined. We can also say :  Because true indivisible units of space have no actual or potential parts, they cannot touch one another without completely coinciding, so, in composing a voidless medium (space), a medium with no holes, their touching must be mediated by something else, something not itself extensive but extending, and that something is the negation-act.
If we thus consider the notion of touching such that it is about the cases in which either nothing is in between (as in the touching of composed units) or where between the mutually touching units there exists something not of the same nature (as that of the two touching points) (but something of a different nature), as it is the case in the mutual touching of real points by means of irreal, mediating, points, then we can clearly understand how simple real space-points can touch one another without falling apart in parts, and without mutually coninciding.
And it is indeed the case that there is a distinction between real and irreal points. This distinction is conceptually possible, because from the assumption of a discretum does not necessarily follow that all points in it must be of the same nature.
This third geometric argument depends on the validity of at least the first, because there is only one species of zero.

These three geometric arguments directly intend to demonstrate the necessity of the absolute continuum (and thus extension without points). They have failed to do so.

Infinity or finiteness of space upwards (i.e. toward the large) is also treated by Petronievics, but we [JB] will here only discuss the infinity of space downward (i.e. concerning the small), insofar as we have not already done so. But where infinity or finiteness of space upwards is conceptually co-determining infinity or finiteness of space downward, then we must surely involve in our discussion the infinity or finiteness of space upward. And this is the case in Petronievics, pp.206 with respect to the second contradiction in the concept of infinity. We now, indeed have arrived at this second contradiction.

Second contradiction :  the contradiction of the finiteness of every infinity.

A finite piece of space consisting of finite parts we may take to be a  middle  in the following sense :  It is infinitely small as compared to the infinitely big, and infinitely big as compared to the infinitely small (the infinitely big and infinitely small taken here as given). Accordingly :  Something that is infinitely small with respect to a next part, and infinitely big with respect to a previous part, is itself finite.
The contradiction, found in the concept of the infinite reads :  Every infinite is finite.
This contradiction pops up as soon as we completely admit the infinite without qualification with respect to numbers. But because in numbers there is, and must be, an absolutely indivisible unit, namely 1, we can ascend to the infinitely big but not to the infinitely small, because 1 is indivisible. [So indeed, here, in exposing the second contradiction in the concept of infinity, we needs involve infinity towards the big]. In fact, 1 is the 'infinitely small' itself, just as that the last indivisible space-unit is 'infinitely small'. Accordingly, while we can go from one to OMEGA, and from there proceed further, we cannot go from 1 to 1/OMEGA and then proceed further down, because 1 is already the beginning.
So if the infinite in numbers [as it is alleged to occur in them] is conceptually taken to be consistent, then we can have the following ascending series of numbers :

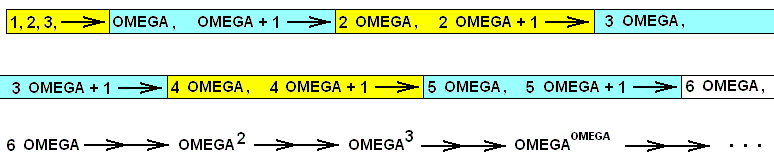
So this series consists of a succession of orders of infinity. In every new order of infinity we have a series that goes from 1 to OMEGA.  If we now let every next order of infinity start with the newly reached or appeared OMEGA, then we can say that every given order of infinity, say,  2 OMEGA,  2 OMEGA+ 1, ==> 3 OMEGA (excl.),  is infinitely big as compared to the previous one, namely  OMEGA,  OMEGA+ 1, ==> 2 OMEGA (excl.),  and infinitely small as compared to the next one, namely  3 OMEGA,  3 OMEGA +1,  4 OMEGA (excl.). "Small" and "big" here do not refer to the number of members of each order (that always is OMEGA - 1), but refer to the magnitude of these members, i.e. to the size of its individual numbers. As to compare things :

(a)    OMEGA,  OMEGA+1 ==> 2 OMEGA (excl.)

(b)    2 OMEGA,  (2 OMEGA)+1 ==> 3 OMEGA (excl.)

(c)    3 OMEGA,  (3 OMEGA)+1 ==> 4 OMEGA (excl.)

The difference of magnitude of number between corresponding members of the consecutive orders of infinity is always OMEGA (for instance [2 OMEGA]+1  minus  OMEGA+1 = OMEGA), and in that sense the order  (b)  is infinitely small as compared to the order  (c)  (i.e. every number of the order  (b) is infinitely small with respect to  3 OMEGA, the lowest number of order  (c) ), and infinitely big as compared to the order  (a)  (i.e. every number of the order  (b)  is infinitely big with respect to even the biggest number of the order  (a),  and so the order  (b)  itself must be  finite, despite the fact that this order, namely  2 OMEGA,  (2 OMEGA)+1 ==> 3 OMEGA (excl.), contains transfinite numbers. But if indeed this order is finite, then also the total of these orders :  1 ==> OMEGA ==> 2 OMEGA ==> OMEGA^OMEGA  . . .   must be finite, because the sum of finite magnitudes is, and always remains, finite [as long as we keep on counting the possible (finite) orders of infinity :  This series of orders is merely potentially infinite, i.e. undetermined  f i n i t e ].
So, indeed, the infinite is finite!
Accordingly, every spatial magnitude (every spatial extensum) must be  finite [because we judge their finiteness/infinity status by means of numbers], and its infinity should therefore only be expressed by the alleged fact that it is composed of an infinite number of finite magnitudes (infinity orders), which (expression) is impossible because however many finite entities we may add up together (connect to each other) the result always remains finite.
Precisely this consequence of the concept of infinity, namely that every infinite magnitude turns out to be finite, demonstrates that the infinite cannot exist, and that it, as soon as one supposes its existence, turns into its opposite.
The essence of the finite magnitude, for example of a given extensum, consists in the fact that it is composed of a finite number of finite magnitudes. When it at the same time would consist also of an infinite number of such finite magnitudes is a contradiction.

If  one wants to prevent the contradiction of the infinite that is nevertheless finite, by taking the  whole  series, toward the small as well as toward the big, as to be  determined  infinite, meaning that then here one also descends from 1 downwards all the way to  1/OMEGA,  1/(2 OMEGA),  1/OMEGA^OMEGA,  etc., and that there exists downwardly as well as upwardly a last member [One then writes this series as, for instance :  1/OMEGA, ..., 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, ..., OMEGA,  where 1/OMEGA and OMEGA indicate the  determined  infinity of the series in both directions. The series itself is then still  ..., 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, ... .],  then there is an  i n t e r m e d i a t e  region, and this region is  f i n i t e  :  ..., 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, ...,  meaning that the intermediate region, taken to be infinite, is nevertheless finite, because every member of this region is infinitely big relative to the last member, 1/OMEGA, counted from 1 to the left, and infinitely small relative to the last member counted from 1 to the right, OMEGA.  Accordingly, also, just as this intermediate region itself, every order of infinity [i.e. containing infinitely small and/or infinitely big numbers] in a given series, i.e. as member of such a series, must be finite, because such an order of infinity stands in the same proportion to its left and to its right as is the case in the mentioned intermediate region.
Only as to the two last orders of infinity ("last" because we here are considering the determined infinite, determined to the left as well as to the right of an infinite series), all the way at the left and at the right, this contradiction no longer is present.
The special feature of the intermediate region, [this region] lying in the determined [at the left and at the right] infinite, accordingly, does not come from that intermediate region itself, but from the fact that here the extremes of the whole infinite (i.e. the last members at the left and right) cannot be in the same way finite (i.e. infinitely big relative to 'this', and infinitely small relative to 'that') as is the intermediate region itself. But this exception certainly does not hold for the intermediate members [i.e. here members of the whole series as well as of the intermediate region], also when they themselves are orders of infinity. These must be finite in the same way as is the whole intermediate region itself (i.e. infinite, but nevertheless finite).
So if thus the infinitely  small  of the  last  order cannot anymore be characterized as finite as can the other orders of the infinitely small, we accordingly must demonstrate the finiteness of that last order of the small in another way. And indeed, this is possible, for the infinitely small of the last order is nothing else than the simple (i.e. not composed) space unit, i.e. the simple space-point itself [such a point is also -- as with other such points composing space -- accepted by the proponents of infinity], and this point is indeed finite, it doesn't consist of parts, it is not further divisible, so with this point the series terminates at its left end. So the series here not merely ends ex hypothesi, but really, for we can explicitly indicate that last member -- the space-point -- to which the continued division approaches (so, albeit that we shall never reach it in this way, we can indicate it, meaning that this last member, the smallest member, is fixed) [Whether the "finiteness" of this smallest member, i.e. its indivisibility, is actually comparable with the finiteness of an order of infinity, I do not know. We might say that the smallest member (lying at the extreme left) is the first member of an order of infinity if we proceed from that member to the right. And if we then are going to count the members of this first order of infinity, then we get :  1, 2, 3, 4, . . . , OMEGA (excl.), and this series is finite].

If this indeed does apply to the infinitely small of the last order (at the extreme left), then it also applies to the infinitely  big  of the last order (entirely to the right). Because also this order has, in common with the finite, the nature of being  determined, and, taken by itself (i.e. without thereby changing into another type, here from finite to infinite), has the nature of being unable to further increase (it cannot grow further) [because it, the last order, is, ex hypothesi, the last member], and that is the predicate of every finite entity. [So also here the infinite is finite, and thus the contradiction remains also when the whole series is taken to be  determined  rendering it having a middle [which it wouldn't have when it was undetermined, unfixed]. So the last member is determined and not augmentable, and thus finite, i.e. a finite number, and so representing a finite order of infinity, and consequently, the 'infinite' series  1/OMEGA, ..., 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, ..., OMEGA  is finite nevertheless.]. So this is the contradiction of the infinite that nevertheless is finite, but there is a restriction :
Only in the case in which one either accepts infinity only toward the small, or only toward the big, this contradiction vanishes [Petronievics, 1904, explains this in p.210-211]. Only then there is a real distinction between the finite and the infinite.
[In space, but also in counting, we have to do with a genuine indivisible unit (space-point, the number 1), and this would then mean that the space series and the number series are infinite only upwards. And then the contradiction (the second contradiction :  the infinite is finite) doesn't exist anymore. This thus is the earlier mentioned qualification of the infinite that we have in mind]. [The just mentioned absence, in certain series, of the second contradiction, does not, however, establish the logical consistency of the concept of infinity as such, because that concept has other contradictions (for example the first and the third), and one contradiction already suffices to demonstrate the inconsistency of the concept of infinity.]

Third contradiction :  the contradiction of the jump from the finite into the infinite.

We now have arrived at the third contradiction of the infinite, namely the contradiction of the  jump  from the finite into the infinite. This contradiction is decisive for the impossibility of the concept of (actual) infinity. It reveals its impossibility and its uselessness.
We have  1, 2, 3, 4, . . . , OMEGA.  [and when we say "we have it", we accept the concept of the actual infinite]. Here we evidently have to do with a leap from  1, 2, 3, 4, ...  to  OMEGA.  In order to remove this leap (this discontinuous transition) we may, to begin with, express the number series (i.e. the series of natural numbers) more completely, namely by explicitly mentioning certain members not yet mentioned. In order to do so, we insert into the series, as it is normally depicted, an infinite sub-series, this in turn in order to bridge the gap between 1, 2, 3, 4, ...  and  OMEGA :

But in fact we still have the jump from  OMEGA-1  (which number is finitely big)  to  OMEGA (which number is infinitely big). So between  OMEGA-1 and OMEGA we must insert a transition series bridging this gap. This means that we, in OMEGA-1 ==> OMEGA, where OMEGA-1 and OMEGA differ by one unit of counting, must divide this unit. This, then, will automatically extend to all individual units, for example between  OMEGA-2 and OMEGA-1, etc., but also between say, 3 and 4,  2 and 3, and 1 and 2. And also this 1 (as being the first number of the series) then must be so divided, rendering the series to continue also to the left (i.e. to the small). But then, of course, we have new units (because we in fact are counting the members of the series), and with these new units we again count, namely everytime  from  such a new unit, let us call it 1',  to  OMEGA  (and in the end also from OMEGA-1'  to  OMEGA). And then we still have a jump from 1' (finite) to OMEGA (infinite)  [ 1' + 1' + 1' + ...  (and thus the result of counting) remains finite, it never reaches the infinite OMEGA (otherwise OMEGA would itself be also finite) ]. So with this we do not get rid of the jump from the finite into the infinite. And it is clear that we cannot improve the situation by again dividing-up the new unit 1' of counting, because we then will obtain yet a new unit of counting, 1'', etc., ad infinitum [By the way, with "ad infinitum" we always mean (expressed by "ad") potential infinity, not actual infinity].
So it is now clear, that, if we want to get rid of the jump from the finite into the infinite, we must eliminate every form of indivisible unit of counting. And then an infinite set would never, even in principle, be  countable  anymore, because we do not then have a unit of counting. Or, the whole said a bit differently, among the infinite sets (i.e. in the set of all infinite sets) there then is no set whatsoever which is in principle completely countable, because during counting we bump into an interruption, an abyss, which can only be bridged (and thus not by continuing counting) by a jump. And if we then want to reconstruct this infinite set such that the jump disappears, then the set has changed from countable to uncountable (and this applies to every infinite set originally considered to be countable), because we then have not a unit of counting anymore. [Presupposing the absolute continuum, there are infinite sets that are uncountable in an even stronger degree, such as the set of real numbers (natural numbers + fractions + irrational numbers). Here, in counting, for every given number we cannot say what number is the next. And even if we make a beginning with a more or less random ordering in the (set of) real numbers (label them with natural numbers), it turns out that there are not enough natural numbers to count or index them!]

Accordingly, if infinite numbers are logically possible (i.e. not containing any internal contradiction), then they are of a fundamental different nature than are finite numbers (this because we cannot get rid of the jump). Then, for instance, OMEGA, would lie outside the series 1, 2, 3, 4, . . . , and so thus not indicating the amount of members (the number of constituent numbers) of this series. It further means that then the series 1, 2, 3, 4, . . . always remains finite how far whatsoever we may continue it, because every (for the time being) last number of it (and thus not OMEGA) always indicates the number-until-now of numbers of the series, and this last number is always finite. So the number of members of the series 1, 2, 3, 4, . . . , that is the number of natural numbers, is finite, and here this means :  undetermined finite (undetermined, because it has no fixed last number), which in turn means :  (merely) potentially infinite.
All this was, in essence, already seen by Aristotle when he rejected the actual infinite, and instead pointing to the potential infinite (= undetermined, unfixed, finite).
So, to say it again, if we want to get rid of the jump from the finite into the infinite we must eliminate (i.e. take to be non-existing) every form of unit of counting, but then (complete) counting of every alleged infinite set has become impossible. If we, however, insist that counting must always be possible, even the set  { 1, 2, 3, 4, ..., OMEGA }  itself, then we must remove OMEGA from this set of numbers (saying that OMEGA, may perhaps exist, but not as a member of the set {1, 2, 3, 4, ...} ),  and then the remaining set is (in principle) certainly countable. And all this demonstrates that if we want to get rid of the jump from the finite into the infinite we must eliminate the infinite!
Cantor (in the 80-ies of the 19th century) indeed does do this, however without the exclusion of infinitely big numbers (i.e. upward infinity in the number series 1, 2, 3, 4, ... ).  He posits that there is a biggest number, he calls it OMEGA, that indicates the number of members of the set {1, 2, 3, 4, ... }  without itself being a member of this set. But this in fact still is a jump afterall, because initially every number of the series 1, 2, 3, 4, ... indicates the until-then number of members of this series, while this cannot be with the number OMEGA because it doesn't belong to the series anymore. OMEGA, may at most be considered to be a  boundary  to which the finite numbers tend without ever reaching it  [This is expressed by the mathematical concept of limit, an important concept in the infinitesimal calculus]. By continuing adding up units, now to OMEGA and further, we obtain the series of transfinite numbers of the form  OMEGA+1,  OMEGA+2,  ...,  OMEGA+ n.  This series, according to Cantor, at last gets to 2 OMEGA, and this must again be a number outside the series  OMEGA+1,  OMEGA+2,  ...,  OMEGA+ n.  (the series tends to 2 OMEGA, but doesn't reach it). In its turn 2 OMEGA leads to the series  2 OMEGA+1,  2 OMEGA+2, ... ,  resulting in the transfinite number 3 OMEGA, and so on up until OMEGA², and then further to OMEGA^OMEGA and beyond, ad infinitum.
So we see that the number series is replete with jumps. And to accept this feature clearly is an ad hoc construction in order to save the infinite.

It is clear that we must abstain from the concept of infinity in the sense of actual infinity, while potential infinity in fact is undetermined finiteness.

We now, in Petronievics, 1904, p. 219, have arrived at the end of the treatment of the three contradictions in the concept of the (actual) infinite :

(1)  The contradiction of the infinite number.
(2)  The contradiction of the absolute finiteness of  every  infinite entity.
(3)  The contradiction of the jump from the finite into the infinite.

But there are still more contradictions.

The contradiction of the true subset being equal to the whole set, in infinite sets.

If we want to determine whether a given set contains an equal number of members as that of some other set, then we must demonstrate that (perhaps after rearranging of the members) a one-to-one correspondence can be set up between them, i.e. between corresponding members of them. For example, if every seat in a theater is occupied by a person and that there are no spectators that have to stand, then we know that the set of spectators is, as to the number of members, equal to the set of seats in the theater. These sets then are, as it is called, of the same cardinality. But, when we apply this criterion to sets that are to be considered infinite (as to the number of members), and thus if one accepts the infinite, something remarkable takes place :
Let us consider two sets taken to be infinite :  {1, 2, 3, 4, 5, ... }  and  {2, 3, 4, 5, 6, ... }. These two sets do not have the same cardinality (they are not equally big) because the second set is the same as the first one except for the fact that in the second set the number 1 is missing, while present the first set. Nevertheless, these two sets can be mapped onto one another by means of a one-to-one correspondence of their members :

So the two sets must, according to the ono-to-one principle, have the same cardinality, i.e. qua number of members they must be equal.
If, as Cantor says, OMEGA expresses the number of members of the set {1, 2, 3, 4, 5, ...} then the following would hold :  OMEGA = OMEGA-1.  And the further equivalence (<==>) :
OMEGA = OMEGA-1  <==>  OMEGA + 1 = OMEGA
Consequently, from OMEGA onwards no further counting is possible.
Cantor concludes from this that transfinite numbers arithmetically behave differently from finite numbers.
And, proceeding this way, we also have the (alleged) infinite sets {1, 2, 3, 4, 5, 6, ...}  and  {2, 4, 6, 8, 10, 12, ...}, and also these have, according to the one-to-one principle, the same number of members :

So also here, a subset (here the set of all positive even whole numbers) has the same number of members as does the whole set of all positive whole numbers (which contains the set of all positive even numbers, as well as the set of all positive uneven numbers).
Instead of seeing in this a right-out  contradiction  (which appears under the supposition of the existence of infinite sets), Cantor (and also Dedekind) uses this phenomenon as a  definition  of the infinite! There may well be a difference between the finite and the infinite, but certainly not when this being-different includes a contradiction.

If we consider  finite  sets, then there is no problem :
{1, 2, 3, 4, 5} and {2, 3, 4, 5, 6} are, qua number of members, completely equal sets, because the members can be one-to-one mapped onto one another. And the one is no subset of the other. Also the sets {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} are, qua number of members, exactly equal to one another. And yet this doesn't imply that then there would be as many even numbers as even+uneven numbers. So the contradiction vanishes in the case of finite sets.
Still more contradictions haunt the infinite :

Suppose we have two circles with different radius :

If we consider lines, also curved lines, to consist of points (and only points), where these points are all of the same nature, then we have, in the case of our two circles, evidently to do with two  unequal  point-sets (unequal as to the number of members, the constituent points), because the one circle clearly has a greater circumference than the other. Nevertheless, for the points of these two circles a one-to-one correspondence can be set up, as the figure illustrates. An thus the two point-sets must have the same cardinality, i.e. they must contain an equal number of members (points). So we have a contradiction. Evidently, the contradiction follows from the supposition that lines, also curved lines, entirely consist of points (of the same nature) (beause this, here, is the only supposition). So, if we consider, and rightly so, lines as representing extension, then we see that extension cannot be formed by means of a concatenation of mere points (of the same nature). Accordingly, space (as extension) cannot be made up from points (of the same nature).
This state of affairs we can also prove with the solution of Zeno's paradox in the racing match between Achilles and the tortoise, in which a fair headstart is granted to the tortoise at the beginning of the game. In order to catch up with the tortoise Achilles must bridge an ever decreasing distance (from the tortoise). Summation of the necessary time does not exceed a finite value, so, based on this calculation, the tortoise must be catched up in a finite amount of time (as is also confirmed by experience). But  spatially  seen, Achilles can never catch up with the tortoise :  He more and more comes closer to it but always remains separated from it by a small distance. This is so under the assumption that space as extension consists of points and only points (of the same nature). [When Achilles reaches the point where the tortoise initially was, the tortoise, in the mean time, has moved a bit to a further point, and when, finally, Achilles has reached this farther point, the tortoise has again moved on a bit further, and so on, and so on. So Achilles never entirely catches up with the tortoise.]. As a result of the contradiction between the calculation of the time needed to catch up and the spatial consideration with points, the assumption that spatial extension is realized by concatenation of points and by points alone, points of the same nature, must be abandoned.
Space consists of small indivisible but nevertheless extensive bits. Therefore, the finite distance that has to be traversed by Achilles in order to catch up with the tortoise contains a finite number of such bits. To traverse every such a bit takes a finite amount of time, and a finite number of such bits also takes a finite amount of time :  In a finite amount of time all these bits can be traversed. And precisely this is the genuine solution of Zeno's paradox.
If space would consist of parts which in turn always and with no end consist of parts, then such a composed part never is completed, resulting in the disappearance of space altogether. Spatial parts that, upon division, continue to consist of parts result in a space being made up of simple points (because a point cannot, by definition, be further divided), and this is, as we have seen, impossible. But it is only so impossible if we take these points to be of the same nature, all being sizeless zero-points. And this impossibility (of space consisting of points, i.e. the punctual nature of space) vanishes as soon as we are going to distinguish two essentially different sorts of points.

Before we are going to treat this new type of space, we must investigate two basic concepts (in fact two pairs of concepts) as to their nature and logical proportion :  The  determined  infinite and the  undetermined  infinite. This is one pair of concepts. The second pair (which corresponds to the first) is :  the  determined  finite and the  undetermined  finite (the latter is the unconcluded infinite, the potential infinite).
Basing oneself on the first member of the second pair, the determined finite, one thinks that there also is something like the determined infinite :  The undetermined infinite becomes the determined infinite. One brings the infinity to a close (which looks like a contradiction). But if one then realizes that, after this closure, the series can be continued nevertheless, one, as a result, upon continuing, obtains a series of consecutive orders of infinity, a series which itself never is concluded :  The infinite remains undetermined.
Only after I have continued the finishedly (completedly) infinite straight line (in) such (a way) that it nowhere has an end anymore, I will obtain the concept of an undetermined and absolutely endless infinite (also that of the line), i.e. the concept of an infinity which truly, in the infinite, has no longer any beginning or end. So the infinite can never be closed. This infinite now is the potential infinite, downwards and upwards. And this potential infinite is the undetermined finite [Indeed, the infinite remains finite, because it nowhere is closed, completed].
Now we are ready to discuss space, discrete space, consisting of two kinds of points [where one of them is not a point at all, i.e. not of a spatial nature, but a negation-act, but still as it were representing the second kind of point].

[While a given discrete entity may, and perhaps should, logically, contain gaps, holes, i.e. interruptions of this entity, a "gapless discretum" looks like a contradiction. But it isn't. It is a heterogeneous continuum, but here "continuum" only in the sense that all the alleged "gaps" in it are not local cases of non-being, they are not "nothings", but only differ qualitatively from their surroundings. So in such a "continuum", such a heterogeneous continuum, "being" is not interrupted. Indeed, if we suppose space to be consisting of points, then already it is a discretum, because these points must be kept apart from one another by something, and this cannot be nothing. Only a space which has no points and no other constituents is truly continuous, but then it cannot have extension, and is then not a space afterall. A true continuum we can only expect (but not know for sure) along an intensive dimension].

As long as we see space as consisting of discretely from one another  separated  parts, the concept of undetermined downward infinity does not apply to such a space. For a space with undetermined infinity would exclusively consist of  composed  parts, and then true parts (in the sense of elements) do not and cannot exist. And then such a space could not exist  ( It would be a discrete Zeno-space in which whatever small finite bit could not completely be traversed ).
Things become entirely different as soon as we suppose that space does not consist of separated discrete parts, and suppose that it is an absolute continuum. Empty space usually, in contrast to the discrete nature of the parts of matter scattered in it, is taken in such a way that, while space would be absolutely without parts, the matter in it only consists of parts which always have between them empty space, or, when these parts may often touch one another, this only happens at certain moments.
In this way one arrives at the concept of continuum (of empty space) and not at the concept of its discretion [i.e. that the continuum is itself interrupted by discrete matter]. While empty continuous space is taken as consisting of absolutely unseparated parts [Between those 'parts' of this space there always is that same space], the matter (in it) is taken as consisting of discrete particles separated from one another by empty space. The concept of the discrete is, after the example of discrete matter, taken such that the "discretum" is completely identified with the concept of an empty-gaps-containing discretum, resulting in the fact that one not at all considers the possibility of a gapless discretum of which the simple (i.e. elementary) parts are absolutely without empty extensive in-between-spaces. An precisely because one cannot comprehend this concept of a gapless discretum as distinguished from the concept of the gap-carrying discretum (a discretum with gaps) of which latter an example (analogue) can be seen in the matter scattered in space, one constantly confuses the concept of the absolute continuum with the concept of the gapless discretum, and we will see that the whole of standard geometry is based on this confusion [By seeing either space+matter-having-voids [wherever these voids are voids of, either of matter or of space], or the absolutely empty space between matter [here the voids are the empty space], one forgets that there still is a third possibility to view space :  Space that is voidless and [nevertheless] discrete. This then would boil down to the fact that space is  c o m p l e t e l y  filled (with Being, with content), or that empty space doesn't exist anywhere, space is its very content (its content-of-Being). Indeed, much earlier in present Part of Website, in the series devoted to natural philosophy, we argued (with Hoenen) that space is not an entity all by itself, but originates from things, beings, namely as a result of their mutual contact.].
And yet the gapless discretum can, as soon as we accept its possibility, be distinguished from the absolute continuum :  If empty space consists of simple indivisible points, then evidently this empty space is not a continuum but a discretum, and then a gapless discretum. That is space identifying itself with content, otherwise an empty space would again be needed that would separate this content, which is absurd. So if we, then, in spite of the Zeno-paradox (speaking against the possibility of a composition of empty space out of simple indivisible points), nevertheless want to accept such points as its constituents, then empty space stops to be absolutely continuous, it then must be taken as a gapless discretum. But if one, in this, assumes the absolutely undetermined infinite number of these points, then empty space evidently stops to be a gapless discretum, beause then there are no simple parts anymore in it (because the divisibility is then endless), and then all the same changes into the absolutely partless continuum afterall. And then there would be no distinction anymore between gapless discretum and absolute continuum afterall. This distinction can only be maintained if we accept the existence of more than one kind of point :  but then, in doing so, the second kind of point is not a spatial point, but a negation-act preventing the coincidence of adjacent space-points, and then finally we have the gapless discretum now truly contrasting with the absolute continuum.

The continuum, just as such, is possible, but the extensive continuum, the spatial continuum, is, however, not possible (whereas an intensive continuum may perhaps be possible). This impossibility can, to begin with, be geometrically proven, and then also be proved purely logically. One of the geometric reasons for the impossibility of an extensive continuum says the following :  The extensive continuum, the spatial continuum, is  upwardly  absolutely impossible, whereas downwardly (i.e. toward the inside, toward the small) it is possible. For, upwardly, expanding space cannot be closed as it is so closed downwardly, and because it is, and remains, thus open upwardly, space upwardly is not a continuum. And instead of then concluding that space cannot be a continuum at all, one merely concludes that that spatial continuum is finite upwardly [potentially infinite, undetermined finite], not realizing that a true continuum cannot be finite.
But now, projective geometry has eliminated the upward openess of continuous space by proving that space upwardly (i.e. toward the big) is just as continuous as it is downwardly :  It only has overlooked the fact that this proof leads to a contradictorial result :  The coincidence of the circle with the straight line (when the radius becomes infinitely long), upon which the upward closure and continuity of space rests, is impossible and contradictory. Just as the circle and the straight line are supposed to absolutely coincide in the infinite [implying that the straight line is not an open structure but a closed one.], so also two parallel straight lines must intersect one another in one point at infinite distance, and based on this, one derives that the very plane, containing these parallel straight lines, must itself become, in the infinite, a point, resulting in the impossibility of continuous spatial expansion into the infinite, and with it, the possibility of the spatial continuum (because it is now closed also upwardly) now becomes clear.
Let us now consider both alleged proofs of the upward closure of space, in order to thereafter lay bare their flaw. We can do this best by considering a one-dimensional extension, i.e. by considering a straight line. See next figure (in which the points are set by us, they are not self-contained points of the line itself) :

If  I, for example, consider the straight segment between the points A and B, then I surely may take this segment as a continuum, because between A and B there is true extension everywhere. On the other hand, viewing the line as a continuum becomes apparently impossible when I, departing from the points A and B, do not go inward, i.e. not go to C, where (in C) both directions AC and BC come together in one and the same point (C), but when I, still departing from the points A and B, proceed outward, that is, in the opposite directions AD (and also CD) and BD' (and also CD'). For these two directions never meet again (they never would lead to coincidence), they  remain  running in opposite directions without ever meeting [This is the upward openess of the line, i.e. one-dimensional space, at the same time exemplifying two- and three-dimensional space.].
If this is indeed the case, then we do not have upward continuity of space (while having inward continuity), for while the spatial segment between the points A and B can be filled towards its interior with spatial extension, the upward completion seems to be absolutely impossible, because upon increasing the length of the line the extreme points will never approach one another. To get rid of this problem one has pondered whether it is really the case that the continued outward extension from the points A and B indeed does result in a steady increase of distance, or whether it turns out to be merely seemingly so, and that the end-points at infinity do at last coincide just as points of the line do inwardly. Well, a simple consideration of the circle, if it is compared with a straight line, teaches us that the bigger the radius of a given circle becomes, the smaller becomes the [degree of] curvature of the circle, resulting in the periphery of the circle to more and more approach a straight line (i.e. becoming a straight line), so that, when the radius becomes infinitely big, the circle's curvature becomes infinitely small and thus becoming a straight line.
We should express this by saying :  The straight line is at infinity in fact a circle (a circle of which the radius has become infinitely big), for we cannot say that the circle  becomes  a straight line, because this would mean a jump (Petronievics, 1904, p. 234). All this means that in following the line AB outwards in opposite directions we, at infinity, will yet see a meeting to take place, and thus will see that the line, also outwards, is closed, rendering a spatial continuum (an extensional continuum) entirely possible, because this space is now closed, inwards and outwards. At infinity the straight line is a circle without being curved.

The flaw in this proof.
The error in the alleged proof that space is a genuine continuum is that this "truly wholly to be a continuum" of space is already presupposed in this proof :  While in the true continuum there is, inwardly (i.e. toward the small), no infinitely small of a last order (it continues to get smaller and smaller), this is also the case outwardly (i.e. toward the big), meaning that in a genuine continuum also toward the big there is no last order of infinity, which is clear from the fact that in proceeding toward the big the radius ever  increases  as to its length while the circle's curvature becomes smaller and smaller, while this is never concluded, meaning that the curvature never becomes zero (it will only become zero if infinity is presupposed), in turn implying that the circle never will become a straight line [So the circle will never become a straight line in such a procedure].
So, as long space is not strictly taken to be continuum (but in fact taken to be a 'discretum') (which is the case as long as one doesn't distinguish between the absolute continuum and the gapless discretum), the circle cannot at last coincide with a straight line, and so long the proof is not stringent. It is only then stringent (in its demonstration that the circle becomes a straight line at infinity, and thus demonstrating that the straight line at infinity is in fact a circle, and thus that space is closed outwards and can thus be continuous) if absolute continuity of extensive space is presupposed [The mentioned coincidence is then demonstrated, but, of course, not the absolute continuity of space, which (continuity) is merely presupposed]. For may the  discretum  consist of an infinite number of simple space-points, these latter will be the infintely small of the  last  order of infinity in the  determined  infinite discretum [because only the determined infinite has, in a given direction, a truly last order of infinity], and the circle with whatever infinitely small degree of curvature will not become a straight line (because for this a continuous getting-smaller, without a last order, is necessary).
As indeed the series of the infinitely small magnitudes is simply undetermined infinite  only  in the absolute continuum, implying that in this continuum only the absolute zero can be the infinitely small of the last order ["last", not in the context of counting, but "last" because no real magnitude can be smaller than zero.], so also the series of the infinitely big magnitudes is simply undetermined infinite  only  in the absolute continuum, and, accordingly, only in this continuum there exists a circle with an absolute infinite radius, a circle whose degree of curvature is absolutely zero (for with the absolutely infinitely big corresponds the absolutely infinitely small, i.e. zero), and therefore this circle really, completely and absolutely coincides with the straight line (only in such a continuum). Indeed, when we say that a spatial (true) continuum implies the fact of  "circle = straight line at infinity", then this is logically correct [In a true continuum prolonged increase of the radius of a given circle will finally transform the latter into a true straight line, instead of merely approaching it]. But because precisely that what is implied by the assumed truly continuous nature of space is a contradictory entity (circle = straight line, resp. non-zero curvature = zero curvature), such a continuum cannot exist.
Something comparable is the case (Petronievics, 1904, pp.236) with two parallel (straight) lines that intersect at infinity (following these lines in both directions, left and right, but because straight lines are circles at infinity, there is only one point of intersection) :  Indeed, when we have two intersecting lines, intersecting under a certain angle, and lying between two parallel lines,

then they will, when the angle between them and the parallel lines steadily decreases, intersect with one another with an ever more smaller angle (between them), and this angle comes to lie farther and farther away from where it was in the beginning. If now the angle between, on the one hand, the parallel lines and the intersecting lines on the other, becomes progressively smaller and passing all orders of the infinitely small (while the distance between their point of intersection and their starting points goes through all orders of the infinitely big), then these lines will at last coincide with the parallel lines. And also here this is only possible when (extensive) space is taken to be absolutely continuous. But further, two parallel lines meeting one another at infinity in one single point, implies that then a  plane,  which justifiably contains infinitely many such parallel lines, will also coincide in that same point, i.e. at infinity being contracted, closed, in that one point. And because space contains infinitely many parallel planes, the whole of space will, at infinity, be contracted into a single line (of which every point represents a plane). However, this line is, at infinity, a circle, i.e. it is closed, and as such this circle encloses a plane. But this plane must become one single point at infinity. Now it is clear, that, and in what way, every space with one or more dimensions will, at infinity, transform into one single point. A one-dimensional space, and thus a line, changes into a space of two dimensions (the plane enclosed by the circle). But this two-dimensional space transforms, because it is infinite, directly into a simple not-extensive point (having zero dimensions), and then every change into more than zero dimensions is once and for all excluded [For a point remains a point, also at infinity]. So, according to what has been said, continuous space of more than two dimensions cannot even be constructed ! (Petronievics, 1904, p 240-241).
And so we have now seen that continuous space (extensive space) cannot exist, and if one nevertheless attempts to construct it, it then necessarily collapses into the simple not-extensive point. What does this mean? Nothing less and nothing more than that the extensive continuum is not possible [A supposed extensum directly falls back to a point which is not an extensum anymore], that the continuum, if it is possible, cannot be extensive [So the continuum either doesn't exist at all, or only in the form of an intensive continuum (such as the true scale of intensity of a quality).]

When speaking about a true continuum, in contrast to a discretum, we must realize that also here there can 'be' parts, but such parts are completely undetermined. They are merely potential parts. Therefore, the true continuum lacks true last (smallest) absolutely indivisible elements. In a discretum, on the other hand, the parts are determined (and therefore actual), and thus it has also absolutely indivisible last (smallest) parts, elements.

The last logical reason rendering the extensive continuum impossible lies in the fact that extension necessarily implies a to-be-outside-one-another of the parts of a continuum (this is what "extension" is). But to-be-outside-one-another is wholly identical to to-be-separated-from-one-another, as size-determinateness is identical to being-separated (from the environment), for what is outside-one-another necessarily also is separated-from-one-another. And the parts of the continuum, because they are unseparated from one another (they are merely potential parts, and, moreover, if it had separate parts it would not be a continuum but a discretum), cannot lie outside one another (and thus do not create extension), they can only lie  inside  one another (creating "intensive space"). So as soon as one takes the continuum to be extensive, its parts lose, together with their inside-one-another (it loses this because it is taken to be extensive), also their being-unseparated (undividedness), they are going to lie outside one another and are then separated, and consequently the extensive continuum stops to be a continuum, it changes into a discretum. [This train of thoughts imagines a given intensive continuum (in which, accordingly, the parts are within one another) which then changes into an extensive continuum revealing the latter's logical impossibility.]
So we must realize that "extension" cannot be extension of merely potential parts, because potential parts are not true parts. Extension can, if it is actually present, only hold apart  actual  parts, meaning that an extensive continuum must have actual parts, but then it is not a continuum anymore, but a discretum.
Accordingly, if a (part of) an intensive continuum (points within one another) can be mapped onto an extensive space, for example an intensive quality onto its extensive (quantitative) effect (heat onto a thermometer scale), then this extensive space cannot be a piece of continuous space, but a piece of a (extensive) discretum (points outside one another).
In the  gapless discretum,  the true alternative of the absolute continuum after the latter has turned out to be logically impossible, is (1) the identity, at infinity, of the straight line with the circle, (2) the intersection, at infinity, of parallel straight lines, and (3) the transformation, at infinity, of the plane into one single point, impossible as long as that discretum is not taken to be as absolutely undetermined infinite.
The  absolute  continuum, on the other hand (which we may imagine in the form of, for example, an intensive dimension) is free from (because such a continuum cannot be modelled anymore by the number sequence 1, 2, 3, 4, 5, ... and that thus we cannot count its alleged actual parts) the three above mentioned contradictions (viz., contradiction of the transfinite number, contradiction of all infinite which is finite, the contradiction expressed by the jump from the finite into the infinite). In the  spatial  continuum (the extensive continuum) a straight line can, at infinity, be a circle, and two parallel lines can intersect one another. If we see these implications (str. line = circle, parallel lines intersecting) of the spatial continuum as representing contradictions (i.e. impossibilities), then space cannot be an extensive continuum [i.e. because precisely that what necessarily follows from it is contradictory, it, extensive absolutely continuous space, cannot exist.]. But, because space surely (namely by definition) is extensive, these just mentioned implications (str. line = circle, etc) point to the fact that space cannot be an extensive  continuum, but an extensive  discretum, and this is, if taken to be  infinite  (but not as absolute continuum), not free from the above mentioned contradictions (contrad. of transfinite number, finiteness of all infinities, jump from finite to infinite), because in the discretum we will, and can, count things in order to determine the finite/infinite status.
Space, i.e. the extensum, is, accordingly, a discretum, and in it the three contradictions appear, and especially the fourth one, namely that in an infinite discretum an infinite part can be of equal size with the corresponding infinite whole (so the spatial discretum must be finite in order to eliminate this contradiction) (see for this  above). Let us now further concentrate on this issue (Petronievics, 1904, p. 244-246).
It is now clear that it is not difficult anymore to establish the strict (conceptual) separation of the infinite in the discretum and the infinite in the continuum :  The true infinite, the true concept of infinity, is exclusively that of the absolutely non-extensional continuum consisting of wholly unseparated parts, whereas the discrete infinite is the erroneous infinite, the faulty concept of the infinite. We have seen how some mathematicians assert that the infinite, because it is simply not the finite, must necessarily have properties that do not apply to the finite. As such this assertion is correct as long as this properties-being-different does not contain contradictions. As soon as the infinite is taken to be discrete (and, the other way around, as soon as the discrete is taken to be infinite), at infinity there appear contradictions rendering discrete infinity impossible. Of the four basic contradictions, present in the concept of the discrete infinite, the most important one is the fourth contradiction (which by Cantor and Dedekind is even elevated to constitute the very definition of the infinite!), in which every infinite discrete set has true subsets which are, as to the number of elements, equivalent to that whole set.
According to this view, the essential difference between the infinite and the finite would then consist in the fact that in the finite domain "part" and "whole" are completely different from each other, whereas in the domain of the infinite "part" and "whole" can also be equal to each other (as to the number of elements), we say "can be", because not every part, but only infinitely big parts, are equal to the infinitely big whole). And precisely here the true distinction between the finite and the infinite is expressed.

So Petronievics allows the actual infinite only in the  intensive  continuum, and not in the extensive continuum (because this forms a contradiction with itself), and also not (allowing the actual infinite) in the  discretum (because here we have the four contradictions of the infinite). Accordingly, infinity would be inseparably connected with the intensive continuum, meaning that we must enquire into the concept of the actual infinity in terms of the intensive continuum. However, to me [JB] it seems problematic to do so, because I do not know what precisely in the intensive continuum is in fact actually infinite. We can only more or less proceed [now I am not following one or another reasoning of Petronievics] if we map this continuum onto an extensive discretum (I would not know how an 'intensive discretum' would look like). The intensive continuum cannot mathematically be depicted straightforwardly, but physically it might be actually present in the form of the dimension of a given intensive quality [An example of an "extensive quality" is a (geometrical) figure], for instance heat. In this form -- dimension, dimension or play of the intensity of the quality -- it might, according to Nicolai Hartmann, be an ontological condition for the possibility of variation in intensity of a quality. If this is correct, then such an intensive dimension cannot  exist  all by itself, but only as "category" (in the Hartmannian sense) together with its "concretum" (= that what is made possible by it, i.e. is determined by the category). This ontological condition for the possibility of variation of the intensity of a quality then has in fact nothing to do with actual infinity, at most with potential infinity, which is undetermined finiteness. So, as such, the intensive continuum does not exist. Not because it would be contradictory, but because it is no more than an ontological condition, which all by itself, i.e. without its concretum (that what it determines), i.e. without a realized value of intension, cannot exist.
In fact we may get to know a bit about this 'intensive continuum' by mapping it onto an extensive dimension, as we do this with the scale of a thermometer which measures the intensity of heat, the temperature, by means of the quantitative effect of heat on physical bodies (dilation of a liquid when it is heated). The extensive dimension cannot, however, be a continuum, i.e. cannot involve infinities because of the inhering contradictions which we have discussed. So it must be a discretum. And then we may conclude, or at least take it as probable, that the (in the mapping) corresponding intensive dimension also is a discretum, i.e. not a continuum. And this would mean that a  continuum  nowhere exists. So all of Reality is 'digital', nothing is analogous.
What then is an "intensive discretum"? We might think of it as being in fact a progressive series of whole numbers, for example natural numbers. This set of numbers, being surely discrete, has no spatial extension whatsoever, but it, apparently, represents a dimension of intensity. And indeed, if we map these numbers onto a space we then get a possible scale of intensity (in which, we may, in order to be able to measure, establish a measuring unit).
So we may view the "intensive" in terms of series of consecutive numbers, progressing series of natural numbers, and this is very well compatible with our idea that the very essence of the  Implicate Order (which as such is the seat of the intensive) in fact consists of the  arithmetic dynamics  of natural numbers  ( This was extensively discussed in  the Theoretic Intermezzo ).  These natural numbers, in their ontological form, form the discrete nature of the intensive dimension.

With all this we have arrived at the end of our discussion of the finite and the infinite. And when thus now, as has been found out, the spatial continuum cannot exist, and the continuum, if it exists, must be non-spatial (non-extensive) (but this can also not exist, as we have seen [because it is possibly only an ontological condition which cannot exist by itself, i.e. without its concretum] ),  then space can only be discrete (and space, extensity, can only exist in the Explicate Order, the unfolded Order, while the non-spatial, the intensive, can only exist in the Implicate Order, the enfolded Order, but then only as intensive discretum, namely in the form of whole numbers). Space can only be discrete, i.e. it must consist of ultimate simple indivisible parts, and we must assess the positive possibility of this discretum (in the Explicate Order) and its inner structure. What we, until now, have established is, firstly, that a spatial continuum is not possible, that space can only be a discretum, and, secondly, that an infinite discretum is also impossible, that the discretum, if it exists, must be a finite discretum.
We must now investigate whether this spatial discretum is one with gaps (voids) or a gapless (voidless) discretum, and how it must be thought of as to its inner structure, and whether it is possible at all.

In anticipating things, it is instructive to expound a few things with respect to the opposition "continuum-discretum" (Petronievics, 1904, pp. 274) :
Because in the extensive continuum (as conventionally taken, i.e. consisting of infinitely many points of the same nature (and only such points)) there are no ultimate simple primary elementary line segments (no non-zero units of extension), there is, in the continuum, no objective difference between rational and irrational straight lines :  The hypotenuse (the oblique side) of, say, a rectangular isosceles triangle is not measurable (incommensurable) with a cathetus of such a triangle. But also the other way around, these catheti are each for themselves incommensurable with the hypotenuse :
According to Pythagoras' theorem, the square of the hypotenuse is equal to the sum of the squares of the catheti, and in further working out things we then have the following (in which 1 is the size of the hypotenuse and x the size of the catheti) :  x² + x² = 1²  <==>  2x² = 1  <==>  x² = 1/2  <==>  x = [square root](1/2),  giving :  [square root]1 / [square root]2  =  1 / ([square root]2), and this is an irrational number. And if the catheti are taken to be 1, we get  1² + 1² = x², meaning that the hypotenuse is now  [square root]2, which is also irrational. So in the continuum there is no objective univocal distinction between rational and irrational lines.
This objective distinction is present, though, in the (inward) finite gapless discretum. For a three-dimensional gapless discretum the arrangement of the real points (and thus not that of the negation-acts) is cubical (piled hexahedrons), whereas for a two-dimensional gapless discretum this point arrangement is that according to equilateral triangles, or squares. In such a discretum we can distinguish "real" and "imaginary" lines, because  real  lines consist of points that all lie at precisely one unit-distance from one another, while this is not the case in imaginary lines. And because here we can identify "real line" with "rational line" (because all these lines are measurable with the one unit-distance), and every "imaginary line" with "irrational line" (because in this discrete geometry every real line is in fact rational by definition and every imaginary line is irrational by definition), it is now clear that in the inwardly finite gapless discretum there exists a univocal distinction between rational and irrational lines. What then in the form of the univocal distinction between rational and irrational straight lines is lost in  continuous space, is copiously made up for by the reality which the irrational straight lines (in addition to the rational lines) enjoy in this space, a reality, which they lack in discrete space. See next Figure, which depicts a small region of two-dimensional triangular (hexagonal) discrete space. The points A, B, C, D, and E are space net-points. The 'point' D' is not a netpoint. The distances AC, AB, BC, BD, CD, BE, and DE are unit distances, they are equal to one another. AD is not a unit distance, neither is it a multiple of it. When we place AD alongside AE (which is two unit distances long), it will end at a location which we have indicated with D'.  And D' is not a real space point. Also M, the location of intersection of the two diagonals, is not a real space point. The triangles ABC, BED and BCD are equilateral triangles.

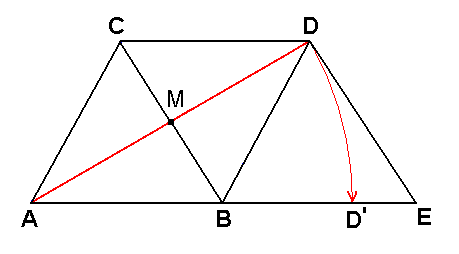
Let us, in discrete space, look to the imaginary straight line AD.  The length of this imaginary line is measured with the unit distance in the discrete (triangular) space. This unit distance we find between the real points A and B,  A and C,  D and C,  B and D,  B and E,  D and E, etc. The length of AD is twice that of AM, and the length of the latter can be determined by means of the rectangular triangle AMB.  We then have according to the theorem of Pythagoras :

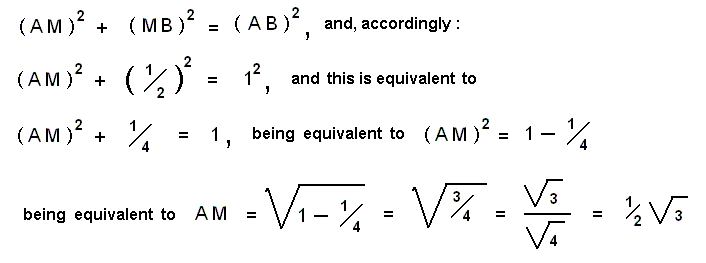
and, accordingly, AD is equal to [square root]3, and consequently, indeed irrational.
The irrational number [square root]3 lies between the rational numbers 1 and 2 (because it lies between [square root]1 and [square root]4 ),  and the point D would then come to lie between the points B and E if we would rotate AD about A until it comes to lie onto AE  (B lies at a distance 1 from A, and E at a distance 2 from A). But because the smallest straight line segments AB and BE are arithmetically and geometrically absolutely indivisible units (of extension), the point D' cannot in fact lie between the points B and E (in that case the section BE would then have to be at least 2 (which it isn't), and then AE would be at least 3 (which it isn't) to make possible that D' can come to lie between B and E).
But things are this way only when we have to do with the punctual discrete nature of space. As soon as we, on the other hand, take space to be absolutely continuous, the segment BE is divisible into the absolutely undetermined infinity (i.e. we can continue dividing it without any limit). Its size then stops to be 1, because in the absolute continuum there are no simple indivisible units, and the irrational point D' may then perfectly well lie between the points B and E.  [The next section is a note to the main text of Petronievics, 1904, p. 275/6].

Dedekind (1892) views in the fact that the irrational straight line can only really exist in continuous space the very essence of continuity, because he asserts that the points together making up the rational segments in the straight line are not all the points of that straight line, that between these points are gaps which are filled in by those points that make up the irrational segments [of that line], rendering this line to be continuous (stetig).
In a comparable way Cantor defines continuity (Stetigkeit) as a "perfectly coherent set". Now it is certainly correct to say that only the total of rational and irrational points of a straight line  - (these points arithmetically taken, i.e. as the result of the mapping of the "continuum" of real numbers (= rational and irrational numbers) onto a straight line (the "line of real numbers"))  - renders this line to be a continuum. But, Cantor, as well as Dedekind, views the notion of continuity (Stetigkeit) as something that may, it is true, easily be confused with [true] continuity, but which itself is not [true] continuity. According to them, namely, [geometric] space consists of simple space-points, and thus is in fact discrete [because these points are not merely potential, but actual, and actually making up the line], and its "continuity" therefore is nothing else than the gaplessness [no holes] of the discretum [And thus they equate "continuity" with gaplessness]. Cantor explicitly rejects the notion of the true continuum [i.e. space without points], in which he sees more of a "religious dogma" rather than a mathematic-logical notion.
The fact, however, that the gapless discretum, may it be infinite or finite, necessarily must have either a triangular or a quadratic structure, together with the fact that in such a structure there is no place for the continuity of the straight line as this [continuity] is taken by Cantor and Dedekind [namely consisting of rational and irrational points] without doubt follows from our [Petronievics'] expositions [for the real points of a gapless discretum all are rational and so also every line connecting them, and this here means every  real  line, a line, exclusively made up of the true indivisible (non-zero) units of extension of discrete space].
And only because these thinkers did not consider more closely the internal geometric structure of their 'continuum', in fact that of the gapless discretum [and then having seen the consequence of their own view of space as a set of points], they could make such a fundamental error. But the true cause, however, of making things obscure to them lies in the fact that they did not reduce the finite line segment consisting of points to a finite number of such points. Cantor, it is true, has seen the impossibility of the infintely small in a  discretum. But according to him there is no smallest finite [line] segment (the "Archimedian axiom"), so that every however small finite segment does consist of an infinite multitude of points, and that it then, as the  gapless discretum  of a straight line segment, as to its arrangement of points, does not differ essentially from the  truly continuous segment, because the only difference between them consists in the fact that the number of points in the truly continuous line segment is simply  undetermined  infinite, whereas in the gapless discretum that number is  determined  infinite [As this discretum is unconsciously created by Cantor and Dedekind]. And that gapless discretum of Cantor is, according to Cantor himself, as to the number of points, of the second high cardinality [a second, higher level or order of infinity], called "C" [of "continuum"], because the total of rational points is of the first cardinality [the lowest level or order of infinity], called OMEGA  [This first order of infinity is the countable infinite as that of the set {1, 2, 3, 4, ...}, whereas the second order of infinity is that of the set of all real numbers, which set cannot be counted], while the total of all rational and irrational points is forming the second order of infinity.
Such an infinite gapless discretum -- [i.e. the gapless discretum of Cantor, and thus in fact the continuum, the continuum, because when of such points there are, not a finite number of them, if so finite then constituting a discretum, but an undetermined infinite number of them,  then it is a true continuum] -- is, as has been proven, completely impossible, because that discretum would then necessarily change into the true continuum.
The  infinite  gapless discretum is in fact an untenable intermediate state between (1) the finite discretum of our geometry [i.e. the discrete geometry of Petronievics], in which a finite [line] segment is made up of a finite number of points, and where there exists a smallest finite segment (namely the elementary line, the diangle), and (2) the absolute spatial continuum, in which every finite [line] segment consists of a simply undetermined-infinite number of points, and in which there is simply no smallest segment, neither of a finitely small nor of an infinitely small magnitude. And if one also takes into account the fact that the internal geometric structure of the discretum-as-such prohibits the existence of irrational points (i.e. arithmetically irrational points, points, accordingly, that represent irrational numbers) in such a discrete segment, and may the number of its points be infinitely big, then one sees that such a spatial discretum (i.e. an inward infinite discretum) is not merely impossible, but also useless and thus superfluous.
[ End of note of Petronievics]

But -- continuing the discussion of the  above figure depicting a small region of discrete triangular space  and following Petronievics, 1904, pp.275 -- not only that the point D' comes to lie between the points B and E  if (geometric) space is continuous, but the segment AD' itself, as such, with it becomes (in continuous space) just as real (as to its ability to exist) as is the segment BE, that is, all distinction in their internal geometric structure vanishes (in the continuous case), for in this case the point D' is not separated by the points B and C from the point A  in such a way  that that point D' cannot touch point A immediately, (not in such a way separated), because the points A, B, and C in continuous space do not have a special position (as connected with this touching) with respect to point D', as is yet the case in discrete space where these three points form the so-called  simplex figure  of discrete two-dimensional space [i.e. the basic simplest, but nevertheless two-dimensional, geometric figure possible in two-dimensional space]. In absolute continuous space the individual points cease to be different -- as to their touching -- from other points by their special positions, which ultimately comes from the fact that they cease to distinguish themselves from one another at all.
So every straight line is, in absolutely continuous space, real because every line may be thought of as consisting of points that immediately touch one another so that there is also no distinction between real and imaginary lines [if this was also the case in discrete space, then also there this distinction would not exist. In discrete space the points do not touch one another immediately, the touching is mediated by negation-acts, but the latter are not themselves points, so between any two consecutive and adjacent points there is no other point, and in that sense these points do touch one another. In the  above Figure  it is the line AD in which the two consecutive points of that line do not touch, that is, its two consecutive points, A and D, are at a distance from each other that is greater than the unit distance, but is not a multiple of it. On the other hand, of the line AB its two consecutive points, A and B, do touch each other, meaning that they lie at unit distance from one another.].
Well, this fact, that the imaginary lines in absolute continuous space become just as real as are the real lines, one might bring up against discrete geometry which necessarily must accept the imaginary status of certain straight lines and justify this by certain "daring" metaphysical assumptions. But things are not like that :  Continuous geometry saves, it is true, the reality of the irrational straight line [such as that of the line segment AD, and also that of the line segment AD' in the above figure] as  straight line, it loses, however, totally the irrational straight line as  irrational  straight line, for in the absolute continuum the irrational straight lines cease to be irrational, they become rational [because in truly continuous space there is no measuring unit except the point. But with the point as unit every line can be measured]. With the suspension of the  geometric  distinction between rational and irrational straight lines also their  arithmetic  distinction is suspended. That is easily demonstrated (Petronievics, 1904, p. 277). The irrational and rational straight lines do not have, it is true, a common divisor [measure] as long as one is in the domain of the finite. They also do not have a common measure as long as one is in the domain of the  determined  infinite [in undetermined infinity we have the point as the 'common measure'] [the determined infinite :  the domain where any finite line segment consists of infinitely many finite units. So there there exists a true distinction between rational and irrational lines.]. They, however, do (all) have a common measure, and are thus commensurable, in the absolutely  undetermined  infinite, because the absolutely smallest infinitely small [entity] is the absolute zero -- the last part [and thus the common measure] of the rational as well as of the 'irrational' line. [So here, i.e. in the absolute continuum, they are not distinguished].
Petronievics, p. 278, adds to all this :
Arithmetically this commensurability of the irrational and rational straight lines in the absolute continuum is expressed by the fact that every number, and thus the rational as well as the irrational number, can be written as a converging infinite series of members reaching its limit value only at absolute infinity [i.e. the members of such a series more and more approach the corresponding number, until, at absolute infinity, they finally obtain this value] [As to irrational numbers, the possibility of expressing them as a converging series is directly clear, for instance as to the number [SQUARE ROOT]2, but for rational numbers this also holds :  for instance, 5 = 4 + 1/2 + 1/4 + 1/8 + 1/16 + . . . . This series progressively approaches 5.].  [Petronievics refers to a note (at p. 280) about the infinitesimal method].
In the absolute continuum rational and irrational magnitudes, respectively segments, qua type coincide in just the same absolute way (in the absolute continuum) as do circle and straight line [i.e. at infinity the straight line is a circle, because its end points meet there, and so the straight line is closed], and just like here the straight line becomes a circle, also the irrational segment becomes rational, and thus the specific distinction between rational and irrational lines vanishes. So with their reality the irrational straight lines obtain in the continuum also rationality.
When, however, space is discrete, there is no common measure between the rational and irrational magnitude anymore, the irrational straight lines can only have an imaginary status there, and in this way the geometry of the discrete is really able to account for this important space-fact of incommensurable straight line segments, whereas continuous geometry is with respect to this totally desperate. [Discrete geometry can explain the occurrence of irrational line segments by means of considering the nature of touching of points, this touching resulting in a non-zero unit distance, which then is the ultimate measuring unit of spatial extension, and because this unit is not infinitely small, is not a mere point, it makes incommensurability of certain line segments possible.]

The  general presupposition  wherefrom we departed -- when discussing coincidence (qua type) of rational and irrational straight lines in the absolute continuum (and also discussed the coincidence of circle and straight line (at infinity), and also the intersection (at infinity) of parallel lines) -- was that the limit value of a variable magnitude can only be reached in that absolute continuum. And this presupposition is then also the principle of explanation of the infinitesimal method which is in such a need for an explanation and justification. The limit value of a variable magnitude cannot, if infinite divisibility of it is presupposed to be possible, be reached as long as this magnitude is finite. It also cannot be reached if it is determined infinite. It can only be reached when this magnitude is simply undetermined infinite, i.e. if it is continuous. Petronievics, p. 281, now is going to explain this (in a note) :

I  [Petronievics] first of all will make this clear by means of a very simple example.
The infinite sequence

1/2 + 1/4 + 1/8 + 1/16 + - - - - - = 1

has the limit value 1, i.e. the sum of the members of this sequence is, at infinity, equal to 1.  [The fractions become progressively smaller, they approach zero :  1/OMEGA.]

[ We indeed can compute the sum of this sequence :

Suppose that this sum is equal to x. Then the following derivation holds :

1/2 + 1/4 + 1/8 + 1/16 + - - - - - = x, implies
1/2 [1/2 + 1/4 + 1/8 + 1/16 + - - - - - ] = (1/2)x, and this implies
1/4 + 1/8 + 1/16 + - - - - - = (1/2)x, implying
1/2 + 1/4 + 1/8 + 1/16 + - - - - - = (1/2)x + 1/2, implying
x = (1/2)x + 1/2, implying
(1/2)x - x = -1/2, implying
-(1/2)x = -1/2, implying
(1/2)x = 1/2, implying
x = 1

So if we could (and actually did) finish the whole sequence [by adding fraction after fraction], then we would obtain a summation of infinitely many fractions, but we cannot finish, so we remain, in following the sequence, to have handled only finitely many fractions, that is :  undetermined finitely many fractions. And the addition of all these fractions would, if we had finished, result in 1  (what we know as a result of our computation, well, not actual computation, but derivation).
OK, so we have the sequence 1/2 + 1/4 + 1/8 + 1/16 + - - - - - = 1, in which 1 is its limit value whereto the sum of the sequence progressively approaches. ]

As long as this sequence  1/2 + 1/4 + 1/8 + 1/16 + - - - - -,  in following it, still is  finite, the limit cannot be reached. There always is a fraction yet to be added to the sequence thus far in order to obtain the sum = 1.  In fact what Petronievics says here is  "that as long as we, in successively adding fractions (or counting them, indexing them), have not yet reached OMEGA, the sum, determined so far, still does not equal 1.  There always will be (how far whatsoever we have already progressed towards OMEGA) at least one finitely small fraction larger than zero that has to be added in order to obtain the sum = 1".  The sequence  1/2 + 1/4 + 1/8 + 1/16 + - - - - -  is undetermined finite (=  potentially infinite).
Evidently, the same holds also in the case when the sequence (as to the number of its members) is  determined infinite [i.e. we saw that it was true of the undetermined finite, but it is also true of the infinite when it is determined-infinite], except that now the fraction to be added is  infinitely  small (not finitely small), infinite(ly) (small), that is, with respect to a certain order of infinity. [If the sequence, as to the number of its members, is of a  determined  infinity, then it concludes itself (i.e. comes to a closure) in some determined higher order of infinity. And as long, in following this sequence, as we are still before that higher order of infinity, at least one fraction has still to be added to the sequence, just like the first case (1 ==> OMEGA), but in the present case (the case in which the sequence is determined infinite) the fractions to be added are infinitely small, infinite(ly) (small) of the previous order of infinity. But also these fractions are  bigger than zero. So also such a sequence (a determined infinite sequence) cannot entirely be traversed, despite the fact that it is closed (at the infinite of a certain higher order).
If the sequence under enquiry is undetermined finite, as is the sequence 1/2 + 1/4 + 1/8 + 1/16 + - - - - -, then the elements become progressively smaller but remain  f i n i t e l y  small, whereas in a determined infinite sequence the members have already gone through one or more orders of the infinitely small (involving, say, fractions like 1/[3 OMEGA]) before ending up at the last, i.e. determined last, order of the infinitely small, the true limit. So the only difference with the first case (undetermined finite) is that now the elements are already infinitely small even before reaching the very limit.]

Only in the  undetermined  infinite (thus when the sequence contains undetermined infinitely many members) the fraction to be added will at last be zero, meaning that we have reached the limit  [In an undetermined infinite sequence the latter never comes to a close in whatever order of infinity, and only then the fraction at last to be added can become zero. Perhaps we should [try to] explain this further :  The sequence 1/2 + 1/4 + 1/8 + 1/16 + - - - - -, taken to be undetermined finite, how far whatsoever we think it to be extended, does not  contain  any fraction that is equal to zero, so the limit, 1, will never be reached, the sum of the members of the series IS never equal to 1.  If this series is taken to be, instead of undetermined finite, determined infinite, whatever that may mean here, then also in this case the series does not contain 0, because somewhere in some order of infinity the series is closed, it doesn't extend further in order to reach 0.  Only a supposed undetermined infinite nature of the sequence extends beyond all limits, beyond all determination, and thus it really contains zero, i.e. the series is so long that its members actually become zero, 0/1 (= 0) and then no further addition, say of fractions such as 0/2, 0/4, 0/8, is needed anymore.]
In the undetermined infinite the limit, which is 1 -- (the sequence 1/2 + 1/4 + 1/8 + 1/16 + - - - - - now, rightly or wrongly, taken to be undetermined infinite, but in all cases the limit, the sum, of the series is 1, and the corresponding limit, namely as to the magnitude of the fraction to be added, is, also in all cases, zero) -- not merely (and unlimitedly closely) is approached, but is really and absolutely reached. [In the undetermined infinite it is not so that we always are still at a distance from the sum = 1 :  At a certain moment (stage) the difference between the sum-until-then and 1 is equal to zero, the limit is then reached. This can, however, only be the case in an  absolute continuum (and in the infinitesimal calculus the undetermined infinite, the absolute continuum, presupposed, and thus the limit can be reached).]. So the limit is reached precisely because then the infinitely small (as to the value of the fraction to be added) of the last order of infinity has really become zero (and cannot become still smaller), and [the limit being reached) not in the way [not caused by the fact] that the infinitely small of a certain order of infinity (the first, the second, etc.) is zero merely relative to the finite (which would mean that it is zero merely as compared with the finite (here, a finitely small fraction).
Because the sequence is [taken to be] undetermined (infinite) we not only arrive at the end of one or another order of infinity but at that of the true last order [And this last order is not as such determined, the series goes beyond every order of infinity whatsoever, and therefore it can and does contain the number 0].
This most simple case [namely of the series  1/2 + 1/4 + 1/8 + 1/16 + - - - - -] demonstrates how we, also in all other cases, must think of the reaching of a limit of possible variables, and how the determination of such limits by means of the infinitesimal method may be justified (Petronievics, 1904, p. 281)  [Such, for instance, the value of the derivative of a function of x, (F(x)) :  when x + h approaches x (and thus h to zero) the rate of increase of the function (its rate of change) tends to a particular value at x, the derivative in x of that function.]

For us [JB] to dwell a little longer at the above simple example, and still further consider the status of rational and irrational straight lines in the continuum and in the discretum :

Every number, whether rational or irrational, can be written as a converging infinite sequence (converging to that number) of members reaching their limit (in the case of the sequence 1/2 + 1/4 + 1/8 + 1/16 + - - - - - the number 0) only in the absolute (undetermined) infinite (domain).
So every number in fact consists of a sequence of numbers, or, is a sequence of numbers. And it is clear that in the case of the finite, i.e. the undetermined finite, (when we are, in 1 ==> OMEGA, still before OMEGA) any two such series (for example 4 + 1/2 + 1/4 + 1/8 + 1/16 + - - - - -, and 1 + 1/2 + 1/4 + 1/8 + 1/16 + - - - - -, respectively expressing the numbers 5 and 2) does not possess a common measure, because continuing decrease of the value of the fractions prohibits to yield an objective measuring unit. Also in the case of the series being [taken to be] determined infinite, no such measure is yielded. Here the infinitely small fractions become progressively smaller still, but without resulting in an indivisible end-element. And only in the undetermined infinite, that is in the absolute continuum, in following the sequence up until the undetermined infinite, we find this common measure, the 0, because such a series (as to the value of its members) actually goes all the way down to 0, in turn because it actually contains it. So both numbers, 5 and 2, in our example, expressed as converging series do have a common measure (in both cases it is the zero), and because we here find things in two randomly chosen finite numbers, the result applies to all numbers [in fact the result universally applies to all numbers because all numbers can each be written as a converging series] :  In the absolute continuum (where we thus have to do with undetermined infinity) there is no difference of type between rational and irrational numbers, and also not between rational and irrational straight lines [because consideration of measuring straight lines and judging their infinite/finite status can only be done by involving numbers]. This difference is present only in discrete space. In the absolute undetermined continuum in the limit (that is, at last) the rational and irrational number, and so also the rational and irrational line segment, as to their type coincide, i.e. in the limit they all are, or become, rational, just as the coincidence in the case of the circle becoming in the limit a straight line.
In the undetermined infinite of the absolute continuum the specific distinction, to say it once again, between the rational and irrational line has been lost. With their reality the irrational straight lines acquire, in the continuum, also rationality. If, on the other hand, space is discrete, then there is no common divisor (measure) between the rational and irrational magnitude anymore, the irrational straight lines can only have, as to their reality as a line, an imaginary status in such a discrete space. They do not fit in such a space, because their length is not compatible with the space's measuring unit. And so the geometry of the discrete, "discrete geometry", is really able to account for the important space effect of the incommensurable line segments, while the geometry of the continuous is desperate in this respect. [Of course, in considering the "common measure", the zero, of all line segments in continuous space, it is so that one cannot actually measure and compare the length of lines by using the zero as a measuring unit. It is only found out that in the limit the distinction between rational and irrational lines vanishes, because in truly continuous space there is such a limit, and therefore it can be reached, and in this sense the limit is zero, it is the final difference between aproaching entities in the continuum. So indeed, all lines in continuous space consist of points and only of points, and moreover, all these points are of the same nature. And this renders all lines compatible with one another (and thus lines of all lengths relative to one another can exist in such a space). In discrete space there is no such zero, it has a last indivisible finite measuring unit making the difference, the incompatibility, between rational and irrational lines possible.]

Also the regular polygon in the limit of the undetermined infinite turns into a circle when the sides become smaller and smaller. And so also the straight line, turning into a curve :  [In a true continuum there can be punctual directions, i.e. directions in individual points of a curve :  derivatives. An thus these derivatives may be different in every next point of a line resulting in a true curve, i.e. smoothly curved line]. So it is without doubt that smooth curves (in contrast to straight lines or broken lines, zigzag lines) can only exist in the absolute continuum, whereas they are completely and absolutely absent in the discretum. If this, however, is true, then it means no more and no less than that the curved lines do not constitute a general geometric fact independent of the structure of space, as is the case with irrational lines :  A rectangular triangle of which the one cathetus is twice as long as the other has a hypotenuse  h  which is irrational :  1² + 2² = h² implies h² = 5, implying that h = [square root]5, independently of the fact whether space is discrete or continuous, and thus constitutes a general geometric fact. But when space is continuous one cannot give an  explanation  of the irrationality of the hypotenuse of a rectangular triangle, because in continuous space the irrational lines cease (in the limit, i.e. considering space at point level) to be different from rational lines, they become rational [that is, during the explanation, when descending into the infinitely small, i.e. considering space at its basic level, the difference between rational and irrational lines vanishes, and thus the explanation]. But a geometry which cannot account for such a fundamental fact must definitely be in error in its fundaments. Discrete geometry certainly can account for that fact. On the other hand, from the inability of discrete geometry to explain the alleged fact of curved lines [i.e. we can think of them and 'see' them, at a macroscopic level] one cannot conclude to its invalidity, because this would only be the case if curved lines also were independent of the actual structure of space as are irrational lines [in every type of space incommensurability may occur, but as to continuous space considered at its most basic level, its points, the incommensurability (in the sense of incompatibility) disappears]. Curved lines are, however, as such only given in continuous space, whereas in discrete space they are completely absent. Accordingly, they do not constitute a geometric fact that is completely independent (of the type of space). They are possible only in continuous space, that is in the spatially extended continuum (Petronievics, 1904, p. 280). In the case of curved lines the continuum is presupposed, and so cannot follow from the existence of curved lines, while the fact of irrational lines renders such a continuum impossible (because the continuum cannot explain such lines [because, again, they vanish as such at the very basis of continuous space], while the discretum can).

With all the foregoing we have now given a good impression of the difference between discrete and continuous space and of certain properties of discrete space. The next discussion summarizes things about the essence of extension in discrete space as we have learned it from Petronievics, and expounded in the foregoing. It will consolidate the reader's picture of discrete space as the matrix of all material reality.

The real, i.e. qualitative content-possessing, points ("monads") of  discrete gapless space  are separated from one another by a unit distance = 1.  If this unit distance were 0, then all the points would coincide. Well, the points do not coincide, but 'touch' one another, i.e. they are at a minimum distance from one another. So there must be something that actively prevents their coincidence, and this is realized by the so-called  negation-acts. Now, as to the spatial distance of points in a point-net, we have a problem :  If we, for simplicity's sake, limit ourselves to 2-dimensional point-space and in particular to the example of triangular point-space (= hexagonal lattice), then we have to do with repeated geometric settings as this one :

The red lines symbolize the unit-distances of the points A, B, C, and D of a small piece of the hexagonal space point-net. These points are real points possessing qualitative content. The minimum distances are all equal to one another, they are all 1, therefore the triangles are equilateral triangles. Indeed, because the points of discrete space lie at the absolutely minimum distance from one another, i.e., in considering only our depicted fragment of discrete space, point A from point C,  A from B,  B from C,  B from D,  and C from D, we can legitimately say that these points 'touch' one another (contrasting with their coincidence). They are separated from one another, not by yet other points, but by real negation-acts. And precisely because these negation-acts are themselves not spatial points they reside outside space itself. But with all that we now have a problem :  How things are as to the distance between A and D? Clearly, they are at a distance from one another that is greater than the unit distance, but not at a multiple of it, as is, for example the distance between the points A and E :

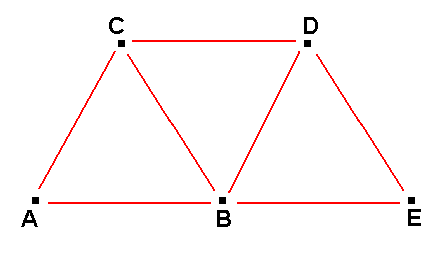
This would imply that this two-dimensional space contains gaps, voids, and so not complying with its definition (gaps in gapless space). In solving this problem we should well distinguish between the relationship with one another of the points A and B,  A and C,  B and D  on the one hand, and the relationship between the points A and D on the other (see Figures) :

• Points A and B (and points B and C, etc.) immediately touch one another, they thus touch primarily.
  Points A an D touch one another mediately, that is, through B and through C, and thus touch secondarily. And the points A and E do not touch one another at all.

• The distance between the points A and B (and between the points B and C, etc) is real, and the line defined by A and B is a real line. And, of course also the line AE is real, consisting of two real unit distances.
  The distance between the points A and D is imaginary, implying that the line, defined by A and D, is imaginary too.

• The points A and B (and the points B and C, etc) are spatially separated from one another by real negation-acts. And negation-acts themselves do not belong to space, i.e. they are not space-points.
  The points A and D are not being separated by any negation-act, because they are already separated from one another by the points B and C.

A negation-act separating two points from one another is, at both 'sides', immediately connected with, and (qualitatively) separated from, those two points. Such a negation-act is not present 'between' the points A and D.  And so the spatial distance is here (i.e. between A and D) nothing more than a formal relation, a relation without actual content. It is a collateral effect of the constitution of point-space, a space with points that primarily touch one another, meaning that the fact of primarily touching implies the occurrence of secondarily, imaginarily, touching. And the imaginarily touching of certain points moreover involves a distance greater then (but no multiple of) the unit distance, and so IS in fact no distance at all (because it is not made up of one touching event nor of a concatenation of them). So between the points A and B we have a distance 1, and between the points A and E we have the distance 2, but directly between the points A and D there is no distance.

Discrete geometry, if it wants to be consistent, must recognize the difference between real and imaginary touching of points. In all this, most imaginary straight lines (as between A and D) are with respect to the real straight lines imaginary magnitudes. Above we saw that AD is equal to [square root]3 and thus is irrational with respect to the unit distance.
In discrete space all imaginary straight lines, geometrically connecting two real points (such as the line AD) are, as to their length, greater than 1.  And only imaginary straight lines can be irrational (Petronievics, 1904, p. 274), whereas the real straight lines can originally be taken only as rational straight lines [If we take some irrational straight line segment as a basis of comparison, then the real straight lines will become irrational, but we do not do this because the real lines form a natural object to compare things with. In discrete space irrational straight lines are imaginary and therefore not real. In continuous space, on the other hand, the irrational straight lines are real (as well as the rational ones), but (in the limit) not distinct from rational straight lines].

We have now arrived at the end of our treatment of the interesting ideas of Petronievics, 1904, as to the discrete nature of the very bottom of material reality. That bottom is a gapless discretum.
In what follows we integrate the results into our theory of the Explicate and Implicate Orders, and close our discussion with some notes about Time. In this we should realize that space and time are only present in the Explicate Order. And in that Order there are no dimensions of intensity, they reside in the Implicate Order. In the Implicate Order there are no extensive dimensions, but this does not mean that all its dimensions are intensive. There are also purely qualitative dimensions, grading different qualities (as they are coded in this Order) from one another.

The discrete nature of the Explicate Order, the Order of space-time reality, which nature here consists in the arrangement of quality-points in a regular space-point network, is perhaps a direct reflection of the nature of the Implicate Order (the Order in which space and time dimensions are enfolded, i.e. not extended), which Order ultimately consists of natural numbers (as we have explained in an earlier document (Theoretic Intermezzo) which also are discrete. And series, each consisting of successively increasing natural numbers in the Implicate Order may form the intensive counterpart of the metric aspect of the extensive in the Explicate Order.

The assumption of space as being discrete has no effect on the forms (angles and directions) as seen in the macroscopic world, because the points of discrete space lie sub-sub-microscopically close to one another (at one unit of extension), so that every macroscopic geometric form can result from them (as we see it also in computer images, that are at their very bottom also discrete).

Space, (explicate) reality, as (1) consisting of quality-points, which are spatially immediately adjacent to one another (as a result of extra-spatial negation-acts) and (2) the quality-points having a magnitude, not of 0, but of 1 (as also the 'gap' between them), seems to be nicely matching up with the theory of Fredkin saying that (material) reality is the display window of a universal cellular automaton, which is constantly being updated. With all this in mind we shall now take a closer look at the dimensional structure of the Explicate and Implicate Orders.
The Explicate Order is at its most fundamental level (below that of Substance in the metaphysical sense) a system of quality-points separated by extensional negation-acts, i.e. acts realizing extension. The Explicate Order is ordered along three extensive dimensions.
The Implicate Order is a system of points (i.e. of natural numbers) separated by intensive and qualitative negation-acts. 'Perpendicular' to the Explicate Order, in the Implicate Order there are intensional dimensions of qualities (as to their intensity). 'Perpendicular' to these dimensions are qualitative dimensions, grading different qualities from one another. For each different quality there is a corresponding intensive dimension, and these dimensions themselves are separated by negation acts, all these in the Implicate Order (in the Explicate Order there are spatial negation-acts as discussed earlier). Also the 'points' in each intensive dimension are separated by negation-acts. All this implies that the Explicate and Implicate Orders are discrete gapless spaces (in the Implicate Order, noëtic space, this is the 'space' of the natural numbers).
For any difference, such as difference of (i.e. as to) spatial distance, difference of intensity, difference of qualities, that may as such become infinitesimally small, negation-acts exist to prevent such a difference to become zero, resulting in smallest indivisible differences rendering the relevant space [i.e. the range of difference, and thus the dimension) to be discrete. The negation of a given quality A results in a quality non-A. What this non-A quality positively will be (B, C, D, etc.) depends on other factors. A point X on the intensity scale dimension (in the Implicate Order) of quality Q is projected into the Explicate Order as a point on the extensive scale dimension of the extensive effect of quality Q in the Explicate Order. So the Explicate Order has only extensive dimensions of various quantities.
The Implicate Order, noëtic space, has an intensive dimension for each true and simple (i.e. elementary) quality. And such a dimension is, as has been said, separated from the intensive dimensions of other qualities by qualitative negation-acts acting on qualitative dimensions (along which different qualities grade off from one quality to another). So the Explicate Order being wholly extensive, does not imply that the Implicate Order is wholly intensive :  apart from intensive dimensions there are, in the Implicate Order, also other non-extensive dimensions, namely the just mentioned qualitative dimensions, which are not intensive (nor extensive).

Qualities can be divided into simple qualities and composed qualities. A simple quality is a most elementary positive content. It is the content of our quality-points, it is distributed among such points, such 'atoms of being'. Many such points together make up a composed quality. Simple qualities are the letters of 'text' that itself is form.
Speaking about qualities, heat, for example, is a quality, but not a simple quality (so also pressure, weight, etc.). It is neither the quality (already) of one quality-point nor the quality of an individual particle (itself made up of quality-points). It is the aggregate resultant of the behavior of a great many of such particles. Although heat and the like is not found in single individual particles, it can nevertheless be reduced to the impetuses of the many particles (expounded in earlier documents on natural philosophy). Precisely the additional effect of all these impetuses (each one of which is a, perhaps already simple, primitive, quality with a given intensity, a quality of a particle), and in fact the overall effect of the molecular motions caused, given, by these impetuses, forms the quality "heat" (of some physical body).

All these remarks on the dimensional structure of the Explicate and Implicate Orders and on qualities and their dimensions, are very preliminary. They only serve to stimulate further thinking about extensive and intensive spaces or dimensions and how they could be thought of in a discrete world.
We  conclude our exposition of natural philosophy  with a few more ideas about the nature of Time.

Time is not something by itself (it is not a being), but the "after one another" of things or conditions of things. Now, it could be imagined that every dynamic entity, dynamical system, in the Explicate Order has its own immanent time. In our standard account of time we, humans, have chosen to rely on the planetary motion of the Earth :  about its axis and about the Sun. This system -- Earth-Sun -- then has its own immanent time, and we then compare the course of all other processes with this immanent time of the Earth-Sun system.
But, perhaps, there is something like a universal time, namely when we suppose that the Explicate Order is the expression or result of one single 'world cellular automaton' (world CA) [For cellular automata as particular dynamical systems, see First Part of Website]. But then it is hard to see where time actually comes from :  What then is the 'next moment' (in the CA updating process) at which the pattern of qualities must be so and so  if  the pattern of the 'present moment' is so and so. Of course it may be that the whole world CA (like any other dynamical system) has its own time, and that in this way the world as a whole (the Explicate Order) has its own time. Anyway, it is so that time is not an essence in itself, not a particular being, just as space also is not an essence of its own :  Space and material being coincide, space is the network of quality-points, these points are not in space but constitute space. But everything, every being, is as spatial as is every other being, the spatiality is the same for all, it has no degrees, things do not have their own specific spatiality, whereas every dynamical system may have its own temporality.
If there is indeed a 'world-CA', ultimately encompassing all processes (sub-CA's), then we have, in addition to all the different temporalities, also a universal temporality, one stream of time, one objective universal time. And this matches well with the fact that in the theory of relativity absolute simultaneity is presupposed in the demonstration that it cannot be measured, not be observed (We have expounded this in some earlier document of the series on natural philosophy in present Part of Website). Absolute simultaneity in turn presupposes absolute and universal time.

When we want to define Time, then such an attempted definition always contains something that presupposes temporality, and thus time cannot be truly defined. Also the process of change in things has its own temporality because change already contains the temporal, rendering it impossible to define time in terms of change. So we can only say that while the spatial is the togetherness of things or parts of them, the temporal is the after-one-another of things or their parts, but this "after one another" also again includes the temporal (like the "being together", the adjacent, presupposes the spatial). So time, and also space, are the ultimate forms of ordering things, and they are not essences all by themselves, the ordering comes from the very things themselves.
The parts of time are evidently given after one another, there can be no togetherness of its parts. And it is by reason of this that time is not infinitely divisible, because ever ongoing divisibility implies ability to be together :  Time must consist of ultimate absolutely simple parts, i.e. time must be discrete. For if a given part of time would in turn be divisible, then these parts cannot be together but only after one another, so that a given divisible part of time cannot exist. The indivisible ultimate part of time, which (part) can exist, always is the NOW moment.
According to Petronievics, 1904, every NOW moment is separated from the previous moment by a transformation act :  The previous moment does not exist (anymore), while the (new) NOW moment exists. The NOW moment is also separated from the next moment because this does not (yet) exist. Also the transformation act, always at both sides of the NOW moment, cannot be divisible, for if it were divisible, then its parts would either be together, which is impossible (because then it is not about change), or (the parts of the transformation act) be after one another, but then one must admit that always only one such a part is actually given, so that ultimately every such part is a simple indivisible transformation act. Of a series of contiguous transformation acts only one (act) 'at a time' is given, and this one act yet changes the NOW into the PREVIOUS, which is the same as the change of the NEXT into the NOW. So the transformation act is indivisible, and time is then a concatenation of NOW moments and transformation acts, in which we may take each NOW moment quantitatively = 1, and each transformation act quantitatively = 0.

Having, in discussing discrete space, "finished the infinite", and having dealt with the very bottom of Reality, it is now perfectly appropriate to let our entire Website (consisting of six chief Parts) end here.
Readers may find the chief theory in it (noëtic space, noëtic evolution) interesting for further development, or may be fascinated by the phenomenon of holism, to which many a page of this Website is devoted. Generally, he or she may continue the search for natural pattern in crystals as well as in organisms, or wherever it exists.
Although some texts are long and quite difficult, they are, in my opinion, well worth the trouble. Most of them, however, are adapted to the general reader, that is, I've done much to explain things as clearly as possible.
In addition, the Website as a whole contains many points for potential development :  many "side-branches" (of thinking), containing different theoretic viewpoints -- for instance Hartmann's Categories -- might be such further-to-be-developed themes, leading into a more or less other direction than that of the Site's main theory, the Implicate and Explicate Orders. Or, the Website may stimulate further study of fossil insects, evolutionary theory, dynamical systems, the theory of crystals, the theory of Being qua Being (metaphysics) and so on.
Having worked on this Website for almost twelve years, I think I've made a fine cultural contribution to natural philosophy, and I hope it will spark off enthousiasm for studying Nature in all her fascinating aspects, and, with it, the realization of the necessity of protection of natural environments.

Jaap Bax, 7 July, 2011.

Second Part of Website

Fourth Part of Website

Fifth Part of Website

Back to Contents (of Sixth Part of Website)

Back to Part I

Back to Part II

Back to Part III

Back to Part IV

Back to Part V

Back to Part VI

Back to Part VII

Back to Part VIII

Back to first part of theoretic intermezzo

Back to second part of theoretic intermezzo Back to Part IX

Back to Part X

Back to Part XI

Back to Part XII

Back to Part XIII

Back to Part XIV, Dipterygia, and conclusion of flight-devices in insects

Back to Part XV, first part of the theory of inorganic nature

Back to Part XVa, second part of the theory of inorganic nature

Back to Part XVb, third part of the theory of inorganic nature

Back to Part XVc, fourth part of the theory of inorganic nature

Back to Part XVd, fifth part of the theory of inorganic nature

Back to Part XVe, sixth part of the theory of inorganic nature

Back to Part XVf, seventh and concluding part of the theory of inorganic nature

Back to Part XVg, Unimol, theory of the organism as one single molecule (first part)

Back to Part XVh, Unimol, theory of the organism as one single molecule (second part)

Back to Part XVi, Unimol, theory of the organism as one single molecule (third part)

Back to Part XVj, Unimol, theory of the organism as one single molecule (conclusion)