e-mail : ( Please write in  ' Subject '  entry :  ' METAPHYSICS ',  in order for me to be able to distinguish your mail from spam )

In the present document we will discuss the nature of  "motion and time", largely as expounded by HOENEN, 1947. Motion and time are closely connected with space, but not necessarily in the way as many authors see it. Space, as well as time are not independent beings or essences. They are, both in their own way, conditions of certain fundamental properties of things and processes. The question whether time, space, and process, are discrete or continuous is not, or at least not at length discussed by HOENEN. We ouselves will do that later.

For we have to distinguish two groups. All change is a transition from a starting-point to an end-point. These two must differ from one another -- otherwise there would be no change at all -- must stand in opposition to one another. If this opposition is one that is called  contradictory,  i.e. an opposition of confirmation and negation of the same entity, of "being" and "not-being" of something (in which "being" has strictly the same sense in both cases), then the transition from starting-point to end-point necessarily takes place in one indivisible moment, because between "being" and its strictly contradictorily opposite "not-being" there is no intermediate. If, for instance, two spheres approach each other, then this motion is gradual. But if they, after having moved for some time, hit each other, the transition from "not-hitting" to "hitting" is instantaneous. If a body switches from the condition of rest into that of motion, this transition is again instantaneous. If a living organism dies, the very transition from living to non-living takes place in an indivisible moment, it is a transition from "being" to "not-being". The same must hold for every change as to substance [= substantial change, i.e. change of one given substance (in the metaphysical sense) into another], of which the dying, the disintegration, of a living being is just one case among others [these others may be, for example, the disintegration of a crystal or of a molecule, both being (inorganic) substances]. To all such changes applies :  If A transforms into B, then the transition consists in nothing else than in the "being" of B immediately after the (ceasing) "being" of A.  But matters are different, as we shall see, in continuous change, motion.
We already have discussed many features of "motion" in  Part XVb of the present series.

Starting-point and end-point may also be opposite to one another according to, what in logic is called :  a "contrary opposition" (in a strict or broader sense). This is the case when the changing entity must, between starting- and end-point run through yet other phases as well. In the cases we have to consider, there is a continuously infinite range stretched out between both extremes ["infinite" here means that the range, lying between the starting- and end-point of the change, is infinitely divisible, i.e. we can keep on dividing that range without ever running against some last indivisible, simple, but still extended, part or unit of it.]
The most evident example of such a change is local motion :  Starting-point and end-point necessarily lie at a distance from one another (except in motion with a closed trajectory), and, how small this distance may be, it is a continuum and thus divisible ad infinitum. The motion along this (open) trajectory shares the continuity of the trajectory itself. It also is, and in the same way, divisible [not divided] ad infinitum. Indeed, motion is possible from the starting-point to the end-point, but also to every intermediate point, and between any two arbitrary intermediate points. But the same continuity we can find in qualitative change :  heating or cooling, increase or decrease of a tension, or of the impetus, which we, in  Part XVb, learned to know as a variable quality. In all these cases, degrees of intensity are possible, and two different degrees of intensity of a same quality always lie at a certain "distance" from one another, i.e. intermediate intensities are possible, and this also ad infinitum [Although we can, as it seems, experience (sense) intensive dimensions (such as that of heat and light), we cannot actually see them. So for an actual and precise measurement of the intensity of a given quality we must resort to its extensive effect or cause. And perhaps also our sensing of an intensity is in fact experiencing the quality's extensive effect or cause.]. Now, a qualitative change in the same way shares the continuity of the intensive dimension. So it is, as is local motion, divisible ad infinitum. Something similar is to be found in quantity, extension, which is continuously variable as a result of (thermal) expansion, shrinking, or of change of shape. These three types of continuous change have been meticulously studied already by Aristotle. He calls them, when strictly using his technical expression,  kinesis.  The technical term of the scholastics is  motus.  The Englisch word "motion", which is the translation of these terms, is only used to indicate local motion. So in Aristotle and the scholastics the corresponding term has a broader meaning. It then refers to every [type of] continuous change. In the present document we too will use the word "motion" in this broader sense. So a continuous qualitative change is also a motion. Change of place is then  local  motion. If we need an example for reading off the features of motion, local motion will do.

Motion,  i.e. the "flowing", or "dynamic", or "successive"  b e c o m i n g ,  brings with it all the problems of the continuum already discussed earlier  ( Part XV (present series) : "Extensionality", metaphysical analysis of the continuum ).
[There, the continuum was defined while taking it, not merely as a continuum, but as an  ens continuum (i.e. not as a mathematical idea, the mathematical continuum, but as a real being). And so the definition of this particular kind of being, of this "ens continuum", was said to be :  an extensum [= a spatially extended thing] that intrinsically is one.  And this implies that every material substance (in the metaphysical sense) is a continuum, because every such substance is -- one is inclined to say by definition -- intrinsically one, i.e. one single ens or being. And this further implies that a substance does not consist of individual material parts (otherwise it would be a many), but of potential parts, provided this view of substance is correct, and, moreover, if such substances do really exist and are really and objectively distinguished from non-substances, i.e. aggregates (of substances). So apart from these latter things, the "continuum taken as extensum-that-is-intrinsically-one" will not be problematic, because as such, no (actual) infinity is involved. The mathematical continuum, on the other hand, is problematic, because of infinities being involved.
There (in Part XV) it was said also that  the parts of a true continuum do not exist  a c t u a l l y,  but are only  p o t e n t i a l l y  present in the one continuum, itself existing actually.  This further implies that the number of these parts is potentially infinite which, however, is the same as :  undetermined finite.]
We, indeed, considered the continuum (in Part XV) while discussing the extensum, which especially there was seen as a "resting", or "static", or "permanent" continuum. So we here presuppose what was discussed earlier. And the "flowing" continuum also has its own problems, to which we now turn.
Like we were able to develop a metaphysics of extensa from considering continuity, we will now, from the continuity of motion, also be able to penetrate into the philosophy of motion. As an example of "flowing becoming" [continuous change] we, as has been said, may, as a rule, take local motion. With some exercise one may read off all this from the growth or from the origin of a quality.
Soon we will find a theorem, discovered in considering static continua, also valid for dynamic continua. There we found namely that a line cannot be constructed of [is not constituted by] a concatenation of points :  Concatenation of nothing (the extensive nothing, which is a point) to nothing cannot result in something (the extensive something). The same applies, by the same reason, to motion of every kind ["motion" always taken as continuous change] :  Rest added to rest does not result in motion, "flowing" is not a sum of (stationary) states. One might believe that motion results as sum of  transitions  between (stationary) states. Here, one of two things hold :  Either those states differ (two points on a line, two degrees of an intensity), or they do not differ. In the first case a transition is possible, but every such a transition still is in the same way a flowing continuum, and still in the same way composed as is the whole, which we want to construct from them. Between every two degrees or points always lie others, indefinitely. In the second case [states do not differ], however, there is no transition, and in this case one would yet again want to compose the something, the continuous motion, from the nothing-of-flowing-extension, which is the stationary state.
For understanding motion, this is an important result. First, we here see the large difference with a change between two contradictorily opposed states (which change cannot be continuous). To understand the transition between these [contradictory opposed states] and to describe it, we only needed :  the "being" of A, immediately followed by the "being" of B, into which A is transformed. The first "being" may be static as well as the second. And the transition itself does not suppose a new, a third "being", a "dynamic being", different from the first two. Not so in the case of a continuous, flowing motion. This type of motion, apparently, cannot be described as a series of consecutive stationary states [because in continuous motion there are no stationary states]. In addition to the stationary state, the static "being", that is the starting- and end-point of the motion (or some "intermediate "being" which results when the motion is interrupted, and thus is being "divided"), we need a special "flowing being", a "continuous becoming", in order to understand and describe motion [i.e. the segment lying between starting- and end-point of the motion wholly consists of continuous becoming]. Therefore, the following description of motion, often encountered, namely "motion is the occupying of different places (states, degrees) at different times or moments", is completely false. It neglects nothing less than the deepest essence of motion :  the "flowing being", which is continuous "becoming".
[Indeed, here, the nature of motion is derived from continuity, i.e. continuity is presupposed and from it follows the 100 percent "becoming" that takes place during motion, to which interruptions (stationary intermediate states) do not as such belong. Earlier, in  Part XVb, section "Motion" (about halfway in the document),  we have described "local motion" in the case that continuity (of motion, space and time) is not only not presupposed, but denied. Space and time, and consequently motion, are taken to be discrete, i.e. consisting of non-zero indivisible units. And then the nature of motion is quite different :  It is an alternation of (1) stationary states and (2) the act of motion itself, [these two] separated by so-called negation-acts (by which the state of rest (stationary state) is negated, resulting in the act of motion, and the act of motion is in turn negated, resulting in the state of rest, etc.). This is supposed to take place at the lowest level of Reality, where Reality consists of a point-net (representing space), where the points are the locations of primary qualities. In this discrete space (where space is derived from real things, i.e. constituted by their extensionality) motion goes from net-point to net-point as a result of the change of the qualitative content of the respective net-points (together forming the "trajectory" of the motion).
At the more macroscopic level of Reality we may stick to the "continuity" of motion, and most other things as found out in natural science (and in Aristotelian-Thomistic metaphysics).]
Let us, in the present discussion (following HOENEN), hold on to this result :  Motion cannot be a sum of (stationary) states, of points, of degrees, and also not a successive sum [increasing while we follow out the motion]. Motion is not "being" allegedly representing a collection of successive  static  existences. Motion is an existency all by its own, a real, but pure, "becoming", a flowing "being", that cannot in any way be reduced to static "being". It surely is connected with static being, though. And this is the big difference between Aristotle's theory and that of Heraclitus (Greek philosopher, 544-483 B.C) or of Bergson (French philosopher, 1859-1941) who has so much emphasized the dynamical character of motion, but missing this connection. Indeed, the flowing "becoming" has static "being" as its point of departure, and this "becoming" only needs to stop in order to let result a static "being". The great merit of Aristotle, in his analysis of motion, is the discovery of this "flowing becoming", not reducible to "static being", but nonetheless leading to a "static being" as to its end-point, and surely to this end-point not only as to its boundary (peras), but as to an end (telos) at which the motion is  aiming  with a passive striving in the motion itself, and active striving in the effective cause, as we will see below. Motion is a "striving" toward a "telos", a goal, because it cannot be constituted of static elements. It is passive, because it is a "becoming" [in which consists this constant "aiming", in fact the "being aimed at".].  [We might think that "being" is a limiting case of "becoming", and that during motion this limit is not reached. It is only reached when the motion ceases.]

Thus we find in motion the unity of continuity [the constant "becoming"] which it derives from the "trajectory" which it describes, in which the word "trajectory" may have its usual meaning so that the motion is local. It may also be used to indicate the possible intensity-range of a quality [not the whole range, but the set of consecutive values, intensities, assumed by that quality.], or to indicate the successive values in the quantity-interval of an extensum [when it expands or shrinks]. Then the motions are changes of quality or quantity.
Considering the permanent continuum, we already said that one is not always able to experimentally observe whether a given extensum is a continuum or a system of two or more contigua. Indeed, if they are genuine contigua, being thus in strict contact with one another, the eye cannot distinguish the boundary between them. So then this system of contigua does, to the eye, not differ from a continuum. Nevertheless, the intrinsic difference is vast. It is the difference between intrinsic unity and intrinsic plurality which [latter] only forms a mere extrinsic accidental unity. But how many contigua there may be, out of which the system is constituted, it must necessarily consist of ultimate  extensa,  which themselves are genuine  continua [Upon division one finally arrives at the last constituent contiguum, and this is itself a continuum], otherwise an extensum could be built up from (or would be constituted of) a sum of non-extensa (points) which is absurd. All this derives from the nature of the continuum as such, and so must also hold for motion. So also in the  flowing  extensum one will not always be able to determine whether it is a series of motions immediately following upon one another (and thus a system of contigua, extrinsically one, intrinsically an actual plurality), or one single motion (thus intrinsically one, a continuum). But this is certain :  If a motion is given, then it is itself either continuous, or it ultimately consists of a group of immediately consecutive motions, which are each for themselves continuous, intrinsically one.
Such a continuous motion thus is an intrinsic unity, containing a multiplicity of [potential] parts [in the sense of being divisible]. So here the main thesis of continua is valid, a thesis derived earlier :  This unity is actual, factual, while the multiplicity is merely potential, is in tendency. Otherwise, the continuum would be destroyed by internal contradiction. The multiplicity of the one single motion is not a "being divided" but only its  divisibility,  just as in a static continuum. Just as Aristotle's notion of potentiality, as we saw earlier, is the key to solve all antinomies of the continuum in general, documented in the history of philosophy, it will also provide the complete solution of all the objections brought against the possibility of motion [continuous change]. But before we deal with these, we must first consider two other questions connected with this unity.

Internal consistency of the continuum.

Here is the place to insert, into the course of discussion - following Hoenen, a short consideration about the very possibility (internal consistency) of the continuum as it is taken by Hoenen. For this we ask whether the continuum (mathematical and physical) is composed or not, and whether it has ultimate parts or not. Further, if there are such ultimate parts, do they have a non-zero size?. If so, we have to do not with a continuum anymore, but with a discretum.
A composed thing which is real draws its reality from the reality of its parts. So here the parts are prior to the whole. But then there must be parts that should be called first, or ultimate parts, because a going back without end along the conditions that must precede in order for the result to be accomplished, is impossible. So there must exist first parts. In the case of a  continuum  these ultimate parts cannot have extension anymore, they must be points, otherwise they will contain parts and are thus not the ultimate parts. So because it is a continuum, its ultimate parts must be points. But points cannot, all by their own, constitute something that has extension, and a continuum has extension. Hoenen, following Aristotle, solves this dilemma by stating that in the continuum the whole is prior to its parts, because the whole is actual (exists actually) while its parts are only potential (exist merely potentially). So we cannot say that the continuum is constituted by parts (because this would make the parts prior to the whole), and so also not constituted by ultimate parts. On the contrary, the continuum is constituted by itself. It has no actual parts, and thus also no actual ultimate parts. So the problem of extentionless points (ultimate parts) constituting the extensive continuum is solved. The physical as well as the mathematical continuum is not divided, but is divisible. So its parts are not real but potential (not really existing, but only potentially existing), while the whole continuum is actual (actually existing). Characterizing the continuum like this boils down to saying that the continuum is  holistic.
From this Hoenenian position we will now shortly enquire whether all this is sufficient for a continuum to be internally consistent, and thus for it to be able to exist (mathematically or physically). If not, the continuum (mathematical and physical) must be replaced by the discretum.  Let us take the line (i.e. a finite segment of a straight line) as an example. It is, it is true, an example of a static continuum, but the results may very well be valid for the dynamic continuum as well. Is such a finite line-segment a continuum or a discretum? This is to ask, after we know that the line cannot consist of points and only of points, whether the line consists of smallest non-zero indivisible units (which makes it to be a discretum), or not (which makes it to be a continuum).
According to Hoenen any given line-segment consists of a potentially infinite number of parts (here "potentially infinite" does not mean that, upon actualization, this infinite number of parts becomes an actually infinite number of parts, but that, upon division, successively every part, initially merely potential, can be actualized), or, equivalently, a line-segment consists of an undetermined (unfixed) finite number of parts. And these parts themselves are, according to Hoenen, not actual but potential parts. He also has shown that indeed a line cannot consist of points (and only of points), because they together cannot yield any extensive entity. Now, a line has potential parts, implying that we can also say that a given line has potentially, say, two parts. If we now place a point (which is a boundary) somewhere on that line, then we can say that this line actually has two parts (the two potential parts have become actual), instead of merely potentially so. The line, in the present situation, now  consists  of two parts. So, by dividing the line by points, we obtain actual parts of that line, and, by continuing division, ultimate actual parts. Let us state this a little differently :  The parts of a line are not actual but potential parts. But saying that something is "potential" does only make sense if this potency can be actualized, realized, otherwise "potential" would be the same as "non-existent". So we must also consider the actualized condition, and this is the line actually consisting, although not of points, but ultimately of non-zero indivisible line-units, meaning that the line is not a continuum, but a discretum (even so from Hoenenian principles). Well, we know the line cannot consist of points. So if the line actually consists of anything at all, it can (1) either actually consist of itself and only of itself (this is the way Hoenen sees things in these matters), or (2) actually consist of smallest indivisible but still non-zero line-segments. And because, according to the above, it makes sense that the line does actually consist of parts -- elementary line-segments -- the second possibility is the most reasonable (because, as we've shown, a line may, and sometime does, actually consist of parts, and potential parts must be such that they can be actualized). So any line-segment is a concatenation of indivisible but still non-zero elementary line-segments. And these elementary line-segments are delimited by points lying at a minimal distance from each other (and so defining the elementary or ultimate line-segment, i.e. the smallest line-segment). Minimal distance of two points from one another means that the points must touch each other. But then they will, as a result of them having zero-size, coincide, eliminating the elementary line-segment. In order to have a truly minimal distance between the points delimiting the unit-line-segment, we must postulate, following PETRONIEVICS, 1904, the presence of so-called "negation-acts", situated as to their effect between every two such points, negation-acts which prevent the coincidence of these two points. And only in this particular way these two points can be said to touch one another without at the same time coinciding. So in this view, the line, and so also space, does consist of non-zero unit-segments, and is thus a discretum, not a continuum.
Things are different, apparently, when we have to do with a  flowing continuum (local motion, continuous change). It may be that something is a true continuum only when it is flowing, that is, flowing may be the very essence of continuity. And if we assume, with Hoenen, that any given motion is a genuine, true unity, then it has no parts, i.e. it doesn't consist of parts but only consists of itself. So in the case of motion the first of the above two possibilities is the most reasonable, and then we have a continuum that intrinsically has no parts, freeing it from contradictions, and being indeed a true continuum, not a discretum. This certainly deserves further inquiry.

The following reasoning, also starting from Hoenen's results, leads to the same conclusion (space must be discrete) by considering the dichotomy of a line (which is supposed to be a static continuum). This (dichotomy) is the division of a given finite line-segment by bisecting it into two halves and bisecting one of these halves again, etc. See Figure.

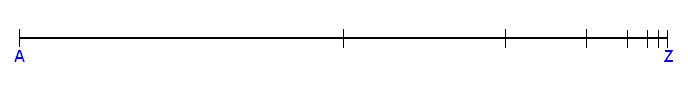
If we dichotomize the line AZ (i.e. if we repeatedly bisect the line) a finite but indefinite number of times, the remaining line-segment still to be divided becomes smaller and smaller. Its length will approach zero without ever reaching it, because reaching it will mean that the last bisection sets a point Y between the last inserted point X and the end-point Z of the line, such that the three points will touch one another and coincide (i.e. fall into each other) into one single point. Of course this just described bisection isn't a true division anymore, implying that the line-segment XZ (and now not inserting point Y anymore) is the shortest indivisible elementary line-segment. This, of course, holds for any given initial line-segment of any length.

So, even starting from HOENEN's position, it is still possible that any line-segment, and thus space itself, is not a continuum, but a voidless (gapless) discretum (voidless, because the unit-segments immediately connect with one another, they are not separated by a gap, i.e. by a nothing. They are separated, it is true, by a negation-act, but this act itself is not spatial).
(end of intermezzo)

We concluded the previous section (before the Intermezzo) with the words :  "Just as Aristotle's notion of potentiality, as we saw earlier, is the key to solve all antinomies of the continuum in general, documented in the history of philosophy, it will also provide the complete solution of all the objections brought against the possibility of motion [continuous change]. But before we deal with these, we must first consider two other questions connected with this unity."
First of all, indeed, we may ask :  What [entity] is able to give intrinsic unity to an extensum [something which is extended] that is flowing, that in virtue of its nature develops successively? For those who have undestood motion [still in the broad sense] as to be a genuine continuum with intrinsic unity, the answer is evident :  Motion is not only a succession of parts reaching an end-point as factual  boundary ("peras" of Aristotle), motion is an intrinsically-one-dynamism, striving  for a particular end-point. Therefore, this end-point is more than a mere boundary, it is an aim or target ("telos" of Aristotle). Reaching the end-point merely by chance cannot give intrinsic unity to the completed motion, only the striving for an aim or target can do this, and, if it is the nearest target, this unity is necessary and intrinsic. A genuine continuous motion -- and in every given motion at least the elementary parts are truly continuous -- is thus a  striving  for an end-point as target, and this target, right from the beginning, gives unity to this striving. This striving is, as already noted, passive in the motion. Indeed, motion is pure "becoming", pure passivity. But it [the motion] depends upon the striving insofar as it is active in the effective cause of motion. The existence of motion proves, in virtue of its unity, the influence of a causa finalis (final cause) alongside the causa efficiens (the effective cause).

The Aristotelian thesis that the purpose or aim determines the motion and its intrinsic unity, provides the metaphysical basis for a theory, dominating all of modern, "non-classical" physics, the quantum-theory of Planck. In its first days this theory has aroused much astonishment, and it still does, because it runs counter to what appears to be so self-evident, namely that every motion [still taken sensu lato, i.e. including all continuous change] is all from itself indefinitely divisible, and that, accordingly, one can expect that, for instance, a body emitting energy -- and here we have a qualitative motion -- can do this with all possible quantities (can emit all possible quantities of energy) and that there is no lowest boundary for this quantity. But since Planck one nevertheless must assume the existence of lowest boundaries, minima of emitted energy or "activity",  quanta.
In Aristotle's theory this is not surprising. Earlier we saw how, in spite of the indefinite divisibility of the static continuum (the body), yet minima could and had to be assumed, minima, demanded and determined by the specific nature of the physical body. Things are similar in the case of the dynamic continuum, for example the emission of energy. Even when this were in itself indefinitely divisible and thus would not in itself demand minima, yet the very nature of the emitting body may demand such minima, such quanta. We saw :  Every truly continuous motion [sensu lato] is a striving for a determined end-point, passive in the motion itself, active in the effective cause, the agent. The one elementary agent [for example the body, emitting energy] will have its own determined specific activity (one or some), the other its own.
And thus, modern atomic theory, the theory of elementary agents and their structural connection in[side] atoms, is completely governed by the theory of quanta (quantum theory). Of course, the  specific  way of activity cannot be determined a priori, it must be studied and become known through experience. But that there indeed do exist such ways of activity determined by quanta is in Aristotle's metaphysics of motion (continuous change) something that is at least plausible. And again we see a confirmation of what we already often had found out :  Metaphysics provides the general principles which must be specified, not a priori, but by experience. And also we find the physical quantum theory to be a specification of aristotelian principles. Also in quantum theory modern physics is aristotelian.

Indeed, by the ancient scholastics the question was already asked whether, as in physical bodies, also in intensities natural minima should be assumed, so by Suárez (Spanish philosopher, 1548-1617).

The fact that a given motion (continuous change), caused by some elementary agent, is a striving for a specifically determined end-state, was also, as to the astonishment of physicists, expressed in the formulas by which the radiation of the atoms of the chemical elements can be calculated. In these formulas does appear, alongside the initial condition, also the end-condition of an electron [referring to the electron's change of energy-level inside the atom, and the radiation -- emisssion of energy -- that follows upon the electron's falling into a lower energy level of the atom.]. This fact in physics brought back to memory the scorned notion of a final cause, the causa finalis, and almost in honor. Let us hear Sommerfeld, 1930 :

" Wenn ich gelegentlich von einer neuartigen oder bedingten Causalität sprach, so gründete sich dies mathematisch darauf, dass wir die Ausstrahlung aus einer Formel zu berechnen habe, in die [Formel] Anfangs- und Endzustand des Atoms gleichberechtigt und symmetrisch eingeht. Das heisst m.a.W., dass bei der Ausstrahlung eine Voraussicht des Endzustandes zusammen mit einer Rückerinnerung and den Anfangszustand als mathematisch Factum vorhanden is. Diese Art Causalität wiederspricht freilich unserer hergebrachten Denkweise, ist aber nur die Wiedergabe eines mathematischen Tatbestandes, der sich bei der Berechnung von Intensität und Polarisation der Ausstrahlung glänzend bewährt hat und dem wir in unseren allgemeinen Vorstellungen Rechnung tragen müssen. Uebrigens ist sie nicht ein völliges Novum :  Aristoteles liess neben der causa efficiens die causa finalis zu, desgleichen Leibniz. Erst im 18. Jahrhundert, offenbar unter dem Einfluss der klassischen Mechanik, setzte sich die uns heute in Fleisch und Blut übergegangene Form des Causalitäts-Begriffes durch, die das Geschehen ausschliesslich durch den Anfangszustand determiniert."

Translation :

" When I sometimes spoke of a new or conditional causality, is was mathematically based upon the fact that we must compute the emission [of light] from a formula in which initial- and end-state of the atom with equal right and symmetrically have their place. This means, in other words, that in the emission there exists, as a mathematical fact, a providence of the end-state together with a recollection of the initial state. This type of causality contradicts, it is true, our traditional way of thinking, but is only the expression of a mathematical fact, which has been wonderfully confirmed by the calculation of the intensity and polarization of the emission, and which, in our general ideas, must be accounted for. Anyway, this discovery isn't something completely new :  Aristotle admitted, alongside the causa efficiens, the causa finalis, and likewise Leibniz. Only from the 18th century onwards, manifestly under the influence of classical mechanics, that form of the causality-concept having today been enshrined in our flesh and blood, pressed ahead, a causality, by which what happens is exclusively determined by the initial condition."

Although much in these words has philosophically been expressed not entirely correctly, the general idea is clear and correct. Indeterminism in Nature is not supposed by the modern methods. They do recognize a (for the time being?) shortcoming in science [i.e. in our capacity to know certain things]. "Voraussicht" (providence) and "Rückerinnerung" (recollection) of intial- and end-state, in the sense of knowledge, does not, of course exist in the material agent. It definitely does have a "nature" in the deep aristotelian sense of the word. As to its deepest essence it [the material agent] is  aimed  at causing a motion to this determined end-point, in these determined conditions. To detect this, is the task of ever progressing science. The fact that such "natures" really exist, is already established by it. These natures themselves do not possess intelligence, but they would not be intelligible, and thus not be, if outside them there was no intelligence which has made them.
[In the macroscopic domain we have so-called "attractors" in certain (iterative) dynamical systems, but these are entities established after the fact. They can be computed by computing the outcome of trajectories of such a dynamical system, trajectories going out from a great many possible initial conditions, by repeated application of the dynamical law (expressing the relation between state and next state of the system). The attractor is then precoley that region of phase-space (collection of system-states) where the system ends up, moves within it, while never leaving it anymore (for example a cycle of states, or just a single state, or a so-called strange attractor [all explained in  First Part of Website ).]

We now will discuss a number of difficulties encountered in the analysis of the concept of motion, difficulties for some so unsolvable that they developed into genuine antinomies, appearing to make the notion of motion impossible. In the end they boil down to the fact that one wants to resolve the "flowing becoming", which is motion, into a series of static states. A human knower tries to think in terms of the "static being". If he perseveres in this consistently, then he, as a result, automatically destroys the proper nature of motion, which, we've seen it, cannot be reduced to this static being. Together and in connection with this first motive, also the other general difficulties of the continuum pop up again :  The notion of the potentiality of the parts of a real continuum is neglected (or is unknown). Already because of that, the continuum as totality is in fact destroyed as to its true conception. Both concepts, continuity and succession, or still better, the unification of them :  continuity in the succession, constituting the essence of motion, we should have in mind, and then indeed the antinomies vanish.

The first antinomy is already discussed by Aristotle. He presents it as a difficulty against the reality of the notion of "time" [said more precisely :  against the reality of that what is intended by the notion "time"], but one may as well bring it up against that what is the fundament of time, namely motion. See here Aristotle's wording [of the antinomy brought forward by philosophers of his time] :  Time would not be able to exist, because the one part of time is already over, and so  is  not anymore, while the other part is still in the future, and so not yet  is.  And from these parts infinite time as well as every special time is composed. But what is composed of non-existing parts does not appear to participate in existence. It is clear that this argument, if it proves anything against the reality of time, would also destroy the possible existence of motion. [According to HOENEN's own principle, this is not necessary, because motion is primary and time is derived from it. It would be necessary if time and motion were equivalent.]. But further thought reveals that the argument (the antinomy) is worthless.
Let us first apply it to a static continuum, a line or a body [for HOENEN, not just any physical body, but those which are at the same time genuine substances in the metaphysical sense. Further we must realize the difference between a line and a body. The latter is not in the same way a continuum as is the former, because for a physical body to be a continuum we must consider its (obvious) parts as merely potential parts. In the present discussion, however, it is clear that HOENEN has, with the word "body", in mind a mathematical body, a "solid", such as a polyhedron.]. And let us consider in such a continuum two parts, the right half and the left half. Of these parts we know, from the general theory of the continuum, that they do not  exist,  only the continuum itself  exists.  The parts are necessarily no more than mere potentialities. Would they exist, then precisely the continuum would not exist. Things would be different if we had to do with a system consisting of  two  contigua.  Precisely that cannot exist when the two constituent parts did not exist. The value of the above argument (the antinomy) is now dependent on the principle used there :  "that what is composed of non-existing parts cannot itself participate in reality". Well, our consideration teaches us that it is false in the case of a continuum [The continuum consists of potential, and thus of non-existing parts, but it nevertheless itself exists.]. Indeed, for to be a continuum, the contrary [that it should not be composed of parts] is  demanded.  For contigua the principle is true [when parts do not exist, neither does the whole]. And again we see how we will arrive at false conclusions [that a continuum cannot exist because its parts do not exist], when we confuse the continuum with contigua [i.e. with a system of contigua]. But motion is, as is time, a continuum. So the argument against the possibility of motion (and time) is worthless [because it is only valid for a system of contigua]. What, however, does follow from it is this :  A given motion cannot be composed of contigua only, because then the argument against it would hold [A motion may be one that has been interrupted a number of times, and thus is then a motion consisting of individual motions (contigua). And if these contigua were the very last elements of the motion, then the argument against (such a) motion would be valid. But in fact these contigua finally must consist of continua, motions, because otherwise they would ultimately consist of points, here stationary points, and adding these up does not result in motion. So every motion is either a continuum or at least consists of continua. And the argument (against motion and time) does not hold for continua.]. But this we already knew, for then an extensum would be the sum of non-extensa [the smallest contigua being points]. So we merely find a confirmation of our earlier thesis.
We may take yet a closer look to this problem and it may free us still more from the delusion of, or striving for, reducing the flowing "becoming" to static "being". Indeed, motion is, in its deepest nature, a flowing continuum. And if we actually divide it, by stopping the motion, then we fix the static "being" resulting from the partial motion, and yes, in that case the previous part of the motion  has  existed, and does not exist anymore. And then (also when we resume motion again) the future part does not yet exist. Then, at that very moment, the motion does not exist [which looks like the argument against motion and time, but it isn't that argument, because we now have actually stopped the motion, amd then, of course, it doesn't exist anymore.]. But when we divide a motion  only in thought,  by fixing a point (the "now"), then the first part  hasn't  existed, and the future part  will  not exist. Only the motion as a whole does exist,  flowing through this "now",  it is there according to its own essence, not as static being, but as flowing being, as "continuous becoming".

Earlier we saw an argument which Leibniz and Kant brought forward against the reality of any sort of continuum, an argument still urged by Lachelier in the 20th century. It reads as follows :  In every composed thing -- and the continuum is composed of parts -- the parts are prior to the whole. The whole is just a collection, an "assemblage" of parts. Then there must be  first  parts which are not composed anymore -- otherwise they wouldn't be  first  parts -- parts, which thus are non-extensa, points. But a concatenation of non-extensa can never result in an extensum, and thus a real continuum is impossible. This is valid for every extensum, also for motion. Leibniz even came to this argument by having first considered the flowing continuum.
Already earlier we said :  if  the parts are indeed always prior to the whole, in whatever way, then, by metaphysical necessity, there must be  first  parts [because these ultimately constitute the whole, and thus are indeed prior to that whole]. Are there first parts, then they must themselves be uncomposed (otherwise they would not be first parts), and then a continuum, or even a real [i.e. physical] continuum will be impossible [because these composing parts would then be points]. With this principle we fully agree. But we saw also that the thesis :  "the parts are prior to the whole" is in its generality untenable [it is the reductionistic thesis]. So for the continuum in general [i.e. taking every kind of continuum] the conclusion that it cannot be real is false [some continua can and do exist, namely those of which the whole is prior to its parts.]. But as to motion, the flowing [dynamic] continuum, it [the argument against continua] seems, at first sight, to hold. There, the parts seem to be indeed prior to the whole, namely in twofold respect :  in virtue of the very nature, the essence, of motion, and according to time [first the parts, then the whole]. For in virtue of its nature motion is successive, there exists an order of succession, of before and after, of priority and posteriority, between the parts themselves, and so also [such an order] between these parts, that is, the provious parts at least, and the whole. And this will express itself in priority, also in time, between those earlier parts and the later ones, and thus also between the earlier parts and the whole [and then there must be first parts, which, for the whole to be a continuum, must be points, and points cannot make up any extensum, so also not any continuum].

[So any given motion, taken to be either local motion or any allegedly continuous quantitative or qualitative change, is a dynamically extended entity, having succesive parts, or states. In a cyclical succession of such parts, those parts that 'still have to appear' are nevertheless constitutive of the parts already formed (because the former come at the same time also before the latter, for in dynamical systems ending up into a cycle of system-states the same states will be visited by the system again and again). So in such a situation, i.e. in the cycle - and a dynamical system's trajectory may in some cases consist entirely of this cycle of system-states -- there are no non-arbitrary first states, and thus no first parts. The parts here presuppose the whole (cycle).
And if, on the other hand, the parts do not presuppose the whole, which may be the case in non-cyclic motions, then also a first part is not necessarily implied, because the whole (motion) is already guaranteed (i.e. determined to be) when  each  individual part is itself guaranteed (determined) by the previous part. But this is only the case when  all  parts are so guaranteed (and then, indeed, there is no need for a non-arbitrary first part to guarantee all other parts), and this, in turn, is only possible when the series comes to an end, and thus its number of parts be finite. But if the number of parts is such that counting them will never end (i.e. if there are potentially infinitely many parts), then for them all to be so guaranteed we must presuppose actual infinity ('all the parts'), which is impossible. So indeed, in this potentially infinite (non-cyclic) case the 'complete' series cannot be. The series is never finished. The number of parts is undetermined but (still) finite. Therefore, here a first part is needed to guarantee the rest of the series. And in order for such parts to be able to constitute the series they must be non-zero. So the series cannot constitute a continuum.]

Yet [as HOENEN continues], on closer inspection, this state of affairs (in motion :  priority of parts, first parts, points, implying the dynamic continuum to be impossible) turns out simply to be incorrect. First, as to nature,  the whole, also in the case of motion, is prior to its parts. After all, motion is, we've seen it, a  striving  for an end-point [in every motion for a particular end-point]. According to the nature of things,  this, i.e. the result, the special end-point to be reached in motion, comes first, and only then the motion as a whole follows, which, as a means, is aimed at this result. And only then, because motion is a continuum, and thus divisible, the parts follow [i.e. potential parts]. So, according to the nature of things, also motion is holistic, i.e. has its whole prior to its parts. But in motion not only the whole has this priority according to nature, but also according to time. Indeed, we also saw :  If a given motion remains continuous and is not interruped by some external cause, the existence of the parts is and remains merely potential [i.e. the parts are not actual parts, but remain potential parts], and that of the motion [remains] actual. But in Time only the actual does exist. That the parts, as to their existence in time, precede the whole, is in such a degree false that their existence is not even actual, neither before, nor during the whole of motion. So the parts of any given single continuous motion surely are not prior to the whole [as to nature, the actual is always prior to the potential, but here also in time, because only the actual can exist in time]. And with this, the antinomy of Leibniz-Kant is completely solved also with respect to motion. We may note, that it finds, also here, its solution in the notion of potentiality [and this is a fundamental notion, which cannot be analysed any further].

Zeno, the Eleate (not to be confused with the famous Stoic having the same name), Greek philosopher, about 490-430 B.C., was a pupil of Parmenides. It is well known how the exorbitant conclusion of the master's metaphysics, that no motion, even no local motion, is possible, shaked the Greek philosophical world. While his metaphysics and its conclusion that intrinsic change [i.e. qualitative change] was impossible was accepted, until the time of Plato and Aristotle, also outside the Eleatic school, such as in thinkers like Leucippus and Democritus, and also Empedocles and Anaxagoras,  the other thesis [of that eleatic metaphysics], saying that local motion was also impossible, which [local motion] was so evident in experience and also so intelligible, was generally opposed to. Now Zeno attempted to eliminate this opposition with his four famous arguments that would destroy the intelligibility of motion. Zeno's own words on these matters are not or hardly known to us. Aristotle did record them succinctly, and they have been given classical names :  the dichotomy, Achilles, the arrow, and the stadium.
The tradition of the last one is very obscure, so that even its sense is difficult or impossible to reconstruct. Therefore, we shall skip it here. To the other three we devote some words.

Dichotomy and Achilles.
According to Aristotle these two arguments boil down to essentially the same. We shall deal with them together in one time. The principle from which Zeno departs is this :  In a finite amount of time the infinite cannot be traversed. It rests on the correct definition of the infinite in quantity :  "that what cannot be traversed".
Here, then, Zeno's dichotomy :  If a thing is to move from A to B, then it must, before reaching B, [first] travel half the distance, i.e. AC.  And before reaching C, again half this distance, AD.  And before this has been traversed, again half of it must be traversed first, and so -- thanks to the infinite divisibility of the continuum -- ad infinitum. To reach an arbitrary point, different from A, an infinite number of points must be passed, which according to the principle, cannot be done in a finite amount of time.
[That it can traverse such an infinity of points in a finite amount of time, can be demonstrated by calculation :  The time needed for every next half to be traversed so rapidly decreases that even an infinite number of stations in a finite distance (AB) can be traversed in a finite amount of time. Let's calculate.
The distances to traverse, when gong from A to B, and expressed as fractions of the distance AB, are respectively, 1/2, 1/4, 1/8, 1/16, etc. And it is clear that the time needed to traverse a given distance is directly proportional with this distance. So the total time, T, needed to go all the way from A to B, -- this needed time given in some arbitrary time unit, -- is then the sum of this infinite series of fractions :  T = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + . . . .
Then, 2T = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + . . . , so 2T = 1 + T, meaning that T = 1.  So the time needed to traverse AB is finite.
The second argument runs as follows :  Zeno lets -- to make things more dramatic says Aristotle -- the speedy Achilles have a match with the slowest of animals, the tortoise, and having given the latter a small headstart. And he proves that Achilles cannot outrun the tortoise. The headstart may be small or large, Achilles needs time to traverse it. In that time the tortoise crawls further and still has a headstart. To traverse this smaller headstart Achilles again needs time. And in that time the tortoise crawls further and still has a headstart. And again :  as a result of the infinite divisibility of the continuum, this story repeats itself ad infinitum. The tortoise always retains a headstart with respect to Achilles. To outrun it, Achilles would have to traverse the infinite, which is impossible in a finite amount of time  [ Here, the actual infinite (of stations or points) is presupposed by Zeno, and this is in itself wrong. But, in the present case (Achilles-Tortoise), even when an actual infinity is presupposed, the time needed to traverse it is still finite, as we saw in the above calculation.].
Both conclusions (dichotomy, Achilles) contradict experience, but both derive from a, seemingly, sound reasoning. So one must, either solve the antinomy, or agree with reason which denies motion against the witnessing senses. The method of Diogenes, who, as a reply to Parmenides' (and thus Zeno's) philosophy, got to his feet and walked away, is insufficient.

Preliminary solution.
The answer to Zeno's own question :  "how can the infinite in a given distance [i.e. a finite distance, but containing an infinite amount of "stations" (to pass through)] be traversed in a finite amount of time?",  is fairly simple. These distances are, in both cases (dichotomy, Achilles) only infinite as a result of their indefinite divisibility [i.e. they are only infinite in the small]. However, time is also a continuum and in the same way indefinitely divisible. And now it is immediately clear :  the distances, which are only infinite as a result of their indefinite divisivility, can be traversed in a time of finite duration because time is indefinitely divisible as well. [So time and motion correspond to each other, which we have shown in the above calculation]. When the problem is stated in this way, the answer is sufficient.

Solution of Descartes.
Since Descartes one also gives a solution, derived from the theory of progressions (series), which, as some hold, is better, and which in fact is totally equivalent with the preliminary solution of Aristotle. Let us consider the match between Achilles and the tortoise. Say, the speed of Achilles is V (centimeters per second), and that of the tortoise  v,  in which V is larger than  v.  Suppose that the headstart of the tortoise is  a  centimeters.  To traverse this distance, Achilles needs a/V [=  a divided by V ]  seconds. During this time the tortoise covers  (v/V)a  cm.  The second amount of time needed by Achilles to traverse this section of the trajectory will then be  (v/V)(a/V), in which time the tortoise makes for  a(v²/V²) cm.  It is now clear that the successive times needed by Achilles are :  a/V, (a/V)(v/V), (a/V)(v²/V²), etc., ad infinitum. These terms form a convergent geometric progression of which we can write the sum of the terms :  (a/V)[1 + v/V + v²/V² + . . . ].  Elementary algebra [see below] can calculate this sum. Its value is :  a/(V-v)  [=  a divided by (V-v) ] seconds. The sum of these times thus is a time with a finite duration  [ but, as we will see, we must still ask the question whether this finite time can be run through, because also any section of time, thus also a finite section, is indefinitly divisible, and thus consists of an infinite number of moments.].

To actually compute the finite time of  a /(V-v)  seconds, i.e. to compute the series  (a/V)[1 + v/V + v²/V² + . . . ], we first determine the sum of  [1 + v/V + v²/V² + . . .]  :  Say this sum is S.
[1 + v/V + v²/V² + . . .] = S, then, multiplying both sides of the equation with  v/V gives :
[v/V + v²/V² + . . .] = (v/V)S, and from this follows :
S-1 = (v/V)S, then we have also :
(S-1)/S = v/V, which is equivalent with :
S/S - 1/S = v/V, which is equivalent with :
1 - 1/S = v/V, which is equivalent with :
-1/S = v/V - 1, which is equivalent with :
1/S = 1 - v/V,which is equivalent with :
S = 1/(1 - v/V).
Now we must multiply this sum with  a/V.  So we get :
(a/V)S = (a/V)/(1 - v/V), and this latter is (multiplying both the denominator (a/V) and the divisor (1 - v/V) by V ) :  a/(V - v), which thus is indeed the finite amount of time that Achilles has to run through in order to catch up with the tortoise.

The point in the trajectory where he outruns it can easily be calculated in a similar way. And in the case of the dichotomy one also finds, by calculation, a finite time.
The solution is completely the same as that of Aristotle. He pointed to the infinite divisibility of a finite (section of) time. With algebra we can compute this time from the parts. This is all what it adds to the preliminary solution of Aristotle. For this computation one even doesn't have to introduce a summation of an infinite series. See here a simple calculation.
V - v  is the distance which Achilles runs through in one second with respect to the tortoise. So he needs, in order to run through the whole distance of  a  centimeters (which is the initial headstart of the tortoise),  a/(V-v) seconds.
And still even more simple it becomes, - simpler, because the speed difference (V-v) is avoided :  Suppose Achilles outruns the tortoise in time X.  Is X finite or infinite? In order to determine the value of  X,  one can easily set up a simple equation. In time X  Achilles runs through the distance VX, and the tortoise vX.  Achilles and the tortoise are now at the same level of the running track (Achilles has catched up with the tortoise). And so the difference between these two distances which they actually had run is equal to the initial headstart of the tortoise, i.e. equal to  a.  So we have the equation  VX-vX = a, which is equivalent to  X(V-v) = a, which is in turn equivalent to  X = a/(V-v).  And X has a finite value.
Aristotle views, as we've said, this solution certainly as a good answer to the question as it was posed by Zeno, but not as a definitive solution of the problem insofar as it may be posed by these data. Because, as he notes rightfully, one could continue in this way :  If this finite time is infinitely divisible, and thus composed of infinitely many parts [Here actual infinity is presupposed], how, then, can it pass on, because then the infinite, which is by definition inexhaustible, must be traversed, and thus be exhausted? And because time in reality is motion, the same question again can be posed for motion. The solution, just given above, thus is not definitive.
We must note that the algebraic solution of Descartes is also not definitive. Because if the sum of an infinite geometric progression indeed should have to result from a repeated addition of a next term to the sum of the previous terms all the way up to uinfinity, then this summation itself would be an inexecutable operation. So a "sum" in this way defined, would be absurd, would not exist. Indeed, the infinite would never become exhausted, the sum not realized, Achilles would not outrun the tortoise. Therefore, modern mathematics, more rigidly than that in earlier centuries, defines the "sum" of such a series as the limit to which the sum of the  n  first terms of it approaches, when  n  increases. By adding a next term to the sum of the previous ones, one can approach the limit as closely as one whishes, but one cannot reach it  [So the impossibility of the summation of any infinite series is admitted and precisely stated by modern mathematics].
The solution of Descartes is as preliminary as is the first one of Aristotle. And if one would view this solution such that the sum would result from the addition of successive terms, then it would even be false, - then that time (needed by Achilles) would never be accomplished. [Indeed, the algebraic reasoning contains the phrase  " Suppose 1 + v/V + v²/V² + v³/V³ + . . . = S ".  Such a summation never could be finished, not even in principle, because the series -- while summation continues -- cannot by definition be run through completely. And this means that the finite time of  a/(V-v)  seconds, the finite duration, will never be gone through, because the summation can never be concluded.]

Definitive solution.
The final solution Aristotle did find from the realization that the continuum, [and thus] also motion and time, contains parts which exist only potentially, in tendency, and not actually, not in fact. The continuum is not  divided  into infinity, but only  divisible  into infinity, and, specifically such that the infinity refers to the potentiality, and never to any result of a division [It is, perhaps better to say that, first, the parts of a continuum exist only potentially, meaning that they, although not yet existing, they could, by some act, be set as parts (for example by insertion of boundaries), and, second (and this is where infinity comes in), that the number of such parts is not determined, has no upper limit, while, nevertheless, always remaining a finite number. We may summarize this by saying that the continuum contains an undetermined but finite number of possible parts.]
In how high a degree whatsoever the continuum is being divided, it always can be divided still further :  ad infinitum [meaning, toward infinity, not into infinity]. And, the other way around, the continuum does not result from adding together an infinite number of parts [A given finite (as to size) continuum may be constructed from a finite number of parts, but these parts are continua as well, so the only parts of a continuum which themselves are not continua must be points, i.e. boundaries separating possible parts of the continuum. And indeed, even an infinite number of points added together does not result in a continuum, because they have no extension and cannot, therefore, create, all by themselves, an extensum, which in our case the continuum is.]
In what way is such a supposed infinity (of the continuum) inexhaustible? [i.e. under what conditions is an infinity inexhaustible?]  Well, it is inexhaustible only when it would have to be brought into actual existence,  [meaning that, during continued actual division, yielding an increasing number of actual parts, every further division, adding new parts to those that have already resulted from all previous divisions, keeps on resulting in a total number of parts that is finite. In this sense infinity is inexhaustible.]. The divisibility is never exhausted. If, thus, motion [a dynamic continuum] had to divide its trajectory as to the latter's  complete  divisibility, or if it itself had to be in this way [i.e. as to its complete divisibility] divided by time, yes, then motion would be an impossible process. But because the trajectory, the motion, as well as the time, are continua, [and thus] are merely divisible, not actually divided, motion is possible, notwithstanding its potential infinity [because no actual division whatsoever is involved].
Let us note, in all this, a false image, which many seem to have, namely that motion automatically divides up its trajectory. It does this only when it is itself divided, i.e. actually or in thought being halted. When it is one and undivided, and thus continuous, it doesn't divide its trajectory [Therefore, motion (s.l.) has nothing to do with a summation of some infinite number of parts, and therefore motion is possible.].
Immediately connected with this, or, rather, being a different expression of the same thing is the following :  If the parts (into which something can be divided) would have priority over the whole, and the whole had to be built from the parts, then we would indeed have an impossibility :  The infinity in the successive construction could not be exhausted, like an infinite series could not have a sum if the latter would have to formed from the addition of that series' terms [because the sum, the limit of this summation, is approximated but never actually reached.].  But if the whole is prior to its parts, this successive construction from the parts is not necessary [because the whole is then more fundamental than its parts], and therefore continuous motion is a possible process. [The parts of it come only after that process, and then still merely in the form of potential parts.]

[So the real possibility of continuous motion is established by HOENEN by the assumed fact that in any continuum the whole is prior to its parts, resulting in these parts to exist only potentially. So the argument here is, neither mathematical, nor physical, but metaphysical. Every continuum is supposed to be holistic as to its constitution. And such a holistic constitution especially applies to motion because motion is supposed to have, in addition to an efficient secondary cause, also a final and primary cause. So motion, being without actual parts, does not divide the space through which it goes, does not divide its trajectory, does not have to exhaust an infinity of stations. In all this, any argument that every continuum is holistic does not need support from the assumed finality of motion (i.e. the finality of the dynamic continuum). Just as we said that the assumed holism of any continuum (static or dynamic) implies the potentiality of its parts, we can also say that the assumed potentiality of the parts of any continuum implies its holism, for in this case the parts are (assumed to be) potential while the continuum as a whole is actual, and because the actual is prior to the potential, the whole continuum is prior to its parts, and thus is holistic.
What a continuum in fact truly is, or should be, is well expressed by HOENEN by insisting that in motion there is no "being", no successive "being", but only "becoming". So allowing for this "becoming", this "flowing", not to be merely an accident, but to be a special state or kind of Being-in-the-broadest-sense, and constituting the very essence of motion (and of continuous change in general), HOENEN makes motion to be a true continuum. And the same then applies to "time" (because time is also flowing, also a flowing continuum). But then all spatial extension, "space", must be continuous too, because if it were discrete, then motion in it would be discrete too. So space, motion and time are continuous, they are continua. But "space" itself, and "time" itself are not beings, but ontological conditions for things to be extended in them. They are "categories" in the sense of Nicolai Hartmann. Space and time are, respectively, a system of "dimensions" and a single "dimension", and a dimension in general is a substrate of extension or, in other cases, of intension. So space and time are themselves not extended, but conditions of things to be extended in them. So if we ask whether space and time are continuous, we in fact ask whether the things which are extended in them are continuous.

It is interesting to realize that, in addition to this solution of the problem of the real possibility of motion, based on the potentiality of the parts of any continuum, there is a second possible solution, saying that space really is constituted of actual parts, and that these parts are the non-zero, but nevertheless indivisible units of space. Such a spatial unit does not have to be traversed by any moving object, because that would imply divisibility of that unit. So these non-zero units of space are the stations, the successive places, which are being passed by, one after the other, by a moving object. And because any finite space, any finite length of it, is constituted of only a finite amount of such non-zero units, motion in this space can be completed and is thus possible. So this solution of the problem of motion boils down to take space to be discrete, to be a discretum, and not a continuum.].

And for such a continuous motion it is thus necessary that the continuum is not merely the sum of its parts. And for this in turn it is necessary that the parts of a continuum are merely potential. And, finally, for this in turn it is necessary that a dynamic continuum is  a  striving  for a [particular] end-point [Because only then such a continuum is a true unity, is holistic.].
Yet another expression of the same thing :  If an extensum were not more than a series of contigua [and thus not a series of small continua touching one another, but exclusively of non-extensa, points, touching one another], then this series should contain an infinite number of such contigua, then all of them would be actual, then they would be prior to the whole, which indeed only then is the sum of its parts, then motion and time had to exhaust the infinite, and thus be impossible. But we have already seen that then every extensum would be impossible [points + points do not add up to an extensum].
If we now see all this together, then we have insight into the continuum, the static and the dynamic, then we see how all the antinomies of both continua find their complete solution in the aristotelian concept of potency, of "being-in-tendency". Then, but only then, all demands of intellectual insight are satisfied, and at the same time experience saved, experience, which so clearly reveals to us the existence of motion.

The arrow.
The third antinomy of Zeno will now not cause trouble anymore. In Aristotle's text [on Zeno] has, it is true, crept in an error, not, however, impeding the understanding and meaning of Zeno's argument. The meaning is this :  A body that is at a place which has the same volume as the body itself, is at rest. Well, a flying arrow is, at every moment at a place that has the same volume as the arrow itself. So at every moment it is at rest, and so it is during the whole time.
After the above discussion Aristotle's short answer will be clear :  Zeno illegitimately supposes that time is composed of indivisible moments. We may add :  If we consider the flying arrow "here and now", then the arrow is not "here" in the "now", but shoots through the "here", while time is running through the "now". [So, in the philosophy of Aristotle-StThomas-Hoenen, motion (i.e. not only local motion, but also any continuous change) is not "being", but "becoming", and it is, apparently, supposed that "becoming" cannot be further analyzed, it is a fundamental concept. Indeed, by introducing this additional type of reality-ingredient, namely "becoming", i.e. "dynamic being", the essence of the "continuous" is metaphysically established, and forms the kernel of the solution of the problem of motion (as proposed by HOENEN). Whatever the value of this solution will turn out to be, there is, as indicated earlier, yet a second possible solution of this problem, a solution based on the supposed discreteness of space (and of motion, and of time).].

In our considerations of motion, repeatedly and automatically the notion of  "time" popped up - a sign, that between these two concepts there must exist an intrinsic connection. So it is natural that we now focus our attention to "time".

Difficulty of the problem.
The treatment of  "time" has been described, already from early on in the history of philosophy, as a work of thinking bringing with it harder difficulties than those concerning other problems. The "existence" of time was then considered as something that was utterly clear, also to the man in the street. But, if one arrives at the question "what is time", then difficulties pile up even for the wise among the wise. Well known are the words of Augustinus  ( Roman patristic philosopher, 354-430 A.D.) :

" With what are we more familiar, and what is better known in our conversations, than time? And when we speak about it, we do -- isn't it? -- understand what we say, and we also understand things when we hear others talk about it. So what is time? When nobody asks me, I know it. When I have to explain it to someone who asks about it, I don't know. Nevertheless, I can confidently say that I know that if nothing went by, there would be no past, and if there were nothing coming, there would be no future, and if there were (and not had been) nothing at all [i.e. no beings at all], there would be no presence."

Nevertheless, Augustinus manages to give (in the series of next chapters of the book from which the quotation was taken), with suppleness of mind and in wonderful language, an answer to the indiscrete question of the "what" of time. The difficulty is, in the end, the same as what we encounter so often in philosophy, where it is about -- in the context of a well known set of ideas -- penetrating, by means of precise analysis, into the first concepts and data lying at the base of this set of ideas, and finding a formulation of them. In what comes next, we shall chiefly follow the analysis of Aristotle, who is working his way more sober-mindedly and also more acutely than Augustinus, and also, chiefly, accept his results. Not because they are of Aristotle, but because it appears to us the best analysis, the only one that gives us satisfaction. In certain points we shall add some corrections indicated by St Thomas Aquinas, and will have to work out the theory still further, such that it can give an answer also to modern formulations of the problem.

Apparently, there exists an analogy between the ways of  Being,  finding an expression in the ways of  predication  such as :  "to be here or there" and those other ways of Being, which we express in words such as :  "to happen now or then", - there is an analogy, but not conspecifity. For, in all similarity there still exists a great difference between the first and the second group. Evidently, they belong to different categories of Being. The first is "to be at  a  place", the second "to happen in  a [moment of]  time". What is meant by these expressions is immediately clear to anyone. Analysis, leading to acuteness of insight, may, however, involve difficulties. That precisely is it what Augustinus expressed above.

Real way of Being.
Both categories are, apparently, groups of  real  ways of Being. Therefore, we earlier had to find a reality which could fulfill the function of  "place". The same we now have to do with the concept "time". Indeed, it is immediately clear that a real difference in "time" is indicated when we say that the Flood happened before the Trojan war, and the latter before the life of Aristotle, precisely as a real difference is indicated when we say that Democritus was born in Abdera and Aristotle in Stagira. Also we indicate a real difference by the words :  "Aristotle reached the age of 62 years and he died in the year 323 before the beginning of our Christian Era". We then indicate quantitatively :  the "duration" of a "motion", namely the life of the philosopher or the "distance-in-time" separating two events, namely his death and the birth of Christ.

We here may insert a good preliminary characterization of "time" as contrasted with "space", taken from PETRONIEVICS, 1904, p.131, where he already established that "time" is not some existing essence alongside real events. In "space" we have a "togetherness of things", while in "time" we have an "after each other of things". This means that in space things, or parts of space, are given together, and thus simultaneously, and in time its parts are given only one after the another, i.e. only successively :

What, then, is the essence of this "after one another" in contrast with "to be together"? Because these relations are very simple [i.e. not composed] they cannot be reduced to more fundamental things, and therefore they cannot be defined. Only with respect to the way of existence, which Being has in these relations, they may be further distinguished and described :  Being, i.e. the things that exist, is, in the pure "to be together" at complete rest, while in the pure "after one another" in perfect motion and change. When parts of Being [i.e. parts of Being in general] are "together", then they are stationary, when they are "after one another", they are in motion (sensu lato), or, when they are "together", they remain unchanged, when they are "after one another", they are changeable.  Rest and motion, unchangeableness and changeableness are the two only possible states of Being which immediately connect with the two orders of  "to be together" and "after one another" of Being. Without rest, the "to be together", without change the "after one another" is unthinkable, and, the other way around, without "to be together" rest, without "after one another" change and motion is unthinkable.

Topological and metric structure.
And thus we already immediately find in "time" a twofold structure :  First, a  real order, the order of  "before or after" (or of simultaneity). Then we find a  measure  for the "duration" of events or for the difference in the order of appearance [how long before it, how long after it]. This twofold structure we will, in terms of modern mathematics, call here :  the  topological  structure, indicating the order of before and after, and the  metric  structure, providing a measure of the duration. In a similar way we can, in the case of static extension and "place", find a twofold structure, but, as will become clear later on, in "time" the topological structure is deeper, more essential, than in extension or "place".

Something extrinsic.
There is yet another thing that place and time have in common. Earlier we established that "place" is something  else  than that what has been placed in it,  it is extrinsic to the placed. And it was also clear that that what has been placed has, in the extension of the place, of its "own place", a measure. Likewise in "time". The time  in  which an event takes place, [the time] which is a measure for that event's duration ( [taken] topologically and metrically), is something  else  than the event itself or its duration, so again it is extrinsic. [place is extrinsic to the placed, and time is extrinsic to the event.]. That what is in this way determined and measured by time is, of course, intrinsic, it is the event itself and the flowing duration of its existence. Indeed, to the question :  " When and how long did Aristotle live?" one cannot, other than joking, answer "he lived in the duration of his life" [The answer should involve something extrinsic to Aristotle's life, something in which his life took place, and this is the general time-frame (independent of the philosopher's life) and the measure (for that life) it provides.]. This, precisely, as we saw it also with "place".
" Time" is thus something extrinsic to that what takes place in it and measured by it, like "place" to the placed.

Imginary time.
Alongside the concept "place" we, earlier, have met, in the same order of things, the concept "space" as being an extensum, a recipient, which, as one says, would remain when the whole extensive world would be destroyed, which [recipient] was already there before the world was created. We have found out that "space" is not an existing essence, not something existing on its own, but a mere product of thought. And so we had found out that the word "space" can at most be applied in one or another sentential connection to  describe  some other real thing connected with "placing". Only in our imagination there remains something when we expel the bodies in it, not so in reality. Something similar is also in our imagination with respect to "time". If we, in our imagination, expel all motion of real bodies, then nevertheless irresistably the impression remains of a flowing continuum, the time of our imagination. However, it will turn out to be a mere being of reason, just like "space". No real entity whatsoever corresponds to that imagination. So as we have alongside the reality "place" the being of reason "space", we have alongside the real "time" also an imaginary "time". It is pitty that we do not possess two words signifying the dynamic continuum to distinguish the real from the imaginary, as we can distinguish "place" from "space". So we have a "time" which is the analogue of  "place", and a "time" which is the anologue of  "space". The latter we shall call the imaginary time. Later we will mention a difference between both beings of reason (space, imaginary time). But first we shall focus our attention to real time. We thus know that "time" must be something real, in such a way that the real content of sayings like "this or that happened in that time, so and so long before or after that other event, and lasted so and so long" is justified. And "time" must, moreover, be something that is extrinsic to these events, taking place in it. We shall have to further determine the nature of time, first as to its general nature, and then also more specifically.

That "time" must be connected with motion was already clear. That this connection must be intrinsic is evident from the fact that our mind, in order for it to form the concept "time", must observe or imagine a motion [local or otherwise]. This is shown by simple introspection. Also the other way around :  If we conceive a motion then the idea of  "time" will easily be formed. So there is a connection.
One might be inclined to simply assume an identity between the two. This would, however, take things too far. Already because of the following reasons :  There are, as we saw earlier, motions of different kinds. Each one of them may be the datum from which we read off the concept of time. Not only local motion, but also increase in quantity and qualitative change. " Time", however, is not multifarious. But also "motion in general" is not identical with "time". After all, motion is in the moved and thus is multiplied with it. Not so time. Two motions running alongside each other take place "in the same time". Also, motions may differ in speed, and one and the same motion may be accelerated or decelerated. Not so with time, which ever and ever flows uniformly [which cannot, however, be objectively determined. According to the theory of relativity the speed of time in some region depends on the strenght of the gravitational field in that region. Perhaps the demonstration of the objective existence of absulute simultaneity, in fact following from the theory of relativity itself (and given in  Fourth Part of Website, part XXIX sequel-5 ),  may force us to accept one single universal time. But we still cannot determine whether this one universal time is accelerated or decelerated in some regions of physical space, although it seems to us very improbable.]. Let this, for the time being, be sufficient to establish a difference. Complete insight must follow from total analysis.

Thus "time" is not simply identical with motion, but must nevertheless be connected with it. We already established :  When we imagine a motion, the concept "time" will often emerge in our mind. To what, then, in motion must we focus our attention in order to arrive at this result? Let us consider an arbitrary motion. For convenience we take a local motion.
" Time" undoubtedly shares with motion the fact that it is a flowing continuum and this property it extracts from motion. Motion in turn extracts its continuity from its trajectory traced out by the object being moved. So in the trajectory we find the origin of continuity of parts, which we recover in motion and in "time". They extract yet more from this trajectory. Indeed, the trajectory is not simply an extensum, a line or curve. It is a line with a direction. It is not simply the distance connecting Athens and Thebe, it is the path  from  Athens  to  Thebe. Considering merely the static continuum, the line, the path, then the path from Athens to Thebe is one and the same thing as is the path from Thebe to Athens, it is the one path between both cities. The two opposite directions are merely aspects of the same reality. Things become different when we consider motion. To go from Athens to Thebe is a different motion from that of going from Thebe to Athens. So " direction" is to motion, to the dynamic continuum, more essential than it is for the static continuum. To the latter the two opposite directions are merely two different aspects of one and the same thing, while motions in these two opposite directions are different motions. This distinction becomes yet even more fundamental in the concept of  "time". Indeed, motions in different directions are certainly possible, but the idea of a reversed course of  "time" is absurd. So " direction" is certainly something very essential in that flowing continuum which is "time".

Before we continue with HOENEN's text, it is perhaps instructive to present (in fact repeat) a quotation [with remarks] from PETRONIEVICS, 1904, p.134, who argues that "time" is not a continuum, but a discretum :

If the parts of time [in contrast to the parts of space] are after one another (and indeed they are, as contrasted with the coexistence of the parts of space [embodied in the extension of simultaneously existing material bodies] ),  then there can be no simultaneous parts of time, i.e. only a single part of time can be really-given. For if more than one part of time could be given, then they would no longer be after one another, but coexistent, because only that is really-given what is given simultaneously (in the "after one another" the past part is not given anymore, while the future part is not yet given, and only the present part (the NOW-part) is given, i.e. only the present really-given part). But if the one given part of time contained in itself parts, i.e. if it were composed of still more simple parts, we may ask whether these parts are coexistent or are after one another. They cannot be coexistent, because there is no coexistence in time [only in space]. They also cannot be after one another, because then they could not all of them be real [always only one of them can be really given, the others are past or future]. So in the one really-given part of time there can be no still simpler parts, it must itself be simple and indivisible.

In another part of this text (p.136) PETRONIEVICS demonstrates that these last parts are really there and that they are not merely points in time but genuine non-zero parts of time :

One might say that the above argument only demonstrates the indivisibility of the last constituents of time, but that it doesn't show that there cannot be an infinite number of such indivisible parts in a finite amount of time [these parts would then be points]. However, in this, one forgets that as soon as one admits a division of a finite magnitude into a first-order infinite number of parts, one then further has to admit, in virtue of the same necessity, the division of every such first-order infinitely small part into an infinite number of second-order infinitely small parts, and so on, into the infinity of all infinities, and that one, in so doing, lets completely vanish the last indivisible parts of time [because then there are no last parts], which, after all, is so clearly demonstrated by the above argument. From this it follows that a finite amount of time can consist only of a finite number of these simple parts of time [implying that these simple parts have non-zero size], that thus time is not indefinitely divisible.

Further, in yet another part of this text (p.137), PETRONIEVICS shows that especially time, because it is interrupted every time when a NOW-moment subsides into the past and a future moment enters the present, cannot be a continuum (he does not consider the possibility of the dynamic, flowing continuum, as HOENEN does) :

The present moment of time is the only one that is really given, while the past moment is not anymore, and the future moment is not yet :  How, then, one can speak of a continuous time when the essence of time is precisely to always consist of one part only. The "after one another" necessarily excludes continuity, because it  completely  excludes the simultaneous existence of the many [time-]parts, and, as a result, [the "after one another"] divides time into real parts, of which always only one [at a time] is given. The "after one another" as negation -- that past part is not this present part, and vice versa, and, also, this present part is not that future part] -- actually separates one part of time from another, implying that time cannot be a continuum :  Wherever in Reality there is negation and separation, it is in the case of time, where the one part is really removed by the negation, and so, only as being removed, makes possible the appearance of another. And - how can it be? - precisely there where separation, where breaking up into parts, is so evident, one dares to speak of a continuum!

The notion of direction in a continuum has some consequences which are, especially to time, of great importance. In addition to starting-point and end-point which are  not  two  equivalent  boundaries anymore, there are intermediate parts and points in such a way that between two arbitrary, different, parts there exists an order. On the directed line the one part or point lies closer to the starting-point of the line than another. The one part lies  before  the other [or, at the rear of the other], the other  after  it [or, in front of it]. There exists a topological difference in rank-order between all consecutive parts. And to motion it is more essential than it is to its trajectory. Reversal of order for the latter brings with it only a difference in aspect, while for the dynamic continuum such a reversal means [the origin of] a new, different motion. And in a corresponding way time with its continuity takes over the topological order of its parts from motion, but now this order is in such a high degree essential, that reversal would be absurd. To every two parts lying [qua spatial position]  before  and  after  on the trajectory, do correspond in motion parts which are  earlier  and  later  in it. So this order of "earlier" and "later" is something essential to time. Indeed we have found something that is  characteristic  of  "time". We asked the question :  to what must we focus our attention in order to let originate from the idea of motion the concept of  "time"? We find as reply :  [we must focus attention] to the topological order of the parts of a given motion according to the "earlier; and later" of these parts. This temporal order of  "earlier and later" of the parts of a motion is determined and defined by the order of the spatial "before and after" of the parts in the directed trajectory, which in turn is determined when the direction is given, or, equivalently, when the trajectory's starting- and end-point are determined.

So in order to apprehend the concept of  "time", the mind must focus its attention to the natural, topological, consecutivity of the parts of a motion. It must discover a first, second, third, etc. part, and must discover in each of these parts in turn a same consecutivity of sub-parts, a first, second, etc. Thus we can, with Aristotle, say :  In order to arrive at the concept "time", the mind must discover in a given motion the natural disposition towards an  indexing  corresponding to the consecutive, i.e. to the earlier and later parts, being objectively present in the motion. " Time" will be something like  a possible indexing of a given motion according to its topological structure.
Aristotle used, to express this, the word "arithmos", of which the general translation reads :  number. This English word is, however, little fit to express the idea of the philosopher. Four and five are numbers. " Time" is not a number. " Time" is much more a  system  of numbers, namely of numbers which first of all (but not exclusively so, as we shall see) are  ordinal numbers  or  indexes, the first, second, third, etc. After all, it is about a topological structure. Such a system is better described by the word  system of indexation  or  indexing.
And then, with the "number" or numbers of this system  abstract  numbers are not meant, numbers, that is, which only exist in the mind, but concrete numbers, i.e. the system of multitude of consecutive parts, insofar as they are fit to be indexed according to the series of consecutive numbers.  Hence the other expression of Aristotle :  "time thus is not (simply) motion, but motion insofar as it can be indexed." [A possible indexing is like a possible observation. So time can be observed by means of indexing.]. Therefore, time remains a continuum, that a series of abstract numbers can never become. After a chief indexing of parts, each one of these can be subdivided and, according to the consecutiveness of the resulting sub-parts, be indexed, and so on and so on. This is expressed in technical terms by the scholastics :  "time" is not  numerus numerans (i.e. an abstract number "by which we count"), but a  numerus numeratus (i.e. a concrete number, or a "multitude which has been counted, indexed").
If we realize all this, then the solution of a difficulty brought against Aristotle's theory, becomes easy. One says :  If time is an indexing, it cannot exist in Nature independently of an observing and counting mind. After all, only the mind can count, can index. The indexing can only exist in the mind, at least not independently of it. The solution is evident. If in the definition-to-be-set-up of  "time", [and if] with "indexing" were meant abstract numbers, the difficulty would be unassailable. They can only exist in the mind. But the "indexing of motion" is concrete [as is especially evident in cyclic motion]. Moreover :  time exists independently of the observing mind, because "indexing" which is necessary and sufficient, is not an indexing that is actually executed -- this would demand the work of the observing mind -- it is merely a succession of parts, bringing with it a possible indexing. And we add :  whose indexing is already indicated by facts in Nature itself, such as the daily motion of the heavens, of which the individual complete revolutions are indicated by the passing of a same star through the meridian of a same location. That the mind must  focus  on this succession as possible indexing, in order, as we described above, to extract the  concept  of time from motion, presents no difficulty. Of course this  concept [as concept] depends on the mind and exists in the mind.
Might someone think that this result of our analysis, which views "time" as an indexing, or a system of concrete numbers, would stand rather far away from the ordinary notion of "time" in daily life, as it is not-analysed living in humans, then he should think of the answer that we return to a question "when", a question as to a certain time. To the question :  "when did St Thomas Aquinas die?" the answer is :  "on the 7th of March 1274". It surely is a question as to a certain time :  "when?". And the answer is nothing more than a numeral, a number, an ordinal number from the indexing of a certain motion. That motion is the daily motion of the heavens, of which each revolution -- one day -- is indicated by one of the consecutive ordinal numbers, while groups of days are united into months and years. It will be clear even more if we formulate the answer, as we do when writing down the date in a letter :  7 III 1274. This certainly is a pure number indicating the time.

" Time" not only has a topological structure, but must also possess a metric structure. Time also serves as a  measure  of the duration of motions and of the distance-in-succession of events. We not only say that Vondel lived in the Golden Century, but precisely from 1587-1679, and these numbers give a measure of the duration of his life, rendering it comparable with others. We not only say that Shakespeare was born before Vondel, but precisely :  the one in 1564, the other in 1587. And again with these numbers we have a measure of the distance-in-succession of both events. The actual indexing of a motion, which, as to the topological structure of time, only has to satisfy the condition that later parts obtain a higher ordinal number, will moreover have to be such that from the difference in ordinal number the duration of the motion (between these numbers) can be read off. The most simple case is then that equal differences in number correspond to equal parts. The indexing, not only representing a system of ordinal numbers, must also obtain cardinal value [meaning that in indexing of a motion, to obtain time, we not only have to do with a succession of the indexing numbers, numbers, in every step increasing by one a unit (resulting in these numbers to express their ordinal aspect), but also [have to do] with quantities, arithmetic quantities, obtained by addition or subtraction of any of the indexing numbers. And while the ordinal aspect of these numbers express the topological structure of time, the cardinal aspect of them expresses its metric structure, and thus allows to determine (measure) temporal duration and distance-in-succession.]

But when, precisely, is a duration equal to another, or longer or shorter than it? In a few cases this is immediately clear. Suppose :  two motions are carried out together, i.e. parallel to each other. They start and end simultaneously. The duration of both is equal, they take place in one single identical [part of] time. Here, not any concept, also not that of simultaneity (with which we will deal later) is not immediately clear. But, what if they are carried out  after  one another, or, if we enquire into the duration of two successive parts of one single motion? The first attempt for a solution would be this one :  The motion derives its continuity as to its parts from its trajectory. A division of the motion (also when it is not interrupted) can only be accomplished by dividing the trajectory. Well, let us assume that equal parts of the trajectory correspond with equal parts of duration, and so with equal parts of time. But then we run into troubles, and even into contradiction. Suppose a case like the one just given, but then such that in the beginning one body lags behind the other one, but catching up again precisely at the end-point. Initially, one motion is faster, later the other is. If we now want to divide this identical time [the identical duration of the two motions] into equal parts by dividing the trajectory into equal parts and then transpose this division onto the motions [and thus indexing them], the we obtain from both operations contradicting results. At least one of the two motions was accelerated/decelarated (maybe both), not uniform. So this attempt to define equal parts of time is incorrect. It will have to be amended.

One might think to amend things quickly, maybe too quickly. A uniform motion must be taken, one will say. And then equal parts of the trajectory will correspond to equal parts of duration and thus of time. And in this way one has a definition of equal parts of time. This is certainly true but one should be careful. After all, then one can and should ask :  What is a uniform motion? And one could be inclined to come up with a very common definition from elementary mechanics, which reads :  "motion is uniform if in arbitrarily chosen equal parts of time equal distances have been traversed". But if one then defines "equal parts of time" with the help of "uniform motion" we need "equal parts of time" again. So we have to arrive at a sharp concept of uniform motion in some other way, because this concept is prior to the concept of time like the concept of motion is prior to that of time.

Correct definition of uniform motion.
This is indeed possible. We began our analysis with the consideration of two bodies which simultaneously started their motion and simultaneously stopped it. To this we shall now add :  bodies that always remain together [i.e. in their motion the two bodies remain at rest with respect to each other.]. Evidently, such a case is possible. Let us call these two motions  congruent.  It is also immediately evident that these two motions may be performed  after  one another, that two congruent motions after one another are possible. The only difference with the first case is :  then [in that case] it could easily be  observed  that the motions are congruent. In the second case such an observation -- such an empirical finding -- already presupposes an entire theory and a knowledge of natural laws. But that is besides our point. In our present discussion it is not about observation, but about certain concepts, and these are clear.
The possibility of the second case derives from the fact that the successive continuum, just like the static extension, is, what one calls :  a principle of individuation. In this sense :  it is immediately clear that a figure which is  here,  in some extensum, realized, could  also be realized in exactly the same way in a different extensum (or in another right part of the same extensum, which may, when needed, be expanded), meaning that congruent figures  can  exist. Such figures only differ as to their  position,  differing purely individually, purely numerically. This is what one means when saying :  extension is a principle of individuation. This is clear to us as a result of a first  insight  of our reason. The same applies to the flowing continuum which is motion. Evidently, motions are possible,  only  differing in  succesive position, [differing] purely individually, purely numerically.  These motions we called mutually congruent.
Well, what applies to two (or more) motions also applies to successive parts of one single motion. Evidently, a case  can  exist in which two (or more) of these parts differ  only in successive position,  they  can  be congruent. Evidently this holds for larger and smaller parts. So a motion is possible in which  arbitrary, mutually equal parts,  whatever their size, are congruent. The equality of parts is defined by equality of pieces of the trajectory.  This motion we define as to be uniform.  And then we can say, without circularity :  equal parts of time correspond to equal parts of a uniform motion.
That all this "exists", i.e. is possible, is clear from our analysis. As a matter of fact, this analysis only makes explicit which is more or less understood in science.
How experimentally to decide whether a given motion is uniform or not, is, of course, a different question whose solution asks for much thinking and knowlege of experimental laws. Here we cannot go into that any further. Here we only analyze the very  concept  of  "time". Surely we may add a remark :  one sees, that the principle of inertia of classical mechanics, about which we have spoken earlier, is not so simple as one often thinks. Indeed, it presupposes the concept of uniform motion.
From way back one has viewed the daily motion of the heavens as to be a realization of a uniform revolution, and read off the division of time in equal parts from it. Possibly, its uniformity is not absolutely precise. But this doesn't bring with it any imprecision in the  concepts  of time and equal parts of time. It is the same imprecision present in all our observations.

The concept of "time" follows from motion (continuous change in general, but especially local motion). Not every "change" involves time. For instance a magnitude may also change with distance. But then it is a relationship, not a process.
Time is motion insofar as it can be indexed. Equal parts of time correspond to equal parts of a uniform motion. So with all this, we have now defined the topological and the metric aspect of time.

Yet a short remark may follow here. The topological structure of  "time" is, evidently, as well expressed by non-uniform as by uniform motions [because both possess the "before and after"]. But also for measuring time, non-uniform motions may be used. In two ways :  One with periodic motion, and the other with any other non-uniform motion.
So first, for measuring time, one uses oscillations or vibrations [i.e. periodic motions, which are special non-uniform motions]. Then each oscillation [i.e. each cycle] (with not too high an amplitude) of such a motion always takes the same amount of time as any other of that same motion. And even half or quarter etc. oscillations do have equal duration [all halves, or all quarters]. Any part of a period repeats itself along with the periods themselves, while within a period the motion is not uniform. Within a period unequal parts of the motion may correspond with equal parts of time. One may, of course, use these oscillations to measure longer times, including a large number of oscillations, even very precisely.
But, secondly :  even an arbitrary motion one could use, also as to its parts, to measure time, provided that one does not let correspond equal differences in numeration with equal parts of the trajectory [in faster motion a larger section of the trajectory is covered in the same time.].  If with faster parts of the motion one lets correspond a proportionally larger part of the trajectory and thus a smaller difference in number of equal parts of the trajectory [The just mentioned "smaller difference" should, according to me, refer, not to the faster, but to the slower parts of the motion, because in those parts of the trajectory representing the slower parts of the motion the consecutive numbers are less crowded than in those representing the faster parts of the motion.], - then  the flow of numbers  will be uniform, and thus with equal numerical differences of the divided trajectory will correspond equal parts of time. Then, while the motion itself doesn't flow uniformly, the artificially applied indexing does. [The irregular motion is divided into equal parts, by having the trajectory divided in conformity with the irregularity of the motion. And thus, even an irregular motion can provede a metric for time.]

In the analysis of the concept "time" we thus found :  "time" is something, within which motions flow, events take place. Something which determines or at least indicates the order of rank of coincidence or succession (simultaneity, before and after). Something that must be extrinsic to those events taking place  in  it [Time is not a thing of its own, not an individually existing essence, but may best be seen as an ontological condition of motion (s.l.), which (condition) we can call a dimension.]. The internal structure of time is this :  Time has something in common with motion. It is, like motion, continuous and flowing, but is nevertheless not identical with motion. Further :  Time primarily has a topological structure as a result of a possible or actual indexing of successive parts. On top of that lies a metric structure, which as such makes special demands on that indexing, such that to equal differences of numbers of this indexing do correspond equal values of time. Indeed, as a result, these  equal parts of motion become equal parts of time. [The trajectory of a motion, (this trajectory) just taken as a geometric figure with direction, itself also already has a topological and metric aspect. In order for time to have a metric aspect, the metrics of two motions (of which one is the one to which the other refers) must be compatible. The motion to which the other refers serves to measure this other motion, like we measure the time of an event by using a clock.].

So there must exist relations between the indexed motion, which is "time", and the events taking place  in  this time, relations, which are precisely indicated by this concept of  "in". What, then is here, the fundamental relation?
In spatial relations, those of nearness [immediately touching] and distance [mediately touching], we have found that they originate from one single fundamental relation :  the relation of  "contact"  between that what is placed and its place. From this we immediately obtain nearness (touching) and from this in turn distance. And notice :  this notion of contact was [found to be] a primitive concept, not reducible to any other, but of which the real possibilty is immediately clear to us by direct insight into the essence of the static continuum. Likewise, it is immediately clear that relations of nearness [direct contact] and distance [indirect contact] are given with it and originate from it.
And so it is also with relations of  "time". Also here we find a primitive concept, not reducible to any other, but itself clear as a result of direct insight, despite the fact that it may be difficult to establish, by way of analysis, what in this order of concepts is precisely the first one, the one that is immediately clear. This first one is also a notion of contact. With a part of that ordered flowing continuum, which is "time", a real motion may be in immediate contact -- like the two motions we discussed above were in immediate simultaneity-contact with each other. This indeed is a new and immediately clear concept, not reducible to any other.
And so it is with every motion with respect to another (potentially or actually indexed) motion serving as "time" :  that motion was not taking place in a previous part of this "time", it is in contact with this part of the same "time", it is not there anymore in a next part [of this time]. With that one part of "time" the motion coincides, like a body coincides with a part of the aether which it occupies. As a result the motion has its position in that "time". And from this, all its temporal relations with other motions come forth. This part of time is a measure of that motion's duration, like the constituent parts of that part of time are a measure of that motion's constituent parts coinciding with these parts of time. Indeed, it is also immediately clear that, first, the consecutive order of different events is topologically the consecutive order of the parts of time with which every one of them is in immediate contact, and that, second, the mutual distance-in-succession of these events is measured by the in-between-times. From the simultaneity-contact of two events [these two events not being simultaneous] with different parts of the "time", i.e. with a (potentially or actually) indexed motion, their distance-in-time results.
This concept of contact, and the [concept of] simultaneity derived from it, and the subsequent resulting distance-in-time, do not cause any trouble when considering events happening at the same place [one event, temporally followed by another event]. Humanity also never has had difficulties with this  concept  of simultaneity of events and motions taking place at a spatial distance from one another. This also points to the fact that also this concept rests on an original and unfailing insight, albeit that one perhaps has not meticulously enquired as to what here the original insight actually is. In the beginning of the 20st century the analysis of Einstein's theory of relativity has raised doubt as to the objectivity of the concept of simultaneity referring to events at a spatial distance from one another. And Einstein even has denied this objectivity [simultaneity of events are held to be dependent on the position and motion of observers]. Later we shall see that this has resulted from the incompleteness of Einstein's analysis. A more complete reflection in these matters clearly demonstrates the objectivity of that simultaneity. For the time being we will presuppose it.

We looked for a reality which can give reality-value to different propositions, propositions as :  " This happened then, in that time". Or :  " This lasted so and so long, so much time". We found out that this "time" must be something extrinsic to these events, being a measure of their duration, something flowing having the intrinsic structure which we have found. Does something like this really exist? Now the answer is easy, yes it exists. First of all, there are "particular times". We read a book from five to six o'clock. This reading is a motion or a complex of motions and events. This complex coincides, i.e. it is in simultaneity-contact with a part of the motion of the hands of our clock, which carries an indexing, which is taken over by the motion from its "trajectory". In a good clock these hands move with a regular circular motion. This "indexed motion" really is thus a time. In  this time, i.e. coinciding with that motion, our reading takes place and it finds in that a topologically known position in time with respect to other activities of the day. Metrically it finds in it a measure of our reading's duration and of its parts. Here, indeed, the  concept  of  "time" is actually realized. When the motion of the clock is not entirely regular -- and practically it isn't -- then it is, as a measuring instrument, imperfect, but its motion remains to be the possible carrier of another indexing, in which equal differences of consecutive numbers would correspond to equal parts of a genuine regular motion. Therefore, the motion remains a real time, although imperfect as a measuring instrument, like all our instruments.
But this is merely a particular time, which itself depends on a more universal, ultimately on  the  universal time. Precisely the same we found when discussing "place".  " Vondel spent a part of his life in Amsterdam". This sentence surely localizes our poet, but not directly into a universal coordinate system. To find his relation with the latter we must focus on the "place" of the town which he inhabited relative to the Earth, relative to the Solar System, and on the place of the latter relative to a universal medium of localisation :  the aether, in which the stars fix a system of coordinates. All this [earth, solar system, etc.], is only to complete our  knowledge.  In itself, as we saw earlier, every physical body is in direct contact with the aether and is, as a result, localized relative to other bodies standing in contact with other parts of the aether.
Something similar, but with some modification, holds for time. Our clock we have set yesterday after the setting of an official clockwork. This in turn is set after a still more universal chronometer. And this one, finally, is fixed by atronomers after a general true universal time :  the daily revolution of the heavens (or the Earth's rotation). And with parts of this time our [activity of] reading is in direct simultaneity-contact, just like a body is in direct local contact with a part of the aether. Indeed, when, during our reading, our clock would halt, our motion [the activity of reading] would not get out of time, it would remain in contact with other clocks, and, when also these would break down, it would still remain in contact with the motion of the heavens. Without astronomical observations we would no longer  know  what time it was and how long our reading had lasted, but our reading surely has taken place during a certain time.
The daily rotation of the Earth thus has the nature of one single universal time, and so the concept of one single time is realized. This time does not only apply to the whole of humanity now, it is universal in yet some other respect. The periodic motion of the heavens goes such a long way back into the past that it comprises the whole history of man ("periëchei", Aristotle says) and it will stretch out into the far future ... unless a catastrophe disturbs it.
But there is also a thorough-going difference between the general medium of localization which is the aether, and universal time being realized in the "[potentially or actually] indexed motion of the heavens" [This motion is, of course, not THE universal indexed motion. It may be the continued expansion of the Universe, the radio-active decay of certain atoms, the march of increasing entropy, or, when we view the world as one giant cellular automaton, its continued updating.]. In addition to being a universal medium of localization, the aether also has decisive  physical  influence upon the bodies. And the laws governing their motion primarily are laws of displacement in the aether. Also in this emphatic sense the aether is a  natural  medium of localization. If it would have vanished, some, if not, all, special natural laws would not hold anymore. Not so with time, realized in the motion of the heavens. Surely, Aristotle thought it was. He was of the opinion that all motion directly and physically depended on the motion of the last heaven and would stop with it. But that is an error, this physical influence does  not  exist. The motion of the heavens only pre-eminently realizes the concept [of time] as a result of the properties [of it] which we discovered above. If it stopped, other motions would still remain, and take over the function of "time". Every motion whatsoever would be fine, even, after Augustine's word, the rotation of the potter's wheel.

There is yet another resemblance-with-difference between "time" and "place". Earlier, we learned about the theory of contact as the only one in which relations of place, nearness, and distance, become intelligible, and so, as theory, must necessarily be accepted. But from this theory necessarily followed that in the supposition of two bodies (or worlds) not being in [physical] contact with each other, not directly, nor as a result of some intermediate real extensum, there can be no local relation between the two. They neither are near to each other, nor at some distance from one another. In a totality-theory as the one of St Thomas this supposition is, as we saw, rejected :  there cannot exist two worlds or bodies without any, unity-producing contact. But the fact that -- this supposition once accepted, [in the sense of  "if ..."] -- the conclusion necessarily follows, was not denied there.
The "space" of our imagination, that remains when all bodies, all real extensa, are eliminated, we recognized to be a mere being of reason, an in itself nothing, which impossibly could provide a fundament of the formation of distances between two bodies or worlds. That in our imagination there also exists an imaginary time, analogous to imaginary space, a flowing continuum which undisturbedly remains when all bodies with their motions are eleminated, we already stated at the beginning of our consideration of  "time". Nothing is easier to read off from our imagination. It even takes an effort, more than it does for "space", to intellectually overcome this imagination and to grasp the non-reality of that imaginary time.
So here we see similar problems as we did with respect to "space". If we make the supposition of two worlds, which  do not exist simultaneously,  and also do not follow upon one another as two contiguous motions, do they, then, still have temporal relations with each other, yes or no? Again there is the danger, as it was in the case of "space", that we interpret the data of our imagination wrongly. We graphically imagine :  a first world which disappears. Then an interval. Then a second world is created. But during these three phases the flowing of the imaginary time unrelentingly continues. There, in our imagination, the two worlds are separated and also connected in and during a certain time. So they necessarily are temporally related to one another. Each one of these worlds stands in simultaneity-contact with a part of this imaginary time. And these two parts are continuously connected with the intemediate part. That time is indeed  real in our imagination.  So it is not surprising that contact with its parts results in temporal relations. But this is not a correct picture of our supposition. After all, in the supposed case there doesn't exist any physical reality between the two worlds, not any real motion anymore. So in reality the time is absent that would connect the two worlds, and which would be a measure of the distance-in-time by which they would be separated, be the measure of the duration of the interval. Precisely as in the case of "space".

But not all is [precisely] as it is in the case of "space". For, albeit that in "time", as a result of the absence of whatever real motion, its metric structure has disappeared, the topological structure, the pure "before and after", is preserved. This is the reason why we already above stated that the topological structure in "time" is more deep-seated than its metrical structure. After all, this is the above supposition :  A world exists and is completely destroyed, a second is created. Let us consider the first datum :  that world  has  existed, and does  not  exist  anymore.  This is true, and will remain true forever. And it remains true forever also when no second world is created. If the second world is actually created [according to the mentioned supposition], then is also true :  the other  has  existed, is thus the first world, was the previous world. So there  is  a topological order of  "before and after" between both worlds. What is connected with this insight and indicating an objective difference between both worlds is this :  what had happened cannot be undone anymore. What has to happen may still be prevented by an agent with sufficient power. And moreover, also in a purely mental world change is possible, which, however, is not a  continuous  motion. But also this change brings with it an order of  "before and after", but an order without extension [In the Implicate Order we may think of this "before and after" to be an order of formal derivation :  the derived or derivable comes "after" that from which it is or can be derived.]. So it is not surprising that when, as a result of the destruction of a world, the extension, also that of motion, disappears, nevertheless the topological structure is preserved. The possibility of  "before and after" already follows from the  existence  of contingent beings [things or worlds] alone. The fact that on top of this  "before and after" does lie yet a metric structure follows from the fact that some of those contingent beings have a continuously-flowing existence. And where only that existence vanishes, only the metric structure vanishes with it, the topological structure remains.
[The argument in favor of the conservation of the topological structure of time is not too convincing. In the question whether one of the two (named and qualitatively distinguished) worlds exists, the "exists" makes sense only in reference to some point in time, either that point in time at which the question was asked :  "does that world exist today?", or some other point in time :  "did that world exist?", "has that world existed?", or "will that world exist?".  So in asking about the existence of some (named) thing or world  the continuous flow of time is presupposed, and then, of course, with it, its topological structure. If we strip off this supposition, then there is no question of "conservation of topological structure". As far as I [JB] can see things now, I would maintain that the (imagined) state of  two (or more) worlds not connected (or separated) temporally  is not as such unintelligible, and doesn't necessarily involve a "before and after". And if we let it be so involved, we have "imaginary time"].

[ ... ]

While introducing the concept of  "simultaneity", we have pointed to the fact that "simultaneity-contact" is a primitive concept, not reducible to other concepts, a concept that is intelligible all by itself. If events are concerned that happen at different but nearby places, one never has encountered any difficulty. Against applying the concept of simultaneity to events happening far from each other in space, humanity also has never objected, until at the beginning of the 20st century the theory of relativity of Einstein came with its objections, which it held to be so conclusive that it even denied the objectivity of "simultaneity" of these events. No thesis of the young theory of relativity did meet so much resistance as this one. Certainly, this is a demonstration that the human mind was convinced of the objective validity of its concept of simultaneity. Einstein and his followers, however, asserted that that conviction only rested on an old habit -- one even spoke of an inherited habit -- which should be abandoned in favor of the results of the analysis of the theory of relativity. However, it is possible that that conviction of human reason does rest on an existing, but not explicitly emphasized, insight which Einstein failed to reach in his analysis. The latter then would be incomplete. So we now know what to investigate next.

Einstein speaks about the only way by which the phycisist -- the human being equipped with the best knowledge of natural laws, with the best theoretically perfect instruments, measuring rods and clocks and all what is needed for their use -- can observe the simultaneity of events far away fom each other [and from the observer]. He uses light-signals to check the course of his clocks and to observe events happening far away from his laboratory. He uses them because he needs them -- for, except by way of messengers, the human mind cannot obtain knowledge of what happens far away from it -- he uses them because they are the best signals having the largest possible speed. But this speed is yet finite. Were the transmission of the signal instantaneously, then Einstein would never have raised any objection against simultaneity-at-distance. In the special theory of relativity also the hypothetical universality of the constancy of the measured speed of light plays a decive role.
Consequently applying the principles -- physical and mathematical -- on which the methods of our phycisist rest, Einstein comes to the conclusion :  two observers -- ideal physicists with perfect measuring instruments -- finding themselves in two systems moving relative to each other with regular motion, necessarily -- in principle, i.e. according these physical principles -- arrive, as to two events, A and B, at contradictory results as to the time relations, if these events take place at different locations. The one observer will, for instance, say :  A is simultaneous with B, while according to the other A has taken place before B.  Or even :  according to one, A was before B, while according to the other, B was before A.  The theory even gives formulas that fix these differences, among other things as a function of the measured speed of light. So what is simultaneous to the first observer, is not so to the second. And there are no means to decide between the two contradictory results. And from this Einstein concludes :  objective absolute simultaneity does not  exist.  Simultaneity of events-at-a-distance-of-each-other is relative to the observer. Initially, Einstein only concluded :  "objective absolute simultaneity does not exist  to the physicist". Soon after, he dropped this restriction and thus he stated as objective, the relativistic thesis :  absolute simultaneity does not exist for these events. One sees that this thesis is more than revolutionary :  not only the metric but -- severe offence! -- even the topological structure of "time" is disturbed :  "A takes place before B or takes place after B" often can be said with equal right. Of course with respect to different observers.

The direct result of Einstein's analysis was this :  absolute objective simultaneity cannot (as a consequence of natural laws) be encountered, cannot be  measured.  He further concluded :  this simultaneity does not  exist.  In order to arrive from the result of the analysis to this conclusion, another principle was needed. And this is indeed explicitly given by Einstein :  To the physicist (later this restriction is cancelled, it becomes :  not only to the physicist), that [thing] does not exist what cannot be measured [where "be measured" means :  be quantitatively observed]. Only when this principle is true, Einstein's conclusion follows from the direct result of his analysis. Usually an essential expression is added to this principle :  thàt [thing] does not exist, what cannot [even] "in principle" be measured [in fact it is necessary, but at the same time evident, that this expression should be added]. This principle is sometimes called (and it is) :  the fundamental principle of  Neo-positivism. Let us further analyze it. A correct understanding of it may also be of service elsewhere. The addition of the expression "in principle" is undoubtedly of importance. Indeed, otherwise the "principle" would be nothing more than a gross falsity. A trivial example which may, however, be of importance :  The moon faces the Earth always with the same half :  the back of the moon cannot only be measured [i.e. mapped], it cannot even be observed. Does it then not exist? To ask the question is to answer it. The fact that it cannot be observed and measured is not the result of a "fundamental" cause, but only of the fact that to our observers it is  technically  impossible to get at the other side of the moon [today one can]. But "in principle" it is possible. Let us make things still more trivial :  Suppose that it is not only technically, but also because of  physical laws,  impossible to get to the moon's other side with measuring equipment. Then one could, in a sense of  "in principle", namely because of physical principles, not measure the moon's other side. Could we then say :  the moon does not  have  an other side? This is nonsense to everybody. Suppose we know the moon only by looking at it, like the savage looks at it, then we might interpret it as being a disc, or perhaps as a semi-sphere. But that it  has  a back-side we  know,  already as a result of  insight  alone, insight into the nature of the extensum as such [The moon is, we can see it, an extensum, and this extensum is with all its sides in physical contact with its place, and so we understand that the moon has a back-side]. To note this, is the valuable aspect of our trivial example. This insight is a principle why we say :  the moon  does have  a back-side. And so we say :  it must in principle be measurable. This "in principle" now refers to that principle that is our insight. Athough the example may be trivial, it is precious, because here we can indicate the principle from which follows the measurability of the moon's back-side. So suppose the second case again, namely that physical laws, and thus not only poor technology, render observation impossible. Then there are physical  principles  present rendering observation and measurement impossible. And then it is in a sense "in principle", i.e. because of  physical  principles, impossible to measure the back-side of the moon. Nevertheless we would have certainty from insight as to its existence, and so we  cannot  say :  "the back-side is in principle (in virtue of a physical principle) unmeasurable, therefore it doesn't exist". From this example it is clear that the added expression, "in principle", does at least not in each if its meanings render the neo-positivistic principle true.
When, then, is this principle true? To "measure" something is :  to learn to know its quantity. Earlier we already saw :  "measure" makes us know the quantity of something. So if something, that should possess quantity, cannot be measured, not as a result of imperfect tools of observation, but by a cause within the object itself, then this object itself is not  knowable, not intelligible. And we already often have applied the metaphysically-epistemological principle :  That what is not intelligible is not an  ens,  not a being, does not exist. So if in the neo-positivistic principle, which we here investigate, the expression "in principle" -- referring to a principle -- does suppose a principle referring to the object-to-be-measured itself, then it is true. Then it is nothing else than that metaphyscally-epistemological principle (non-intelligible ==> non-existent).[That is, if the object -- here always some material object -- is in virtue of itself unmeasurable, then it is unintelligible, and therefore cannot exist].
Does, on the other hand, the expression "in principle" refer to a principle that only is about either the imprecision of the human ability to observe, or about the poorness of the physical tools of observation [and then the principle of the "in principle" does not refer to the object itself anymore], then one  cannot  apply the above mentioned metaphysically-epistemological principle [saying :  what is not intelligible, does not exist] anymore. In this sense the neo-positivistic principle is false. [If the non-observability of an object does not follow from what the object in itself is, but only from what precisely is an observer, in the sense of what precisely is the very act of observation and measurement, then the object has not become unintelligible, and thus we cannot say without more ado that that object doesn't and cannot exist :  indeed, it might exist.]. This is already fully clear from the example we have considered. But it may be instructive to bring in yet another example, which is of decisive importance in the measuring sciences.

Measuring of lengths.
This is theoretically surely the most simple measurement. It boils down to measuring the ratio in length of two rods or of the distances between two pairs of points. That these ratios do exist in Nature is a supposition that can be encountered in almost every physical reasoning. Einstein's observers continually apply them.
Can this ratio be measured? Certainly not with absolute precision. The ratio may be irrational (and then in fact not being a true ratio at all), but even when this is not the case, it can be measured at most up to a certain number of decimals, meaning that the next decimals remain uncertain as to their value, or totally unknown. Absolute precision is impossible in such a measurement. And, certainly, this impossibility is physically "in principle". It originates from physical principles. First of all there is an intrinsic limit of our capacity of observation. And because the last observation [to carry out], also when very ingenious instruments are being used, will be :  an observation of the coincidence of two calibrations or of the coincidence of a pointer with a calibration, this [last] observation is "in principle" bound to a limit of precision. And to which is added that also physical laws, like those of light refraction or deflection, governing the display of our optical instruments, set limits to the precision of these displays. So the ratio in length of two rods or two distances is "in principle", that is, because of certain physical principles, not precisely measurable. If we now would, following the neo-positivistic principle, conclude :  "therefore the precise ratio does not exist", we would apply the principle there where it cannot be used -- after all, it concerns principles, not referring to the object-to-be-measured, but only to the methods of observation -- and in the present case we know, and the positivists know it with us, that the conclusion would be not only illegal, but also false. Therefore, Einstein assumes that his ideal physicists with their perfect instruments carry out measurements of lengths and read off from clocks with absolute precision [He thus assumes that lenghts and the like are precisely determined in Nature]. So this is certainly clear :  If the impossibility of an absolutely precise measurement originates from physical principles  only,  controlling our tools of observation, the conclusion :  "therefore that quantity does not exist"  is  illegal.  Does one nevertheless draw it, in a case like the above, in which we know from insight that that quantity, with its relations, does exist, then we know moreover that the conclusion is  false.
Let us now, in the light of all this, investigate the problem of absolute simultaneity.

To what result did Einstein's analysis lead? He finds (if the hypothesis of the constancy of the measured speed of light is indeed  univerally  valid) a fundamental impossibility to measure with absolute precision simultaneity-at-distance. But the reasons from which this impossibility derive are  physical  principles [controlling our means of observation. The principles do not come from the events themselves]. Our observations and settings of clocks are dependent on the speed of the signals. The most perfect signals are those that propagate with the speed of light [but it has still the disadvantage to be finite]. The impossibility "in principle" thus is one that we above called physical, demonstrating the fact that the principle "what in principle cannot be measured, does not exist" cannot be applied here. The conclusion would be  illegal.  So mistakenly it was concluded that absolute objective simultaneity does not exist. And thus Einstein's analysis is  incomplete,  because the nature of the "in principle" which he has discovered was not further investigated, and therefore his further reasoning became  illegal.
All this is also expressed in this :  In the formulas, of which we spoke above, also appears the speed of light "c". When it increases (i.e. when it could be replaced by a higher speed), the deviations between [the findings of] different observers decrease. In the case of infinite speed of the signals (as one expresses this philosophically less fortunately), thus for an observer of the same events who wasn't dependent on signals at all, the differences [of the findings] would vanish and absolute simultaneity would be directly observed.
But we can go yet one step further, for upon closer analysis we indeed find -- which doesn't surprise us -- the insight guaranteeing the existence of absolute simultaneity [see further below], precisely as we have insight from which we read off the existence of absolutely precise ratios of lengths [in Nature], or the existence of the back-side of the moon. And then our further conclusion must be :  the assertion that absolute simultaneity of events at a distance does not exist is not only an  illegal  conclusion, but it is  false.  And this results from the incompleteness of Einstein's analysis [in which he, first, should have enquired into the "in principle", and, secondly, into our insight.]

To see this, we shall consider a principle which, as far as we know, is nowhere  explicitly  formulated, also not in the over-rich literature on the theory of relativity. But nevertheless a principle so clear that anybody reflecting on it will see that it is true. We mean the principle saying that a distance results immediately, instantaneously  (from a contact originating elsewhere). With this, the creation of a new  distance  differs from the resulting [the realization] of an  effect  at a distance. The latter needs time to propagate itself. This principle was considered already earlier.
Here is a concrete example from which we read off this insight :  Suppose that a material point moves along a trajectory perpendicular to a line AB.  We consider the moment at which the moving points intersects the line AB at the point P lying at a distance  a  from the point A.  We now have the insight that the moving point  immediately, at the same moment,  finds itself at a distance  a  from the point A and, the other way around, that A finds itself at the same distance from the moving point. A little earlier, these distances were other differences. From the contact of the moving point with the point P the new distance results instantaneously. This is so clear that it may sound trivial to even mention it. That it is nevertheless important, can be seen from the following :  If we were to speak about an  effect,  things would be different. Suppose that the moving point emits light when it is at P (on AB). That effect will reach A only after a certain time when the moving point has already left the line. Not so in the creation of distance. If the moving point is a sun coming, through P, above the plane horizon of AB, this sun will, just a little after having crossed the line AB, already  be  above the horizon of A, but not yet  seen  in A.  From this insight the principle is clear :  distances result instantaneously.

Let us apply this principle to the two systems discussed in the theory of relativity, systems that move relative to each other. With each system a coordinate system is rigidly connected. We take a random point P(1) of the first system (just lying at its border), and we look, while the motion is still going on, to the one moment at which P(1) coincides with the point Q(2) of the second system :

This moment is thus objectively completely determined by the coincidence of those points. If we now take a random point A(2) from the second system, then the point P(1) has, according to the "principle of the instantaneous realization of distances", at the same moment  [i.e. simultaneous with the coincidence of P(1) and Q(2) ]  the distance Q(2)A(2) from A(2), where Q(2)A(2) is constant, because Q(2) and A(2} both belong to the same system, the second system,  and, the other way around, A(2) the same distance from P(1) [because P(1) has coincided with Q(2)].  Only at this one moment. The indexes 1 and 2 indicate to what system the points belong. If we do away with these indexes and other references to these systems, then the just given statement will read :

If we now take a random point A from the second system, then the point P has, according to the "principle of the instantaneous realization of distances", at the same moment  [i.e. simultaneous with the coincidence of P and Q ]  the distance QA from A (where QA is constant), and, the other way around, A the same distance from P [because P has coincided with Q].  Only at this one moment. [When the motion of the systems continues, the distance PA will not be the same anymore as that of QA]. The distance needs not to be measured, it is simply there. This holds for any point of the second system. At  the same moment  P has the distances QA, QB, QC, etc. from the points A, B, C, etc. of the second system, and these points in turn have these distances from P.  Only at this moment. (that a given point may later obtain the same distance from P is, of course, immaterial in the present discussion).
The expressions such as :  " If A has a distance AQ from P,  B the distance BQ from P", etc. (AQ and BQ are constant magnitudes), each determine a moment, and, surely, the same moment, namely the moment at wich P goes through Q.  In the same way for all points of the first system a same moment is determined by their distances from Q (of the second system), which moment is also the same as that at which P goes through Q.  And this holds for any point such as P and Q, and thus for any moment of the motion. So indeed there  does exist  absolute objective simultaneity for all points of both systems [Accordingly, the facts that P obtains the distance QA from A, and that P obtains a distance QB from B, and that P obtains a distance QC from C, happen simultaneously. This is clear without any measurement. Perhaps the problem with this argument consists in the fact that "obtaining of distances" is in itself not a physical event -- and it is precisely "events that are observed" the theory of relativity speaks of. In this, we might perhaps imagine that at these points A, B, C (of the second system), certain physical events take place as a result of the distances they, at that moment, come to have, the distances QA, QB, QC from P (of the first system). These distances might trigger certain physical events at the points A, B, C.].

We were, in order to arrive at this result, looking at the motion of the two systems with respect to each other, a motion as carrier of a division (an indexing), and this indexing then is itself a time. So we may express the incompleteness of Einstein's analysis also in this way :  He supplies his ideal observers plentyfully with perfect clocks. But one clock, one carrier of time, he neglects :  the motion itself of his two systems. And if we consider this motion in the light of the "principle of the instantaneous resulting of distances", then, indeed, we find that there exists objective simultaneity. And to the motion of the two systems one may of course link a second, third, fourth motion.
Are observers really able to read off from this "clock" perfectly? No, it is not possible. For this [i.e. in order to measure] -- it is about human observers -- they need signals, coming from a distance. So the first result of Einstein's analysis remains unchanged. With these signals they can still not  measure  whàt events-at-a-distance are simultaneously. But we also see clearly that this fundamental imprecision is of the same kind as the others, imprecisions which are necessarily present to us in all physical measurements, imprecisions of the same kind as is present even in measurements of lengths. Instead of the revolutionary discovery which Einstein thought he'd made, namely the absence of objective simultaneity-at-a-distance, there only remains a new imprecision in the  observation  of this simultaneity, an imprecision joining up with the ones already known.
We now can formulate things also in this way :  In the formulae themselves of Einstein is included :  If we had at our disposal signals with "infinite speed", i.e. if we could observe instantaneously across a distance, then we could actually  find  absolute simultaneity [there where it actually is the case]. To explain this, we shall here insert a part of the consideration of Van MELSEN, 1955, discussing these formulae (pp.225) :

The Galileï- and Lorentz-transformations.
[It is about expressing the coordinates of the one system moving with respect to another, into those of that other system.]
Suppose that one wants to indicate the speed of someone, walking on the deck of a moving ship into the direction of the bow. If the ship has a speed of 15 km/h and the walking person a speed of 5 km/h, then the speed of the latter with respect to the shore is 20 km/h. So in this case the Galileï-transformation boils down to adding up both speeds. [The transformations with respect to location and time are respectively :  x' = x - vt  and  t' = t,  where  x  and  t  are the location (the space-coordinate) and (moment of) time (read off) in the first system, while  x'  and  t'  are those in the second system which moves with speed  v  relative to the first system. The coordinate in the second system is found by back-calculating where the corresponding point must lie in that second system.]. The consequence of this is that the determination of the speed of the walking person turns out to be different depending on the choice of system of reference, the ship or the shore.
However, in measuring the speed of light the Galileï-transformation does not hold. It has turned out that light has always the same speed [in vacuo] with respect to whatever systems of reference. To remedy this difficulty, Lorentz set up a transformation formula, which was such that in it the speed of light is always the same. Notable in this formula is the fact that not only the space-coordinates are being transformed (which is also the case in the Galileï-transformation, albeit that there the equations are different), but that also the time-coordinate is changed. This boils down to the fact that time [i.e. the moment of time at which some event is supposed to take place] in the one system is different from that in the other system. If, for the sake of convenience, we assume that the one coordinate system II moves into the direction of the X-axis of the other coordinate system I, then the formula reads as follows :

In this formula  t'  means the [moment of] time in system II,  t  the [moment of] time in system I,  x  the space-coordinate in system I,  while  v  is the speed of system II with respect to system I,  and  c  the speed of light (about 300000 km/sec). This formula is remarkable in more than one respect :
First it turns out from this formula that when  v  is not very large, v/c²  and  v²/c²  are almost equal to zero, as a result of the very large value of  c, the speed of light. The formula becomes  t' = t, implying that we notice the transformation of time [the moment of time] only when the speed of system II is very large with respect to that of system I.  Otherwise the Lorentz-transformation becomes equal to the Galileï-transformation.
Further, it follows from the formula that when two events, A and B, in system I take place at the same time and very close to each other [x then virtually the same] they also are seen by the observer in system II as simultaneous, even when  v  is very large.[Here we then have :  If t(A) = t(B) and x(A) = x(B), then t'(A) = t'(B)]. But he will record another moment in time in which this simultaneity takes place than does the observer in system I, because t' is not equal to t.
If, on the other hand, the two events, A and B, in system I happen at the same time but in different (far away) locations -- in this case  t  is the same, but  x  different -- then an observer in system II will not see them as simultaneously happening [as can be seen in the formula :  t'  is dependent on  x, so if we have two different values of  x,  we obtain two different values of  t', namely t'(A) and t'(B), so for the observer in system II event A takes place at time t'(A), while event B takes place at time t'(B). For the observer in system I the events are simultaneous, t(A) = t(B).]  But (all this) not so when  c, the speed of light, would be infinite, because then, in the assumed case of simultaneity, the formula does neither contain  v, nor  x  anymore. So in this case, if direct, instantaneous observation was possible, then simultaneous events would also be  o b s e r v e d  as simultaneous. (then, not only we would have t(A) = t(B), but also, because now t = t',  t'(A) = t'(B).

But there aren't such (infinitely fast) signals. Nevertheless, instantaneous realization of states does occur. Indeed, - now we know that  distances  are realized with "infinite speed", i.e. do result instantaneously, - this simultaneity does  exist.  Of it we have intellectual insight, although we cannot experimentally establish precisely whàt concrete events are simultaneous, like we cannot  observe  the existing accurate lengths with absolute precision. In the case of simultaneity-at-a-distance yet a new cause of imprecision is added, which we may perhaps not mitigate as a result of new findings.

The principle :  "what in principle cannot be measured does not exist" (or :  what cannot experimentally be verified does not exist) is only true if  "in principle" refers to a principle that is about  the quantity-to-measure  itself. Not if it is only about our methods of observation and tools, i.e. if it is only "physically in principle" as we called it above. So in this second case applying the principle [not measurable ==> not existing] is illegal and may lead to false conclusions. That the conclusion actually  is  false will be evident when we, from elsewhere, by intellective insight, know about the existence of the quantity-to-be-measured and of its relations. In this way one should distinguish between the two senses of the "in principle".
In the case of simultaneity-at-a-distance the impossibility-in-principle of measurement is merely a "physical" impossibility, and applying the principle  "not measurable ==> not existing"  is illegal. That that application leads to a false conclusion is evident from the principle of the instantaneous realization of relations of distances.

The above given definition of time and also the just given elaboration on it, seems to be contradicted by the theory of relativity, especially the notion of simultaneity. But, there is a caveat here :  While the philosophical definition of time admits of the possibility of the existence of objective and absolute simultaneity and therefore holds that there is just one universal time, the theory of relativity says, and rightly so, that absolute simultaneity cannot, even in principle, be measured. And, as has been said, it is now important not to jump to the conclusion that it then doesn't  exist. On the contrary, absolute simultaneity, is, although not measurable, presupposed by the theory of relativity :
This is because in the theory of relativity the possibility of  transformation  is assumed. Transformation here means that the location (place) and moment in time of a given event, i.e. one and the same event in the universe, can be determined in more than one system of reference (coordinate system). And this means that observers in different systems of reference that move with respect to each other, all can observe and record this event, be it that they will find different values of place and time, at which this event takes place. Transformation formulae admit to express time and place as measured within one particular reference system to be expressed in terms of another reference system that moves with respect to the first one.
The ensuing argument, demonstrating that absolute simultaneity is -- because transformation is (by the theory of relativity) supposed to be possible -- presupposed in the described situation, was first given by Van MELSEN, A., 1955, Natuurfilosofie (written in Dutch). There is an English edition of this work -- not a translation -- preceding Natuurfilosofie :  Van MELSEN, A., The Philosophy of Nature, 1954).

If we, for the sake of convenience, limit ourselves to two systems of reference, I and II, that move with respect to each other with a uniform motion (i.e. with constant speed), then the possibility of transformation presupposes that every event, recorded in I, can also be recorded in II. The transformation equations then exactly determine what the values of registration in II will be, when given in I, or vice versa. One can now express the presupposition, based on every transformation-possibility, also as follows :  The two systems (which move with respect to each other) should be constantly in contact with each other (i.e. penetrate each other), otherwise not every event could be recorded in I as well as in II. This being constantly in contact, however, means that at whatever chosen moment of time all points of II coincide with certain (though unknown) points of  I.  After all, there must be a constant correspondence ( = transformation possibility) between the two reference systems.
Precisely the existence of such correspondence presupposes something with respect to time, still apart from its measurement. It is, namely, presupposed that  at the same moment  when, say, point P₁ in system I coincides with point P'₁ in system II,  another point P₂ (in system I )  necessarily coincides with one or another point in system II. Otherwise the two systems would not be in contact with each other at that particular moment, implying that there does not exist any sensible application of the transformation equations. See next Figures.

Figure above :  Two systems of reference, I and II, moving with respect to each other. Both systems must be imagined to be extended indefinitely. See also next Figure.

The systems of reference (with respect to the assessment of place) should be understood as coordinate systems (For three-dimensional reality they must be three-dimensional) :

Figure above :  Two systems of reference, I (black) and II (red), moving with respect to each other. Both systems must be imagined to be extended indefinitely. They are coordinate systems, each provided with an origin (indicated by a green point). From such an orgin the location of some object can be indicated (with two coordinates), i.e. it can be measured.

So the application of the transformation equations presupposes that at every given moment, let us say the moment that is marked by a certain event at point P₁ in system I, all points of  I,  whatever their distance is from P₁ ,  coincide with certain points of system II. And in this fundamental sense (and only in this sense) one can legitimately speak of absolute simultaneity. This simultaneity does not mean that clocks indicate a same point in time. It means that a given moment in time is not limited to one place, one point in a system. Or, expressed in other words :  Absolute simultaneity, according to its fundamental philosophical meaning, expresses nothing more than the fact of the  coexistence  of the parts of the universe (Van MELSEN, 1955, p.236).
In fact, in virtue of the discovery of the presupposition, a simultaneity is discovered, that is objective (partly) due to the fact that the simultaneity was not found by means of signals (such as light). The simultaneity is, in this case, found in a direct way, and therefore it is absolute.

REMARK :  In the above argument we considered two events that occurred simultaneously, viz., the coincidence of point P₁ of system I with point P'₁ of system II on the one hand, and of point P₂ of system I with point P'₂ of system II on the other. But these are not really events in a physical way. So one could conclude that the implied simultaneity is not of a physical nature either, and therefore not real. And thus the argument, which was supposed to be about real simultaneity, seems to be invalid.
However, I don't think that things are that bad. The systems of reference, I and II, of the argument,  m o v e  with respect to each other, making them enough physical for the argument to be relevant.
Moreover, we could tentatively add the following :  Suppose that at the location and moment of the coincidence of point P₁ of system I with point P'₁ of system II, there happens to take place some physical event, and that at the location of our point P₂ of system I, while coinciding with point P'₂ of system II, there also happens to take place a physical event. Then from the fact of the simultaneity (here in the sense of [mathematical] coexistence) of the two coincidences (P₁ with P'₁, and P₂ with P'₂ )  it follows that also the two  physical  events took place simultaneously.

It is of great importance to realize that the above described presupposition (present in the theory of relativity, and based upon the supposed possibility of transformation) of the simultaneous coincidence of points of one reference system with those of another (that moves with respect to the first), does not mean that this coincidence can be objectively registered. To see this, let us analyse the following case :
Suppose we have two systems of reference, I an II, as described above, which uniformly move with respect to each other. If we take into account the possibility that the (constant) speed involved in this motion can be very high, i.e. can approach the speed of light, then the transformations that relate these two reference systems must be (according to the theory of relativity) the so-called Lorentz transformations for place and for time.
Suppose further (see this Figure above ) that at a certain moment point P₁ of system I coincides with point P'₁ of system II, while this moment of coincidence is recorded as  t₁ .  If we further, for the sake of convenience, suppose that system II moves in the direction of the x-axis of system I, then, with respect to the position of P₁ in system I only the x-coordinate counts. We suppose that, by measurement in system I, it is assessed that the involved coordinate is  x₁ .  And now, according to what has been said above, at the same moment when  t₁  is measured, another point P₂ of system I will necessarily coincide with one or another point of system II. Let us call this point P'₂ .  (a little later we say something about its position). The difficulty, now at hand, is that observers in I and II will not agree among each other as to which points P₂ and P'₂ of both systems will coincide at the time  t₁ .  The position of point P₂ of system I and with respect to I, at the time  t₁  is measured to be  x₂ .  This point will coincide with a point P'₂ of system II. This point thus becomes identical to the point with location  x₂ ,  but the location of this point as assessed within system II is different. It is different according to the Lorentz transformation of a coordinate. The new coordinate (x'₂) then is :

What we, until now, have is that the observer in system I maintains that point P₂ with the coordinate  x₂  coincides, at time  t₁  with a point P'₂ of system II.
However, the observer in system II sees the coordinate of the point P₂ as being not  x₂ ,  but  x'₂  (the value of which is given by the above formula). So they disagree about the position of the point P₂, and they explain this by maintaining that the measurement of the coinciding of the points P₂ and P'₂ was not done at the same time.
Observers in system II, that find themselves at the points corresponding with P₁ and P₂ of system I will maintain that their colleagues in system I at P₁ and P₂ did not assess the point in II, that coincides with P₂ in system I, at the same moment as that moment in which P₁ and P'₁ coincide. According to the observers in system II the time  t₁ ,  that the observer in system I at point P₁ uses, has (according to the Lorentz transformation for time) the value :

while the time used at P₂ (by observers in system I )  according to them (i.e. the observers in system II) has the value :

So according to the observers in II these moments differ, and they conclude therefore that the observers in system I were wrong about the simultaneity of the two events, viz., the coincidence of P₁ with P'₁ on the one hand, and the coincidence of P₂ with P'₂ on the other.
The observers in I will, however, maintain that they have measured at the same moment. So according to them the coincidence of P₁ with P'₁ took simultaneously place with the coincidence of P₂ and P'₂ (Van MELSEN, 1955, p.236--237).

So indeed we see that the necessary presupposition of the existence of objective simultaneity, in the sense of being implied by every accepted possibility of transformation between systems of reference, namely that the places of one given coordinate system are continually in contact with those of another coordinate system, doesn't say anything about the possibility to actually and objectively measure this simultaneity.
There is no possibility to measure this simultaneity. And this is a true result of the theory of relativity. Therefore the concept of simultaneity does not make sense in natural science, but it does make sense as one of its presuppositions, and as such it is a truly philosophical concept.

So in our metaphysical (and thus philosophical) analysis of reality, which is a consideration of the way and status of Being and beings, we can accept the existence of absolute simultaneity.
And such a simultaneity implies the existence of absolute place (absolute position), because of the following reason :
If at location  x₁  an event  g₁  takes place, then a simultaneous event  g₂  cannot take place at location  x₁ .  It can, however, in principle, take place at any other location (i.e. at any location which is not  x₁ ). And this shows that the location  x₁  is unique with respect to a given event. In the same way we can couple a different event to another point, say  x₂ ,  and so on with respect to every point whatsoever. All this means that  place  is something absolute. And this means that we have found with all this a second indication of the truth of the contact theory  ( The first indication was conceptual in nature, it drew from the concept of ens extensum). And after having established objective place, absolute motion follows as a consequence, because motion is continuous change of place.
As we have said, absolute simultaneity cannot be objectively measured, and so, consequently absolute place and absolute motion cannot be so measured. And that's why the outcome of the famous Michelson-Morley experiment was negative.

We want to conclude this exposition about simultaneity and the theory of relativity with a short remark. In the years of youth of the theory of relativity one often -- today less often we think -- has wanted to fuse together space and time into one single amalgam. Time would be something like a fourth dimension, not only in a graphic display, to which we do not object, but in reality. Time would be inseparable from space, in the same way as the three dimensions of the spatial things themselves. Time would be a dimension, homogeneous with the spatial dimensions. A different perspective would yield a different time, just as valid as the time of every other perspective. This became even more emphasized as a result of the elegant mathematical construction of Minkowski, introducing time as an imaginary fourth coordinate. Minkowski himself expressed this in his well-known words :  "Von Stund an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren." [Translation :  "From now on space in itself and time in itself will sink into mere shadows, and only a kind of union of both will retain entity."]. This is certainly strongly expressed but not, therefore, necessarily true. We keep on understanding that time, as a flowing continuum, essentially is something different from the static extensum. Complete homogeneity will not be urged by anybody anymore. Einstein himself was working out a fairly separated state of both continua, as his words (1928) do witness [Here directly translated from French into English] :  " Time and space are well founded upon a same and unique  continuum, but this [continuum] is not isotropous. The characters of the element of spatial distance and those of duration remain distinct from one another. And this up into the formula giving the square of the interval of universe of two events infinitely close to each other."
Anyway, also a complete separation of time and spatial dimensions is realized in Nature. We now sufficiently know that, in addition to local motion, also purely qualitative motion (of course in an extensum) exists. Well, the range of intensity of a quality has nothing to do with spatial dimensions. The qualitative motion of increase of an intensity (at a same point) also has nothing to do with spatial dimensions, and it takes place in time.  Time is also not homogeneous with the dimension of a range of intensity as it is [not homogeneous] with those of space. Otherwise, these themselves [range of intensity, space] would be homogeneous, which is absurd.

Back to Homepage

Back to Contents

Fifth Part of Website

Back to Part I

Back to Part II

Back to Part III

Back to Part IV

Back to Part V

Back to Part VI

Back to Part VII

Back to Part VIII

Back to first part of theoretic intermezzo

Back to second part of theoretic intermezzo Back to Part IX

Back to Part X

Back to Part XI

Back to Part XII

Back to Part XIII

Back to Part XIV, Dipterygia, and conclusion of flight-devices in insects

Back to Part XV, first part of the theory of inorganic nature

Back to Part XVa, second part of the theory of inorganic nature

Back to Part XVb, third part of the theory of inorganic nature

Back to Part XVc, fourth part of the theory of inorganic nature