e-mail : 
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
Index of the Sections presented in the present document.
This document (and the next one) summarizes and further extends our noëtic theory of evolution. But because it is a long and rather complicate exposition of that theory (so far developed), it may be convenient to present an index of all the various Sections in it, in order to lay bare this documents's structure.
|
Having now given an index of the Sections of the present document, the reader may now proceed to actually study this document.
Introduction
According to our theory, evolution is said to be rooted in the Implicate Order, that is, in the immaterial domain of Reality. Therefore it is grounded in Metaphysics, to be precisely in ontology, i.e. the metaphysics of Being. And if this theory is correct, then natural science cannot grasp the very essence of organic evolution, because natural science is an empirical science. It attempts to explain material phenomena (including organisms) that are actually observed. And its theories are verified exclusively by in principle observable phenomena (observation and experiment). It has set out its scope precisely by limiting itself to observable phenomena and their explanation, whereby the explanation must be rooted in other observable phenomena. This does not, however, mean that phenomena that are, even in principle, unobservable cannot exist, because this assertion would be based on some 'sneaked-in' philosophical position that says that Being is equivalent to being (directly or indirectly) observable. But within natural science this assertion itself can never be demonstrated to be true, because it cannot empirically be tested. So such an assertion falls outside the scope of natural science.
Returning to organic evolution, only the successive appearance, in the Explicate Order, of organismic species and types is determined by physical and biological conditions existing in that Order [the only Order of Being or Reality accepted by conventional natural science], and can be recorded and mapped out by natural science. It can try to uncover correlations between existing climatic and ecological conditions on the one hand, and the appearance of particular organic types on the other. It may also, where possible, compare genomes of different organisms, because DNA is telling us much about its bearers [In our theory much of the DNA in a given organism is part of the strategy of the species to which that organism belongs. It contains the information of how to build up the individual of the species. The information, stored in the DNA is retrieved, to begin with, by the DNA-ribosome mechanism in the cell. So there exists an isomorphy between genotype and phenotype. But the existence of an exact mapping of DNA structure onto the structure of the phenotype is not directly evident, because the decoding process is extremely complex. Within the material organism, the phenotype is the meaning or interpretation of the genotype.].
Natural science can then set out to explain observed similarities obtaining among the species of a given group of organisms by common descent. And indeed, it has an elaborated theory of common descent, based on random genetic mutation and natural selection.
In our noëtic theory, on the other hand, materialized strategies -- organismic species -- simply do appear just like that, in the Explicate Order, in their proper ecological environments, i.e. in their proper ecological niches, without having descended one from another. So, according to our theory, at least in the Explicate Order (i.e. just the whole of empirical reality of natural science) there is no common descent, no evolution, at all. Physically this is wholly ununderstandable, because the complex must somehow have been evolved from the simplex. According to noëtic theory the very 'making' of the strategies -- the transformation of original immaterial forms into (still) immaterial but fully-fledged strategies [i.e. noëtic descriptions of them] -- takes place ["takes place" not referring to an event or process but to details of existing structure] in the Implicate Order as part of the 'process' of the materialization of those original immaterial forms. And only when suitable physical and ecological conditions actually exist in the Explicate Order to make these immaterial strategies effective, the latter will be projected, i.e. they appear as organismic species in the Explicate Order. Natural science, and especially Biology, may study the successive appearance of organismic species as this is determined by the presence of the proper ecological niches in which the strategy precisely fits. It may therby study the nature of adaptation of a given organismic species or type to its environment. It may further study the geographical and geological distribution of species or types as depending on ecological factors, such as barriers, climates, content of existing biocoenoses, etc. And, finally, it may study the morphology, physiology, and life-history of a given species or type, i.e. it may study the nature of its strategy to exist and persist. But it cannot investigate the very g e n e s i s of strategies, because that is, as has been said, something metaphysical, and therefore falling outside natural science's proper scope. [if, of course our noëtic theory is accepted].
So, as to the question in what way immaterial forms develop, in the Implicate Order, into (and until then still immaterial) true strategies, we can only set up conjectures, which may, it is true, be rendered more plausible by certain observed phenomena, but which cannot finally be confirmed or proved empirically. We need not be embarrassed by this, because even current evolutionary theory is replete with conjectures. The only thing that might disturb a scientifically-minded reader is the fact of the intrinsic nature of our conjectures, namely that they cannot, even in principle, be confirmed by observation or experiment. This makes our theory to be, not merely yet another scientific theory added to the set of already existing theories, but to be, in its very kernel, a metaphysical theory, and a new one indeed.
As to conventional theory, one holds that its hypotheses are such that they potentially may be confirmed by observation or experiment, and so are truly scientific hypotheses or theories. But is this truly the case in conventional evolutionary theory? Is it not just a collection of speculations without any prospect of empirical confirmation? Indeed, trying to have -- as conventional theory does -- complex organisms evolved from simple ones, or complex functions from simple functions, is pure r e d u c t i o n i s m [ which is, by the way, when it succeeds, the only way to explain material phenomena in a genuine scientific way (which sticks to observable fact), in contrast to a philosophical way (which allows for immaterial forms as well ], because in this (reductionistic) way complex organisms -- complex strategies -- are reduced to [i.e. explained in terms of] simple ones ('primitive' ones]. Precisely this is also the case in monophyletic evolutionary theory : A given group of organisms is reduced to one single and primitive (often hypothetical) ancestral species. The latter unfolds, in the course of history, eventually resulting in its present condition : the mentioned group or taxon. This is done in phylogenetic as well as in typological evolutionary taxonomy. And in doing so, inevitably one falls into the trap of the "reductionistic nightmare" : because, even if, to quote a more general example, we actually k n e w the 'ultimate formula' (equation, dynamical law) of the World as a whole, and if we also had knowledge of its initial condition, we still could not make long-term predictions from them [dyn. law, init, cond.] (because such a World-system is certainly highly sensitive to changes in initial conditions, and the dynamical law very complex) as to how precisely the World will unfold [this is already evident in much more simple dynamical models]. The only thing we can do is sit and watch. And if we would, in some way, k n o w for sure that our present World has indeed actually evolved from the supposed initial condition by the successive changes of it according to the supposed ultimate formula, equation, or dynamical law, then our inability to make predictions from them, i.e. to actually u n d e r s t a n d the course of the world's history, is, it is true, merely an e p i s t e m o l o g i c a l reductionistic nightmare, but a nightmare all the same. But when we actually do not know whether the World has actually evolved from these supposed conditions (init. cond., dyn. law), i.e. when these conditions are completely hypothetical, then we really have to do, not only with an epistemological, but also with an o n t o l o g i c a l (i.e. concerning facts) reductionistic nightmare. Explaining from supposed initial conditions we soon end up in an impenetrable tangle completely obscuring the end-condition that we had wished to derive from these initial conditions.
And this, in my opinion, is precisely also the case in reductionistic evolutionary theory (whether it be about the ancestral line(s) of genomes (DNA) or of whole organisms), because not only all of the alleged stem-species (of groups or taxa), or stem-genomes, are hypothetical, but also the way along which these stem-species should have evolutionarily diversified, developed, and complexified, and eventually, allegedly, having resulted in certain given modern groups of organisms. The problems of letting (in this reductionistic theory) random genetic mutations and natural selection drive the whole evolutionary process, and all the problems that arise when one attempts to formally derive later organisms from earlier ones, make up the reductionistic nightmare of evolutionary biology. And here the nightmare is not only an epistemological one, but a factual one as well, because we do in fact not know whether later organismic species have actually descended from earlier ones (or later genomes from earlier, more simple ones, for that matter). So all this has led us to our "noëtic theory of evolution". Of course a theory with its own mysteries. It is, however, not so that we simply are replacing the 'lucid and evident current theory of evolution' by some obscure metaphysical alternative full of mysteries, because although our theory is indeed metaphysical, this fact alone is not sufficient for its dismissal [as a scientifical theory it may be dismmised, but not as just a theory, embedded in a broader setting], and we have done and will continue to do our utmost best to make our theory as lucid and plausible as possible, and further be completely honest and objective with respect to these matters.
As has been said, what precisely happens in the Implicate Order we also don't know, but we can make some clarifications and conjectures.
Because, so we then theorize, immaterial existence is inferior to material existence (in contrast to what was held in classical Greek philosophy) by reason of immaterial entities being ontologically incomplete (they lack [prime] matter), immaterial forms always aspire to become material, and this means for them to exist in the Explicate Order. And precisely because of all this, the Implicate Order is intrinsically attuned to the Explicate Order, that is, to its superior Being. The Implicate Order is not transcendent (as Plato supposed), but immanent with respect to the Explicate Order. It is wholly entangled with, and, as it were, wholly residing within, the Explicate Order. And we may, perhaps, conjecture that being attuned to it (i.e. the Implicate Order being attuned to the Explicate Order), is in fact to know it, i.e. we may conjecture that the Implicate Order knows the Explicate Order. And this makes it possible to have, in the Implicate Order, original immaterial forms automatically developing into strategies to exist in the Explicate Order. It is a noëtic 'process' driven by the metaphysics of Being.
This process, because it is noëtical, is not an event taking place in time. It is no more than just a derivational structure of some section of the Implicate Order. And this section has this structure because it constitutes a formal system of noëtic strings (of symbols). Some of these strings are axioms, other are theorems derived from these axioms by having applied the production rules of this system. As we will argue later on, this formal system of noëtic strings is defined not by or in the Implicate Order, but by the Explicate Order as a result of the former being fully attuned to the latter.
The generalities of the 'machinery' of the Implicate Order and its relationship with the Explicate Order, especially when all this concerns the production of (noëtic descriptions of) organic strategies (from elements or from other such strategies) have been described in the parts LXa (formal systems and meaning), LXb (typographic number theory [TNT] ), and LXc (formal system of noëtic strategy-strings) of "Organic Evolution" in Fifth Part of Website. In the present document we will give a summary of the results obtained in these parts, by reproducing certain important sections from them (and referring to other such sections by a link) and adding further considerations. Perhaps, before reading the following summary, the reader should study the mentioned parts in Fifth Part of Website. For having access to the left frame as well of that Part of Website, click HERE.
The biological formal system in Noëtic Space
( From Part LXa of "Organic Evolution" in Fifth Part of Website )Earlier we had established that the Implicate Order is an immaterial range of Being -- noëtic space -- where the patterns present in it are, to begin with, elementary immaterial patterns, or products of noëtic reactions having (noëtically) taken place between either these elements among each other, or between these elements and certain products, or between products among each other. Still other noëtic patterns may be the result of a so-called one-reactant noëtic reaction giving rise to one or more products different from the one reactant. And in all these noëtic reactions no reactants are exhausted (because this is a matter pertaining to the Explicate order). And of course these 'reactions' do not take place in time, they are purely noëtic, and can best be compared with mathematical derivations.
In the present document we want to investigate further the general structure and nature of noëtic space. That is to say that we'd like to sort out the possibility that noëtic space -- the Implicate Order -- is a collection of "formal systems" [ We must realize that our context - when discussing noëtic theory -- is always strictly ontological (that is, is always about the objective and independent existence (independent from being known) of things and patterns, generally of b e i n g s. So for "formal systems" their "reason to be" here, that is, to exist in the Implicate Order, and the reason for us of going to consider them, has, in the present context, nothing directly to do with things like axiomatic theory, the theory of cognition, or epistemology : In the present context of noëtic theory (of evolution) the status of "formal systems", in so far as they are considered to reside in the Implicate Order, is throughout o n t o l o g i c a l ]. Each such a formal system has one or more (noëtic) Starting Patterns ('Axioms'), and one or more Rules of Derivation (producing new patterns from 'old' patterns [first of all from the starting pattern] ). Here we will concentrate on that particular formal system (or systems) in the Implicate Order (noëtic space) that is associated somehow with organisms in the Explicate Order. Already earlier we had established that (at least) the noëtic patterns in noëtic space associated with organisms are connected with each other by relations of (formal) derivation. These derivations are the result of so-called "two-or-more-reactant noëtic reactions" or of "one-reactant noëtic reactions". This derivational structure of (at least) 'organic' noëtic space is, as we had established, expressed by the "noëtic trajectory" (or trajectories). This trajectory is in fact tracing out the evolution of organisms as it, first of all, takes place in the Implicate Order. But the result of this evolution, now as seen in the Explicate Order, forced us to assume that the sequence of noëtic derivations, the noëtic trajectory, cannot be unbranched. So the general process of noëtic derivation of one noëtic pattern from another must allow for branching, and is therefore quite unlike the trajectory of states in a deterministic dynamical system, which (trajectory) is unbranched. So these dynamical systems, in their mathematical form, could not serve as an analogue of the noëtic processes. Consequently, we had to find a kind of (formal) derivation that allows branching (and in fact we already knew that "reactions" of some kind, resulting in new noëtic patterns, are compatible with branching, because A can give B as a result of reacting with N, while it can give C as a result of reacting with M ). And more completely and more evidently, we have found legitimate branching in formal systems with more than one derivational rules [ For example, from A can be derived B, using Rule 1, but from A can also be derived C, using Rule 2 ]. Here branching of the derivational trajectory is quite natural. It is therefore worthwhile to investigate more closely the general nature of formal systems (and combining their Rules with the affinity or lack of it between reactants of noëtic reactions). In all this we must assume that the Explicate-Order-counterparts of the Implicate-Order-noëtic patterns [the latter in our (biological) case being strategies, present as noëtic descriptions] are not only these patterns-materialized, but also their . . . "meaning" (still in an ontological, not a linguistic, sense). That is to say, these Explicate-Order-counterparts -- organisms -- form the meaning of corresponding noëtic strategies, a meaning based on natural (= ontological) 'interpretation' of the 'symbols' of the mentioned noëtic descriptions. We also may perhaps say that the biological part of the Explicate Order is analogous to a system of 'true' propositions based on a natural interpretation of the mentioned symbols. These 'true propositions' are isomorphous counterparts of the axioms and theorems of the noëtic biological formal system.We had found out that in the Implicate Order (noëtic space) the immaterial patterns -- existing in it -- strive for ontological completion. They can achieve this by being projected into the Explicate Order. Then pure Forms will -- as a result of being unrolled along the space and time dimensions of the Explicate Order -- "inform" Prime matter. Each such a Form will then be manifested as a collection of material "individuals", variable in number and place of occurrence. But projection of a given immaterial pattern -- a Form -- from the Implicate Order into the Explicate Order can only take place if prevailing existential conditions in the Explicate Order are compatible to and receptive for this pattern. So it is expected that most immaterial patterns, noëtic patterns to be sure, -- and especially very complex patterns -- will never be projected, because they have the greatest chance to lack any compatibility with the Explicate Order. But, as we have explained earlier, some such complex patterns will nevertheless manage to be projected, because they are in fact patterns of a special sort : they are "descriptions", descriptions that is, in a strictly ontological sense, meaning that they are not written down by some one author. And they are not only just descriptions, but each one of them a description of a particular "strategy" of how for this very description itself to exist and persist in the Explicate Order. And, upon projection into the Explicate Order, they appear there materialized as o r g a n i s m s. The organism (including its internal chemistry, physiology, morphology, and behavior) is the manifestation or meaning, in the Explicate Order, of that noëtic description. So we must imagine such a "strategy", as it is in the Implicate Order, that is, as it is a noëtic description, to be a s t r i n g (with a definite direction) of consecutive "symbols", a string located in a definite 'place', that is, at a set of definite noëtic coordinates, in noëtic space, as we had already explained in Fifth Part of Website, the"noëtics" section of Part LVII of "Organic Evolution" :
Figure 1 : Greatly simplified and schematic sketch of a STRING in a 2-dimensional analogue of noëtic space (which itself is not spatial and which is multidimensional, where a "dimension" is a scale or range of a given qualitative parameter). Each red rectangle represents a symbol of this string. The identity and nature of each symbol is determined by its position in noëtic space, that is, by its noëtic coordinates. The coordinates in any rectangle (white or red) are those of a single representative point of the rectangle (for instance its upper left corner). Here the string possesses only nine different symbols. In reality, however, that is, in noëtic space, it will, when it expresses a strategy, consist of a great many such different symbols of course.
Any string consisting of more than one symbols has a fixed direction. So the consecutiveness of the symbols in any given string is fixed (like the letters or the words in a description). We will indicate this by the direction of the noëtic trajectory (going from one string to its derivative) passing through the string :
Figure 2 : Noëtic trajectory. The fixed direction within a STRING in noëtic space. The fixed consecutiveness of the symbols in the string (resulting from, or representing the STRING's internal direction) can be given by their consecutive (representative) noëtic coordinates : (6,14), (7,15), (8,15), (9,14), (10,13), (11,13), (12,13), (13,13), (14,13).
In certain cases it might be more convenient to represent the symbols in our diagrams not by their noëtic coordinates, but simply by letters (which are suggestive of the fact that the STRING is a (noëtic) description) [but there will remain many cases where using the coordinates is more instructive].
(end of quote from part LXa of Fifth Part of Website)
We theorize that all these noëtic strings together form the elements a formal system, residing in the Implicate Order, in which (formal system) strings are produced from other such strings by applying a set of production rules inherent in the system. The strings themselves are descriptions or elements of them of biological strategies. We may, then, imagine that each string is composed of symbols -- the symbols of the formal system. We may call this system the "Formal System of Noëtic Strategy Strings" ( FSNSS ). And although its name suggests that the elements of this formal system are only the descriptions of fully-fledged strategies, certain 'not-yet-strategies' also are supposed to be elements of the system.
It is possible for us to assign to each symbol of this system a natural number and to arithmetize its production-rules, and so embedding the whole of FSNSS in number theory (N). Ontologically we indeed assume that it is actually so embedded. With this we further assume that all natural numbers are actually existing in noëtic space (the Implicate Order), and, for convenience, we keep on calling this actually existing set of natural numbers and their inherent properties "number theory" (N). And then each coordinate of noëtic space, as depicted in the above diagrams, should correspond with a natural number, now resulting in our having a collection of individual number-strings each having a definite direction (of 'reading' them) and a determined beginning and end. But the definite direction and beginning-and-end of such a number-string, i.e. its definite delimitation, are not imposed by number theory, but by FSNSS, which itself is delimited -- defined -- by the Explicate Order. In what way precisely such an embedding -- of FSNSS in N -- is accomplished is expounded in part LXb of "Organic Evolution" in Fifth Part of Website. And because we actually do not know much of FSNSS, we have taken there an analogy of it, viz., the MIU-system, which is a formal typographical system made up by HOFSTADTER in his Gödel, Escher, Bach (GEB) (and which is expounded in Part LXa of "Organic Evolution" in Fifth Part of Website ), in order to explain, not, of course, our FSNSS, but to expound the very nature of typographical formal systems in general (systems considered in number theory and mathematical logic) and how to embed such a system in number theory. Having selected Hofstadter's MIU-system as an analogy of our Formal System of Noëtic Strategy Strings (FSNSS) we must realize that the MIU-system is for many purposes far too simple to serve as an analogy of our supposed FSNSS, but as long as it is appropriate to let it so serve, we will use it in our expositions.
We take the rules of FSNSS to be such that in it from non-strategies true strategies are produced, further, that from already produced strategies are produced other strategies, and finally, that in the production of these other strategies the noëtic trajectory (the path of successive derivations) tends to follow an increase of internal integration of successively derived strategies. Internal integration of a given strategy means that its parts are closely attuned to each other and to the whole strategy. We suppose that a higher degree of internal integration renders the strategy -- still as a noëtic description -- noëtically more stable, meaning that the transition from a lower to a higher degree of internal integration (not exhausting thereby the strategy with the lower degree of integration) is spontaneous or is built-in in the production-rules of FSNSS. Upon projection of a series of strategies with increasing internal integration, we see, in the Explicate Order, the phenomenon of evolutionary higher-development (anagenesis), as we see it, for example, in the evolutionary series Fish-Amphibian-Reptile-Bird-Mammal.
Of much importance are two possible states of affairs that follow from the fact that all formal systems allow themselves to be 'arithmetized' (i.e. allow themselves to be mapped onto number theory (N)). First, this very fact itself may point to the possibility that the organic noëtic formal system (FSNSS), of which the "strings" are "organic strategies" or their elements (i.e. non-strategy strings), which in turn are noëtic descriptions (involving noëtic symbols or 'letters'), is ultimately such that the "derivations" of given (noëtic) strategies or elements of them, from other (noëtic) strategies or their elements, are in fact arithmetical transformations (that make them, by the way, truly noëtical!). Second, the possibility for us (and now thus in a (human) cognitive content) to successfully arithmetize formal systems -- by assigning so-called Gödel-numbers to their symbols and arithmetize their production-rules -- makes us able to show, following HOFSTADTER's expositions, that, as told in part LXa of Fifth Part of Website, certain strings of a given formal system express something of other strings of the same system. For us this means that a (noëtic) strategy can involve in its intrinsic description other strategies, and this involvement will reappear in the isomorphic material version of it in the Explicate Order and is a key-feature in ecology.
In working-out the present summary of the noëtic 'machinery' still further, it is now time to dwell a little longer upon the cognitive, and, especially, the ontological status of several formal systems relevant to us, and upon the location of MEANING in them. For this we will reproduce a section written already in part LXb in Fifth Part of Website :
In order correctly to judge the status of number theory (N) and its formalization TNT, especially how MEANING functions in them, it is important to distinguish two viewpoints or contexts, from or in which we see them :"Ontological" (context, or domain) means "viewpoint from things or patterns as objectively existing" (in the Implicate or Explicate Order), that is, existing independently of being (or not being) known.
"Cognitive" (context, or domain) means "viewpoint from things or patterns insofar as they are, can, or cannot, be known, or insofar as they are mere instruments of knowledge".In the present exposition we have to do with five systems that are related to each other by MEANING. These systems are :
N (number theory) may represent an informal theory about the properties of natural numbers. Here these numbers are real, but the theory about them is conceptional, that is, man-made. This is the cognitive view of N.
- The ontological system of material organic strategies in the Explicate Order.
- The ontological formal system of noëtic strategy-strings in the Implicate Order (FSNSS).
- The concocted typographical formal system "MIU". It will serve here as a (poor, it is true) analogue of FSNSS.
- Number theory (N), embodying the domain of natural numbers which are supposed to objectively exist in some domain.
- Formalized number theory (TNT [= Theoria Numerorum Typographica]).
In addition, N may also be the objectively existing set of natural numbers with their fixed properties that are what they are, independently of being known. This is the ontological view of N. And in it we may still point to N as "number theory".
TNT (formalized number theory) may represent a man-made conceptional device to establish the truth or falsity of statements in number theory (these statements can [or cannot] be proved in TNT). This is the cognitive view of TNT.
In addition, TNT (not necessarily in the form of how it was set up by man) may also be the very essence and fine-structure of N-as-the-existing-set-of-natural-numbers. This is the ontological view of TNT.
TNT is fully expounded in part LXb in Fifth Part of Website.Both viewpoints should exist side by side, that is, they should not exclude each other. If we pass from one viewpoint to the other, that is, from the cognitive to the ontological viewpoint, or vice versa, MEANING, connecting the mentioned systems, changes its nature (that is : not the meaning (of something) changes, but the very nature of "meaning" itself). Thus, in the cognitive domain MEANING is the statement-decoded, while in the ontological domain MEANING is the (revealed) essence of something objectively existing.
We will explain this further in the next section of this REMARK on the status of TNT :In Hofstadter's book ( "Gödel, Escher, Bach" ) the expositions about "metamathematics" -- a mathematics that is in fact not just mathematics, but is a b o u t mathematics, in the present case about number theory -- concern how things are with respect to our possible knowledge of the properties of natural numbers. TNT is defined by mathematicians in order to analyse or dissect facts of natural numbers, and thus to analyze true statements about natural numbers, into the most basic ('primitive') constituents. In this sense TNT is devised to speak about number theory -- which we call N -- in terms of the most basic entities. So N is what TNT means for mathematicians. TNT ==> N (TNT means N). It is a cognitive characterization of the relationship between N and TNT.
If we now transpose things from the cognitive domain into the ontological domain (while still preserving the cognitive viewpoint alongside it), we must hold that N as well as TNT are objectively existing (not, conceptual, not man-made) entities in the Implicate Order : N and TNT (stripped from errors of course, and thus consistent) ARE what they ARE in themselves, and, this being so, we must reverse the semantic relationship : TNT itself, that is, all by itself, describes (and thus IS) the very essence of N. Indeed, TNT is precisely what N in fact means. N ==> TNT (N means TNT). So in this context TNT has ontological priority. And if we, in this ontological context, leave out strict self-references in TNT -- [And this is easy to do, because truth or falsity of a symbol-string is attuned to the interpretation of the symbols. But in an ontological context the symbols of TNT do not have any interpretation. They have an interpretation in a cognitive context only. Thus the above given statement on self-reference is relevant in a cognitive context only, i.e. it refers to the cognitive context. So investigating completeness (of a formal system) demands a cognitive context, and thus that TNT ==> N ( TNT means N).] -- that is cases in which a given TNT-string expresses something about itself, especially a string G saying (about itself) "G is not a theorem of TNT", then we can be pretty sure that TNT is complete, that is, TNT is then the complete essence of N.
So, consequently, also in the context of our noëtic theory (in which we have thus "ontologized" certain metamathematical findings of Hofstadter) N -- number theory -- means TNT, that is, TNT is what N in fact is, TNT is the very essence of N (while in the cognitive context [in which TNT is not objectively existing, but devised in order to understand N] the meaning of TNT, that is what its symbols and symbol-strings mean, is to be found in N, that is, in the ordinary language of number theory).
But, still also in the context of our noëtic theory, N has yet another meaning too, or better, it is meant by something else, a meaning that is stretched out into another direction : The noëtic strategies -- assumed to reside as immaterial patterns in the Implicate Order, where these patterns are held to be 'descriptions' (of strategies of how to be able to exist in the Explicate Order) and thus some sort of typographical strings -- together constitute a formal system (think, as an analogy, of the MIU-system), that is, to begin with, a set of pre-existing, 'primitive', strings (strategies) -- axioms -- and a set of typographical rules. The rest of the strings (theorems) are now derived from the axioms by having the rules applied (About these rules, where they come from, we will speak later on). And -- thinking again of the MIU-system as an analogy -- this noëtic formal system of 'typographical' strings and rules can be isomorphically expressed in number theory -- N -- (by having the strings coded by natural numbers and the rules arithmetized). And in our noëtic context (the Implicate Order) we then hold that this system of strategy-strings IS in fact so coded, which here means that this system IS in fact part of number theory ("number theory" here not taken to be a theory devised by humans, but an existing state of affairs), that is, it means a certain part of number theory, or, said differently, its essence is in number theory. And this in turn implies (as already found out earlier) that the derivations of noëtic strategies from one another are in fact arithmetical transformations. These arithmetical transformations are fully determined by the arithmetized rules of the formal system of noëtic strategy-strings (FSNSS), and are thus specific combinations of the basic arithmetical operations (addition, multiplication, etc.), as we saw it in the arithmetized MIU-system (see Fifth Part of Website, near the end of part LXa at "Rules I, Rule II, Rule III, Rule IV" ).
So the o n t o l o g i c a l symbol-meaning relationships between number theory (N), formalized number theory (TNT), and the Formal System of Noëtic Strategy-Strings (FSNSS) (in the Implicate Order), are :
FSNSS ==> section of N, and N ==> TNT
and thus also :
FSNSS ==> section of TNT Thus, what happens in the system of noëtic strategy-strings -- derivation of strategy-strings from other such strings -- has its essence in number theory which in turn is essentially TNT.
But the formal system of noëtic strategy-strings (FSNSS) has, in addition to its meaning (residing) in the Implicate Order, also a meaning outside this Order, that is, in the Explicate Order. There the meaning of each noëtic strategy-string is represented by existing material individuals of some definite organic species, characterized by a definite biochemistry, physiology, internal and external morphology, morphogenesis, behavior, and ecology. This meaning is ontologically revealed by the phenomenon of projection (from the Implicate into the Explicate Order). In fact, projection of a given strategy can only take place when an appropriate ecological context actually exists (containing also the evolutionary precursor of that strategy) somewhere in the Explicate Order, and it is thus in fact this ecological context that reveals ('decyphers' or 'decodes') the meaning of that given noëtic strategy-string.
So, in the ontological context we can write :
Material Strategies <== FSNSS ==> section of N, and N ==> TNT In terms of ontological priority we can express this as follows :
TNT ==> N ==> FSNSS <== Material Strategies where we assume that a material strategy -- present in the set of existing organic individuals of a given species -- has ontological priority with respect to the corresponding noëtic strategy, which is ontologically still incomplete.
FSNSS is embedded in N, and, consequently, also in TNT. But there is nothing in N, neither in TNT, that causes or defines FSNSS. The delimitation of FSNSS comes from outside, that is, from outside N or TNT, and thus from outside the Implicate Order. And this means, of course, that the delimitation of FSNSS comes from the Explicate Order.
In the cognitive domain, on the other hand, there is, of course no talk about ontological priority, and the above symbol-meaning relationships (first line of the above two chains) are partly the other way around :
TNT ==> N, and section of N ==> FSNSS ==> Material Strategies Strings expressing things of other strings of the same system.
Anticipating the fact (later to be proved) that strings of TNT can express things of other TNT-strings (and thereby thinking about the MIU-system as an analogue of FSNSS) :
If we consider the MIU-system, then we can say the following :"The string MIU is a theorem of the MIU-system"
(because we can produce MIU from the axiom MI )This whole statement is itself not an MIU-string (because it does not consist solely of MIU-symbols). Thus it is not so that this whole 'MIU-string' expresses something about the (other) MIU-string MIU, because, again, this whole string is not an MIU-string.
The same can be said about the MIU-strings MII, MIIIIU, MUIU, and all other theorems of the MIU-system.
Further we have statements like"The string MU is not a theorem of the MIU-system"
Also here something is expressed about the MIU-string MU (namely that it is not a theorem). But also here this is not expressed by another MIU-string. It is said by the statement "MU is not a theorem of the MIU-system", but this statement (this series of symbols) is itself not an MIU-string.
And because, us speaking about MIU-strings, expressions about being or not being a theorem are the only expressions in the context of the MIU-system we can think of, it is not possible that in the MIU-system any given MIU-string expresses something about another MIU-string. But in TNT this is possible (as will be shown later). But also no TNT-string can have as its meaning that a given MIU-number expresses something about another MIU-number.The MIU-system has no interpretation in some part of (physical or mathematical) Reality, but we can see it as an (albeit poor) analogue of FSNSS (formal system of noëtic strategy-strings).
In a cognitive context the typographical MIU-strings and rules together form the meaning of their arithmetic counterparts ("311110" means MIIIIU ), these counterparts obtained by assigning Gödel numbers to the system's symbols and by arithmetizing its production rules.
In an ontological context, on the other hand, the MIU-system and all its derivations can be said to mean some section of number theory ("MIIIIU" means 311110) and thus a corresponding section of TNT, and so essentially being that section of TNT. Nevertheless, pure MIU-strings cannot express things of other MIU-strings, because this system is much too simple. On the other hand, we can expect of FSNSS (formal system of noëtic strategy-strings) that it is rich enough to contain strings that express things about other such strings. And then we can say that these FSNSS-statements in fact mean statements in N, and consequently in TNT. So now we can say that if indeed TNT (which ontologically is basic to N and to FSNSS) turns out to be capable of having several TNT-strings that each express something about other TNT-strings, then we can hold that FSNSS too is so capable.
(end of quote from part LXb in Part V of Website)
And indeed, TNT-strings are certainly capable of expressing things of other TNT-strings, as is proven in part LXc of Fifth Part of Website. But to prove that certain TNT-strings might, or might not express something, whether it be about other strings or not, can only be done when the system, TNT, is interpreted. So in other to get to know something about some formal system we need it to be interpreted, which in the case of TNT means that it must be taken, not in its ontological, but as it shows itself in its cognitive status. And by doing so we come to know something as to how TNT really is in itself ( TNT as objectively existing ).
Let us continue to quote from part LXb of "Organic Evolution" in Fifth Part of Website :
Embedding of the formal system of noëtic strategy-strings in number theory.
In order to further elaborate the status of N and TNT in the context of our noëtic theory of evolution, that is, in an ontological context, it is necessary to work out the way in which FSNSS is "essentially a part of N, and therefore of TNT", that is, how the formal system of noëtic strategy-strings (in the Implicate Order) is embedded in the existing system of natural numbers and their fixed properties. In exactly what way is FSNSS a part of number theory? Because we do not know the detailed nature of FSNSS, we must answer this question by consulting an analogue of it. For this we take the MIU-system. Like it was supposed for FSNSS to consist of 'symbol strings' (each being a noëtic 'description' of a strategy) and a set of 'typographic' production rules, the MIU formal system also consists of symbol strings and a set of typographical production rules. Now, in order to understand in what way FSNSS is embedded in number theory (resulting in one able to say : "derivations in FSNSS are in fact arithmetical transformations"), we must see in what way the MIU-system is embedded in number theory. We already did ourselves (following Hofstadter) embed the MIU-system in N by assigning Gödel numbers to each symbol and by arithmetizing its production rules. And it is the latter that hold the key to the understanding what precisely this "embedding" is. We know that 31 is the number we possess right from the beginning (this number was obtained by Gödel-coding for the axiom MI ). The arithmetized rules (as we had given them in Fifth Part of Website, part LXa ) of the arithmetized MIU-system were :Rule I : If we have made 10m + 1, then we can make 10 x (10m + 1).
Rule II : If we have made 3x10m + n, then we can make 10m x (3x10m + n) + n.
Rule III : If we have made k x 10m+3 + 111 x 10m + n, then we can make k x 10m+1 + n.
Rule IV : If we have made k x 10m+2 + n, then we can make k x 10m + n.
In these rules, m and k are arbitrary natural numbers, and n is any natural number which is less than 10m. In the formulae 'x' means "multiplied by".
We can see that these four numerical transformations are each a certain combination of arithmetical operations. And these latter are just the operations allowed in N and defined in TNT. So the very possibility of these numerical transformations is rooted in number theory, and ultimately in TNT. But the precise combinations of these arithmetical operations (that is, precisely those combinations, and not other potential combinations) are NOT determined nor sanctioned by N, neither are they by TNT, that is, these actually existing combinations fall outside the realm of N or TNT.
So it seems that the general laws and definitions in N and (formalized in) TNT are in some way harnessed by the MIU-system (respectively by FSNSS). The MIU-system (and thus FSNSS) imposes its special structure onto N (and ultimately onto TNT) without violating any of its laws and definitions. So the MIU-system (and thus FSNSS) come from outside N and TNT but is written in their language (that's why we can say that the MIU-system (and thus FSNSS) is "in fact an arithmetical system"). And indeed, the MIU-system was made up by Hofstadter!
N or TNT cannot cause or express the MIU-system (and thus FSNSS) as to what it specifically is. So although the existence of TNT (and therefore N) implies the existence of natural numbers and their properties, it does not imply any specific combination and recombination of arithmetical operations (addition, multiplication, etc.), and thus does not imply any system such as MIU or FSNSS. It only i m p l i c i t l y implies these systems (and possibly others as well).Of course WE can (although it is hard) express in TNT that, say, a given number "is a MIU-producible number", but only when we explicitly specify in TNT what a MIU-producible number in fact is. This can be done only in the cognitive context of TNT.
TNT itself does not define the MIU-system (and so also not FSNSS) neither in a cognitive nor in an ontological context.In a cognitive context WE take the MIU-system, forged by Hofstadter, and encode it in number theory (by assigning arbitrary Gödel numbers to its typographical symbols, and by arithmetizing its typographical production rules).
In an ontological context, on the other hand, we assume the objective existence of FSNSS (formal system of noëtic strategy-strings) -- and thus, analogously, that of the MIU-system -- and then hold that it is automatically encoded in N, that is, not by us, but by and in noëtic space itself (by a 'method' that is supposed to be more or less similar to that of assigning 'Gödel numbers' and of our arithmetizing the production rules of the system). So FSNSS (and analogously the MIU-system) appears in noëtic space as arithmetized. Thus such a system of noëtic patterns, and all other noëtic systems that might be present in the Implicate Order, ARE in noëtic space essentially arithmetic entities obeying the g e n e r a l laws of TNT (all TNT-laws are general), and also obeying their own s p e c i a l laws (production rules) harnessing these general TNT laws.
So our theory is that noëtic space (the Implicate Order) is in fact "arithmetical space". And this is what makes this space truly "noëtical". The existence of systems like FSNSS in noëtic space gives structure to this space. It is a property of this space itself. The Formal System of Noëtic Strategy Strings ( FSNSS ) with its own production rules is, as is also the MIU-system, imposed upon number theory (N), and, consequently, also upon TNT, i.e. it is imposed from outside the Implicate Order, that is, it is imposed upon it by the Explicate Order, and it leads, among other things, to the evolution of organisms in that Order. And FSNSS is so imposed from the Explicate Order upon the Implicate Order because the latter is totally attuned to the Explicate Order as a result of nothing less than the metaphysics of Being, i.e. the aspiration of immaterial forms to become ontologically complete, and thus become material. [We may rephrase this by saying that the Implicate Order "knows" the Explicate Order. And it is on the basis of this knowledge that genuine organic strategies (of forms) to exist in the Explicate Order can, and will, indeed be formed.]
(end of quote from part LXb in Part V of Website)
Every theorem derived in the Formal System of Noëtic Strategy Strings ( FSNSS ) from its (many) axioms, is a description -- and we here concentrate on descriptions of organic strategies -- which as such are complex propositions. Such a proposition is true upon interpretation in terms of the Explicate Order, and that means that it is at least compatible with the structure of the Explicate Order. And, of course, the theorem is always so compatible because the Implicate Order, together with its production-rules, is, as has been said, wholly directed to the Explicate Order.
The conventional status of TNT.
So, as has been said, formalized number theory, TNT, is devised by mathematicians in order to be able to investigate the properties of natural numbers. And the latter are, by most mathematicians, supposed to somehow objectively exist 'somewhere', and that's why they can be investigated by anyone, at any time, and anywhere. The natural numbers are what they are, independent(ly) of being, or not being, known.
To illustrate the conventional status of TNT, as a devised instrument of knowledge of the properties of natural numbers, we can best reproduce a figure, drawn by Hofstadter in Chapter III Figure and ground, p.71. TNT consists of a small number of axioms, and a relatively large number of rules for manipulating strings. From these axioms new strings --theorems -- can be produced by the rules, and applying rules to already produced theorems generates still more theorems. In themselves these theorems are neither true nor false, they are just symbol-strings, but when the agreed interpretation is involved the theorems can be said to be true. Cognitively, they prove the corresponding statements in number theory to be true. And perhaps there are true statements in (non-formalized) number theory that cannot be so proved, that is, in TNT no corresponding theorems do exist. Or, even worse, perhaps there are false statements in number theory that appear as theorems in TNT!
Let's now reproduce Hofstadter's figure.Figure 1 : Cognitive picture of formalized number theory, TNT.
Considerable visual symbolism is featured in this diagram of the relationship between various classes of TNT strings. The biggest box represents the set of all TNT strings. The next-biggest box represents the set of all well-formed TNT strings. Within it [that is in the most inner box] is found the set of all sentences of TNT. Now things begin to get interesting. The set of theorems is pictured as a tree growing out of a trunk (representing the set of axioms). The tree-symbol was chosen because of the recursive growth pattern which it exhibits : New branches (theorems) constantly sprouting from old ones. The fingerlike branches probe into the corners of the constraining region (the set of truths), yet can never fully occupy it. The boundary between the set of truths and the set of falsities is meant to suggest a randomly meandering coastline which, no matter how closely you examine it, always has finer levels of structure, and is consequently impossible to describe exactly in any finite way (It is a fractal boundary). The reflected tree (the tree at the right-hand side of the diagram) represents the set of negations of theorems : All of them false, yet unable collectively to span the space of false statements. The bottom part of the right-hand tree represents the set of negated axioms. The black area on the left half of the diagram represents the set of unreachable truths, while the white area on the right half of the diagram represents the set of unreachable falsehoods.
(After HOFSTADTER, 1979)In an ontological context, on the other hand, TNT only consists of its set of axioms, its transformation rules, and its derived theorems. It is the existing essence of natural numbers an their properties, and, as this essence is in itself, does not contain statements that are neither true nor false, or both true and false for that matter, for if it did, it could not EXIST. But for such an argument we need the cognitive view of TNT, because only in this view TNT has an interpretation [rendering questions about truth and falsity meaningful]. With respect to all this, we may theorize that TNT is, apart from representing N's essence (in the ontological view), N's way, and thus the Implicate Order's way, to know about itself, in the sense of : What does the essence of N tell N about itself? For this, we must revert to the cognitive view of TNT again, and realize that TNT cannot tell us, and cannot tell N, everything. We know this from Gödel's Incompleteness Theorem. Whether the things TNT (or we) does not know of N are important to the structure of FSNSS (formal system of noëtic strategy-strings), I do not dare to say. The most we can tell is, that although the Implicate Order knows the Explicate Order (as a result of it being attuned to it), it has not a complete self-knowledge. We might theorize that this fact renders the Implicate Order a bit unstable and a bit wavering. Perhaps this condition is responsible for a touch of irrationality to be present in the Explicate Order (indeed, in some organisms we have discovered some oddities-of-design of certain organs or parts thereof (morphological dysteleology).Having now placed TNT in the proper context of our noëtic theory of evolution, we can proceed, following Hofstadter (Chapter VII), to establish what exactly is expressed by formalized number theory, TNT.
(End of Introductory Remark)Gödel's construction depends on describing the form, as well as the content, of strings of the formal system we have defined in part LXb of Fifth Part of Website -- Typographical Number Theory ( TNT ). The unexpected twist is that, because of the subtle mapping which Gödel discovered, the form of strings can be described in the formal system itself. Let us acquaint ourselves with this strange system with the capacity for wrapping around.Before starting, however, we might ask whether Number Theory -- and a fortiori TNT -- is the same in all conceivable worlds. Although this question is not relevant within an ontological context (where only one single objectively existing world is assumed -- for us a single world consisting of two interacting Orders, the Implicate and Explicate Orders) it is certainly important within the cognitive viewpoint, or, we might say, within pure mathematics. If we assume that at least logic is part of every conceivable world --- however, "Intentional Logic", as defined and expounded in the "Logic Series" (Formal Elements of Cognition, Part II--VII) of the present (Part of) Website, is fully geared to the objectively existing world and only this world --- is that all? That is, are the other logic-related or mathematical disciplines not part of every conceivable world, but more or less change when we go from one world to another? Concerning Number Theory, is it really conceivable that, in some worlds, there are not infinitely many primes (In standard number theory it is indeed proved that there are infinitely many prime numbers)? Would it not seem necessary that numbers should obey the same laws in all conceivable worlds? Or ... is the concept "natural number" better thought of as an undefined term, like "POINT" or "LINE"? In that case, number theory would be a bifurcated theory, like geometry (where we have one standard -- euclidian -- and several non-euclidian geometries) : there would be standard and nonstandard number theories. But there would have to be some counterpart to absolute geometry : a "core" theory, an invariant ingredient of all number theories which identified them as number theories rather than some completely other theory. It seems to be the consensus of most modern mathematicians and philosophers (so Hofstadter, 1979, reports on p.100) that there IS such a core number theory, which ought to be included, along with logic, in what we consider to be "conceivable worlds". This core of number theory, the counterpart to absolute geometry, -- is called Peano arithmetic, and formalized it is known as TNT. Also, it is now well established -- as a matter of fact as a direct consequence of Gödel's Theorem -- that number theory IS a bifurcated theory, with standard and nonstandard versions. Unlike the situation in geometry, however, the number of "brands" of number theory is infinite, which makes the situation of number theory considerably more complex.
For practical purposes (Hofstadter, p.100), all number theories are the same. In other words, if bridge building depended on number theory (which in a sense it does), the fact that there are different number theories would not matter, since in the aspects relevant to the real world, all number theories overlap. And we know that the same cannot be said of different geometries : The geometry of the Universe is determined by its content of matter, so that no one geometry is intrinsic to space itself. From this it is clear that in an ontological context there is, contrary to geometry, only one number theory, represented by the Peano arithmetic. Let us now turn to its formalization.
[In this formalization the notation of many number-theoretic entities is changed. This is done in order not to confuse number theory (N) with its formalization (TNT). Ontologically TNT is just the essence of N, that is, it is N, but then in terms of N's very elements. And because N is (by us) assumed to represent the basic structure of noëtic space (the Implicate Order) (or at least its "organic" part), TNT is this same basic structure analysed into its very elements.
Cognitively TNT is is a man-made device with which one may prove the truth of propositions of and in N.][. . .]
For our noëtic theory of organic evolution -- as it is so far developed on this website -- it is important to realize the following : Our theory assumes that the set of noëtic strategies, existing as string-patterns in the Implicate Order, constitutes a formal system with its own production rules, a system that is, however, essentially arithmetic, with its symbols standing for natural numbers and its production rules being, to this system, intrinsic and unique combinations of arithmetical operations. These operations are the 'usual' arithmetical operations, that is, addition, multiplication, and carrying-to-a-higher-power (which is special case of multiplication), as they are defined -- and ontologically, as they naturally are what they are -- in the theory of natural numbers, and, again, ontologically, in the objectively existing system of natural numbers and their properties : The rules of the noëtic system of strategy-strings harness the laws of objective 'ontological' number theory. So the noëtic system of strategy-strings, although it has its own typical nature, is rooted in (ontological) number theory. But this 'harnessing' coming -- it must be stressed -- from outside number theory, that is, from the Explicate Order.
Now TNT is the formalization of number theory, that is, here, of man-made number theory, and is devised by mathematicians in order to extract the very essence of natural numbers and their properties. So from the cognitive standpoint TNT, with its axioms, rules, and theorems, is a means to study the realm of natural numbers. But from an ontological point of view -- the view of our noëtic theory (but not denying the cognitive point of view) -- TNT is the objectively existing essence of the objectively existing set of natural numbers and their properties, but not necessarily in the form, or forms, as it happens to be devised by mathematicians (and shown in part LXb of Fifth Part of Website). In this form it is purely a cognitive device. Ontologically we do not have to suppose that in the Implicate Order there actually exist TNT axiom-strings, TNT theorem-strings, and TNT production rules, as we will meet them later on in our exposition of TNT. Ontologically we must hold that the existing set of natural numbers and their properties ('ontological number theory') has an essence, a core, a basic structure, that makes it what it in fact is. By means of TNT mathematicians try to lay bare this core. So, according to our noëtic theory TNT is as such not an objectively existing formal system. It is not the essence itself of 'ontological number theory' but represents that essence. So by studying the results of (the science of) TNT we will gain some insight into the essence of 'ontological number theory' and with it an insight into the very depths of the Implicate Order.[. . .]
When we look to the rules of TNT that are shared with the Propositional Calculus (see part LXb in Fifth Part of Website ), and also to the new rules of TNT, the ones that have been given until now, and all the ones that will come a little later on, we see that these rules formalize steps of the reasoning process. So the formal system TNT consists of axioms from which (and from theorems already derived from the axioms) we can derive all the theorems of TNT by using these rules, that is by the allowed reasoning steps. So the rules of TNT are not entities that objectively exist somewhere, or, perhaps better expressed, not entities that are objectively inherent in the set of natural numbers and their properties. We assert that the axioms and theorems, and only the axioms and theorems, of TNT should express the fundamental and objectively existing properties of natural numbers. We expect that the rules of TNT, as established (and later, when needed, perhaps partly amended) by the enquiring subject (= "we", that is, mathematicians and logicians), lead us to these existing properties.
On the other hand, the rules in the supposed "formal system" of noëtic strategies existing in the Implicate Order (which rules are ultimately special combinations of arithmetical operations) are not held to be principles of human reasoning. They are fully ontological (i.e. independent of any [general and individual] knowing-subject) and contribute to the special features of the Implicate Order. (end of quote from part LXb in Fifth Part of Website).
We've now seen that the Implicate Order is, as to its essence, arithmetic space. It obeys the laws of natural numbers. But these laws may, 'somewhere' in the Implicate Order be harnessed [by something coming] from outside (without violating them). And indeed, in the Implicate Order we suppose the Formal System of Noëtic Strategy-Strings ( FSNSS ) to be present, being completely embedded in number theory, and being therefore essentially a system that is arithmetic, but receiving the special combinations of arithmetic operations (as the latter are determined by the properties of natural numbers) making up its production-rules, from outside number-theory, and that means from outside the Implicate Order. And it is by and in FSNSS that [descriptions of organic] strategies are produced, either from non-strategies (axioms) or from already produced strategies (theorems). And upon projection of such a strategy-string from the Implicate Order into the Explicate Order, the very meaning of that strategy-string becomes explicitly expressed. It becomes so expressed in the form of an organismic species materially existing in the Explicate Order.
Summary, and further conclusions of noëtic theory
Our general noëtic theory of evolution, if it is correct, explains a number of inconsistencies in conventional evolutionary theory, such as (1) the wide-spread phenomenon of underivability of later organisms from earlier ones, as a result of specialization-crossing, and such as (2) cases where insects of a definite type are distributed on Earth in widely-separated localities, such as the Archimylacridae occurring in the palaeozoic coal basins, showing that they could not have been originated at one particular location only, and then, from that one locality having migrated to geographically and ecologically widely separated swamps of the late Palaeozoic. They must have been originated independently in several such locations, which is perfectly possible and natural in our noëtic theory. Also the often utterly 'worked-out' and subtle adaptations and life-strategies of many organisms fit in perfectly well in our theory, while often unexplainable in conventional theory with its random genetic mutations and natural selection and subsequent migration of the new species or type across large distances.
According to our theory, ready-made strategies project into the Explicate Order, where, in that Order the ecological conditions happen to be appropriate to 'receive' these strategies, and where they then appear as new organismic species. These ready-made strategies are, following our theory, produced in the Implicate Order. This production is in its generality, i.e. in its gross features, driven by the Formal System of Noëtic Strategy-Strings ( FSNSS ) residing in the Implicate Order and embedded in arithmetic space. And arithmetic space is 'ontological number theory', that is, the complete set of truly and objectively existing natural numbers (and their properties), that can encode 'sentences' (symbol-strings with interpretation [meaning] ). So FSNSS is a section of number theory (N), with the elements of its production-rules being just the 'ordinary' arithmetic operations. But the particular combinations of these operations, composing FSNSS's production-rules, are extrinsic to number theory. They are imposed from outside (without violating the rules of arithmetic), that is, imposed from the Explicate Order onto number theory, because the Implicate Order, being itself arithmetic space, is wholly attuned to the Explicate Order as a result of the metaphysics of Being.
Now the Formal System of Noëtic Strategy-Strings ( FSNSS ) is certainly strong enough to be vulnarable to Gödel's Incompleteness Theorem, meaning that there may be formed statements in the language of FSNSS that definitely are true, meaning that their interpretation is at least compatible to the Explicate Order, but that cannot be produced (as theorems) by FSNSS. But because such statements must be of the form "'I am not a theorem of FSNSS", we cannot suppose that they have any important relevance to the biological world (which is the domain of meaning or interpretation of FSNSS ). So here we need not investigate the consequences of Gödel's Incompleteness Theorem.
But matters are different in the deeper levels of the Implicate Order, i.e. in the deeper levels of arithmetic space. The properties of the general structure of this space -- ontological number theory, N -- may be described by formalized number theory, TNT. And if TNT is correct, we may ontologize it, and then hold that it constitutes, or at least represents, the very essence or core of number theory (N), i.e. of arithmetic space. And, as has been said, TNT might be N's way to know itself. And now Gödel's Incompleteness Theorem (which applies perfectly well to TNT) becomes ontologically relevant, not because of the special content of the true statements that cannot, as theorems, be produced by TNT, but because of the general state of affairs such statements do imply. This general state or situation consists in the very fact that N, and thus the Implicate Order, has no complete self-knowledge, and may, as a result of this, be in some degree unstable. And because FSNSS is fully embedded in N, and has the biological section of the Explicate Order as its domain of interpretation, this instability might in the end also affect the Explicate Order, and might as such be responsible for a touch of irrationality especially apparent in the biological domain of that Order. We may mention, for instance, the crossing-over of the air- and swallow-channels (tubes) in at least mammals, which may cause choking. Further we may mention the position of the photo-sensitive rods in the eyes of at least mammals, which are placed upside-down, with their photo-sensitive ends turned away from the incoming light, and with their outcoming wiring lying all over the retina. And we may mention also the many animal species having evolutionarily developed grotesk structures (such as horns or teeth) rendering them unfit for further evolution (evolutionary dead-ends). Even the human species is biologically and evolutionarily a dead end, because precisely his intelligence does not inhibit irrational behavior, soon leading to his extinction. Finally, all non-functional structures (detrimental or not) in organisms carry a touch of irrationality.
Such cases of irrationality are constant features at many points in the animal kingdom, and they should be distinguished, of course, from mere here-and-now accidents and coincidences so characteristic of the Explicate Order.
And of course the mentioned irrationalities, as well as the mere (here-and-now) accidents, do not violate natural laws, i.e. the laws prevailing in the Explicate Order (laws of physics and chemistry), but do violate biological rationality.
So our theory of noëtic formal systems does account for oddities and irrationalities in the Explicate Order, in contrast to conventional biological theory, because in conventional theory all more or less persistent (i.e. specific, in contrast to individual) structures in organisms are supposed to be functional, and therefore rational, while evidently non-functional, or even admittedly detrimental structures are supposed to be inevitable remnants of earlier structures.
In the POSTSCRIPT of part LXc of "Evolution", in Fifth Part of Website we, against Hofstadter, demonstrated that TNT cannot, among its strings, recognize those that typically belong to some other formal system that is embedded in number theory and thus also in TNT (i.e. such strings do exist in TNT, but TNT cannot recognize them as such). And, "some other formal system" is, for instance, out supposed Formal System of Noëtic Strategy-Strings ( FSNSS ) (including, of course, its, undoubtedly, many and complex (arithmetized) rules of production). So although this system is embedded in number theory, and thus in the Implicate Oerder, it is there imposed by teh Explicate Order. This finding is so important that we here reproduce the mentioned POSTSCRIPT of part LXc (at the end of our intermezzoing three-document exposition of formal systems, number theory and their ontologization). The reader should be aware that it is based on the exposition of TNT (including its production rules) put down in part LXb.
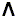means "and", 
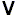means "or", 
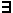means "existential quantor", and 
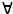means "for all ..., does hold ...".
Postscript
[ We have now come to an end of Hofstadter's discussion of how any formal system can be embedded in number theory, and that with TNT -- formalized number theory -- we have "the usual kind of step-by-step reasoning as it applies to natural numbers" by which reasoning we may solve problems concerning arithmetized formal systems such as the MIU-system and our assumed formal system of noëtic strategies.
We may now, as promised , analyze more precisely in what way the MIU-system (serving as a rough and simplified analogy of our "formal system of noëtic strategy-strings") can be/is embedded in number theory and what aspect of it is extrinsic to number theory. What follows is a more or less tentative and informal analysis, not explicitly found in Hofstadter's exposition.] :Recall from the previous-previous document, i.e. from here [Six Part of Website] to be quoted as part LXa of Fifth Part of Website, that the MIU-system is a typographic formal system consisting of the symbols M, U, and I, the given string (axiom) MI, and the following typographical rules by which other strings (theorems) can be derived :
The MIU-system can then be embedded in number theory (as fully explained in previous-previous document ( part LXa of Fifth Part of Website ) by assigning (arbitrary) Gödel-numbers to its symbols :
- : ... I ==> ... IU
- : Mx ==> Mxx
- : ... III ... ==> ... U ...
- : ... UU ... ==> ......
M <==> 3 I <==> 1 U <==> 0 and by arithmetizing its rules :
Let us now consider the typographical statement
- Rule I : If we have made 10m + 1, then we can make 10 x (10m + 1).
- Rule II : If we have made 3x10m + n, then we can make 10m x (3x10m + n) + n.
- Rule III : If we have made k x 10m+3 + 111 x 10m + n, then we can make k x 10m+1 + n.
- Rule IV : If we have made k x 10m+2 + n, then we can make k x 10m + n.
" The string MIUIU is a theorem of the MIU-system" As a number-theoretical statement it reads :
"31010 is a MIU-number" where "a MIU-number" means "a MIU-producible number".
[The sentence "31010 is a MIU-number" is a pure number-theoretical statement, that is, a statement about numbers (or a number) (here) in plain English, provided that we circumscribe in it what, in plain English, "to be a MIU-number" arithmetically means. In order to do so, we will rephrase the sentence "31010 is a MIU-number" by its pure number-theoretic equivalent (thereby demonstrating that the sentence can be reduced to a pure a number-theoretic statement) :
" If we multiply the number 31 by the number 10, and multiply the resulting number (310) by the number 100, we get the number 31000. If we then add to this number the number 10, we get the number 31010."This is indeed a pure number-theoretic statement, i.e. a statement in N.]
Of course, number theory does not a priori know what "a MIU-producible number" is. So in the number-theoretical statement this must be described. [We just did this in plain English but] Let us try to do so [more formally] by using the transcribed axiom and the arithmetized rules of the MIU-system :
First we do this in a global way :
If we take the number 31 (transcribed axiom of the MIU-system) and take into account the arithmetical rules I and II, then we can produce the number 31010.
And now in a more detailed version, using some logical symbols :
< < 31 And because number theory does not know what these rules are, we must put things in a still more detailed way (where 'x' means 'times') :
< < 31
But the value of the variable m is in the present case different in the application of the two rules. To apply rule I, m must be specified as 3, while to apply rule II, m must be specified as 2. So we have to name this variable differently, we chose m and m' :
< < 31
The variable n does not appear in rule I, but it does so in rule II. Its value must be 10.
So specifying the variables m, m', and n, with respectively 3, 2, and 10, we get :< < 31
and further worked out we get :
< < 31
And still further worked out we, finally, get :
< < 31 So this is the full number-theoretic statement saying that 31010 is a MIU-producible number, and, according to its second-level meaning, saying that MIUIU is a theorem of the MIU-system.
If we now want to translate this statement into TNT-notation, we only have to translate the numerals in it, such as 31 = SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS0, etc. And with this translation we then have a TNT-string saying something about the MIU-system (namely that the string MIUIU is a theorem of the MIU-system).However, this conclusion is a bit rash, as the following considerations will show.
The last formula is in effect the following statement :
If we have 31 together with < 31 ==> 310 > and < 310 ==> 31010 >, then we have 31010 It is directly evident that this statement, so formulated, is true (according to the Rule of Detachment : if x and < x ==> y > are both theorems, then y is a theorem) [ The statement expresses only a special case, that is, a particular instance, of what the Rule of Detachment expresses generally]. And thus the TNT translation of the above string -- < < 31
But although TNT can see that 31010 necessarily follows from a given 31 and the two implications, and thus having the whole statement
"If we have 31 together with < 31 ==> 310 > and < 310 ==> 31010 >, then we have 31010" (when properly translated into TNT-language) as one of its theorems, it cannot recognize the number "31" as the axiom of precisely the MIU-system, nor can it recognize that "< 31 ==> 310 >" is (an instance of) Rule I of precisely that system, and it can also not recognize "< 310 ==> 31010 >" as (an instance of) Rule II of that system. So we cannot hold that there is a TNT-string that says :
"31010 is a MIU-number"
let alone
"MIUIU is a theorem of the MIU-system" Let us illustrate this further. If we had the following statement :
< < 31 then (when transcribed into TNT-notation) it would also be one of the theorems of TNT (according to that same Rule of Detachment). But in this case "< 310 ==> 3101010 >" does not correspond with any rule of the MIU-system. But this cannot be discerned by TNT. And indeed, 3101010 is not an MIU-producible number. Also this TNT cannot discern.
Yet another example might be following :
If we had the statement :
< < 30 we would recognize in "< 30 ==> 300 >" Rule II of the MIU-system. Likewise we would recognize in "< 300 ==> 3 >" Rule IV of the MIU-system. But we would also directly see that "30" is not the axiom of the MIU-system, and neither can it be a theorem ( This we are sure of, because we know that MU is not a theorem of the MIU-system.). Also 3, although it follows from < 30
The here established fact that TNT cannot speak about the MIU-system (because it cannot distinguish between things belonging to this system and those that do not) (and generally about any other formal system different from TNT itself) runs counter some of Hofstadter's assertions. Let us reproduce what he said in this respect (already produced at the beginning of the present document) :
Could it be, therefore, that the means with which to answer any question about any formal system lies within just a single formal system -- TNT ? It seems plausible. Take, for instance this question :And we -- the author of this website -- had found out that TNT is not capable of "speaking in code about the MIU-system". Although I am not a professional mathematician or logician, I think that my conclusion is valid or, in any case, I take into account that it might be correct. Of course TNT contains all the derivations in the MIU-system, but cannot distinguish them from derivations in other systems. So we may perhaps say that TNT speaks about the MIU-system (only) implicitly (and in so far Hofstadter is right). It is in fact we [the knowing subject] who recognize that it does so.
Is MU a theorem of the MIU-system? Finding the answer is equivalent to determining whether 30 is a MIU-number (that is, a MIU-producible number) or not. [30 is the overall Gödel number of the string MU which overall Gödel number resulted by assigning (arbitrary) numbers -- Gödel numbers -- to the symbols of the MIU-system, as was established in the first intermezzoing document i.e. (here to be quoted as) part LXa of Fifth Part of Website.]. Because it is a statement of number theory (N), we should expect that, with some hard work, we could figure out how to translate the sentence "30 is a MIU-number" into TNT-notation, in somewhat the same way as we figured out how to translate other number-theoretical sentences into TNT-notation. I should immediately caution the reader that such a translation, though it does exist, is immensely complex. If you recall, I pointed out [...] that even such a simple arithmetical predicate "b is a power of 10" is very tricky to code into TNT-notation -- and the predicate "b is a MIU-number" is a lot more complicated than that! Still, it can be found, and the numeral SSSSSSSSSSSSSSSSSSSSSSSSSSSSSS0 [30 S's and 0] can be substituted for every b (where it appears in the resulting TNT-string). This will result in a MONstrous string of TNT, a string of TNT which speaks about the MU-puzzle. Let us therefore call that string "MUMON". Through MUMON and strings like it, TNT is now capable of speaking "in code" about the MIU-system.
On the other hand, when we 'Gödelize' TNT itself (and arithmetize its rules) then we find (with Hofstadter) that TNT can speak about itself. It then speaks by its metalanguage, and its metalanguage is embedded within it. And it is clear that the metalanguage of TNT cannot be such that in and through it it can speak about another formal system.
So what we have found is that although TNT, and thus number theory itself, cannot in its strings explicitly speak about other formal systems, it can speak about itself.If we now think of the "formal system of noëtic strategy-strings" (FSNSS) residing in the Implicate Order, we can hold that --like it was the case with the MIU-system -- (the essence of) number theory (as the objectively existing natural numbers and their properties) cannot speak about FSNSS. It cannot recognize its axioms and especially not its production rules. And while the axioms can come from within the Implicate Order (without them being recognized as such by that Order) the rules are, like the rules of the MIU-system, extrinsic to (ontological) number theory, and therefore as regards their origin, extrinsic to the Implicate Order. They must therefore come from the Explicate Order.
We can analyze the relation between the MIU-system and TNT still further :
Above we had the true statement
< < 31 In it the elements < 31 ==> 310 > and < 310 ==> 31010 > are not "logical", that is, not any of the Rules of TNT (which are [its] logical rules) legitimizes these two transformations, that is a transformation of 31 into 310, and of 310 into 31010 ( They are legitimized not by logical or rational reasons but by the particular rules of the MIU-system). But the derivation 31010 from 31 is logical (is rational), because, given 31, and given both < 31 ==> 310 > and < 310 ==> 31010 >, logically implies that then 31010 will be obtained (according to the logical Rule of Detachment). So within the (arithmetized) MIU-system the derivation of the number 31010 from the number 31 is logical or rational in its nature, and consequently also the derivation of the string MIUIU from the string MI. These derivations are therefore ultimately based on TNT, that is, on TNT's logical production rules. This is precisely the way the MIU-system is implemented in number theory. The same, then, can be said of our supposed "formal system of noëtic strategy-strings", residing in the Implicate Order : This system has its own rules (ultimately coming from the Explicate order) but is nevertheless implemented in ontological number theory, meaning that the derivations in it of (everytime) a strategy-string from another are logical, that is, take place according to logical rules (namely those of ontological TNT ).
This may suggest that the logical rules of TNT are, or reflect, the basic structure of the Implicate Order (and thus not only reflect the basic structure of mathematical number theory). That is, if we suppose that there is indeed something like "ontological number theory" -- the objectively existing natural numbers and their properties -- (studied by "mathematical number theory" by means of its formalization, TNT ), and if we suppose, moreover, that the Implicate Order is in fact ontological number theory, then we must admit that the logical rules of TNT are, or more or less reflect, the basic structure of the Implicate Order. So, although the particular form in which mathematicians created TNT and its rules of inference does not necessarily need to be the form in which it really exists in the Implicate Order, it is at least a possible representation (of ours) of the basic logical structure of the Implicate Order [Perhaps, because no human knowledge is considered here, we may replace "logical structure" by "rational structure"]. And in this sense we can legitimately speak of "ontological TNT ". And because we do not know the particular form in which TNT (as the essence of ontological number theory) actually exists in the Implicate Order, all we can do is simply assume that the form in which TNT is created by mathematicians actually is the from in which it exists in the Implicate Order. There is, probably a small number of slightly different forms in which number theory is, and was, formalized by mathematicians, but that is not really important. We chose the form in which it is presented by Hofstadter, and which is expounded in the previous document. Being so, we can then assume that the very rules of TNT, as formulated by Hofstadter, are actually present in the Implicate Order as to their very content. And as to what specific symbols are chosen here, such as S, 0, <, >,So we can say that the very basic structure of the Implicate Order is ontological TNT and its logical rules, as we see them in Hofstadter's presentation of them.
In our noëtic theory we have taken the freedom to assume that there are objectively existing structures (ranging from immaterial to material) that are, in their overall general structure, that is, as to their type, completely isomorphic with a typographical formal system as such systems are forged in conventional mathematics and mathematical logic. [ That is, we hypothetize that certain formal systems, or certain types of formal systems, as they have been created in mathematics and in mathematical logic, do actually exist in rerum natura (in the real world), and thus appear not only in the usual cognitive fashion but also appear ontologically.] For many a researcher this may sound too hypothetic to swallow. I can imagine that. But I want to place organic evolution in precisely such a metaphysical context (by assuming the Implicate and Explicate Orders) in order to account for all of the 'sophisticated' adaptations, typogeneses and anageneses ('higher-developments') that are encountered in it. Many, if not all, of such adaptations, typogeneses, and anageneses, seem to defy any explanation in terms of the material world alone (and that is, in terms of random genetic mutations and natural selection). I did not, however, seek for one or another mystical explanation by assuming some deity-like "higher order" that allegedly had forged all this : The Implicate and Explicate Orders are not supposed to be ontologically completely separate domains : they are in constant interaction by the assumed processes of injection and projection (that is, 'traffic' across their common boundary). Indeed, we had just established that the derivational rules of the formal system of noëtic strategy-strings (FSNSS) cannot have been originated (derived) from the Implicate Order itself, but must in some way have come from the Explicate Order, that is, from the material space-time world.
And that our attempt to compare a typographical formal system with some objectively existing pattern is not some crazy idea of mine is indicated by the fact that something like that is already done by at least someone else, namely by Hofstadter (who is certainly an expert on the general nature of formal systems) in his book "Gödel, Escher, Bach". There in Chapter XVI he describes the isomorphy between the basic genetic system in organisms and the typographical number theory ( TNT, that is, formalized number theory).
[This 'ontologization' of a (initially man-made) formal system is shown in part LXc in Fifth Part of Website.]
Qualitative delimitation of a formal system implemented or embedded in number theory
If some typographically defined formal system, say the MIU-system, has, by us, been embedded in number theory (N), by assigning (arbitrary) Gödel-numbers to its typographical symbols and arithmetizing its typographical production-rules, and of which system we may then say : "It is (and was) in fact not more than just some section of number theory", -- we then have worked our way, let's say, "forwardly", i.e. from typographic to arithmetic (without thereby having changed the qualitative content of the system). And, as we had found out above, in its arithmetized form its number-strings, i.e. its own number-theoretic patterns, do not particularly stand out (as a group) among all the many other number-theoretic patterns. This means that the system, viewed from and within number-theory cannot be recognized as a particular system at all, i.e. it cannot be recognized or distinguished by number-theory as : 'in fact being' the MIU-system. It is not qualitatively delimited by number-theory, although it is based on it. The MIU system, in its arithmetic guise has harnessed number-theory. When we take 'number-theory' ontologically, we may say that the MIU-system, although residing in the Implicate Order, is not qualitatively delimited there. Indeed, it was so delimited by Hofstadter!, i.e. delimited from outside the Implicate Order. The MIU-system is, of course, how it is in itself not important to us, -- but as an analogy of our supposed Formal System of Noëtic Strategy-Strings ( FSNSS ) it is very important indeed, especially because its typographic symbols have not obtained explicit or implicit interpretation (in contrast to those of FSNSS) and, as a result, do not divert us when arguing about typographic formal systems embedded in number-theory. And of course, if we consider FSNSS in its arithmetized form, it, just like the MIUsystem, does not in any way stand out, as a particular group, among all the other number-theoretic structures in the Implicate Order. Like the MIU-system it is not qualitatively delimited, and not qualitatively distinguished from those other number-theoretic structures. But unlike the MIU system, FSNSS is supposed not to be made up by someone, but actually and objectively existing in the Implicate Order. And now, especially in the case of FSNSS, we have the problem of its objective delimitation. If it cannot be so delimited, recognized, or distinguished by and in number-theory, and thus by and in the Implicate Order, (and it indeed cannot be so distinguished), by what IS it distinguished? It must be delimited and recognized from outside number-theory, but by what features of it?.
Well, we solve this problem by still taking the MIU-system as to be an analogy of FSNSS, and forgetting the fact that the MIU-system was in fact made up (by Hofstadter), made up, that is, in order to help us understanding the true nature of formal systems. Having thus forgotten this, we may ask by what precisely this system is qualitatively delimited.
The qualitative delimitation of the MIU-system (delimitation from outside number-theory) becomes evident if we work our way, instead of forwards, i.e. instead of from MIU to N, backwards, i.e. if we work our way from N to MIU (and thus also from N to FSNSS). Let's do this (what comes next is in fact more or less trivial, but nevertheless very important indeed) :
The structure (pattern, or string), to take an example already presented above,
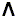< 31 ==> 310 > 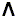< 310 ==> 31010 > > ==> 31010 >
is a true number-theoretic statement, and as such, i.e. as a string, existing in the Implicate Order (it represents numbers embedded in logical space, therefore we have, in our presentation of that string, in addition to numbers also placed logical symbols, of which "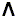" means and, and of which " ==>" means implies. The brackets serve to indicate the substructure of the string).
The statement's truth can be proved in N's formalization, TNT.
As such there is nothing in particular with this statement, i.e. it does not stand out as a member of a special group of statements among all the other number-theoretic statements. But if we assign to the number 3 the typographic symbol M, and to the number 1 the typographic symbol I, and, finally, to the number 0 the typographic symbol U, i.e. if we backwardly 'Gödelize', then we get :
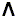< MI ==> MIU > 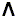< MIU ==> MIUIU > > ==> MIUIU >
And only then we recognize that the statement is also a MIU-statement, i.e. a statement of which the context is the typographic MIU-system. Equivalently we may say that the string is number-theoretic, and, more particularly, of the MIU-sort.
Indeed, we recognize MI as the (one) axiom of the MIU-system. Further we recognize in MI ==> MIU its first typographical production-rule, and, finally, in MIU ==> MIUIU its second typographical production-rule.
So we now see the meaning of the above number-theoretic statement (string), its meaning being :
( because the statement demonstrates that the string MIUIU is derived (produced) from the axiom of the MIU-system by applying two of its production-rules).
So the above pattern or statement -- < < 31 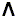< 31 ==> 310 > 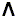< 310 ==> 31010 > > ==> 31010 > -- exists in the Implicate Order (alongside many other number-theoretic patterns or structures). And in working back upon it (as we just have done) the symbols M, I, and U (not being number-theoretical symbols) were mentioned ('retrieved') by us o n l y to express the fact that although < < 31 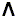< 31 ==> 310 > < 310 ==> 31010 > > ==> 31010 > is just a number-theoretic structure, it turns out, at the same time to be a derivation (production) of a theorem of the MIU-system. By this we, in particular mean that the symbols M, I, and U do not actually exist in the Implicate Order : Of them we see, in the Implicate Order, only their respective number-theoretic counterparts, the numbers 3, 1, and 0.
So to express the delimitation of the MIU-system (as we name it, seen from the Explicate Order), -- this system being a particular formal system embedded in number-theory, but (a system) not as such recognized by number-theory, -- we, in still working backwards, say that 3 means M, 1 means I, and 0 means U, and that the arithmetic transformations mean the MIU-system's typographical production-rules, -- (whereas when working forwards, we embed the MIU-system in number-theory by assigning (arbitrary) Gödel-numbers to its symbols, and by arithmetizing its typographical production-rules).
All this, what has been said about delimitation of the MIU-system precisely holds -- mutatis mutandis -- also for our Formal System of Noëtic Strategy-Strings ( FSNSS ). This system is delimited by the Explicate Order because this Order recognizes that the strings are noëtic descriptions of organic strategies or of their noëtic precursors. And this 'recognizing' is possible at all because the organic part of the Explicate Order is the domain of interpretation, the (domain of) meaning, of FSNSS.
Noëtic Chreodes in the Implicate Order.
Our "noëtic theory of evolution" is meant to present an alternative of conventional evolutionary theory, i.e. it is designed to get rid of the great difficulties undeniably present in that theory. Conventional theory is in fact unable to explain and describe the genesis, in the material world, of organic species, organic types, and of the many subtle adaptations, nor is it able to explain many geographic distributional patterns of them, patterns existing or having existed in the present or in the past.
Problematic distributional patterns (such as that of the Archimylacridae in the coal basins of Siberia, Europe, and North America) are, on the contrary, well accounted for by our noëtic theory, especially by the elaborated idea of polyphyletic development.
But is the very genesis of organismic species, strategies, types, and adaptations, so very well accounted for by our alternative theory? Well it is accounted for, but, sadly enough, still in very general terms only, namely in terms of the number-theoretic structure of the Implicate Order, which structure, although allowing for some irrationalities, is logical (because we can describe it with TNT) and (detaching it from the human mind) rational, and (accounted for in terms) of projection into the Explicate Order of noëtically produced organic strategies.
It is our conviction (but hoping that it turns out to be misplaced) that science, and even philosophy (metaphysics) can, in explaining or describing organic evolution, hardly go beyond stating mere generalities, as has done so far in our noëtic theory.
In earlier documents (mainly in Fifth Part of Website) we have attempted to be more specific as to the genesis of organismic species and strategies, but, admittedly, with only little success. It may, for example, turn out that our earlier (conceived) idea of derivational branching in the Implicate Order of the noëtic trajectory (following the derivation of strategies) is not entirely correct, and it may also turn out that the earlier idea of "holistic simplification" in the Implicate Order, coupled with "reductionistic complexification" in the Explicate Order, must be abandoned. Further, we had tried out in what way noëtic reactions, just as reactions (as analogues of those in chemistry), i.e. without placing them in the context of formal systems, may create strategies in the Implicate Order. Also we probed the idea of noëtic interactions between immaterial forms and noëtic counterparts of ecological existential conditions, allegedly resulting in adapted strategies, - and so on. All these efforts met with only little success because they all were of rather an ad hoc nature without much explanatory value. Indeed, the Implicate Order cannot simply be a noëtic copy of the Explicate Order.
Nevertheless, despite these difficulties, inherent in our theory, we may go a little beyond the level of generality so far developed, if we take as our point of departure the above summarized Noëtic Theory of Formal Systems in the Implicate Order :
Above we had found out that the Formal System of Noëtic Strategy-Strings ( FSNSS ) was delimited by the Explicate Order by, as it were, assigning typographical symbols to the elements of the number-theoretic strings of this system, i.e. recognizing the fact that these strings are noëtic biological descriptions. It could do so, because biological structures in the Explicate Order do in fact form the meaning, i.e. do belong to the domain of interpretation, of these noëtic strings. So the Explicate Order 'recognizes', which here means actively delimits, these strings as to belong to the Formal System of Noëtic Strategy-Strings and its production-rules (this system is, from the outset, hyper-implicitly present in the Implicate Order, but is recognized by the Explicate Order only). It is, of course especially these rules that determine the qualitative nature and content of the system. But why and how, then, do descriptions of non-strategies (axioms) turn into descriptions of true organic -- but still noëtic -- strategies?
In answering this question we theorize that the special nature of the production-rules of FSNSS creates, that is, automatically implies, a canalization of part of the Implicate Order, i.e. it implies the presence of so-called "chreodes" in that Order through which (chreodes) the derivations (formal productions) are being canalized in order to result in precisely such theorems that are noëtic descriptions of organic strategies. We must imagine chreodes as to be (noëtic) funnels, each containing at its bottom an axiom of FSNSS and at its end a fully-fledged noëtic description of a particular organic strategy as (the last) theorem derived from such an axiom (itself a non-strategy string). The axioms of the supposed FSNSS are in fact the earlier described "original immaterial forms" aspiring to become ontologically complete, i.e. to become material. And they can become material when they have developed into strategies-to-exist-in-the-Explicate Order. And when appropriate existential conditions (in which such a strategy precisely fits) do actually exist in the Explicate Order these strategies will be "projected" into that Order (from the Implicate Order) and appear there as material individuals of organismic species.
We theorize that the special nature of the production-rules of FSNSS --- these rules existing in an arithmetic version in noëtic, that is, in arithmetic space, the Implicate Order, and in which version it is the very c o m b i n a t i o n of 'ordinary' arithmetic operations that is recognized, in fact delimited, by the Explicate Order --- is such as to determine their consecutive order of application to the axioms or to the already derived theorems (not-yet-strategies) of FSNSS. This is in fact the noëtic chreode in each case. And this particular succession of rules-to-be-applied in the end leads, in each individual case, to a theorem that, as such, is a noëtic description of a true organic strategy, by which the original immaterial form, an axiom, is able to materially exist in the Explicate Order upon subsequent projection of it (but now embedded in the strategy) into that Order.
And so, even in the Implicate Order the (noëtic) development has proceeded strictly polyphyletically (parallel noëtic trajectories, derivational sequences), - from axioms to theorems, and finally to theorems that are complete descriptions of true organic strategies.
Determination of the consecutive order of application of the production-rules of FSNSS may take place in the following way :
To a given axiom more than one rule may equally well be applicable, but only the one that does not bring the noëtic trajectory outside the chreode, is actually applied. The same holds for intermediate theorems to which more than one rule may be applied. So inside the chreode only one single noëtic trajectory is running, leading from the particular axiom to intermediate theorems and, finally, to the last theorem. Strictly, in this proposed scenario, branching of the noëtic trajectory inside the chreode (if it is wide enough), and so perhaps resulting in more than one strategies, is possible, but is less probable to occur because that would in the end lead to some groups of organisms that could be derived from each other. Indeed, common experience in evolutionary taxonomy has to do with at least many, if not all, organismic species resisting complete derivation from each other (specialization-crossings).
The production-rules of FSNSS are supposed to be of such a nature that their application (as being in fact noëtic reactions) results in the noëtic construction of (descriptions of) organic strategies from bottom to top. Or, said differently, their successive application to a given original immaterial form (a number-theoretic string), an axiom, and to its intermediates, renders that original immaterial form to be able to inform Prime Matter, and that is the same as rendering it -- now as a strategy -- to exist in the Explicate Order.
All this is an 'evolution' of, in each case, a given original immaterial string toward a description of a true organic strategy including the description of the basic molecular machinery of living cells, i.e. the DNA-protein machinery, and the expression of the macroscopic phenotypic morphological structure of the organism. The derivation from FSNSS axiom to strategy-theorem is therefore a sequence of increasingly complicated descriptions, and the production-rules of FSNSS are precisely geared to accomplish this. And it is the particular physical structure of the Explicate Order, especially certain details of it -- its ecological existential conditions -- that imposes upon the mentioned rules their particular nature, despite the fact that they are in the end prescriptions of merely arithmetic transformations of given number-theoretic strings, but nevertheless transformations of a very special kind. But the content of these rules is not only determined by Explicate Order conditions, but first of all by the overall metaphysics of Being.
So at last we have succeeded in "to be more specific" as to the genesis of organic strategies. But still things remain more or less general, and our hypothesis of noëtic chreodes is admittedly a bit ad hoc. This is unavoidable, because as has been said, our theory is for a large part metaphysical, implying that we cannot go for observation and experiment to confirm it. The only directing and restricting (and thus controlling) factor in our theorizing is the demand for conformity, i.e. non-contradiction, with documented observed facts. Our idea of the Formal System of Noëtic Strategy-Strings comes from the empirical fact that the realm of organisms shows it to have some degree of derivational structure (not only between features in different organisms but also between features of a same organism) having led to the idea of evolution especially that of Charles Darwin. And of course, already before him, not to mention Lamarck, there were the 'rational morphologists' such as Cuvier and his followers, having already detected the derivational nature of the animal kindom as a result of the discovery of homologous morphological structures (in fact isomorphisms) in different and in the same animals. Based on such facts they did not conclude that a material evolution had actually taken place on the Earth's surface, but merely the presence of an idealistic rational relationship between structures of different (fore-feet -- wings) and the same (repeating body segments) animals. We, in our theory, also speak of the presence of 'ideal', 'rational' derivational patterns in organisms, and also not take them as evidence of actual material descent of organismic species from one another. We do recognize true derivational patterns to be present in the Implicate Order, not derivations from one strategy to another, but from one immaterial form (a not-yet strategy), through a series of derived theorems (also not-yet-strategies), ultimately to a theorem that is a (description of a) true organic strategy to have, upon projection, this initial immaterial form materially existing in the Explicate Order in the form of a particular organismic species.
With all this we'd like to urge the reader to try to see the evolution, not only of insects, but of all organisms, in the context of the described noëtic machinery, and indeed conclude that, insofar as the Explicate Order is concerned, all organisms developed polyphyletically, because they just result from projections of ready-made strategy-strings [i.e. noëtic strategies, noëtic descriptions of strategies, theorems of FSNSS ], and that the formal system producing -- in the Implicate Order -- the (noëtic descriptions of) organic strategies, has its particular rules, not from the Implicate but from the Explicate Order. Further, the reader should realize the importance and validity of the above finding that natural numbers and the logical (rational) production rules of TNT, are, respectively represent, the very nature of the Implicate Order, and the fact that, finally, there inevitably exists some degree of irrationality in at least the biological domain of the Explicate Order.
Further elaboration of the supposed noëtic generation of strategy-strings and their projection into the Explicate Order.
The nature of an organic strategy.
After all the above considerations about the nature of the Implicate Order it is still necessary to again ponder about how strategies in it develop from non-strategies, i.e. what it exactly means to be a non-strategy and in what way precisely they, as axioms of FSNSS, do manage to transform into organic strategies. And, of course, for this to understand we must know what exactly is meant by saying that something is an organic strategy.
Well, the construction of a noëtic organic s t r a t e g y is the step-by-step formation of a complex form that is, upon projection, able to a c t i v e l y keep itself far from thermodynamic equilibrium, whereas simple forms such as crystals, upon their projection, can, and indeed must, exist while being in thermodynamic equilibrium. If the complex form is not in some way able to keep itself far from thermodynamic equilibrium it will disintegrate, ultimately resulting in fragments and transformed fragments, that are, each for themselves in thermodynamic equilibrium and stable, implying that the original complex form (that subsequently had been disintegrated) could not as such (i.e. as complex form) stably exist in the Explicate Order. So the material strategy must have its individual instances (which is the way every such strategy exists in the Explicate Order) to be active, replacing the loss of matter and energy, a loss resulting from dissipation, by new matter, and especially new energy (in a form that can be used to fuel processes, in contrast to dissipating heat) to keep them away from thermodynamic equilibrium, i.e. by actively ingesting energy-rich materials, either by synthesizing them from inorganic matter and solar energy (that's what green plants do) or by ingesting other organisms or parts or products of them (done by fungi and animals).
This is the first main part of the strategy, i.e. the main condition for something to be a strategy.
The second main part is more typically organic : Although managing themselves as far-from-thermodynamic-equilibrium structures, constantly replacing matter-energy losses, the material organic individuals (instances of the species's strategy) are only moderately stable. Sooner or later they will slide down into thermodynamic equilibrium, i.e. they will disintegrate. So the second part of the strategy, made up to keep the very s p e c i e s going, is the phenomenon of reproduction, resulting in new, fresh individuals of the same species (these new individuals participating in the same strategy). This main part of the strategy is probably the most intricate and subtle one, and certainly one of the main conditions for a complex form to be a strategy.
A large part of the overall strategy of an organismic species is, in the form of instructions, stored in organic molecules, the DNA. It triggers at the right places in the body, and at the right time, the production of the right proteins, wherby some of these directly serve as building material of the organism's body, and others as start-signals to, in turn, trigger many very specific biochemical reactions resulting in the organism's ability to grow and perform the necessary functions of sensing, feeding, excretion, and reproduction. Accordingly, much of the species' strategy is stored in the DNA, which, of course, itself -- as a specific kind of molecule, suited to store information -- is also part of that particular strategy.
In order for such a strategy to develop in the Implicate Order from a non-strategy, the noëtic chreode (canalizing the production) must be such -- as determined by the production-rules of FSNSS -- that by (only) going up in it, a form (a string) increasingly becomes more able to inform Prime Matter (= the ultimate ontologic content-free 'carrier' or substrate of Form (content)), meaning that, while being step-by-step transformed according to the production-rules, it eventually becomes c o m p l e t e l y able to inform Prime Matter, i.e. it is able to exist in the Explicate Order, it is a strategy. And the rules themselves are such that they, starting to act on some given original immaterial form, an axiom of FSNSS, determine their own consecutive order of application, resulting in a, in the chreode upgoing, sequence of theorems, the last one of which is a true strategy. And we know that the rules -- the production-rules of FSNSS -- being precisely such that they indeed accomplish such transformations, results from the fact that their intrinsic content stems from the Explicate Order.
Projection of a noëtic strategy-string into the Explicate Order in terms of simulation and computation.
In the practice of natural science mathematics is used to simulate observed natural processes and structures. And when the result, the simulation, conforms with such a natural process or structure, that process or structure is said to be understood. So what is simulated is the material process or structure, and it is simulated by a mathematical model, nowadays implemented in a computer, which, by means of an algorithm (a set of computer instructions) solves the equations of the model.
For our theory we can use the practice of simulation to establish an analogue of the projection of a noëtic form from the Implicate Order into the Explicate Order, that is the transformation of an immaterial form -- a mathematical string -- into a corresponding material form. But for this we must turn the simulating-simulated relation upside down. That is, ontologically, mathematics does not simulate material processes or structures (as it does in science), but material processes or structures simulate existing mathematical 'processes' or structures, i.e. immaterial forms. In this we may theorize that for a given immaterial form "to be fully able to inform Prime Matter" is, to begin with, equivalent to that form "being able to materially exist in the Explicate Order", and then, for this materially existing form, i.e. for the existing material configuration, equivalent to actually s i m u l a t e that immaterial form. Precisely that material configuration that simulates the immaterial form and is at the same time its simulacrum, is necessarily i s o m o r p h i c with that immaterial form and consequently its m e a n i n g (significatum). So for an immaterial form "being fully able to inform Prime Matter" is equivalent to this form "being such that it can be simulated by a material configuration" which in turn is equivalent for it to be able to project into the Explicate Order, and so precisely appearing as that same material configuration. And if an immaterial form, i.e. a mathematical structure, sequence, or function, can be simulated by some material configuration (which we may call the "computer"), then that immaterial form is computable. So the computability of this form is equivalent to the fact that it can be simulated by some material configuration. And so, in turn, for an immaterial form to be computable (i.e. to be materially produced by computing that form) means that this form can materially exist in the Explicate Order. And, further, for some immaterial form to be computable, it must at least be non-random, it must internally be a true and definite pattern of elements. To define randomness in terms of information we might say : If an intrinsically r a n d o m immaterial form, which [form] is non-algorithmically defined in some way (i.e. a form, either just posed or given, or described in words, that is, a form not expressed in computer-instructions), for example a (so) given number expressed as a series of digits, - has more information content than the axiomatic system with which it is associated, then that form is random (in case of a number : as regards the consecutive order of its digits). ( See COVENEY and HIGHFIELD, Frontiers of Complexity, The Search for Order in a Chaotic World, 1995, p. 32-34, and BARROW, Pi in the Sky, Counting, Thinking, and Being, 1992, 134-137 ). Such a random immaterial form is interesting when it is associated with the Formal System of Strategy-Strings ( FSNSS ). It is then an axiom of this system, and being internally not ordered or patterned it cannot be simulated by any material device, meaning that it is not a strategy, and cannot therefore be projected into the Explicate Order.
Because every definite immaterial pattern (such as a description of something) can be encoded by a single whole number, it is interesting to ask when a given number is such that it is truly random, that is whether its consecutive order of digits is in fact a random sequence. A number, for example written in binary digits, is indeed random if the sequence of 0's and 1's is indistinguishable from a series of heads and tails obtained by tossing a coin. Each outcome of a coin toss tells you nothing about any future outcomes or past outcomes. In such a string of digits there is no 'Fibonacci-like' rule telling you how to everytime compute the next digit, i.e. the sequence of digits, or in other cases the consecutive numbers of a number sequence for that matter, cannot be determined by some recursive function, not even by a much more complex one than that what determines the Fibonacci numbers [ this is a sequence of numbers, of which the first two numbers are given : 1 and 2, and of which each next number can be obtained by calculating the sum of the two previous numbers. This number series is one that pops up in some features of growth in plants]. The series accordingly is : 1, 2, 3, 5, 8, 13, 21, 34, 55, . . . ].
What does it exactly mean that a given number is uncomputable? To answer this, it is perhaps instructive to give an example of a truly random, that is, uncomputable number, i.e. a number that does have a non-algorithmic definition, but cannot be computed on the basis of that definition :
The number OMEGA (as we might call it), thought of as written in binary notation (which choice is theoretically immaterial) is d e f i n e d as follows :
Given is a so-called Diophantine equation with a large number n of variables, say 17000, and a whole number Q which could be 1, 2, 3, 4, . . . etc.
Thus X1 + X2 + X3 + X4 + . . . Xn = Q (where the X's are raised to fixed integer powers) is in fact a family of Diophantine equations in which the members are distinguished by the value of Q. Now take each value of Q in turn and write 0 if the corresponding Diophantine equation (thus having the particular value of Q) has a finite number of solutions in whole numbers, and write 1 if that number is infinite. The result then is a binary string of ones and zeros, so if we place a point at the very beginning of the string, we indeed have defined a number, in this case a number between zero and one.
( By the way, this number, so defined, also expresses the probability that a randomly chosen computer program with a random[ly chosen] input will eventually stop after a finite number of steps. And this probability cannot, therefore, be known.)
The number just defined has infinitely many binary digits and is called OMEGA. And the sequence of its digits is totally random, and thus indistinguishable from a series of heads and tails obtained by tossing a coin. No machine that merely follows a given rule or program possesses the ingredient of novelty that is required to create the next digit of the sequence.
So this was an example of uncomputability of a number. That is, a number that is defined, but is nonetheless uncomputable. It is uncomputable because its series of digits has no pattern, it is fully random. Even when some initional series of its digits were known, the next digits cannot be computed (with the same computer program, acting according to the definition of OMEGA).
For each value of Q in the corresponding Diophantine equation a new approach must be followed to answer the question whether the equation with this particular value Q has a finite or infinite number of positive whole-number solutions.
If we want to know the complexity of a (defined) sequence of numbers, or a sequence of digits (each one of them being itself a number) of a (defined) number, we ask what is the length, in computer bits, of the shortest program (algorithm) that can generate the sequence.
A particular random sequence of digits or numbers (random, but nevertheless definite) may either be non-algorithmically defined such as the sequence of digits constituting the number OMEGA, or, not defined, but simply given, such as, for instance, the number-sequence 3, 56, 6, 23, 78, . . . (which we here indeed give as to its beginning, but which is supposed to have been given here in its entirety -- where "entirety" should not point to actual infinity, but to potential infinity : meaning that the series can be extended indefinitely because "we see no end".). In both cases there is no special (single) rule for generating (any)one entry from another. And the shortest computer program to generate such a sequence can be nothing less than the mere listing (i.e. not the consecutive computation of its members) of the sequence itself, which is, of course not a generation of it.
If, on the other hand, the (chosen) sequence is ordered, then the required program (algorithm) can be much briefer than the given, or defined sequence. Indeed, to give an example, the sequence 2, 4, 6, 8, 10, 12, . . . is ordered, and a program can be written to just print all [i.e. as far as we want] the even numbers [ PRINT 2N, for N = 1, 2, 3, 4, . . . ].
A sequence is random if its complexity equals the length of the sequence itself (both written in, for example, binary notation).
Sometimes a definition of a number or of a sequence of digits is as such non-algorithmic but turns out to be implicitly algorithmic, and then, of course, the number can be produced after we have unearthed the algorithm. For example we have the number or digit sequence
This (unfinished) number (or series of digits) really looks completely random, but in fact it is not so, because the series really is the beginning of the decimal expansion of the number pi / 4, where "pi" is the ratio between the circumference and diameter of any circle. And what then is the algorithm to actually compute this decimal expansion? Well, it is the sum of the following numbers :
This sequence of numbers (the number one and the many fractions) can easily be extended as far as we like (i.e. it is itself not random). The next number evidently is +1/17, and the number following it is -1/19, etc. If we calculate the sum of these numbers we are generating the above seemingly random series of digits, and are thus computing the number pi / 4.
So a truly random number cannot be computed, which means that it cannot be produced by any material configuration, which in turn means that there cannot exist any material configuration that can simulate that number, and this further implies that it has no material meaning, i.e. a meaning in the Explicate Order. The only significance it might have is that it, as an individual immaterial structure, is one of the many axioms of the Formal System of Noëtic Strategy-Strings ( FSNSS ), in which such an axiom is step-by-step being transformed into a (still) immaterial structure (pattern) that is now such that it can be simulated by some material configuration, which material configuration is then the immaterial structure's (material) meaning. It is the materialized strategy, and as such the organismic species.
[As to inorganic entities existing in the Explicate Order, they stem from immaterial forms (in the Implicate Order) that are already such that they are fully compatible with explicate order conditions, and so do not need to develop into a strategy (which is, when having been projected into the Explicate Order, an active strategy, an organismic species). And such immaterial forms are thus already all by themselves computable.]
A simulation of "some sort of reality" indeed represents that sort of reality (here simulation-simulated taken in the usual [but not our's] sense), because it is the algorithmic product of a mathematical model. It is generated by processes that are ultimately independent of human intervention, except for the choice of the model. The logical structure of the mathematical model is indeed independent of human intervention.
In all this, but now taking things ontologically, we say that the mathematical model itself is simulated by the algorithm that computes the model, whereby the (already material) outcome -- the product -- is made visible by some video display device. The mathematical model is -- as a result of this simulation -- made material. And after having us placed things into the dynamics between the Implicate Order and the Explicate Order, we take the mathematical model not to be merely a model [set up by humans] anymore, but to be an objectively existing immaterial form (where "existing" here means "immaterially being" of such a form).
As to the idea that organic strategies -- developed in the Implicate Order as a result of formal production according to arithmetical rules harnessed by the Explicate Order -- become material[ly realized] as a result of [some analogue of] simulation, we, of course, do not know in what form the noëtic strategy is represented in the Implicate Order. And although we have assumed that this form is that of a "description" of the strategy (= the noëtic counterpart of an organismic species), this way of imagining that form is still very unspecified. But this is precisely how far we can go. In fact the noëtic organic strategy is (supposed to be) a particular whole number. And it has a material meaning because it is computable and can be simulated. It is not so that that particular whole number, that is going to represent the noëtic description of an organic strategy, can be materially simulated precisely in virtue of its meaning that it is supposed to have in the Explicate Order (in the sense that another meaning would make it unable to be so simulated). It obtains material meaning as a result of the fact that it is materially simulated in the Explicate Order. And only then the mentioned whole number codes for a noëtic description of a particular strategy. The simulation consists in actually and materially producing that noëtic description, producing it in the Explicate Order, resulting in the appearance of a particular organismic species. Such a species is then represented by a various number of material individuals and only they are actually alive. The simulation of the strategy thus consists in computing it, i.e. materially producing it.
The preconditions of computation as such, include (according to LANGTON, and discussed in EMMECHE, The Garden in the Machine, 1991, p.123) include
We have theorized about the nature of the projection of noëtic strategy-strings into the Explicate Order in terms of materialization, simulation, and computation.
The greatest enigma, however, is the very formation (in the Implicate Order) of those strategy-strings from non-strategy strings. The heart of the enigma lies of course in the precise nature and content of the production-rules of FSNSS. The content of these rules is derived from explicate-order-conditions, while (this content) having as it substrate (ontological) number theory, itself constituting the Implicate Order. Ultimately, the content of these rules is determined by the immaterial forms' aspiration (we might say 'need') to become ontologically complete. Of course we cannot even speculate how these rules look like, and how, as a result of their application, the sequence of noëtic forms, starting with some random form (one of FSNSS's axioms), goes through a series of already partially non-random, but partially still random, and thus explicate-order-incompatible, forms, and ends up with a true strategy-string, noëtically describing an organismic species.
Relevance of uncomputable mathematical functions and of non-algorithmically defined numbers to the material world.
We had spoken of computable and non-computable mathematical entities in the context of these entities to be (or not to be) projected into the Explicate Order. In this theoretical context we have said that non-computable mathematical forms cannot be simulated by any matter-energy device (and then this very device itself constituting a material simulacrum of that mathematical structure), while all computable mathematical forms are so simulated in the Explicate Order (as seen from the timeless Implicate Order).
But what if there do exist (many important) material configurations (i.e. definite configurations) in the Explicate Order which are completely random as to their internal 'structure' or are supposedly correctly described by mathematical equations whose solutions are uncomputable? This problem is adressed by COVENEY and HIGHFIELD, 1995, in Frontiers of Complexity, pp. 40. [comments of mine in square brackets] :
Very little work has been done to find out how the theoretical limitations on mathematics [unsolvable mathematical problems, incompletenes of formal systems, uncomputability of certain mathematical forms, uncompressibility, randomness] [...] restrict our ability to describe real-world [here the material world] complexity [in our context such restrictions would imply that some of this complexity cannot be the result of simulation, i.e. of material simulation, as defined above]. Perhaps the most serious suggestion that they do pose problems comes from the work of Marian Pour-El and Ian Richards at the University of Minnesota. They have shown noncomputable solutions do exist for certain well-known equations of mathematical physics, including the wave equation, which describes the way in which electromagnetic waves propagate -- such as light, ultraviolet, infrared, X-ray, and radio waves.
Yet it is difficult to see how this finding will restrict the study of complexity [meant is here complexity of structures and processes in the Explicate Order]. The (computable) initial conditions necessary for yielding noncomputable solutions are somewhat unusual. But as these mathematicians point out, an experimenter [who does not let unusual initial conditions being involved) would observe a computable sequence of events and so would see nothing unusual occurring. Since science is about what we observe, even these peculiar mathematical results do not place significant limitations on the computer in its application to science. Even though pure logic has shown the limits of mathematical reasoning, it is significant that Turing himself [one of the inventors and investigators of the concept of digital computers] never took these limits very seriously in his writing on artificial intelligence. Chaitin [another, more recent, explorer of randomness and computational limitedness] also believes that the arithmetical randomness he discovered is a feature of the Platonic world, not the one we inhabit. [ We would say it is a feature 'here and there' occurring in the Implicate Order, existing there, for example, as the axioms of our assumed Formal System of Noëtic Strategy-Strings ( FSNSS ) ].
The problems of mathematicians all stem from the relationship between the finite and the infinite [especially the actual infinite, and still more so the uncountable (actual) infinite], or the discrete and the continuous. Turing's concept of a computer is based on a discrete, digital device with a finite number of internal states. With the possible exception of quantum computers, his universal machine defines the limits of what is mathematically computable. Nevertheless, physical systems that run on "classical", that is, Newtonian, laws, are continuous rather than discrete. They therefore have access, in principle, to an infinite number of internal states [even a non-countable infinite number of states]. Such analog computers could therefore be expected to outperform the universal Turing machines [one should better say "the universal Turing machine", because it is a single concept] by computing results that digital computers cannot. Examples of this enhanced ability would include solving halting problems [deciding whether a given program, once fed in, will ever stop and give results], and generating noncomputable numbers. (COVENEY and HIGHFIELD, 1995)
Our idea of seeing projection, - from the Implicate Order into the Explicate Order, of immaterial forms (such as those that stand for descriptions of strategies-to-exist-in-the-Explicate Order), and these forms then becoming material, - in terms of simulation and computation, may not be more than just an analogy, i.e. an analogy of the real process of projection. It is nevertheless instructive because it at least attempts to demystify our concept of projection. A given organismic species (as such representing a material(ized) strategy) "simulates" (without us necessarily seeing it as a "computer") its noëtic counterpart (immaterial form), where the latter is the noëtic description of the strategy immaterially derived and residing in the Implicate Order. The material entity (in the Explicate Order) that simulates the immaterial form (in the Implicate Order) is at the same time the simulacrum of that immaterial form (i.e. that what computes the immaterial form is at the same time the result of that computation). Therefore, the actual activity of a Turing machine (conceptually representing a computer fed with some program) in terms of simulation and computation might show us the way to understand the phenomenon of a form's transition from an immaterial domain of (mere potential) existence into a material domain of (true) existence.
And indeed, our analogy is perhaps a well-chosen one, because in natural science one indeed links nature's (i.e. the Explicate Order's) complexity with computation (COVENEY and HIGHFIELD, 1995), i.e. the emergence of complex organized behavior from the many simpler cooperative and conflicting interactions between the microscopic components concerned, whether they are atoms, bits of logic, or spinning electrons.
The Implicate Order knowing the Explicate Order
Introduction
Especially in organisms we see, in addition to neutral or non-functional characters and structures, many biologically functional ones. And I expect that a truly functional character or structure, -- such as, for instance, a specialized ovipositor as it is present in many insects (such as in ichneumon flies), and also, for instance, the whole flight-apparatus in winged insects (especially as we see it in Diptera and Hymenoptera, whose flight-apparatus is characterized by the, later to be described, highly advanced type called "dipterygia"), and, above all, the functional behavior of the higher Hymenoptera as to their care and provision for their offspring, in short, ( I expect that) all these functional characters and structures, -- cannot mechanically come into being. And in the relatively few cases where they did come into being in this way, we may hold that they merely happened to be biologically functional (to assist the organism in its existence) after the fact so to say, i.e. it turned out that they could be used to perform certain functions, just by accident. However, most functional structures present in organisms cannot be so interpreted.
This is in fact acknowledged even in Darwinian theory. And that's precisely why it does not suppose truly linear evolutionary lines definitively leading, step by step, to such a functional structure (and to a whole organic strategy for that matter, of which it is but a part). For such structures to come into being Darwinian theory admits of mere random changes (of the phenotype as a result of such changes in the genotype) being all what is needed. And indeed a random change is one that is caused by factors that just happened to be present instead of factors that must be present. So no mysterious final causes need to be assumed. As such, it is true, a process of repeated (but different) random changes can never result in the formation of a functional structure relevant and useful to the individuals of the species concerned. So Darwinian theory, while insisting that the material world is capable of creating such functional structures, calls for continued natural selection of mutants that phenotypically represent an incremental increase of the overall fitness of these mutant individuals. These individuals are supposed to be just a part, a population, of the original species, while the other part remains unchanged, as is assumed in Hennigian phylogenetic systematics (as being the macroscopic phenotypical consequence of Darwinian theory), and which is evident when comparing taxa that are 'advanced' in certain characters with other related taxa which are not, in the same respect. And so the process of creating a given functional structure does not, in this Darwinian theory, proceed like this :
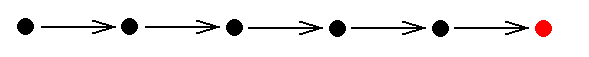
but rather like this :
This process is not a straightforward one, and the creation of the functional structure depends on the right order of appearance of the right and relevant genetic mutations (expressed and selected upon in the phenotype), and also on the completeness of this series of mutations. Moreover, it will be expected that other quite different genetic mutations (as expressed by the phenotype) will mess up with the selection process (when they happen to have a somewhat greater selection value), resulting in the original series to be broken off somewhere along the line and being continued in some other direction quite different from the original one, which (other direction in turn) may, subsequently also be broken off (i.e. cut short prematurely), etcetera.
All this, together with the fact that most genetic mutations are either phenotypically indifferent, or even harmful to the organism, it is clear that functional structures (or at least the most subtle of them) cannot be produced by the mechanism of random genetic mutation and natural selection. They must have been produced in some other way. But because the Darwinian process of creating functional structures is, according to me, the only serious candidate for having the material world to produce functional structures, and if, indeed, we cannot accept such a Darwinian process to be (fully) responsible for the origin of such functional structures in organisms, we must look elsewhere for the origin of these structures. And this means that it must take place in some immaterial environment, i.e. in some immaterial order of things, where indeed there is final causality, namely in the form of every immaterial form or pattern aspiring to become ontologically complete, that is, to become material. And to achieve this it must somehow come to exist in the Explicate Order, and in order to become able to so (materially) exist (and persist) it must develop into a strategy. Precisely such considerations had led us to our theory of the (immaterial) Implicate Order (where we have been inspired by the works of David Bohm, who first -- on the basis of an interpretation of quantummechanics -- proposed this dual order of Reality, but where the noëtic theory of evolution is completely a proposal of our own).
So a functional structure has to be produced in the immaterial Implicate Order and in the context of the construction (if we may use such a mechanical expression) of a whole complete organic strategy of which that functional structure is just a part. And, as we know, the constructed strategy may subsequently be projected (also a term of Bohm's) into the Explicate Order where it appears as an organismic species. But such a functional structure, and indeed most organic strategies for that matter, cannot be constructed in the immaterial Implicate Order without that Order having knowledge of the Explicate Order. Said differently, for the construction of a biologically functional structure there must needs be some in-flow of information from the Explicate Order into the Implicate Order, because the functionality of the mentioned structure is only relevant in a material and biological context, not in the purely immaterial context of the Implicate Order. Only in the material and biological context (and that is the context of the Explicate Order) the structure may truly be functional. So there must be some in-flow of information, or perhaps some causal influence, from the Explicate Order into the Implicate Order, in order for the latter Order to be able to produce biologically functional structures (and thus organic strategies). And all this is an expression of immaterial forms to become increasingly more appropriate to inform Prime Matter, i.e. to (materially) exist in the Explicate Order. What is this in-flow of information? What is the nature of the necessary contact of the Implicate Order with the Explicate Order? Of course it must be some kind of knowledge : The Implicate Order must be able to know (about things and patterns in the) Explicate Order. One might feel of this idea as to be a serious concession and capitulation in the enterprise to mechanically explain the bewildering complexity of, and functionality in, organisms, and their functional relationships and interactions. But it seems the only way out, and we have done our utmost best to preserve Nature as a unity. We, in our theory, endow the Implicate Order (which is not supposed to transcend the material world, but to be ordered to it) with natural rationality and some power of knowledge, to better for us to understand and describe the organic world as we observe it in the Explicate Order.
Organic strategy-contents and their existential conditions in the Explicate Order.
The exact matching of the organismic species in its environment.
The Implicate Order's knowledge of the presence of organismic species in the Explicate Order.
This section is, among other things, about the origin and nature of the rational aspect of the organic world as the latter is (historically) structured in the Explicate Order. It especially concerns the perfect match between any given organismic species and its biological and physical environment forming its existential condition or ecological niche.
It is the Implicate Order's intrinsic aspiration to have all its immaterial forms materialized, which means having them maximally determined all the way down to individuals. And this can only take place in the Explicate Order. For this to be possible, the many immaterial forms which are not by themselves capable to inform Prime Matter, and thus to become material, must first turn into 'strategies' to exist in that Order, where they then appear as organismic species. And (the content of) each such an organic strategy will not only refer to necessary in-organic existential conditions (such as climate) but also to other organic strategies, strategies that support it. In this way each strategy will define an existential condition for the corresponding organismic species, i.e. (will define) its proper ecological niche. And just as an organismic species is not merely one particular individual at some place and time, its ecological niche is a general condition that may be instantiated in different and even widely separated locations.
An organismic species is here seen as the basic biological entity or unit that possesses a qualitative content (essence, strategy) of its own, distinguished from that of other organismic species. And an organismic species acts or behaves according to its qualitative content through that species' existing individuals. That is to say, in the Explicate Order it is not a species, as species, that acts or behaves, but its individuals, but they act according to the commonly possessed qualitative content (strategy) of their species, a content forged in the Implicate Order, while things like individual variability, all kinds of contingencies, and indeed the very individuality of the members of the species, and also, of course, place and time, are typical of the Explicate Order. They are not to be found in the Implicate Order.
The placing of organismic species in their proper ecological niche, i.e. their precise match with existential conditions, must bring-in some sort of 'knowledge' from the side of the Implicate Order. 'Knowing the Explicate Order' is one of precisely those intrinsic properties of the Implicate Order (these properties determining what it really is) determining it to be wholly geared into (i.e. wholly ordered to) the Explicate Order (already evident in the nature of the production-rules of FSNSS ( Formal System of Noëtic Strategy-Strings)). So the Implicate Order must possess certain cognitive instruments or logical tools intending structures in the Explicate Order.
Human knowledge of the material world is ultimately based on sense experience. A material object is entirely given to the senses, meaning that the sense data (such as smell, color, etc.) presented to the senses are apprehended by the intellect to belong to some existing object. As to which (kind of) object it is we might sometimes be mistaken. It can be determined by judging additional sense data.
As for the Implicate Order, on the other hand, we cannot assume it to have senses, i.e. we cannot assume its knowledge of the Explicate Order to be based on sense experience, because sense experience as such is about, i.e. is ordered to, external individual (i.e. one-off) material cases, configurations, or events, while the Implicate Order, being itself immaterial, is, -- although being fully ordered to the Explicate Order (its forms strive to become material) and thus to individuality as such (as it is implied by materiality), -- not fixed up for dealing with one-off individual cases, configurations, or events. Its knowledge is rather comparable with knowledge of mathematical entities, such as prime numbers or sets. So it needs not 'abstract' from sense data some common qualitative content. It directly intends this content as it is the case in mathematical knowledge.
The following account of the cognitive abilities of the Implicate Order will not be easy to fully apprehend and will be in need of further development, but is, I think, nevertheless inspiring, interesting and instructive to read, despite some necessary repetition (sorry!) of the general idea to be expounded.
Theory of the Implicate Order knowing the Explicate Order
Before further considering the possibility that the Implicate Order is able to k n o w the Explicate Order as to existing material patterns in it, and in this way being able to return, on the basis of this knowledge, new structure, and thus to imbue the Explicate Order with a r a t i o n a l s t r u c t u r e as far as the o r g a n i c w o r l d is concerned, we must first recapitulate our theory so far developed.
Earlier we had established the presence in the Implicate Order of the noëtic process of a (large) number of initial immaterial forms becoming increasingly more adapted to inform Prime Matter. In each case this process starts with some given form (axiom) which is totally random as to its internal structure : As such, it cannot be materially simulated because it is uncomputable, and thus is totally unfit to inform Prime Matter. The increase of this fitness to do so is a necessary consequence of every immaterial form's aspiration to become ontologically complete. Therefore, the trajectory of the immaterial form's change follows a noëtic chreode (as described above), and in doing so the form necessarily ends up as a pattern that can materially exist in the Explicate Order, i.e. it ends up as a strategy-to-exist-materially-in-the-Explicate-Order.
In this way, starting in each case from some internally random immaterial form (and in other cases from other, qualitatively different, internally random immaterial forms), and thus, collectively, starting from a virtually unbounded set of such initial forms, FSNSS (the Formal System of Noëtic Strategy-Strings) ultimately produces all possible strategies, i.e. it generates the complete collection of strategies ready to be projected into the Explicate Order.
But maybe we should mitigate this claim (concerning "all possible strategies") a bit : A very large number of strategies is indeed so constructed in the Implicate Order, but not necessarily all strategies exhaustively. This accounts for the fact that in the Explicate Order in all probability there exist vacant ecological niches never to be occupied by a particular organic species.
Strategies that have been so formed in the Implicate Order will be projected as soon as the corresponding existential conditions (ecological niches) for these strategies to fit in are actually present in the Explicate Order. That is to say, as soon as some vacant ecological niche has somehow been formed or simply happens to be present, the corresponding strategy, if present in the mentioned collection of strategies produced by FSNSS, will be projected into the Explicate Order. And it will be so projected at all the sites (or at least at many of them) where the vacant ecological niche happens to be represented (i.e. instantiated). There the strategy will be simulated (i.e. materially computed) and consequently appears there as a new organismic species (the same species in all the individual instances (sites) of this vacant ecological niche).
So far so good.
Having said that a large number of strategies have been produced in the Implicate Order, and together constituting the collection of (still) immaterial strategies, 'noëtic strategies', we may now turn to the s e l e c t i o n, by the Implicate Order, of particular strategies from this collection, and their subsequent projection into the d e t e c t e d vacant ecological niches. This detection / selection can only be accomplished when the Implicate Order is able to obtain k n o w l e d g e of the changing situation in the Explicate Order with respect to the destruction or creation in it of existential conditions, i.e. of ecological niches. For this, the Implicate Order, as a subject, must be able to know the structure of each strategy as it is materialized in the Explicate Order, and to know its inherent relationships with other strategies, that is, it must know the essence (qualitative content) of each organismic species as this essence is present in the individuals representing that species, and know all interactive relationships between existing species, (it must know all this) in order for it (i.e. for the Implicate Order) to be able to recognize a still vacant ecological niche and to select (from the above mentioned collection) the right strategy for that niche to be occupied, i.e. to pick out a strategy for which this niche is precisely its existential condition.
If we admit the power of obtaining knowledge to be possessed by the Implicate Order, we must enquire after its tools of knowledge-acquisition, i.e. we must enquire into its supposed logic.
Concerning such logical tools, we suppose that s i g n s do exist in the Implicate Order that intend things-to-be-known, i.e. genuine intentional signs (in contrast to mere instrumental signs), whose qualitative content is not in fact their own's, but that of what they (are supposed to) intend or signify, that is, they are exclusively about something else, and that something else is their m e a n i n g (i.e. that what they signify). In Fifth Part of Website, " Logic, formal elements of cognition" part I-VII we have given a complete treatment of Intentional Logic insofar as it concerns human knowledge. Much about the necessity of intentionality of logical signs is written there.
When in the Implicate Order a given strategy is formed from some original immaterial form, it is itself still immaterial, it is the noëtic prescription of that strategy for how itself to exist in the Explicate Order. When this strategy subsequently has been p r o j e c t e d into the Explicate Order it means that the strategy, as being a qualitative content or essence, has been taken up in existing individuals, i.e. it has been materialized. And we may now theorize that the content or essence, now being present in individuals in the Explicate Order, is no longer explicitly present in the Implicate Order, because it has changed into an intentional sign pointing to that content as it is now in the Explicate Order. This is indeed yet another way of describing the phenomenon of 'projection' : as the transfer of a form, i.e. a content, from the Implicate Order to the Explicate Order, resulting in a sign-signified structure. And if the organismic species subsequently happens to become extinct, its strategy-content is injected back into the Implicate Order, where it is then not an intentional sign anymore, but will become such a sign again when the content is again projected.
Maybe we should qualify this a bit more : A projection of a strategy-content is always immediately followed by an injection temporarily switching off the corresponding intentional sign only to having it switched on again upon subsequent projection (of that same strategy-content). In this way there is a continuous alternation of projection and injection taking place. And, as we will explain in the next document, this alternation plays a part in the further refinement of the strategy-content. And only after extinction of the species the intentional sign ceases to exist until the strategy is projected (later) again as conditions again permit.
To explain things further, we may start from a situation in which a number of strategies have already been projected into the Explicate Order, implying that some more or less primordial communities (biocoenoses) of living organismic species do exist (each one of such communities existing as one ore more individual instances of it, and each species in such a community being present in the form of a number of existing living individuals).
Let us consider one such more or less primordial community, and the Implicate Order's logical instruments to intend such a community.
Each species of this community is the result of projection of the corresponding noëtic strategy-content. As explained, the latter has, in the Implicate Order, thereby become an intentional sign, while the corresponding organismic species is its meaning. So through the presence of the intentional sign, the Implicate Order knows that the organismic species signified by it is (still) present in the Explicate Order.
But the strategy-content (as such intended by the Implicate Order) intrinsically implies a pattern of interaction with other strategy-contents (in the Explicate Order visible as predator-prey relationship, phytophagan-foodplant relationship, parasite-host relationship, protection-enemy relationship, etc.). So the description of the strategy does refer to other strategies. In this way many potential causal patterns (potential causal relations) are involved in making up every single strategy-content (i.e. each strategy-content refers to many other strategy-contents). So any given strategy-content intrinsically refers to other strategy-contents, either as necessary supporters of it, or as those that should be protected against, or as those that should be absent in its habitat because they are in one way or another incompatible to form part of its ecological surroundings. And when all other strategies necessary for supporting a given strategy, and consequently being ecologically adjacent to that given strategy, are, as organismic species actually present together, here meaning not only being co-existent in the Explicate Order but also spatially adjacent to each other, then these other strategies together constitute the biological existential condition of that given strategy-content, i.e. they form the ecological niche of the corresponding organismic species. So the biological existential condition of a given organismic species (and thus of its strategy-content) consists in the fact that all other organismic species that are indispensible to support the very existence of this given species and to which reference is made in its strategy are present in its habitat, whereas all other species that are absolutely incompatible with its strategy are absent in its habitat. And the complete existential condition must, of course, include inorganic conditions as well, such as climate, and also the nature of the medium or substrate of living (water, air, soil, bodies of living or dead organisms, etc.). The strategy of the given organismic species is then precisely ordered to this existential condition so that it exactly fits into it, resulting, together with the supporting and other species, in an ecological community of interacting species. Also each of the supporting species referred to in the strategy are themselves materialized strategy-contents as well, and will refer to still other supportive species, some of them being among the species already referred to in the first mentioned strategy, while others being indifferent to the latter. And in this way each species occupies its own ecological niche, that is, an organismic species is exactly defined by its specific ecological niche. And such a whole web of co-existing and interacting strategies can be detected by the Implicate Order, detected as to be actually present in the Explicate Order. Moreover, in such a web there may, in addition, exist still v a c a n t existential conditions for strategies not yet projected, i.e. there may exist not-yet-occupied, that is, potential ecological niches. And we must theorize that the Implicate Order is, upon having detected this, able to d e d u c e the precise nature of these potential niches, or, better, able to deduce the content of the strategies that precisely would fit into these niches, or, expressed in yet another way, is able to recognize a vacant ecological niche as being an existential condition for a particular not yet projected strategy-content. Such unoccupied niches are 'holes' in the pattern of already occupied ecological niches. So by intending the collection of the materially co-existing strategy-contents, the Implicate Order can deduce the content of other strategy-contents that may materially be inserted into the existing collection.
Thus, (again saying this a little differently) the Implicate Order knows which strategy-contents are present (in the Explicate Order) in a pattern of filled-in existential conditions and then deduces the content of the strategies that can fill the 'holes' in this pattern, and is then able to select these strategies from the collection of strategy-contents already present in the Implicate Order and produced by FSNSS. As a result, these noëtic strategies will be projected and end up as new organismic species occupying the initially vacant ecological niches in the Explicate Order.
Let me clarify some things a bit further.
If a particular biological existential condition does not happen to exist anywhere in the Explicate Order at a particular point in time, then we say that there is no ecological niche for a particular organismic species to occupy, and so, at that same point in time this species does not, and cannot, exist at that point in time. And if, at some other point in time, such an existential condition, such an ecological niche, is somehow created at one or more locations, and if, subsequently, one or more of them are being occupied by (individuals of) an organismic species, then this species is considered to be a new species, i.e. a species now having appeared for the first time in the Explicate Order. Other existential conditions (existing ecological niches) may subsequently be destroyed or altered, leading to the extinction of the corresponding organismic species.
So, as seen in and from the Explicate Order, all kinds of contingencies taking place in it, may change the existing patterns of existential conditions (ecological niches) by destroying or altering some of them and creating new ones. And in the same way as just described, the new ecological niches may be filled with new organismic species, while other species become extinct. And this, i.e. the succession, alternation and replacement of different organismic species in the history of the Explicate Order, is what we actually see on the basis of the fossil record. It is not the origin of species from one another, but merely the appearance of species as a response to changing inorganic and organic conditions. And all this is fully compatible with the polyphyletic origin of organic taxa, such as families. It explains, for instance, that the same cockroach family Archimylacridae has been found in the upper Carboniferous of such ecologically isolated and geographically widely separated (even in pangean times) regions as the Saar basin (Europe), the basin of Kuznets (Asia), and the Dunkard basin (North America).
The type of knowledge that can be attained by the Implicate Order is not of an individual nature
Although in the Explicate Order all things are local and individual (no universals do exist there), the knowledge, attainable by the Implicate Order about the Explicate Order we hold to be a knowledge of universal relations and contents, and universal only, that is, knowledge of features commonly present in a number of individuals or individual cases, meaning here that that knowledge is not about individuals, individual cases or individual instances, and not about one-off events. And insofar as the organismic world in the Explicate Order is concerned, it is always a knowledge (attained by the Implicate Order) about biologically determined organismic species, not about particular organic individuals.
So it is (1) the identity of, and the relationships between, organismic species living in a particular type of biocoenosis, not in some here-and-now biocoenosis, that possible knowledge of the Implicate Order is about, and (2) this knowledge is about the morphological, physiological, and behavioral structure as it is defined in the organismic species, i.e. about the features of its strategy (of existing).
The Implicate Order cannot inspect or find out where a particular individual of a given species finds itself at a particular point in time, neither what this individual is doing at that time. It only can determine what the organismic species is meant to do in virtue of (and in accordance with) that species' intrinsic strategy, i.e. it can identify that species and distinguish it from other species. It does so by intending the species' intrinsic content as it exists in its individuals. And all this means that no contingencies can be known or detected (in the Explicate Order) by the Implicate Order. It (as a logical subject) can 'speak' about a given individual in universal terms only, signifying necessary consequences of the intrinsic structure of the strategy of the species to which that individual belongs. So the Implicate Order (again as a logical subject) can only assert, i.e. know, things about a given individual insofar as that individual belongs to a given organismic species. And thus the subject-term of such an assertion is, accordingly, not that individual at all, but the species (the latter not merely being some class of individuals, but the biologically determined organismic species).
In the next document we will stress the universality of this knowledge possessed by the Implicate Order again, when discussing the further perfection and delimitation of the strategy as a result of one or another particular additional behavior taken up by individuals of the species becoming, instead of mere one-off events, a habit of more and more of them resulting in the precise homing-in of the species into its ecological niche in setting up its precise ecological station within its habitat. And it is indeed only such additional behavior that has eventually turned into a habit (i.e. having been universalized) that can, as an additional part of the strategy and with this strategy, be injected into the Implicate Order, and then, upon subsequent projection, be known by it.
Actual construction of strategies in the Implicate Order revisited
Above we had described the ability of the Implicate Order to select from the collection of already produced strategy-contents the right strategy to be projected into a vacant ecological niche detected by it. But in addition to this ability we will ascribe to the Implicate Order also its ability to actually construct (additional) rules or adjust existing rules of the Formal System of Noëtic Strategy-Strings ( FSNSS ) active in that Order. Of course we already had ascribed to the Implicate Order the ability to construct strategy-contents, namely through FSNSS embedded in it. But this ability was supposed to completely stem from the immaterial forms' aspiration to become material, that is, the rules of FSNSS were ordered to that aspiration. The new feature to be ascribed to the Implicate Order is its ability to (further) shape the rules of FSNSS on the basis of its knowledge of vacant ecological niches detected by it.
Let us go into this additional ability in more detail.
We had theorized that in the Implicate Order strategies are formed by this formal system [in which (symbol) "strings" are immaterial forms developing into noëtic descriptions ('texts') of strategy], where this formation is driven by every immaterial form's 'aspiration' to become material. We had further theorized that because there is a virtual infinity of immaterial forms to serve as axioms of this system, all, or at least a very large number of, possible strategies will eventually be produced by FSNSS, creating a large collection of strategies waiting to be selected and to be projected into the proper ecological niche as a result of the Implicate Order's detection of such a (vacant) niche in the Explicate Order.
We have further theorized that the detection of a vacant niche makes possible for the Implicate Order to deduce or derive a strategy-content that would, when materialized, fit into this niche. And then the Implicate Order knows where to look in the mentioned collection of produced strategies in order to find this particular strategy to be projected into the vacant ecological niche.
However, we may, in theorizing, proceed in a slightly different way as just described :
Already much earlier we had conjectured that the particular content or nature of the production-rules of FSNSS does come, not only from outside this very system, but also from outside the Implicate Order itself, i.e. it comes from the Explicate Order. Now we had conjectured too that the nature of these rules is, precisely because it stems from the material Order, exhaustively determined by the immaterial form's aspiration to become such that it is able to inform Prime Matter (the ultimate ontological substrate of forms), resulting in each case in an ascending series of immaterial forms that are increasingly becoming better adapted to inform Prime Matter, and eventually ending up as a form that is a strategy of some kind, a strategy to exist in the material Order.
But maybe this is not enough for the production-rules of FSNSS to be such that they can produce (all possible) organismic strategies. Maybe additional knowledge attained by the Implicate Order of the Explicate Order is needed to mould the rules into true strategy-producing determinants. Perhaps the above mentioned ability of the Implicate Order to deduce or derive, but not yet actually produce, a strategy-content from the nature of some detected vacant ecological niche is taken up for it to determine (change or create) some of the production-rules of FSNSS, resulting in one of the ascending series of forms (axiom ==> theorem ==> theorem ==> . . . ) to end up with precisely that particular strategy that fits into the vacant ecological niche.
Indeed, in the case of a (man-designed) formal system such as TNT (a system describing whole numbers and their properties) one uses it to prove theorems. That is to say, one has some statement about numbers in mind that one wants to prove to be true, and that means to derive it from the axioms of the formal system by applying its rules of transformation, i.e. to actually produce that statement in the system. For this to do, one chooses, to begin with, one or two axioms of the system that seem to be fit to do the job, and in the process of derivation one selects precisely those (applicable) production-rules of the system that might eventually lead to the production of the statement, which, when they (i.e. the rules) do, is then taken to be a theorem of the system.
A similar proceeding we may, mutatis mutandis, expect to take place in the production of strategy-contents in the Implicate Order. The particular strategy-content deduced by the Implicate Order from the nature of the vacant ecological niche, i.e. the strategy which the Implicate Order 'has in mind', is in this stage not actually produced by it, but known, known not as such, but as a set of directives that will guide it to select, in a particular ascending series of forms in FSNSS, the right production-rules to be applied in the right order, and then to project the produced strategy into the vacant ecological niche.
This 'meddling' of the Implicate Order with the rules of FSNSS, in fact their determination and construction by it, is in fact one of the aspects of the nature of these rules "to stem, as to their content, from the Explicate Order". So the chreode, in the Implicate Order, of a given ascending series of forms (in FSNSS) is not only determined by the commonly possessed aspiration of immaterial forms to become material (and thus become strategies), but also determined by shaping the rules on the basis of the Implicate Order's detection of a vacant ecological niche in the Explicate Order.
The Implicate Order (as a whole, and thus including FSNSS) then in fact produces the right strategy to be projected on the basis not only of the overall course of immaterial-forms-to-become material, i.e. not only for reasons intrinsic to the Implicate Order all in itself, but also on the basis of certain types of existential conditions being present in the Explicate Order. When the Implicate Order thus is going to produce that strategy-content it takes care of FSNSS to derive a theorem that describes all the adaptations and functional structures necessary for a new organismic species to be able to exist in that ecological niche. In all this, the Implicate Order picks out precisely that particular ascending series of immaterial forms which (series) already most closely comes near the strategy-to-be-formed, and directs the selection of appropriate production-rules to be successively applied. And the noëtic descriptions to be thus formed are descriptons of morphological, physiological and behavioral adaptations. In this way the description of the right strategy is step by step constructed.
REMARK :
As to "constructed" : Precisely this 'activity' of the Implicate Order to generate a description of a particular strategy, and thus of all the functional structures pertaining to it, is the "non-mechanical aspect" of it, referred to earlier.
And, again, these noëtic descriptions are based upon the structure of the detected vacant ecological niche in terms of food resources, protection, etc. The new organismic species must have all the features that make it able to exist and persist in that niche. And in order to be so able, its strategy-content must be a reflection of the whole existential condition represented by that niche. Such a niche might, for instance, be a particular species of plant (defined by its own strategy) that can serve as an appropriate food source for the representatives of such a new organismic species. So the strategy of such a new species of organism should contain adaptations to that plant's integument (to pierce through) and to the nature of the potential nutrients that the plant contains. Moreover, the strategy of that new species must contain resistence and immunity against possible toxins in the plant, and also a protection (such as camouflage) against predators already living on the plant or in the environmental type of it, etc. Also the new species' mode of reproduction must be taken care of, and thus be properly defined in its strategy-content. Another vacant ecological niche for some other organismic species might be the body of some animal species that could be parasitized, bringing with it all the needed adaptations for the new species to be able to do so. Further, also existing social communities of animals, such as ants, create new ecological niches for new organismic species to be occupied.
We may further theorize that the first simple organismic strategies have been directly produced by FSNSS, and projected into the not-yet-so-narrowly defined existential conditions in the Explicate Order, without a vacant ecological niche needed to be detected first, i.e. such a strategy has been evolved (in FSNSS ) wholly and exclusively in virtue of the ontological aspiration of immaterial forms to become materialized. But as new organismic species arise on the scene, new existential conditions for other species are created. And this indeed is 'evolution' according to our noëtic theory.
We have described things in the Implicate Order as : immaterial forms "developing into" strategy-contents by the application of "production-rules", and also as the right strategy being "step by step constructed ", etc. But we must realize, however, that the Implicate Order (and thus also FSNSS) is completely timeless, meaning that what we describe in more or less dynamical terms is in fact a (static) structure, i.e. a certain set of structural features of the Implicate Order.
The incentive to posit such speculative ideas such as of the Implicate Order "knowing" the Explicate Order, and on the basis of such knowledge steering the 'materialization process' of FSNSS into the direction of the right strategies ecologically fitting into certain "detected" vacant existential conditions in the Explicate Order, is the well-known fact of the often very clever nature of many plant and animal strategies, making it possible for organismic species to be able to live in the most diverse and often forbidding environments on Earth. Indeed, it is unlikely that such wonderful and subtle adaptations in morphology, physiology, and behavior would have been originated merely by the process of random genetic mutations and natural selection (of most fit mutants). Some elements of natural rationality must have played an important role in their formation, 'howso'ever unscientific such an idea may sound.
Polyphyletic development of strategy-contents and their noëtic construction in the Implicate Order
Already earlier, namely in Fifth Part of Website, we developed the idea explaining in what way organic strategies may develop in the Implicate Order. They do not develop from one another, but develop polyphyletically from independent axioms of the Formal System of Noëtic Strategy-Strings ( FSNSS ) [where "strings" are 'written' contents]. And the well-known approximately derivational order visible in existing (or once having existed) groups of organisms helped us to more or less reconstruct the step by step construction of strategies in the Implicate Order. We do not derive organisms from each other, and also do not derive noëtically expressed true strategy-contents from each other. On the contrary, we have to do with parallel series, starting from 'axioms', in which (ascending series) all kinds of morphological and other biological structures are going to be noëtically described, i.e. noëtic texts get written and overwritten, in the course of this immaterial process. In the ascent all the way up to true insect-strategies the wing-venation is one of these structures, and different wing-venations, as noëtic descriptions, have certainly been derived from one another. And the wing-venation of existing or having existed related insects will certainly help to more or less reconstruct the noëtic ascent from axiom-string to strategy-string, albeit in very general terms only. And so we have done in Fifth Part of Website. For example, we had set up (based, as explained, on wing-venation) a particular collection of parallel ascending noëtic series, each one of them leading to a specific dipteran strategy [in the present case that particular part of it that is commonly possessed by all the species of some given genus]. Here we reproduce a diagram expressing these ascending series, a diagram made in Fifth Part of Website, part LXXIIa :
Diagram above :
Polyphyletic development (construction) of strategy-contents (strategy-strings) within a particular group of Diptera (two-winged insects) in the Implicate Order (blue arrows).
When the strategy (red disc) has finally been formed by the noëtic process of making the initial immaterial form (at the beginning of each ascending series) to be more and more suitable to inform Prime Matter, i.e. transforming, in each sequence, the initial immaterial form into a strategy prescribing how for itself to materially exist in the Explicate Order, - the strategy-content is projected into the appropriate and vacant ecological niche in the Explicate Order, if this niche actually does exist in that Order. The projection is represented in the diagram by green vertical lines.
It is assumed that the approximately derivational order, detectable in a number of related genera of flies, existing in the Explicate Order, more or less reflects the series of productional noëtic stages as they are being derived in the ascending lines leading, in the Implicate Order, from axioms to true strategies.
For example, the immaterial strategy-content F gives, upon projection, rise to a species of the genus Chiromyza of the dipteran family Stratiomyiidae, a species, that is, consisting of a number of material individuals. So this species F, as such residing in the Explicate Order, does not descent from immediate material ancestors (in the Explicate Order) of a species of, say, the genus Hermione (also of the family Stratiomyiidae) as their wing-venation might suggest, but is the result of the projection of the strategy-content F, itself having been produced in the Implicate Order. And, similarly, this immaterial strategy-string F, as such residing in the Implicate Order, is not derived from the immaterial strategy-content E, but produced from the immaterial not-yet strategy-string E1 which is, as to its content, similar to, but not identical with, the strategy-string E. And in the same way the not-yet strategy-string E1 is not derived from the not-yet strategy-string D1, but from the not-yet strategy-string D2 which is not identical to D1 but merely similar to it. And this D1 is similar to the strategy-string D which, upon projection, gives rise to a species of the genus Cibotogaster also of the family Stratiomyiidae. Further, the not-yet strategy-string D2 has been derived (produced) from the not-yet strategy-string C3 which is similar to, but not identical with, the not-yet strategy-string C2 which is itself similar to C1, which in turn is similar to the strategy-string C which, upon projection, gives rise to a species of the genus Craspedometopon of again the family Stratiomyiidae.
Similarly, E, representing a species of the genus Hermione, and as such residing in the Explicate Order, did not originate from the immediate ancestors -- in the Explicate Order -- of a species of the genus Cibotogaster ( D ), but is the result of the projection of the strategy-content E, as such residing in the Implicate Order, into its appropriate ecological niche in the Explicate Order. And this immaterial strategy-string E has been produced from the immaterial not-yet strategy-string D1, which is similar to, but not identical with, the immaterial strategy-string D. And D1 has been produced from the immaterial not-yet strategy-string C2 which is similar to, but not identical with, C1, and so on, and so on.
If we continue this, we are working our way back along the sequence of genera of Stratiomyiidae (and ending up with Rhagionidae), and, indeed, with the help of them obtain insight in the polyphyletic development of the flies of this family, i.e. in the independent construction of the respective strategy-strings in the Implicate Order.
It is, perhaps instructive to the reader to study the relevant documents in Fifth Part of Website on the phenomenon of polyphyletic development as it is held to take place according to our noëtic theory of evolution. And, of course, this theory will have to be worked out, and perhaps changed, still further. We will do that in later documents.
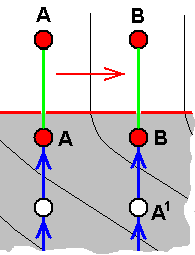
In the same way, for the next wing-venation C (possessed by a species of our group under investigation) we find out that, in the Implicate Order, it cannot have been produced from B but from B1 which is similar to, but not identical with, B. And so we proceed -- A, B, C, D, E -- until we arrive at our target-species F with its wing-venation "F". And indeed, in constructing and expanding the diagram in this way we obtain a significant part of the noëtic 'ancestral' line of construction of the wing-venation of our target-species :
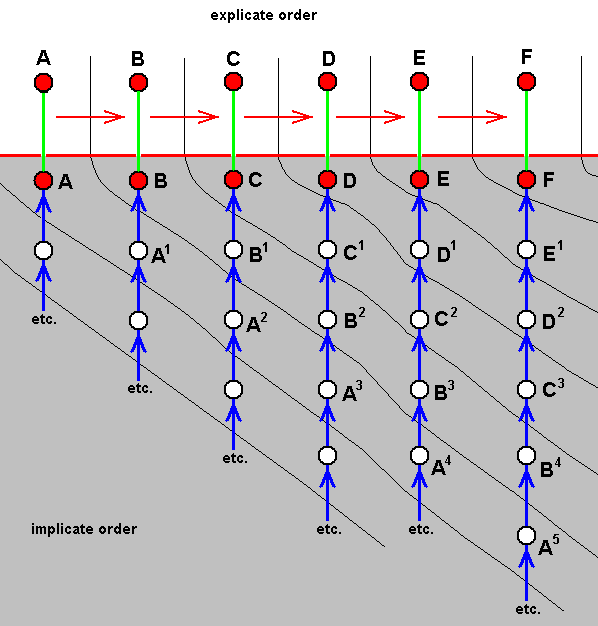
Now the ascending series F, E1, D2, C3, B4, A5, etc., so obtained, shows the probable noëtic construction of the wing-venation in species F from, ultimately, a wing-venation more or less similar to A.
And also of the species B, C, D, and E we have found a part of their noëtic history as to the construction of their respective wing-venations.
Of course this does not yet depict the noëtic construction of a complete strategy-content from some initial not yet strategy-content. It only shows the possible construction of one single element of the strategy, in the present case the insect's wing-venation. So in theory we must follow the same procedure with all other (functional) characters of the same group of insects. But then we will certainly encounter specialization-crossings :
If we follow, for instance, the structure of the mouthparts as they are found in this same group of insects, we will almost always find out that when we study the mouthparts possessed by the existing species of this group while arranging these species in the same order A, B, C, D, E, and F (as they were approximately arranged as to their wing-venation), no derivational series of mouthpart-structures will result at all, even if we admit for hypothetical members in this series, because in most cases there is no 'synchronicity' or correlation in development between wing-venation and mouthparts at all within a particular group of existing insect species (at least it is not a priori to be expected).
But in fact this is not a real problem at all, because we are not looking for a series of existing (and having existed) organismic species that directly (but, of course, always via immediate ancestors, because species cannot evolve from other species when they are precisely contemporaneous) have descended sequentially from one another : The existing species of our group are not supposed to have been descended from one another, that is, it is not supposed that species F arose from the immediate ancestor of species E, and species E from the immediate ancestor of species D, etc. They have developed independently from one another, but nevertheless reflect in some way (and by some reason) the noëtic construction series having resulted in them. So we, in our search for the noëtic construction of strategy-contents in the Implicate Order, can happily rearrange the species of our group until they show a step by step increase of apomorphy as to their mouthparts. And if it is necessary to replace some members of this series of mouthpart-structure by hypothetical ones (because of persistent specialization-crossing with respect to mouthpart-structure) we do so. In this way we obtain a progressive series of mouthpart-structures, and if we now take care that the last member of this series is a mouthpart-structure identical with that of species F representing the last member of the progressive series of venational patterns that we had obtained earlier (derived from the species of the same group of insects), then, by putting together these two series (i.e. by superposition of them), we have obtained a (single) series of increasingly apomorphous venational patterns AND of increasingly apomorphous mouthpart-structures. And although such a series is still not a series of increasingly apomorphous 'complete' strategies, it is already a step closer to such a series. And indeed, the ascending series to be obtained need not be a series of complete strategies, because our noëtic theory considers only the last member to be a strategy at all. The strategy is gradually constructed by transformation of still not-yet strategies.
The following polydiagram symbolically depicts the noëtic construction (vertical blue arrows) of the wing-venation and mouthparts in the species A, B, C, D, E, and F. (If, in such a diagram, not only wing-venation and mouthparts, but all (functional) characters appearing in this group of species would have been considered, then we would have uncovered the noëtic construction, in the Implicate Order, of the (complete) s t r a t e g y of each of these species.) :
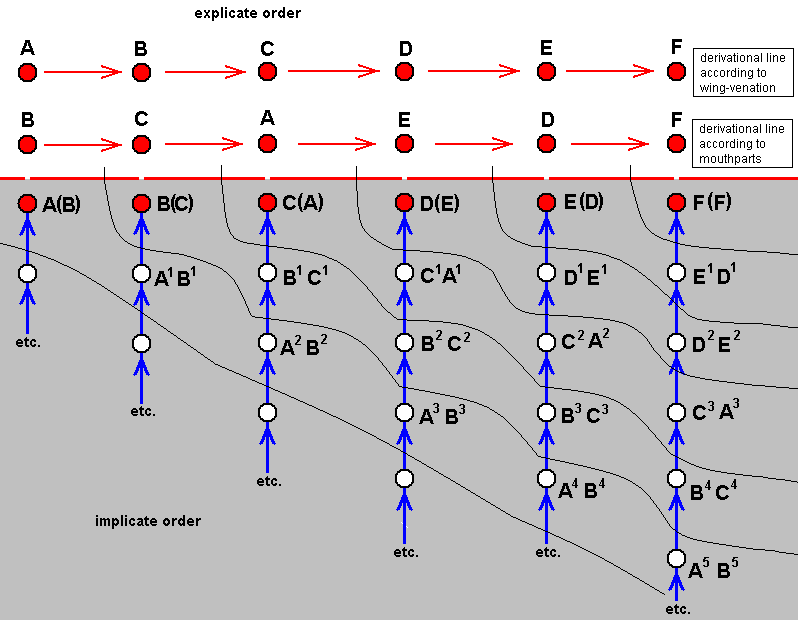
In this diagram we can see that the noëtic construction of the wing-venation is in the Explicate Order approximately reflected by the venational derivational line (series) A ==> B ==> C ==> D ==> E ==> F, whereas the noëtic construction of the mouthparts is, also in the Explicate Order, approximately reflected by the mouthpart derivational line (series) B ==> C ==> A ==> E ==> D ==> F.
In the Explicate Order we have the species A, B, C, D, E, and F, forming two derivational series as to respectively wing-venation and mouthpart structure.
In the diagram, the noëtic construction of strategies, taken only insofar as wing-venation and mouthpart-structure do play a part in this construction, consists of six ascending series, each terminating (still in the Implicate Order) with a strategy. These strategies are respectively A, indicated by A(B), B, indicated by B(C), C, indicated by C(A), D, indicated by D(E), E, indicated by E(D), and F, indicated by F(F). Upon projection into the Explicate Order (now when the strategies are considered to be complete) they appear there as the organismic species A, B, C, D, E, and F.
In the Implicate Order we have, in the diagram, indicated the structure of strategies and not-yet strategies in terms of wing-venation (first entry) and of mouthparts (second entry). For example :
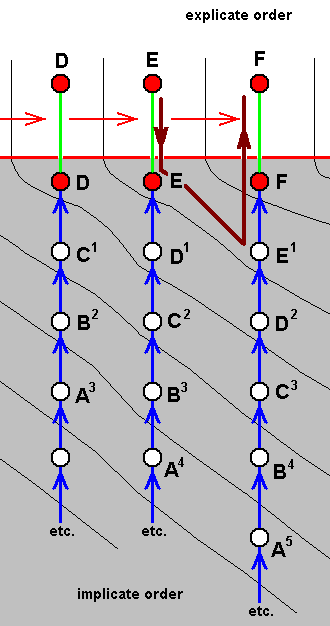
And the same can be said about venation E having immaterially descended from venation D, etc.
We cannot say, however, that the species F has so descended from the species E (and species E from D, etc.) because the noëtic construction of the (description of the) mouthparts is (ex hypothesi) not 'synchronous' with that of the venation : For the mouthparts F we have an immaterial descent through the Implicate Order as follows :
D (Expl. Order) ==> D (Impl.Order) ==> D1 (Impl. Order) ==> F (Impl. Order) ==> F (Expl. Order).
See next Figure.
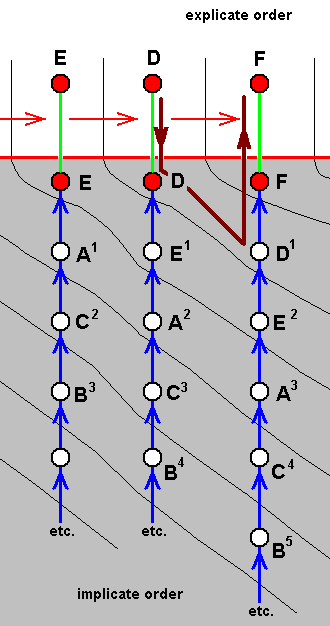
And in the same way we have such a descent through the Implicate Order of D from E, etc.
So we see that the strategies A, B, C, D, and E do contribute, in the way described, to the noëtic construction of the wing-venation as well as to that of the mouthparts of F.
This is quite significant. It means that as a consequence of our noëtic theory the noëtic construction of a given strategy is not entirely independent of that of other related strategies. Morphological (and other) structures of a given organismic species in the Explicate Order have been constructed from states of corresponding structures in other, related, species, but constructed immaterially through (mediation of) the Implicate Order. This means that although species as species do still develop independently of each other, their characters (such as wing-venation, mouthparts, etc.) do not. They are inherited from various other species, but non-mechanically so, and, taken together, not forming one single line of descent but forming a criss-cross of such lines.
This 'seizing' of features from other strategies hither and thither dispersed, is, of course, possible in the noëtic order only, because (the structure of) the Implicate Order is non-local. This might also explain the phenomenon of atavism, i.e. the re-adoption of a primitive state of a character, but then in a new evolutionary setting (and thus not violating Dollo's Law of irreversibility).
So all this theorizing about obtaining an ascending series -- in the Implicate Order -- of increasingly apomorphous states of certain characters, is merely done to gain some general insight into how indeed a true strategy-content might be noëtically constructed in the Implicate Order, that is, in and by the Formal System of Noëtic Strategy-Strings ( FSNSS ) all the way up from initial or original immaterial forms (axioms) that are no strategies at all and cannot inform Prime Matter all by themselves and thus cannot exist in the Explicate Order, but must turn into strategies in order to be able to do so. Each such an initial immaterial form keeps on being altered until at last a true strategy-content is formed which may then be projected into the appropriate and vacant ecological niche in the Explicate Order if such a niche is actually present in that Order.
And "completeness", as discussed further above as to laying bare the noëtic construction line resulting in a given strategy, must refer not to the strategy as such, but to the totality of ALL characters involved in such a given strategy. Above we had 'done' things for wing-venation and mouthparts only, in a given group of related insects. And in order to be complete, we must do it also with, for instance, the antennae, the legs, the internal and external structures of the larvae, and so on, and so on. And in all this, we take the same species as 'target species', in which the state (apomorphy, plesiomorphy) of each of these characters is taken to be the 'end-state' of the corresponding noëtic construction line.
In this way we would (if all the necessary data were indeed available for the group under investigation) obtain a thick bundle of derivational lines, each one of them approximately reflecting the noëtic construction of a single character or morphological structure, and together reflecting the noëtic construction of the strategy.
And in all this, we should realize that to set up a more or less formal derivational line of increasing apomorphy of the states of a given character, we must set up a derivational order as it is more or less seen in existing (or having existed) species of the group. And in this, for each character we must presuppose the d i r e c t i o n of morphological derivation leading to increased apomorphy. And of course this may be different in different groups. In the insect Order Neuroptera, for example, the tendency in the wing-venation is toward proliferation of veins, whereas in most other Orders it consists in the reduction of them, or in costalization (shifting of veins to the anterior wing-margin).
So to set up noëtic construction lines in polydiagrams for species of a given group, the latter must be studied first in order to assess the tendency in each morphological system in that group.
Construction of strategies from one another through the Implicate Order.
As to their evolutionary relationships with each other, that is to say, evolutionary relationships through the mediation of the Implicate Order, the species A, B, C, D, E, and F, figuring in the last three polydiagrams, especially in the first one of these , are, with respect to wing-venation and mouthparts, connected with each other as follows :
Conclusion
While, further back, us having (1) seen how the noëtic production of strategy-contents and their selection (as to which one of them is to be projected) is steered by the Implicate Order's knowledge of existing ecological conditions in the Explicate Order, and (2) further having seen that the general driving force that transforms immaterial forms into true strategies is the 'aspiration' of the Implicate Order to have all its immaterial forms materialized, - we now have (as symbolized by polydiagrams) at least some idea as to how the different noëtic stages of the noëtic process resulting in true strategy-contents will look like, by reading them off from the (horizontal) derivational line (in fact, ideally, from the bundle of derivational lines). And if we are satisfied with such a more or less general idea, then we may even confine ourselves -- when investigating winged insects in this respect -- to the wing-venation alone, especially because the wing-venation is, in contrast to other characters, often so well preserved in fossil insects, and so well studied in recent ones. See for an application of all this to the venation of palaeozoic Cockroach forewings part IIIbb, Noëtic construction of palaeozoic Blattarian tegmina.
As regards a strategy, precisely as strategy, we might perhaps hold that the characters used to compile an ascending noëtic series leading to a strategy must be functional. Is the wing-venation of an insect functional? We had found that in many cases it seems not to be so at least as to its details. But even in these cases the particular wing-venation that has actually developed may well be the necessary by-product of the generation of a true strategy, and in this way it does belong to the strategy sensu lato of the insect species. Moreover, our exposition of wing-types shows these types to be functional at least as to their overall structure (number, relative size, shape, and hardening of the wings, and the connection of the hindwings by hooks or spines to the forewings). And because most wing-venations in existing (and fossil) insects are very intricate, and thus 'elaborated' indeed as to their detailed structure, this also may point to their functionality even with respect to their details, apart from individual variations or small differences between species of the same genus.
In the next document we will continue and conclude our theoretic intermezzo.
e-mail :
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
To continue click HERE for the sequel of the theoretic intermezzo.
