e-mail : 

This page (and what follows) is a continuation of the Philosophy Website of Jaap Bax.
It is the Third Part of the Website.
What precedes this Part can be found when the "back to homepage" link is used. The adress is :  http://home.hetnet.nl/~heackel.
What will then be found is the First Part of this Website. When one clicks there on the last link of the contents (left frame), the Second Part of the Website can be reached. The address is :  http://home.hetnet.nl/~turing. To find the latter directly, one can click on the following link :  back to Second Part of this Website.

The First Part of this website was concerned with a revision of the Aristotelian-Thomistic Substance-Accident Metaphysics. That revision was accomplished by introducing and integrating into it of the Theory of Dynamical Systems. The search for the intrinsic essence of things resulted in the establishment of that essence -- i.e. the intrinsic essence of a given thing -- namely as being the dynamical law of that dynamical system that has produced, or can produce, that given thing. This dynamical law is already inherent in the elements of the relevant dynamical system. Only things that are intrinsic unities (in contradistinction to being just aggregates) can be considered as possessing such an intrinsic essence.
The dynamical law of a given dynamical system that generates the thing is responsible for the intrinsic features of that thing (while external, non-intrinsic factors determine the non-intrinsic properties ("accidents") of that thing).
An intrinsic thing was called a "totality", i.e. an intrinsic unity of parts and features resulting in a uniform thing.
The philosophical investigation concentrated on such things as organisms and crystals. Both are products of dynamical systems.

In order to go into more detail -- after the general metaphysical theory had been set up -- we started to investigate two important and interrelated general effects of the dynamical law in a totality-generating dynamical system :  STRUCTURE and SYMMETRY (in and of the generated totality or uniform thing (for instance an individual organism or an individual crystal)).
We started with CRYSTALS.
The six Crystal Systems and the 32 Crystal Classes were treated extensively, and after that we embarked on the study of the internal structure and symmetry of crystals. It turned out that this should be preceded by a study of imaginary two-dimensional crystals, in order to ease the (much harder) study of three-dimensional real crystals. Twenty documents were devoted to these two-dimensional crystals. And with that the First Part of the website came to a conclusion.

The Second Part of the website continued the study of the symmetry and structure of crystals, but now preparing for those of three-dimensional crystals.
It was realized, however, that, to understand the symmetries of three-dimensional crystals, especially the total symmetry of any given crystal, i.e. the symmetry taken up by the internal structure of such a crystal, a study of Group Theory must be included. The reason for this is that explaining the total symmetry of three-dimensional crystals could not be accomplished by just presenting elaborate and detailed drawings, as we did with respect to two-dimensional crystals, because drawings of complicated three-dimensional structures will get unclear, and will likely to confuse the reader instead of revealing insight to him or her.
More than twenty documents were devoted to group theory, and it turned out that group theory is a power full general description and analysis of the symmetry, not only of crystals but also of that of organisms.
After three-dimensional crystals had been treated, together with some notes on their generation from melts or solutions, we began considering the second category of intrinsic things as products of dynamical systems :  Organisms. Also of organisms we concentrated on their general structure (Tectology), and their basic symmetry (Promorphology).
The Tectology of Organisms is a general structural doctrine, that sees each organism being built up by morphological units, each of them possessing a certain degree of individuality within the one organism.
This tectological structure of an organism reveals that the organism is composed of similar parts (morphological units) that are repeated non-periodically in the organism (whereas in crystals we can see a periodic repetition of certain units). The way these morphological units are configured within the organism can be seen as determining the organism's basic symmetry. The latter will be studied as Promorphology, i.e. the study and systematization of the stereometric basic forms of organisms (We could say a kind of 'crystallography' of organisms).
We have then set up a Promorphological System of organic stereometric forms, which means that we express the basic symmetries of a given organism in terms of the simplest geometric body that has these symmetries.
In this Promorphological System we also included crystals, which is possible because although crystals do not directly show a tectological non-periodic structure, this structure is nonetheless implicit in them. We retrieved this tectological structure by conceptually removing all translational symmetries in crystals, and so eliminating the periodic aspect of them. What we then get is a motif (which is some chemical unit) that has indeed a tectological, i.e. non-periodic, structure. And of this structure we determined the basic stereometric form. Having done that, we were then able to incorporate the crystal in question into the general Promorphological System. With all this we concluded the Second Part of the website.

The present Part of the website -- the Third Part -- will be devoted to a thoroughly holostic view of all of reality, based on the Theory of the Implicate Order(s) of the quantum physicist David BOHM.

In the First Part of our website we established a general view of Reality based on an updated Substance-Accident Metaphysics. There the focus was on macroscopic individual intrinsic beings like crystals and organisms. Their metaphysical structure was investigated, and it was established which conditions must be met in order for something to represent a real genuine being (So the "metaphysical structure" of something means the composition of that something, not of physical parts but of principles -- metaphysical causes -- of being). It turned out that (macroscopical) aggregates as well as quantum entities were not genuine beings. The latter were seen as "deficient beings" because of their partial indeterminateness, while the former were not considered to be beings at all because their causes were external to them.
Three general remarks can be made about that metaphysics :

• The ultimate generative ground -- if such a ground exists -- for all real beings was not investigated thoroughly. We took for granted the existence of system elements, and discussed the generation of more complex entities from those elements in the context of dynamical systems. The system elements themselves were, however, also supposed to be genuine beings, be it more simpler beings. Thus the whole approach was of a rather reductionistic nature, even though the emergence of new properties and structures was granted.

• The ultimate ground of all (material) things was seen by the notion of prime matter, which is pure potentiality for form, i.e. it is the ontological substrate or carrier for any qualitative and quantitative content ("ontological" means being-theoretic, i.e. figuring in the theory of being in sofar being). Only when in-formed, a being will result, and this in-forming was not considered to be a physical process, but an expression of the basic constitution of things (real beings) out of entities which are not themselves things : neither prime matter, nor form is a thing. In what way the 'first' system elements were created from prime matter was not discussed, because, as has been said, it was not considered to be a process but an ontological constitution.

• In the metaphysics referred to above the World was conceived of consisting of relatively separated and more or less autonomous beings (things) with definite boundaries and identities. These beings can at times interact with each other, sometimes resulting in more complex beings. While interacting, we could say that those beings were less autonomous : they then were heteronomous. So in spite of there being dynamical processes going on, the World also consists of more or less static objects. And the interaction of those objects (things, beings, system elements) was supposed to be based on immutable eternal laws of nature. A possible totally dynamic world, that is moreover one indivisible whole was, for the time being, rejected, on the ground of the principle of the Co-existence of Motif and Background, which says that for every motif there is also a background, and for every background there is some motif, which in particular means that if we have dynamics we must also have statics (static entities), and if there is some whole there must be some parts either (See for this the First Part of the website -- accessible by the Back to Homepage link -- the document The Substance-Accident Metaphysics and the totally dynamic world in the Critical Series of documents).

If I -- or anyone else -- say that nature (or some aspect of it) is so and so, it (in fact) isn't, it is always more than that, and different.

In fact this is a statement about our always limited knowledge and about the fundamental creativity and utmost sublety of nature. Reality is always much more subtle than any theory can grasp. This means that any theory about the workings and the constitution of nature is either false or else incomplete, in the sense that its domain of validity is limited.
This means that we have to be modest when proposing broad theories about the whole of existence. And this implies that we must be prepared to nourish several different views about the world, allowing them to engage in dialogue with each other, provided of course that such views are the result of serious thinking.
So also on this website (consisting of the mentioned three Parts) we will not stick to just one position, as if it were the one and only truth about the constitution of the World. We will investigate other views, thereby, however, not mixing them up, because when we would do that we automatically incorporate contradictions into such a mixed view. So we keep them separate.

In fact the most general and fundamental physical theories, Relativity Theory and Quantum Theory, both, each in its own way, point to the World as an undivided and dynamical whole, although not yet thoroughly in every respect. This deserves serious attention, and guarantees the relevance of investigating how such a dynamical whole, not involving separate more or less autonomous but interacting parts, is supposed to be constituted, even if it violates the mentioned principle of the co-existence of motif and background. Perhaps motif and background merge into each other because of their common enfoldment in an indivisible whole. This interplay of motif and background could find its expression also in the two opposing world views (reductionism and holism) which could also merge together into a single theory after they have communicated with each other, exchanged ideas and have removed remaining contradictions.

In the present series of documents we will investigate how a thoroughly dynamic world, which is one undivided whole, should look like. In such a world view all the seemingly separate and autonomous or heteronomous things are seen as just abstractions from, or approximations to, an absolutely undivided and dynamic whole that is holonomous, which means that the laws are laws of the whole. And even such broad theories like relativity and quantum theory are just approximations valid in a limited context. Indeed it seems that if we consider the broadest possible context those theories manifest difficulties in explaining some features of the world, or they end up in attributing fundamentality to randomness and chance. With respect to the latter it is our conviction that everything happens in some order, which means that there is in fact no disorder in the fabric of Reality.

As is known, quantum theory, in its conventional interpretation, says that the indeterminatenes and randomness of features which it finds all over the microscopic domain, are fundamental. Indeed within its domain of investigation indeterminateness and randomness cannot cannot be reduced to determinateness and order, not even in principle. But, according to the above, every theory, how fundamental it looks like (like in earlier times the newtonian mechanics looked like), is always an abstraction and approximation from a broader order of things. It is established that the randomness of quantum theory cannot be explained by the presence of 'hidden variable'. But we must add not by the presence of hidden variables within the order of the current theory. There might be a further order, much more subler than that within which current quantum theory works, and this order could be responsible for the apparently random behavior concluded from current quantum theory. So the hidden variable could be in such a further order.

An example of a certain species of order is our familiar order in which there are local things interacting in a continuous time flow, so this order is essentially sequential. Another species of order could be a timeless order, where everything is present together.

Take Brownian motion. This motion we can see when we observe for example pollen grains in water. Under the microscope the grains turn out to be in a very irregular zig-zak motion. This motion is so irregular that one could say it is random (We will however prefer to call such a motion one of infinite order (i.e. of infinite complexity)). Suppose that we did not know of the existence of molecules (in our case, water molecules), then we could consider this random motion fundamental. Indeed in the context of the absence of any molecular theory this would be the end of the story : the grains are -- because of intrinsic reasons -- moving totally irregularly when they are immersed in, or floating on, a liquid, and this motion apparently is dependent on pure chance, i.e. it is apparently indeterministic. And because the liquid would be considered to be a homogeneous continuous medium which, when not locally heated or stirred in any way, is at rest, it does not affect the condition of motion of the grains that are in it. But when we now broaden our context, and include the new theory of molecules, which means that every liquid is composed of molecules that are moving because of thermal energy, then we see that the pollen grains are constantly being kicked to and fro by the collisions of very many molecules (In our case, water molecules). And the motion of each individual water molecule in itself is deterministic and just a motion of low order (which means that we only need to specify a few parameters to determine such a motion, in contradistinction to the resulting very complex motion of the pollen grain which is kicked from every direction by millions of water molecules). The trajectories, each of themselves, of such individual molecules can be regarded as low-order ones. Thus the random motion of the pollen grains is now explained by the molecular theory. The chance movement of the pollen grains can be causally reduced to a deterministic movement of the water molecules.
Such an interplay of low-order motion (regular motion) and infinite-order motion (often called random motion) is visible in any isolated dynamical system consisting of interacting particles :  In a narrow context where the details are not taken into account the order of motion is of infinite degree. It can even be, under suitable conditions, totally random. But in a broader context, in which these details (which would be, in the absence of any theory about these details, 'hidden variables') are taken into account, it is possible in principle to obtain a deterministic account of the inner movement of particles within the dynamical system. A random order can thus be explained within such a system without the need to take into account any contingencies which are external to the whole system.
So we see, that in a way chance is equivalent to necessity.
The above treatment, while valid up to a certain point, is, however, still an abstraction and an approximation. For no system can corectly be regarded as totally isolated and self-determined. Thus, most systems of appreciable complexity are capable of developing instabilities, so that they may be profoundly affected even by weak external interactions. And even more important, no specified statement of the laws of nature will be completely and universally valid. For, as has been said already, whatever we say anything is, it isn't -- it is also something more and something different. So it could for instance be that the deterministic motion of the particles of the dynamical system is just an abstraction from a much more subtle and compex motion, for instance one that is like Brownian motion. If that were the case a new order would be revealed in which new structures are possible.
And it is evident that between the two extremes -- random order and lowest-degree order -- there is a rich spectrum of intermediate orders.

Thus, there is no need to fall into the assumption of complete determinism (although this may in certain fairly broad contexts to be a correct abstraction and approximation). Nor is there any need to assume that chance and indeterminism rule absolutely (though these too will provide correct abstractions and approximations in their appropriate contexts). No matter which system of law may be appropriate in the context that is currently under investigation, there is always room for something more and something different -- something that will be more subtle and that has the ultimate potential for being a manifestation of creativity. (D. BOHM and F. PEAT, 1987, Science, Order and Creativity ).

The ideas of David Bohm about new fundamental and more subtle orders that figure as levels of being, from which eventually our 'explicate order' (our directly observed world) emerges, is mainly inspired by the unsatisfactory interpretations of current quantum theory (quantum mechanics). These interpretations involve the need of observers for a quantum event to be actual, they involve fundamental indeterminism (chance), or the splitting up of the whole universe after each observed quantum process.

Figure 1.  David Bohm in 1987 during a reading about the foundations of quantum mechanics.

It is important to put what follows in perspective. In other areas of the study of Nature, especially in biology, there are serious problems with the current attemps to explain all biological features mechanistically, i.e. reductionistically. So for example in evolutionary theory. The key idea of mechanistic evolutionary theory is that organismic types change under the influence of natural selection of certain (progressive) mutant organisms. The (genetic) mutations of such organisms are supposed to be induced randomly by the action of certain environmental agents (for example radiation). So the source of the appearance of new biological types (like birds having apparently evolved from certain reptiles) is in fact randomness. This, however, seems unlikely to be the main mechanism for the evolution of major types in the animal and plant kingdom. This is because for such a transformation (say from reptiles to birds) to take place very many diverse mutations should more or less simultaneously occur, because when initially only a few of them would take place (and later on the others), they would certainly be lethal to the animals having undergone such initial mutations. Indeed it is unclear how many major groups (types) of animals have evolved from other types within this mechanistic paradigm. So problems crop up, and the reason could be that the paradigm has only limited value (It could for instance be more or less valid with respect to minor transformations between closely related types (closely related species)).
Already as a result of such problems (which keep on being very persistent indeed) one could look for a new paradigm involving new and more subtle orders. Orders in which organisms depend for their evolution (but perhaps also for their individual development) on some sort of timeless creative whole. And in this way -- and without falling back to obsolete or mystic ideas -- the idea of an implicate order as the holistic ground for all living beings, including their morphology, physiology, behavior and evolution, could arise and be worked out. But it is admitted that that would be a very difficult task to accomplish.
However, in physics one indeed has already found two implicate orders, conceptually derived from current quantum theory :  and indeed in this way we must see the meaning and relevance of the causal interpretation (of quantum theory) of David Bohm.
The next account concerning this causal interpretation in its first form (the 'particle form') is almost litterally taken over from the above mentioned book of BOHM and PEAT (Bantam Books, 1987, pp. 88), because I am not myself a quantum theorist. I am using the results of others, and I am sincerely grateful to them.

First form of the causal interpretation of quantum theory

Unlike the familiar particles of Newtonian physics (as they are legitimately allowed there to be (as abstractions and approximations)), the electron (as a quantum particle, treated in quantum theory) is never separated from a certain quantum field (here the mentioned abstraction cannot be made anymore) which fundamentally affects it, and exhibits certain novel features. This quantum field satisfies Schrödinger's equation, just as the electromagnetic field satisfies Maxwell's equation. It, too, is therefore causally determined.
Within Newtonian physics, a classical particle moves according to Newton's laws of motion, and the forces that act on the particle are derived from a classical potential V. The basic proposal of the causal interpretation is that, in addition to this classical potential, there also acts a new potential, called the quantum potential Q . Indeed all the new featues of the quantum world are contained within the special features of this quantum potential (This is indeed an interpretation of the results of current quantum theory. It is one of the several possible interpretations). The essential difference between classical and quantum behavior, therefore, is the operation of this quantum potential. Indeed, the classical limit (i.e. classical range) of behavior is precisely that for which the effects of Q become negligible. The quantum potential is given by :

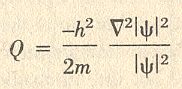
In this expression we see a small triangle. This is the so-called vector gradient operator. We further see the greek letter PSI. It stands for the quantum field, and is formally identical to the wave function derived from Schrödinger's equation (The latter is the law governing the changes with time of the wave function, or the Hilbert space vector). Further we see the letter  h ,  it is Planck's constant, i.e. the quantum of action. And the letter  m  finally, stands for the mass of the electron or other particle. Clearly the quantum potential is determined by the quantum wave field, or wave function. But what is mathematically significant in the above equation (concerning the quantum potential Q) is that this wave function is found in both the numerator and the denominator. The curious effects that spring from this relationship will be pointed out in due course.
At first sight, it may appear that to consider the electron as some kind of particle, causally affected by a quantum field, is to return to older, classical ideas which have clearly proved inadequate for understanding the quantum world. However, as the theory (i.e. the causal interpretation) develops, this electron turns out not to be a simple, structureless particle but a higly complex entity that is affected by the quantum potential in an extremely subtle way. Indeed the quantum potential is responsible for some novel and higly striking features which imply qualitative new properties of matter that are not contained within the conventional quantum theory.
The fact that PSI is contained both in the numerator and the denominator for Q means that Q is unchanged when PSI is multiplied by an arbitrary constant. In other words, the quantum potential Q is independent of the strength, or intensity, of the quantum field but depends only on its form. This is a particularly surprising result. In the Newtonian world of pushes and pulls on, for example, a floating object, any effect is always more or less proportional to the strength or size of the (water) wave. But with the quantum potential, the effect is the same for a very large or a very small wave and depends only on its overall shape.

By way of illustration, think of a ship that sails on automatic pilot, guided by radio waves. The overall effect of the radio waves is independent of their strength and depends only on their form, i.e. on the modulation that is superimposed onto a carrier wave. The essential point is that the ship moves with its own energy (while also the automatic pilot works in virtue of its own energy, obtained from its power plug), but that the information within the radio waves is taken up and used to direct the much greater energy of the ship. In the causal interpretation, the electron moves under its own enegy, but the information in the form of the quantum potential directs the energy of the electron. Clearly the term causal is now being used in a very new way from its more familiar sense.

The result is to introduce several new features into the movement of particles. First, it means that a particle that moves in empty space, with no classical forces acting on it whatsoever, still experiences the quantum potential and therefore need not travel uniformly in a straight line. This is a radical departure from Newtonian theory. The quantum potential is itself determined fom the quantum wave PSI, which contains contributions from all other objects in the particle's environment. Since Q does not necessarily fall off with the intensity of the wave, this means that even distant features of the environment can affect the movement in a profound way.
As an example, consider the famous double slit experiment. This is generally taken as the key piece of evidence of the wave-particle duality of quantum particles, and that this duality is intrinsic to such a particle ( In the current interpretation one says, it is either a particle -- or shows particle-like behavior -- or a wave -- or behaves in a wave-like fashion -- dependent on the way it is observed). When electrons are sent from a source to a screen with two slits, they exhibit a wave-like interference pattern on a screen placed behind the screen with the two slits, which is quite "incommensurable" with the classical behavior of particles : An electron from the source encounters the double slits and can evidently only go through one of the slits. It ends up being registered on the screen that is placed some distance behind the double slit screen. After very many of such individual events a pattern begins to built up on the screen. The conventional interpretation is that this interference pattern is evidence of the wave-like nature of the electron. In the causal interpretation, however, the pattern is a direct result of the complex quantum potential :  The electron travels toward the screen containing two slits. Again, clearly it can go through only one slit or the other. But the quantum wave can pass through both. On the outgoing side of the slit system, the quantum waves interfere to produce a higly complex quantum potential which does not generally fall off with the distance from the slits. The potential is illustrated below.

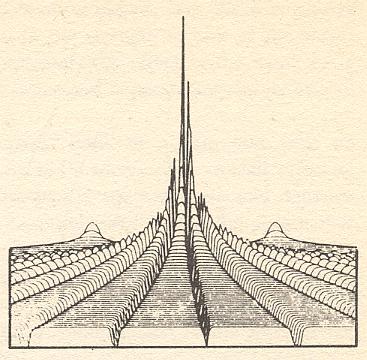
Figure 2.  The quantum potential for the two slit system.
After BOHM and PEAT, 1987.

Despite the new features of the theory, and the possibilities for further modifications, the majority of physicists have not considered the causal interpretation to be a serious alternative to other interpretations of the quantum theory (As such reported by BOHM and PEAT, 1987, p. 97). Why should this be? One of the main reasons is that perhaps it does not cohere with their general way of using the informal language of physics, to which they have become habituated over long periods of application of the usually accepted interpretations. There seems to be little place in their thinking for the causal interpretation, which is therefore ruled out as being irrelevant and not worthy of serious study
(However, I think that the main reason of not considering the causal interpretation as a serious candidate, is that it postulates one or several "new levels of Reality" (that cause the quantum effects). Such a postulation tends to make the quantum theory imcomplete because of "hidden variables" or "hidden orders". In all this, current quantum theory could turn out to be just an abstraction and approximation to the real state of affairs. This really must disturb the quantum theory devotees. But in fact they should welcome it, because if correct, the new theory makes the world an even more interesting and subtler place than it already is. And the men of science should be modest about the theories they nurture, and be content with the almost certain fact that those theories are just approximations, how far they may be developed. An extra reason for not taking the causal interpretation seriously is that the mentioned new fundamental levels of Reality are more complicated and subtler than the less fundamental levels -- among which the explicate order of everyday objects. This is contrary to the well accepted notion that more fundamental levels are more simple in structure and behavior. Indeed, some general elements in BOHM's view of "all of Reality" reminds us very much of a Neoplatonic motif as we see it for example in the writings of the ancient Greek philosopher Proklos (fifth century) ).
A particular objection appears to arise from what scientists call the non-local nature of the approach. This can be explained in the following way. When several particles are treated in the causal interpretation then, in addition to the conventional classical potential that acts between them, there is a quantum potential which now depends on all the particles. Most important this potential does not fall off with the distance between particles, so that even distant particles can be strongly connected. This feature, in which very distant events can have a strong influence, is what is meant by a non-local interaction and is strongly at variance with the whole spirit of classical mechanics.
There is a great reluctance on the part of the physicists (1987) to consider such non-locality seriously, even though it does lie at the heart of the formal implications of quantum theory. Because theories in terms of local interactions have been so successful over the past few centuries, the concept is now seen as both necessary and inevitable. But, in fact, there does not appear to be any intrinsic reason to rule out non-local forces. However, a general attitude has arisen out of the tacit infrastructure of ideas over the last few centuries which prejudices scientists to any serious consideration of non-locality.
If the objections to non-locality are based on an almost subliminal prejudice, can they be backed up by physical argument? One suggestion is that non-locality is inconsistent with the basic tenets of relativity (i.e. Einstein's theory of relativity). Non-locality implies an instantaneous connection between distant events, and this appears to violate the basic principle of relativity that no signal can travel faster than light. However, a more detailed analysis shows that the quantum potential is very 'fragile' and unstable to alternations. In other words, if any attempt is made to impose a form on the potential and thereby use it as a signal, this form will become mixed up and lose all order and meaning. The quantum potential cannot therefore be used to carry any signal between distant effects and therefore its instantaneous connection of distant particles does not violate the theory of relativity.
Indeed, there is suggestive evidence that rather than violating physical laws, non-locality does in fact operate in nature. An experiment initially suggested by Einstein, Rosen, and Podolsky depends upon measuring the non-local effects of one distant quantum particle on another (These two particles must once have belonged to one and the same system). In 1981 this experiment has been carried out in Paris by Alan Aspect and interpreted with the aid of a theorem of J.S. Bell. It provides strong evidence for a non-local form of interaction. This result follows in a natural way, within the causal interpretation, as a result of the non-local quantum potential that directly connects distant particles.

On the basis of the causal interpretation of quantum theory we must indicate a new level of Reality that is associated with the quantum potential, and as such responsible for the behavior of quantum particles as found in quantum theory. This new reality level can be imagined as a new order, in the sense that it is timeless, although it is in a thorougly 'dynamic' state or flux. It is in a sense a hidden order and at the same time the dynamical ground for at least many quantum processes, or, in other words, a generative order for several quantum features. BOHM calls it the (first) implicate order. As such it carries the explicate order which comprises our everyday objects and processes, but also apparent trajectories of elementary particles. Within the implicate order everything is connected. We can also say that everything in the explicate order is (more or less) connected via the implicate order (or orders). There is a constant 'dynamics' of enfoldment and unfoldment :  relative autonomous subtotalities unfold from the implicate order into the explicate order, only to be enfolded again later on into the implicate order. So because of the non-local nature of the implicate order and its tight dynamic connection with the explicate order, the world is undivided wholeness. Later we will present a very instructive analogy to the implicate order, which especially throws much light on the unfold-enfold dynamics.

In the foregoing we have given BOHM's first version of the causal interpretation of quantum mechanics. There we departed from the particle. But in modern quantum theory the field has become more fundamental than the particle, because the particle emerges from the field. And so we have quantum field theory. Let us say something more about those fields.
Maxwell's equations concerning the electromagnetic field, constituted the first fully worked out field theory, one that applies to both electricity and magnetism, and that says that magnetism is equivalent to moving (dynamic) electricity. It is the classical (meaning non-quantum) theory of electrodynamics. Einstein's General Theory of Relativity describes the other force familiar from everyday life (gravity) and is another classical (in the same sense) field theory, this time of gravity. In the old, classical view of the world there were two basic components :  material objects and the fields that linked them.
But the field is now the ultimate, fundamental concept in physics, because quantum physics tells us that particles (material objects) are themselves manifestations of fields. One of the first great surprises of quantum physics was the realization that a particle, such as an electron, had to be treated like a wave. In this first application of quantum principles we learn to treat these matter waves as fields, with one field corresponding to each type of particle. For example, there is a general matter field filling the Universe, which is described by the wave function of an electron (Strictly speaking, the wave function describes electron-positron pairs). But, as the discovery that electromagnetic waves must also be regarded in particle terms showed, a field can be directly responsible for the existence of particles. Indeed, in the quantum world a field must give rise to particles. Quantum physics says that the energy in the field cannot be smoothly changing from place to place, continuously, as in the classical picture. Energy comes in definite lumps called quanta, and every matter field must have its own quanta, each with a definite amount of energy, or mass. The particles are energetic bits of the field, confined to a certain region. A photon is a quantum of the electromagnetic field. In the same way, by applying quantum principles a second time to the matter fields of electrons, we find that we recover the idea of the electron as a particle, as the quantum of the electron matter field. This interpretation of particles as "field quanta" is known as second quantization. It tells us that there is nothing else in the Universe except quantum fields.
(GRIBBIN, J., 1987, In Search of the Big Bang, Quantum Physics and Cosmology,  p. 256/7.)

Returning now to the implicate order, to obtain a deeper and more extensive understanding of that order, it is necessary to start from quantum mechanical field theory. This is, in essence, the most basic and general form of the modern quantum theory that is available to date (as BOHM and PEAT report, 1987). Such a step will lead to an extension of the implicate order, called the superimplicate order. This is much subtler than the implicate order and goes deeper. In addition, it is capable of further extensions in ways that go beyond quantum theory altogether.
As with the quantum mechanical particle theory, it is necessary to proceed from the standpoint that the mathematical formalism of the quantum field theory is essentially correct, at least within some suitable limits. However, the informal language describing physical concepts is even more unclear in the field theory than it is in the particle theory.
The causal interpretation will therefore be extended in order to obtain a clear physical notion of the quantum field theory, as well as to gain insight into the superimplicate order.
To be more specific, the key new property treated by quantum field theory is the appearance of discrete particle-like quanta (as a result of second quantization), in what was initially assumed to be a continuous field. In the causal interpretation, a clear and well-defined physical concept of the appearance of discrete particle-like quanta in a continuous field can be given. This interpretation fully and faithfully expresses the meaning of the mathematical equations.
It must be emphasized, however, that although the particular example of the superimplicate order is obtained from the causal interpretation of quantum field theory, the essential idea of the superimplicate order is not restricted either to the causal interpretation or to the quantum theory itself. Rather, these are only special forms of the more general superimplicate order.
The basic discussion of quantum field theory in terms of the implicate order and the causal interpretation is quite simple.
Instead of taking a particle as the fundamental reality, start with the field. And instead of having a particle acted on by a quantum potential, suppose that the field is acted on by a superquantum potential. This superquantum potential is far subtler and more complex than the quantum potential, yet the basic principles governing its behavior are similar. Its net effect is to modify the field equations in a fundamental way so they become non-linear and non-local. This brings about the new quantum properties of the field. The field is continuous and by itself would tend to spread out from any source. However, because the superquantum potential is non-linear and non-local, it is able, under certain conditions, to provide a very subtle kind of immediate connection between distant regions of the field. Suppose, for example, that the field meets an atom that can absorb a definite amount of energy. The superquantum potential will 'sweep in' energy from the whole field, in a definite amount equal to what can be absorbed by the atom. This explains how a continuous field can act in matter as if it were made up of discrete elementary units.
In the particle treatment (i.e. the first form of the causal interpretation discussed above), the wave-particle duality was explained as an effect of the quantum potential on the particle. But the wave-particle duality can now be treated as an effect of the superquantum "field" on the original field itself. Therefore, the particle is no longer used as a basic concept, even though the field manifests itself in discrete units, as if it were composed of particles (The field becomes a quantum field by the action of the superquantum potential.).
So far the implicate order has not been brought in. In the causal interpretation of the field theory there are two implicate orders in a specified relationship. The first implicate order is just the field itself, and its movement, as described by so-called Green's functions, is just a form of the implicate order. The second implicate order is then obtained by considering the superquantum wave function. This is related to the whole field as the original quantum wave function is related to the particle (The mentioned wave functions figure in the corresponding potentials.). A more detailed treatment shows that the superquantum wave function also moves in a kind of implicate order which is, however, far subtler and more complex than is the first implicate order. This then comprises the second implicate order.
In the earlier version of the causal interpretation, the quantum potential represents information which guides the self-active movement of the particles. In the field case, the superquantum potential now represents information that 'guides' or organizes the self-active movement of the field.
The first implicate order applies to the original field (considered as not quantized) which, however, now has new features brought about by the action of the superquantum potential. And the second, or superimplicate, order applies to the 'super field' or information, that guides and organizes this original field.
A good analogy to the first and second implicate orders is provided by considering a computer or video game. The first implicate order corresponds to the television screen, which is capable of showing an indefinite variety of explicate forms, which are essentially manifestations of an implicate order. In earlier television sets this could clearly be seen through the action of the synchronizing adjustment. When synchronism failed, the images would be seen to enfold into an apparently featureless background. But when the correct adjustment was made, the hidden images would suddenly unfold into explicate forms again.
The second implicate order corresponds to the computer, which supplies the information that arranges the various forms -- spaceships, cars, and so forth -- in the first implicate order. Finally the player of this game acts as a third implicate order, affecting the second implicate order. The result of all this is to produce a closed loop, from the screen to the player to the computer and back to the screen. Such a loop is, in a certain sense, self-sustaining, for with only the computer and the screen in operation, all that would happen would be an unfoldment of a predetermined program. But when the player, as third implicate order, is introduced, a closed loop results and the possibility is opened up of a genuine dynamic developement in time, in which creative novelty may enter.
We could speculate that, in nature, there is something like a third implicate order that affects the second and is affected by the first, thus giving rise again to a closed loop. Or more generally there is an indefinite series, and perhaps hierarchies, of implicate orders some of which form relatively closed loops and some of which do not. Of course such an idea implies that the current quantum theory is of limited validity. This theory is covered only by the first and second implicate orders. Where anything beyond the second implicate order is active, then quantum theory would no longer be valid. (BOHM and PEAT, 1987).
In the quantum field version of the causal interpretation, an elementary particle is taken to be the manifestation of an underlying quantum field. The particle therefore represents the folding of a field into a localized region. Likewise the annihilation of the particle is the unfolding back into the field. In this way the complex reactions of elementary particles can be thought of as enfoldings and unfoldings within a dynamic background (See PEAT, 1987, Synchronicity, The Bridge between Matter and Mind).

In the above expositions we have seen that modern physics calls for at least two implicate orders that are responsible for the behavior of quantum entities. But in the usual interpretations of quantum theory it does not seem to be possible to maintain the notion of the interweaving of the orders of chance and necessity as abstractions from infinite order with unlimited creative potential, as is attributed to the implicate and generative orders. The principal difficulty arises because a system of particles cannot simply be treated by analysis into independently existent but interacting constituent particles. Rather, the quantum theory implies a certain quality of wholeness in the sense that a system cannot be dealt with properly as a set of separate parts. Hence in the usually accepted interpretation, there is no way to discuss how randomness might arise. Randomness (as deduced from quantum mechanical experiments) is therefore assumed to be a fundamental but inexplicable and unanalyzable feature of nature, and indeed ultimately of all existence. Such an approach complements Bohr's notion of the inherent ambiguity of concepts at the quantum mechanical level. For within the range of this ambiguity, the quantum theory implies that the experimental results will fluctuate with an irreducible kind of randomness. And thus the very nature of the quantum mechanical ambiguity will imply a coresponding limit to the possibility of meaningful order.
On the present more or less alternative Part of our website -- alternative with respect to the First and Second Parts -- however, we, along with BOHM and PEAT, propose the notion that everything that happens takes place in some order (which, however, depends on broader contexts for its meaning). Therefore, while there is ambiguity within particular contexts, the notion of an ultimate limit to the meaning of order, a limit that holds in all possible contexts, is not admitted (while in the current interpretation of quantum mechanics one identifies such a limit with respect to quantum mechanical concepts). For example, above, the causal interpretation of quantum theory was discussed in which a further kind of order is proposed. This order, which underlies the randomness implied in the probabilistic laws of the quantum theory, can be understood as the causally determined motion of the particle under the quantum potential. Because this latter potential gives rise to a complex and highly irregular force, the motion will in general be fairly chaotic. In such complex systems, an essentially random order is to be expected which explains the probabilistic assumptions of the theory. Deterministic movements at a lower level explain and determine the random movements at a higher level (The former is the implicate order, while the latter is the explicate order in which observations take place).
However, such a simple deterministic theory (involving the causal action of the quantum potential) is an abstraction, which is valid only up to a point. Beyond this point, one may have to consider the possibility that even the basic laws of the particles involve orders of infinite degree, which reflect levels of reality beyond those treated adequately by the current quantum theory. In a certain approximation, this may be considered as a random order. But the motion may more generally be in an order of very large or infinite degree, which is in the rich domain between simple orders of low degree and infinite chaotic or random orders. When understood in terms of the causal interpretation, the quantum theory is therefore capable of fitting into the general notion of the interweaving of chance and necessity, considered as lying at the extremes of an infinitely rich order that is context-dependent. In quantum theory this order is at present hidden in the context available so far in physics, because -- as say BOHM and PEAT -- science has not been able to respond with the necessary subtlety of meaning. But in contexts that may one day be discovered, new possibilities for creativity within such orders may be revealed, and these context orders will then cease to be 'hidden'.
The notion that both simple regularity and randomness in a given context may contain orders that are 'hidden' in that context, but which can be revealed in other contexts, is of quite general significance. For example, the order of a language or music cannot be found by studying the regular orders of vibration in sound waves, or the almost random orders of motion of the molecules in the air that carries them. Indeed, unless the mind is free of rigid commitments to familiar notions of order, it cannot provide a context within which basically new orders might be perceived. (BOHM and PEAT, 1987).

It is in our context instructive to ask oneself the question as to what the status is of natural laws (physical laws). Of course in science they are first of all mathematical descriptions, i.e. abstractions in thought. They refer to more or less idealized and often simplified situations, and express certain definite restrictions, under which certain processes proceed. It is only by restrictions that we get something definite, i.e. that we can expect that processes follow certain definite pathways, and not others. Whether such laws are correct(ly stated) (by scientists), experience and experiments will decide. In the following discussion we assume those laws to be correct, and ask ourselves whether as such they subsist somewhere in Reality, or are still just descriptions of fundamental restrictions, descriptions toward which scientists strive to finally obtain. In other words are natural laws immanent in matter (or in Reality as such), or not?
Well, it seems, to treat physical laws as if they were somehow immanent in matter has all the appearance of a logical blunder. To argue, for example, that the Second Law of Thermodynamics causes the running down of a clock, or of the steam engine, seems to be as muddled as to suppose that a football commentary actually determines the state of the game.
Science has always treated its laws as just mathematical abstractions, descriptions after the fact, rather than laws in the judicial sense that determine and direct behavior. Therefore to speak of such laws as being manifest or realized in matter, so that they play a formative role, sounds absurd.
But suppose that this orthodox view of science is strictly limited. Suppose that, at some level, a formative and ordering principle does indeed operate within the universe. Such a principle would act to generate the novel forms and structures of nature and would be the motivating force behind all patterns and conjunctions. Clearly a formative principle must be very different from what is normally meant by "a law of nature", which is the abstraction and generalization of scientific experience. But what then could it be, this principle of animation and generation that differs in such a radical way from the conventional laws of physics?
This question, and the foregoing discussion, was put up by PEAT, in Synchronicity, The Bridge Between Matter and Mind, 1987. My preliminary answer would be that genuine dynamical laws, each of them governing a certain dynamical system, that generates one or another intrinsic pattern, could be at least an aspect of such a principle of animation (formative principle). As stated in the First Part of our website, such a dynamical law is immanent in the elements of the given dynamical system. So what, if at least such laws, provided they are correct, are not simply abstractions of experience but are the realization of something that is creative, generative, and formative, i.e. of something that lies beyond language and thought?
This generative power cannot lie within the mental or material worlds alone but rather has its place in some, as yet unexplored, ground that lies beyond the distinctions of either. The nature and name of this generative power should by now be recognizable to the reader on the basis of the above discussions about the explicate and implicate orders. We could, alternatively, refer to it as 'objective intelligence' or 'creative ordering' that manifests itself in both the mental and the physical realms. Normally this ordering is only dimly grasped.

The Implicate Order (or set of such orders) is ultimately carried by the Holomovement (Holoflux). This Holomovement is an unbroken and undivided totality. In certain cases, we can abstract particular aspects of the Holomovement (e.g. light, electrons, sound, etc.), but more generally, all forms of the Holomovement merge and are inseparable. Thus, in its totality, the Holomovement is not limited in any specifiable way at all. It is not required to conform to any particular order, or to be bounded by any particular measure. Thus, the Holomovement is undefinable and immeasurable.
To give primary significance to the undefinable and immeasurable Holomovement implies that it has no meaning to talk of a fundamental theory, on which all of physics could find a permanent basis, or to which all the phenomena of physics could ultimately be reduced. Rather, each theory will abstract a certain aspect that is relevant only in some limited context, which is indicated by some appropriate measure.

Figure 3.
Above :  Reductionistic Physics finds ultimate simple building blocks out of which all of Reality has emerged.
Below :  The ultimate ground of all Reality is unbounded, undefinable and immeasurable. It is the Holomovement, out of which everything emerges and to which everything returns, in an ever to and fro process.

The theory of the Implicate Order can be philosophically developed along several directions. These developments may then serve as tests as to whether the theory as such is or is not on the right track leading to a global understanding of Reality.
One of the possibilities for further development is to combine it with the ontology of Nicolai HARTMANN (1940) which is about spheres and layers of Being within all of Existence (whether ideal or real). This ontology is highly interesting and promising, but it also presents several difficulties. In  Fourth Part of Website  Part I, we have tried to remedy these difficulties, resulting in a long, but -- I think -- interesting discussion of Layers of Being. And in  Part XXIX Sequel-1  (of this same Fourth Part of Website) we have, on the basis of some very plausible assumptions, finally solved these difficulties by combining HARTMANN's theory with the theory of the Implicate Order, and with MEYER-ABICH's theory (1948) of Holistic Simplification. All this results in a general theory of coupled orders of form generation :  Reductionistic Complexification (Explicate Order) coupled with Holistic Simplification (Implicate Order), and Layers of Being. In Part XXIX Sequel-2, Part XXIX Sequel-3 and Part XXIX Sequel-4 of the menioned Fourth Part of Website, this theory is further exemplified by the structure of plants (phyllotaxis) and the symmetries of snow crystals.

Recently, I have picked up the idea of the Implicate Order again, especially in an attempt to rationalize the perplexing phenomenon of organic evolution. It is argued for in  Fifth Part of Website , in the Series on Evolution (after the issues of Aristotelian logic and metaphysics, and Intentional Logic). It is argued there that the current neo-darwinian explanation of the driving force of organic evolution, namely by seeing this force exclusively to be random genetic mutation and natural selection, only -- if at all -- holds for events at merely the sub-species level. For explaining all long-time evolutionary lineages it fails miserably. It cannot explain in this way the many intricate and 'clever' adaptations having arised in the animal and plant world in the course of geologic time. In conceptually isolating one such adaptation in a given organismic species, that is, when neglecting the evolution of all the other organ-systems and behavior of the individuals of such a species, the neo-darwinian explanation of the evolutionary origin and generation of such an adaptation by a succession of random genetic changes and subsequent natural selection, appears, when not too critically looked at, plausible. But as soon as the true nature of random genetic changes is taken into account, this explanation of that (chosen) adaptation fails. And things become even worse when it is (rightly) demanded that, considering evolution, the whole organism must be taken into account, beause all its many different organ-systems and behavior are subjected to evolution in a constantly changing environment (especially its biotic part). And then explanation by random genetic mutation and subsequent natural selection of the 'fittest' mutants breaks down and is drowned in a mass of ad hoc assumptions.
The organisms chosen by me to consider in this respect are the insects, because, firstly, they offer almost all aspects of evolution, secondly because they are by far the largest and most diverse organisms, with a long evolutionary history (from the Carboniferous onwards), and thirdly, because I am well acquainted with these creatures.
My alternative general theory of organic evolution is step-by-step developed on that Fifth Part of Website while considering the morphology and behavior of, to begin with, the representatives of the insect Orders Diptera (mosquitoes, gnats, and true flies) and Hymenoptera (wasps, ants, and bees).
In my theory it is assumed that Reality consists of two interacting Orders of Being, the Explicate and the Implicate Orders. It is then further assumed that the processes of organic evolution do not actually take place in the Explicate Order (the material, physical world) but in the Implicate (the immaterial, "noëtic" order). There it takes place in the form of formal derivations of certain noëtic patterns (themselves each being a 'description' of a certain strategy to exist in the Explicate Order) from other such patterns. Upon 'projection' from the Implicate Order into the Explicate Order this derivational sequence appears in the Explicate Order as a succesive appearance of different organisms and organismic types.
As has been said, this theory is being gradually developed in Fifth Part of Website during the many considerations about the morphology and way of life (in hymenoptera especially that of reproduction) of concrete Diptera and Hymenoptera. Only near the end of treating of the Hymenoptera (where the evolution of ants and their social behavior is discussed) the general theory of evolution -- the noëtic theory of evolution -- attains a more complete form. And there the original conception (by BOHM) of the Implicate Order, and also that of the mutual interaction of the two Orders, is, as conscientious as possible, changed a bit.
We hope to have succeeded in better (than neo-darwinism) rationalize the phenomenon of organic evolution by placing it in a broader metaphysical context, without introducing any theological or related considerations.
For the reader who is interested in this new "noëtic theory of evolution" it would be useful to start with the present document on the Implicate Order, and then move on to the Series on organic evolution in Fifth Part of website.

e-mail : 

back to homepage

back to Second Part of this Website