Having given an introduction to these ideas in the previous document, we will first elaborate a little more on what has been said in that introduction, and then give a very instructive analogy of the relation between the implicate and explicate orders, namely the ink-in-glycerine model.

A part of the mentioned elaborations stems from a published discussion in a book about morphogenetic fields of Rupert SHELDRAKE, A new Science of Life, The Hypothesis of Formative Causation, 1981 and 1987. The theory of BOHM is in certain respects very much alike that of SHELDRAKE. Both are holistic. Whereas the theory of the latter mainly focuses on the development and evolution of organisms, the theory of BOHM concentrates for a large part on inanimate physical entities (and cursorily involves organisms and consciousness). BOHM's theory can be considered to be more fundamental than that of SHELDRAKE. A synthesis of both theories, then covering Cosmology, Physics, Chemistry, Biology, Psychlogy and Sociology, can be very promising indeed.
The mentioned discussion took place between BOHM and SHELDRAKE, and was about possible connections between the two theories. A part of that discussion will be given here, together with comments and explanations.

We begin with an editor's note about an(other) analogy of how the implicate order provides for processes in general, that are as such not clearly figuring in current quantum mechanics. The latter really deals with one moment only, one observation, and the probability that one observation will be followed by another one : There is no genuine connection between a past event and a present event.
Take the ocean and its waves. Each wave arises or is 'projected' from the whole of the ocean. That wave then dips back into the ocean, or is 'injected' back into the whole, and then the next wave arises. Each wave is affected by past waves simply because they all rise and fall, or are projected and injected, by the whole ocean. So there is a type of 'causality' involved, but it is not that wave A linearly causes wave B, but that wave A influences wave B by virtue of being absorbed back into the totality of the ocean, which then gives rise to wave B. In BOHM's terms, wave B is in part a 're-projection' of the 'injection' of wave A, and so on. Each wave would therefore be similar to previous waves, but also different in certain aspects -- exact size, shape, etc. BOHM is suggesting that there is a type of 'causality', but one that is mediated via the totality of the implicate ocean, and not merely via the separated, isolated, explicate waves. This means, finally, that such 'causation' would be non-local, because what happens at any part of the ocean would affect all other parts.

.   .   .

[After BOHM having stated that current quantum theory does not treat time adequately] :
Sheldrake :  But don't you get time in physics when you have a collapse of the wave function? (This is supposed to happen when an observation is made in a quantum mechanical experiment. And because of this, one of the several superposed possibilities for the experiment's outcome will be realized.)

Bohm :  Yes, but that's outside the framework of qunantum physics today. That collapse is not treated by any law at all, which means that the past is, as it were, wiped out altogether. [Editor's note :  This is the point where BOHM discusses some of the inadequacies of present-day (1987) quantum mechanics -- in particular, its incapacity to explain process, or the influence of the past on the present. He then suggests his re-formulations -- injection, projection, the implicate order, etc. -- that might remedy these inadequacies. And these re-formulations, apparently, are rather similar to Sheldrake's theories.]
You see, the present quantum mechanics does not have any concept of movement or process or continuity in time. It really deals with one moment only, one observation, and the probability that one observation will be followed by another one. But there is obviously process in the physical world. Now I want to say that that process can be understood from the implicate order as this activity of re-projection and re-injection. So, the theory of the implicate order, carried this far, goes quite beyond present quantum mechanics. It actually deals with process, which quantum mechanics does not, except by reference to an observing apparatus which in turn has to be referred to something else.

Sheldrake :  Would you say that process at that level is a re-projection?

Bohm :  Yes.

Sheldrake :  And a re-injection at the same time?

Bohm :  Re-injection is exactly what the Schrödinger equation is describing (This equation represents a domain of potentials, in the sense that several outcomes are in fact possible. When an observation is done the wave function, derivable from that equation, collapses and then corresponds to one of these possible outcomes.). And re-projection is the next step, which quantum mechanics doesn't handle (except by the arbitrary assumption that the wave function 'collapes' in a way that has no place in the physical laws, such as Schrödinger's equation).
Now, there's one other thing that modern (1987) quantum mechanics doesn't handle. Oddly enough, physics at present has no contact with the notion of actuality. You see, classical physics has at least some notion of actuality in saying that actuality consists of a whole collection of particles that are moving and interacting in a certain way. Now, in quantum physics, there is no concept of actuality whatsoever, because quantum physics maintains that its equations don't describe anything actual, they merely describe the probability of what an observer could see if he had an instrument of a certain kind, and this instrument is therefore supposed to be necessary for the actuality of the phenomenon. But the instrument, in turn, is supposed to be made of similar particles, obeying the same laws, which would, in turn, require another instrument to give them actuality. That would go on an infinite regress. Wigner has proposed to end the regress by saying it is the consciousness of the actual observer that gives actuality to everything.

Sheldrake :  But that doesn't seem very satisfactory to me.

Bohm :  Nor to me, but apparently Wigner feels happy with this, as do some others. The point is, unless you extend quantum mechanics, there is no room in it for actuality, no room for any of the things you are talking about. So quantum mechanics as it stands now, I want to say, is a very truncated, limited, abstracted set of formulae which gives certain limited results having to do with only one moment of an experiment. But out of this truncated view, physicists are trying to explain everything, you see. The whole thing simply has no meaning at all. Think about it : modern physics can't even talk about the actual world!

Sheldrake :  But how do you think we get to a concept of actuality?

Bohm :  Well, I think through the implicate order. We have a projection of the whole (This at the same time also means a projection of something from the multi-dimensional implicate order onto three-dimensional space, which explains the phenomenon of non-local connection between different things.) to constitute a moment. A moment is a movement. And we can say that that projection is the actualization. In other words, the thing that physics doesn't discuss is how various successive moments are related, and that's what I say the implicate order is attempting to do. If we extended quantum mechanics through the implicate order, we would bring in just that question of how past moments have an effect on the present (i.e., via injection and re-projection). At present, physics says the next moment is entirely independent, but with some probability of being such and such (indeed, being such and such, and not becoming such and such!). There's no room in it for the sort of thing you're talking about, of having a certain accumulated effect of the past. But the implicate order extension of quantum mechanics would have that possibility. And further, suppose somehow I were to combine the implicate order extension of quantum mechanics [which would account for the accumulated effects of the past] with this quantum potential [which would account for these effects being non-local in nature], then I think I would get things very like what you are talking about.

Sheldrake :  Yes, that would be very exciting! Of all the ways I've come across I think that's the most promising way of being able to mesh together these sorts of ideas. I haven't come across any other way which seems to show such possible connections.

Bohm :  If we can bring in time, and say that each moment has a certain field of potentials (represented by the Schrödinger equation) and also an actuality, which is more restricted (represented by the particle itself), and then say that the next moment has its potential and its actuality, and we must have some connection between the actuality of the previous moments and the potentials of the next -- that would be introjection, not of the wave function of the past, but of the actuality of the past into that field from which the present is going to be projected. That would do exactly the sort of thing you're talking about. Because then you could build up a series of actualities introjected which would narrow down the field potential more and more, and these would form the basis of subsequent projections. That would account for the influence of the past on the present.

By the implicate order theory it is supposed that the implicate order (and all (other) additional implicate orders that are beyond it) forms a multi-dimensional reality, while the explicate order (the order that is known by sense experience) is a three-dimensional projection of certain subtotalities of the implicate order.
The next Figure explains this for the (analogous) case of a certain subtotality of (i.e. inhabiting) a two-dimensional explicate order that is a projection from (a certain subtotality of) a three-dimensional implicate order.

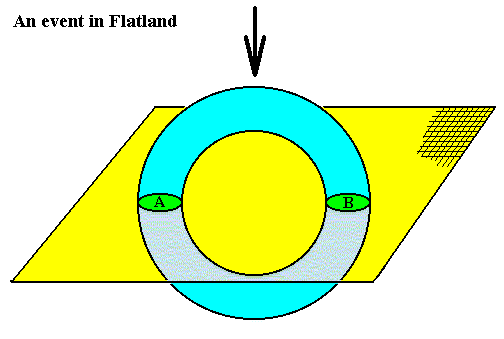
Figure 1.  A three-dimensional donut-like object present in three-dimensional space moves downward (arrow) through two-dimensional 'flatland'.
The areas A and B are two-dimensional projections of the object onto two-dimensional Flatland. As the downward movement continues the inhabitants of Flatland observe two circular objects approaching each other, till they finally merge to become one oval object, which becomes smaller and finally disappears altogether. The mentioned inhabitants study this movement (and several other such movements occurring in other cases), and try to set up laws of motion between their observed objects. One of them, however, named MHOB, says that those laws are only abstractions and approximations from a state of affairs occurring in a higher-dimensional reality, in which those two objects are just one object, also when observed as actually separate (i.e. also when it is observed as two separate objects that later collide). Because the 'real' object is just one simultaneously existing whole, the apparent interactions between the objects A and B are of a non-causal and non-local nature.

Bohm :  That's exactly where we started. These matter waves are the formative cause, and that was what DeBroglie originally suggested. However, he wanted to regard the matter wave as just simply a real three-dimensional wave in time, and that doen't work well. The formative field is a far better interpretation (Bohm had said earlier : The formative field could not be put in three-dimensional [or local] space, it would have to be in three-n dimensional space, so that there would be non-local connections, or subtle connections of distant particles, which we see in the Einstein-Podolsky-Rosen experiment) (See Figure 1). The quantum potential is the fomative field which we derive from the generalized DeBroglie waves. And we say that the particle is the actuality, affected by the formative field. The set of particles, the whole structure of all the particles forming a system, is the actuality of that formative field.
But that model by itself still ignores time, so the next step is to bring in time, to say that there's a succession of moments of time in which there is a recurrent actuality. And we would say that what recurs is affected by the formative field. But then that formative field is affected by what has previously happened, actually. Now that would help to remove most of the problems in physics, if we can manage it. And it would tie up closely with the sort of thing that you are talking about.
See, at present we say that the wave function as potential spreads out very fast and then it suddenly collapses into some definite actual state for reasons totally outside the theory (current quantum theory). So we say it requires a piece of measuring apparatus to do so. Then another collapse, and the only continuity of this system would be achieved by an infinite set of measurement apparatuses that would keep it in observation all the time, and these observation apparatuses in turn would have to be observed to allow them to exist actually, and so on. And the whole thing vanishes in a fog of confusion. Because people take the present mathematics as sacred, they say these equations in their general form are never to be altered, and then they say here we are with all these strange problems. But you see almost no one wants to introduce anything fundamentally different into this general framework.

Sheldrake :  So the DeBroglie interpretation is the way you're thinking of developing. You'd have this recurrent actualization of something which is continually associated with the formative field.

Bohm :  And the present formative field is affected by past actualizations. In the present quantum mechanics there is no way to have the formative field affected by anything at all, including the past, because there's only one moment that you can talk about. You can't find anything that would affect the formative field, and that's the problem.

.   .   .

(end of dialogue excerpt.)

The current approach in biology and the theory of evolution is to treat explicate and sequential orders as basic. It is assumed that ultimately everything in nature can be reduced to explanations using such orders, for example, in terms of atoms, molecules, DNA, cells, and other structures. But if the generative order -- (The already discussed first and second implicate orders mainly apply to physical features in quantum mechanics, and are special cases of generative orders or formative fields. Deeper orders must be assumed for all other phenomena, especially biological ones.) -- is basic to inanimate matter, then it is even more essential for the understanding of life. In the explicate and sequential orders, life appears to arise as a fortuitous chance combination of molecules which leads, in a more or less mechanical determined way, to further developments which produce ever higher and more complex forms. While this approach can be admitted as significant for study, it is now seen as an abstraction and an approximation in the light of the generative order. Its deeper meaning is to be understood by exploring how it reveals the inward generative order of the 'whole stream' that is constantly present (Here we see that the implicate order in general is dynamic, but all the dynamics is as a whole already present, so that dynamics is not according to a time-succession.).
In this connection some scientists, notably Erwin Schrödinger, have suggested that the quantum theory, with its new feature of wholeness, could explain the basic qualities of life. However, current work in biology hardly takes the quantum theory into account, even though it is necessary for understanding the very existence of molecules. The current approach is (however) justified by pointing out that the relatively high temperatures at which life becomes possible make long-range quantum connections (as we see it, for example in superconductivity, taking place at very low temperatures) not particular important (although it may turn out that in certain macromolecular process, such as protein folding, long-range quantum correlations may indeed be relevant). In conclusion, therefore, it does not appear likely that the essence of life is to be understood in terms of the details of conventional quantum theory.
Rather it is necessary, for the understanding of life, to go beyond the quantum theory and the superimplicate order, into an infinity of generative and implicate orders from which present (biological) theory has been (as it were) abstracted. In doing so, however, it is not intended to seek the 'ultimate origin of life' in a reductionist way by going, for example, to an even more fundamental microscopic theory than the quantum theory. Rather it is being proposed that a deeper generative order is common to all life and to inanimate matter as well. It is not therefore an attempt to explain life in terms of matter, but rather to see how both emerge out of a common overall generative order. Within this order there is room for new kinds of 'pools of information' from which life could be generated. The wholeness of the living being, and even more of the conscious being, can then be understood in a natural way, rather as the wholeness of the molecule and the superconductive system is understood (although it must not be forgotten that life is much subtler and more complex than molecules and superconducting systems). Life is no longer seen as the result of somewhat fortuitous factors, which perhaps happened only on an isolated planet, such as Earth. Rather it is seen to be enfolded universally, deep within the generative order. (BOHM and PEAT, 1987, pp. 200).

It must be emphasized that the domain of implicate and generative orders is not a transcendent domain (like, for instance, Plato's domain of Ideas), i.e. it is not separately existing, separate from the things that we can observe with our senses (and instruments), but is immanent in those things. In other words, the implicate orders are immanent in the explicate order. Those orders (explicate and implicate) form one indivisible dynamic whole.

It is perhaps instructive to bring in some elements of the closely related theory of morphogenetic fields of SHELDRAKE into the discussion of implicate orders (which is not carried as far by BOHM, and BOHM & PEAT, as I would wished they had).
Although matter in general has evolved (from the Big Bang onwards), crystals and the like do not evolve (further). But organisms do. They have experienced an evolution having lead to ever more complex forms all the way to conscious beings. How do we relate this to the above mentioned generative orders (or formative fields)? Well, existing organisms are connected (we could say, 'tuned-in') to their respective formative fields (implicate generative orders) that sustain them. But a change in the environment of a population of an organismic species can trigger a tuning-in to new ranges of the generative order, resulting in a new sequence of genetic changes (which are thus not the result of random mutations, but of directed and ordered mutations, although under certain circumstances random mutations -- which are often disadvantageous or lethal -- can and will occur). These genetic changes will give rise to a new sequence of successive organisms (in the explicate order). So analogously as is the case in quantum mechanical experiments, the observed randomness is caused by an underlying enfolded order, an order, one is only dimly aware of. All the cases of apparent 'cooperation' between a host of changes that together must result in, for example, the transition from Reptiles to Birds, must be attributed to the enfolded generative orders or formative fields. The tuning-in to such a field by an explicate entity (which is always partly enfolded into the generative order) is in fact (further) enfoldment, injection (into the generative order), while the resulting action of the formative field is an unfoldment from the implicate to the explicate order. At the same time we must assume that the formative field is itself changed by it being tuned in. This language of "tuning-in" is very relevant. It stems from the radio technique that a part of the radio is able to resonate with a particular frequency of an incoming radio wave. And because it is reasonable to assume that everything whatsoever is in fact one or another vibration (which can form interference patterns), we can imagine that such a 'tuning-in' can take place. (For the theory that everything is in fact a certain vibrational phenomenon, see ZWART, Het Wezen van het Zijn (The Essence of Being) (in Dutch)).
The mentioned phenomena of "cooperation" of parts in creating a whole is widely encountered in biological phenomena. But even in inanimate things we sometimes find such a cooperation :
There are many solids (crystals) whose atoms can adopt more than one kind of orderliness. In such solids, one orderliness is usually more stable above some definite temperature, another below it. As the solid (in the form of a crystal) is heated through that temperature, the crystal structure may change abruptly from one form to the other (HOLDEN & MORRISON, p. 219 -- this source is more fully cited below). So some crystal species can undergo a spontaneous transformation while they remain in a solid state. A beautiful example of this can be observed in mercuric iodide. It is especially spectacular because the change of crystal structure brings with it a change in color from red to yellow. The red tetragonal form, stable at room temperature, changes to a yellow form belonging to the orthorhombic crystal system as the temperature rises through 126⁰ centigrade. On cooling, the yellow form transforms more slowly back to the red. HOLDEN & MORRISON, 1982, Crystals and Crystal Growing, p. 221, remark the follwing about this crystal transformation :

"When we visualize what the atoms must do to accomplish a structural transformation of a solid, it seems even clearer than in visualizing melting that co-operative action of the atoms might be necessary. In the structural transformation the atoms must not only move, they must move to the new 'right places'. Since the locations of its neighbors determine what is the right place for an atom, the atoms must feel one another out quite extensively in the course of the transformation."

So also in such inanimate cases one could suspect the action of some formative field.
Now if we go down the complexity ladder within the explicate order, we get the sequence  CONSCIOUS BEINGS,  LIVING BEINGS,  MOLECULES and CRYSTALS,  ATOMS,  and, finally,  ELEMENTARY PARTICLES.  These entities, in order for them to be generated and sustained, reach back to their corresponding levels of (and in) the implicate order(s), as the next diagram illustrates :

Figure 2.  Each type of explicate structure depends for its generation and sustenance on its own 'layer' of implicate generative order. These layers are not transcendent but immanent with respect to the explicate structure. This means that the explicate structure is tuned in to the  a c t i v e   i n f o r m a t i o n  of the relevant 'layer' in the implicate order.

We will now outline the promised (mechanical) analogy (given by BOHM, 1980) that visualizes the relationship between the explicate and implicate orders.
Suppose we have two glass cylinders, a smaller one placed concentrically inside the other. We fill the space between the two cylinders with a viscous fluid, like glycerine. Then we take insoluble ink (for example ink composed of carbon particles). We then place a droplet of that ink onto the surface of the fluid. So what we then see is a dark more or less circular droplet floating on a colorless medium. If we now rotate the outer cylinder slowly, then any fluid element (i.e. any small region of the fluid) will be drawn out, because the parts of that fluid element that are closer to the outer cylinder are moving faster than those that lie more inward. And with this fluid element the ink droplet will also be drawn out. After prolonged rotation the ink droplet will be stretched into a long thread, and as the process proceeds, the droplet will finally disappear, and the thread will be so thin that it becomes invisible to the naked eye. For the latter the ink has been totally mixed up with the glycerine.

Figure 3.  The ink-in-glycerine model for explicate and implicate order. Two concentric cylinders (top view) of unequal size. The space between the cylinders is filled with glycerine, and a droplet of insoluble ink is placed onto the fluid. When the outer cylinder is rotated (arrow), the ink droplet will be drawn out into a long thread.

With this mechanism we can simulate several phenomena (thereby sometimes using more than one ink droplet, or colored droplets, etc.).

First we will describe the more or less prolonged explicate (local) existence of an object (say a particle, represented by an ink droplet), and its non-local existence in the Implicate Order.
In the next four Figures the implicate entities are indicated by threads. These threads must not be taken literally. They are supposed to symbolize the enfolded condition of entities in the Implicate Order, i.e. the entities are homogeneously diffused all over the Implicate Order. The different colors of the thread (and the explicate object) does not symbolize a qualitative difference, but only a sequential difference reflected in the order of appearance in the Explicate Order. In the present case the degree of enfoldment of a droplet is weak when it is in the vicinity of location A, and stronger for enfolded droplets further away from that location. The four Figures represent successive situations of enfoldment (injection) and unfoldment (projection), resulting in this particular case in a relative constant local presence of the (same) object in the Explicate Order and at the same time a non-local presence of the enfolded state of the same object in the Implicate Order. The latter is carried by the Holoflux, like the modulation of a radio wave is being carried by the carrier wave.

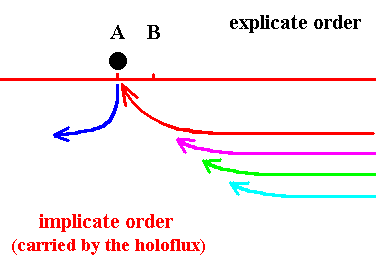
Figure 4.  The object (indicated by a black ball) is explicate(d) in virtue of the unfolding of a black thread at location A .  Just a moment before, it had been made explicate by the unfolding of a blue thread, which is now being enfolded back again into the Implicate Order. In the next moment the object will become represented by the unfolding of the red thread leaving the black thread implicate again (See next Figure). We imagine here that in this particular process of unfolding and enfolding no new objects are being created. The 'replacements' represent the same object, and this same object is non-locally, and in an implicate way, present in the Implicate Order, and locally present in the Explicate Order at location A.
The next images relate to what happens further during prolonged rotation of the outer cylinder.

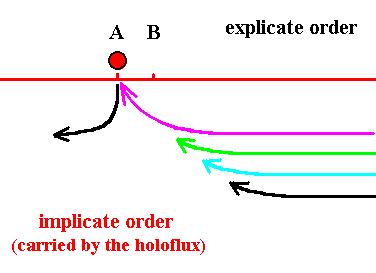
Figure 5.  Now the red thread is contracted, resulting in its becoming explicate as a droplet at location A, while the previous droplet (black) has become implicate again and (in the model) present as a black thread in the glycerine. But, already the next thread (purple) is in the process of contracting.

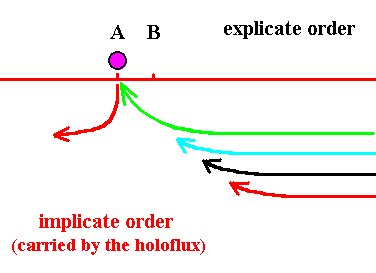
Figure 6.  The purple thread has now become fully contracted and appears as droplet in the Explicate Order at location A, while the red droplet is again drawn out into a thread and is implicate again. But the green thread is already in the process of contracting and will soon become explicate.

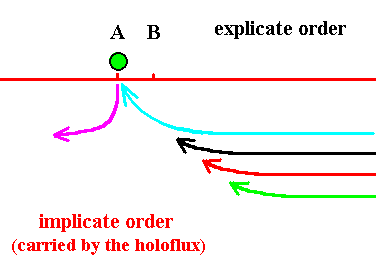
Figure 7.  The green thread is now fully contracted and has become explicate as a droplet at location A, while at the same time the purple droplet is drawn out again into a thread and so is implicate again. But the blue thread is already contracting . . . .

As has been said, the above four Figures symbolize the more or less sustained existence of the same object in the Explicate Order. But -- and now considering another possible state of affairs -- the four Figures can also be interpreted as replacements of that object by another object, by the successive unfoldment and enfoldment of qualitatively different threads, this qualitative difference now being indicated by the different colors. In this interpretation we see -- in the Explicate Order -- an object that is gradually changing on the spot (i.e. at location A). In both cases, however, the object in the Explicate Order is just an abstraction from the Implicate Order (and ultimately from the Holoflux). As such it is just a relatively and temporarily stable and isolated object, which in fact is not isolated but connected with the whole which is everywhere in the Implicate Order. It is like a semi-stable vortex in a steam, enjoying a transient explicate existence, while being integrated with, and dependent on, the implicate whole which sooner or later will absorb it again within itself. The condition of unfoldment depends on the pattern of degrees of implication of the 'threads' inside the Implicate Order. As has been said, the threads must not be taken literally as threads, but as some sort of diffused entities wholly taken up by the Implicate Order, but, in contrast with the case of real diffusion, they can be recovered again and become explicate. The pattern of degrees of implication is an expression and consequence of the laws that reign in the Implicate Order. These laws are approximated by the laws of Quantum Mechanics. Maybe not all known natural laws governing observable processes, can be reduced to the laws of present-day quantum mechanics, because, even without considering the possible existence of the implicate and generative orders, the quantum theory cannot be the final theory about all of Reality, in virtue of the fact that it, as it stands today, cannot be harmonized with the theory of relativity. Anyway, we can imagine the 'real' laws to be present in the implicate and generative orders in the form of mathematical entities, to which structures in the Explicate Order can tune in as it were, in order to be 'guided' in their processes. With respect to the individual development of crystals, for example, we could say that the locally existing chemical motifs (atoms or sets of bonded atoms) are guided by 'group theory' -- present in the implicate generative order as a set of principles of symmetry (symmetry groups) -- in order to find their minimum-energy configuration (demanded by quantum laws), by actually taking up one or another particular symmetry corresponding to that minimum-energy configuration. With the mentioned "real laws" we could mean all the laws that we earlier have called "Dynamical Laws", namely in the documents of the First Part of our website. Such a dynamical law represents the so-called "Essence" of that intrinsic thing that is generated by the dynamical system that is governed by that law.
In this vision of deeper levels of enfolded generative orders that organize, by their active information, the entities in the Explicate Order, it is demanded that those entities, particles, atoms, molecules, etc., must be of sufficient complexity in order to be able to respond to this active information. The order of matter has in this vision (but also already in quantum mechanics) become far removed from that of the billiard balls and falling apples of the Newtonian world. Rather than nature being reduced to the material, the whole notion of the material has been extended into regions of indefinite intangibility. While in material processes, like, say, crystallization, the actual driving force is still the quantum mechanical desire to minimize energy by moving toward the configuration of atoms that corresponds to the lowest-energy valley, the actual process is given form by information in the enfolded generative orders (or formative fields) themselves. So in in principle quantum mechanics can say something about how a lowest-energy configuration (of atoms) must look like, but to actually find this configuration, i.e. to actually take up this configuration (by the relevant atoms themselves, which must move to certain places), is accomplished by the active information from the enfolded order. Thereby the atoms (chemical motifs) move in virtue of, so to say, their own energy, but this energy is directed by the much weaker energy of the formative field.
The still deeper and most subtle enfolded orders, or formative fields, are, it seems, close to some form of objective intelligence that wells up from an underlying creative source.
So we see that in this vision the whole philosophy, as presented in the First Part of this website, is, in a way, turned upside down :  Matter, in a way, stems from some mind-like 'substance', instead of mind ultimately stemming from matter. The discrepancy between the two visions (in one and the same website) should not be taken negatively, but positively. It means that it makes possible a fertile dialogue, between, say, (self-critical) 'reductionists' and (self-critical) 'holists'.

After having had this intermezzo, we continue with the ink-in-glycerine model of the explicate and implicate orders.
And we will once and for all set that in all ensuing images of explicate and implicate ink droplets (unless stated otherwise), each droplet must -- without drawing all that again -- be imagined as consisting of a whole ensemble of implicate threads, all belonging to the same explicate object. This implies that whatever droplet we draw as explicate, it is at the same time also implicate in virtue of its fellow threads, which means that every object, visible in the Explicate Order, is at the same time present everywhere in the Implicate Order. And because of this it is not an isolated particle, but represents the Whole.

The transformation of becoming implicate of something explicate, and vice versa, must be considered to be a radical one. Therefore we will call it a metamorphosis rather than just a transformation. Such "just transformations" are for example linear displacements (translations), rotations, reflections, dilations, etc., while a metamorphosis can be best compared with what we see in certain insects, for instance the change from caterpillar to butterfly.
Metamorphosis often results in different orders. To see what this means, let us first illustrate a case where this is not so (In these illustrations we investigate the process of enfolding, and the orders that can result therefrom, and for clarity in these cases (only) we assume that when something is explicate it is not implicate, and vice versa) :
The simplest notion of order is that of a sequence or succession. The essence of such an order is in the series of relationships among distict elements :

A : B = B : C = C : D .  .  .  .

For example, if A represents one segment of a line, and B the succeeding one, etc., the sequentiality of segments of the line follows from the above set of relationships.
Returning to our ink-in-glycerine analogy, suppose that we have inserted into the fluid a large number of droplets, set close to each other and arranged in a line. These we label as A, B, C, D, E, . .  .  . . See next Figure.

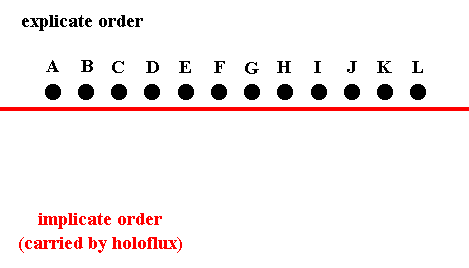
Figure 8.  A row of explicate droplets.
After they all are thus placed at the surface of the glycerine, rotation of the outer cylinder will begin.

We then turn the outer cylinder many times, so that each of the droplets gives rise to an ensemble of ink particles, enfolded (as infinitely thin threads) in so large a region of space (of glycerine) that particles from all the droplets intermingle.
We label the successive ensembles A', B', C', D', E', . .  .  . . See next Figure.

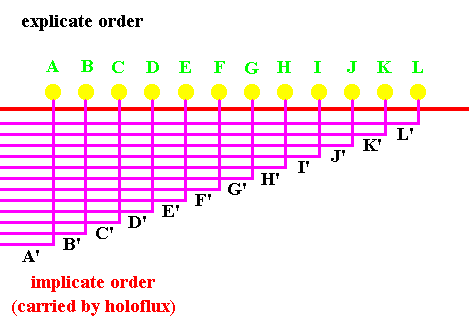
Figure 9.  In virtue of the rotation of the outer cylinder, all droplets have simultaneously become implicate. Although the ensembles of ink particles (infinitely thin threads(purple)) are intermingled with each other, they can be recovered back into the Explicate Order, by reversing the rotation of the outer cylinder. The earlier explicate state of the droplets is indicated by soft colors.

It is clear that, in some sense, an entire linear order has been enfolded into the fluid. This order may be expressed through the relationships

A' : B' = B' : C' = C' : D' .  .  .  .

This order is not present to the senses. Yet its reality may be demonstrated by reversing the motion of the fluid, so that the ensembles, A', B', C', D', .  .  .  .  , will unfold to give rise to the original linearly arranged series of droplets A, B, C, D, .  .  .  . .
In the above, we have taken a pre-existent explicate order, consisting of ensembles of ink particles arranged along a line, and transformed (i.e. metamorphosed) it into an order of enfolded ensembles, which is in some key way similar.
We shall next consider a more subtle kind of order, not derivable from such a transformation (metamorphosis).
Suppose now that we insert a droplet, A, and rotate the outer cylinder  n  times. We then insert a second ink droplet, B, at the same place, and again rotate the cylinder  n  times. We keep up this procedure with further droplets, C, D, E, F, .  .  .  . . The next Figure schematically shows what happens. When later droplets are inserted and the cylinder is rotated, the degree of implication increases for earlier droplets. One should read the Figure from top to bottom.

Figure 10.  Intrinsically implicate order.
From top to bottom :
We insert a droplet A onto the fluid at location X.
We rotate the outer cylinder  n  times. The droplet A becomes implicate. It becomes the ensemble (thread)  a .

Then we insert a droplet B onto the fluid again at location X.
We rotate the outer cylinder  n  times. The droplet B becomes implicate. It becomes the ensemble (thread)  b . The degree of implication of A increases.

Then we insert a droplet C onto the fluid again at location X.
We rotate the outer cylinder  n  times. The droplet C becomes implicate. It becomes the ensemble (thread)  c .The degree of implication of A increases still further, and that of B increases.

Then we insert a droplet D onto the fluid again at location X.
We rotate the outer cylinder  n  times. The droplet D becomes implicate. It becomes the ensemble (thread)  d .The degree of implication of A and B increases still further, and that of C increases.

Then we insert a droplet E onto the fluid again at location X.
We rotate the outer cylinder  n  times. The droplet E becomes implicate. It becomes the ensemble (thread)  e .The degree of implication of A, B and C increases still further, and that of D increases.

Then we insert a droplet F onto the fluid again at location X.
We rotate the outer cylinder  n  times. The droplet F becomes implicate. It becomes the ensemble (thread)  f .The degree of implication of A, B, C and D increases still further, and that of E increases.
We can, if we want, continue this procedure.

The resulting ensemble of ink particles, a, b, c, d, e, f, .  .  .  .  , will now differ in a new way, for, when the motion of the fluid is reversed, the ensembles will successively come together to form droplets again in an order opposite to the one in which they were put in. For example, at a certain stage the particles (i.e. the carbon particles of the ink) of ensemble  d  will come together (i.e. the thread, forming that ensemble, contracts, and becomes an explicate droplet again, after which it will be drawn out into a thread again). This will happen for the particles of  c ,  then to  b ,  etc. It is clear from this that ensemble  d  is related to  c  as  c  is to  b ,  and so on. So these ensembles form a certain sequential order. However, this is in no sense a transformation of a linear order in space (as was that of the sequence A', B', C', D', .  .  .  . , that we considered earlier), for in general only one of these ensembles will unfold at a time. When any one is unfolded, the rest are still enfolded. In short, we have an order which cannot all be made explicate at once and which is nevertheless real, as may be revealed when successive droplets become visible as the cylinder is turned.
Bohm (Wholeness and the Implicate Order) calls this an intrinsically implicate order, to distinguish it from an order that may be enfolded but which can unfold all at once into a single explicate order. The just temporal (i.e. time-successive) order in the Explicate Order in the present case corresponds to a simultaneous order in the Implicate Order. So we have here an example of how an explicate order is a particular case of a more general set of implicate orders.

Let us now go on to combine both of the above-described types of order.
We first insert a droplet, A, in a certain position and turn the cylinder  n  times. We then insert a droplet, B, in a slightly different position and turn the cylinder  n  more times (so that A has been enfolded by  2n  turns). We then insert C further along the line AB and turn  n  more times, so that A has been enfolded by  3n  turns, B by  2n  turns, and C by  n  turns. We proceed in this way to enfold a large number of droplets. We then move the cylinder fairly rapidly in the reverse direction. If the rate of emergence of droplets is faster than the minimum time of resolution of the human eye, what we will see is apparently a 'particle' moving continuously and crossing the space. See next Figure (which only depicts the enfoldment of the droplets)

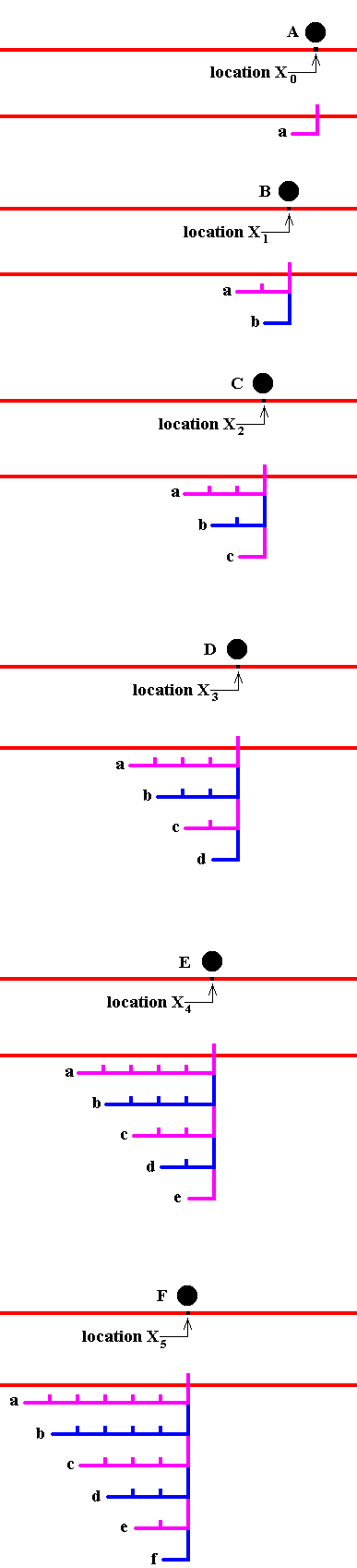
Figure 11.  Movement in the Explicate Order.
This Figure, reading it from top to bottom, illustrates the successive enfoldment of droplets at sequential locations, that lie very close to each other on a straight line
(When, such an enfoldment of a large number of droplets has thus been accomplished, the cylinder is rapidly turned in the opposite direction. The droplets will then become explicate again, one after the other, while at the same time they will -- also one after the other -- be enfolded back again into the glycerine. What we then actually see (i.e. see what happens in the Explicate Order) is a continuous movement of a droplet along a straight line.).
The sequential locations X₀ , X₁ , X₂ , X₃ , X₄ , X₅ , etc., are supposed to be very close to each other, while lying on a straight line.

From top to bottom :
We insert a droplet A onto the fluid at location X₀ .
We rotate the outer cylinder  n  times. The droplet A becomes implicate. It becomes the ensemble (thread)  a .

Then we insert a droplet B onto the fluid at location X₁ .
We rotate the outer cylinder  n  times. The droplet B becomes implicate. It becomes the ensemble (thread)  b . The degree of implication of A increases.

Then we insert a droplet C onto the fluid at location X₂ .
We rotate the outer cylinder  n  times. The droplet C becomes implicate. It becomes the ensemble (thread)  c .The degree of implication of A increases still further, and that of B increases.

Then we insert a droplet D onto the fluid at location X₃ .
We rotate the outer cylinder  n  times. The droplet D becomes implicate. It becomes the ensemble (thread)  d .The degree of implication of A and B increases still further, and that of C increases.

Then we insert a droplet E onto the fluid at location X₄ .
We rotate the outer cylinder  n  times. The droplet E becomes implicate. It becomes the ensemble (thread)  e .The degree of implication of A, B and C increases still further, and that of D increases.

Then we insert a droplet F onto the fluid at location X₅ .
We rotate the outer cylinder  n  times. The droplet F becomes implicate. It becomes the ensemble (thread)  f .The degree of implication of A, B, C and D increases still further, and that of E increases.

We continue this for a large number of droplets.
As has been said, when the cylinder is now rapidly rotated in the reverse direction, we see a droplet moving continuously along a straight line.

Such enfoldment and unfoldment in the Implicate Order may evidently provide a new model of, for example, an electron, which is quite different from that provided by the current mechanistic notion of a particle that exists at each moment only in a small region of space and that changes its position continuously with time. (We must not be confused by the fact that the described model is itself wholly mechanical. The model is supposed to be an analogy. The status of the ink ensembles must be interpreted as totally implicate in the fluid, just like the image of an illuminated object is genuinely implicate (enfolded) in the interference pattern of a hologram, discussed earlier.). What is essential to this new model is that the electron is instead to be understood through a total set of enfolded ensembles, which are generally not localized in space. At any given moment one of these may be unfolded and therefore localized, but in the next moment, this one enfolds to be replaced by the one that follows. The notion of continuity of existence is approximated by that of very rapid recurrence of similar forms, changing in a simple and regular way (rather as a rapidly spinning bicycle wheel gives the impression of a solid disc, rather than of a sequence of rotating spokes). Of course, more fundamentally, the particle is only an abstraction that is manifest to our senses. What is is always a totality of ensembles, all present together, in an orderly series of stages of enfoldment and unfoldment, which intermingle and inter-penetrate each other in principle throughout the whole of space. It is further evident that we could have enfolded any number of such 'electrons' in different ways, so that we could then mimic a set of interacting particles.
Since classical physics traditionally aims to explain everything in terms of interacting systems of particles, it is clear that in principle one could equally well treat the entire domain that is correctly covered by such classical concepts, in terms of this new model of ordered sequences of enfolding and unfolding ensembles.
What this theory of the Implicate Order proposes here is that in the quantum domain this model is a great deal better than is the classical notion of an interacting set of particles. Thus, although successive localized manifestations of an electron, for example, may be very close to each other, so that they approximate a continuous track, this need not always be so. In principle, discontinuities may be allowed in the manifest tracks -- and these may, of course, provide the basis of an explanation of how an electron can go from one state to another without passing through states in between. This is possible, of course, because the 'particle' is only an abstraction of a much greater totality of structure. This abstraction is what is manifest to our senses (or instuments) but evidently there is no reason why it has to have continuous movement (or indeed continuous existence).
The form of a moving object, as we saw in the above experiment, appears in immediate perception primarily because the eye is not sensitive to concentrations of the ink lower than a certain minimum, so that one does not directly see the 'whole movement' of the ink, i.e. its droplets being drawn out into threads, and being contracted again. Rather, such perception relevates a certain aspect, where "relevates" means making relevant. That is to say, it makes this aspect stand out 'in relief' while the rest of the fluid is seen only as a 'grey background' within which the related 'object' seems to be moving.
Of course such an aspect has little interest in itself, i.e. apart from its broader meaning. Thus, on the present example, one possible meaning is that there actually is an autonomous object moving through the fluid. This would signify, of course, that the whole order of movement is to be regarded as similar to that in the immediately perceived aspect. In some contexts, such a meaning is pertinent and adequate (e.g. if we are dealing in the ordinary level of experience with a rock flying through the air). However, in the present context (a context such that we give primary relevance to the Implicate Order), a very different meaning is indicated, and this can be communicated only through a very different kind of description.
Such a description has to start by conceptually relevating certain broader orders of movement, going beyond any that are similar to those relevated in immediated perception. In doing this, one always begins with the Holomovement, and then one abstracts special aspects which involve a totality broad enough for a proper description in the context under discussion. In the present example, this totality should include the whole movement of the fluid and the ink as determined by the mechanical stirring device (with respect to the rotation of the outer cylinder), and the movement of the light, which enables us visually to perceive what is happening, along with the movement of the eye and nervous system, which determines the distinctions that can be perceived in the movement of light.
It may then be said that the content relevated in immediate perception (i.e. the 'moving object') is a kind of intersection between two orders. One of these is the order of movement that brings about the possibility of a direct perceptual contact (in this case, that of the light and the response of the nervous system to this light), and the other is an order of movement that determines the detailed content that is perceived (in this case, the order of movement of the ink in the fluid). Such a description in terms of intersection of orders is evidently very generally applicable.
In our present example it is appropriate to describe the movement of the ink in terms of implicate and explicate. That is to say, in the movement, certain implicate orders (in the distribution of the ink) become explicate, while explicate orders become implicate.
To specify this movement in more detail, one could introduce here (as BOHM, 1980, has done) a new measure (A measure is a chosen unit that can be used to measure along a certain order, for example a cm to measure along the linear order of a line.), namely an implication parameter, denoted by T. In the fluid, this would be the number of turns needed to bring a given droplet of ink into explicate form. The total structure of the ink present in any moment can then be regarded as an ordered series of substructures, each corresponding to a single droplet N with its implication parameter T_N.
Evidently, we have here a new notion of structure, for we no longer build structures solely as ordered and measured arrangements on which we join separate things, all of which are explicate together. Rather, we can now consider structures in which aspects of different degrees of implication (as measured by T) can be arranged in a certain order.
Such aspects can be quite complex. For example, we could implicate a 'whole picture' by turning the outer cylinder  n  times. We could then implicate a slightly different picture, and so on indefinitely. If we then rotate the outer cylinder rapidly in the opposite direction, we could see a 'three-dimensional scene' apparently consisting of a 'whole system' of objects in continuous movement and interaction.
In this movement, the 'picture' present at any given moment would consist only of aspects that can be explicated together (i.e. aspects corresponding to a certain value of the implication parameter T). As events happening at the same time are said to be synchronous, so aspects that can be explicated together can be called synordinate, while those that cannot be explicated together may then be called asynordinate. Evidently, the new notions of structure under discussion here involve asynordinate aspects (namely there where we had the 'moving paricle'), wheras previous notions (there where we implicated a whole linear succession of ink droplets together) involve only synordinate aspects.
It has to be emphasized here that the order of implication, as measured by the parameter T, has no necessary relationship to the order of time (as measured by another parameter,  t ). These two parameters are only related in a contingent manner (in this case by the rate of turning the outer cylinder of our ink-glycerine device). It is the T parameter that is directly relevant to the description of the implicate structure, and not the  t  parameter.
When a structure is asynordinate (that is, constituted of aspects with different degrees of implication), then evidently the time order is not in general the primary one that is pertinent for the expression of law. Rather, as one can see by considering the previous examples, the whole implicate order is present at any moment, in such a way that the entire structure growing out of this implicate order can be described without giving any primary role to time. The law of the structure will then just be a law relating aspects with various degrees of implication, and only that, i.e. the change of degree of implication, is in time. But the explicate-implicate dynamics has a derived status, derived from the holomovement. Such a law will, of course, not be deterministic in time. But determinism in time is not the only form of ratio or reason. And as long as we can find ratio or reason in the orders that are primary relevant, this is all that is needed for law (BOHM, 1980/88, Wholeness and the Implicate Order).

Remark :  I must stress once again that these brilliant ideas are wholly due to the thinking of David Bohm. So, full credit is to be given him. That's why I have presented his texts almost literally here. Those ideas couldn't be expressed any better, and moreover, I am not authorized in dealing with these matters all by myself. The intention, in this document is to bring out his interesting ideas to a wider audience. In the next document, where I will apply his theory to the development of crystals, I am largely on my own again..

Let's continue.
It is important to realize that the projection-injection-reprojection-reinjection phenomena, i.e. the explicate-implicate dynamics of unfoldment and enfoldment, is not a movement, which means that it does not involve spatial trajectories. It is not a change of place, but a change of degree of implication, or, if one whishes to express oneself, a change of degree of explication.
The whole structure of, say, a crystal, is already present, albeit in a high degree of implication. The process of crystallization of a certain chemical compound, as we see it in the Explicate Order, is then an evolving dynamics of projection and injection from the implicit pattern of the crystal lattice to its explicate state, where different sets of implicate ensembles have corresponding different explicate destinations.

In a crystallization process (to be described in detail in a following document) we are supposed to see the chemical units moving to their proper location, and forming an incipient crystal lattice. In a following document we will speculate that the chemical units will be 'guided' toward their lowest-energy arrangement by a 'patch' of Group Theory, consisting of a pattern of symmetry elements of the given Group, enfolded within the Implicate Order.
The movement of the chemical units to their proper locations in accordance with the mentioned pattern of symmetry elements of the given Symmetry Group is in fact also not a genuine movement at all, but a constant projection, followed by injection, of ensembles or subunits with respect to different explicate destimations, suggesting a movement through explicate space.
Two or more chemical units of the same type can be synordinate, and thus can appear in their explicate form simultaneaously at different explicate destinations (locations).
But each individual chemical unit itself consists of a series of asynordinate subunits, of which never more than one can become explicate at the same time, also not at different explicate positions, i.e. at different explicate destinations. The asynordination of the subunits is, however, such that the involved different implication parameters (indicating the degree of implication) of the subunits form an ordered series of increasing or decreasing degree of implication. All this guarantees that when a given chemical unit (or any intrinsic thing for that matter) is explicate, it is at the same time also implicate, thanks to all its subunits that have different degrees of implication. And in this way such an explicate chemical unit is always connected with the Whole.
For how long a chemical unit is visible (i.e. explicate) at one particular location depends on the number of asynordinate subunits taking part in the projection-injection dynamics.
When such a location turns out not to be the proper location for the chemical unit to be at, the subunits receive a different explicate destination. When that indeed happens, then no subunits will become explicate anymore at the original location. The explicate destination is now changed, and we now see the chemical unit at that new, generally slightly different, location.
When this location in turn is not proper in the given context, the asynordinate subunits once more receive a new explicate destination, etc., until, finally, the proper location has been attained. And then the number of subunits partaking in the process of projection and injection, and having the same explicate destination, will be large, resulting in the persistence of the chemical unit at that particular proper location.
In this context "proper place" or "proper location" in the Explicite Order, do not mean an absolute location according to some system of cosmic coordinates, but apply to proper surroundings. In this sense the same 'place' can be at successively different absolute locations in space.
The ink-in-glycerine model will help us visualize all this. Thus in the next eight Figures we first see a number of asynordinate subunits successively ending up at location A (Figures 12--15). Then the destination changes (from A) to location B (anticipated in Figure 15), and now the subunits successively end up at B (Figures 16--19) :

Figure 12.  The object (indicated by a black ball) is explicate(d) in virtue of the unfolding of a black thread at location A .  Just a moment before, it had been made explicate by the unfolding of a blue thread, which is now being enfolded back again into the Implicate Order. In the next moment the object will become represented by the unfolding of the red thread leaving the black thread implicate again (See next Figure). We imagine here that in this particular process of unfolding and enfolding no new objects are being created. The 'replacements' represent the same object, and this same object is non-locally and in an implicate way present in the Implicate Order, and locally present in the Explicate Order at location A.
The next images relate to what happens further during prolonged rotation of the outer cylinder.

Figure 13.  Now the red thread is contracted, resulting in its becoming explicate as a droplet at location A, while the previous droplet (black) has become implicate again and (in the model) present as a black thread in the glycerine. But, already the next thread (purple) is in the process of contracting.

Figure 14.  The purple thread has now become fully contracted and appears as droplet in the Explicate Order at location A, while the red droplet is again drawn out into a thread and is implicate again. But the green thread is already in the process of contracting and will soon become explicate.

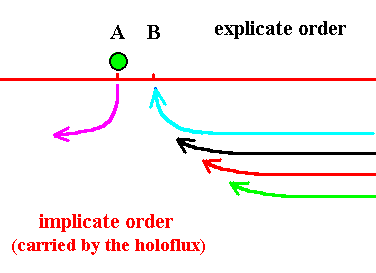
Figure 15.  The explicate destination of the blue thread (and of all the next threads) has changed. From now on the explicite destination has become location B.

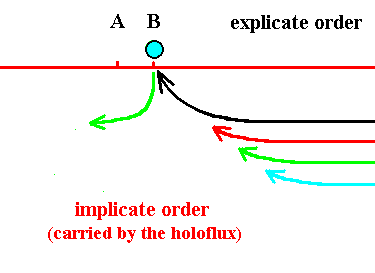
Figure 16.  The blue thread (asynordinate subunit) has become explicate (at location B), and the green has become implicate again. Soon the black thread will become explicate (at location B).

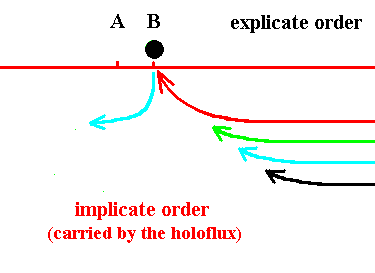
Figure 17.  The black thread (asynordinate subunit) has become explicate (at location B), and the blue has become implicate again. Soon the red thread will become explicate (at location B).

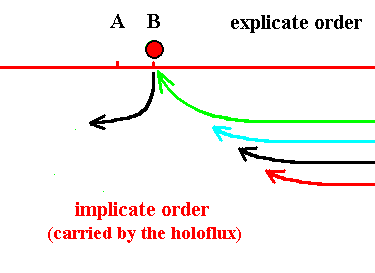
Figure 18.  The red thread (asynordinate subunit) has become explicate (at location B), and the black has become implicate again. Soon the green thread will become explicate (at location B).

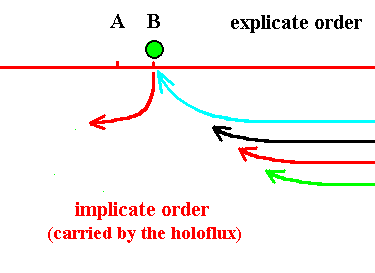
Figure 19.  The green thread (asynordinate subunit) has become explicate (at location B), and the red has become implicate again. Soon the blue thread .  .  .  .

So now we have described the 'movement' of some object, for example a chenical unit, from the explicate location A to the explicate location B, completely in terms of the ink-in-glycerine model. As is clear from the Figures, the chemical unit is in any case always and everywhere present in the Implicate Order, which means that, also when it is explicated, it keeps in contact with the Whole.
The implicate aspect that is guiding a particle must be seen as relatively autonomous subtotality.
In a quantum context we can consider such an implicate subtotality as a wave that governs a quantum experiment. It is like a radar beam directing an airoplane into position. This guide wave acts non-locally and is responsible for guiding the particles into their patterns, as for instance in the famous double slit experiment (where the electrons, when fired one at a time at the double slit screen, end up at the screen behind the latter, forming a pattern recognizable as an interference pattern). When combining BOHM's theory with the theory of SHELDRAKE, we could say that in a similar (or even identical) way the morphogenetic field guides either atoms, larger chemical units, or organic cells, into place, in order to form a structure or pattern. BOHM believes the guide wave (and hence the morphogenetic field) is actually a very 'subtle' form of energy. It is energy from the Implicate Order and so exists in the multidimensional reality beyond our three-dimensional space and time (An explicate object is a three dimensional projection (and thus unfoldment) from a multidimensional reality which is the Implicate Order). This implicate energy is subtle but, because it is multidimensional, it is powerful. The guide wave of implicate energy is a formative wave. It is a wave that forms things (i.e. gives them form and shape), like particle patterns. So it is a morphogenetic wave or 'cosmic memory'. This cosmic memory wave is a relatively autonomous subtotality in the Implicate Order.

e-mail : 

To continue click HERE for further study of the totally dynamic and holostic nature of Reality.

back to homepage

back to Introduction

****************