• Organisms are extremely complex entities, the general features of which are in many cases not well understood, or even mysterious, especially the complete chain of reactions that leads from (the instructions of) the DNA to the full phenotypical expression of the organism.
  
• When we would focus on organisms, and discussing the holistic theory along with them, we could spark off the impression that we wanted to introduce a fundamental line of division between the animate and inanimate worlds, by for example, saying, that organisms are holistic entities, while inanimate things are not. And that's precisely what we do not want to proclaim. According to the theory of the Implicate Order, all things, whether animate or inanimate, are holistic in nature, although there are things, especially in the inanimate world, that allow for an approximate description and explanation along reductionistic lines.

Crystals, their internal structure and symmetries, and their external symmetries, as well as their degree of individuality, are extensively treated in the First and Second Parts of our website :
In the First Part, accessible with  back to homepage, we discussed :

1. Their individuality in the document Crystals and Metaphysics in the Non-Classical Series of documents (Essays),
2. Whereas in the Special Series of documents we introduce the reader to the internal structure of crystals in the document The Structure of Crystals revisited.
3. The latter is followed by a large sequence of documents about the external (intrinsic) shape of crystals, where all the Crystal Systems and their Classes are being expounded.
4. And this is follwed by a preparation to the detailed study of the internal structure of crystals, done by considering (the more simple) imaginary two-dimensional crystals.

1. First we have given a general exposition of Group Theory, which, although covering a wide area of phenomena, is, in addition to those, the very theory on symmetry. In this general exposition we very often refer to crystals.
2. Then we proceed further with a symmetry theory of three-dimensional crystals, making extensively use of the concepts of Group Theory as we have expounded them.
3. This is followed by some additional documents on the thermodynamics of crystal growth, on twinned crystals, and some other topics related to crystals.

A growing crystal is in thermodynamic respect an equilibrium system. When the crystallization process has come to an end, the system is in thermodynamic equilibrium (This in contrast to organisms who remain always far from thermodynamic equilibrium, i.e. they constantly import energy and matter and export matter and entropy. This makes it possible for organisms to deliver work, which equilibrium systems can't.). A crystallization process begins when in a melt the temperature and pressure come into a certain range. In a solution crystallization begins when the concentration of the dissolved substance is supersaturated. Such a system of crystallization always means that the melt or solution have become unstable (because of lower tempratures, supersaturation, etc.). This means that the system tends spontaneously to reorganize itself such that the resulting configuration of constituents form a lowest-energy configuration. And such a configuration is then stable under the given conditions (of temperature etc.) : A certain definite crystal lattice will then be formed in which the constituents (atoms, ions, molecules) are being arranged in a periodic pattern.
More precisely, all this is supposed to go as follows :
We suppose the case of homogeneous nucleation, which means the emergence of a crystal, not onto an already existing crystal of a different sort (which is called heterogeneous nucleation), but in a melt or solution containing no crystals at all. With homogeneous nucleation, the growth of a mineral grain (or just any other crystalline substance) requires that the appropriate atoms and ions must find each other and then chemically bond to form what will become the nucleus of a crystal. The nucleus must then grow by progressively adding additional atoms / ions to its surface. In any chemical system, such as a melt or an aqueous solution, the atoms are constantly moving about, bumping into neighbors, and forming a variety of chemical combinations. It is generally assumed that some of these combinations, called embryos, will, by chance, have the composition and structure of a substance that could crystallize from the melt. Most of the embryos will be small, consisting of only a few atoms, but some will be larger. In general, the size distribution of embryos decreases exponentially with size. Whether these embryos will ultimately grow to form mineral grains depends on both the stability of the mineral and the size of the embryos. With respect to a melt, at a given temperature, the embryos must, for energetic reasons, have a certain minimum size already. When the size of such an embryo is below that minimum, further growth of it will increase its energy, causing the embryo to be unstable (Note that the embryo emerged by chance, as a fluctuation, which means it emerged, while in fact it shouldn't under the present circumstances). And then it will disintegrate again. At lower temperatures the minimum size of embryos can allowed to be smaller. Above this minimum size further growth (at that lower temperature) now causes the energy to decrease, and so the embryos are stable and continue to grow.
Let us analyse all this.
A first condition for the emergence of a crystal (in the case of homogeneous nucleation) is that there be some embryos in the first place, which means that, just by chance collisions of atoms, an incipient crystal lattice of a substance that can in principle crystallize from the given melt, is formed. We see that, in assuming this, one relies on pure chance for this to happen. And although this is not a priori impossible, this chance will not be so great, because the embryos must moreover be of sufficient size. The latter is the second condition -- and is itself dependent on temperature -- for the crystal to get started. The third condition (linked to the second) is that the energy of that crystalline substance is lower than that of the corresponding melt. Indeed, when these three conditions are not satisfied, the emergence of a macroscopic crystal is not possible at all. When, on the other hand, they are satisfied we have a potential crystal. But of course this potentiality must be converted into actuality, i.e. while the atoms can indeed go their way to form a crystal (i.e. they, as it were, received the green light to do so), they now must actually accomplish the further growth of the very small initial incipient crystal structure in accordance with the appropriate lattice, of which a small fragment had been already formed by chance. This further growth consists of the apposition of atoms onto the fragment. Generally, however, namely in complex crystals, it must be an apposition of complex structural chemical units (not just single atoms). These units must be formed and correctly aligned to the existing fragment in such a way that the overall lattice structure is conserved and extended. And even when this can in principle be accomplished, it is coupled with energetic problems, especially when starting a new layer on the crystal. This is because when a certain individual chemical unit starts to build up a new layer, it is sitting all alone on the previous layer, which implies that many of its chemical valences are left unsatisfied, which in turn implies a (locally) higher energy configuration. In fact it seems that in real crystals the growth proceeds on existing crystal defects, namely so-called screw dislocations, which have an effect of there being always a edge available for new chemical units to attach on. But even then there is still a -- but now somewhat mitigated -- energy problem.
All this should make it clear that the actual formation and further growth of the crystal lattice will not be easy to understand on the basis of local forces alone.
In order to apprehend this claim we must first state some general facts concerning crystallization.

We know that one and the same chemical substance can crystallize in several different ways, dependent on the thermodynamic condition.
For example the substance Calcium Carbonate, CaCO₃, can crystallize as the mineral Calcite in the Class 3* 2/m (In the crystallographic and mineralogical literature the asterisk is substituted for a score above the numeral to which it belongs, in our case, a score above the numeral 3, meaning a 3-fold roto-inversion axis.), of the Hexagonal Crystal system.
Its total symmetry (thus including translational symmetries as well) is according to the Space Group R3* 2/c (or, for short, R3*c).
But Calcium Carbonate can -- under other thermodynamic conditions -- also crystallize as the mineral Aragonite in the Class 2/m 2/m 2/m of the Orthorhombic Crystal System.
Its total symmetry is then according to the Space Group P 2₁ / n  2₁ / m  2₁ / a  (or, for short, Pnma).
This means that the constituents of Calcium Carbonate do not have only one possible way to combine chemically in a crystal lattice, but several.

In the same way we see that the substance Aluminum Silicate, Al₂SiO₅, can come about in three mineral phases, namely :

• Sillimanite, crystallizing in the Class 2/m 2/m 2/m of the Orthorhombic Crystal System, while its total symmetry is according to the Space Group P 2₁ / n  2₁ / m  2₁ / a  (or, for short, Pnma).
• Kyanite, crystallizing in the Class 1* of the Triclinic Crystal System, while its total symmetry is according to the Space Group P1*.
• Andalusite, crystallizing in the Class 2/m 2/m 2/m of the Orthorhombic Crystal System, while its total symmetry is according to the Space Group P 2₁ / n  2₁ / n  2 / m  (or, for short, Pnnm).

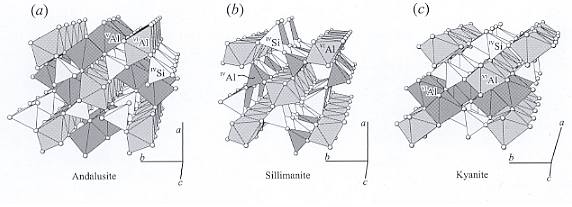
Figure 1.  Structure of the Aluminum Silicates, Al₂SiO₅ .
(a) Andalusite.  (b) Sillimanite.  (c) Kyanite.
(After NESSE, W., 2000, Introduction to Mineralogy)

When the solution or a melt of a certain chemical substance becomes unstable, crystallization will eventually set in. The system must go into a lowest-energy configuration. In such a (chemical) system, the different possible arrangements of atoms (or atomic clusters of bonded atoms) have different potential energies owing to the electrical and other interactions between them. As has been said earlier, the system will spontaneously tend to take up the structure with the minimal potential energy (minimal, under the given thermodynamic conditions). In a simple system, with only a few possible alternative structures, one may have a distinctly lower energy than the others. It 'falls' in the lowest 'energy well'. In addition to this, there are often some less stable possibilities, represented by local minima (higher up) on the side of the well (See Figure 1a (A) below). In systems of increasing complexity -- for example, involving complex minerals like Augite, (Ca, Na)(Mg, Fe, Al)(Si, Al)₂O₆), crystallizing in the Class 2/m of the Monoclinic Crystal System, with a total symmetry according to the Space Group C 2 / c -- the number of possible structures increases. As it does so, the chance of there being a unique minimum-energy structure seems likely to diminish. Then we can have situations that several different structures would be equally stable from an energetic point of view, under the same circumstances (thermodynamic conditions)(See next Figure (D)). (Note, that the situation described here is different from the above examples, because there the different structures correspond to different thermodynamic conditions.).

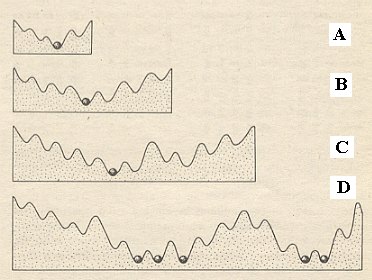
Figure 1a.  A diagrammatic representation of the possible structures of systems of increasing complexity. In A there is a unique minimum-energy structure, but in D several possible structures are equally stable.
(After SHELDRAKE, 1987.)

When a crystal is growing in a supersaturated solution it will grow on all its faces, at rates corresponding to the atomic aspects presented to the growing environment by the faces of the given crystal. But the act of growth, withdrawing material from the solution, sets up a density current, which climbs up the side of the crystal. As it climbs (Low density patches are going up, because their density is lower), it loses still more material to the crystal, and soon the solution bathing the crystal has a lower degree of supersaturation near the top of the crystal than at the bottom. The growth rates on faces near the top become less than the rates on corresponding faces at the bottom, and when a steady state of current flow has been established, the new growth rates effect that corresponding faces will not have corresponding sizes anymore.
Well, we could ask, if the growth rate varies with the degree of supersaturation, and the degree of supersaturation varies from top to bottom of a single face, how can all parts of that face continue to grow outward at the same rate? In fact, it is extraordinary how well the various parts of a face seem to keep track of one another and succeed in arriving at compromises. But, they cannot be pushed too far. As a face grows larger, it has increasing difficulty letting its left hand know what its right hand is doing, because they are farther apart. Moreover, there is room for larger differences in the degree of supersaturation between its parts (HOLDEN & MORRISON, (1960), 1982, Crystals and Crystal Growing,  p. 129/130).
Also here, i.e. in the case of the growing of single faces, there is, as long as such a face is not too large, a certain cooperation at work resulting in an evenly developed face.

The "hopper growth" is a spectacular result of a variation of growing conditions over the parts of a crystal face. The schematic diagrams in the next Figure will help you to see what has happened.

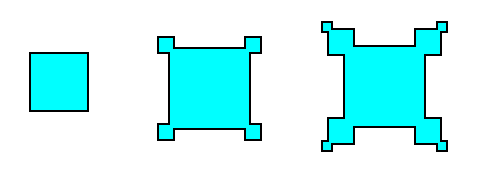
Figure 1b.  Idealization of hopper growth.
Faster growth at corners and edges than on faces can be self-perpetuating when it partly shields the center of the face from a fresh supply of dissolved material.

One of the most spectacular phenomena in crystals that clearly show that (long-range) cooperation must be at work, are the structural transformations, that many crystal species can undergo in the solid state, when the thermodynamic conditions change. The following example was already given earlier in the previous document, but for the sake of completeness and because of its importance, we give it again :
There are many solids (crystals) whose atoms can adopt more than one kind of orderliness. In such solids, one orderliness is usually more stable above some definite temperature, another below it. As the solid (in the form of a crystal) is heated through that temperature, the crystal structure may change abruptly from one form to the other (HOLDEN & MORRISON, p. 219). So some crystal species can undergo a spontaneous transformation while they remain in a solid state. A beautiful example of this can be observed in Mercuric Iodide. It is especially spectacular because the change of crystal structure brings with it a change in color from red to yellow. The red tetragonal form, stable at room temperature, changes to a yellow form belonging to the Orthorhombic Crystal System as the temperature rises through 126⁰ centigrade. On cooling, the yellow form transforms more slowly back to the red. HOLDEN & MORRISON, 1982, Crystals and Crystal Growing, p. 221, remark the follwing about this crystal transformation :

"When we visualize what the atoms must do to accomplish a structural transformation of a solid, it seems even clearer than in visualizing melting that co-operative action of the atoms might be necessary. In the structural transformation the atoms must not only move, they must move to the new 'right places'. Since the locations of its neighbors determine what is the right place for an atom, the atoms must feel one another out quite extensively in the course of the transformation."

We're now going to speculate about the possible nature of the formative fields or implicate (generative) orders, that 'guide' the particles (atoms, ions, molecules) such that they can quickly realize their minimum-energy configuration in the form of an incipient crystal lattice.
In fact we cannot say anything specific about the physical nature of such formative fields, beyond the fact that they are implicate structures possessing very little energy, and can apply active information to direct explicate structures in their behavior, by means of some sort of resonance.
About the formal content we can speculate a little more. This content must be something like a network of principles, principles, that can be activated by one or another event in the Explicate Order. For such explicate objects like  c r y s t a l s  we could postulate a generative order containing principles of lattice symmetries. In mathematical terms we could say that this particular generative order (as one among the many orders) contains the principles of Group Theory especially those of the various Symmetry Groups.
Group Theory is very fundamental, in the sense that it describes universal and basic mathematical structures, that are in all respects objective, so that one can (and does) investigate them, for example as to how many basic types of Groups there actually are.

A Group is a set of abstract elements for which one operation is defined to combine them. Such combinations of elements must, however, always result in one of the elements of the mentioned set. We say that the set must be closed under the group operation.
Further, an identity element must be present, so that a*1 = a, for all elements a of the set (where 1 is the identity element, and * is the group operation).
Also the inverse of every element of the set must be present in that set, so that the following holds :  a*a^-1 = 1 (where a^-1 is the inverse of a ).
Finally, the operation must be associative, which means that for any triple of elements a, b and c the following holds :  (a*b)*c = a*(b*c) for all elements a, b, c of the set.

When these conditions are met, the set is structured. And the specific way it is structured causes the set to be a Group, and the elements of this set can now be called group elements.
These group elements can remain abstract, which means that their only meaning lies in the way they combine according to the given group operation.
If, however, the group elements are symmetry transformations -- and the group operation consists in the successive application of two such symmetry transformations -- then we have a symmetry group.
A  s y m m e t r y   t r a n s f o r m a t i o n  with respect to a given object is a rigid transformation of the object (i.e. a transformation such that the object is not deformed), such that after thus being transformed, the object occupies the same patch of space as it did before it was transformed. For example, if we take an equilateral triangle, and rotate it 120⁰ about its center, then the triangle will occupy the same patch of space as it did before it was so rotated.
Such symmetry transformations (being the group elements of a given symmetry group) can thus be rotations, roto-inversions, reflections, inversions, and -- when we have to do with infinite patterns -- translations, glide reflections and screw rotations. The set of such transformations that let the object occupy the same patch of space as before (i.e. let the object be covered onto itself) defines the symmetry of that object, and has the (algebraic) structure of a Group.
A  s y m m e t r y   e l e m e n t  is a point, a line or a plane to which the given symmetry transformation refers, i.e. with respect to which the symmetry transformation is defined. So symmetry elements are :  rotation axes, mirror lines, mirror planes, glide lines, glide planes, inversion points, etc.
So if we have, say, a three-fold rotation axis (expressing a three-fold symmetry of some object), then this means that we have one symmetry element, namely that rotation axis, and that we have three symmetry transformations (i.e. three group elements of the relevant symmetry group), namely a rotation of 0⁰ about that axis (This zero rotation can figure as identity element in the relevant symmetry group), a rotation of 120⁰ about that axis, and finally, a rotation of 240⁰ about that same axis.

There are finite and infinite symmetry groups, depending on the number of group elements (and that is here the number of different symmetry transformations that figure in the given group).

In order to grasp what follows, the reader should consult the documents on two-dimensional crystals in the First Part of this website, and the documents on Group Theory in the Second Part of the website. See the following links :
First Part of Website.
Second Part of Website

A point symmetry (i.e. the point symmetry of a given object) is a set of symmetry transformations, which are such that at least one point is not moved by any such transformation. The Group that is formed by a set of such symmetry transformations is called a point group.
If, on the other hand, we have a group with group elements such that among these elements (symmetry transformations), there is at least one that moves all points of the object to another place, then we have a Plane Group (for two-dimensional patterns), or a Space Group (for three-dimensional patterns).
One may wander how a rigid transformation that moves all points of an object, can be such that the object still occupies the same patch of space after it has been subjected to such a transformation. Well this is possible only for homogeneous infinite objects, or, when such an object is not fully homogeneous, for an infinite periodic object.
Although  c r y s t a l s  are not infinite objects, they can nevertheless be considered as infinite, because from a microscopic perspective they contain an almost unlimited number of microscopically small translations (distance of lattice points), so that a shift according to one such translation leaves the crystal virtually in the same patch of space as it was before being shifted (over such microscopic distance).
These translational symmetries (simple translations, in contrast to glide reflections and screw axes) of a crystal define a lattice. A crystal lattice is an imaginary set of equivalent points ("equivalent" here means that every point has the same kind of surroundings :  The lattice looks exactly the same from one such point or from any other such point). These points we call nodes.
Each node can now be associated with a certain motif (generally consisting of motif units, and representing in our case chemical units). This associated motif must be the same everywhere in order to preserve the equivalence of the nodes. When indeed a lattice is thus provided with motifs (motifs having a symmetry that is compatible with that of the lattice), we have a Plane Group (two dimensions) or a Space Group (three dimensions), because we can then indicate the motif units as relating to each other by rigid transformations of the whole pattern, and all these transformations leave that whole pattern occupying the same patch of space as it did before, so these transformations are symmetry transformations and together form a Group in which they figure as group elements.

In order to speculate on the formative field insofar as the individual developement of  c r y s t a l s  is concerned, let us first of all confine ourselves to imaginary two-dimensional crystals, because their symmetries are easier to visualize. Let us begin with those two-dimensional crystals that have a total symmetry content according to the Plane Group P4. We can visualize the internal structure of the crystal as an infinite set of motifs (representing chemical units), motifs, that are repeated according to a square point lattice (net). This Square Net can accommodate for a motif, having a point symmetry 4, and representing the Class 4 of the 2-D Tetragonal Crystal System. See nextFigure.

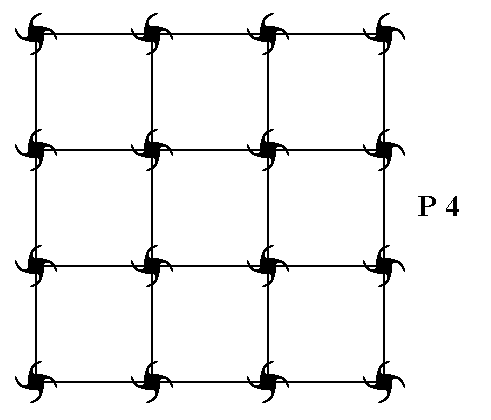
Figure 2.  A periodic pattern of motifs based on a 2-D square lattice (net). This particular pattern represents the Plane Group P4. It must be imagined to extend indefinitely over the 2-D plane.

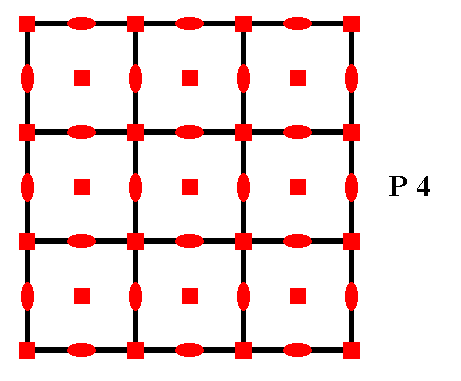
Figure 3.  The total symmetry content of any pattern representing Plane Group P4. There are neither mirror lines, nor glide lines present.
Small solid squares indicate 4-fold rotation axes.
Small solid ellipses indicate 2-fold rotation axes.
The black line segments, connecting the nodes of the net, indicate horizontal and vertical simple translations.

In Figure 2 the motifs are depicted as black four-fold structures, but in fact also the proper surroundings belong to such a motif. Together (motif in the strict sense + proper surroundings) we will call it a motif s.l., i.e. a motif in the broad sense. The next Figure depicts one such motif s.l.

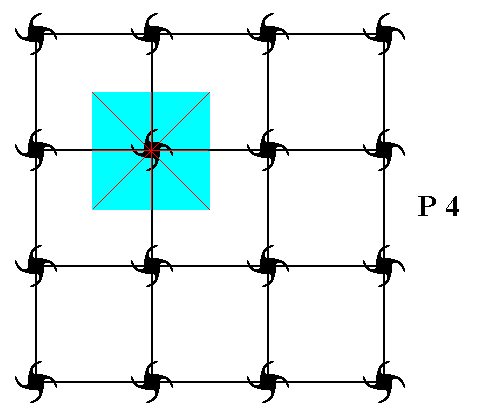
Figure 4.  A complete motif (motif s.l.) of the pattern of Figure 2.
( The auxiliary lines, drawn within the motif, do not belong to it.)

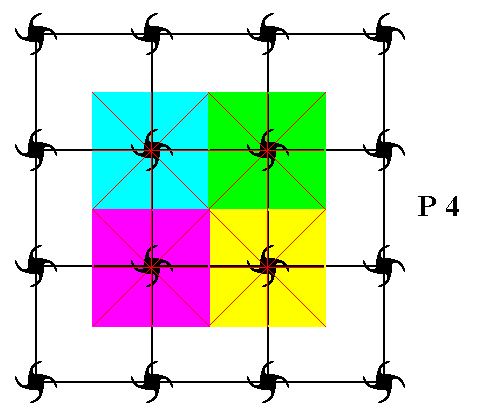
Figure 5.  The complete motifs (motif s.l.) of the pattern of Figure 2 fill up the whole plane as they are periodically repeated. Four such motifs are highlighted.
( The auxiliary lines, drawn within the motifs, do not belong to them.)

Figure 6.  The plane covered with complete motifs (motifs s.l.), which repeat periodically, and as such representing the Plane Group P4.
The red and blue motifs (s.l.) are considered to be totally equivalent.

Figure 7.  When we place four-fold motifs (in the present case motifs, each consisting of four partly overlapping commas) at the nodes of a square point lattice (square point net), we obtain a pattern according to the Plane Group  P4 .  A unit cell is indicated (light blue). The point  R  is the location of a four-fold rotation axis ( There are more such axes). The group element  p  is defined by an anticlockwise rotation of 90⁰  about the point  R , and is chosen as a generator of the group. A second generator is needed. We choose it to be the horizontal translation  t ,  which is a horizontal shift of the whole pattern to the right over a distance that is equal to that between two horizontally adjacent nodes of the lattice ( The pattern must be imagined to extend indefinitely over 2-D space). The inverse of this translation (which is, consequently, an equal shift to the left) is denoted by  t^-1 .
The group elements, and with it the whole pattern, can then be generated, by applying the symmetry transformations represented by the generators, over and over again, and starting with the initial motif unit 1 .

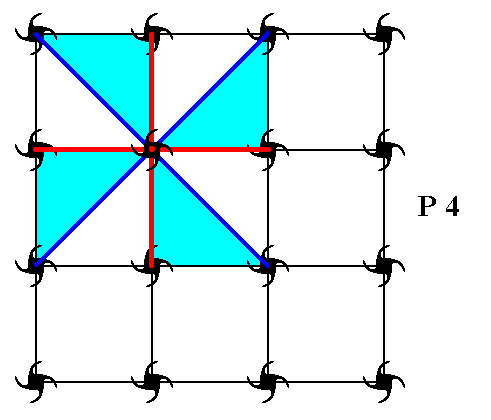
Figure 8.  This Figure shows the four-fold symmetry at the point  R ,  which means that the whole pattern returns as it was before (i.e. it will occupy the same space as it did before), after it has been anticlockwise rotated either by 90⁰, 180⁰, or 270⁰ about the point  R  (indicated in the previous Figure). The group element representing a 90⁰ rotation about this point  R  maps the initial element  1  (See previous Figure) onto the location that is denoted by  p  (See previous Figure), and, letting  p  represent the mentioned rotation, it is chosen as a generator of the group (in addition to this generator a second one is needed).  A 180⁰ rotation (about R ) of the initial element generates the group element  p²  (represented by the motif unit denoted as  p² )(See previous Figure),  while a 270⁰ rotation (about R ) generates the element  p³ (represented by the motif unit denoted as  p³ )(See previous Figure). Finally a 360⁰ rotation about R is equivalent to 0⁰ rotation, which means that we can say :  p⁴ = 1.
As the second generator we have chosen the translation  t  (See subscript of previous Figure).

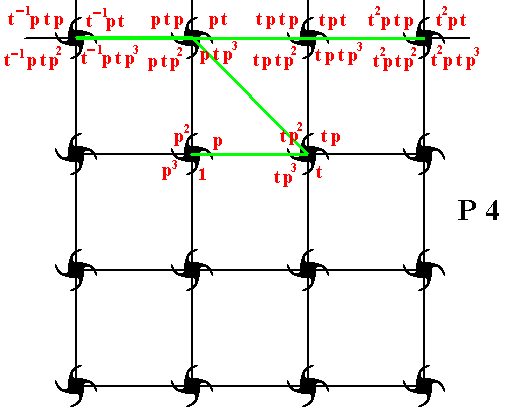
Figure 9.  Generation of five new motifs (each one is a composed motif, consisting of four motif units), from the initial motif (which also consists of four motif units :  the initial motif unit, and the motif units  p, p², p³ ). (Explanation is given directly below)

• The initial motif unit, denoted by  1 .
  
• The motif unit  p , formed as an image of  1  under anticlockwise rotation of 90⁰ about the point  R .
  
• The motif unit  p² , formed as an image of  1  under anticlockwise rotation of 180⁰ about the point  R .
  
• The motif unit  p³ , formed as an image of  1  under anticlockwise rotation of 270⁰ about the point  R .

Our intitial composed motif consists of the four motif units  1 ,  p ,  p²  and  p³ .  If we produce the coresponding images of these under the translation  t  (which is a shift to the right along a certain fixed distance), then we get respectively  t ,  tp ,  tp² ,  tp³ ,  which form a new composed motif to the right of the initial composed motif (See Figure 9).

We're now going to produce the image of this new composed motif under an anticlockwise rotation of 90⁰ about the point  R ,  i.e. we subject it to the transformation  p .  This means that
t  becomes  pt
tp  becomes  ptp
tp²  becomes  ptp²
tp³  becomes  ptp³

In this way we have obtained yet another new composed motif consisting of  pt ,  ptp ,  ptp² ,  ptp³ ,  which we can find as the second composed motif of the top row in Figure 9.

When we now subject this last found composed motif to successively the translations  t^-1 ,  t ,  and  t² ,  we get the following :

Application of  t^-1 :
pt  becomes  t^-1pt
ptp  becomes  t^-1ptp
ptp²  becomes  t^-1ptp²
ptp³  becomes  t^-1ptp³

An this yields yet another new composed motif, which we can see as the first one in the top row of Figure 9.

Application of  t :
pt  becomes  tpt
ptp  becomes  tptp  =   (tp)²
ptp²  becomes  tptp²
ptp³  becomes  tptp³

This yields the third composed motif in the top row of Figure 9.

Application of  t² :
pt  becomes  t²pt
ptp  becomes  t²ptp
ptp²  becomes  t²ptp²
ptp³  becomes  t²ptp³

And this yiels the fourth composed motif in the top row of Figure 9.
So we now have indeed generated five new composed motifs from the initial composed motif.
Next we shall generate still more composed motifs of our P4 pattern :

The third row of composed motifs can be generated along the same lines as we did it for the first row. The difference is that we now use an (anticlockwise) rotation (about the point  R (As it is denoted in Figure 7 )) by  270⁰  (instead of 90⁰) of the earlier obtained composed motif, the motif at the right of the initial composed motif. See next Figure.

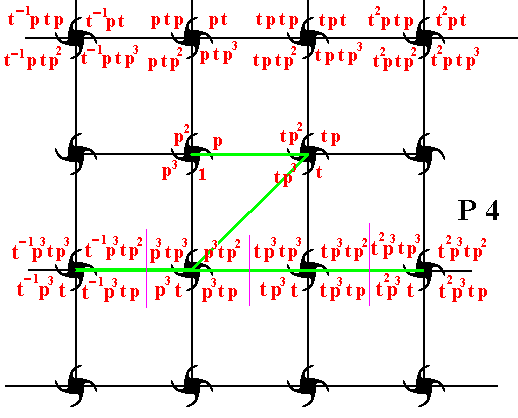
Figure 10.  To the composed motif to the right of the initial motif the transformation  p³  is applied, resulting in a new composed motif (second of the third row). From this new composed motif three other composed motifs are generated repectively by the transformations  t^-1 ,  t ,  t² .

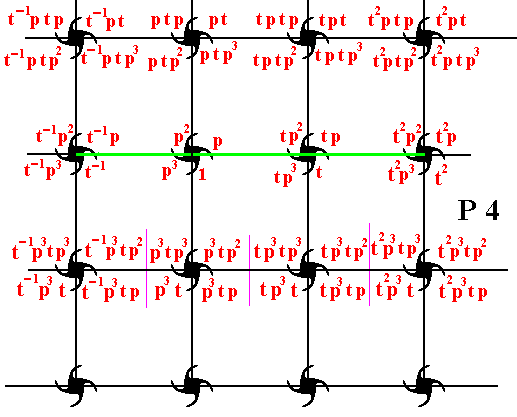
Figure 11.  Two more composed motifs of the second row are generated by the translations  t^-1  and  t² .

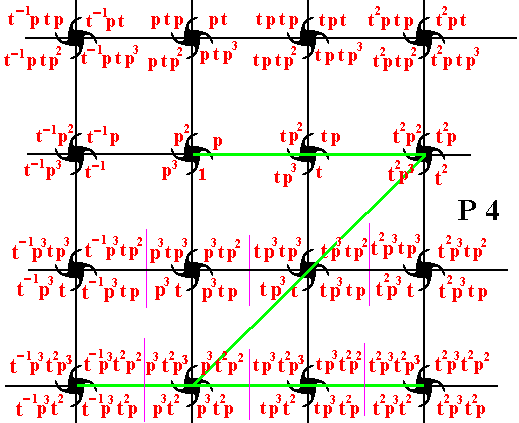
Figure 12.  The fourth row of composed motifs can be generated from the fourth composed motif of the second row, using the transformations  p³ ,  t^-1 ,  t  and  t² .

Figure 13.  Relationship of group elements with motifs s.l., in a periodic pattern, representing Plane Group P4. The red squares and the blue squares (both representing motifs s.l.) are totally equivalent. They are the motifs s.l. that are repeated according to the point lattice (which is a square net).

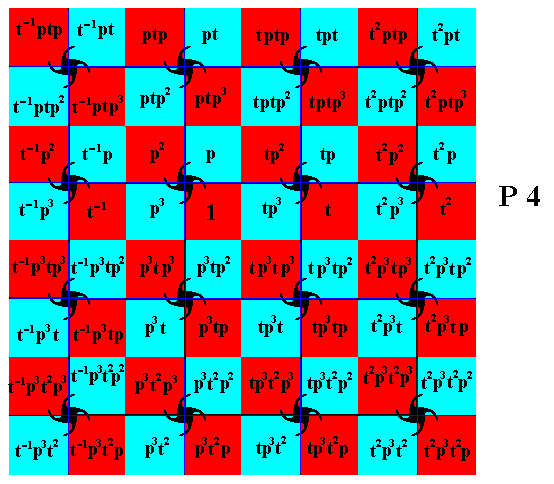
Figure 14.  The red and blue squares represent the group elements of the pattern according to the Plane Group P4.  The square marked by 1 is the bottom right quadrant of the corresponding motif s.l.  That quadrant is associated with the initial motif unit (comma), and represents the identity element of the Group. By subjecting it to the generators  p  and  t ,  and then continually applying those generators to the results, will produce the Group. However, because this Group is infinite, the process of generating new group elements will never end.

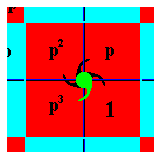
But of course a more abstract association of the group element 1 with the motif s.str. can be considered ( and the same for all other group elements):

Remark :
The rest of this document will adress the guiding process that directs chemical units to their proper places. This guiding process takes place just in virtue of the fact that all interactions take place via the Whole, forcing us -- as observer -- in some cases to speak of "cooperation between parts", i.e. to speak in a holistic fashion. Along the way we will speculate about the metaphysical form and status of these guiding agents, i.e. we will slowly built up some proposals -- maybe we'd better say, trials -- as to putting those guiding agents into a broader philosophical context. This is not an easy matter, because it turned out that we have to characterize these agents in many diverse ways (which is, by the way, typical for genuine philosophical concepts), for example as "quantum potential", "implicate order", "formative field", "active information", "generative order", "objective mathematical structure", "objective thought structure", "objective thinking dynamics" (the latter, of NOUS as it subject, the Second Hypostasis of the Neoplatonic metaphysics), etc. Because all this could become highly confusing, we have repeated (i.e. said the same, but shifted the context a little) some expositions about the guiding agents -- active in crystal formation -- in order to expose all this from several more or less different angles. We further must stress that the guiding activity as such is not very evident (i.e. does not reveal itself clearly to us) in the explicate order of crystals, i.e. it is not evident, because this guiding activity is apparently such as to allow a classical chemical description of crystal formation (i.e. with moving parts) to be a good approximation, except in cases of observed cooperation.
The hints to (parallels with) Neoplatonic metaphysics, will, in a later document, be more fully worked out. The meaning of what follows is to train ourselves to talk about such common a process like crystallization fully in terms of the theory of the Implicate Order.

In order to apprehend the following discussion about the crystallization process, we begin with stating succinctly the general conclusion, about how to visualize the crystallization process in terms of the Theory of the Implicate Order :

1. Because of supersaturation of a solution, or because of a decrease in temperature in a melt, the system of chemical units becomes unstable.

2. Quantum mechanics prescribes how a stable situation (stable arrangement of chemical units) must look like.

3. The potential field of the ordinary forces can now going to become actual, in virtue of the instability.

4. The ordinary (explicate) relatively strong forces, coming from, and acting on, the chemical units, are now being modulated by the much weaker, though more subtle, forces of the activated group theoretic formative field, resulting in the actual attainment of the stable end destination of the chemical units. This stable destination is the (periodic) arrangement of the chemical units according to the appropriate lattice, such that the symmetries, associated with the activated Group (as field aspect present in the Implicate Order), are satisfied.

5. The situation of point 4, is such that it demands to be described in a number of alternative ways, in order to fully express its subtlety and complexity.

6. In crystal formation, the action of the formative field is often such that it allows for a conventional chemical description to be a good approximation, except in observed cases of "cooperation".

7. Group Theory, at least insofar as it deals with the symmetry groups concerning the symmetries of three-dimensional crystals (and also the basic stereometric forms of organisms), can be seen as an aspect of the metaphysical generative order of those crystals (and organisms). It is at the same time an aspect of Nous (Objective Intelligence), the Second Hypostasis of the Neoplatonism of the Greek philosopher Plotinus (third century). And Nous can be identified with an aspect of, or the whole of, the Implicate Order(s). The latter is carried by the Holomovement as its modulation, and this undefinable and unmeasurable Holomovement can be identified with The One, being the First Hypostasis of the Neoplatonism of Plotinus.
   The One is the ultimate creative source of all there is.

Figure 15.  The total symmetry content of any pattern representing Plane Group P4. There are neither mirror lines, nor glide lines present.
Small solid squares indicate 4-fold rotation axes.
Small solid ellipses indicate 2-fold rotation axes.
The black line segments, connecting the nodes of the net, indicate horizontal and vertical simple translations.

Figure 16.  A periodic pattern of motifs based on a 2-D square lattice (net). This particular pattern represents the Plane Group P4. It must be imagined to extend indefinitely over the 2-D plane.

Figure 17.  The pattern of Figure 16, with (the distribution of) its symmetry elements indicated (according to Figure 15).

Figure 18.  The particular complexification of the motif s.l. , as shown here, is not possible, because the 4-fold rotation axes in the centers of the meshes are destroyed. Here it is show for the addition of a 3-fold motif unit in the center of each mesh of the net. This motif unit is incompatible with the 4-fold rotation axis which must be present (and preserved) in the center (and corners) of every mesh of the square net. As can be easily seen, the same impossibility applies to the insertion of 6-fold motif units.

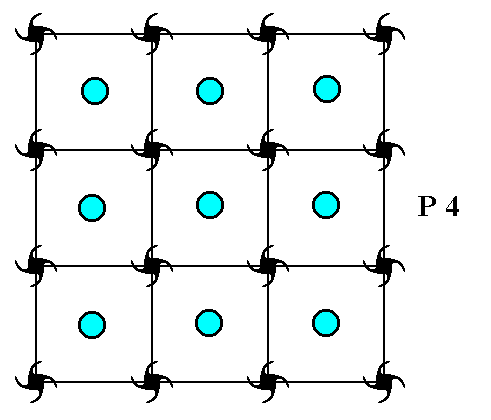
Figure 19.  Allowed complexification of the motifs s.l. of the pattern of Figure 16, by means of the insertion of additional motif units, having the form of circular discs (We have brought some structure into those discs by letting them be bounded by a black circumference, but that does not disturb the symmetries of a pure homogeneous disc).

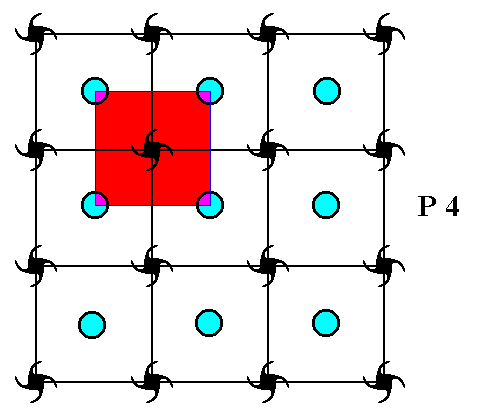
Figure 20.  Boundaries of one of the complexified motifs s.l. indicated. Such a motif consists of one 4-fold structure (black) and four quarter discs.

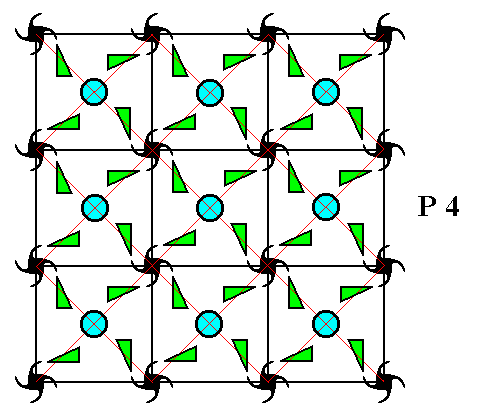
Figure 21.  The original motif s.l. is further complexified :  In addition to the previously added motif units, new asymmetric motif units (green) are being added, such that the symmetry distribution of the Plane Group P4 is preserved. ( The thin red auxiliary lines are not supposed to belong to the present pattern).

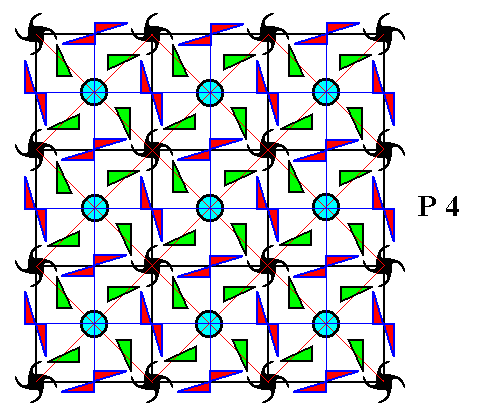
Figure 22.  Further complexification of the motifs s.l. by adding 2-fold motif units (red) at the proper places in the lattice, i.e. such that the P4 symmetry distribution will be preserved. ( The thin auxiliary red and blue lines do not belong to the pattern).

Figure 23.  Final result of the complexification of the original motifs s.l. (as in Figure 6), by addition of motif units, in such a way that the P4 symmetry distribution, as is required for all patterns of the Plane Group P4, is preserved.

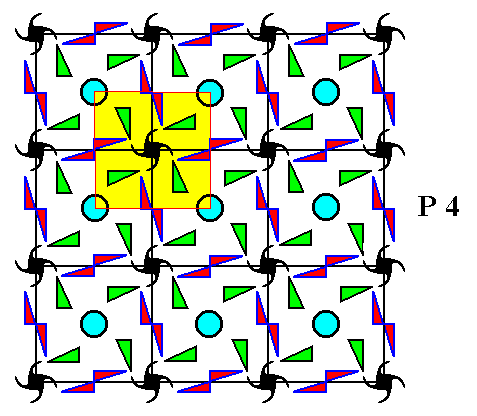
Figure 24.  The boundary of one of the new motifs is indicated, and this applies to all those motifs. So the pattern is now built up out of square motifs with a complex inner structure. These motifs are, as before, arranged according to the Square Point Lattice. The Plane Group to which this pattern belongs is still P4.

Figure 24a.  The boundary of the motif s.l. can be harmonized with those of the chemical motifs. Like with respect to the motif s.l. of Figure 24, the pattern can be built by periodically stacking these motifs s.l.  The motifs s.l. of the present Figure, cannot, however, be considered as consisting of four group elements.

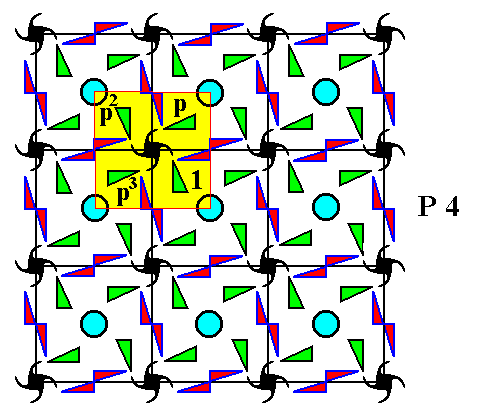
Figure 25.  Each (complexified) motif s.l. represents -- as before -- four group elements. In the highlighted motif these are :  1,  p,  p²,  p³ .See also Figure 13.

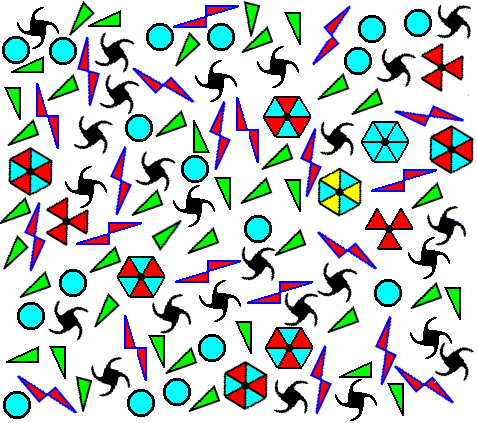
Figure 26.  Solution, containing chemical motifs. The solution is supposed to be about to crystallize for the compound consisting of the chemical units symbolized by
.
In addition to these units, some alien units are also present.

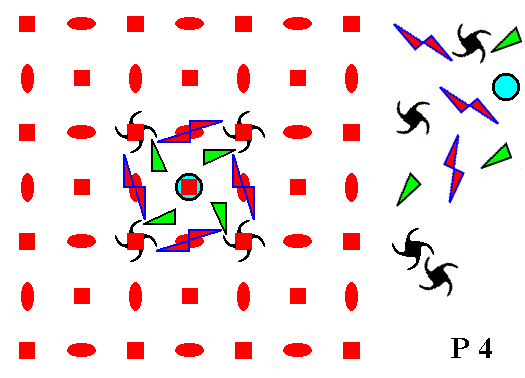
Figure 27.  Chemical motif units are being arranged by, and in accordance with, the P4-pattern of symmetry elements as an aspect of a (more general) generative field. Or, in other words, the relatively strong forces, present in the dynamical system of chemical motif units, are being modulated by the much weaker, though more subtle, forces of the group theoretical generative field, such that a thermodynamically stable situation is being attained, in about the same way that a ship can be guided by radar waves to be directed toward a certain destination.

In the context of the theory of the Implicate Order, movement, and in our case the movement of chemical units as they are arranging into a pattern, is an asynordinate structure, i.e. it is constituted of aspects with different degrees of implication. The time order is then just a derived feature, and not in general the primary one that is pertinent for the expression of law. Rather the whole Implicate Order is present at any moment. The law of structure will then just be a law relating aspects with various degrees of implication, and only that (i.e. the varying of the degree of implication) takes place in time, but that is a derived situation, because the explicate-implicate dynamics is itself derived, not primary. The explicate-implicate dynamics is not a movement, i.e. it is not a change of place, but a change of degree of implication. So the developing crystal, and with it the movement of the chemical units, is just an aspect relevated ('singled out') by our senses or instruments. The whole implicate order of the crystal is present at any moment, though for the larger part only implicitly, i.e. for the larger part the crystal is enfolded in its implicate order. Its explicate order is just an intersection of the implicate order of the whole crystal and an implicate order of distinctions that are relevated in sense perception.
All this becomes much more pronounced in a quantum context (i.e. at the quantum level), because on that level the discontinuity of movement (which is then in fact no movement at all) becomes significant. At the quantum level therefore, a description in terms of moving and interacting particles that are more or less autonomous, is not even an approximation to the real state of affairs.

Let us recap some findings, and add more details.
The movement of the chemical units to their proper locations in accordance with the pattern of symmetry elements of the given Symmetry Group, is in fact not a genuine movement at all, but a constant projection, followed by injection, of ensembles or subunits.
Two or more chemical units of the same type can be synordinate, and thus can appear in their explicate form simultaneaously at different explicate destinations (locations).
But each individual chemical unit itself consists of a series of asynordinate subunits, of which never more than one can become explicate at the same time, also not at different explicate positions, i.e. at different explicate destinations. The asynordination of the subunits is, however, such that the involved different implication parameters (indicating the degree of implication) of the subunits form an ordered series of increasing or decreasing degree of implication. All this guarantees that when a given chemical unit (or any intrinsic thing for that matter) is explicate, it is at the same time also implicate, thanks to all its subunits that have different degrees of implication. And in this way such an explicate chemical unit is always connected with the Whole.
For how long a chemical unit is visible (i.e. explicate) at one particular location depends on the number of asynordinate subunits taking part in the projection-injection dynamics.
When such a location turns out not to be the proper location for the chemical unit to be at, the subunits receive a different explicate destination. When that indeed happens, then no subunits will become explicate anymore at the original location. The explicate destination is now changed, and we now see the chemical unit at that new, generally slightly different, location (This is illustrated in the previous document).
When this location in turn is not proper in the given context, the asynordinate subunits once more receive a new explicate destination, etc., until, finally, the proper location has been attained. And then the number of subunits partaking in the process of projection and injection, and having the same explicate destination, will be large, resulting in the persistence of the chemical unit at that particular proper location.
In this context "proper place" or "proper location" in the Explicite Order, do not mean an absolute location according to some system of cosmic coordinates, but apply to proper surroundings. In this sense the same 'place' can be at successively different absolute locations in space.

To emphasize the different orders involved in the above described formation of the initial crystal lattice, we again go over the above account, and pay attention to the pattern of enfoldments and unfoldments.
In the emerging crystal lattice, emerging in virtue of the ordering of the chemical units into a thermodynamically and quantum mechanically suitable arrangement, the time order (about which we will say more further down),  t,  is primary when we consider all this in the Explicate Order. But when we give primacy to the Implicate Order, then the time order is secondary, because the whole Implicate Order, and thus also the whole crystal lattice under consideration, is present at any moment. So now we have to do with a different order that is primary, namely the order that expresses the different degrees of implications (as measured by the implication parameter T ) :
Those chemical units that have 'arrived' at their proper locations consist of many asynordinate subunits that either are soon becoming explicate (i.e. having already a low value of  T ), or are explicate (with T = 0), or are not explicate anymore (i.e. having also a low value of  T, which will, however, increase in due course). The chemical units that are still in the process of 'moving' to their proper locations, consist at any moment of relatively few asynordinate subunits that become successively explicate at a certain location (which is not yet the proper location). At a next moment the explicate destination changes to a location that is generally closer to a proper location, and again that chemical unit consists of relatively few subunits that successively end up at the new explicate location. And, as has been described above, this goes on, until a proper location has been reached.
So if we take the whole situation into account (which means that we consider the Implicate Order as fundamental), we continually have to do with the whole crystal lattice, that is present at any moment. It is represented by a pattern of entities finding themselves in different degrees of implication. And only this pattern changes in time (i.e. changes within the time order) :  The distribution of degrees of implication across that whole set of entities (chemical units and subunits) changes in time.
So in the Explicate Order we see the lattice actually emerging, piece by piece, while, seen in the Whole, it is already present in its entirety.
When, in the Explicate Order, the lattice is being formed, we have the following situation :  While the subunits of a chemical motif (chemical unit) are all asynordinate, the chemical units that are already in place in the lattice, are synordinate, and the law of structure will then, when seen from the perspective of the Whole, just be a law relating aspects with various degrees of implication, without giving any primary role to time.

To return to Group Theory, the pattern of symmetry elements, such as the one depicted in Figure 15, indeed defines the given Group. But this pattern must be conceived as wholly implicit. We should imagine it as an abstract set of rules as to how to realize the given Group in the Explicate Order.
And this image of directing the chemical units to their proper places, is totally equivalent to the generally more abstract notion of the generation of the Group, which here means the generation of all its group elements, by means of one or more generator elements, from some initial element, and, if needed, with the help of some defining relations. In our present case, namely with respect to the Plane Group P4, we could choose as generators (1) the element  p ,  representing a rotation of 90⁰ about some specified axis, and (2) the element  t ,  representing a horizontal translation. So we have two generators (which is sufficient).
The element  p²  is then  p  applied two times (and consequently a rotation of 180⁰), while  p³  is then  p  applied three times (and consequently a rotation of 270⁰). Finally  p⁴  is a rotation of 360⁰, which is group theoretically identical to no rotation at all, i.e. a rotation of 0⁰ (because in considering symmetry transformations, only the final result of such a transformation is what counts).
We now can generate the Group P4, with respect to its realization involving the above chemical units. As has been said, this generation of the Group must be seen as the same guiding process that we considered earlier with respect to the pattern of symmetry elements, determining the proper locations of the chemical units in order to obtain a lowest-energy arrangement. The guiding process expressed as the generation of the Group, is a bit more abstract, because generally the group elements (which are being generated) do not coincide with the involved chemical motifs, or motif units.

We begin by indicating an initial group element, represented by the corresponding chemical entities (Here the group elements are abstract, their boundaries do not necessarily coincide with the boundaries of chemical units or subunits).

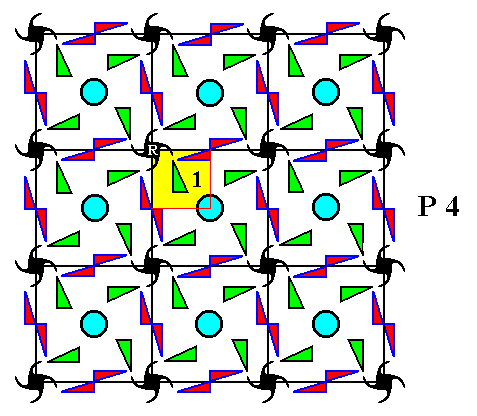
Figure 28.  We choose an initial group element (1) (representing the identity element), from which the other group elements can be generated by the generators  p  and  t . The element  p  is an anticlockwise rotation of 90⁰ about the point R , while the element  t  is a fixed horizontal translation.

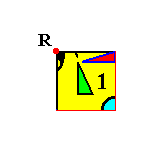
Figure 29.  The inital group element, chemically represented.

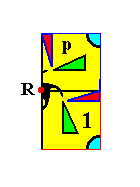
Figure 30.  Generation of the group element  p  from the initial element  1  by applying the symmetry transformation  p ,  which is an anticlockwise rotation of 90⁰ about the point R .

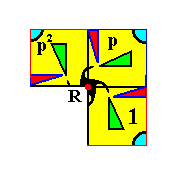
Figure 31.  Generation of the group element  p²  from the initial element  1  by two times applying the symmetry transformation  p  (to the initial element),  which is an anticlockwise rotation of 90⁰ about the point R .

Figure 32.  Generation of the group element  p³  from the initial element  1  by three times applying the symmetry transformation  p ,  which is an anticlockwise rotation of 90⁰ about the point R .

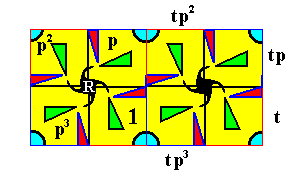
Figure 33.  Generation of the group elements  t,  tp,  tp²  and  tp³  from the elements  1,  p,  p²  and  p³  by applying the symmetry transformation  t ,  which is a horizontal translation.

So we have now described two equivalent ways of guiding the chemical units into their appropriate arrangement :  One by means of the pattern of symmetry elements, and another by the generation of chemically represented (though in a formal abstract way) group elements. The essence and origin of such guidance lies in the fact that the principles of symmetric arrangements are permanently (but in a dynamic way) present in the Implicate Order.
As we have done it with respect to imaginary two-dimensional crystals of the Plane Group P4, so it goes mutatis mutandis with crystals of the other Plane Groups, and, in a comparable way, with real crystals.

The implicate structures, for example the group theoretic structures, present in the Implicate Order, represent a common pool of information, with respect to the organizing of explicate entities, such as chemical units (which themselves are also organized in this way). As has been explained, chemical units can actually attain their lowest-energy arrangements, in this way, and form crystals, or other chemical entities, such as larger molecules (also a crystal can be seen as a large molecule consisting of units that are periodically repeated to result in macroscopic entities).
So in chemistry the properties of molecules and crystals critically depend on the corresponding pool of information which is enfolded in their wave function and which may extend into wider and wider contexts. Therefore, the Explicate Order cannot give a complete account of the emergence of new chemical properties and structures, just as it cannot account for the emergence of for example, superconductivity. This implies that the general goal of absolute reductionism is not feasable, if by this is meant the proposal that all properties of matter can be explained through explicate structures alone. This limitation arises because the generative and implicate orders are involved in an essential way, even at this rather elementary level of physics and chemistry.
It is known that there is a limit (i.e. a range) in which the contributions from the quantum potential (which is associated with the (first) Implicate Order) can be neglected. In this limit ordinary classical (Newtonian) motions provide a good description, which is as such reductionistic in character. On the whole they give a good approximation to the domain of common, large-scale experience (In terms of the ink-in-glycerine model, as decribed in the previous document :  If we do not zoom in, then we see the ink-droplet describe a continuous trajectory, and thus Newtonian mechanics (when not dealing with very high speeds or very strong gravitational fields) applies. But at close range (i.e. when we zoom in) the movement is seen to be discontinuous, which in fact is not a movement at all.). Nevertheless under special conditions, for example extremely low temperatures, the quantum potential may be significant even on the large scale. Superconductivity and superfluidity, for example, are large-scale manifestations of the effects of the quantum potential. More generally, this potential plays a significant role in many other ways. Without it, it would not be possible to account for the stability of atoms and the chemical properties of molecules that constitute bulk matter. Nor could many of the basic properties of solids, such as crystals and metals, be explained. In addition, the possibility must be kept open that in macromolecules, and in other contexts, certain properties, as yet unexplained (for example protein folding), may be very sensitive to the quantum potential. But, it must be emphasized, in spite of all this, that a suitable classical limit (range) does exist, in which explicate forms appear to dominate (especially in the areas of physics and chemistry). This explains why generative and implicate orders are not significant in the broad areas of experience in which classical physics is valid.
The causal interpretation of quantum mechanics (discussed in the first document) has been discussed as a particular way of describing the generative order in physics. But even if this particular theory is sooner or later replaced, the essential idea of the generative (implicate) order, which operates through various levels of information, will still be relevant. Indeed, in the present website (which is called Part Three) it is being suggested (following BOHM and PEAT) that such a generative order goes far beyond the quantum theory and is a key feature of the general notion of order that is relevant for understanding creativity, not only in objective Reality, reflected in theories proposed by science, but in all areas of (personal) life. (See BOHM and PEAT, 1987, Science, Order, and Creativity).

What has all this to say about the deeper nature of time (about which we already spoke above)? Science has, up to now, emphasized the sequential order of successive changes. In the larger scale this includes, for example the theory of evolution, and on a smaller scale also the crystallization process. In the generative order (as an aspect of the overall Implicate Order or orders), however, time is not put into the first place (Like it is also not put in the first place in the Neoplatonic Metaphysics of the ancient Greeks, of which we will speak in later documents). Rather, time has to be related in a fundamental way to the generative order. The image of a stream (a river) is helpful in this respect. The stream can be studied by following an object that floats along it, in a time process. However, it is also possible to consider the entire stream all at once, to reveal the overall generative order that goes downstream from the source or origin.
But the stream is only an image (as was used, for example by the early Greek philosopher Heraclitus, to emphasize the flowing and dynamic nature of Reality). The essential flow is not from one place to another but a movement within the implicate and superimplicate (generative) orders (and within what goes beyond them). At every moment, the totality of these orders is present and enfolded throughout all space so, just as with the successive enfoldments of the ink droplets, they all interpenetrate. The flux or flow is therefore between different stages and developments of these orders. However, because of the possibility of loops, this flow may go in a pair of opposite 'directions' together.
The temporal process of evolution of the universe is constantly generated within this flow from a 'source' or 'origin' that is infinitely far into the implicate and generative orders. To see the universe in this way is to see 'the whole stream at once' and this perception may be called timeless, in the sense that what is seen does not involve time in an essential way. However, the modes of generation and unfoldment in the stream imply that everything changes in successive moments in time. So in the flux described above, the timeless order and the time order enter into a fundamental relationship. However, because this relationship is now seen through the generative order, the time order appears very different from what it is in the traditional approach. It is not primarily a transformation within a given level of organization and explication. Rather it is, in the first place, a transformation of the entire 'stream' of the implicate and generative orders, that takes place from one 'moment' to the next.
This discussion (as we see it in BOHM and PEAT, ibid.) appears, at first sight, to reduce the time order so that it could, in principle, be derived completely from the timeless order. This would indeed be so, if the 'flow' in the implicate, generative stream were only in the 'direction' from the source or origin down to ever more explicate orders of succession. However, because of the two-way nature of this flow, there is an inherent dynamism in the theory and such a reduction is not actually possible (This two-way flow we also find, in a way, in the Neoplatonic doctrine of emanation, where everything at least strives to return again to "the One"). The timeless order and the temporal order therefore both make essential contributions to the overall order.
As has been said, all explicate processes, including crystallization, must be seen in this general context, involving timeless orders and their intermingling with temporal orders.

With respect to  c r y s t a l l i z a t i o n,  especially the emergence of the initial crystal lattice, representing the lowest-emergy arrangement of given chemical units, under certain (thermodynamic) conditions, we can say that a relevant patch of group theoretic structure -- which is an implicate structure, and an aspect of a larger more encompassing group theoretical structure -- is unfolding from the Implicate Order into the Explicate. The guidance of the chemical units into such an arrangement is the expression of the fact that this explicate incipient pattern of chemical units is not really separate from the implicate structure. They are different dimensions of the same thing. Or, in other words, the fact that we have to do with just one and the same thing (as relative autonomous subtotality) lets us describe it in terms of the cooperation of (explicate) parts :  In the Explicate Order it is cooperation, but in the context of the Whole (explicate and implicate orders, carried by the Holomovement) it is not. It is the unfolding of something that is already there, though in an implicit form, the chemical units as well as their possible symmetries. The latter in the form of certain group theoretical structures. And not only the latter, but the whole of Group Theory, i.e. all the possible Groups and their interrelations -- a number of which one has discovered and stated as theorems -- is present in the Implicate Order as one of its many aspects. As such this Group Theory is very general and abstract, and is the structure or substructure of many widely diverse entities, including many mathematical structures themselves. With respect to symmetry there are the Symmetry Groups. Only a part of these groups is relevant to (3-D)crystals, because the periodic structure of the latter excludes most symmetry groups, leaving only 32 Point Groups and 230 Space Groups.
Group Theory is about a certain type of general structures -- mathematically, algebraic structures -- that are objectively present somewhere. That they are not just inventions or mere methods, can be apprehended by the fact that it was possible to investigate how many different types of (finite) Groups there actually are :
The fundamental building blocks in Group Theory are the Simple Groups. By means of the method of 'telescoping', every finite group may be split into a unique set of simple groups in much the same way that a composite number is decomposed into its prime factors. Now one has investigated the classification of the finite simple groups. As a result it is now known that the finite simple groups consist of the groups which make up 18 regular, infinite families of groups (i.e. families with an infinite number of groups), together with 26 sporadic groups, and no more (This result took up 500 articles and almost 15000 pages in mathematical journals). (DEVLIN, 1988, Mathematics :  The New Golden Age).
From this it is evident that Group Theory describes abstract, but objectively existing fundamental structures. Where then, are these structures? According to me they exist in an implicit way in the Implicate Order as one of its many aspects. And some of these abstract structures play a role in the formation of (explicate) crystal lattices, as described above.

If we descend deeper and deeper (or, higher and higher, if one prefers) into the intermingled sequences of implicate generative orders, we will discover that we arrive at purely mathematical structures (such as the just discussed group theoretic structures), and these are nothing less than objective thought structures, i.e. we arrive at what Neoplatonists call the "hypostasis of Intelligence" (the Second Hypostasis). We must imagine this to be a logical sphere, consisting of the basic logical ingredients, basic logical units. These logical ingredients constantly combine, disconnect and rearrange, resulting in all kinds of more or less broader (mathematical) thought structures. The 'manipulation' of such logical units is thus a never ending timeless 'process', or dynamics, taking place in the Implicate Order, and which we could call 'cosmic thinking'. This ability of combining, integrating, disconnecting and reconnecting of logical units, has no limit with respect to the possible diversity of resulting thought structures, and this then is equivalent to creativity on the part of the Intelligence hypostasis (Nous). Ancient philosophy tells us the following about this 'thinking sphere' :
The Second Hypostasis (Intelligence, Nous) of the Neoplatonists (especially Plotinus, third century) originates from "the One" (which we can interpret as being the Holomovement, carrying all implicate orders). It is, while striving back to the One, halted by the One, and, through that being-halted, it obtains Being, which is Being itself. The essence of Nous (Intelligence) is the act of thinking, intuitive knowledge, contemplation. The thinking activity of Nous is the thinking of Being, i.e. of itself. Nous is what it contemplates and vice versa. The order of Thinking and the order of Being coincide in it. The Ideas, in which, by its thinking, Nous anatomizes Being, thus reside within it, and represent (and comprise), together with it, the one true reality (SASSEN, F., 1965, Geschiedenis van de Wijsbegeerte der Grieken en Romeinen (in Dutch)) (We will, in later documents, further elaborate on this theme).
Explicate states of affairs can trigger the activation of one or another such thought structure, resulting in an act of organization within the Explicate Order. When we see a sequence of genetically related organisms, i.e. a line of descent, we can describe it by an explicate process of evolution, involving the environment, the genes, the physiology and the behavior of the relevant organisms in the context of natural selection of viable mutants. But in fact this is just an approximation to what really happened when we put it in the context of the Whole. In that context we have to do with the fact that everything goes via the Implicate Order, where everything is one, in the sense that all entities are interpenetrated into each other. There we have to do with the mentioned combination, integration and disintegration of logical units and higher thought structures, that partially unfold into the Explicate Order when triggered to do so.
Thus to describe the formation of the given sequence of organisms, we do better to proceed along the lines of the 'rational idealistic morphologists' of the early nineteenth century (at least we should do that in addition to the conventional approach).

Because crystals do not have the tendency to evolve into higher and higher forms within the Explicate Order, and thus do not show lines of descent, a rational idealistic morphology is even more appropriate to them. This rational morphology will consist of certain relevant implications (results) of Group Theory, which itself is, or should be -- as a disciplin -- an aspect of a wider structural algebra.
Objective (i.e. as subsisting within the Implicate Order) group theoretic structures can be considered as one of the many products of the mentioned 'cosmic thinking' within the Implicate Order. In this cosmic thinking, complex Groups are 'derived' from less complex Groups, as a kind of rational process of 'hereditary' descent, itself a part -- i.e. an aspect -- of the grand timeless dynamics within the hypostasis of Intelligence.
When we ourselves do mathematics, we recreate -- or simulate -- those structures with our limited resources ( The human intelligence is a reflection from the thinking ability of Nous, and thus, like every other explicate entity, derived from, and an aspect of, the Whole).
Thus an incipient crystallization, or, better, the appearance of instability of a melt or solution, activates some group theoretic thought structures insofar as symmetry is concerned. The crystallization process will then go along relatively smooth lines, resulting in a full-fledged crystal, the internal pattern of which representing the lowest-energy arrangement of its chemical constituents under the given thermodynamic conditions. As has been said, this lowest-energy configuration (not its actual formation) is dictated by quantum mechanical laws.
A multiple repetition of this process (i.e. the formation of many such crystals, on many occasions) will, as a kind of feed-back, stabilize the relevant thought structures in Nous.

For the time being, this is all what we can say about the crystallization process in general --and illuminated with two-dimensional crystals belonging to the Plane Group P4 -- as seen in the context of the Theory of Wholeness and the Implicate Order.

e-mail : 

back to Introduction

back to the Ink-in-Glycerine Model