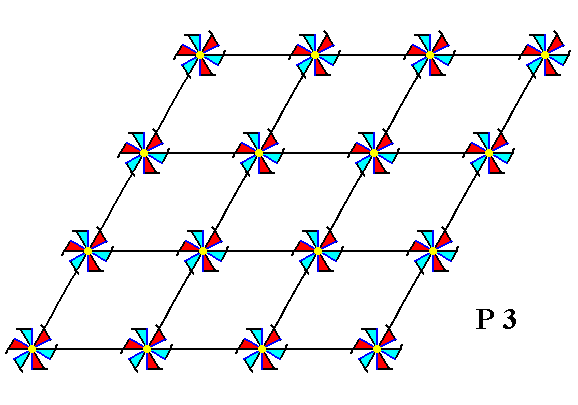
If we place motifs, having a point symmetry 3 (i.e. the only symmetry element each one of them has is a 3-fold rotation axis), in a hexagonal net, then we obtain a periodic pattern (of motifs) representing the Plane Group P3. See Figure 1.

Figure 1.  Arranging motifs with point symmetry 3 in a hexagonal 2-D lattice yields a pattern that represents Plane Group P3.
The symmetry of the motifs is indicated by their shape and by their coloration.  So these motifs have a three-fold symmetry, not a six-fold symmetry.

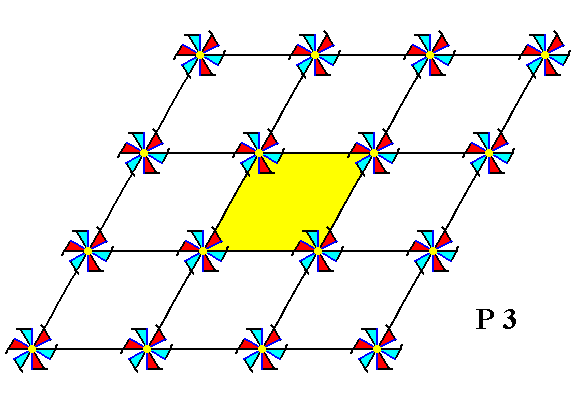
Figure 2.  A unit mesh is chosen (yellow), it is primitive and has point symmetry 1, i.e. it has no symmetry whatsoever. The sides of the unit mesh are equal in length, and include angles of 60⁰ and 120⁰.

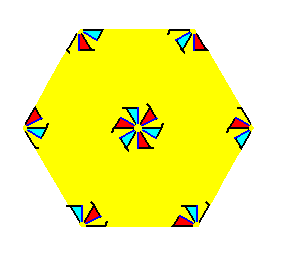
Figure 3.  Translation-free residue of the pattern of Figure 1. It represents the Point Group of the Plane Group P3.

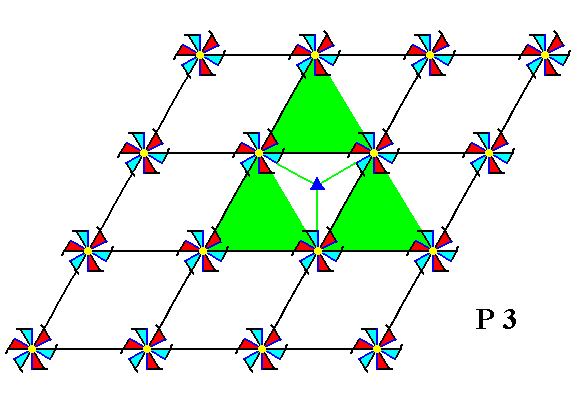
Figure 4.  A pattern representing Plane Group P3 has 3-fold rotation axes. One of them is shown (small blue solid triangle).

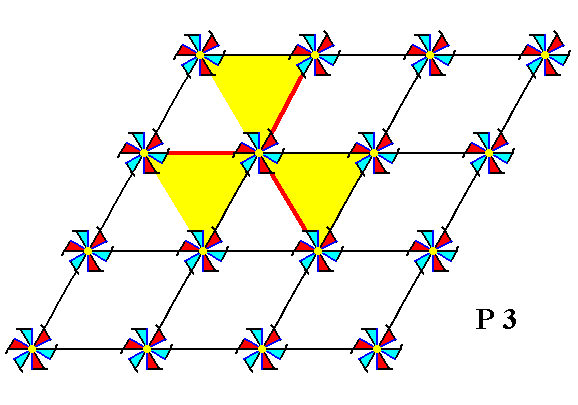
Figure 5.  A pattern representing Plane Group P3 has 3-fold rotation axes. One of them is indicated. It is situated at a node of the net.

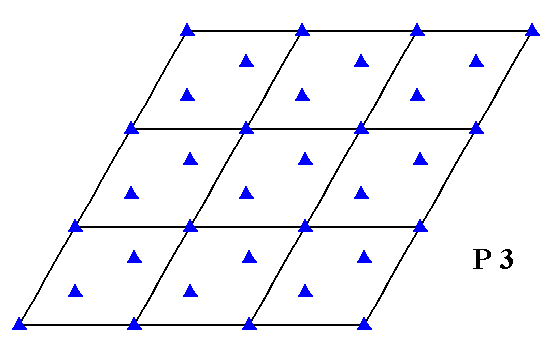
Figure 6.  Total symmetry content of the Plane Group P3.
There are no mirror lines and also no glide lines. The Plane Group only possesses 3-fold rotation axes.

Figure 7.  Arranging motifs with point symmetry 3 in a hexagonal 2-D lattice yields a pattern that represents Plane Group P3.  (We have here used somewhat different motifs than those used above, but with the same symmetry). The pattern must be conceived as to be indefinitely extended in two-dimensional space.
A unit cell (unit mesh), outlined by the hexagonal net, is indicated (light blue).
Each motif consists of three motif units. One such unit is considered as the initial motif unit, and is indicated by the numeral  1.
As generators, for building up this pattern, we choose a (horizontal) translation  t  and an anticlockwise rotation of 120⁰, denoted by  p  about the point  R .
So from the initial motif unit  1  (representing the identity element of the group) the motif unit  p  is generated (which represents the group element  p ).  And when -- on the initial motif unit -- the rotation  p  is twice applied, we get the motif unit  p²,  and with it the corresponding group element  p². Three times applying  p  yields the identity element, so  p³ = 1.
Wherever we have some (already generated) motif unit (representing a group element), we can generate a new motif unit (representing a new group element) by rotating it 120⁰ about the point  R .  Another new motif unit can be produced by shifting it according to the translation  t.  (See also Figure 8).

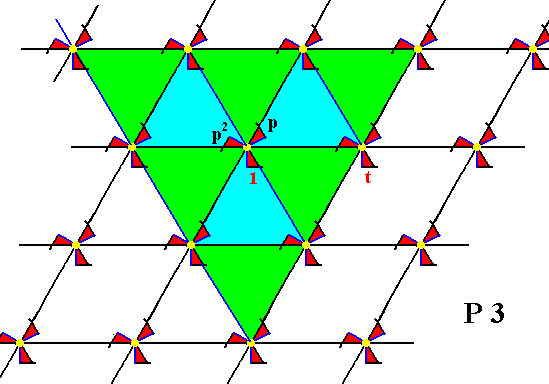
Figure 8.  This Figure shows the  tri-radiate  nature of the P3 pattern with respect to the point  R .  ( That point is explicitly indicated in the previous Figure). The whole pattern returns as it was before (i.e. occupies the same space as it did before), when we rotate it 120⁰ about  R .  The point  R  is not the only point with this property :  There are many such points.  But the rotation about the specific point  R  by 120⁰ anticlockwise, is chosen as a generator of the group. Any already existing motif unit (representing a group element) of the pattern yields a new motif unit (representing a new group element), when it is subjected to rotation of 120⁰ or of 240⁰ about the point  R .  In addition to this particular generator a second generator is needed, which is chosen to be a horizontal translation to the right (and implying also such a translation to the left). By this translation the motif units (representing group elements)  t^-1,  t ,  t²,  etc. are generated from the initial motif.

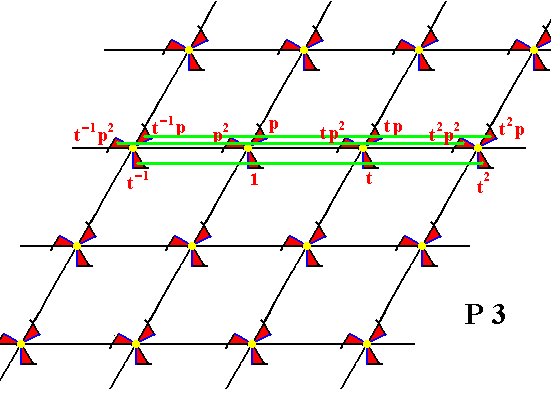
Figure 9. 
From the element  1  the elements  t^-1 , t,  t² ,  etc. are generated by the element  t .
From the element  1  is generated the element  p  by applying the transformation  p , which is an anticlockwise rotation by 120⁰ about the point R (indicated in Figure 7).
From the element  p  is generated the element  p²  by (again) applying  p .
From the element  p  are generated the elements  t^-1p ,  tp ,  t²p  , etc. by applying  t .
From the element  p²  are generated the elements  t^-1p² , tp² ,  t²p² ,  etc. by the element  t .

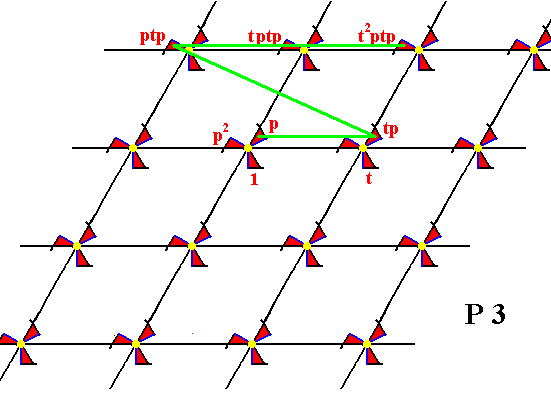
Figure 10. 
From the element  p  the element  tp  is generated by applying  t , and from  tp  the element  ptp  is generated by applying  p , i.e. an anticlockwise rotation of 120⁰ about the point  R  (as indicated in Figure 7).
From the element  ptp  the elements  tptp ,  t²ptp , etc. are generated by applying  t .

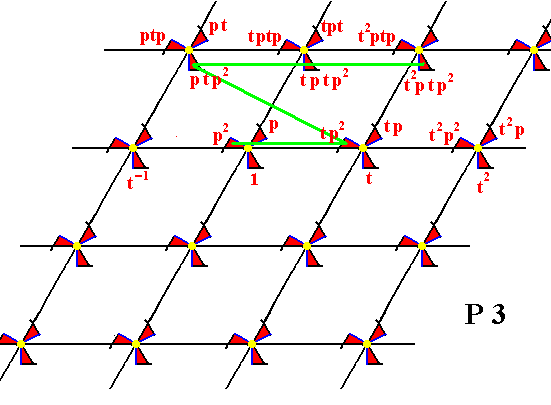
Figure 11. 
From the element  p²  the element  tp²  is generated by applying  t , and from  tp²  the element  ptp²  is generated by applying  p  (rotation of 120⁰ anticlockwise about R ), and from  ptp²  the elements  tptp² ,  t²ptp² , etc. are generated by  t .

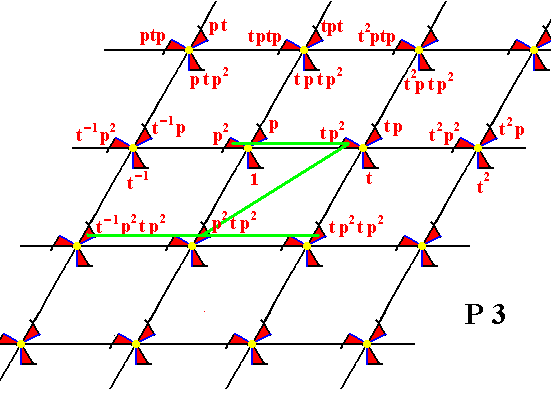
Figure 12. 
From the element  p²  the element  tp²  is generated by applying  t , and from the element  tp²  the element  p²tp²  is generated by applying  p²  (A rotation of 240⁰ anticlockwise about the point  R  (As given in Figure 7).
From   p²tp²  are generated the elements  t^-1p²tp² ,  tp²tp²  , etc. by applying  t .

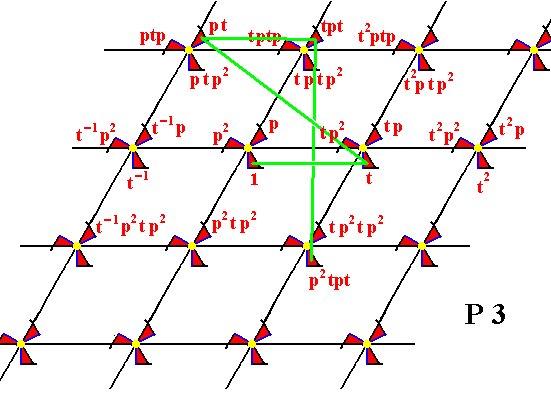
Figure 13. 
From the element  1  the element  t  is generated by applying the translation  t , and from the element  t  the element  pt  is generated by applying the rotation  p  about the point  R  (see Figure 7), and from the element  pt  the element  tpt  is generated by applying the translation  t . From the element  tpt  the element  p²tpt  is generated by applying the rotation  p²  (about the point  R ).

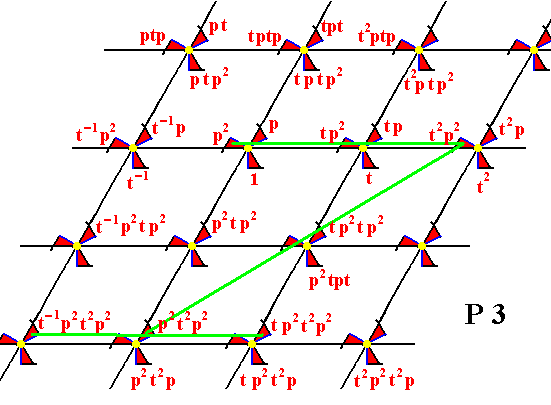
Figure 14. 
From the element  p²  the element  t²p²  is generated by applying the translation  t² , and from the element  t²p²  the element  p²t²p²  is generated by the rotation  p² .  And from the element  p²t²p²  the elements  t^-1p²t²p² ,  t p²t²p² , etc. are generated by applying the translation  t .

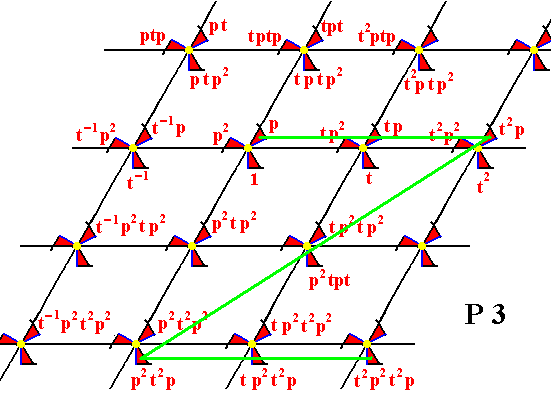
Figure 15. 
From the element  p  the element  t²p  is generated by applying the translation  t²  (i.e. applying the translation  t  two times), and from the element  t²p  the element  p²t²p  is generated by the rotation  p² .  And from the element  p²t²p  the elements  t p²t²p ,  t² p²t²p  , etc. are generated by applying the translation  t .

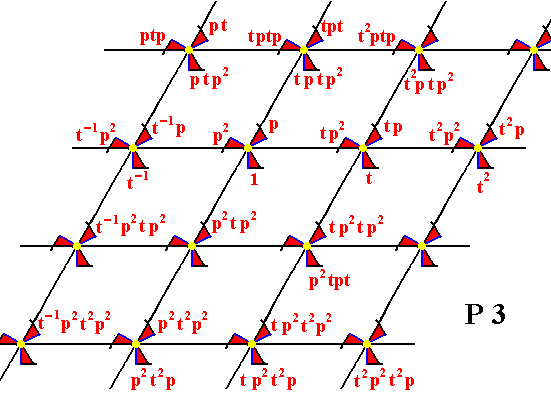
Figure 16.  The  P3  pattern, generated by the transformations  p  and  t .
( The pattern must be conceived as becoming to be extended indefinitely in 2-D space)

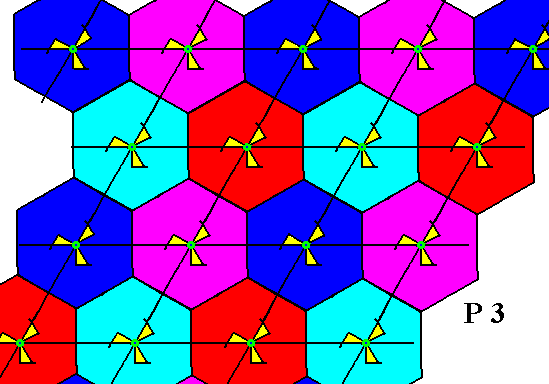
Figure 17.  Motifs s.l.  (colored hexagons) of the  P3  pattern of Figure 7.  They tile the plane in a periodic manner. The different colors do not signify qualitative differences. The pattern must be imagined to extend indefinitely over the plane.

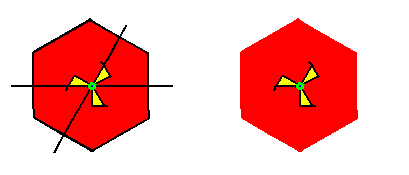
Figure 18.  Motif s.l.  isolated.
Left image :  Isolated motif s.l. with lattice lines and other auxiliary lines.
Right image :  Isolated motif s.l. without those lines.

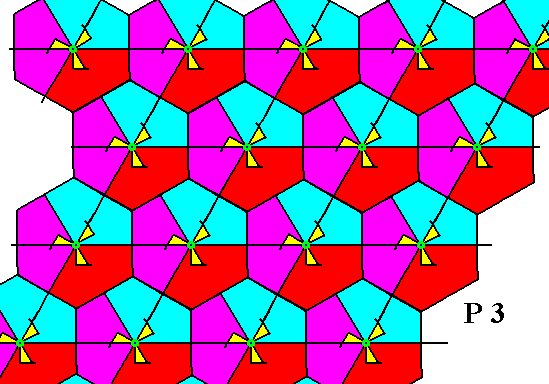
Figure 19.  Partition of the motifs  s.l.  and with it a partition of the  P3  pattern of Figure 7.  The resulting areas (each of them is one third of a hexagon) can represent group elements.
The different colors of the areas do not signify qualitative differences.

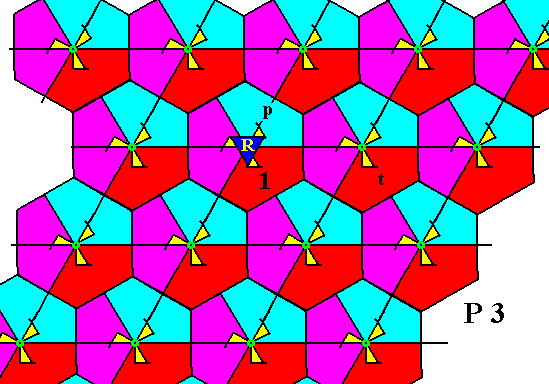
Figure 20.  The  P3  pattern of Figure 7 is partitioned into areas representing group elements (as was already the case in the previous Figure). Three group elements are explicitly indicated (i.e. specified), namely the initial element (initial motif unit s.l., identity element), and two generator elements.

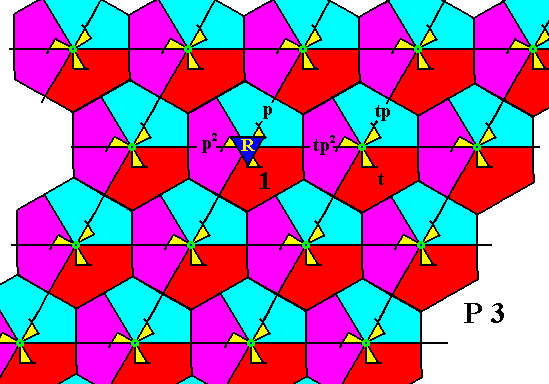
Figure 21.  Generation of the group elements  p²  and, by translation, the elements  tp  and  tp² .

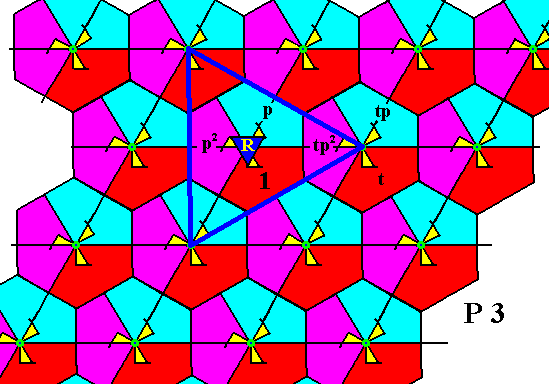
Figure 22.  Indication how new group elements can be generated by applying the rotations  p  and  p²  to the elements  t, tp, tp² .

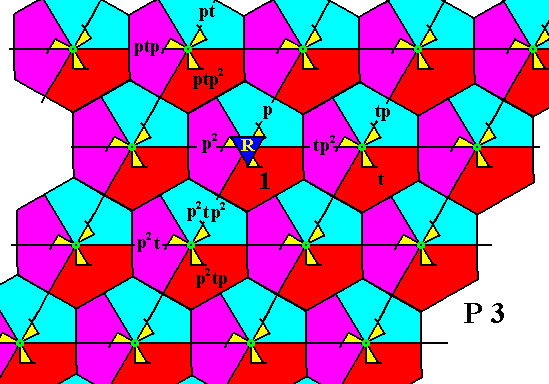
Figure 23.  Generation of new group elements by applying rotations about the point  R .

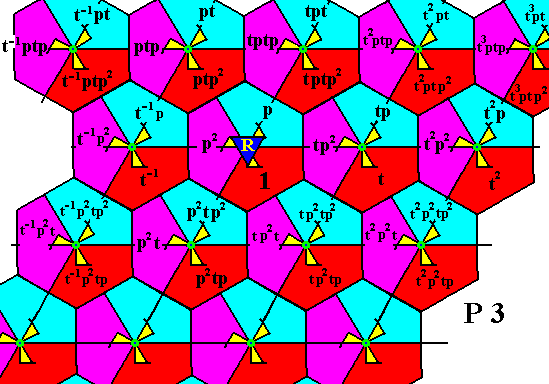
Figure 24.  Generating the rest of the group elements of the first three rows of motifs s.l.

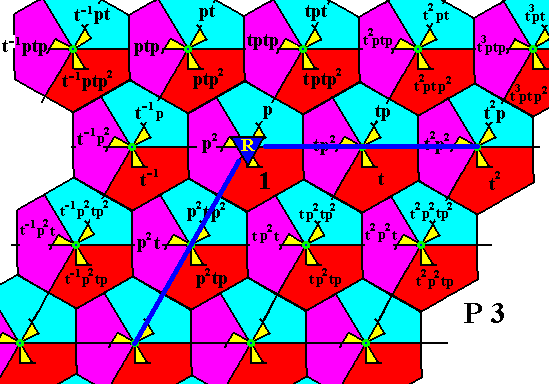
Figure 25.  Indication of the performance to be done to the group elements, i.e. to the motif units, of the last motif s.l. of the second row. This performance consists in applying the generator  p  two times to those motif units (s.l.), i.e. a rotation of 240⁰ anticlockwise about the point  R .

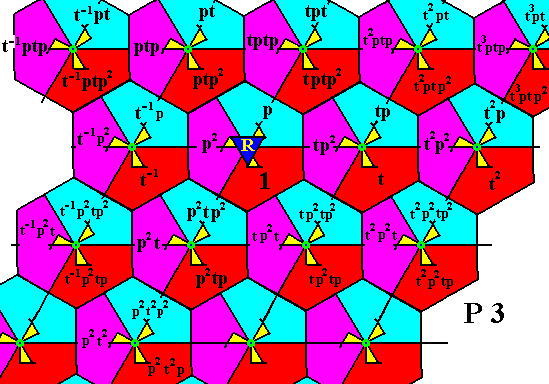
Figure 26.  Generation of some group elements of the fourth row of motifs s.l. of the pattern representing Plane Group  P3 .

Figure 27.  Completion of the fourth row of motifs s.l. by applying translations.

The origin and growing of a crystal -- which is here exemplified by means of imaginary two-dimensional crystals -- is the gradual explication of a structure that is already present in its entirety within the Implicate Order (Here we 'relevate' only one aspect of such a crystal, namely its internal symmetry. The same goes for the other aspects pertinent to the origin and growing of such a crystal). This process of explication -- which in direct perception we experience as the coming into being and growing of a crystal in a solution, vapor or melt -- can apparently only proceed along certain more or less definite lines, making it possible to state certain laws governing such a process, in our case certain crystallization laws. Indeed the ultimate laws of the Holomovement, carrying all implicate orders, is apparently such as to force such a specific order of explication. So the crystallization law apparently at work when we see a crystal emerge and grow is just an aspect of a much larger Whole, and is as such not a primary law as soon as we give primacy to the Implicate Order. When we give this primacy then we must consider the presence of the whole crystal at once, while its components -- seen just as aspects of the whole crystal -- form a pattern of different degrees of implication that changes in time. But the role of time is not primary, because the whole crystal is already present, albeit that certain components are still in an implicate condition. This implies a different description of structure, different from what is usually done in this respect. In this new description the structure of the (whole) crystal concerns the pattern of different degrees of implication at a certain moment. This degree of implication varies over the different components (aspects) of the crystal. This means that even when the crystal is only at the point of emerging, or is just very small, i.e. still a microscopic fragment, its description is about the whole crystal, i.e. the fully formed crystal. In this way the description is holistic. So if we describe an emerging crystal in the latter way, we are considering it in a broader context than just focussing on its explicate state. In the explicate state we consider operations like reflections rotations, translations, dilations, etc, which are one-to-one correspondences of points. We can denote these operations as transformations, and, more specifically as Euclidean transformations. These transformations describe lengths, angles, congruence, similarity, etc.  When, on the other hand, an aspect of, say, a crystal becomes implicate, i.e. when we compare the explicate state of that aspect with its corresponding implicate state, then we have to do with an altogether different operation, in which there is no one-to-one correspondence between points, and we will call such an operation a metamorphosis (We can obtain an idea of it -- in the sense of an analogy -- when thinking of the changes as we see them in holometabolic insects, for example the metamorphosis of a caterpillar into a butterfly, in which everything alters in a thorough going manner while some subtle and highly implicit features remain invariant. But, as has been said, this is only an analogy, because when we observe the changes in these insects in the usual way, i.e. remaining in the Explicate Order, then we can in principle observe a one-to-one correspondence between points in the caterpillar to points in the butterfly).
So explicate objects can be described by the above mentioned Euclidean transformations  E₁ ,  E₂ ,  E₃ .  . . . .  When such objects are subjected to a metamorphosis  M (which, as has been said, is a special operation) they become, in virtue of that, implicate. The resulting implicate structure, as such residing in, and according to, the Implicate Order, can in turn be described by operations that are appropriate to the (conditions of the) Implicate Order. The metamorphosis  M  effects the transform (in the group theoretical sense)  E'  of an Euclidean operator  E  according to the relation

resulting in a similar (but different) operation (E') (Because operations can together form algebraic structures like groups, we can use the above relation which expresses the 'tranformation of a transformation') . What the just mentioned similarity means is that if any two operations, say,  E₁  and  E₂ ,  are related in a certain way in the description of a specified structure, then there is a set of operations  E₁'  and  E₂' ,  describing non-local 'enfolded' operations that are related in a similar way :

The non-locality of the operations  E₁', E₂'  (as supposed by BOHM, Wholeness and the Implicate Order, 1988, Ark edition, p. 165) means that the relations between the 'parts' of the implicated object cannot be described by Euclidean operations, in which distances and the like play a role. And this way of implicatenes (i.e. its non-locality) fits well with the conjecture that implicate structures are immaterial objective thought structures (See below).
BOHM, 1988, (Op. cit.) suggests that the explicate and implicate conditions of something are equivalent to each other in the sense that they are implicate relative to each other (or explicate relative to each other), and so extending the principle of relativity with respect to coordinate systems corresponding to different velocities to implicate and explicate conditions. We cannot, however, agree with him on this point :  The implicate condition represents a different ontological status, different from the explicate condition. In the Implicate Order everything is enfolded into everything else, while this is not so in the Explicate order. The idea of (ordinary) space is a space constituted of a set of unique and well-defined points, related topologically by a set of neighborhoods and metrically by a definition of distance. This idea is (also according to BOHM) no longer adequate as an absolute and universal description. Indeed, each set of Euclidean operations  E  defines such a set of points, neigborhoods, measures, etc., which are explicate in an absolute sense (and not in a relative sense as BOHM proposes), while those defined by another (corresponding) set  E'  (related by E' = MEM^-1) are implicate in an absolute sense. So the notion of space as a set of points with a topology and a metric is thus merely (also according to BOHM) an aspect of a broader totality which includes explicate and implicate order.
In this way the emerging crystal must be seen as a totality including both explicate and implicate conditions, and in this way the whole crystal is present at any moment, which explains the cooperative phenomena observed in crystal growth.

Along Neoplatonic lines, the general state of implication, i.e. the state of something that is implicated (in a stronger or lesser degree), can be imagined as being an immaterial discursive thinking process taking place in Soul (i.e. the World-Soul), a process that we have imitated by our generation of group elements of the relevant symmetry Group. In Nous, the next higher metaphysical level with respect to Soul, this thinking is intuitive, i.e. without step by step derivation, and as such the relevant symmetry Group is present there all at once, and constitutes a genuine Idea in the Neoplatonic sense. While the several Ideas in Nous are distinguished from each other, in The One they are also present, it is true, but no longer as distinguished from each other, because The One is totally one. As has been said in previous documents, The One can be more or less equated with the Holomovement which carries all the implicate and generative orders. So an Idea is present in all the metaphysical levels (hypostases), but always in a way according to the conditions of the relevant hypostasis. And only the final explication, i.e. the emanation from Soul to Prime Matter (which is pure potentiality for receiving form), results in concrete separate structures as seen at that level, i.e. at the Explicate Order.

e-mail : 

back to Introduction

back to the Ink-in-Glycerine Model

back to Part I of The Crystallization process and the Implicate Order

back to Part II of The Crystallization process and the Implicate Order

back to Part III of The Crystallization process and the Implicate Order

back to Part IV of The Crystallization process and the Implicate Order

back to Part V of The Crystallization process and the Implicate Order

back to Part VI of The Crystallization process and the Implicate Order

back to Part VII of The Crystallization process and the Implicate Order

back to Part VIII of The Crystallization process and the Implicate Order

back to Part IX of The Crystallization process and the Implicate Order

back to Part X of The Crystallization process and the Implicate Order