We will now investigate the generation of the Plane Group P4mm, i.e. the generation of its group elements.
The Plane Group P4mm
Square Net
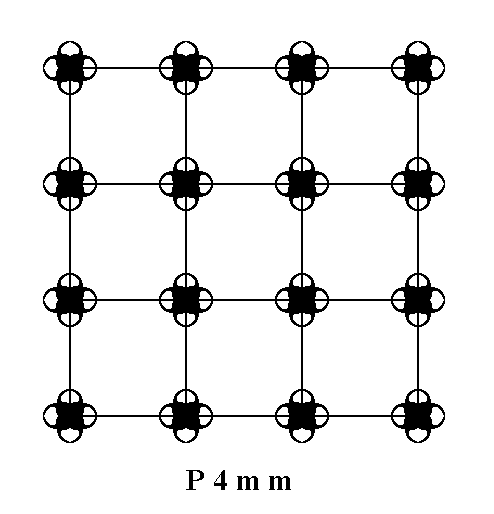
The Square Net (2-D Square Lattice) has point symmetry 4mm, so it does support 4-fold rotation and two types of mirror line. Consequently it surely can accommodate the insertion of a motif that has 4mm symmetry. This results in a periodic pattern that represents the Plane Group P4mm. See Figure 1.
Figure 1. Placing 2-D motifs with point symmetry 4mm into a square 2-D lattice yields a pattern that represents the Plane Group P4mm.
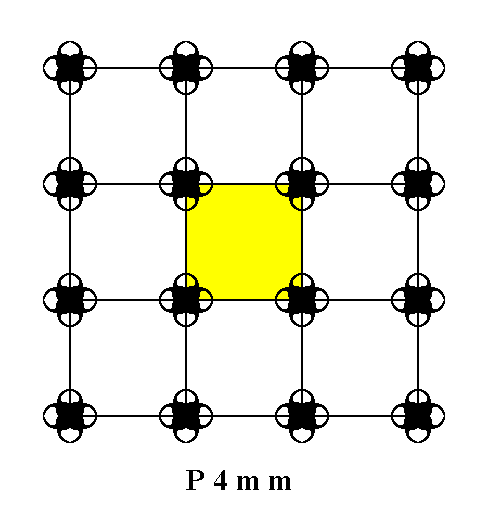
Figure 2. A unit mesh choice is given in yellow. This unit mesh contains four 1/4 motifs, which is equivalent to it containing precisely one motif. This unit mesh, not containing a motif in its center, is primitive and is denoted by the symbol P. Its point symmetry is 4mm .
The motif s.str. and motif s.l. are depicted in the next Figure.

Figure 3. Repeated motif with point symmetry 4mm in the pattern of Figure 1.
This is, in the present case, also the figure that emerges when all translations are eliminated. Its point symmetry is 4mm and as such gives the point symmetry of the pattern of Figure 1.
Besides simple translation the periodic pattern representing the Plane Group P4mm contains glide lines. The next Figure depicts one of these glide lines.
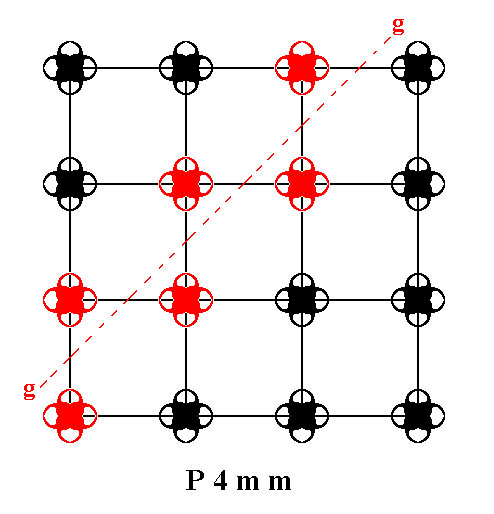
Figure 4. One of the possible glide lines in the pattern of Figure 1.
The total symmetry content of the Plane Group P4mm consists of simple translations, glide lines, 4-fold rotations and two types of mirror line. See Figure 5.
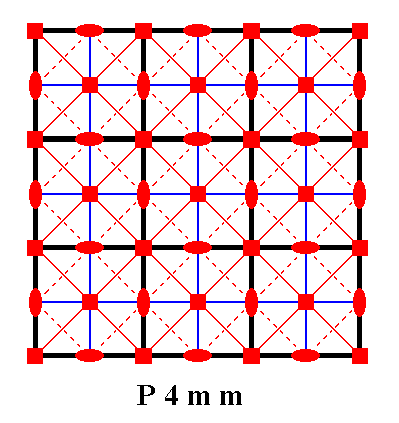
Figure 5. Total symmetry content of the Plane Group P4mm.
All continuous lines, including those that represent (the lines connecting the nodes of) the net, are mirror lines. There are two types of them, diagonal and non-diagonal. Dashed lines signify glide lines, small solid ellipses signify 2-fold rotation axes perpendicular to the plane of the drawing, and small solid squares signify 4-fold rotation axes perpendicular to the plane of the drawing.
Generation of the group elements of the Plane Group P4mm
In the realization of a P4mm pattern as given in Figure 1, we see that each motif s.str. consists of eight motif units (partly overlapping commas). Each such motif unit can represent a group element.
To generate the pattern we can choose the following generators :
An anticlockwise quarter-turn (900 rotation) about some chosen point.
A reflection in some mirror line.
A horizontal translation.
The next Figure shows : The motif unit chosen as initial group element (identity element), the group element representing the translation (generator), the group element representing the quarter-turn (generator) and the group element representing the mirror reflection (generator). The symmetry elements associated with the latter two transformations are also given : The point about which the chosen quarter-turn takes place, and the line in which reflection takes place.
Figure 6. Each motif s.str. of the P4mm pattern of Figure 1 consists of eight motif units. Each such unit can represent a group element. In the present Figure four such elements are explicitly indicated :
The initial group element 1 representing the identity element.
The group element representing an anticlockwise quarter-turn q about the point R . This element is chosen as a generator.
The group element representing the reflection m in the horizontal line m . It is chosen to be the second generator.
The group element representing the horizontal translation t . It is chosen to be the third generator.
The next Figure shows how two more group elements (motif units) are generated by repeatedly appling the quarter-turn q to the initial element 1 .
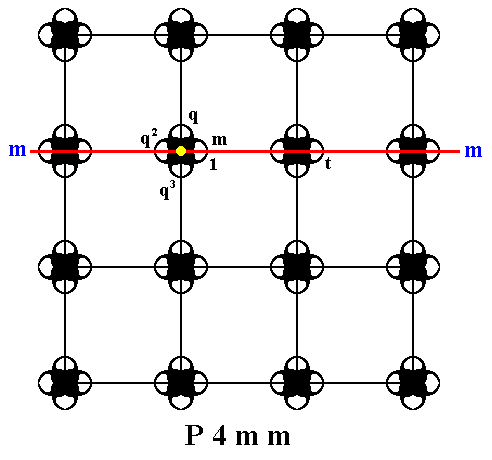
Figure 7. Generation of the group elements (motif units) q2 and q3 .
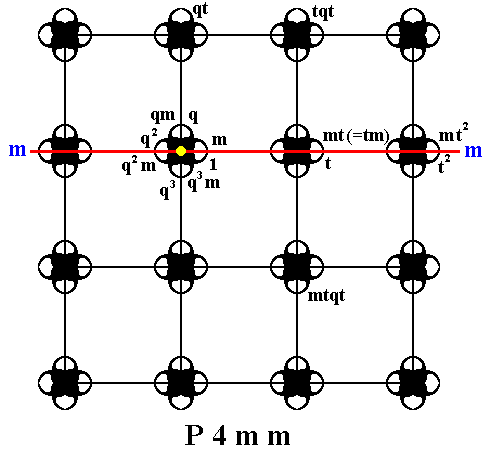
Figure 8. Some more group elements (motif units) of our P4mm are generated.
Instead of concentrating further on the units of the motifs s.str., we will bring in the motifs s.l. as we have done in the previous documents, in order to let every part of the pattern play a role in representing the group elements, which means that the pattern (its motifs + complete background) will be partitioned into areas in such a way that each such an area represents a group element.
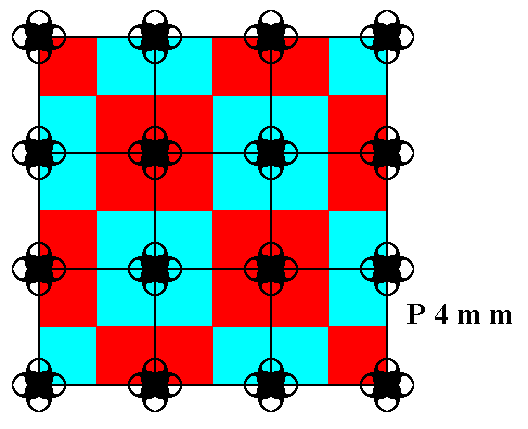
Figure 9. Motifs s.l. (red and blue squares) of the P4mm pattern of Figure 1.
( The red and blue colors do not signify qualitative differences)
The next Figure divides each motif s.l. into eight parts, each of them representing a group element.
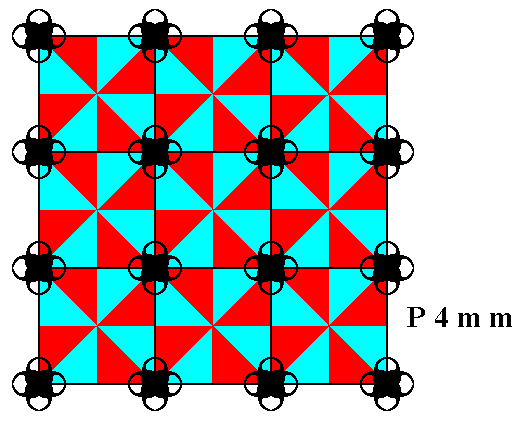
Figure 10. Division of the motifs s.l. results in (red and blue) triangular areas each representing a group element.
( The colors red and blue do not signify qualitative differences)
In the above Figure we're now going to indicate the initial group element and the three generators as established in Figure 6, and insert the relevant symmetry elements (mirror line and rotatation point) associated with the generators.
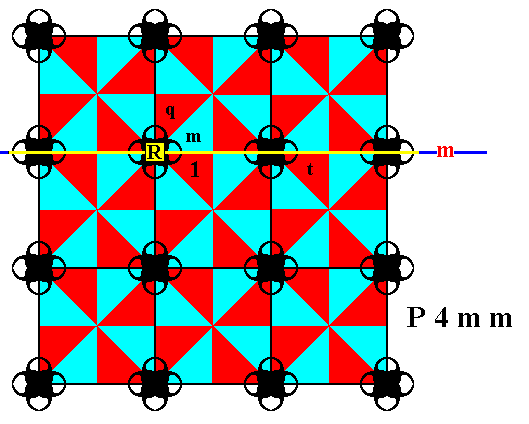
Figure 11. The P4mm pattern of Figure 1 is partitioned (as it was already in the previous Figure) into triangular areas, each representing a group element. Four such elements are explicitly indicated :
The group element 1 representing the identity element.
The group element m representing the reflection in the line m . It is chosen as a first generator.
The group element q representing an anticlockwise quarter-turn about the point R . It is chosen as a second generator.
The group element t representing a horizontal translation. It is chosen as a third generator.
We will now start to generate more group elements, by applying the generators to the initial group element, and (again) to the results.
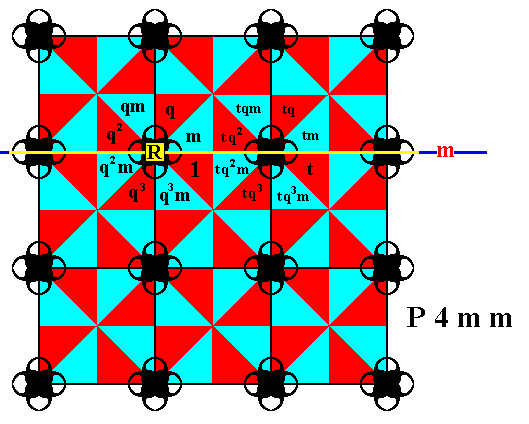
Figure 12. Some group elements of the P4mm pattern are generated by using the defined generators.
The next Figures depict our P4mm pattern enlarged in order to obtain enough space for the markings of the group elements.
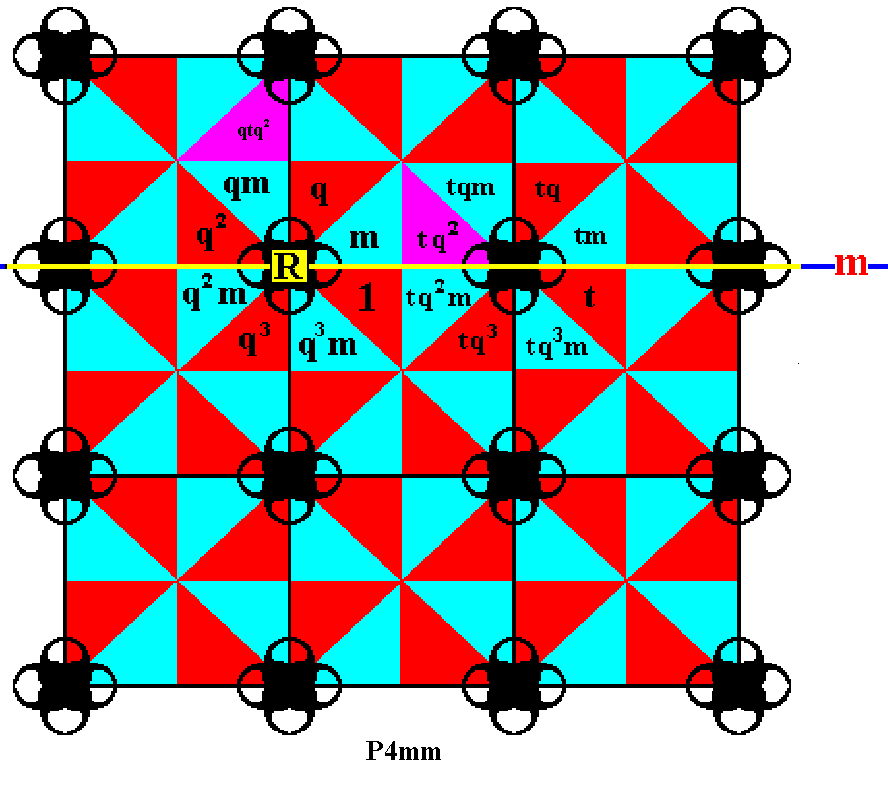
Figure 13. To reach the first row of group elements, we must use the generator q .
So we take the already generated element tq2 and rotate it anticlockwise by 900, resulting in the element qtq2 .
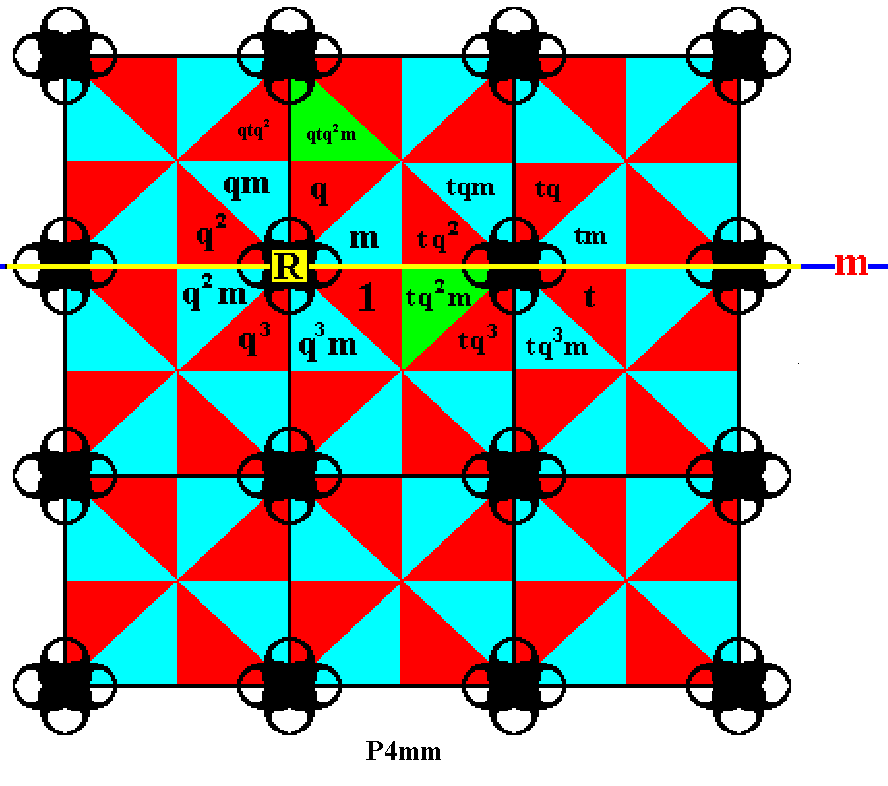
Figure 14. In the same way we take the already generated element tq2m and rotate it anticlockwise by 900, resulting in the element qtq2m .
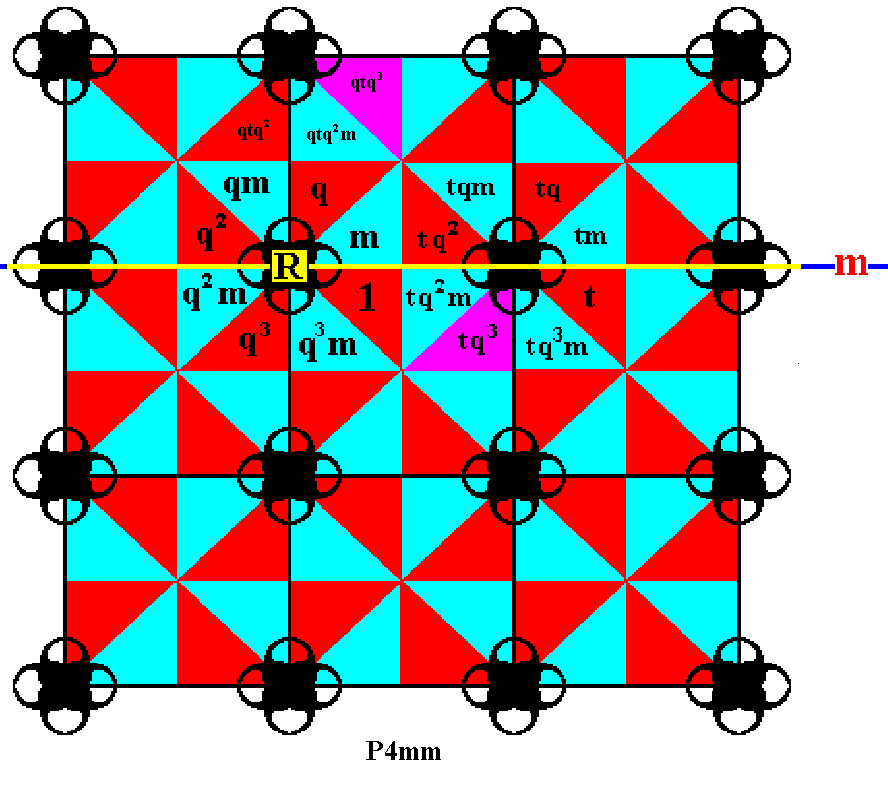
Figure 15. In the same way we take the already generated element tq3 and rotate it anticlockwise by 900, resulting in the element qtq3 .
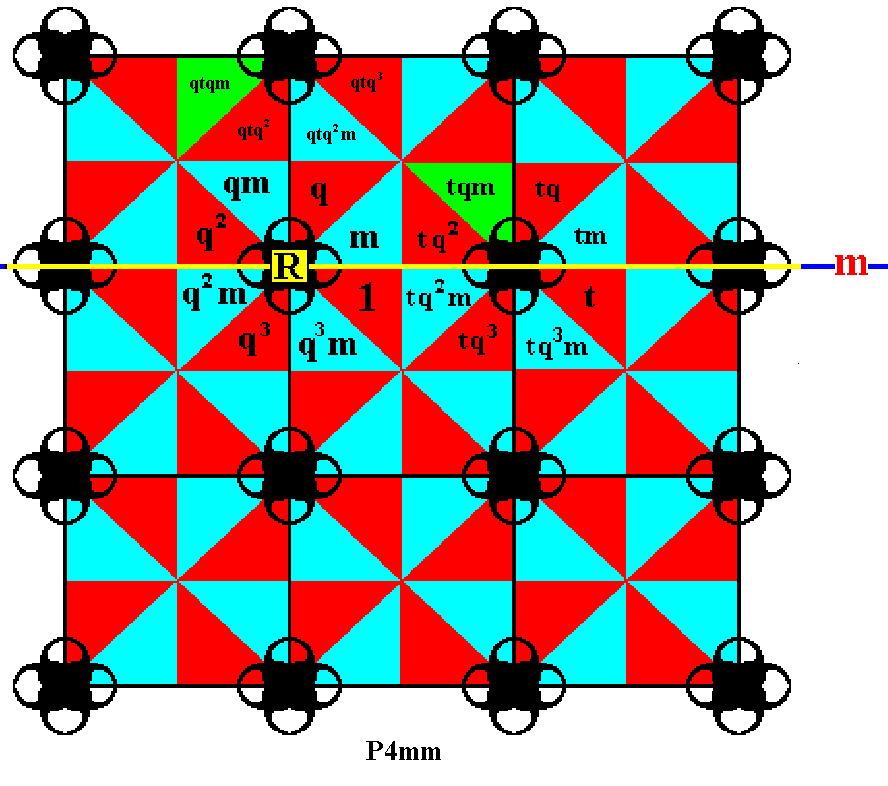
Figure 16. Again, in the same way we take the already generated element tqm and rotate it anticlockwise by 900, resulting in the element qtqm .
By using the translations t and t-1 , we can fill in the rest of the first row of group elements :
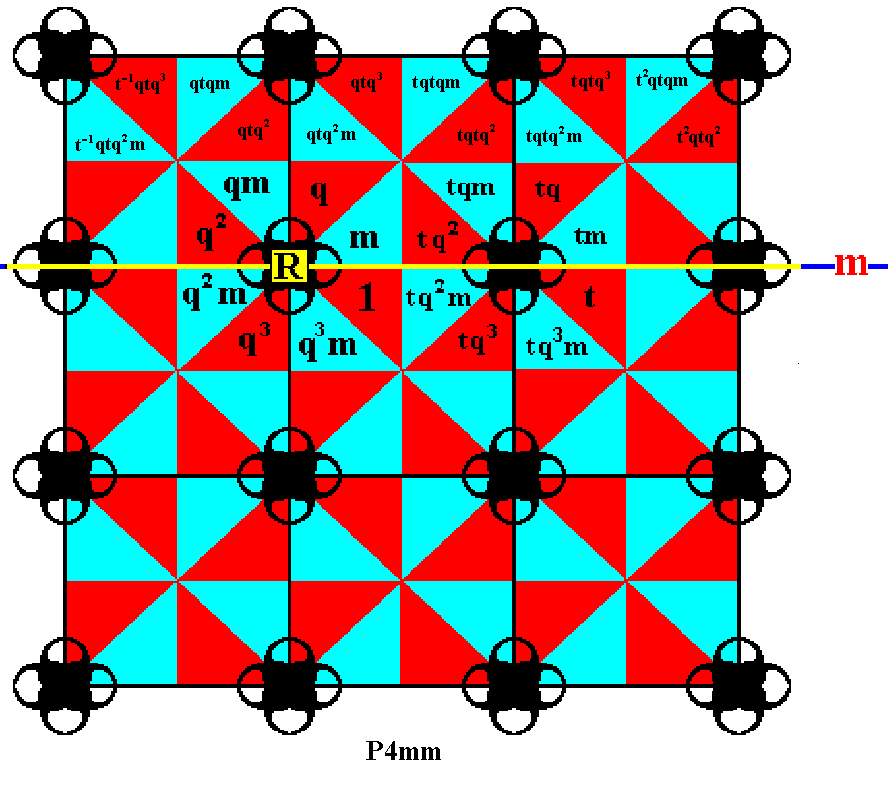
Figure 17. The (displayed part of the) first row of group elements is completed by applying translations.
The second and third rows of group elements can also be completed by applying translations :
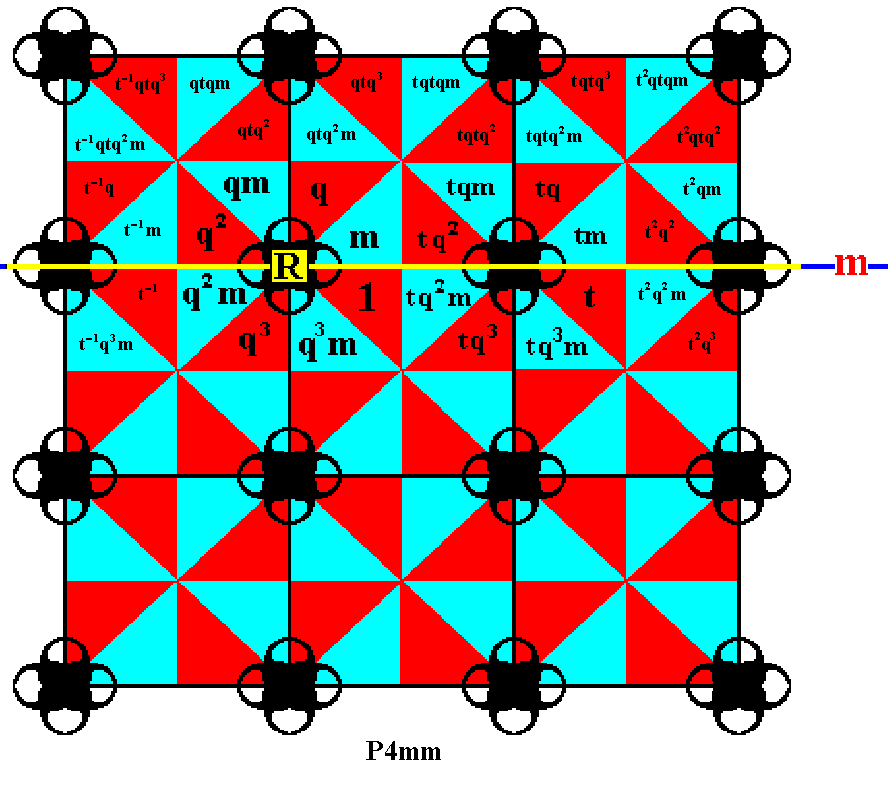
Figure 18. More group elements are generated, completing the first three rows of the displayed part of the pattern ( P4mm ).
To reach the fourth row of group elements, we must again apply the rotation q about the point R , but now applying it three times, which means that we rotate anticlockwise by 2700 (or, which is wholly equivalent, 900 clockwise). And this transformation is denoted by q3 . Alternatively, this fourth row can also be reached by applying the reflection m to the elements of the first row.
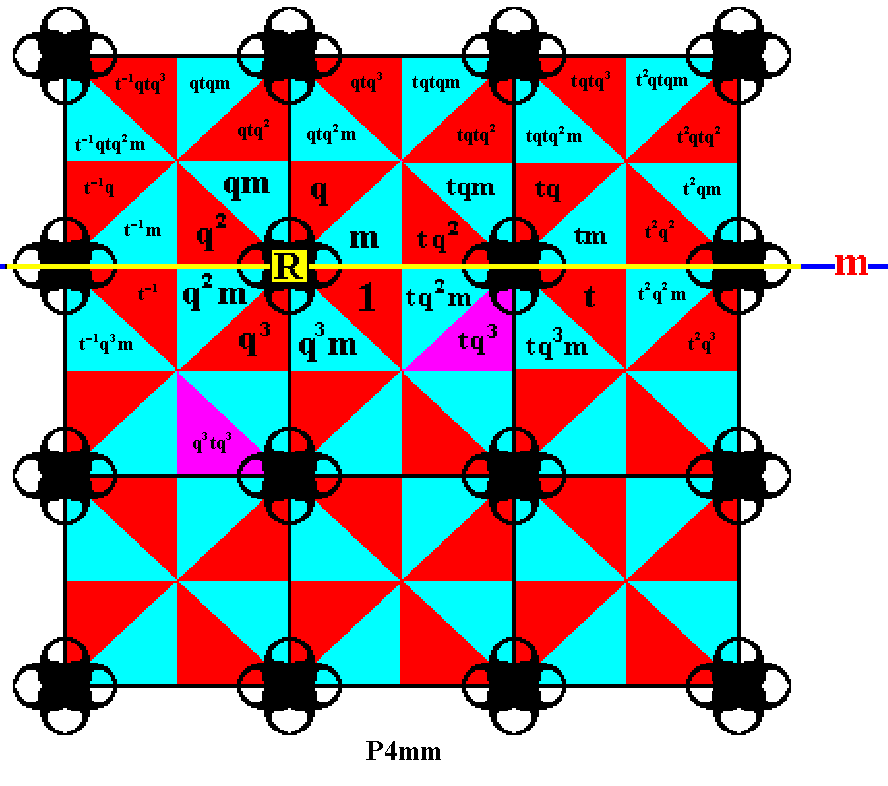
Figure 19. Applying r3 to the (already generated) group element tq3 , which means rotating the latter anticlockwise by 2700 about the point R , results in the element q3tq3 .
By appling q3 to another element we again get a new group element.
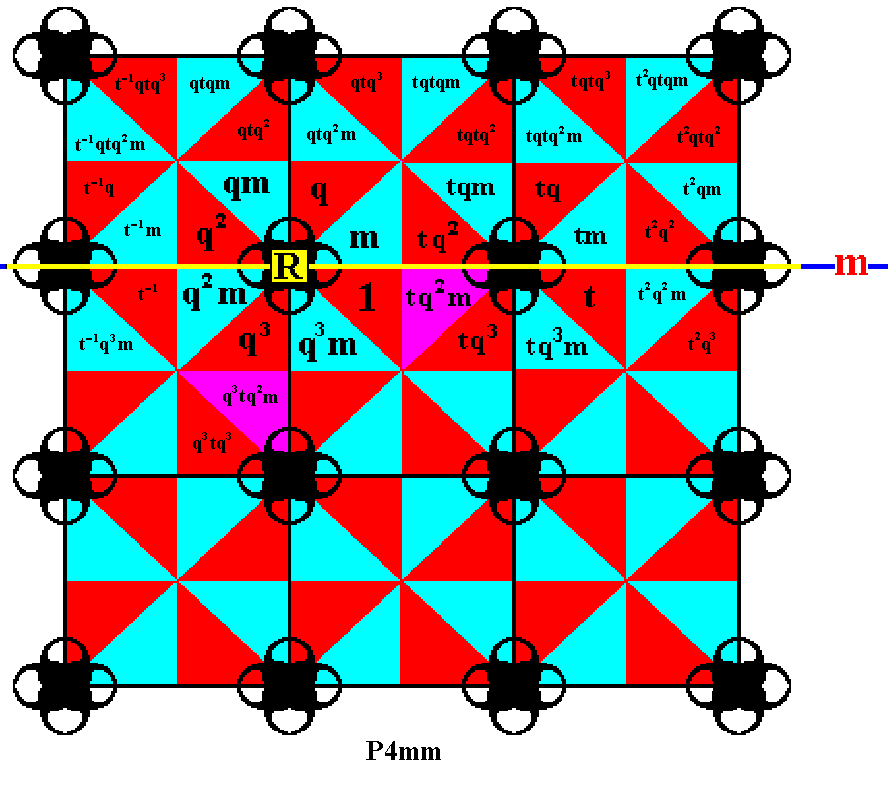
Figure 20. The element q3tq2m is obtained by applying q3 to the element tq2m.
We choose the generator m -- reflection in the horizontal line m -- to generate the rest of the fourth row.
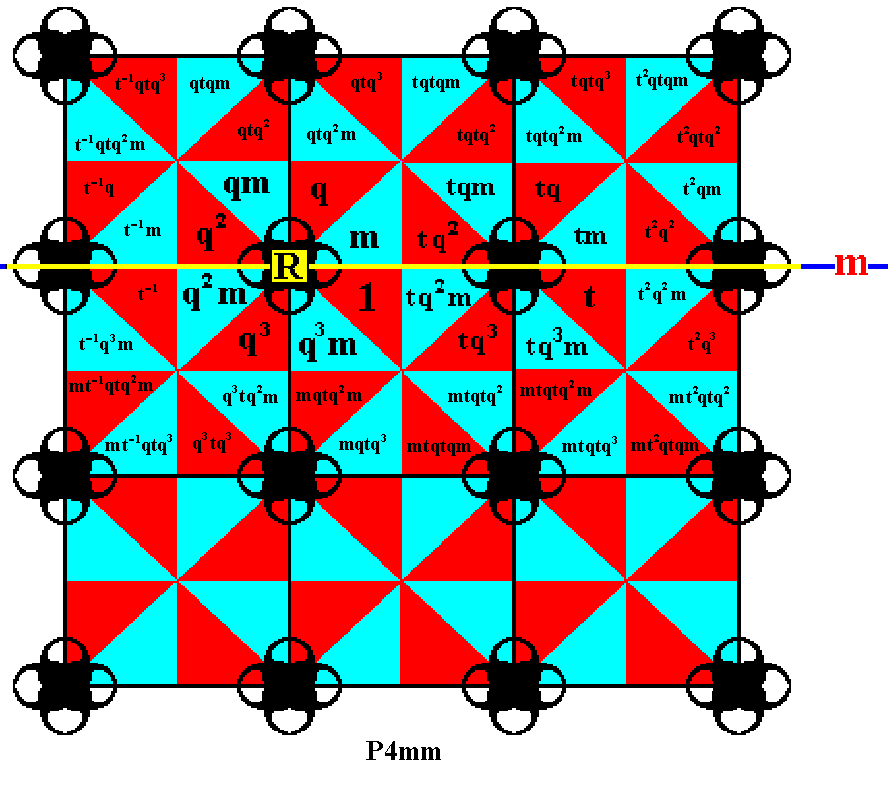
Figure 21. The fourth row of the displayed part of our P4mm pattern is completed by applying the generator m to the elements of the first row.
To reach the fifth row of group elements we must again apply the element q3 , i.e. three times applying the generator q ( 3x900 = 2700 anticlockwise rotation about the point R ).
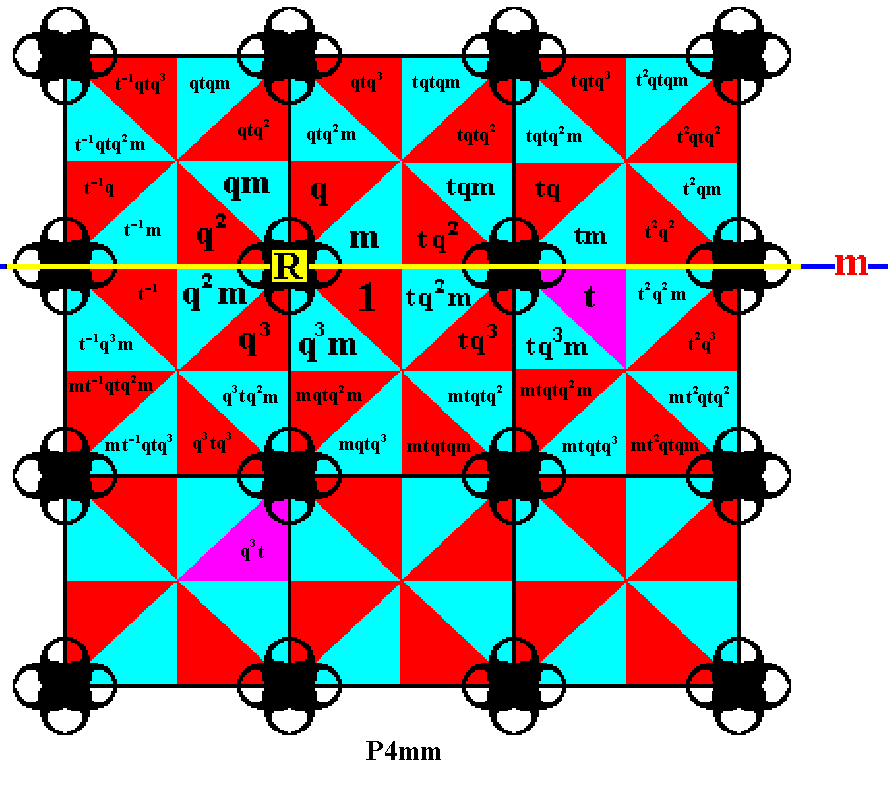
Figure 22. The group element q3t is generated by applying the element q3 to the element t .
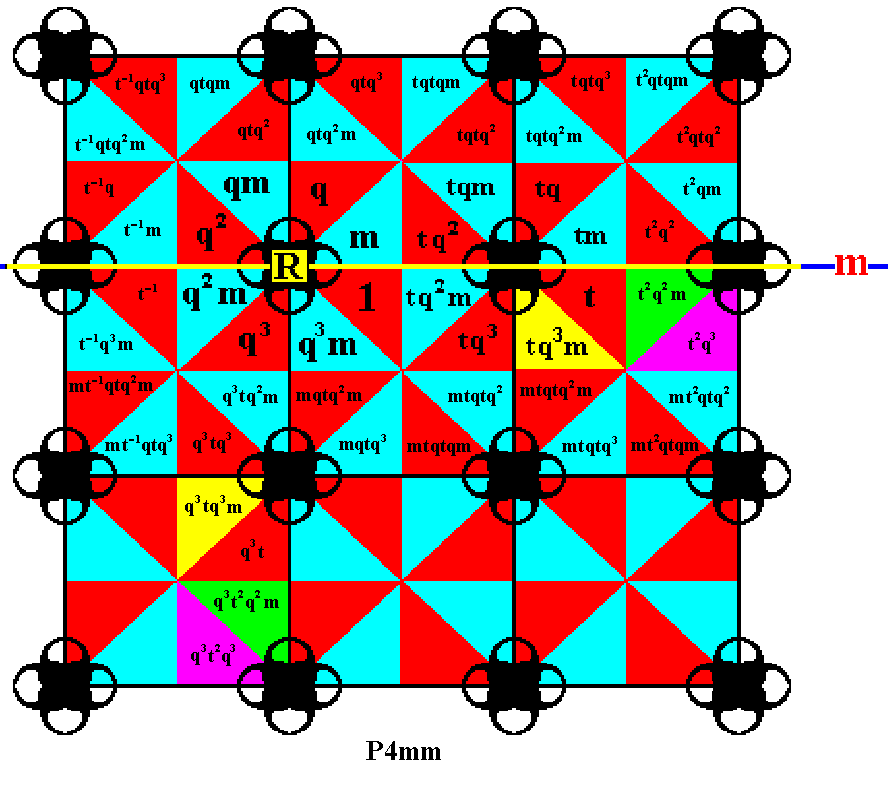
Figure 23. In the same way as in the previous Figure some more elements are generated.
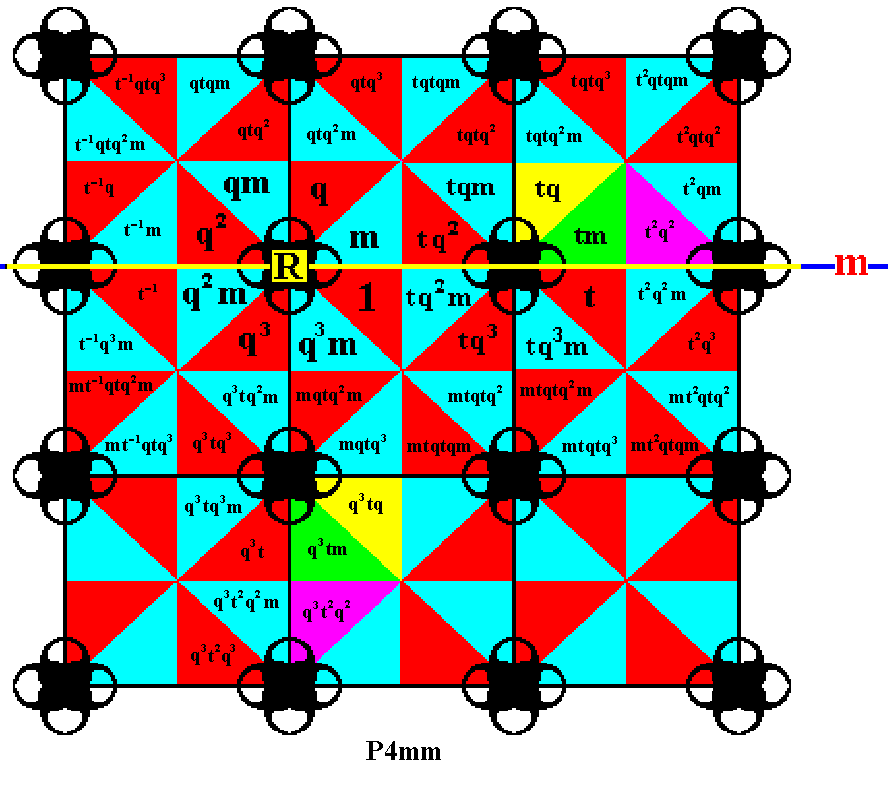
Figure 24. Again, in the same way as in the previous Figure some more elements are generated.
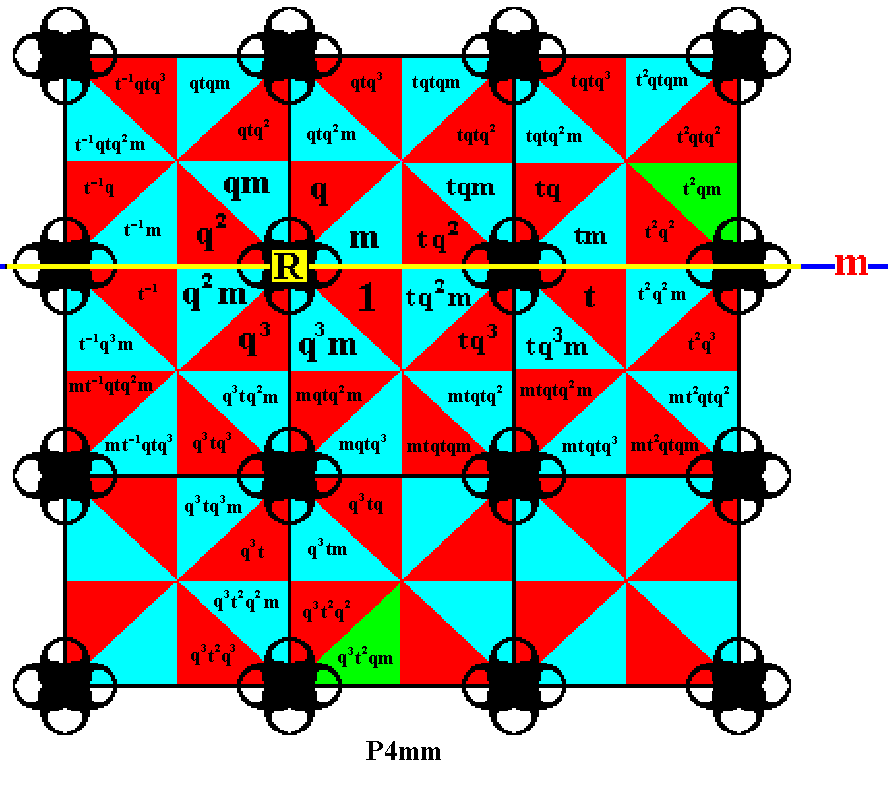
Figure 25. Finally, in that same way, one more element is generated.
We can now complete the last two rows of the displayed part of our P4mm pattern by means of translations :
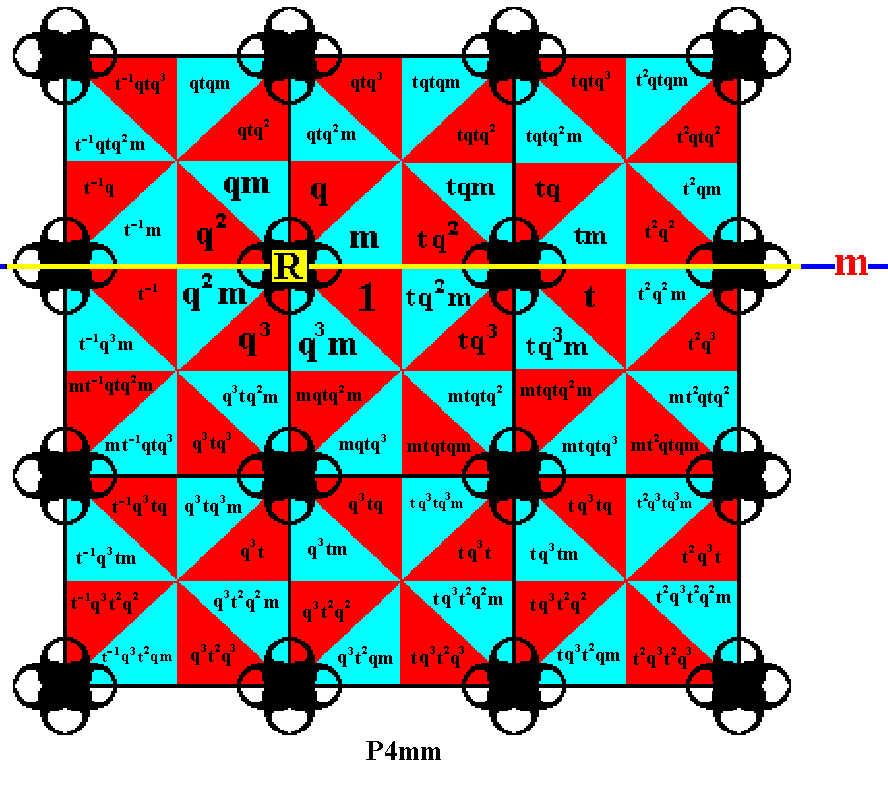
Figure 26. Completion of the last two rows of group elements in the displayed part of the P4mm pattern (as represented in Figure 1) (with the just mentioned "as represented" we mean the choice of motifs s.str. We could have chosen different motifs as long as they have 4mm symmetry).
So we have now generated the group elements of the Plane Group P4mm . Again, the process should continue indefinitely, because the group is infinite.
In the next document we will generate the elements of the Plane Group P4gm .
e-mail : 
To continue click HERE for further study of the totally dynamic and holistic nature of Reality.
back to homepage
back to the Ink-in-Glycerine Model
back to Part I of The Crystallization process and the Implicate Order
back to Part II of The Crystallization process and the Implicate Order
back to Part III of The Crystallization process and the Implicate Order
back to Part IV of The Crystallization process and the Implicate Order
back to Part V of The Crystallization process and the Implicate Order
back to Part VI of The Crystallization process and the Implicate Order