implicate order 14

Wholeness and the Implicate Order

The Crystallization Process and the Implicate Order
(Part Fourteen)

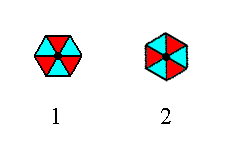
We continue our investigation concerning the generation of group elements of the Plane Groups.

The Plane Group P31m

The next motif we're going to insert into a 2-D hexagonal lattice has the same point symmetry as the one we used for the exposition of Plane Group P3m1 in the previous two documents. But with respect to the connecting lines of the net our new motif is oriented differently : It is rotated 30⁰ with respect to the one used earlier. See Figure 1.

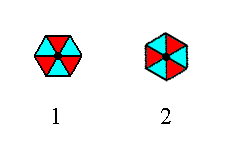
Figure 1.
(1). Orientation of the 3m motif, compatible with the Plane Group P3m1 (discussed in the previous two documents).
(2). Orientation of the 3m motif, compatible with the Plane Group P31m .

Placing two-dimensional motifs with 3m symmetry into a (primitive) hexagonal net (2-D hexagonal lattice), such that the orientation of these motifs differs by 30⁰ from that of the motifs of the Plane Group P3m1 (discussed in the previous two documents), yields a periodic pattern representing Plane Group P31m. See Figure 2.

Figure 2. When motifs, having point symmetry 3m (i.e. having a 3-fold rotation axis and three equivalent mirror lines), are inserted into a (primitive) hexagonal net, in the way (i.e. the orientation) shown, a pattern of repeated motifs will emerge that represents Plane Group P31m .
Each (composed) motif consists of three augmented motif units, in such a way that the symmetry of the composed motif is 3m . Each augmented motif unit represents a subgroup or a coset.
The symmetry of the motifs is indicated by their shape and by their coloration.
The pattern must be conceived as extending indefinitely in two-dimensional space.

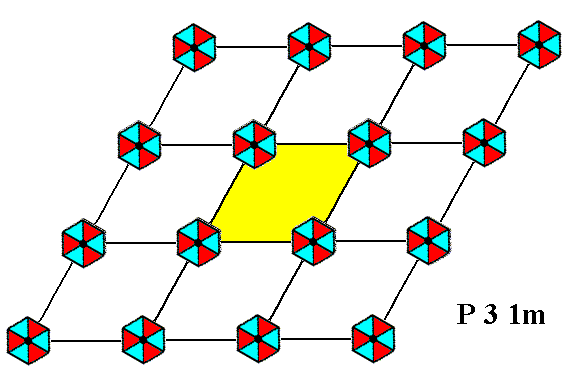
Figure 3. A unit mesh is chosen (yellow). This unit mesh is primitive, and its point symmetry is m, i.e. the only symmetry element it possesses is a mirror line.

If the pattern representing Plane Group P31m is contracted such that all translations are eliminated, then we end up with a figure that has 3m symmetry. It is the translation-free residue of that Plane Group, and as such represents the Point Group to which that Plane Group belongs. See Figure 4.

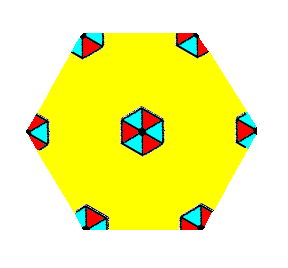
Figure 4. The translation-free residue of the pattern -- representing Plane Group P31m -- of Figure 2. The point symmetry of this residue is 3m , and as such it represents the Point Group 3m to which the present Plane Group belongs. The translation-free residue is at the same time the motif s.l. and tiles the 2-D plane completely.

The symmetry elements involved in a pattern representing Plane Group P31m are 3-fold rotation axes, mirror lines and glide lines. See next Figures.

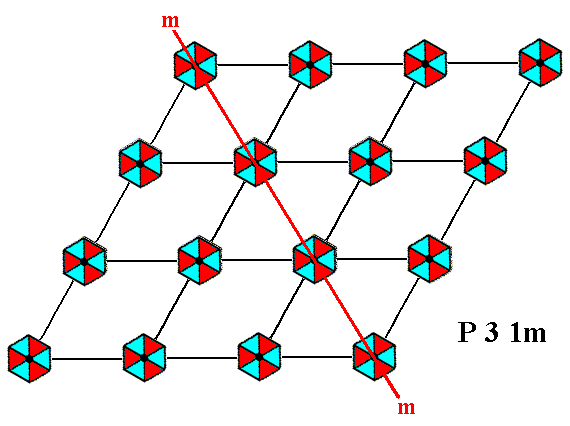
Figure 5. A pattern representing Plane Group P31m has mirror lines. One of them is depicted here.

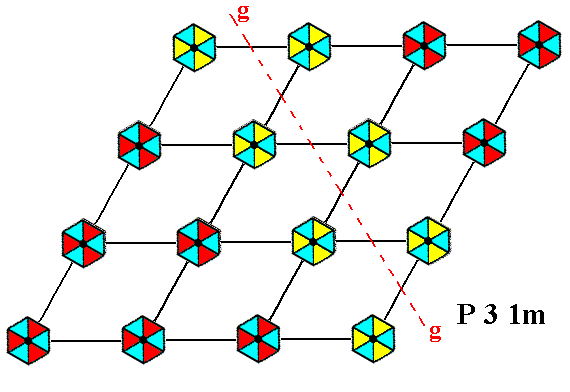
Figure 6. A pattern representing Plane Group P31m has glide lines. One of them is depicted here.

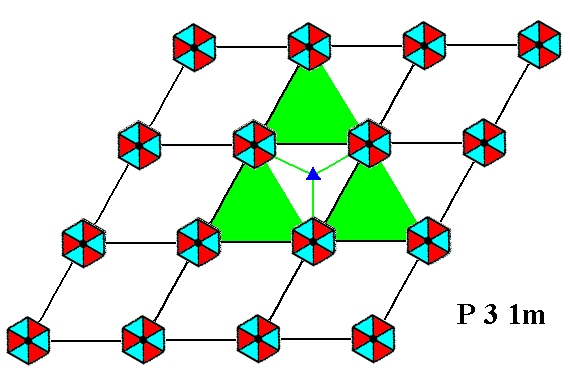
Figure 7. A pattern representing Plane Group P31m has 3-fold rotation axes. One of them is depicted here.

The total symmetry content of the Plane Group P31m is given in the next Figure.

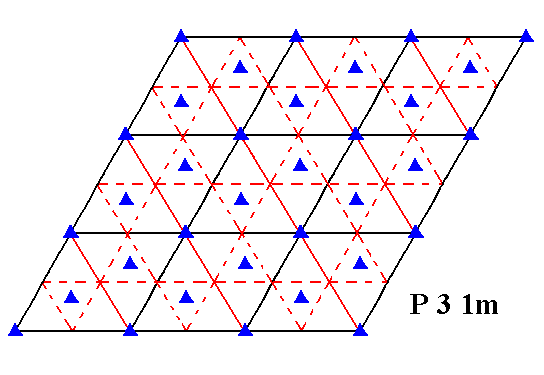
Figure 8. Total symmetry content of Plane Group P31m .
Mirror lines are indicated by solid lines (red and black).

Generation of the group elements of the Plane Group P31m

Now we will show the generation of the group P31m by means of basic motif units that legitimately represent group elements (i.e. elements of the full group P31m). In Figure 2 we had motifs, each consisting of three units, making angles with each other of 120⁰, and providing the composed motif with 3m symmetry (Which is equivalent to a D₃ group structure). But such a motif unit is still symmetric in itself, so in fact it is composed of still more basic motif units : It is an augmented motif unit. And indeed the basic units, as can be obtained by dividing the augmented motif units, do not have (and ought not to have) any symmetry at all. They're going to build up a symmetric pattern from scratch. They can legitimately represent group elements (i.e. elements of the full group P31m). The next image shows a composed motif, equivalent to the ones in Figure 2, but partitioned into six basic motif units.

This type of motif can perhaps be more clearly expressed as follows :

The two basic motif units composing an augmented motif unit (of which three together make up the full composed motif) can conveniently be distinguished by colors, provided we do not interpret the difference between colors as expressing an asymmetry. The two basic motif units, red and blue in the next Figures, are symmetrically related to each other :

The latter motifs we will now place in a hexagonal lattice (That lattice having the same orientation as that used for depicting the pattern of the group P3m1 ), resulting in the periodic pattern according to the group P31m. The effect is that both patterns, P31m and P3m1, have the same type of composed motif (and also of basic motif unit for that matter), but in each case those motifs are differenly orientated with respect to the lattice lines (i.e. the edges of the unit cell). This difference in orientation is 30⁰.

Figure 9. Pattern according to the Plane Group P31m .
The (composed) motifs consist of six basic motif units (red and blue), each representing a group element (i.e. an element of the group P31m). The difference in color should not be interpreted as an asymmetry.
The pattern must be conceived as extending indefinitely in two-dimensional space.

The next Figure gives this same pattern. Some lattice points are marked : R, S, X, U, W. One basic motif unit (of the composed motif at point R) is chosen to be the initial motif unit, representing the identity element 1 of the group. Three other basic motif units are chosen as generators :
The basic motif unit p representing an anticlockwise rotation of 120⁰ about the lattice point R .
The basic motif unit m representing a reflection in the mirror line m .
The basic motif unit t representing a horizontal translation t .

Figure 10. Pattern according to the Plane Group P31m .
The initial motif unit, three generators and some lattice points are indicated.

The next Figure depicts an enlargement of the composed motif at the lattice point R. The initial basic motif unit, 1 , the generators p and m , and the mirror line m are indicated.

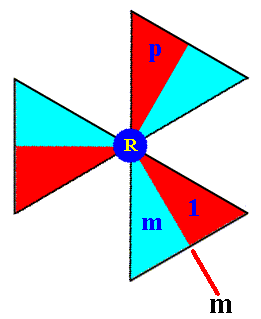
Figure 11. Composed motif (consisting of six basic motif units) of the P31m pattern at the point R in Figure 10.

The identity of the remaining basic motif units of the composed motif at the lattice point R can now be determined ( p³ = 1 ) :

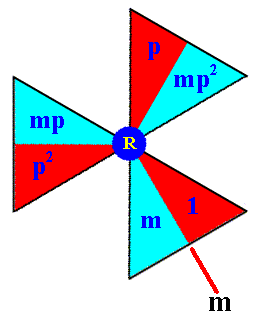
Figure 12. The group elements of the composed motif at the point R .
Together they form the subgroup {1, p, p² , m, mp, mp²} , having the structure of D₃ . The elements 1, p, p² form a subgroup with the structure of C₃ .
The elements 1, m form the subgroup C₂ .

We will now produce the composed motif at the point S (Figure 10). We'll do this by subjecting all the elements (basic motif units) of the composed motif at the point R to a translation t , i.e. we will form the left coset of the subgroup D₃ (materialized as the composed motif at the point R) by the element t . See next Figure.

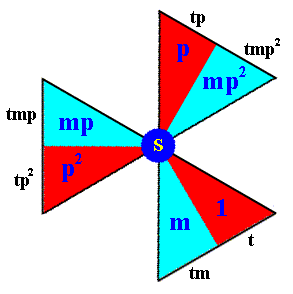
Figure 13. The elements (basic motif units) of the composed motif at the lattice point S . They form the left coset of the D₃ subgroup by the element t . The notations (i.e. identities) of the newly generated elements are placed at the perimeter of the image (i.e. outside the image).

Next we determine the elements of the composed motif at the lattice point U (Figure 10).
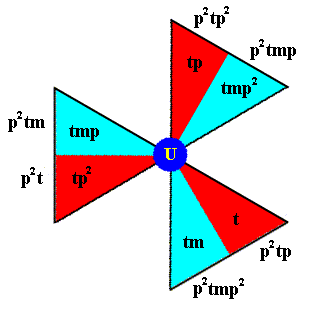
To generate those elements we must subject the elements of the composed motif at the point S to an anticlockwise rotation of 240⁰ about the point R, that is to say, we must apply the transformation p² . In this way we form the left coset of the subgroup D₃ by the element p²t . See next Figure.

Figure 14. Generation of the basic motif units of the composed motif at the lattice point U . The names of the newly generated elements are given at the perimeter of the image (i.e. outside the image).

The second and third row of composed motifs (Figure 10) can now be completed by applying the translations . . . t^-2, t^-1, t, t², t³, . . . etc.
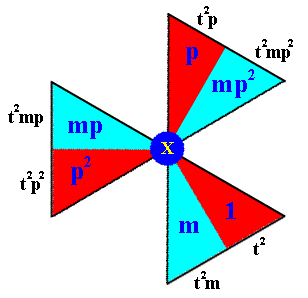
We will do so with respect to the composed motif at the point X :

Figure 15. Generation of the elements of the composed motif at the point X . Together they form the left coset of the subgroup D₃ by the element t² .
The notation of the newly generated elements is given at the perimeter of the image.

From this lastly obtained composed motif we can reach the fourth row (Figure 10) of composed motifs (to be generated), by applying p² to that lastly obtained composed motif. See next Figure.

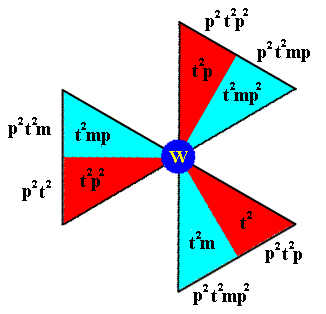
Figure 16. Generation of the elements of the composed motif at the lattice point W . Together they form the left coset of the subgroup D₃ by the element p²t² .
The notation of the newly generated elements is given at the perimeter of the image.

The fourth row can now be completed by translations. Continuation of this procedure will generate in principle the whole group P31m , "in principle", because the order of the group is infinite.

What follows next is the generation of that same group P31m by means of augmented motif units.
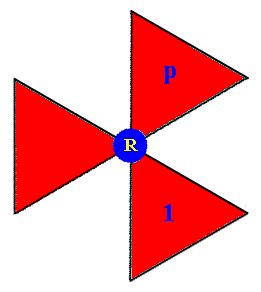
Here an augmented motif unit means two symmetrically related basic motif units taken together as one motif unit that can generate the pattern. See Figure 17 (Augmentation could be pursued still further, for example when we were to take the whole composed tri-radiate motif as initial unit to build up the P31m pattern).

Figure 17. Composed motif (at the lattice point R (For its position, see Figure 10)), consisting of three augmented motif units. One is chosen to be the initial motif unit 1 , representing the identity element of the group P31m , another such augmented motif unit is chosen to be the generator p representing an anticlockwise rotation of 120⁰ about the lattice point R (See Figure 10).
As a second generator we choose the horizontal translation t .

Because we now use augmented motif units to generate the group, we do not need the transformation m (reflection, see Figure 10) anymore, so we can do it with two generators ( p and t ).

The next Figure shows the two chosen generators in the context of the lattice :
The 'element' (augmented motif unit) p , resulting from the 'element' (augmented motif unit) 1 , by an anticlockwise rotation of 120⁰ about the point R .
The 'element' t (augmented motif unit), resulting from the 'element' 1 by the translation t .

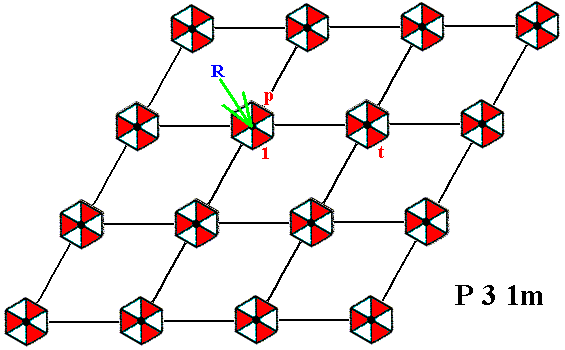
Figure 18. The two chosen generators p and t for the P31m pattern.

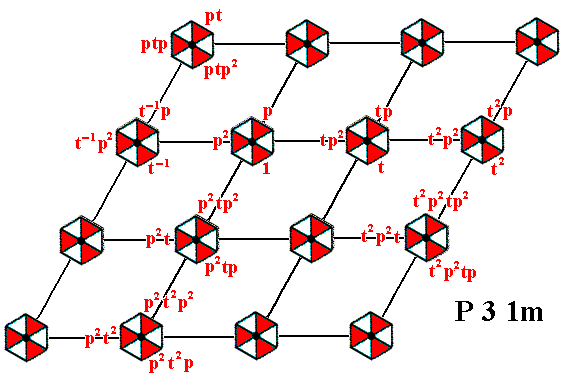
Figure 19. The whole P31m pattern can be produced by the generators p and t .

As can be seen from the above results, we can say the following :
As abstract groups, the groups P3m1 and P31m are identical, but the orientation of the motifs is different with respect to the hexagonal point lattice in each case, i.e. different with respect to the edges of the rhomb-shaped unit cell (unit mesh).

We're now going to generate our group P31m again, but now letting the group elements be represented not only by a basic unit of the motif s.str., but by a basic unit of a motif s.l. in such a way that a group element is represented by a maximal area of the pattern, an area containing one basic unit of the motif s.str. PLUS its corresponding background. The maximality of such an area means that it tesselates the plane completely (without leaving any gaps, and without any overlappings). To accomplish this we first determine the tesselation of the pattern by an appropriate choice of motif s.l. The next Figure depicts these motifs.

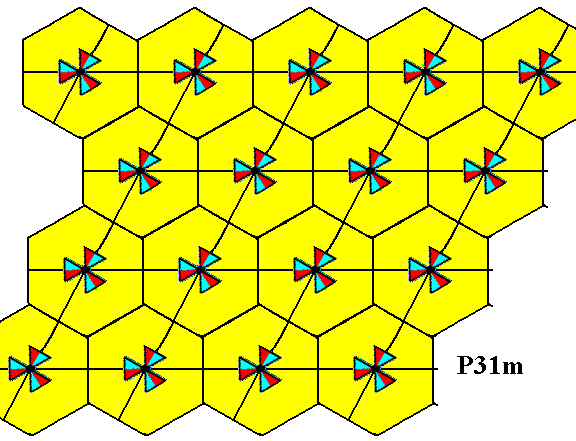
Figure 20. (Choice of) Motifs s.l. (yellow hexagons) of the P31m pattern of Figure 9.

In the next Figure we partition the motifs s.l. in such a way that the resulting areas (plus their content) can represent group elements.

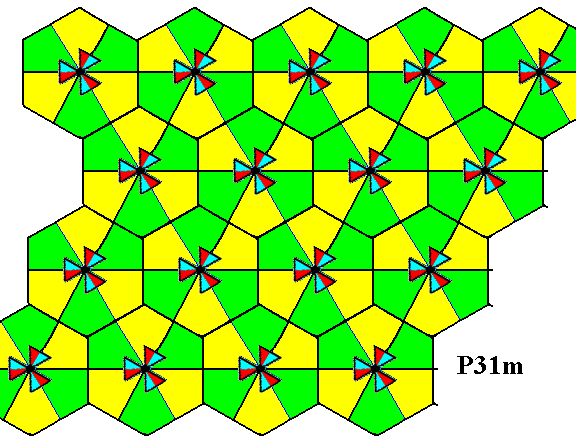
Figure 21. Division of each motif s.l. of the previous Figure into six equally sized and shaped areas (yellow and green bi-isosceles triangles) that can legitimately represent group elements. Each such area contains one basic unit of the motif s.str. PLUS corresponding background.

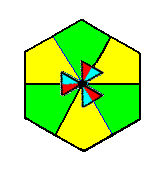
Figure 22. A partitioned motif s.l. isolated. It consists of six basic units of the motif s.l. Each such unit contains one basic unit of the motif s.str. PLUS corresponding background.

In the next Figure we indicate explicitly the initial group element and the generators p , m and t .

Figure 23. The P31m pattern of Figure 9 is partitioned in areas (bi-isosceles triangles) that can represent group elements (as was already done in Figure 21). Four such group elements are explicitly indicated :
The initial element 1 (identity element).
The generator p , which is an anticlockwise rotation of 120⁰ about the point R .
The generator m , which is a reflection in the line m .
The generator t , which is a horizontal translation.

In the next document we will generate the group elements (as represented by the above determined areas) of the group P31m from the given initial element by means of (repeatedly) appling the generators to it and to the results.

e-mail :